The heat and mass transfer characteristics of superheated steam in horizontal wells with toe-point injection technique

Abstract

Little efforts were done on the heat and mass transfer characteristics of superheated steam (SHS) flow in the horizontal wellbores. In this paper, a novel numerical model is presented to analyze the heat and mass transfer characteristics of SHS in horizontal wellbores with toe-point injection technique. Firstly, with consideration of heat exchange between inner tubing (IT) and annuli, a pipe flow model of SHS flow in IT and annuli is developed with energy and momentum balance equations. Secondly, coupled with the transient heat transfer model in oil layer, a comprehensive mathematical model for predicting distributions of pressure and temperature of SHS in IT and annuli is established. Then, type curves are obtained with numerical methods and iteration technique, and sensitivity analysis is conducted. The results show that (1). The decrease in SHS temperature in annuli caused by heat and mass transfer to oil layer is offset by heat absorbtion from SHS in IT. (2). SHS temperature in both IT and annuli increases with the increase in injection pressure. (3). IT heat loss rate decreases with the increases in injection pressure. (4). Increasing pressure can improve development effect.

Introduction

Steam injection is one of the most effective methods for heavy oil recovery (Sun et al. 2017a, b, c). When steam is injected from ground to oil layer, one of the foremost tasks for engineers is to predict the distributions of pressure and temperature along the wellbores (Sun et al. 2017d, e). However, the predicting task is never easy due to the complexity of the non-isothermal flow characteristics of thermal fluid in wellbores (Sun et al. 2017f, g).

Willhite (1967) developed an important model for calculating overall heat transfer coefficient during the steam injection process. Ejiogu and Fiori (1987) and Tortike and Farouq Ali (1989) presented empirical formulas for calculating steam thermophysical properties. Sagar et al. (1991) proposed a simplified model for predicting temperature distribution of saturated steam along the vertical wellbores based on the Coulter–Bardon equation, and Alves et al. (1992) developed a new model describing the relationships between enthalpy and pressure in wellbores. Bahonar et al. (2010, 2011) took vertical heat transfer into consideration and proposed their numerical model which was later compared with previous models.

Satter et al. (1965) presented a mathematical model for predicting steam quality. However, they ignored the kinetic energy change in their energy balance equation. Pacheco et al. (1972) developed an improved model with consideration of friction losses. Farouq Ali (1981) presented a model that can be used to predict steam pressure and temperature for both downward and upward flow in the vertical wellbores. Durrant and Thambynayagam (1986) proposed another method for calculating transient thermal conductivity with superposition method. Based on previous works, Livescu et al. (2010a, b) proposed a semi-analytical model for predicting multiphase flow pressure and temperature. Hasan (1995), Hasan and Kabir (1991, 1992, 1994, 2007, 2009, 2010, 2012) and Hasan et al. (2007a, b) did a series of works on the steady-state heat conduction rate and transient heat conduction rate in the formation. Cheng et al. (2011, 2012, 2013, 2014) presented several models for predicting heat loss rate in the formation. All of these great works laid a solid foundation for later study. However, they were focused on saturated steam, which is not applicable for superheated conditions.

In recent years, Zhou et al. (2010), Xu et al. (2013a, b), Fan et al. (2016) and Sun et al. (2017h, i) developed different models to predict the distributions of pressure and temperature of SHS in the vertical wellbores. However, it is a constant mass flow process in the vertical wellbores. Dong et al. (2014, 2016) proposed a numerical model for predicting steam pressure in the horizontal wellbores. However, it is conventional heel-point steam injection technique, and they focused on the flow characteristics of multi-component thermal fluid. Gu et al. (2015) proposed a numerical model for predicting superheated steam pressure along the horizontal wellbores. Besides, it is also focused on the heel-point steam injection technique.

It is proved by field practices that conventional heel-point steam injection technique may lead to serious fingering phenomenon (Sun et al. 2018a; Wu et al. 2012). Consequently, the alternative steam injection technique was proposed to overcome these shortcomings (Sun et al. 2018a). However, the mass and flow transfer characteristics of SNG in IT and annuli of the horizontal wellbores are quite complex (Sun et al. 2018a).

This paper has mainly three contributions to the existing body of the literature: (1). A novel model is developed to predict SHS pressure and temperature along the horizontal wellbores with toe-point SHS injection technique. (2). Effect of SHS flow in IT on the profiles of SHS pressure and temperature in annuli is taken into consideration. (3). Influence of injection pressure on the distributions of SHS pressure and temperature is discussed in detail.

Model description

General assumptions

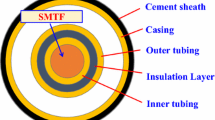
A schematic of SHS flow in toe-point SHS injection wellbores is shown in Fig. 1. In order to establish the model, some basic assumptions are listed below.

Fig. 1

A schematic of SHS flow in horizontal wellbores with toe-point SHS injection technique

• (1). Injection parameters of SHS at the heel point of IT are constant.

• (2). Heat flow from SHS in annuli to the outside wall of casing is steady state (Sun et al. 2017j).

• (3). Heat flow in oil layer is transient state.

• (4). Heat conduction in the horizontal direction is ignored.

Modeling of SHS flow in IT

It is a constant mass flow process of SHS flow from the heel point to the toe point in IT. The mass balance equation can be expressed as (Sun et al. 2018a):

$$\frac{{\partial w_{IT} }}{\partial L} = \pi r_{ITi}^{2} \frac{{\partial \left( {\rho_{IT} v_{IT} } \right)}}{\partial L} = 0$$

(1)

There exists heat exchange between SHS in the IT and annuli (Sun et al. 2018a). The energy balance equation of SHS flow in IT can be given as :

$$\frac{{{\text{d}}Q_{IT} }}{{{\text{d}}L}} = - w_{IT} \frac{{{\text{d}}h_{IT} }}{{{\text{d}}L}} - w_{IT} \frac{\text{d}}{{{\text{d}}L}}\left( {\frac{{v_{IT}^{2} }}{2}} \right) + w_{IT} g\sin \theta$$

(2)

The impulse of external force equals the change of SHS momentum (Sun et al. 2018a). The momentum conservation equation can be given as :

$$\frac{{{\text{d}}p_{IT} }}{{{\text{d}}L}} - \rho_{IT} g\sin \theta + \frac{{\tau_{f} }}{{\pi r_{ITi}^{2} {\text{d}}L}} + \frac{{{\text{d}}\left( {\rho_{IT} v_{IT}^{2} } \right)}}{{{\text{d}}L}} = 0$$

(3)

Modeling of SHS flow in annuli

It is a variable mass flow process of SHS flow from toe point to heel point in annuli (Sun et al. 2018a). The mass balance equation can be given as:

$$w_{an} = w_{IT} - \int {\rho_{an} I_{an} }$$

(4)

The sum of heat loss from annuli to oil layer and heat conduction from IT to annuli is equal to the total energy change of SHS in annuli (Sun et al. 2018a). The energy balance equation in annuli can be given as:

$$\frac{{{\text{d}}Q_{an} }}{{{\text{d}}L}} - \frac{{{\text{d}}Q_{IT} }}{{{\text{d}}L}} + \frac{{I_{an} \rho_{an} \left( {h_{an} + {{v_{r}^{2} } \mathord{\left/ {\vphantom {{v_{r}^{2} } 2}} \right. \kern-0pt} 2}} \right)}}{{{\text{d}}L}} = - \frac{{{\text{d}}\left( {w_{an} h_{an} } \right)}}{{{\text{d}}L}} - \frac{\text{d}}{{{\text{d}}L}}\left( {\frac{{w_{an} v_{an}^{2} }}{2}} \right) + w_{an} g\sin \theta$$

(5)

The momentum balance equation of SHS flow in annuli can be given as:

$$\frac{{{\text{d}}p_{an} }}{{{\text{d}}L}} = \rho_{an} g\sin \theta - \frac{{\tau_{f} }}{{\pi r_{wi}^{2} {\text{d}}L}} - \frac{{{\text{d}}\left( {\rho_{an} v_{an}^{2} } \right)}}{{{\text{d}}L}} - f_{perf} \frac{{\rho_{an} v_{an}^{2} }}{{4r_{wi} }}$$

(6)

Solving method of the mathematical model

The mathematical model is solved with numerical method. Firstly, Eqs. (2, 3, 5, 6) are converted into different equations, as shown below.

$$\frac{{\Delta Q_{IT} }}{\Delta L} = - w_{IT} \frac{{\Delta h_{IT} }}{\Delta L} - w_{IT} \frac{\Delta }{\Delta L}\left( {\frac{{v_{IT}^{2} }}{2}} \right) + w_{IT} g\sin \theta$$

(7)

$$\frac{{\Delta p_{IT} }}{\Delta L} - \rho_{IT} g\sin \theta + \frac{{\tau_{f} }}{{\pi r_{ITi}^{2} dL}} + \frac{{\Delta \left( {\rho_{IT} v_{IT}^{2} } \right)}}{\Delta L} = 0$$

(8)

$$\frac{{\Delta Q_{an} }}{\Delta L} - \frac{{\Delta Q_{IT} }}{\Delta L} + I_{an} \frac{{\Delta \rho_{an} \left( {h_{an} + {{v_{r}^{2} } \mathord{\left/ {\vphantom {{v_{r}^{2} } 2}} \right. \kern-0pt} 2}} \right)}}{\Delta L} = - \frac{{\Delta \left( {w_{an} h_{an} } \right)}}{\Delta L} - \frac{\Delta }{\Delta L}\left( {\frac{{w_{an} v_{an}^{2} }}{2}} \right) + \Delta w_{an} g\sin \theta$$

(9)

$$\frac{{\Delta p_{an} }}{\Delta L} = \Delta \rho_{an} g\sin \theta - \frac{{\tau_{f} }}{{\pi r_{wi}^{2} dL}} - \frac{{\Delta \left( {\rho_{an} v_{an}^{2} } \right)}}{\Delta L} - f_{perf} \frac{{\Delta \rho_{an} v_{an}^{2} }}{{4r_{wi} }}$$

(10)

Then, the pressure and temperature of SHS in IT and annuli at the outlet of mth segment are obtained by iteration technique. Finally, these outlet results are input as inlet values of the (m + 1)th segment, and the distributions of pressure and temperature in IT and annuli are obtained from toe point to heel point.

Results and discussion

Type curve analysis

In this section, type curves of SHS flow in IT and annuli are obtained and discussed in detail (Huang et al. 2017, 2018a, 2018b; Feng et al. 2018; Sun et al. 2017k, 2017l, 2018b; Zhang et al. 2017a, 2017b; Chen et al. 2015, 2016, 2017). The injection pressure, temperature and mass flow rate at the heel point are 4.231 MPa, 566.6 K and 3 kg/s, respectively. The predicted results are shown in Figs. 2, 3, 4, 5 and 6.

Fig. 2

Predicted SHS pressure in IT and annuli

Fig. 3

Predicted SHS temperature in IT and annuli

Fig. 4

Predicted heat exchange rate between IT and annuli

Fig. 5

Predicted superheat degree in IT and annuli

Fig. 6

Predicted mass flow rate in IT and annuli

As can be seen from Fig. 2, SHS pressure decreases with the increase in distance from heel point. As shown in Fig. 3, SHS temperature in IT decreases with distance from heel point. However, while there exists heat loss from SHS in annuli to oil layer, SHS temperature in annuli increases when SHS flows from toe point to heel point. This is because the wellbore heat losses are offset by energy absorbed from IT, as shown in Fig. 4. The heat flow rate from SHS in IT to annuli is obviously higher at the heel point than that at the toe point. Consequently, SHS temperature in annuli has an increase at the heel point. Figure 5 shows the distributions of superheat degree in IT and annuli. It is found that superheat degree decreases when SHS flows from heel point to toe point in annuli, while it increases when SHS flows from toe point to heel point in annuli. This is because the lower-temperature SHS in annuli absorbs huge amount of energy from the higher-temperature SHS in IT. Figure 6 shows clearly that it is a constant mass flow process in IT and it is a variable mass flow in annuli. This is because a certain amount of SHS in annuli is injected into oil layer due to the pressure difference between annuli and oil layer.

Effect of injection pressure

In order to study the effect of injection pressure on the profiles of thermophysical properties of SHS in wellbores, different injection pressure is tested (3.5, 4.0, 4.5 and 5.0 MPa) based on no change in values of injection rate or temperature. The predicted results under different injection pressure are shown in Figs. 7, 8, 9, 10 and 11.

Fig. 7

Effect of injection pressure on the profiles of SHS pressure in IT and annuli

Fig. 8

Effect of injection pressure on the profiles of SHS temperature in IT and annuli

Fig. 9

Effect of injection pressure on the profiles of IT heat loss rate

Fig. 10

Effect of injection pressure on the profiles of superheat degree in IT and annuli

Fig. 11

Effect of injection pressure on the profiles of mass flow rate in IT and annuli

As can be seen from Fig. 7, SHS pressure in both IT and annuli increases with the increase in injection pressure at heel point in IT. Figure 8 shows that SHS temperature in both IT and annuli increases with the increase in injection pressure. This is because the SHS density increases with the increase in injection pressure, which causes the decrease in flow velocity. And the friction losses decrease accordingly with the decrease in flow velocity, which causes the increase in SHS temperature in IT and annuli. Besides, the temperature difference between IT and annuli decreases with the increases in injection pressure, which causes the decrease in heat exchange rate between IT and annuli, as shown in Fig. 9.

Figure 10 shows that superheat degree in IT decreases with the increase in injection pressure. However, superheat degree in annuli increases slightly with the increase in injection pressure. This means that the injection pressure does little effect on superheat degree of SHS that is injected into oil layer. But the amount of SHS injected into oil layer increases significantly with the increase in injection pressure, as shown in Fig. 11.

Conclusions

In this paper, a novel numerical model is proposed to analyze the heat and mass transfer characteristics of SHS in horizontal wellbores with toe-point SHS injection technique. Some meaningful findings are listed below.

• (1). The decrease in SHS temperature in annuli caused by heat and mass transfer to oil layer is offset by heat absorbtion from SHS in IT.

• (2). SHS pressure in both IT and annuli increases with the increase in injection pressure at heel point in IT.

• (3). SHS temperature in both IT and annuli increases with the increase in injection pressure.

• (4). The temperature difference between IT and annuli decreases with the increase in injection pressure, which causes the decrease in heat exchange rate between IT and annuli.

• (5). In order to obtain a satisfactory oil recovery ratio, field engineers are suggested to increase the injection pressure to a reasonable level.

Appendices

Appendix 1: Supplementary materials

SHS tables used for calculation in this paper can be seen online: http://webbook.nist.gov/chemistry/fluid/.

Appendix 2: Heat exchange rate between IT and annuli

Based upon previous studies (Sun et al. 2017a; Gu et al. 2014), the heat exchange rate between IT and annuli can be expressed as:

$$\frac{{{\text{d}}Q_{IT} }}{{{\text{d}}z}} = 2\pi r_{ITo} U_{ITo} \left( {T_{IT} - T_{an} } \right)$$

(11)

where

$$U_{ITo} = \left[ {\frac{{r_{ITo} }}{{\lambda_{IT} }}\ln \frac{{r_{ITo} }}{{r_{ITi} }} + \frac{{r_{ITo} }}{{h_{fITi} r_{ITi} }} + \frac{1}{{h_{fITo} }}} \right]^{ - 1}$$

(12)

Appendix 3: Volume injection velocity and transient heat transfer rate in oil layer

Based upon previous works (Dong et al. 2014; Gu et al. 2015; Gu 2016; Chen et al. 2007; Liu 2013), the volume flow velocity can be given as:

$$I_{\text{an}} = J_{\text{an}} I_{\text{r}} \left( {p_{\text{an}} - p_{\text{r}} } \right)$$

(13)

$$J_{\text{an}} = \beta \frac{{2\pi \sqrt {{{K_{\text{h}} } \mathord{\left/ {\vphantom {{K_{\text{h}} } {K_{\text{v}} }}} \right. \kern-0pt} {K_{\text{v}} }}} K_{\text{v}} {\text{d}}L\left( {{{K_{\text{ro}} } \mathord{\left/ {\vphantom {{K_{\text{ro}} } {B_{\text{o}} \mu_{\text{o}} }}} \right. \kern-0pt} {B_{\text{o}} \mu_{\text{o}} }} + {{K_{\text{rw}} } \mathord{\left/ {\vphantom {{K_{\text{rw}} } {B_{\text{w}} \mu_{\text{w}} }}} \right. \kern-0pt} {B_{\text{w}} \mu_{\text{w}} }}} \right)}}{{\ln \frac{{0.571\sqrt {A_{\text{d}} } }}{{r_{\text{wi}} }} + S - 0.75}}$$

(14)

$$I_{\text{r}} = \frac{{2\ln {{A_{\text{d}} } \mathord{\left/ {\vphantom {{A_{\text{d}} } {r_{\text{wi}}^{2} }}} \right. \kern-0pt} {r_{\text{wi}}^{2} }} - 3.86}}{{\ln {{A_{\text{d}} } \mathord{\left/ {\vphantom {{A_{\text{d}} } {r_{\text{wi}}^{2} }}} \right. \kern-0pt} {r_{\text{wi}}^{2} }} - 2.71}}$$

(15)

The heat transfer rate from annuli to oil layer can be expressed as (Liu 2013):

$$\frac{{{\text{d}}Q_{\text{an}} }}{{{\text{d}}L}} = 2\pi \lambda_{\text{e}} \frac{{T_{\text{an}} - T_{\text{ei}} }}{f\left( t \right)}$$

(16)

where $\lambda_{\text{e}}$ denotes reservoir thermal conductivity, W/(m K); $T_{\text{ei}}$ denotes the initial reservoir temperature, K; and $f\left( t \right)$ is the function of injection time (Cheng et al. 2012).

Appendix 4: Shear stress in IT and annuli

In this paper, shear stress is calculated according to Yuan (1982) where it is given as:

$${\text{d}}\tau_{\text{f}} = \frac{1}{4}\pi r_{\text{wi}} f\rho_{\text{IT,an}} v_{\text{IT,an}}^{2} {\text{d}}L$$

(17)

where

$$\left\{ {\begin{array}{*{20}l} {f = \frac{64}{{N_{\text{Re}} }},} \hfill & {N_{Re} \le 2000} \hfill \\ {f = \left[ {1.14 - 2\lg \left( {\Delta + 21.25N_{Re}^{ - 0.9} } \right)} \right]^{ - 2} ,} \hfill & {N_{Re} > 2000} \hfill \\ \end{array} } \right.$$

(18)