Simultaneously modelling steam flow and heat transfer in vertical and horizontal wellbores during SAGD cyclic pre-heating stage

Abstract

Steam-assisted-gravity-drainage (SAGD) is currently an effective technology for heavy oil recovery. The pre-heating stage is important to affect the overall process of SAGD development. In this paper, flow and heat transfer model in vertical well section and horizontal well section and thermal connectivity judgment model during cyclic pre-heating stage were established. Model calculation results are in good agreement with actual measurement results. The effects of steam injection rate and steam quality on the distribution of steam parameters along the whole wellbore and the distribution of heat transfer were compared. Besides, the optimization of steam injection parameter combination was provided. Ultimately, the effect of horizontal well spacing on pre-heating thermal connectivity was discussed. The results show that: With the increase of steam injection rate and steam injection quality, the pressure and temperature drop of the fluid increase. Wellhead required steam injection pressure and temperature increases and even superheated steam appear with the increase of steam injection rate and steam injection quality. The position where the pre-heating backflow turns from wet steam to subcooled water gradually shifts to the wellhead. With the increase of steam injection rate and steam injection quality, the heat transfer between annulus and reservoir decreases, but the uniformity of pre-heating in the horizontal section increases. The time required for cyclic pre-heating to form thermal communication between double wells increases significantly as the horizontal well spacing increases. To simultaneously integrate the uniformity and economy of pre-heating on the oilfield site, the steam injection quality at the heel end of the horizontal section of 0.7, the steam injection rate of 80 t/d, and the horizontal well spacing of 5 m were recommended.

Appendices

Appendix A. dυ/dz for fog two-phase flow

The gas volume flow is much greater than the liquid volume flow in the mist flow state, thus the ideal gas equation can be applied in fog flow:

$${{d(}}\frac{1}{{\rho}}){ = }\frac{1}{{\rho}}\left( {\frac{1}{T}\frac{{{{d}}T}}{{{{d}}p}} - \frac{1}{p}} \right){{d}}p$$

(20)

$${T_{{s}}} = 210.2376{p_{{s}}}^{0.21} + 243.15$$

(21)

$$\frac{{{{d}}T}}{{{{d}}p}} = 44.15{p^{ - 0.79}}$$

(22)

where T_s is saturation temperature of wet steam, K; p_s is saturation pressure of wet steam, MPa.

For fog two-phase flow, dv/dz can be expressed as:

$$\frac{{{{d}}\upsilon }}{{{{d}}z}} = \frac{{{d}}}{{{{d}}z}}\left( {\frac{{{i_{{s}}}}}{\rho A}} \right){ = }\frac{{{i_{{s}}}}}{A}\frac{{{d}}}{{{{d}}z}}\left( {\frac{1}{{\rho}}} \right){ = }\frac{{{i_{{s}}}}}{{A \cdot {\rho}}}\left( {\frac{1}{T}\frac{{{{d}}T}}{{{{d}}p}} - \frac{1}{p}} \right)\frac{{{{d}}p}}{{{{d}}z}}$$

(23)

where υ is two-phase fluid velocity, m/s; ρ is two-phase fluid density, kg/m³; T is wet steam temperature, K; p is wet steam pressure, Pa.

Appendix B. Annulus characteristic length

The annulus characteristic length can be expressed as:

$${d_o}{ = 4}\frac{{\pi \cdot {d_{{{si}}}}/2{^2} - \pi \cdot {d_{{{to}}}}/2{^2}}}{{\pi \cdot {d_{{{si}}}} + \pi \cdot {d_{{{to}}}}}} = {d_{{{si}}}} - {d_{{{to}}}}$$

(24)

where d_o is the annulus characteristic length, m; d_si is the inner diameter of screen tube, m; d_to is the outer diameter of long tubing, m.

Appendix C. Flow friction coefficient

The frictional work between the steam and the pipe wall can be expressed as:

$${{d}}W = \tau ^{\prime} \cdot {{d}}z \cdot {\left( {\frac{{2{{d}}z}}{\upsilon [i] + \upsilon [i + 1]}} \right)^{ - 1}} = \frac{\tau ^{\prime}}{2}(\upsilon [i] + \upsilon [i + 1])$$

(25)

$$\tau ^{\prime} = f^{\prime} \cdot \rho \cdot \frac{{\pi d \cdot {{d}}z}}{8}{\left( {\frac{\upsilon [i] + \upsilon [i + 1]}{2}} \right)^2}$$

(26)

where υ[i], υ[i + 1] are the average velocities of the section located at the i and i + 1 nodes respectively, m/s.

f ' is friction coefficient between fluid and pipe wall, dimensionless:

$$f^{\prime} = \left\{ {\begin{array}{*{20}{c}} {54/{{\operatorname{Re} }_{{s}}}} \\ {{{\left[ {1.14 - 2\lg (\Delta + 21.25\operatorname{Re}_{{s}}^{ - 0.9})} \right]}^{ - 2}}} \end{array}} \right. \, \begin{array}{*{20}{c}} {{{\operatorname{Re} }_{{s}}} \leqslant 2000} \\ {{{\operatorname{Re} }_{{s}}} > 2000} \end{array}$$

(27)

where Re_s is Reynolds number of single-phase flow, dimensionless; ∆ is the relative roughness of pipe wall, dimensionless.

Steam is injected from point A of the long tubing, dissipating heat to the oil reservoir along the way, and may be converted into subcooled water in the annulus. If the steam transforms into supercooled water during the flow, the pipe wall friction coefficient is related to the casing wall roughness, the Reynolds number and the flow pattern of the fluid. The calculation formula of the single-phase pipe flow friction coefficient can be found in the literature [1]. If it is a two-phase flow in the flow process, the density and resistance coefficient of two-phase flow are calculated by B-B method [2]. The calculation of other physical parameters of two-phase flow and single-phase flow can refer to the Witney given method [3]. The calculation of forced convection heat transfer coefficient of two-phase flow and single-phase flow can refers to the Akers given method [4].

Appendix D. Heat exchange in the vertical wellbore

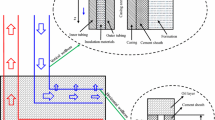
The double-tube structure wellbore section is shown in Fig. 15.

Fig. 15

Section of a vertical wellbore

The heat dissipation of injection pipe per unit length can be expressed as:

$$\frac{{{{d}}{Q_{{{s1}}}}}}{{{{d}}z}} = \frac{{{{d}}{Q_{{{t1c}}}}}}{{{{d}}z}}{ + }\frac{{{{d}}{Q_{{{1cir}}}}}}{{{{d}}z}}{ + }\frac{{{{d}}{Q_{{{12r}}}}}}{{{{d}}z}}$$

(28)

The calculation of the radiation heat of the production pipe refers to the above method and the heat dissipation of the production pipe per unit length is as follows:

$$\frac{{{{d}}{Q_{{{s2}}}}}}{{{{d}}z}} = \frac{{{{d}}{Q_{{{t2c}}}}}}{{{{d}}z}}{ + }\frac{{{{d}}{Q_{{{2cir}}}}}}{{{{d}}z}}{ + }\frac{{{{d}}{Q_{{{21r}}}}}}{{{{d}}z}}$$

(29)

The natural convection heat exchange between the outer wall of the injection pipe and the annulus per unit length dQ_t1c/dz in Eq. (28) can be expressed as:

$$\frac{{{{d}}{Q_{{{t1c}}}}}}{{{{d}}z}} = 2\pi {r_{{{tl}}}}{h_{{c}}}({T_{{l}}} - {T_{{{an}}}})$$

(30)

$${h_{{c}}} = \frac{{\lambda \cdot 0.049{{(Gr \times Pr)}^{0.33}}P{r^{0.71}}}}{{{d_{{o}}}}}$$

(31)

where r_t1 is the outer radius of the injection pipe, m; T_an is the average annulus temperature, K; T₁ is the steam temperature in the injection pipe, K; $\lambda$ is the thermal conductivity of the annulus, W/(m·K).

The radiation heat exchange of injection pipe surface to production pipe surface per unit length dQ_12r/dz in Eq. (28) can be expressed as:

$$\frac{{{{d}}{Q_{{{12r}}}}}}{{{{d}}z}} = 2{\uppi }{r_{{{tl}}}}{h_{{{12r}}}}({T_{{l}}} - {T_{2}})$$

(32)

$${h_{{{12r}}}} = \frac{{\alpha \sigma ({T_{{l}}}{ + }{T_{2}})({T_{{l}}}^2{ + }{T_2}^2)}}{{{\uppi }\left[ {\frac{1}{{{\varepsilon_{{{t1}}}}}}{ + }\frac{{2\alpha {r_{{{t1}}}}}}{{({\uppi } - 2\alpha ){r_{{{t2}}}}}}{(}\frac{1}{{{\varepsilon_{{{t2}}}}}} - {1)}} \right]}}$$

(33)

where T₂ is the steam temperature in production pipe, K; r_t2 is the outer radius of production pipe, m; σ is the Stefan-Boltzmann constant, 5.67 × 10^–8 W/(m²·K⁴); ε_t1 is the radiation coefficient of outer surface in injection pipe, dimensionless; ε_t2 is the radiation coefficient of outer surface in production pipe, dimensionless; a is the half of the radiation angle of the injection string to the production string, rad; The relationship between a and β is shown in Fig. 15.

The radiation heat exchange of injection pipe surface to the inner wall of casing s per unit length dQ_1cir/dz in Eq. (28) can be expressed as follows:

$$\frac{{{{d}}{Q_{{{1cir}}}}}}{{{{d}}z}} = 2{\uppi }{r_{{{tl}}}}{h_{{{1cir}}}}({T_{{l}}} - {T_{ci}})$$

(34)

$${h_{{{1cir}}}} = \frac{{({\uppi } - \alpha )\sigma ({T_{{l}}}{ + }{T_{{{ci}}}})({T_{{l}}}^2{ + }{T_{{{ci}}}}^2)}}{{{\uppi }\left[ {\frac{1}{{{\varepsilon_{{{t1}}}}}}{ + }\frac{{(2{\uppi } - 2\alpha ){r_{{{t1}}}}}}{{(2{\uppi } - 2\beta ){r_{{{ci}}}}}}{(}\frac{1}{{{\varepsilon_{{{ci}}}}}} - {1)}} \right]}}$$

(35)

where T_ci is the temperature of the casing inner wall, K; r_ci is the inner radius of casing, m; ε_ci is the radiation coefficient of the casing inner surface, dimensionless;

The temperature of casing inner wall can be expressed as:

$${T_{{{ci}}}} = \frac{{2\pi {\lambda_o}({T_{{h}}} - {T_o})}}{{f(t) \cdot {k_{{{cih}}}}}} + {T_{{h}}}$$

(36)

f(t) can be calculated by Chiu formula [5]:

$$f(t) = 0.982\ln \left( {1 + 3.62\frac{{\sqrt {at} }}{{{d_{so}}}}} \right)$$

(37)

where T_o is the temperature of the oil layer, K; λ_o is the formation thermal conductivity, W/(m·K); a is oil reservoir thermal diffusivity, m²/s; T_h is the temperature at the outer edge of cement ring, K.

$${k_{{{cih}}}} = {\left\{ {\frac{1}{{2\pi {\lambda_{{c}}}}}\ln \left( {\frac{{{d_{{{co}}}}}}{{{d_{{{ci}}}}}}} \right) + \frac{1}{{2\pi {\lambda_{{{cem}}}}}}\ln \left( {\frac{{{d_{{{cemo}}}}}}{{{d_{{{cemi}}}}}}} \right)} \right\}^{ - 1}}$$

(38)

where λ_c is the thermal conductivity of casing, W/(m·K); λ_cem is the thermal conductivity of cement ring, W/(m·K); d_ci, d_co are the inner diameter and outer diameter of casing respectively, m; d_cemi, d_cemo are the inner diameter and outer diameter of cement ring respectively, m;

According to Ramey’s approximate solution, the radial heat flux density at the interface between the outer edge of the cement ring and the formation:

$${{d}}{\phi_{{s}}} = \frac{{2\pi {\lambda_o}({T_{{h}}} - {T_o}){{d}}z}}{f(t)}$$

(39)

Heat exchange from casing inner wall to the outer edge of cement ring:

$${{d}}{Q_{{{cih}}}} = {k_{{{cih}}}}({T_{{{ci}}}} - {T_{{h}}})dz$$

(40)

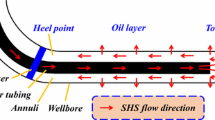
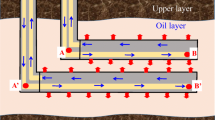
Appendix E. Heat exchange in the horizontal wellbore

Heat exchange between the steam in the long tubing and backflow in the annulus can be expressed as:

$${{d}}{Q_{{s}}} = {k_{{t}}}\left( {{T_{{t}}} - {T_{{{an}}}}} \right) \cdot {{d}}z$$

(41)

$${k_{{t}}} = {\left\{ {\frac{1}{{{\uppi }{d_{{{ti}}}}{h_{{{ti}}}}}} + \frac{1}{{2{\uppi }{\lambda_{{t}}}}}\ln \left( {\frac{{{d_{{{to}}}}}}{{{d_{{{ti}}}}}}} \right) + \frac{1}{{{\uppi }{d_{{{to}}}}{h_{{{to}}}}}}} \right\}^{ - 1}}$$

(42)

where T_t, T_an are the fluid temperature of long tubing and annulus respectively, K; h_ti, h_to are the forced convection heat transfer coefficients of the inner wall and the outer wall in the long tubing respectively, W/(m²·K); λ_t is the thermal conductivity of long tubing, W/(m·K).

Heat exchange between the backflow in the annulus and the outer edge of the screen tube:

$${{d}}{Q_{{{m1}}}} = {k_{{{an}}}}({T_{{{an}}}} - {T_{{{so}}}})dz$$

(43)

$${k_{{{an}}}} = {\left\{ {\frac{1}{{\pi {d_{{{si}}}}{h_{{{an}}}}}} + \frac{1}{{2\pi {\lambda_{{s}}}}}\ln \left( {\frac{{{d_{{{so}}}}}}{{{d_{{{si}}}}}}} \right)} \right\}^{ - 1}}$$

(44)

where T_so is the temperature of the screen tube outer edge, K; h_an is the forced convective heat transfer coefficient of the inner wall of the annulus, W/(m²·K); λ_s is the thermal conductivity of screen tube, W/(m·K); d_so is the outer diameter of screen tube, m.

According to Ramey's approximate solution, the radial heat flux density at the interface between the screen and the oil layer:

$${{d}}{\phi_{{s}}} = \frac{{2\pi {\lambda_{{o}}}({T_{{{so}}}} - {T_{{o}}}){{d}}z}}{f(t)}$$

(45)

The temperature of the screen tube outer edge:

$${T_{{{so}}}} = \frac{{2\pi {\lambda_{{o}}}{T_{{o}}} + {k_{{{an}}}}{T_{{{an}}}}f(t)}}{{2\pi {\lambda_{{o}}} + {k_{{{an}}}}f(t)}}$$

(46)