Skip to main content

Advertisement

SpringerLink
Log in

A Diffuse Interface Framework for Modeling the Evolution of Multi-cell Aggregates as a Soft Packing Problem Driven by the Growth and Division of Cells

  • Special Issue: Multiscale Modeling of Tissue Growth and Shape
  • Published:
Bulletin of Mathematical Biology Aims and scope Submit manuscript

Abstract

We present a model for cell growth, division and packing under soft constraints that arise from the deformability of the cells as well as of a membrane that encloses them. Our treatment falls within the framework of diffuse interface methods, under which each cell is represented by a scalar phase field and the zero level set of the phase field represents the cell membrane. One crucial element in the treatment is the definition of a free energy density function that penalizes cell overlap, thus giving rise to a simple model of cell–cell contact. In order to properly represent cell packing and the associated free energy, we include a simplified representation of the anisotropic mechanical response of the underlying cytoskeleton and cell membrane through penalization of the cell shape change. Numerical examples demonstrate the evolution of multi-cell clusters and of the total free energy of the clusters as a consequence of growth, division and packing.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Notes

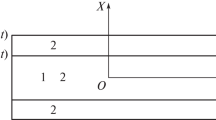
  1. In some simulations, a buffer zone, \(\Omega ^{'}\), is needed around the simulation domain to inhibit unrealistic cell shapes resulting from the enforcement of \(\kappa {\varvec{\nabla }} c_k \cdot {\varvec{n}}= 0\) on \(\partial \Omega \). In addition, this buffer zone also acts as a membrane around the cell cluster. In the buffer zone, an additional term of the form \(\sum _{k=1}^{N}\lambda c_k^2\) is added to the free energy density to penalize the movement of any cells from the active simulation domain (\(\Omega \)) to the buffer zone (\(\Omega ^{'}\)).

  2. In this initial boundary value problem, \(\partial \Omega \) is composed of only a Neumann (flux) boundary (\(\partial \Omega ^{h} = \partial \Omega \)) and hence the Dirichlet boundary is a null set (\(\partial \Omega ^{g} = \varnothing \)).

References

  • Allen SM, Cahn JW (1979) A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening. Acta Metall 27(6):1085–1095

    Article  Google Scholar 

  • Alt S, Ganguly P, Salbreux G (2017) Vertex models: from cell mechanics to tissue morphogenesis. Philos Trans R Soc Lond B Biol Sci 372(1720):20150520

    Article  Google Scholar 

  • Bangerth W, Hartmann R, Kanschat G (2007) deal. II—a general purpose object oriented finite element library. ACM Trans Math Softw 33(4):24/1–24/27

    Article  MathSciNet  MATH  Google Scholar 

  • Brezzi F, Fortin M (1991) Mixed and hybrid finite element methods. Springer, Berlin

    Book  MATH  Google Scholar 

  • Brodland GW (2004) Computational modeling of cell sorting, tissue engulfment, and related phenomena: a review. Appl Mech Rev 57:47–76

    Article  Google Scholar 

  • Cahn JW, Hilliard JE (1958) Free energy of a nonuniform system. I. Interfacial free energy. J Chem Phys 28(2):258–267

    Article  Google Scholar 

  • Fletcher A, Osterfield M, Baker RE, Shvartsman SY (2014) Vertex models of epithelial morphogenesis. Biophys J 106(11):2291–2304

    Article  Google Scholar 

  • Gilbert SF (2000) Developmental biology, 6th edn. Sinauer Associates, Sunderland

    Google Scholar 

  • Glazier JA, Graner F (1993) Simulation of the differential adhesion driven rearrangement of biological cells. Phys Rev E 47:2128–2154

    Article  Google Scholar 

  • Goel NS, Rogers G (1978) Computer simulation of engulfment and other movements of embryonic tissues. J Theor Biol 71(1):103–140

    Article  Google Scholar 

  • Goel N, Campbell RD, Gordon R, Rosen R, Martinez H, Yaas M (1970) Self-sorting of isotropic cells. J Theor Biol 28(3):423–468

    Article  Google Scholar 

  • Graner F (1993) Can surface adhesion drive cell-rearrangement? Part I: biological cell-sorting. J Theor Biol 164(4):455–476

    Article  Google Scholar 

  • Graner F, Glazier JA (1992) Simulation of biological cell sorting using a two-dimensional extended Potts model. Phys Rev Lett 69:2013–2016

    Article  Google Scholar 

  • Heroux M, Bartlett R, Hoekstra VHR, Hu J, Kolda T, Lehoucq R, Long K, Pawlowski R, Phipps E, Salinger A, Thornquist H, Tuminaro R, Willenbring J, Williams A (2003) An overview of Trilinos. Technical report SAND2003-2927, Sandia National Laboratories

  • Honda H (1978) Description of cellular patterns by Dirichlet domains: the two-dimensional case. J Theor Biol 72(3):523–543

    Article  MathSciNet  Google Scholar 

  • Honda H (1983) Geometrical models for cells in tissues. Int Rev Cytol 81:191–248

    Article  Google Scholar 

  • Honda H, Yamanaka H, Eguchi G (1986) Transformation of a polygonal cellular pattern during sexual maturation of the avian oviduct epithelium: computer simulation. Development 98(1):1–19

    Google Scholar 

  • Itskovitz-Eldor J, Schuldiner M, Karsenti D, Eden A, Yanuka O, Amit M, Soreq H, Benvenisty N (2000) Differentiation of human embryonic stem cells into embryoid bodies compromising the three embryonic germ layers. Mol Med 6(2):88

    Article  Google Scholar 

  • Kamrin K, Rycroft CH, Nave JC (2012) Reference map technique for finite-strain elasticity and fluid–solid interaction. J Mech Phys Solids 60(11):1952–1969

    Article  MathSciNet  Google Scholar 

  • Li XS (2005) An overview of SuperLU: algorithms, implementation, and user interface. ACM Trans Math Softw 31(3):302–325

    Article  MathSciNet  MATH  Google Scholar 

  • Mills KL, Kemkemer R, Rudraraju S, Garikipati K (2014) Elastic free energy drives the shape of prevascular solid tumors. PloS ONE 9(7):e103245

    Article  Google Scholar 

  • Mirams GR, Arthurs CJ, Bernabeu MO, Bordas R, Cooper J, Corrias A, Davit Y, Dunn S-J, Fletcher AG, Harvey DG et al (2013) Chaste: an open source C++ library for computational physiology and biology. PLoS Comput Biol 9(3):e1002970

    Article  MathSciNet  Google Scholar 

  • Mochizuki A, Wada N, Ide H, Iwasa Y (1998) Cell-cell adhesion in limb formation, estimated from photographs of cell sorting experiments based on a spatial stochastic model. Dev Dyn 211(3):204–214

    Article  Google Scholar 

  • Mosaffa P, Asadipour N, Millán D, Rodríguez-Ferran A, Muñoz JJ (2015) Cell-centred model for the simulation of curved cellular monolayers. Comput Part Mech 2(4):359–370

    Article  Google Scholar 

  • Mosaffa P, Rodríguez-Ferran A, Muñoz JJ (2017) Hybrid cell-centred/vertex model for multicellular systems with equilibrium preserving remodelling. Int J Numer Methods Biomed Eng 34(3):e2928

    Article  MathSciNet  Google Scholar 

  • Nonomura M (2012) Study on multicellular systems using a phase field model. PLOS ONE 7(4):1–904

    Article  Google Scholar 

  • Reya T, Morrison SJ, Clarke MF, Weissman IL (2001) Stem cells, cancer, and cancer stem cells. Nature 414(6859):105

    Article  Google Scholar 

  • Rudraraju S, Mills KL, Kemkemer R, Garikipati K (2013) Multiphysics modeling of reactions, mass transport and mechanics of tumor growth. In: Holzapfel G, Kuhl E (eds) Computer models in biomechanics. Springer, Dordrecht, pp 293–303

    Chapter  Google Scholar 

  • Schierenberg E (2006) Embryological variation during nematode development (2 Jan 2006), WormBook, ed. The C. elegans Research Community, WormBook

  • Swat MH, Thomas GL, Belmonte JM, Shirinifard A, Hmeljak D, Glazier JA (2012) Multi-scale modeling of tissues using compucell3d. In: Asthagiri AR, Arkin AP (eds) Methods in cell biology, vol 110. Elsevier, Amsterdam, pp 325–366

    Chapter  Google Scholar 

  • Vedantam S, Patnaik BSV (2006) Efficient numerical algorithm for multiphase field simulations. Phys Rev E 73(1):016703

    Article  Google Scholar 

  • Verner SN, Garikipati K (2018) A computational study of the mechanisms growth-driven folding patterns on shells, with application to the developing brain. Extreme Mech Lett 18:58–69

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Mechanical Engineering, University of Michigan, Ann Arbor, USA

    J. Jiang

  2. Mechanical Engineering and Mathematics, University of Michigan, Ann Arbor, USA

    K. Garikipati

  3. Mechanical Engineering, University of Wisconsin-Madison, Madison, USA

    S. Rudraraju

Authors
  1. J. Jiang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. K. Garikipati
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. S. Rudraraju
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to K. Garikipati.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jiang, J., Garikipati, K. & Rudraraju, S. A Diffuse Interface Framework for Modeling the Evolution of Multi-cell Aggregates as a Soft Packing Problem Driven by the Growth and Division of Cells. Bull Math Biol 81, 3282–3300 (2019). https://doi.org/10.1007/s11538-019-00577-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11538-019-00577-1

Keywords

Search

Navigation