Cell-centred model for the simulation of curved cellular monolayers

Abstract

This paper presents a cell-centred model for the simulation of planar and curved multicellular soft tissues. We propose a computational model that includes stress relaxation due to cell reorganisation (intercellular connectivity changes) and cytoskeleton remodelling (intracellular changes). Cells are represented by their cell centres, and their mechanical interaction is modelled through active non-linear elastic laws with a dynamically changing resting length. Special attention is paid to the handling of connectivity changes between cells, and the relaxation that the tissues exhibit under these topological changes. Cell–cell connectivity is computed by resorting to a Delaunay triangulation, which is combined with a mapping technique in order to obtain triangulations on curved manifolds. Our numerical results show that even a linear elastic cell–cell interaction model may induce a global non-linear response due to the reorganisation of the cell connectivity. This plastic-like behaviour is combined with a non-linear rheological law where the resting length depends on the elastic strain, mimicking the global visco-elastic response of tissues. The model is applied to simulate the elongation of planar and curved monolayers.

1 Introduction

The dynamics of multicellular systems is governed by a myriad of parameters, including genetic, chemical and kinematic factors. In recent years though, it has become apparent that cells are also highly influenced by mechanical stimuli, and therefore, the stress state of the cell and its neighbourhood mediate important cell shape changes during cell migration [5, 45], embryo development [8, 13, 39] or organogenesis [43]. These facts have motivated the development of computational tools that allow scientists and engineers to analyse the intra- and inter-cellular forces during tissue dynamics [11, 34, 35, 37].

The computational models developed so far for the analysis of multicellular systems and single cells can be classified into continuum based models [30, 38], usually discretised with finite element techniques, and discrete models that assume ab initio a discontinuous material. The latter may be in turn subdivided into vertex models [17, 32, 34, 44], Potts models [14, 24], cell-centred models [11, 27, 31, 37], or sub-cellular models [12, 25, 43], where particles do not represent cells, but material points of the cell. For a discussion and overview of these models, see for instance [10, 25].

In this paper we aim to simulate global embryogenetic cell shape changes such as invagination or germ-band extension [9]. Motivated by the need to represent hundreds or even thousands of cells (Drosophila fly embryo for instance is formed by around 6000 cells during gastrulation), and the self-organisation of the tissue when undergoing topological changes, we have resorted to a cell-centred model, where each cell is represented by a particle, and each cell–cell interaction is modelled through a bar element connecting two particles. This element carries all the interactions at the junctions between the cells, and also the internal active and passive forces produced by the cytoskeleton. Since topological changes are commonly observed during embryo development, and may determine the global tissue deformations [19], the proposed model aims to handle these changes in a robust manner.

The cell-centred approach adopted here is substantially different from vertex models, where forces are located at the cell boundaries [17, 34, 35]. In our model, forces are exclusively acting at the cell centres, whose positions are found resorting to mechanical equilibrium. We also present here a methodology to compute the cell boundaries from the cell centres, which, in contrast to standard vertex models [27, 34], is also valid for curved three-dimensional monolayers. Our choice aims to simplify the definition of the three-dimensional geometry when cell neighbours are dynamically changing, a task that is significantly simpler for cell-centred models. Although no equilibrium is searched at the cell–cell boundaries, we envision to couple intra- and inter-cellular forces by using the methodology described here.

We implement a constitutive law of the bar elements that mimics the non-linear mechanical response of multicellular systems. This is the result of multiple local phenomena acting at different scales. At the micro-scale, the cytoskeleton can undergo (de)polymerisation process [22], cross-link reorganisation [7], or affect the cytoplasm flow [28]. At the macro-scale, cell motility is driven by cell–cell and cell-extracellular matrix adhesive forces, lamellipodia activity or other intercalation forces. The combination of these multi-scale forces results into global changes during embryogenesis such as convergent extension [3, 36], or anisotropic tissue growth [4].

We do not intend to include all this range of multi-scale forces in the bar elements of our model, but just a subset of the observed mechanisms that may be sufficient to reproduce some of the observed morphogenetic movements. In our model we control the cell–cell reorganisation, and also implement a strain-dependent evolution of the resting length, in a similar manner to a time-varying reference configuration in continuum models [30, 40].

The paper is organised as follows. Section 2 describes the ingredients of the computational model: the bar elements being employed, the equations to be solved, and the definition of the cell–cell connectivity. Section 3 applies the model to a flat and to a curved monolayer, and Sect. 4 concludes the paper with some final remarks.

2 Computational model

2.1 Model definition

We will henceforth consider that the cellular system satisfies the following assumptions:

• (a) The system forms a monolayer, modelled as a planar or curved manifold.

• (b) Cells are packed with no extracellular space in between.

• (c) Cell centres are considered as dimensionless points (later mentioned as nodes) by which the location of each cell is defined in space.

• (d) Contact between two cells i and j is defined by the presence of a one-dimensional bar element connecting the two cell centres, providing a connected graph as a whole.

• (e) The total number of cells (nodes) N is constant.

Assumption (a) is based on the fact that during the early stages of embryogenesis, prior to any mesenchymal transformations, cells tend to form a monolayer [9]. This may be eventually internalised and cells may turn into a cell aggregate, but this situation is not studied here. Assumptions (b–d) are considered to simplify the computations, while assumption (e) is consistent with the fact that when cells undergo drastic deformations, no proliferation takes place, that is, the number of cells remains approximately constant [21].

The configuration of the model at each time-step $t_n$, denoted by ${\varvec{C}}_n$, is defined by the nodal position of the N nodes, ${\varvec{X}}_n=\{{\varvec{x}}^1_n,{\varvec{x}}^2_n,...,{\varvec{x}}^N_n\}$, and the connectivity between the nodes, indicated by a connectivity matrix, ${\varvec{T}}_n$. The two sets of variables, ${\varvec{X}}_n$ and ${\varvec{T}}_n$ may vary between time-steps, and are computed from the previous variables ${\varvec{C}}_{n}$ according to the following scheme:

• 1. Compute nodal coordinates ${\varvec{X}}_{n+1}$ by finding mechanical equilibrium between the particles, while keeping the connectivity ${\varvec{T}}_n$ constant.

• 2. Update the connectivities ${\varvec{T}}_{n+1}$ resorting to a Delaunay triangulation of the new positions ${\varvec{X}}_{n+1}$.

Figure 1 shows the two-step update process. Note that according to the scheme above, equilibrium at time $t_{n+1}$ is computed for the connectivity defined at time $t_n$. The connectivity at ${\varvec{T}}_n$ may not be suitable for the new positions ${\varvec{X}}_{n+1}$, and for this reason the cell–cell contacts are updated, yielding a new connectivity ${\varvec{T}}_{n+1}$. We will next describe in detail the two steps: mechanical equilibrium (Sect. 2.2) and connectivity definition (Sect. 2.3).

Fig. 1

A schematic view of Delaunay triangulation for a set of four nodes. a Primary Delaunay triangulation. b New configuration in equilibrium. c Recovering Delaunay triangulation for the new configuration

2.2 Mechanical equilibrium

2.2.1 Equilibrium equations

The connectivity matrix ${\varvec{T}}_n$ defines a set of $N_E$ elements $E=\{1,\ldots , e_{N_E}\}$, each one connecting a pair of nodes i and j. In order to ease the notation, we will drop in this section the subscript n. For each element e we have used the elastic potential $U^{ij}$

$$\begin{aligned} U^{ij}=\frac{1}{2} k\left( \varepsilon ^{e,ij}\right) ^2, \end{aligned}$$

(1)

with k a material parameter representing the material stiffness, and $\varepsilon ^{e,ij}$ the scalar elastic strain between nodes i and j, and given by

$$\begin{aligned} \varepsilon ^{e,ij}=\frac{(l^{ij}-L^{ij})}{L^{ij}}. \end{aligned}$$

Here,  $l^{ij}=||{\varvec{x}}^i -{\varvec{x}}^j||$ is the current length between nodes i and j, and $L^{ij}$ is the resting length between the two nodes, to be discussed in the next section. By computing the traction forces at the two ends of element ij, denoted respectively by ${\varvec{t}}^{ij}_i$ and ${\varvec{t}}^{ij}_j$ and obtained as,

$$\begin{aligned} {\varvec{t}}^{ij}_i&=\partial _{{\varvec{x}}^i} U^{ij}=k\varepsilon ^{e,ij}\frac{1}{L^{ij}l^{ij}}(\varvec{x}^i-\varvec{x}^j), \end{aligned}$$

(2)

$$\begin{aligned} {\varvec{t}}^{ij}_j&=\partial _{{\varvec{x}}^j} U^{ij}=k\varepsilon ^{e,ij}\frac{1}{L^{ij}l^{ij}}(\varvec{x}^j-\varvec{x}^i), \end{aligned}$$

(3)

the global equilibrium of the system is computed by assembling at each node all the confluent forces, that is solving the set of equations

$$\begin{aligned} \sum _{ik\in I_i} {\varvec{t}}^{ik}_i&={\mathbf {0}}, i=1,\ldots ,N \end{aligned}$$

(4)

where $I_i\subset E$ denotes the subset of elements connected to node i. The Eq. in (4) are tantamount to minimise the total elastic energy $U=\sum _{ij\in E} U^{ij}$. Note that due to the non-linear dependence of $l^{ij}$ on the positions ${\varvec{x}}^i$ and ${\varvec{x}}^j$, the equations are non-linear. We resort to a Newton-Raphson scheme for finding the solution of (4).

2.2.2 Active rheological model

The actin cytoskeleton is a network of protein-polymers, which is responsible for the mechanical stability of cells and, due to its remodelling and (de)polymerisation of the actin filaments, may strongly affect cell rheology. Indeed, it has been shown that inhibition of the actomyosin cytoskeleton increases the tissue viscosity [1, 22].

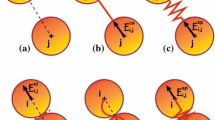
From the physical perspective, when a set of cross-linked actin filaments in the cytoskeleton is subjected to a macroscopic strain, it stretches mainly as a result of two combined phenomena: (i) a reversible (elastic) deformation and a (ii) non-reversible remodelling and lengthening, due to the remodelling of the cross-links and (de)polymerisation process of the filaments. Figure 2 illustrates schematically this two combined effects for a pair of cross-linked polymers under a stretch process.

Fig. 2

a Schematic of network of actin filaments connected by flexible cross-links. b Schematic of strain induced changes in the resting length L of a reduced system with two filaments and a cross-link (white circle). a Initial configuration with resting length equal to $L_0$. b Configuration under an applied load. c New unstrained configuration with modified resting length $L > L_0$

Consistent with this observation, we propose the following evolution law for the resting length $L^{ij}$ between two connected nodes i and j,

$$\begin{aligned} \dot{L}^{ij}=\gamma \varepsilon ^{e,ij} L^{ij}=\gamma (l^{ij}-L^{ij}). \end{aligned}$$

(5)

That is, the relative changes of the resting length $L^{ij}$ are proportional to the elastic strain $\varepsilon ^e$, which we point out that is different from the apparent strain $\varepsilon ^{ij}=\frac{(l^{ij}-L_0^{ij})}{L_0^{ij}}$, with $L_0^{ij}=l_0^{ij}$, the initial length. The parameter $\gamma$ will be called the remodelling rate, and represents the ability of the network to adapt its resting length when subjected to stress. It has been shown that this evolution law is equivalent to a Maxwell-like rheological model [29].

The evolution law in (5) is combined with a purely linear elastic constitutive law in (1). This is implemented by discretising the differential equation in (5) using a $\theta -$scheme [18]

$$\begin{aligned} L^{ij}_{n+1}-L^{ij}_n={\varDelta }t\gamma (l^{ij}_{n+\theta } -L^{ij}_{n+\theta }), \end{aligned}$$

(6)

with $(\bullet )_{n+\theta }=(1-\theta )(\bullet )_n+\theta (\bullet )_{n+1}$. Due to the varying resting length, the nodal tractions at end i, denoted by ${\varvec{t}}^{ij}_i$ and given in (2), become now

$$\begin{aligned} {\varvec{t}}^{ij}_i&=\partial _{{\varvec{x}}^i} U^{ij}=k\varepsilon ^{e,ij}\frac{1}{L^{ij}l^{ij}}(1-F)(\varvec{x}^i-\varvec{x}^j),\\ {\varvec{t}}^{ij}_j&=\partial _{{\varvec{x}}^j} U^{ij}=k\varepsilon ^{e,ij}\frac{1}{L^{ij}l^{ij}}(1-F)(\varvec{x}^j-\varvec{x}^i), \end{aligned}$$

with $F=(1+{\varDelta }t\gamma \theta )^{-1}{\varDelta }t\gamma \theta l^{ij}/L^{ij}$. The elemental active length $L^{ij}$ can be statically condensed [31], so that only displacement degrees of freedom are globally solved.

2.3 Cell–cell connectivity: modified Delaunay triangulation

2.3.1 Triangulation of planar monolayer

We resorted to Delaunay Triangulation (DT) [2] of the set of nodes ${\varvec{X}}_{n+1}$ obtained from the mechanical equilibrium described in the previous section. This triangulation connects the nodes in such a way that the circumcircle of any triangle does not contain any other node in it, providing triangles with optimal aspect ratio [2, 33]. Figure 3 illustrates a schematic view of this triangulation for a set of four nodes (cell centres).

Fig. 3

Filtering process of Delaunay triangulation: a configuration at time $t_n$, b nodal positions at time $t_{n+1}$, in equilibrium while holding the Delaunay triangulation at $t_n$, c Delaunay triangulation updated for the new positions, with unrealistic connectivities on concave edges d unrealistic connectivities being filtered

Since Delaunay’s algorithm yields the convex hull of all the points, a basic Delaunay triangulation $\tilde{\varvec{T}}_{n+1}=DT({\varvec{X}}_{n+1})$ of the cell centres may invariably lead to distant boundary cells being unrealistically connected, i.e. covering non-convex boundaries (see Fig. 3c). In order to overcome this problem, those elements with very high aspect ratio were eliminated by defining a filtering process. The ratio of in-radius, r, to circumradius, R, of each triangle in 2D problem and each tetrahedron in 3D problem has been considered as an appropriate criterion to filter undesirable simplexes. In our case, we have used a tolerance $tol=0.2$ and imposed that wherever $\frac{r}{R}<tol$, the element is removed.

After applying this filtering process, denoted by ${\varvec{F}}$, a new connectivity ${\varvec{T}}_{n+1}={\varvec{F}}(DT({\varvec{X}}_{n+1}))$ is obtained, which does not include the unrealistic elements on the boundary. Figure 3 shows schematically the sequence of all the process described in Sect. 2.2 and the planar triangulations described here for a set of nine nodes. Configuration in Fig. 3b is computed after imposing mechanical equilibrium on the triangulation in (a). The connectivity in Fig. 3c is obtained by basic Delaunay triangulation, while the one in Fig. 3d is obtained after applying the filtering process.

2.3.2 Triangulation of curved manifold

To obtain the new triangulation at step (c) in Fig. 3, within the filtering process of Delaunay triangulation, we resort to a non-linear dimensionality reduction method (NLDR) to embed the three-dimensional scattered set of points describing the cell centres in a two-dimensional embedding. In general, NLDR techniques suppose that the input high-dimensional point-set either lies on or is close enough to a low-dimensional manifold that also is an open set [6, 20, 23].

Here we use a robust and efficient variation of the well known local linear embedding (LLE, [42]) technique, that is the modified local linear embedding (MLLE, [46]). LLE-based methods assume that each point of the manifold can be locally approximated by a linear combination of its k-nearest neighbours (k-nn). LLE ignores metric information producing low-dimensional embeddings of unit covariance through a minimisation process that involves eigenvalue decomposition of sparse matrices. The reader is referred to [41, 42, 46] for full details, and to [26] for a concise description and performance comparison with other NLDR methods in the manipulation of point-set surfaces.

As we have mentioned, a remarkable feature of LLE-based methods is the lack of a clear metric relationship between the low-dimensional embedding and the original data (see Fig. 4b). In the problems tackled in this work this is not problematic as can be noticed in Fig. 4c, even when the input point-set describes an elongated surface as that shown in Fig. 4a. Finally, the resulting Delaunay triangulation from the filtering process is attached to the input point-set surface as depicted in Fig. 4d.

Fig. 4

a Arbitrary point-set configuration from a proof of concept example in 3D. b Two-dimensional embedding obtained by using MLLE [46] (k-nn = 8). The lack of a metric related to the input data, that is, different distances between points in the real and mapped domain, and its unit covariance (mapped points are distributed on a squared region) are apparent from the picture. c Two-dimensional embedding nodes and connectivity after applying the filtering described in Sect. 2.3.1. d 3D initial point-set configuration with resulting connectivity. The colour-map, which indicates the identifier of each sample of the point-set, is provided for visual inspection

2.3.3 Post-processing: voronoi tessellation

To represent the cells boundaries, we resort to standard Voronoi tessellation algorithm of the set of nodes ${\varvec{X}}_{n+1}$: each Voronoi face is perpendicular to the connecting line of the Delaunay triangulation, and splits in half this line [2].

However, when it comes to constructing the boundaries associated with the cells at the boundary of the cell aggregate, Voronoi faces form unbounded regions closing at infinity. To resolve this issue, a set of off-set nodes were added to the original set of nodes at the boundary of the filtered Delaunay triangulation. Each face (edge in two dimensions) at the boundary was duplicated by adding nodes at a constant off-set distance.

For a curved three-dimensional monolayer configuration, the Voronoi tessellation was performed at two stages. At the first stage, a set of off-set nodes were constructed at each side of the monolayer. At the second stage, after defining the nodes at the boundary of the monolayer, a second set of off-set nodes were added on the plane of the monolayer.

The Voronoi tessellation was constructed taking into account the original and the additional off-set nodes, ensuring the formation of bounded regions for the original nodes of the monolayer. Figure 5a illustrates a schematic view of a set of three nodes primarily connected by a Delaunay triangulation. Figure 5b shows the unbounded regions created by directly applying a Voronoi tesselation. Figure 5c indicates the off-set nodes with smaller circles, while Fig. 5d shows the Voronoi regions formed by this extended set of nodes, which after removing the unbounded regions and the off-set nodes results in the final Voronoi regions of the cells for the original set of nodes (Fig. 5e). The off-set nodes are finally removed.

Fig. 5

Voronoi tessellation: a Delaunay triangulation of original set of nodes, b open Voronoi tessellation, c setting up off-set nodes, d Voronoi vertices set on original nodes and off-set nodes and e closed Voronoi boundaries for surface nodes after eliminating off-set nodes followed by Voronoi vertex at infinity being excluded

In summary, the steps followed to form the Voronoi tessellation are:

• 1. Form off-set layer of nodes. The external normal $\varvec{n}_\xi$ to each boundary $\xi$ is computed and the new set of nodes $\varvec{x}_{off-set}^{\xi }$ is built according to

  $$\begin{aligned} \varvec{x}_{off-set}^{\xi }=\varvec{x}^{\xi }+\epsilon \varvec{n}^{\xi }. \end{aligned}$$

  The new set of nodes is denoted by $\check{\varvec{T}}_{n+1}$, which includes $\varvec{X}_{n+1}$ and the nodes a the off-set layer $\varvec{x}_{off-set}^{\xi }$ (see Fig. 5c). In our numerical results we have used the value $\epsilon =1$, which gives a reasonable cell shape for the cells at the boundaries in our examples. We note that, in general, the choice of this parameter should be made dependent on the actual size of the cell, and other values such as one half of the cell-to-cell distance. In our current implementation, where the Voronoi vertices are not included in the mechanical equilibrium, the value of $\epsilon$ does not affect the deformed configurations, but just the aspect of the cell region.

• 2. Build a new Delaunay triangulation from $\check{\varvec{X}}_{n+1}$, i.e. $\check{\varvec{T}}_{n+1}=DT(\check{\varvec{X}}_{n+1})$(see Fig. 5c).

• 3. Build Voronoi tessellation of $\check{\varvec{T}}_{n+1}$, that is $\check{\varvec{V}}_{n+1}=Voronoi(\check{\varvec{T}}_{n+1})$ (see Fig. 5d).

• 4. Remove Voronoi vertices connected to vertex at infinity (see Fig. 5e) and remove nodes of the off-set layer.

2.3.4 Update of active length for active rheological model

The time discretisation of the evolution law in (5) requires the evaluation of the active length at times $t_{n+1}$ and $t_n$, respectively, denoted by $L_{n+1}^{ij}$ and $L^{ij}_n$. However, due to the redefinition of the cell–cell connectivity, it may well be that the element ij exists at time $t_{n+1}$ but not at time $t_n$. For this reason, we compute a nodal Active Length Tensor ${{\mathbf {L}}}^i$, which will allow to compute the active length along direction ${\varvec{n}}_j$ as

$$\begin{aligned} L^{ij}={{\varvec{n}}_j}\cdot {{\mathbf {L}}}^i{{\varvec{n}}_j}. \end{aligned}$$

(7)

This relation allows for interpreting tensor ${{\mathbf {L}}}^i$ as a strain tensor, where the quantity ${\varvec{n}}_j\cdot {{\mathbf {L}}}^i{\varvec{n}}_j$ corresponds to the stretching along ${\varvec{n}}_j$. Since the skew part of ${{\mathbf {L}}}^i$ does not affect the value of $L^{ij}$ in (7), and in order to keep the similarity between ${{\mathbf {L}}}^i$ and a deformation tensor, we will assume that ${{\mathbf {L}}}^i$ is symmetric.

It is clear that for a given node i, the existence of an active length tensor ${{\mathbf {L}}}^i$ satisfying exactly relationship in (7) for all current cell–cell connections ij may not be possible. Therefore, the tensor ${{\mathbf {L}}}^i$ is computed by minimising the following quadratic error function:

$$\begin{aligned} E_i=\frac{1}{2}\sum _{j=1}^N||{{\mathbf {L}}}^i{\varvec{n}}_j-L^{ij}{\varvec{n}}_j||^2. \end{aligned}$$

(8)

We note that, in view of Eq. (7), we could alternatively aim to minimise the error function $\tilde{E}_i=\sum _j || \varvec{n}_j^T{{\mathbf {L}}}^i\varvec{n}_j-L^{ij}||^2$. We have not done so for reasons that will be explained below, when commenting the uniqueness of the minimiser.

Due to the symmetry of tensor ${{\mathbf {L}}}^i$, we will write this tensor in the forms

$$\begin{aligned}&\bar{{{\mathbf {L}}}}_{2D}^i\!=\!\left\{ L_{xx}, L_{yy}, L_{xy}\right\} ^T,\quad \nonumber \\&\bar{{{\mathbf {L}}}}_{3D}^i \!=\!\left\{ L_{xx}, L_{yy}, L_{zz}, L_{xy}, L_{xz}, L_{yz}\right\} ^T, \end{aligned}$$

so that ${{\mathbf {L}}}^i{\varvec{n}}_j={{\mathbf {N}}}_j\bar{{{\mathbf {L}}}}^i$, with ${{\mathbf {N}}}_j$ a matrix that contains the components of the unit vector ${\varvec{n}}_j$. Then, the error $E_i$ reads as

$$\begin{aligned} E_i=\frac{1}{2}\sum _{j=1}^N||{{\mathbf {N}}}_j\bar{{{\mathbf {L}}}}^i-L^{ij}{\varvec{n}}_j||^2, \end{aligned}$$

and its derivative with respect to each one of the components of ${{\mathbf {L}}}^i$ gives rise to the system of equations

$$\begin{aligned} {{\mathbf {A}}}\bar{{{\mathbf {L}}}}^i={{\mathbf {b}}}\end{aligned}$$

(9)

with

$$\begin{aligned} {{\mathbf {A}}}=\sum _{j=1}^N{{\mathbf {N}}}_j^T{{\mathbf {N}}}_j\quad ,\quad {{\mathbf {b}}}=\sum _{j=1}^NL^{ij}{{\mathbf {N}}}_j^T{\varvec{n}}_j. \end{aligned}$$

The error measure $E_i$ in (8) is a quadratic function that has a unique minimiser as far as the vectors ${\varvec{n}}_j$ span ${\mathbb {R}}^{n_{sd}}$, with $n_{sd}$ the number of space dimensions. Appendix 5 gives a proof of this fact. The symmetry of ${{\mathbf {L}}}^i$ is not required in the proof of uniqueness, which opens the possibility for considering a non-symmetric tensor ${{\mathbf {L}}}^i$. However, in this case, the system of Eq. in (9) would contain more unknowns, without any qualitative improvement in the retrieved active lengthening $L^{ij}={\varvec{n}}_j\cdot {{\mathbf {L}}}^i{\varvec{n}}_j$. Furthermore, and although we do not prove it here, we point out that other alternative error measures as the function $\tilde{E}_i$ mentioned above would not guarantee a unique minimiser, even if the vectors ${\varvec{n}}_j$ span ${\mathbb {R}}^{n_{sd}}$.

3 Numerical results

3.1 Flat monolayer

In order to test the effects of the connectivity changes and also the active rheological law, respectively described in Sects. 2.2.2 and 2.3.1, we have simulated the stretching of a flat square monolayer with dimensions $(L_x, {L_z})=(10,11)$, and subjected to an increasing displacement $u_z$, $0\le u_z\le 20$ at the end $Z=11$, with the end $Z=0$ fixed (see Fig. 6).

Fig. 6

Example of flat monolayer. Top Initial geometry. Bottom deformed geometry

We have analysed the following two material models:

• M1: $\gamma =0$. Pure elastic material with $k=0.8$.

• M2: $\gamma =0.8$. Elastic material with $k=0.8$ and evolving resting length L.

We have measured the sum of all the reactions along direction Z for the nodes that are initially at the boundary $Z=11$. The evolution of this sum, denoted by $R_{TOT}$, is plotted in Fig. 7(a, b) for the two material choices M1 and M2. We have also tested the effect of allowing cell–cell remodelling. When remodelling is allowed, we have in turn implemented two possible regimes: with stress relaxation and with no relaxation, which corresponds to update the resting length of the new elements according to the expressions in Table 1.

Fig. 7

Total reaction at the boundary with increasing imposed displacements for the flat monolayer. a Purely elastic model, b rheological model with active lengthening. The symbols ($\times$) and ($+$) indicate the number of connectivity changes per time-step for the two simulations with remodelling

Table 1 Update of length L for new bar elements when remodelling is activated, with and without stress relaxation

It can be drawn from the trends of the curves in Fig. 7 that the stress relaxation does not have a strong effect on the total reaction, while the remodelling rate $\gamma$ does have an impact in the non-linear response, introducing by itself an apparent stress relaxation. Figure 7(a, b) also indicate with the symbols ($\times$, no relaxation) and ($+$, with relaxation) the number of connectivity changes that take place during the simulation for the cases when remodelling is activated. The height of the symbol corresponds to the number of connectivity changes divided by 10 for each time-step. It is clear that the jumps of the response are directly correlated with the changes of neighbours between cells. Since these are in general independent on the relaxation regime of the remodelling, it can be inferred that the relaxation of $R_{TOT}$ is mostly due to the presence of these new connections, which has a stronger contribution on the minimisation of the stored elastic energy than the reduction of the stretching onto the new directions when relaxation is allowed.

In order to demonstrate the equivalence between the active rheological model and the Maxwell model, we have applied the displacement history shown in Fig. 8a, and plotted the corresponding total reaction in Fig. 8b, which indeed relaxes to zero. It has been observed in laboratory experiments that monolayers do relax, but to a non-zero stress level [15]. This is associated to the elastic component of the polymeric structure of the cytoskeleton, and its inherent contractility. In our active model, which mimics the Maxwell model, the reactions tend to a zero value. In future works we envision to include this elastic character of the response with more sophisticated rheological laws.

Fig. 8

a Time history of the applied strain. b Evolution of the total reaction as a function of time for the flat tissue and active rheological law

We have compared in Fig. 9 our numerical results with the experimental measurements in [16]. This figure shows the non-linear response of the tissue during an increasing applied displacement, which induced a loss of cell–cell integrity. In our case, this tissue rupture is represented by a decrease in the number of cell–cell connectivities. The trend of the two curves agree qualitatively up to the measured experimental extension. Due to the adopted linear elastic model, our simulations do not capture the initial stiffening of the material. This may be recovered by modifying the quadratic potential in (1).

Fig. 9

Comparison between the averaged stress value in the experimental results [16] and using the numerical model with a linear elastic material ($k=9$) and connectivity changes

3.2 Curved monolayer

We have tested a curved monolayer that has the shape of half a cylinder, with the axis on the Z direction, and with the same number of nodes and similar dimensions: the projected area occupies the same domain $D=\{(X,Z) | 0\le X\le 10, 0 \le Z \le 11\}$ (see Fig. 10). The monolayer is stretched along direction Z, up to the diplacement $u_{z}=20$.

Fig. 10

Example of curved monolayer. Top Initial geometry. Bottom deformed geometry

The same material models and the mapping of the surface described in Sect. 2.3.2 has been employed in order to apply the Delaunay triangularisation. Figure 11 shows the evolution of the total reaction $R_{TOT}$ and the number of connectivity changes. Similarly to the previous case, the trend of the curves is hardly affected by the update of the active length. However, in the three-dimensional case, the effect of remodelling has a more acute effect on the reduction of the total reaction than in the two-dimensional case, although this effect is only observed for larger imposed displacements.

Fig. 11

Total reaction at the boundary with increasing imposed displacements for the curved monolayer. a Purely elastic model, b rheological model with active lengthening

The reduction of $R_{TOT}$ may be attributed to two contributions. First, the sides $Z=0$ and $Z=11$ are fixed on the $X-Y$ plane, and since Delaunay triangulation minimises the aspect ratio of the resulting triangles, no elongated triangles can be created. As a result, larger cells are built in the middle of the monolayer, which reduces the number of bars per cross-section and consequently also the resulting stiffness of the monolayer. Second, and although the number of cells is constant, these are intercalated as the stretching process takes place: new connections are being created transversally to the stretching direction (X axis), which replace bars aligned on the Z direction. We recognise that the first contribution is unrealistic, and we are currently extending the model in order to imposing kinematic constraints that preserve the total volume of each cell. The second contribution, the intercalation process, has been observed in real embryogenetic movements of curved monolayer such as the endoderm of Drosophila Melanogaster during germ band extension [19]. We notice that this effect is more pronounced in the three-dimensional case than in the flat monolayer, which is restrained to remodel on a flat surface.

We finally point out that the stress relaxation, due to either the active rheological model or the intercalation process, solely takes place along the direction of stretching. The material thus remodels anisotropically, as it has been observed on tissues during cell motility [45].

4 Conclusions

We have shown that the non-linear response of epithelial cells can be simulated by modelling the relative position of cell centres and their topological changes without unnecessarily dealing with complicated rheological laws at the cells boundaries. In the tests analysed here, the plastic response of tissues has been reproduced by implementing a cell reorganisation of monolayers (connectivity changes) in two and three dimensions, and also by adding a strain dependent intra-cellular active lengthening. In addition, and as a result of the stretching process, anisotropy emerges due to the unsymmetrical boundary conditions being applied.

In the examples analysed here, it has been shown that even with a purely elastic material, the tissue relaxes due to the intercalation process. Although this relation between tissue relaxation and cell intercalation is experimentally well known [19, 39], the model described here may help to quantify this relationship, and also predict significant differences when it occurs on a flat or on a curved monolayer.

Further mechanical analysis of the cell–cell boundaries and implementation of the kinematic constraints is currently being investigated. This may be achieved by imposing mechanical equilibrium and the volumetric constraints onto the Voronoi tessellation. We also aim to include more sophisticated rheological laws in order to simulate the observed softening and hardening response of monolayers, in conjunction with cell proliferation. The latter may be simulated by adding new cells (particles) to stretched bar elements or elongated Voronoi regions.

Appendix

1.1 Proof of the uniqueness of active length tensor ${{\mathbf {L}}}^i$

We will here prove that the solution of the system of Eq. in (9) at a given node i is unique if the vectors ${\varvec{n}}_j$ that define the cell–cell connectivities at node i and that form matrix ${{\mathbf {A}}}$ span ${\mathbb {R}}^{n_{sd}}$.

By definition, matrix ${{\mathbf {A}}}$ is semi-positive definite (SPD) and symmetric. We will here prove that matrix ${{\mathbf {A}}}$ is in fact positive definite (PD) when the vectors ${\varvec{n}}_j$ span ${\mathbb {R}}^{n_{sd}}$, and hence gives a unique solution. Matrix ${{\mathbf {A}}}$ is PD if the following implication holds:

$$\begin{aligned} \bar{{{\mathbf {L}}}}^i{}^T{{\mathbf {A}}}\bar{{{\mathbf {L}}}}^i=0\Rightarrow \bar{{{\mathbf {L}}}}^i=0. \end{aligned}$$

(10)

But, by setting ${\varvec{l}}^{ij}= {{\mathbf {L}}}^i{\varvec{n}}_j$, we have that,

$$\begin{aligned} \bar{{{\mathbf {L}}}}^i{}^T{{\mathbf {A}}}\bar{{{\mathbf {L}}}}^i =\sum _{j=1}^n{{\mathbf {L}}}^i{\varvec{n}}_j\cdot {{\mathbf {L}}}^i{\varvec{n}}_j=\sum _{j=1}^n||{\varvec{l}}^{ij}||^2. \end{aligned}$$

So,

$$\begin{aligned} \sum _{j=1}^n{{\mathbf {L}}}^i{\varvec{n}}_j\cdot {{\mathbf {L}}}^i{\varvec{n}}_j=0\Rightarrow {\varvec{l}}^{ij}={\mathbf {0}}, \forall j, \end{aligned}$$

(11)

i.e., implication in (10) may be also expressed as,

$$\begin{aligned} \sum _{j=1}^n{{\mathbf {L}}}^i{\varvec{n}}_j\cdot {{\mathbf {L}}}^i{\varvec{n}}_j=0\Rightarrow {{\mathbf {L}}}^i{\varvec{n}}_j\cdot {\varvec{e}}_k=0, \forall j,k. \end{aligned}$$

Setting ${\varvec{n}}_j = \alpha _j^l{\varvec{e}}_l$ we have that,

$$\begin{aligned} {{\mathbf {L}}}^{i}{\varvec{n}}_j\cdot {\varvec{e}}_k =\alpha _j^l{{\mathbf {L}}}^i{\varvec{e}}_l\cdot {\varvec{e}}_k =\sum _l\alpha _j^l L^i_{kl} \end{aligned}$$

with $L^i_{kl}={{\mathbf {L}}}^i{\varvec{e}}_l\cdot {\varvec{e}}_k$ the component kl of tensor ${{\mathbf {L}}}^i$. Therefore, Eq. (11) is equivalent to,

$$\begin{aligned} \sum _l\alpha _j^l L^i_{kl} =0, \forall k,j. \end{aligned}$$

By denoting by ${{\mathbf {L}}}^i_k$ the k-th row of the tensor ${{\mathbf {L}}}^i$, this condition may be also expressed as,

$$\begin{aligned} {\varvec{n}}_j\cdot {{\mathbf {L}}}_k^i =0,\forall k,j, \end{aligned}$$

that is, the vectors ${\varvec{n}}_j$ are orthogonal to each one of the rows of ${{\mathbf {L}}}^i$. If the vectors ${\varvec{n}}_j$ span the whole space ${\mathbb {R}}^{n_{sd}}$, this is only possible when ${{\mathbf {L}}}^i_k= 0$, as we wanted to prove. If the tensor $\bar{{{\mathbf {L}}}}^i$ is not assumed symmetric, the uniqueness of the solution can be also proved by considering an alternative matrix ${\mathbf {N}}_j$ in the definition of matrix ${\mathbf {A}}$, but following very similar steps.