Abstract
As sea level is rising along many low-lying and densely populated coastal areas, affected communities are investing resources to assess and manage future socio-economic and ecological risks created by current and future sea level rise. Despite significant progress in the scientific understanding of the physical mechanisms contributing to sea level change, projections beyond 2050 remain highly uncertain. Here, we present recent developments in the probabilistic projections of coastal mean sea level rise by 2100, which provides a summary assessment of the relevant uncertainties. Probabilistic projections can be used directly in some of the decision frameworks adopted by coastal engineers for infrastructure design and land use planning. However, relying on a single probability distribution or a set of distributions based upon a common set of assumptions can understate true uncertainty and potentially misinform users. Here, we put the probabilistic projections published over the last 5 years into context.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
For the more than 600 million people living in low-elevation coastal areas less than 10 metres above sea level, sea level rise is one of the primary damaging aspects of climate change (IPCC 2014). The global coastline is characterized by high population density, a substantial fraction of global economic activity and the presence of critical infrastructure (IPCC 2014, Hallegatte et al. 2013; Hinkel et al. 2014). Changes in mean sea level affect the height and frequency of extreme water levels (Woodworth et al. 2011), thus altering flood and inundation risks for low-lying areas (Nicholls and Cazenave 2010). Impact and risk assessment, adaptation policies and long-term decision-making in coastal areas are crucially informed by projections of coastal mean sea level and extreme water level events. (IPCC 2014; Nicholls et al. 2014; Hinkel et al. 2014, 2015; Kopp et al. 2014, 2017; Jevrejeva et al. 2016, 2018; Le Cozannet et al. 2017a). There is thus considerable societal demand for projections of future mean sea level and extreme water level changes with well communicated uncertainties.
Since the Intergovernmental Panel on Climate Change’s Fifth Assessment Report (IPCC AR5), there has been considerable progress in observing mean sea level changes and the different components contributing to it (Cazenave and WCRP Global Sea Level Budget Group 2018). Advances in climate and ice sheet models (Griffies et al. 2016; Nowicki et al. 2016; Nowicki and Seroussi, 2018) have also led to improved understanding of the oceanic and cryospheric response to radiative forcing and better characterization of their associated uncertainties. Despite recent progress in climate change and sea level science, projections of long-term future sea level changes under different emissions scenarios remain highly uncertain, mainly due to the large uncertainty in estimates of future mass loss from the Greenland and Antarctic ice sheets. Recent publications reveal an increase in observed Antarctic sheet mass loss (e.g., Shepherd et al. 2018; Cazenave and WCRP Global Sea Level Budget Group 2018; Rignot et al. 2019), while model projections range widely (e.g., Ritz et al. 2015; Golledge et al. 2015; DeConto and Pollard, 2016; Edwards et al. 2019). These have fuelled a discussion about the increasing possibility of considerably higher future sea level rise than suggested in IPCC AR5 (Church et al. 2013a; Kopp et al. 2017; Horton et al. 2018; Garner et al. 2018). As a consequence, there has been an increase in the number of publications constructing regional and local mean sea level projections (e.g., Kopp et al. 2014, 2017; Grinsted et al. 2015; Slangen et al. 2016; Carson et al. 2016). This reflects the need for mean sea level rise projections suitable for risk assessment and decision-making by policymakers, planners, coastal engineers and general public in coastal areas (Hinkel et al. 2015, 2019).
Recent coastal and local sea level rise projections (e.g., Kopp et al. 2014, 2017; Grinsted et al. 2015; Jackson and Jevrejeva, 2016; Le Cozannet et al. 2017b) have moved away from IPCC AR5’s focus on median and central range projections (Church et al. 2013a; Slangen et al. 2014). IPCC AR5 focused particularly on the “likely range” of projections. Under the IPCC’s calibrated uncertainty language (Mastrandrea et al. 2010), likely refers to a probability of at least 66%. An exegesis by the authors of AR5′s sea level rise chapter (Church et al. 2013a) indicates that, in the context of sea level rise projections, IPCC AR5 ascribed a probability of about two-thirds to the likely range (Church et al. 2013b). However, for impact assessment, risk management and adaptation strategy in coastal areas there is a need for the low-probability, high-impact upper range of future sea level rise, which is not provided by AR5 IPCC “likely range” sea level projections.
Probabilistic sea level projections provide probability density functions (PDFs) that are conditional upon emissions pathways, which self-consistently project both likely values of mean sea level rise and the likelihood of high-risk, low-probability conditions such as those associated with rapid ice mass loss of Antarctica or Greenland which are physically poorly understood. Those projections explicitly labelled “probabilistic” include not only central or “likely” ranges, but also the tails of these distributions; Garner et al. (2018) empirically distinguish them as studies reporting more than three quartiles of a projected distribution. Probabilistic projections also provide a summary assessment of the relevant uncertainties, which are consistent with some of the decision frameworks used by coastal engineers for infrastructure design and land use planning (e.g., Hunter et al. 2013; Buchanan et al. 2016). In this paper, we also discuss that for many stakeholders, probabilistic projections require simplification into a range-spanning set of sea level scenarios (Nicholls et al. 2014; Hinkel et al. 2019). Unlike probabilistic projections, which are explicitly conditional upon emissions scenarios, sea level scenarios may or may not be tied to emissions scenarios (e.g., Representative Concentration Pathways) or other climate change scenarios (e.g., 1.5 °C above pre-industrial global mean surface temperature).
In this paper, we present an overview of recent work on probabilistic projections of changes in mean sea level and extreme sea levels by 2100. We discuss the user needs for multiple probabilistic sea level projections at the coast and the main challenges for coastal sea level projections including future changes in extreme sea levels.
2 Probabilistic Approach to Sea Level Changes
In many ways, the IPCC has become authoritative in assessing climate change; thus, unsurprisingly, its assessment, including the statements on uncertainties, influenced decision makers (Nicholls et al. 2014). A number of regional- and national-level assessments build upon the IPCC framework (e.g., Tran et al. 2016) or have developed their own along similar lines of reasoning, but often from a more national perspective (e.g., Katsman et al. 2011; NYPCC15; Hall et al. 2016). Notwithstanding the difficulties in producing them, probabilistic projections have been recognized as potentially useful information to support adaptation and mitigation since the 1990s (Titus and Narayanan 1995). This utility is due in part to the desire amongst the decision/planning community to gain insight into possible futures in which a low-probability, high-impact sea level rise occurs—discussed further in Sect. 4: Challenges for coastal sea level projections.
Several modelling frameworks exist to produce sea level projections. For example, process-based projections estimate the contribution of each process causing sea level rise (e.g., Katsman et al. 2011; Church et al. 2013a), while semi-empirical projections are simulated by reduced-form models calibrated to historical observations (e.g., Rahmstorf 2007, Jevrejeva et al. 2012; Kopp et al. 2016; Mengel et al. 2016). In a process-based approach, such as that used by Church et al. (2013a), various sources of information, including numerical simulations, are combined to model the evolution of different sea level components. Global mean sea level (GMSL) changes over time (t) are represented as the sum of projected sea level components, including thermostatic expansion (T), ice mass loss from different glaciers (GICi), ice mass loss from the Greenland Ice Sheet (GrIS), ice mass loss from the Antarctic Ice Sheet (AIS), often separated into East and West (EAIS and WAIS), and the contribution from land water storage (LWSj) changes:
In some studies, the individual PDFs of each term are considered independent. This assumption could result in underestimation of the upper tail of the projections (see Le Bars et al. 2018 for a review of dependence and correlation schemes used so far in the area of probabilistic sea level rise projections). In Church et al. (2013a), the sum of these components, with their uncertainties, provided an estimate of the median and 90% range (5th–95th percentiles) of sea level change under each representative concentration pathway (RCP) scenario (Moss et al. 2010). This range was then assessed as a likely range (~ 2/3 probability) within the IPCC framework. Different research groups have taken alternative approaches to tackling this interpretation to “fill in” the remaining approximately one-third of the distribution (e.g., Kopp et al. 2014, 2017; Jevrejeva et al. 2014; Grinsted et al. 2015; Jackson and Jevrejeva, 2016; Le Cozannet et al. 2017b).
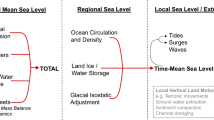
Regional sea level (RSL) rise displays complex spatial patterns due to atmosphere/ocean dynamics and the gravitational, rotational and crustal deformation effects of the redistribution of ocean mass, associated with ice loss from mountain glaciers, ice mass changes in the Greenland and Antarctic ice sheets and changes to land–water storage by artificial reservoirs and groundwater extraction.
RSL projections at locations x can be represented as:
where RSL(x,t) is relative sea level, DSL(x,t) is the dynamic sea level contribution and \( F_{{{\text{GIC}}_{i} }} \), FGrIS, FWAIS, FEAIS and \( F_{{{\text{LWS}}_{j} }} \) are the normalized gravitational, rotational and deformational fingerprints associated, respectively, with different glacial regions, GrIS, WAIS, EAIS and different land water storage regions. Bkgd references to background processes, unassociated with contemporary climate change that contribute to local sea level changes; in some projections, this includes only glacial isostatic adjustment (GIA), whereas in others it includes localized processes such as sediment compaction.
In general, the process-based modelling approach for regional sea level projections sums the contribution of sea level components. The mass contribution (e.g., glaciers, ice sheets, land water) is scaled by spatial “fingerprints” associated with gravitational, deformation and rotational effects (e.g., Mitrovica et al. 2001). In studies prior 2013 (e.g., Katsman et al. 2011), contributions from Greenland and Antarctica ice sheets are represented by “low” and “high” (“modest” and “severe” in Katsman et al. 2011) scenarios, mainly due to lack of ice sheet model simulations of ice mass loss from ice sheets with emission or climate scenarios. The RSL changes associated with dynamic sea level effects are determined from an ensemble of global climate models, with the spread between individual model ensemble members often used as an estimate of the uncertainty. This approach was taken by Katsman et al. (2011) and Slangen et al. (2014).
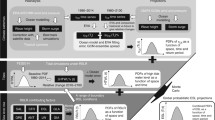
Kopp et al. (2014), Grinsted et al. (2015) and Jackson and Jevrejeva (2016) further developed this approach by embedding it into a probabilistic framework, such that the global mass and volume contributions were represented as PDFs (Fig. 1). The PDFs were then sampled using a Monte Carlo approach (e.g., Kopp et al.. 2014; Grinsted et al. 2015) or a semi-analytical method (De Winter et al. 2017), and draws across components to yield total sea level at either a global scale (Fig. 1) or individual locations (Fig. 2). These summed draws define a new PDF for a given point in time and space, thus providing the probabilistic regional sea level projections.
Probability density functions for global sea level and its components in 2100 for two scenarios: warming of 1.5 °C and RCP8.5 (after Jevrejeva et al. 2018). Note that the land-based water component is scenario independent
Kopp et al. (2014), Grinsted et al. (2015) and Jackson and Jevrejeva (2016) utilized the expert elicitation by Bamber and Aspinall (2013) to introduce non-Gaussian uncertainty into the tails of Greenland and Antarctic ice sheet contributions. Kopp et al. (2014) used information about tail shape, while retaining the central range of AR5; Grinsted et al. (2015) and Jackson and Jevrejeva (2016) used the full distribution of Bamber and Aspinall (2013). Both cases yielded a heavy-tailed distribution for the Antarctic ice sheet and hence total sea level. Additional interpretation of Bamber and Aspinall (2013) was made by De Vries and Van de Wal (2015; see also response by Bamber et al. 2016) and was consequently used by de Winter et al. (2017). Several other probabilistic projections have been made based on a recent Antarctic ice sheet modelling studying by DeConto and Pollard (2016) (e.g., Kopp et al. 2017).
In a scaling approach (Perrette et al. 2013), authors sample distributions for the global contributions and use a Monte Carlo to combine these with the spatial fingerprints. The spread mostly comes from the sampled global distributions (Model for assessment of greenhouse gas induced climate change (MAGICC) probabilistic projections), whereas the global circulation model (GCM) spread only imprints in the scaling relationships (ocean heat uptake to steric expansion, global mean temperature to local ocean dynamic). In fact, this study describes a regional SLR emulator, to make flexible, probabilistic projections, in the same spirit as Nauels et al. (2017). Probabilistic projections have also been constructed using semi-empirical sea level models (e.g., Rahmstorf 2007, Jevrejeva et al. 2012; Kopp et al. 2016; Mengel et al. 2016), simple climate models (e.g., Goodwin et al. 2017) and statistical emulators (e.g., Nauels et al. 2017). Because these approaches are not directly dependent upon the RCP-driven projections of global climate models, they are more flexible with respect to scenarios considered (e.g., Kopp et al. 2016; Jevrejeva et al. 2018; Nauels et al. 2017). One limitation of most semi-empirical approaches is that they simulate only global sea level. The advantage of all these methods is their computational efficiency and their ability to explore numerous future pathways with policy intervention (e.g., Rasmussen et al. 2018; Mengel et al. 2018). In all cases, these methods, when embedded into a Monte Carlo or Bayesian framework, allow projection of a distribution under the assumptions of the model formulation.
3 Sea Level Projections and Scenarios: A User Perspective
3.1 Current Uses of Sea Level Projections and Scenarios
Coastal adaptation practitioners have had access to sea level information for decades (Hoffman et al. 1983). While the first probabilistic projections were produced nearly 25 years ago (Titus and Narayan, 1995), current adaptation planning largely relies on discrete scenarios, often informed by IPCC projections, defining possible future trajectories of sea level rise (Nicholls et al. 2014; Le Cozannet et al. 2017b). In some countries, sea level rise scenarios are defined at a national level and used across government agencies, as in the Netherlands (Van den Hurk et al. 2014). In other countries, such as the USA, sea level rise scenarios may differ amongst entities. For example, in the USA, the US Department of Defense (Hall et al. 2016), the US National Climate Assessment process (Sweet et al. 2017) and different states may employ different projections (see Hall et al. 2019, for a review). Furthermore, sea level rise scenarios can eventually be included in the regulation or design guidance, as in California, New York City or France (Rosenzweig et al. 2011; Le Cozannet et al. 2017b).
The overall process producing these sea level projections is driven by a demand of coastal users on the one hand and by efforts of the scientific community to produce these projections and transfer them to the practice of coastal adaptation on the other hand. In fact, the coastal engineering community has long used probabilistic approaches to estimate extreme water levels at the coast and design infrastructures with appropriate safety levels (e.g., extreme value analysis).
Probabilistic sea level projections are useful for analysing, understanding and communicating the cascade of uncertainties that propagate from sea level rise and other forcing factors throughout coastal impact models applicable at global to local scales. In this area, sensitivity analyses are especially useful to help identify input parameters or modelling assumptions that drive the variability of model outcomes such as the magnitude of shoreline retreat or the frequency and intensity of coastal flooding (e.g., Hallegatte et al. 2013; Hinkel et al. 2014). Typical sensitivity analyses are based on variance, which is relatively insensitive to the tail of the distribution. For that reason, as long as sea level projections considering Marine Ice Cliff Instability (DeConto and Pollard, 2016) are excluded (Fig. 3), the results of these variance-based sensitivity analyses remain relatively insensitive to different assumptions in probabilistic sea level projections, because projections mainly differ in their upper tail (Le Cozannet et al. 2015).
Projections of globally mean sea level rise (GMSL, in m) by 2100 under RCP8.5 represented in a cumulative distribution diagram. (Church et al. 2013a; Kopp et al. 2014; Jackson and Jevrejeva, 2016; Kopp et al. 2017; Le Bars et al. 2017). Here, the curve labelled as “Hunter et al. (2013), based on IPCC (Church et al. 2013a)”, is a modification of the median and likely range provided by Church et al. (2013a), following the interpretation of Hunter et al. (2013), which assumes a symmetric Gaussian extrapolation of the IPCC likely range and median values. DP16 is reference to the estimate of contribution from Antarctica ice sheet by DeConto and Pollard (2016), which is used in studies by Kopp et al. (2017) and Le Bars, et al. (2017); JJ16 is reference to Jackson and Jevrejeva, 2016 (including RCP8.5 scenarios, labelled as JJ16 RCP8.5 projection, and the high-end scenario, labelled as JJ16 High-end projection)
3.2 Dealing with Multiple Probabilistic Sea Level Projections: A User Perspective
Today, the processes that will cause sea level rise during the twenty-first century remain imperfectly understood. In particular, the dynamic response of the Antarctic ice sheet is a critical unknown, as its contribution to global sea level rise by 2100 could be either limited to a few tens of centimetres (Ritz et al. 2015), or reach one metre or more if ice shelf hydrofracturing and marine ice cliff instability lead to a dramatic increase in melt (DeConto and Pollard, 2016). Producers of probabilistic sea level projections need to choose which processes are included in their projections. Furthermore, they need to make assumptions about the dependencies between the different contributions of sea level rise. These choices can have a strong impact on the final probabilistic sea level projections produced for time periods after 2050 (Church et al. 2013a, Kopp et al. 2017; Le Bars, 2018), as well as on the coastal impacts to be expected.
Hence, several probabilistic sea level projections are available for users concerned with adaptation. Figure 3 displays a few probabilistic global sea level projections for RCP 8.5 in 2100 published recently. This figure is only for illustration, because coastal adaptation practitioners need sea level projections applicable locally and not global sums. However, this figure shows clearly that two very different subsets of probabilistic sea level projections coexist today:
-
Those assuming that Antarctic dynamics will be mostly driven by marine ice sheets instability (red curves in Fig. 3)
-
Those involving marine ice cliffs instability and ice shelf hydrofracturing (blue curves in Fig. 3).
At the level of the median, the difference between the two subsets of sea level projections is close to one metre. Importantly, coastal adaptation practitioners usually do not have the expertise to estimate the likelihood of the assumptions underpinning each sea level projections.
Instead of trying to identify a single probabilistic sea level projection corresponding to a “best estimate”, coastal adaptation practitioners may choose to consider all existing probabilistic sea level projections or a set of projections that span the range of probability distributions, for example, in order to test the robustness of their adaptation options against a suite of probabilistic projections (Horton et al. 2018). It follows that for coastal adaptation practitioners, the challenge is to identify the particular probabilistic projection that is best aligned with their level of risk aversion (Buchanan et al. 2016; Hinkel et al. 2019). For example, managers of critical infrastructures with long lifetimes (e.g., nuclear power stations) may consider the most pessimistic probabilistic projection in order to test their resilience to the full range of future possible sea level changes. These different probabilistic projections could be used within flexible adaptation pathways approaches (e.g., Haasnoot et al. 2013), employing probability distributions for the time period of good agreement (through about 2050) and developing structured contingency plans to follow as the fate of future sea level becomes clearer.
3.3 Strengths and Weaknesses of Probabilistic Projections in Operational Contexts
Today, many potential users of probabilistic projections have questions regarding the maturity and the transferability of probabilistic projections to operational practices and still remain reluctant to move from scenarios to probabilistic projections. For example, suggestions to consider probabilistic projections or scenarios besides the regulatory 60-cm sea level rise scenario defined by regulation for 2100 in France have not surpassed the level of technical reports so far (BRGM 2018). This example, amongst others, shows that scenarios are used in the practice of adaptation (Le Cozannet et al. 2017a).
Building on the review of current coastal climate services conducted within the framework of the World Climate Research Programme (WCRP) Grand Challenge on sea level rise, it appears, however, that probabilistic projections could be directly useful for several applications (Table 1), with the caveat that relying on a single probabilistic projection may not be sufficient (see Fig. 3). The first line in this table highlights that using existing probabilistic projections in combination with global coastal impact models to assess the benefits of mitigation in coastal area is a straightforward research avenue. Probabilistic projections can also be used to quantify and rank sources of uncertainties and identify which research is needed to reduce uncertainties in coastal impacts and adaptation assessments. Other needs listed in Table 1 relate to global or local adaptation. In this area, there is a need for probabilistic prediction (i.e. probabilistic description of sea level rise unconditional to greenhouse gas emissions) in order to address adaptation needs and optimize investments to prevent chronic flooding occurring during the highest tides, as this is increasingly occurring in low-lying sheltered areas (Table 1, line 4; Sweet and Park, 2014). The needs in this area may be that further efforts involving users with sea level information providers to co-design appropriate projections will be essential in this area.
4 Challenges for Coastal Sea Level Projections
The primary sources for a sea level rise beyond one metre this century are the polar ice sheets though a key aspect of the uncertainty is how they will respond to further warming. This is reflected in a significant spread amongst the research community’s opinion (e.g., Bamber and Aspinall, 2013), a wide range of estimates for potential ice mass loss simulations (e.g., DeConto and Pollard, 2016; Edwards et al. 2019; Golledge et al. 2015; Ritz et al. 2015; Church et al. 2013) and the latest estimates of ice mass loss from observations (e.g., Shepherd et al. 2018; Cazenave and WCRP Global Sea Level Budget Group 2018; Bevis et al. 2019; Rignot et al. 2019). The current state of ice sheet modelling and reasons for the large uncertainty is presented by van de Wal et al. (2019) and discussed in several recent publications (Horton et al. 2018; Kopp et al. 2017; Jackson et al. 2018).
While the future of the ice sheets remains a prominent uncertainty, other challenges for coastal sea level projections remain. Current climate and Earth system models (e.g., Coupled Model Intercomparison Project Phase 5 (CMIP5, Taylor et al. 2012)), used for sea level projections, lack both the horizontal and vertical resolution to resolve small-scale processes, which may be important for sea level rise. One such a challenge relates to the ability of ocean models to simulate realistic sea surface height (changes) in coastal areas. Part of the reason for this issue is the coarse resolution (the average across CMIP5 models is ~ 1°) compared to the length scale desirable for coastal analysis. Most of the models in CMIP5 are not eddy permitting and require parameterizations for eddy-induced transport of mass, heat and freshwater (Landerer et al. 2014; Griffies et al. 2016). This issue is compounded by coarse bathymetry on the continental shelf and the lack of physical mechanisms modelled in large-scale climate simulation driving coastal sea level variability on time scales of seasons to years.
In addition, mean sea level rise projections are often focused on long-term averages over extended periods. In most coastal locations (Carson et al. 2016, Church et al. 2013a), observations reveal the presence of strong seasonal, interannual and decadal variability. Carson et al. (2016) show that internal variability is also present in individual simulations of the models, but the variance in the models is underestimated (Hay et al. 2013) (Fig. 4).
Observed (black, based on monthly mean tide gauge data) and projected (thick blue line represents the median and blue shows 5–95th percentile) sea level changes with RCP8.5 at Newlyn (UK). Note that projections are usually presented as mean annual values excluding the temporal variability at higher frequencies
Ocean dynamics can be misallocated or appear as diffuse features whose signal is smeared coastward. For example, Landerer et al. (2014) showed the meridional maximum sea surface height gradient of the Antarctic circumpolar current was shifted equatorward by ~ 4 degrees in CMIP5 models, which was correlated with a positioning bias in the zonal wind stress maxima. Many of these dynamic issues are likely to be resolved by using high resolution ocean models (e.g., Roberts et al. 2016) that resolve long-standing biases in the mean ocean state, which is critical for reliable climate projections.
One key issue is related to the combining of regional sea level projections with local land motion to project local relative sea level change (e.g., Kopp et al. 2014). A crucial shortcoming is that at present there is no global, coastal field of continuous subsidence or uplift. While simulations of the global field of global field of glacial isostatic adjustment (GIA) are available from a number of research groups, it forms only one component of uplift (Fig. 5) and is frequently presented without uncertainties in the context of probabilistic projections. At local scales, the uncertainty in GIA may be up to 6 mm yr−1, which is a substantial fraction of the total rates of regional sea level at those locations even for high scenarios at the end of the century. For the global mean, it is a small source of uncertainty.
Difference between the GIA from ICE6G-VM5a (Peltier et al. 2015) and ICE5G-VM2 (Peltier 2004) at coastal locations. Choice of GIA model is critical for the locations in North America and Europe, where the difference could be up to 6 mm·yr−1 (North American coast) and up to 3 mm·yr−1 (European coast). The largest differences occur at places where sea level will drop substantially due to GIA which are rather sparsely populated (Hudson Bay and Barents Sea), while for most locations of interest with a substantial GIA signal (US East Coast, Western Europe, etc.), the uncertainty is often only on the order of 1 mm·yr−1 or less
Besides GIA, natural and anthropogenic processes such as tectonics, volcanism, groundwater extraction and mining activity can cause vertical land motion. The land motion resulting from these processes is difficult to model quantitatively; thus, coastal adaptation often relies on geodetic observations such as permanent Global Navigation Satellite System (GNSS) stations, levelling surveys or synthetic aperture radar interferometry (InSAR) to estimate the future contribution of uplift/subsidence to sea level rise (Wöppelmann and Marcos, 2016). These data sets are complementary: for example, the pointwise measurements in a geocentric framework obtained from GNSS records can be complemented with levelling or InSAR deformation maps, which are relative to a local terrestrial framework. Ultimately, the combination of these techniques allows one to obtain up to sub-millimetre estimates of coastal vertical land motions (e.g., Dixon et al. 2006; Erban et al. 2014; Wöppelmann et al. 2013).
Coastal vertical land motion remains a major unknown when it comes to producing sea level projections applicable to individual locations because (e.g., Raucoules et al. 2013): (1) maps of vertical land motion are often lacking; (2) nonlinear vertical land motion remains difficult to predict. All projections that include non-GIA vertical land motion implicitly assume that rates occurring over the observational record will continue in the future (e.g., Kopp et al. 2014), though in some cases rates of vertical land movement are closely tied to human activities (e.g., groundwater extraction) and exhibit significant variability over the historical period. In areas where vertical land motion is fairly steady but the observational record is short, geological data can in some cases provide a useful additional constraint (e.g., Horton et al. 2018). In the coming years, the SAR Sentinel 1 data, which are characterized by a more frequent revisit time and larger swaths, are expected to produce nation-wide ground deformation maps, at least in Europe.
5 Probabilistic Projections for Coastal Extremes
For coastal communities, knowledge about the expected changes in the height and frequency of extreme sea level (ESL) events is of importance to decide on sufficient and cost-effective adaptation strategies in coastal communities (Hinkel et al. 2014). The height and return frequency of ESL events are mostly driven by tides, storm surges, waves and river discharge (Wahl et al. 2015; Ward et al. 2018; Williams et al. 2016; Melet et al. 2018). Since for most locations mean sea level is expected to change relative to the present-day level, the height and frequency of ESL events relative to present-day mean sea level at a specific location are expected to change as well. Furthermore, the characteristics of tides, surges, waves and river discharge can be affected by changes in the climate system. All aforementioned processes are subject to uncertainty, and probabilistic projections of the height and frequency of future extreme water level events are needed to incorporate these uncertainties.
Changes in ESL events are often expressed as changes to the return curves. A return curve shows height above present-day mean sea level (or another reference level) as a function of the return period (inverse of the expected frequency) of ESL events that exceed that height. Figure 6 shows estimated return curves for three coastal locations. These return curves can be derived from tide gauge observations or from hydrodynamic models. Changes in ESL events due to climate change will result in a changing return curve, relative to present-day mean sea level. These changes can be caused by changes in mean sea level or by changes in the characteristics of tides and surges. The green lines in Fig. 6 show the effect of a 30-cm rise of MSL on the return curves: they shift vertically, which results in higher exceedance frequencies for a given height above present-day mean sea level.
Example of the statistical method to project future ESL events for three stations. The black crosses show the height and return frequency of observed ESL events from tide gauge records (Woodworth et al. 2016). The blue lines show the return curve for the Gumbel (light) and generalized extreme value (GEV, dark) distribution fitted to the annual maximum water levels under present-day conditions. The green lines show the return curve for a sea level rise of 30 cm. These lines have been computed following the procedure in Wahl et al. (2017). The red arrow shows the 100-year allowance, and the purple arrow denotes the 100-year amplification factor
Two quantities are widely used to characterize these changing return curves. The first one is the frequency amplification factor (AF) (Tebaldi et al. 2012; Buchanan et al. 2016). The AF describes how many times more or less often a specific event is expected to occur in a future scenario compared to present-day conditions. This factor is a metric of the increase in flood risk when assets and defence structures are not adapted to sea level changes. The purple arrows in Fig. 6 show these changes in return frequencies, from which the amplification factor can be directly inferred. The second quantity is the sea level allowance, which describes the height change (unit metres) for which the projected exceedance frequency stays constant under sea level changes (Hunter 2012; Hunter et al. 2013; Buchanan et al. 2016; Slangen et al. 2017). The red arrow in Fig. 6 depicts the allowances. Projections of future ESL events have been traditionally modelled using statistical frameworks based on high-frequency tide gauge observations. Another approach consists in using hydrodynamical models to provide estimate of extreme water levels and flooding heights and velocities where no tide gauge records are available. Here, we discuss both modelling and statistical approaches.
5.1 The Statistical Approach
The statistical approach is grounded on the assumption that the distribution of water level extremes relative to the mean sea level do not change significantly. It is thus assumed that the tidal, wave and storm surge regime does not change significantly in a future climate. Observations over the last century provide support for this assumption, since variations in the occurrence of ESL events have been dominated by changes in mean sea level (Menendez and Woodworth 2010), although the changes in the climate system over the last century were significantly smaller than those foreseen in the twenty first century.
Critical in the approach is the fitting of the characteristics of ESL events with an extreme value distribution (EVD) to the tail of high-frequency sea level observations, generally obtained from high-frequency tide gauge records. Since tide gauges are often mounted in stilling wells or use similar low-pass filtering techniques, and the sampling frequency is typically a few minutes or more, the effects of waves are commonly not included in this type of analysis. Commonly used distributions are the Gumbel, generalized extreme value and generalized Pareto distributions (Wahl et al. 2017). These distributions are fitted to a number of extreme events, which are determined using a threshold approach or the annual or monthly highest values. These distributions all have a location parameter, which relate the height of a typical ESL event to mean sea level. To simulate ESL events under a future scenario, the location parameter is changed by the projected mean sea level change.
The curves in Fig. 6 have been computed using the GEV and Gumbel distributions. The shape of the return curve has a profound effect on the resulting amplification factors (AFs): for locations where the ESL events have an upper limit, such as in Honolulu, small changes in mean sea level lead to large amplification factors. In this example, the distribution parameters and mean sea level change are considered deterministic. Various methods have been derived to compute probabilistic estimates of the allowances and amplification factors. Hunter et al. (2013) computed allowances for a global set of tide gauge locations with the uncertainty in mean sea level projections taken into account. As a consequence, the allowance is always larger than the projected median mean sea level change. This method can also be applied to mean sea level projections with non-Gaussian confidence intervals (Slangen et al. 2017). A further extension of the concept has been introduced by Buchanan et al. (2016) and Rasmussen et al. (2018) who also combine uncertainty in the projected MSL changes with uncertainties in the fitted EVD parameters into account when computing allowances and AFs.
The advantages of the statistical methods are the low computational costs, the ease of implementation and inherent consistency with the observational record. When using observed ESL events, no direct care has to be taken of the possible joint probability of the individual processes, such as compound river-discharge–surge–waves–tide events. A limitation is that the available tide gauge records only sparsely cover the global coastline, with large parts of the global coasts ungauged, especially along the African coast (Woodworth et al. 2016). In addition, the length of the tide gauge records is generally only about a few decades, and the EVD is thus fitted through a limited number of ESL events. One way to use the short observational records more effectively is to separate the observations into a tide and surge component, which could uncover surges that occurred during low tides (Tawn et al. 1989; Tawn 1992; Batstone et al. 2013; Mazas et al. 2014). Since tides and surges can be dependent, the distributions of tides and surges cannot be added directly. The skew surge, which is the difference between the highest observed sea level and the predicted tidal high water, instead of the surge height, can be used as a good estimate of the tide-independent surge level (Williams et al. 2017).
Furthermore, the treatment of the data and the choice of a specific EVD and which water level extremes are used to fit the EVD have a considerable impact on the estimated return frequencies (Arns et al. 2013; Wahl et al. 2017), especially for events with small return frequencies. The two distributions shown in Fig. 6 show this divergence at low frequencies, which strongly affects the estimated return levels at those frequencies. Another challenge for the statistical method is the modelling of ESL behaviour in locations that are prone to tropical cyclones and hurricanes. These events are very rare, but can generate very high surge levels. The highest observed surge in Charleston in Fig. 6 was caused by Hurricane Hugo in 1989. The EVD does not adequately model these events, and for locations prone to similar events, the statistical method likely underestimates the flood frequencies. Also in regions not affected by these events, the inclusion of single surge events could have a significant impact on the projected EVD behaviour (Dangendorf et al. 2016).
5.2 Towards Global Hydrodynamical Modelling of Extreme Sea Level Events
To obtain estimates of ESL changes along ungauged coastlines, and to avoid the assumption that the ESL characteristics are invariant under future changes in the climate system, the use of hydrodynamic models to project future changes has gained popularity over the last few years (Wahl, 2017). Multiple studies show that the assumption of invariant ESL behaviour is generally not valid: from regional to local scales, mean sea level changes cause changes in tidal regimes (Pickering et al. 2017; Du et al. 2018), surges (Arns et al. 2017) and waves (Vitousek et al. 2017; Melet et al. 2018) so detailed coastal modelling is required for accurate coastal impact assessments (e.g., Barnard et al. 2019). Additionally, various environmental models indicate future changes in tropical cyclones, wind patterns and river discharge, which will modulate surge and wave conditions in the regions affected by these changes (Nohara et al. 2006; Wang et al. 2014; Piecuch et al. 2018).
By replacing the observed present-day ESL curves and using model results rather than a shift in the location parameter to project future ESL characteristics, the aforementioned limitations due to sparse tide gauge records can be resolved. The improved resolution of atmospheric reanalysis data sets and hydrodynamical models have been used to reconstruct present-day tide and surge levels during extreme events (Muis et al. 2016, 2017). Regional ESL projections have been developed for the German and European coastlines: Arns et al. (2017) forced a hydrodynamic model of the German Bight with updated mean sea level projections and found that due to the nonlinear response of tides, waves and surges to mean sea level changes in most locations, the changes in required coastal design heights exceeded the mean sea level change with an average of about 50 per cent. For RCP scenarios Vousdoukas et al. (2016) used wind fields from CMIP5 model simulations and global mean sea level projections to estimate ESL changes, finding that changes in wind patterns result in higher ESL projections along a majority of the European coastlines.
Recently, two studies investigated the global changes in ESL characteristics based on hydrodynamic models. In the first study by Vitousek et al. (2017), a combination of tide, surge and wave models were used to estimate present-day ESL return curves on a global grid. They subsequently combined these return curves with regional mean sea level projections to derive a grid of expected amplification factors to obtain a global estimate of ESL change projections. Vousdoukas et al. (2018) built on this approach by explicitly modelling the changes in surge, tide and wave characteristics that result in changes in mean sea level and wind forcing under various climate scenarios. Changes in ESL characteristics and the accompanying confidence intervals were derived using a Monte Carlo approach. They found that under both RCP4.5 and RCP8.5 scenarios, AFs above 100 are expected along most of the world’s coastlines. On average, the largest changes in ESL are driven by regional mean sea level changes. They also found that the mean sea level changes form the largest source of uncertainty for determining future ESL changes.
The use of models to project future changes in ESL behaviour at broad scale is a recent area of research, and not all relevant processes, such as river discharge, are included in the models. Since ESL events are often a combination of multiple contributing processes, the probability of these events is based on the joint probability of the individual processes, which are often not independent (Wahl et al. 2015; Little et al. 2015), and some processes, such as local subsidence and changes in river discharge, are not present in the current generation of hydrodynamic models. Similar to challenges faced by the statistical model, tropical regions still pose questions for hydrodynamic models, which is partially caused by the atmospheric reanalysis products whose resolution generally falls short to simulate the large gradients in winds during tropical hurricanes and cyclones. A solution to this problem is to combine the hydrodynamic model with synthetic cyclone forcing. Using this approach, Haigh et al. (2014a, 2014b) were able to compute an exceedance curve for the Australian coastline which is subject to both tropical and extratropical storms and in agreement with tide gauges in the region. Synthetic tropical cyclones have also been used in studies of the New York City area (e.g., Garner et al. 2017) and La Réunion island (Lecacheux et al. 2012).
6 Ways Forward
6.1 Probabilistic Sea Level Projections at the Coast
In this review, we have demonstrated that probabilistic sea level projections in coastal areas are a valuable solution and a step forward for the risk assessment and decision-making of stakeholders, providing a probability density function, conditional upon emissions, that self-consistently projects likely outcomes and also the likelihood of high-risk, low-probability states of the world. However, there are several challenges for probabilistic sea level projections in coastal areas. In addition to the uncertainties in global sea level projections, e.g., ice mass loss from ice sheets in Greenland and Antarctica (Church et al. 2013a; Jevrejeva et al. 2014) and the large uncertainties in regional sea level projections (e.g., due to ocean circulation), which have been widely discussed (Kopp et al. 2014; Grinsted et al. 2015; Jackson and Jevrejeva, 2016), there are a wide range of specific uncertainties for coastal and local projections.
Currently, interactions between some of the sea level components (e.g., the interaction between fresh water fluxes due to ice mass loss from ice sheets and ocean dynamics) are not represented in standard climate model experiments. The understanding and modelling of ocean dynamic processes and incorporation of fresh water forcing as a result of ice sheet mass loss in climate models is a goal of CMIP6 experiments (Eyring et al. 2016). In addition, CMIP5 models lack both the horizontal and vertical resolution and representation of the main physical mechanisms driving the variability in sea level in shallow areas of continental shelf and along the coast. This leads to difficulties providing probabilistic projections for marginal seas, such as the Baltic Sea (Grinsted et al. 2015) and the Mediterranean Sea (Slangen et al. 2016). Interactions between fundamental physical mechanisms in coastal areas such as river run-off, tide, waves, storm surges and their link to the changes in mean sea level are still poorly understood and currently not included in coastal sea level projections and the projections of extreme water levels (Zhang et al. 2017).
The lack of local vertical land movement measurements in the areas vulnerable to sea level rise, e.g., river deltas, low-lying island and coastal cities, and inability to project the future change in local vertical land movement introduces additional uncertainties to sea level projections for individual locations. In some areas, especially those affected by significant groundwater extraction activity (e.g., Jakarta, Manila and Bangkok) the rate of local subsidence is larger than any projected rate of sea level rise by 2100 (Chaussard et al. 2013; Raucoules et al. 2013; Phien-wej et al. 2006; Jevrejeva et al. 2016).
Moreover, there are currently considerable challenges modelling high-end ice sheet contributions to sea level rise. Alternative physical characterizations in the period since AR5 have led to Antarctic ice sheet projections for 2100 that span 30 cm (Ritz et al. 2015) to more than a metre (DeConto and Pollard, 2016). In particular, DeConto and Pollard (2016) introduced new physical mechanisms that had not previously been represented in continental-scale ice sheet models, leading to model projections that included potential metre-scale contributions to sea level by the end of the twenty-first century. The wide spread of the Antarctic projections reflects the deep uncertainty surrounding these processes, and while subsequent papers and conference presentations suggest increasing convergence amongst continental-scale projections (Edwards et al. 2019), it would be premature to assume that this will be the last episode in which new physical insights lead to substantial changes in projected ice sheet behaviours. This deep uncertainty highlights both the need for an improved physical understanding of the problem as well as the value of structured expert judgement studies focused on characterizing tail risk of deeply uncertain sea level components (e.g., Bamber and Aspinall, 2013), and the use of extra probabilistic methods, discussed below.
6.2 Needs for Sea Level Information Beyond Probabilistic Projections
The previous sections have shown that the various probabilistic projections available today can display large differences. Globally, this is due primarily to differences in the treatment of ice mass loss contributions from ice sheets. Regionally, ocean dynamics and local vertical land movement are key drivers of both uncertainty within projections and differences amongst projections. As mentioned in Sect. 3, this poses a particular difficulty for coastal adaptation practitioners, who do not necessarily have the expertise to select a particular sea level projection amongst those available. To overcome this issue, coastal adaptation has adopted for at least 30 years a pragmatic approach consisting of considering a few sea level rise scenarios, including some corresponding to the most unfavourable cases considered by sea level science (Nicholls et al. 2014; Hinkel et al. 2015; Sweet et al. 2017). Here, it can be noticed that probabilistic projections may not meet the need for information of the most risk-averse users, because their highest quartile remains poorly constrained (Hinkel et al. 2015; Le Cozannet et al. 2017b). For example, estimating the value of sea level rise corresponding to an exceedance of 1% by 2100 would require a large confidence in the tail of the distributions. Here, we suggest that defining actionable sea level scenarios requires identifying interlinkages between sea level and coastal impact science and the operational workflows of users (Le Cozannet et al. 2017b), for example, by crossing sea level scenarios with the desired security margins and decision time horizon (Hallegatte, 2009). Flexible adaptation pathways, which in advance identify triggers (e.g., when sea level exceeds a given height) for key decisions (e.g., when to replace a storm barrier) and chart out possible options, provide another key tool for coping with this deep uncertainty (Haasnoot et al. 2013).
Extraprobabilistic approaches can be seen as an attempt to reconcile probabilistic sea level projections and sea level rise scenarios into a single mathematical object (see Ben Abdallah et al. 2014 for a first application in the area of sea level rise). Recognizing that the probability of sea level rise cannot be precisely estimated, extra probabilistic approaches assign an uncertainty to this probability and provide the analytical tools to work with families of probabilistic projections. Such approaches can be used when conflicting expert opinions (whether probabilistic or not) need to be considered and represented (Ben Abdallah et al. 2013; Le Cozannet et al. 2017b). Extra probabilistic projections can be visualized in the form of probability boxes, which bound all probability functions considered possible at a given date. In Fig. 7, the extra probabilistic projection is presented in the form of a probability box (p-box), which bounds all possible probability functions compliant with a set of assumptions. In this case, these assumptions are the IPCC AR5 likely range as defined by the guidance of the IPCC AR5 (Mastrandrea et al. 2010), as well as more recent studies attempting to provide maximum and minimum values for sea level rise by 2100 for RCP8.5. As these boundaries are uncertain, different weights are associated with maximum values as given in Table 3 of Le Cozannet et al. (2017a). Importantly, Fig. 7 shows that probabilistic projections relying on DeConto and Pollard (2016) are not included in the probability box and therefore disagree with the IPCC likely range. To summarize, instead of attempting to provide minimum and maximum values for future sea level rise the extra probabilistic approach attempts to provide constraints to probability functions in particular considering the needs of the most risk-averse users (Hinkel et al. 2019), and they allow for performing propagation of uncertainties and sensitivity analysis even when different probability functions coexist, which is hardly achievable within a scenario approach with complex coastal impact models (Rohmer et al. 2019). This example shows that approaches in the area of mathematical theories of uncertainties can be beneficial to support coastal adaptation to sea level rise, in particular if large differences remain between probabilistic projections of sea level rise over the coming years to decades.
Probability box (p-box; grey area bounded by dark lines) displaying the uncertainty of global sea level rise projections in 2100, conditional to the RCP 8.5 scenario, with respect to 1986–2005. These p-boxes are compared with probability functions shown in Fig. 3
7 Conclusions
This paper has reviewed the current status of probabilistic sea level projections. Initially, probabilistic projections were demanded by some users who required a more complete description of uncertainties than existing products, especially the IPCC projections that were limited to a “likely range”. However, probabilistic projections are themselves uncertain, and the differences are very large as their mean can differ by up to one metre or so (see Figs. 3, 7). So far, the large differences of probabilistic assessments have often prevented users from replacing their standard sea level scenarios with state-of-the-art probabilistic sea level projections. This means that research is still needed to tailor probabilistic projections to the needs of adaptation practitioners.
We identify four research challenges potentially beneficial for coastal adaptation:
-
include coastal processes in probabilistic SLR projections, e.g., changing meso-scale ocean processes acting at the scale of the continental shelf and semi-enclosed seas in regional probabilistic projections or vertical land motions at regional to local scales;
-
provide information regarding future changes in extreme water levels;
-
beside 2050 and 2100, address other timescales relevant to adaptation according to each user requirement;
-
conduct research at the interface between decision-making and sea level science to provide uncertainty assessments relevant to user needs and ultimately support operational adaptation.
References
Arns A, Wahl T, Haigh ID, Jensen J, Pattiaratchi C (2013) Estimating extreme water level probabilities: a comparison of the direct methods and recommendations for best practise. Coast Eng 81:51–66. https://doi.org/10.1016/j.coastaleng.2013.07.003
Arns A et al (2017) Sea-level rise induced amplification of coastal protection design heights. Sci Rep. https://doi.org/10.1038/srep40171
Bamber JL, Aspinall WP (2013) An expert judgement assessment of future sea level rise from the ice sheets. Nat Clim Change 3(4):424
Bamber JL, Aspinall WP, Cooke RM (2016) A commentary on “how to interpret expert judgment assessments of twenty-first century sea-level rise” by Hylke de Vries and Roderik SW van de Wal. Clim Change 137(3–4):321–328
Barnard PL et al (2019) Dynamic flood modeling essential to assess the coastal impacts of climate change. Sci Rep. https://doi.org/10.1038/s41598-019-40742-z
Batstone C et al (2013) A UK best-practice approach for extreme sea-level analysis along complex topographic coastlines. Ocean Eng 71:28–39. https://doi.org/10.1016/j.oceaneng.2013.02.003
Ben Abdallah N et al (2014) Combining statistical and expert evidence using belief functions: application to centennial sea level estimation taking into account climate change. Int J Approx Reason 55:341–354
Bevis M (2019) Accelerating changes in ice mass within Greenland, and the ice sheet’s sensitivity to atmospheric forcing. Proceedings of the national academy of sciences of the united states of america, vol 116, pp 1934–1939. https://doi.org/10.1073/pnas.1806562116
BRGM (2018) Annula report, BRGM, the French geological survey. http://www.brgm.eu/news-media/2017-annual-report
Buchanan MK et al (2016) Allowances for evolving coastal flood risk under uncertain local sea-level rise. Clim Change 137(3–4):347–362. https://doi.org/10.1007/s10584-016-1664-7
Carson M et al (2016) Coastal sea level changes, observed and projected during the 20th and 21st century. Clim Change 134(1–2):269–281
Cazenave A and WCRP Global Sea Level Budget Group (2018) Global sea-level budget 1993–present. Earth Syst Sci Data 10:1551–1590. https://doi.org/10.5194/essd-10-1551-2018
Chaussard E et al (2013) Sinking cities in Indonesia: aLOS PALSAR detects rapid subsidence due to groundwater and gas extraction. Remote Sens Environ 128:150–161. https://doi.org/10.1016/j.rse.2012.10.015
Church FN et al (2013a) Sea level change. In: Stocker TF, Qin D, Plattner G-K, Tignor M, Allen SK, Boschung J, Nauels A, Xia Y, Bex V, Midgley PM (eds) Climate change. The physical science basis. Contribution of working group I to the fifth assessment report of the intergovernmental panel on climate change. Cambridge University Press, Cambridge
Church JA et al (2013b) Sea-level rise by 2100. Science 342(6165):1445–1445. https://doi.org/10.1126/science.342.6165.1445-a
Cozannet Le et al (2015) Evaluating uncertainties of future marine flooding occurrence as sea-level rises. Environ Model Softw 73:44–56. https://doi.org/10.1016/j.envsoft.2015.07.021
Cozannet Le et al (2017a) Sea level change and coastal climate services: the way forward. J Mar Sci Eng 5(4):49
Cozannet Le et al (2017b) Bounding probabilistic sea-level projections within the framework of the possibility theory. Environ Res Lett 12(1):014012
Dangendorf S et al (2016) The exceptional influence of storm ‘Xaver’ on design water levels in the german bight. Environ Res Lett 11:054001. https://doi.org/10.1088/1748-9326/11/5/054001
De Vries H, van de Wal RS (2015) How to interpret expert judgment assessments of 21st century sea-level rise. Clim Change 130(2):87–100
DeConto RM, Pollard D (2016) Contribution of Antarctica to past and future sea-level rise. Nature 531(7596):591
Dixon TH et al (2006) Space geodesy: subsidence and flooding in New Orleans. Nature 441(7093):587
Du J et al (2018) Tidal response to sea-level rise in different types of estuaries: the importance of length, bathymetry, and geometry: tidal response to sea-level rise. Geophys Res Lett 45:227–235. https://doi.org/10.1002/2017GL075963
Edwards TL et al (2019) Revisiting Antarctic ice loss due to marine ice cliff instability. Nature. https://doi.org/10.1038/s41586-019-0901-4
Erban LE, Gorelick SM, Zebker HA (2014) Groundwater extraction, land subsidence, and sea-level rise in the Mekong Delta, Vietnam. Environ Res Lett 9(8):084010
Eyring V et al (2016) Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci Model Dev 9:1937–1958. https://doi.org/10.5194/gmd-9-1937-2016
Garner AJ et al (2017) Impact of climate change on New York City’s coastal flood hazard: increasing flood heights from the preindustrial to 2300 CE. Proc Natl Acad Sci. https://doi.org/10.1073/pnas.1703568114
Garner AJ et al (2018) Evolution of 21st century sea-level rise projections. Earth’s Future 1:1. https://doi.org/10.1029/2018EF000991
Golledge NR et al (2015) The multimillenial Antarctic commitment to future sea-level rise. Nature 526:421–425. https://doi.org/10.1038/nature15706
Goodwin P, Haigh ID, Rohling EJ, Slangen A (2017) A new approach to projecting 21st century sea-level changes and extremes. Earth’s Future 5(2):240–253
Griffies SM et al (2016) OMIP contribution to CMIP6: experimental and diagnostic protocol for the physical component of the Ocean Model Intercomparison Project. Geosci Model Dev 9:3231–3296. https://doi.org/10.5194/gmd-9-3231-2016
Grinsted A et al (2015) Sea level rise projections for Northern Europe under RCP8.5. Clim Res 64:15–23. https://doi.org/10.3354/cr01309
Haasnoot M et al (2013) Dynamic adaptive policy pathways: a method for crafting robust decisions for a deeply uncertain world. Glob Environ Change 23(2):485–498. https://doi.org/10.1016/j.gloenvcha.2012.12.006
Haigh ID et al (2014a) Estimating present day extreme water level exceedance probabilities around the coastline of Australia: tropical cyclone-induced storm surges. Clim Dyn 42:139–157. https://doi.org/10.1007/s00382-012-1653-0
Haigh ID et al (2014b) Estimating present day extreme water level exceedance probabilities around the coastline of australia: tides, extra-tropical storm surges and mean sea level. Clim Dyn 42:121–138. https://doi.org/10.1007/s00382-012-1652-1
Hall JW et al (2012) Robust climate policies under uncertainty: a comparison of robust decision making and info-gap methods. Risk Anal 32:1657–1672
Hall JA et al (2016) Regional sea level scenarios for coastal risk management: managing the uncertainty of future sea level change and extreme water levels for Department of Defense coastal sites worldwide. Department of Defense, Strategic Environmental Research and Development Program, Alexandria
Hall JA et al (2019) Rising sea levels: helping decision-makers confront the inevitable. Coast Manag. https://doi.org/10.1080/08920753.2019.1551012
Hallegatte S (2009) Strategies to adapt to an uncertain climate change. Glob Environ Change 19(2):240–247
Hallegatte S et al (2013) Future flood losses in major coastal cities. Nat Clim Change 3:802–806. https://doi.org/10.1038/nclimate1979
Hay CC, Morrow E, Kopp RE, Mitrovica JX (2013) Estimating the sources of global sea level rise with data assimilation techniques. Proc Natl Acad Sci 110(Supplement 1):3692–3699
Hinkel J et al (2014) Coastal flood damage and adaptation costs under 21st century sea-level rise. Proc Natl Acad Sci 111:3292–3297. https://doi.org/10.1073/pnas.1222469111
Hinkel J et al (2015) Sea-level rise scenarios and coastal risk management. Nat Clim Change 5:188–190
Hinkel J et al (2019) Meeting user needs for sea-level rise information: a decision analysis perspective. Earth’s Future 1:1. https://doi.org/10.1029/2018EF001071
Hoffman JS, Keyes D, Titus JG (1983) Projecting future sea level rise; methodology, estimates to the year 2100, and Research needs. Environmental Protection Agency, Washington, pp 115–121
Horton BP et al (2018) Mapping sea-level change in time, space and probability. Ann Rev Environ Resour. https://doi.org/10.1146/annurev-environ-102017-025826
Hunter J (2012) A simple technique for estimating an allowance for uncertain sea-level rise. Clim Change 113(2):239–252. https://doi.org/10.1007/s10584-011-0332-1
Hunter JR et al (2013) Towards a global regionally varying allowance for sea-level rise. Ocean Eng 71:17–27
IPCC (2014) Summary for policymakers. In: Field CB, Barros VR, Dokken DJ, Mach KJ, Mastrandrea MD, Bilir TE, Chatterjee M, Ebi KL, Estrada YO, Genova RC, Girma B, Kissel ES, Levy AN, MacCracken S, Mastrandrea PR, White LL (eds) Climate change 2014: impacts, adaptation, and vulnerability. Part A: global and sectoral aspects. contribution of working group II to the fifth assessment report of the intergovernmental panel on climate change. Cambridge University Press, Cambridge, pp 1–32
Jackson LP, Jevrejeva S (2016) A probabilistic approach to 21st century regional sea-level projections using RCP and High-end scenarios. Global Planet Change 146:179–189
Jackson LP et al (2018) 21st century sea-level rise in line with the Paris accord. Earth’s Future 6:213–229. https://doi.org/10.1002/2017EF000688
Jevrejeva S, Moore JC, Grinsted A (2012) Sea level projections to AD2500 with a new generation of climate change scenarios. Global Planet Change 80:14–20
Jevrejeva S, Grinsted A, Moore J (2014) Upper limit for sea level projections by 2100. Environ Res Lett 9:104008
Jevrejeva S et al (2016) Coastal sea-level rise with warming above 2 degree. Proc Natl Acad Sci. https://doi.org/10.1073/pnas.1605312113
Jevrejeva S, Jackson LP, Grinsted A, Lincke D, Marzeion B (2018) Flood damage costs under the sea level rise with warming of 1.5° C and 2° C. Environ Res Lett 13(7):074014
Katsman CA et al (2011) Exploring high-end scenarios for local sea level rise to develop flood protection strategies for a low-lying delta—the Netherlands as an example. Clim Change 109:617–645
Kopp RE et al (2014) Probabilistic 21st and 22nd century sea-level projections at a global network of tide-gauge sites. Earth’s Future 2(8):383–406
Kopp RE et al (2016) Temperature-driven global sea-level variability in the Common Era. Proc Natl Acad Sci 13:E1434–E1441
Kopp RE et al (2017) Evolving understanding of Antarctic ice-sheet physics and ambiguity in probabilistic sea-level projections. Earth’s Future 5(12):1217–1233
Landerer FW, Gleckler PJ, Lee T (2014) Evaluation of CMIP5 dynamic sea surface height multi-model simulations against satellite observations. Clim Dyn 43(5–6):1271–1283
Le Bars D (2018) Uncertainty in sea level rise projections due to the dependence between contributors. Earth’s Future. https://doi.org/10.1029/2018ef000849
Le Bars D, Drijfhout S, de Vries H (2017) A high-end sea level rise probabilistic projection including rapid Antarctic ice sheet mass loss. Environl Res Lett 12(4):044013
Lecacheux S et al (2012) A method to characterize the different extreme waves for islands exposed to various wave regimes: a case study devoted to Reunion Island. Nat Hazards Earth Syst Sci 12(7):2425–2437
Lempert R, Schlesinger ME (2000) Robust strategies for abating climate change. Clim Change 45:387–401
Lin N, Shullman E (2017) Dealing with hurricane surge flooding in a changing environment: part I. Risk assessment considering storm climatology change, sea level rise, and coastal development. Stoch Env Res Risk Assess. https://doi.org/10.1007/s00477-016-1377-5
Little CM et al (2015) Joint projections of US East Coast sea level and storm surge. Nat Clim Change 5(12):1114–1120. https://doi.org/10.1038/nclimate2801
Mastrandrea MD et al (2010) Guidance note for lead authors of the IPCC 5th assessment report on consistent treatment of uncertainties. Intergovernmental Panel on Climate Change. Available at https://archive.ipcc.ch/pdf/supporting-material/uncertainty-guidance-note.pdf
Mazas F et al (2014) Applying POT methods to the Revised Joint Probability Method for determining extreme sea levels. Coast Eng 91:140–150. https://doi.org/10.1016/j.coastaleng.2014.05.006
Melet A et al (2018) Under-estimated wave contribution to coastal sea-level rise. Nat Clim Change 8(3):234–239. https://doi.org/10.1038/s41558-018-0088-y
Menéndez M, Woodworth PL (2010) Changes in extreme high water levels based on a quasi-global tide-gauge data set. J Geophys Res. https://doi.org/10.1029/2009JC005997
Mengel M et al (2016) Future sea level rise constrained by observations and long-term commitment. Proc Natl Acad Sci 113:2597–2602
Mengel M, Nauels A, Rogelj J, Schleussner CF (2018) Committed sea-level rise under the Paris Agreement and the legacy of delayed mitigation action. Nat Commun 9(1):601
Mitrovica JX, Tamisiea ME, Davis JL, Milne GA (2001) Recent mass balance of polar ice sheets inferred from patterns of global sea-level change. Nature 409(6823):1026
Moss RH et al (2010) The next generation of scenarios for climate change research and assessment. Nature 463(7282):747
Muis S et al (2016) A global reanalysis of storm surges and extreme sea levels. Nat Commun 7:11969. https://doi.org/10.1038/ncomms11969
Muis S et al (2017) A comparison of two global datasets of extreme sea levels and resulting flood exposure. Earth’s Future 5(4):379–392. https://doi.org/10.1002/2016EF000430
Nauels A et al (2017) Linking sea level rise and socioeconomic indicators under the Shared Socioeconomic Pathways. Environ Res Lett 12(11):114002
Nicholls RJ, Cazenave A (2010) Sea-level rise and its impact on coastal zones. Science 328(5985):1517–1520
Nicholls RJ et al (2014) Sea-level scenarios for evaluating coastal impacts. Rev Clim Change 5:129–150
Nohara D et al (2006) Impact of climate change on river discharge projected by multimodel ensemble. J Hydrometeorol 7(5):1076–1089. https://doi.org/10.1175/JHM531.1
Nowicki S, Seroussi H (2018) Projections of future sea level contributions from the Greenland and Antarctic Ice Sheets: challenges beyond dynamical ice sheet modeling. Oceanography 31:2. https://doi.org/10.5670/oceanog.2018.216
Nowicki SMJ et al (2016) Ice sheet model intercomparison project (ISMIP6) contribution to CMIP6. Geosci Model Dev 9:4521–4545. https://doi.org/10.5194/gmd-9-4521-2016
Peltier WR (2004) Global glacial isostasy and the surface of the ice-age Earth: the ICE-5G (VM2) model and GRACE. Annu Rev Earth Planet Sci 32(1):111–149. https://doi.org/10.1146/annurev.earth.32.082503.144359
Peltier WR, Argus DF, Drummond R (2015) Space geodesy constrains ice age terminal deglaciation: the global ICE-6G_C (VM5a) model: global glacial isostatic adjustment. J Geophys Res Solid Earth 120(1):450–487. https://doi.org/10.1002/2014JB011176
Perrette M et al (2013) A scaling approach to project regional sea level rise and its uncertainties. Earth Syst Dyn 4(1):11–29
Phien-wej N, Giao PH, Nutalaya P (2006) Land subsidence in Bangkok, Thailand. Eng Geol 82:187–201
Pickering MD et al (2017) The Impact of future sea-level rise on the global tides. Cont Shelf Res 142:50–68. https://doi.org/10.1016/j.csr.2017.02.004
Piecuch CG et al (2018) River-discharge effects on united states atlantic and gulf coast sea-level changes. Proc Natl Acad Sci. https://doi.org/10.1073/pnas.1805428115
Rahmstorf S (2007) A semi-empirical approach to projecting future sea-level rise. Science 315(5810):368–370
Rasmussen DJ et al (2018) Extreme sea level implications of 1.5° C, 2.0° C, and 2.5° C temperature stabilization targets in the 21st and 22nd centuries. Environ Res Lett 13(3):034040
Raucoules D et al (2013) High nonlinear urban ground motion in Manila (Philippines) from 1993 to 2010 observed by DInSAR: implications for sea-level measurement. Remote Sens Environ 139:386–397
Ritz C et al (2015) Potential sea-level rise from Antarctic ice-sheet instability constrained by observations. Nature 528(7580):115
Rignot E et al (2019) Four decades of Antarctic Ice Sheet mass balance from 1979–2017. PNA. https://doi.org/10.1073/pnas.1812883116
Roberts MJ et al (2016) Impact of ocean resolution on coupled air-sea fluxes and large-scale climate. Geophys Res Lett 43(19):10–430
Rohmer J et al (2019) Addressing ambiguity in probabilistic assessments of future coastal flooding using possibility distributions. Clim Change. https://doi.org/10.1007/s10584-019-02443-4
Rosenzweig C, Solecki WD, Blake R, Bowman M, Faris C, Gornitz V, Horton R, Jacob K, LeBlanc A, Leichenko R, Linkin M (2011) Developing coastal adaptation to climate change in the New York City infrastructure-shed: process, approach, tools, and strategies. Clim Change 106(1):93–127. https://doi.org/10.1007/s10584-010-0002-8
Shepherd A et al (2018) Mass balance of the Antarctic Ice Sheet from 1992 to 2017. Nature 556:219–222
Slangen ABA et al (2014) Projecting twenty-first century regional sea-level changes. Clim Change 124(1–2):317–332
Slangen ABA et al (2016) A review of recent updates of sea-level projections at global and regional scales. Surv Geophys 38:385
Slangen A et al (2017) The impact of uncertainties in ice sheet dynamics on sea-level allowances at tide gauge locations. J Mar Sci Eng 5(2):21. https://doi.org/10.3390/jmse5020021
Sweet WV, Park J (2014) From the extreme to the mean: acceleration and tipping points of coastal inundation from sea level rise. Earth’s Future 2:579–600
Sweet et al (2017) Global and Regional Sea Level Rise Scenarios for the United States. NOAA technical report nos CO-OPS 083. https://tidesandcurrents.noaa.gov/publications/techrpt83_Global_and_Regional_SLR_Scenarios_for_the_US_final.pdf Cited 6 January 2018
Tawn JA (1992) Estimating probabilities of extreme sea-levels. Appl Stat 41(1):77. https://doi.org/10.2307/2347619
Tawn JA, Vassie JM, Gumbel EJ (1989) Extreme sea levels: the joint probabilities method revisited and revised. Proc Inst Civ Eng 87(3):429–442. https://doi.org/10.1680/iicep.1989.2975
Taylor K, Stouffer RJ, Meehl GA (2012) An overview of CMIP5 and the experiment design. Bull Am Meteorol Soc 93(4):485–498. https://doi.org/10.1175/BAMS-D-11-00094.1
Tebaldi C et al (2012) Modelling sea level rise impacts on storm surges along US Coasts. Environ Res Lett 7(1):014032. https://doi.org/10.1088/1748-9326/7/1/014032
Titus JG, Narayanan VK (1995) The probability of sea level rise; US Environmental Protection Agency: Washington, DC, USA; Office of Policy, Planning, and Evaluation: Bethesda, MD, USA; Climate Change Division, Adaptation Branch: Washington, DC, USA, 1995; vol 95
Tran T et al (2016) Climate change and sea level rise scenarios for Viet Nam. Viet Nam Institute of meteorology, hydrology and climate, http://www.imh.ac.vn/files/doc/2017/CCS%20final.compressed.pdf
van den Hurk B et al (2014) Climate change scenarios for the 21st century—a Netherlands perspective Scientific Report WR2014-01 KNMI, De Bilt, the Netherlands. www.climatescenarios.nl
van de Wal RSW, Zhang X, Minobe S, Jevrejeva S, Riva, REM, Little C, Richter K, Palmer M (2019) Uncertainties in long-term process-based coastal sea-level projections, Surv Geophys 40 (in review)
Vitousek S et al (2017) Doubling of coastal flooding frequency within decades due to sea-level rise. Sci Rep. https://doi.org/10.1038/s41598-017-01362-7
Vousdoukas MI et al (2016) Extreme sea levels on the rise along Europe’s coasts. Earth’s Future 5(3):304–323. https://doi.org/10.1002/2016EF000505
Vousdoukas M et al (2018) Global probabilistic projections of extreme sea levels show intensification of coastal flood hazard. Nat Commun. https://doi.org/10.1038/s41467-018-04692-w
Wahl T (2017) Sea-level rise and storm surges, relationship status: complicated! Environ Res Lett 12(11):111001. https://doi.org/10.1088/1748-9326/aa8eba
Wahl T et al (2015) Increasing risk of compound flooding from storm surge and rainfall for major US cities. Nat Clim Change 5(12):1093–1097. https://doi.org/10.1038/nclimate2736
Wahl T et al (2017) Understanding extreme sea levels for broad-scale coastal impact and adaptation analysis. Nat Commun 8:16075. https://doi.org/10.1038/ncomms16075
Wang XL et al (2014) Changes in global ocean wave heights as projected using multimodel CMIP5 simulations. Geophys Res Lett 41(3):1026–1034. https://doi.org/10.1002/2013GL058650
Ward PJ et al (2018) Dependence between high sea-level and high river discharge increases flood hazard in global deltas and estuaries. Environ Res Lett 13(8):084012. https://doi.org/10.1088/1748-9326/aad400
Williams J et al (2016) Tide and skew surge independence: new insights for flood risk. Geophys Res Lett 43(12):6410–6417. https://doi.org/10.1002/2016GL069522
Winter De et al (2017) Impact of asymmetric uncertainties in ice sheet dynamics on regional sea level projections. Nat Hazards Earth Syst Sci 17(2125–2141):2017. https://doi.org/10.5194/nhess-17-2125-2017
Woodworth PL, Menéndez M, Gehrels WR (2011) Evidence for century-timescale acceleration in mean sea levels and for recent changes in extreme sea levels. Surv Geophys 32(4–5):603–618
Woodworth PL et al (2016) Towards a global higher-frequency sea level dataset. Geosci Data J 3(2):50–59. https://doi.org/10.1002/gdj3.42
Wöppelmann G, Marcos M (2016) Vertical land motion as a key to understanding sea level change and variability. Rev Geophys 54(1):64–92
Wöppelmann G et al (2013) Is land subsidence increasing the exposure to sea level rise in Alexandria, Egypt? Geophys Res Lett 40(12):2953–2957
Zhang X et al (2017) Sea level projections for the Australian region in the 21st century. Geophys Res Lett. https://doi.org/10.1002/2017gl074176
Acknowledgements
This paper arose from the workshop on “Understanding the Relationship between Coastal Sea Level and Large-Scale Ocean Circulation” held at the International Space Science Institute (ISSI), Bern, Switzerland on 5–9 March 2018. Parts of this research (TF) were carried out at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration and a NWO-NPP grant. REK was supported by National Aeronautics and Space Administration (NASA) Grant 80NSSC17K0698 and National Science Foundation grant ICER-1663807. GLC and RvdW were supported by the ERA4CS ECLISEA and INSeaPTION projects (Grant 690462). SJ was supported by the Natural Environmental Research Council under Grant Agreement No. NE/P01517/1 and by the EPSRC NEWTON Fund Sustainable Deltas Programme, grant number EP/R024537/1. LPJ is funded by the Robertson Foundation through the Climate Econometrics project (Grant Numbers: 9908921 and 9907422). RvdW received funding from NWO, grant 866.13.001.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Jevrejeva, S., Frederikse, T., Kopp, R.E. et al. Probabilistic Sea Level Projections at the Coast by 2100. Surv Geophys 40, 1673–1696 (2019). https://doi.org/10.1007/s10712-019-09550-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10712-019-09550-y