Efficient temperature field evaluation in wet surface grinding for arbitrary heat flux profile

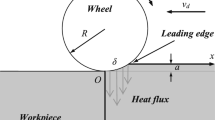
Abstract

We consider the heat transfer in surface wet grinding, assuming a constant heat-transfer coefficient over the workpiece surface, as well as the usual heat flux profiles entering into the workpiece given in the literature, i.e. constant, linear, parabolic and triangular. On the one hand, we calculate in the stationary regime, the temperature distribution on the workpiece surface in series form. These series converge only for Biot numbers less than unity. By using convergence acceleration, these series can be computed more rapidly than its equivalent integral form without any appreciable loss of accuracy. Also, we avoid the numerical integration problems found in the expressions given in the literature. Moreover, the expressions found can be used to compute the maximum temperature of the workpiece very rapidly. On the other hand, we have refined some approximations for the relaxation time in wet grinding, and we have derived some new expressions for dry grinding. The relaxation time has been applied to compute the temperature field inside the workpiece in the stationary regime, obtaining a more rapid numerical evaluation without any appreciable loss of precision.

Appendices

Appendix A: A useful expansion

The $w\left( z\right)$ function is an entire function defined as [23, Eq. 7.2.3]

$$\begin{aligned} w\left( z\right) =\mathrm{e}^{-z^{2}}\mathrm {erfc}\left( -\mathrm{i}z\right) . \end{aligned}$$

(98)

This function has the following expansion [23, Eq. 7.6.3]

$$\begin{aligned} w\left( z\right) =\sum _{n=0}^{\infty }\frac{\left( \mathrm{i}z\right) ^{n}}{\varGamma \left( \frac{n}{2}+1\right) }. \end{aligned}$$

(99)

Therefore, taking $z=\mathrm{i}x$ in (98) and (99), and equating both results, we obtain

$$\begin{aligned} \mathrm{e}^{x^{2}}\mathrm {erfc}\left( x\right) =\sum _{n=0}^{\infty }\frac{\left( -x\right) ^{n}}{\varGamma \left( \frac{n}{2}+1\right) }. \end{aligned}$$

(100)

Notice that from (100), we have

$$\begin{aligned} 1-\sqrt{\pi }x\,\mathrm{e}^{x^{2}}\mathrm {erfc}\left( x\right) =1+\sqrt{\pi } \sum _{n=0}^{\infty }\frac{\left( -x\right) ^{n+1}}{\varGamma \left( \frac{n}{2} +1\right) } =1+\sqrt{\pi }\sum _{n=1}^{\infty }\frac{\left( -x\right) ^{n}}{\varGamma \left( \frac{n+1}{2}\right) }. \end{aligned}$$

(101)

Now, using the fact that $\varGamma \left( \frac{1}{2}\right) =\sqrt{\pi }$ [23, Eq. 5.4.6], we finally arrive at

$$\begin{aligned} 1-\sqrt{\pi }x\,\mathrm{e}^{x^{2}}\mathrm {erfc}\left( x\right) =\sqrt{\pi } \sum _{n=0}^{\infty }\frac{\left( -x\right) ^{n}}{\varGamma \left( \frac{n+1}{2} \right) }. \end{aligned}$$

(102)

Appendix B: The $\mathrm {Yu}\left( x\right)$ function

Let us define the function, $\forall m=0,1,2,\ldots$

$$\begin{aligned} \widetilde{\mathrm {Yu}}_{\nu }^{\left( m\right) }\left( x\right) =\int _{0}^{x}\mathrm{e}^{-t}t^{m}\left| t\right| ^{\nu }K_{\nu }\left( \left| t\right| \right) \mathrm {d}t. \end{aligned}$$

(103)

To calculate the above integral (103), we use the following result [24]

$$\begin{aligned} {\mathcal {J}}_{m,\nu }^{\pm }\left( x\right)&=\int _{0}^{x}\mathrm{e}^{\pm t}t^{\nu +m}K_{\nu }\left( t\right) \mathrm {d}t \nonumber \\&=\mathrm{e}^{\pm x}x^{\nu +m+1}\left\{ K_{\nu }\left( x\right) \Phi _{\nu }^{\left( m\right) }\left( \mp x\right) \pm K_{\nu +1}\left( x\right) \Psi _{\nu }^{\left( m\right) }\left( \mp x\right) \right\} +A_{m,\nu }^{\pm }, \end{aligned}$$

(104)

where the following polynomials in 1 / x have been defined:

$$\begin{aligned} \Phi _{\nu }^{\left( m\right) }\left( x\right) =\frac{1}{2\nu +m+1} \left[ 1-\frac{m}{2\nu +2m+1}\,_{3}F_{1}\left( \left. \begin{array}{c} 1,1-m,-1-m-2\nu \\ 1/2-m-\nu \end{array} \right| \frac{-1}{2x}\right) \right] , \end{aligned}$$

(105)

and

$$\begin{aligned} \Psi _{\nu }^{\left( m\right) }\left( x\right) =\frac{1}{2\nu +2m+1} \,_{3}F_{1}\left( \left. \begin{array}{c} 1,-m,-m-2\nu \\ 1/2-m-\nu \end{array} \right| \frac{-1}{2x}\right) . \end{aligned}$$

(106)

Also, the integration constant is set as

$$\begin{aligned} A_{m,\nu }^{\pm }=\left( \mp 1\right) ^{m+1}2^{\nu +m}\frac{m!\varGamma \left( \nu +m+1\right) \varGamma \left( 2\nu +m+1\right) }{\varGamma \left( 2\nu +2m+2\right) }. \end{aligned}$$

(107)

$\forall x>0$, it is clear that we can drop the absolute value bars in (103), and thus

$$\begin{aligned} \widetilde{\mathrm {Yu}}_{\nu }^{\left( m\right) }\left( x\right) =\int _{0}^{x}\mathrm{e}^{-t}t^{m}t^{\nu }K_{\nu }\left( t\right) \mathrm {d}t={\mathcal {J}} _{m,\nu }^{-}\left( x\right) . \end{aligned}$$

(108)

Also, $\forall x<0$, we can replace the absolute value bars by a “−” sign, so that by performing the change $t=-\tau$, we arrive at

$$\begin{aligned} \widetilde{\mathrm {Yu}}_{\nu }^{\left( m\right) }\left( x\right)= & {} \int _{0}^{x}\mathrm{e}^{-t}\left( -t\right) ^{m}t^{\nu }K_{\nu }\left( -t\right) \mathrm {d}t =\left( -1\right) ^{m+1}\int _{0}^{-x}\mathrm{e}^{\tau }\tau ^{m}\tau ^{\nu }K_{\nu }\left( \tau \right) \mathrm {d}\tau =\left( -1\right) ^{m+1}{\mathcal {J}}_{m,\nu }^{+}\left( -x\right) . \end{aligned}$$

(109)

Then, from (104), (108) and (109), and using the property $x=\mathrm {sgn}\left( x\right) \left| x\right|$, it is easy to verify that $\forall x\ne 0$

$$\begin{aligned} \widetilde{\mathrm {Yu}}_{\nu }^{\left( m\right) }\left( x\right) =x^{m+1}\left| x\right| ^{\nu }\mathrm{e}^{-x} \left\{ K_{\nu }\left( \left| x\right| \right) \Phi _{\nu }^{\left( m\right) }\left( x\right) -\mathrm {sgn}\left( x\right) K_{\nu +1}\left( \left| x\right| \right) \Psi _{\nu }^{\left( m\right) }\left( x\right) \right\} +A_{m,\nu }^{+}. \end{aligned}$$

(110)

Now, taking limits in (103) as $x\rightarrow 0$, we have

$$\begin{aligned} \lim _{x\rightarrow 0}\widetilde{\mathrm {Yu}}_{\nu }^{\left( m\right) }\left( x\right) =\lim _{x\rightarrow 0}\int _{0}^{x}\mathrm{e}^{-t}t^{m}\left| t\right| ^{\nu }K_{\nu }\left( \left| t\right| \right) \mathrm {d}t. \end{aligned}$$

(111)

$\forall \nu \ne 0$, we can use the limiting form [23, Eq. 10.30.2]

$$\begin{aligned} K_{\nu }\left( x\right) \approx \frac{2^{\nu -1}\varGamma \left( \nu \right) }{ x^{\nu }},\quad x\rightarrow 0, \end{aligned}$$

(112)

thus, using the definition of the lower incomplete gamma function $\gamma \left( a,z\right)$ [23, Eq. 8.2.1], we arrive at

$$\begin{aligned} \lim _{x\rightarrow 0}\widetilde{\mathrm {Yu}}_{\nu }^{\left( m\right) }\left( x\right) =2^{\nu -1}\varGamma \left( \nu \right) \lim _{x\rightarrow 0}\int _{0}^{x}\mathrm{e}^{-t}t^{m}\mathrm {d}t =2^{\nu -1}\varGamma \left( \nu \right) \lim _{x\rightarrow 0}\gamma \left( m+1,x\right) =0. \end{aligned}$$

(113)

$\forall \nu =0$, we can use the limiting form [33, Eq. 5.16.4]

$$\begin{aligned} K_{0}\left( x\right) \approx \log \left( \frac{2}{x}\right) ,\quad x\rightarrow 0, \end{aligned}$$

(114)

thus

$$\begin{aligned} \lim _{x\rightarrow 0}\widetilde{\mathrm {Yu}}_{0}^{\left( m\right) }\left( x\right) =\lim _{x\rightarrow 0}\int _{0}^{x}\mathrm{e}^{-t}\left( \log 2-\log t\right) \mathrm {d}t. \end{aligned}$$

(115)

Splitting (115) in two terms, on the one hand, we have

$$\begin{aligned} I_{1}=\log 2\int _{0}^{x}\mathrm{e}^{-t}\mathrm {d}t=-\log 2\left( \mathrm{e}^{-x}-1\right) . \end{aligned}$$

(116)

On the other hand,

$$\begin{aligned} I_{2}=\int _{0}^{x}\mathrm{e}^{-t}\log t\ \mathrm {d}t=\underset{-\gamma }{\underbrace{ \int _{0}^{\infty }\mathrm{e}^{-t}\log t\ \mathrm {d}t}}-\int _{x}^{\infty }\mathrm{e}^{-t}\log t\ \mathrm {d}t, \end{aligned}$$

(117)

where, according to [33, Eq. 1.3.19], the first integral of (117) is just $-\gamma$, and the second integral can be integrated by parts, obtaining

$$\begin{aligned} I_{2}=-\gamma +\mathrm{e}^{-x}\log x+\underset{\varGamma \left( 0,x\right) }{\underbrace{ \int _{x}^{\infty }\frac{\mathrm{e}^{-t}}{t}\mathrm {d}t}}, \end{aligned}$$

(118)

where we have applied the definition of the upper incomplete gamma function $\varGamma \left( a,x\right)$ [23, Eq. 8.2.2]. Inserting in ( 115) the results (116) and (118), we get

$$\begin{aligned} \lim _{x\rightarrow 0}\widetilde{\mathrm {Yu}}_{0}^{\left( m\right) }\left( x\right) =\lim _{x\rightarrow 0}\left( \log 2+\gamma +\mathrm{e}^{-x}\log \left( \frac{ x}{2}\right) +\varGamma \left( 0,x\right) \right) . \end{aligned}$$

(119)

Using the limiting form [22, Eq. 45:3:2]

$$\begin{aligned} \varGamma \left( 0,x\right) \approx -\gamma -\log \left( x\right) +x,\quad x\rightarrow 0, \end{aligned}$$

(120)

we finally conclude that

$$\begin{aligned} \lim _{x\rightarrow 0}\widetilde{\mathrm {Yu}}_{0}^{\left( m\right) }\left( x\right) =0. \end{aligned}$$

(121)

Therefore, collecting the results (110), (113) and (121), we have

$$\begin{aligned} \widetilde{\mathrm {Yu}}_{\nu }^{\left( m\right) }\left( x\right) =\int _{0}^{x}\mathrm{e}^{-t}t^{m}\left| t\right| ^{\nu }K_{\nu }\left( \left| t\right| \right) \mathrm {d}t =\left\{ \begin{array}{ll} x^{m+1}\left| x\right| ^{\nu }\mathrm{e}^{-x}F_{\nu }^{\left( m\right) }\left( x\right) +A_{m,\nu }^{+} &{}\quad x\ne 0, \\ 0 &{}\quad x=0, \end{array} \right. \end{aligned}$$

(122)

where we have set

$$\begin{aligned} F_{\nu }^{\left( m\right) }\left( x\right) =K_{\nu }\left( \left| x\right| \right) \Phi _{\nu }^{\left( m\right) }\left( x\right) -\mathrm { sgn}\left( x\right) K_{\nu +1}\left( \left| x\right| \right) \Psi _{\nu }^{\left( m\right) }\left( x\right) . \end{aligned}$$

(123)

Notice that we can drop the integration constant $A_{m,\nu }^{+}$ if we are integrating in a definite interval $\left( a,b\right)$. Thereby, if we define the function

$$\begin{aligned} \mathrm {Yu}_{\nu }^{\left( m\right) }\left( x\right) =\left\{ \begin{array}{ll} x^{m+1}\left| x\right| ^{\nu }\mathrm{e}^{-x}\left\{ K_{\nu }\left( \left| x\right| \right) \Phi _{\nu }^{\left( m\right) }\left( x\right) -\mathrm {sgn}\left( x\right) K_{\nu +1}\left( \left| x\right| \right) \Psi _{\nu }^{\left( m\right) }\left( x\right) \right\} &{} \quad x\ne 0, \\ 0 &{}\quad x=0, \end{array} \right. \end{aligned}$$

(124)

then

$$\begin{aligned} \left. \mathrm {Yu}_{\nu }^{\left( m\right) }\left( x\right) \right| _{x=a}^{b}=\int _{a}^{b}\mathrm{e}^{-t}t^{m}\left| t\right| ^{\nu }K_{\nu }\left( \left| t\right| \right) \mathrm {d}t. \end{aligned}$$

(125)

1.1 Appendix B.1: Convergence condition for ${\mathcal {T}}^{\left( k\right) }\left( X,0\right)$

To see that the series given in (29) for ${\mathcal {T}} ^{\left( k\right) }\left( X,0\right)$ converges if and only if $\mathrm {Bi\, }<1$, it suffices to prove the following theorem, recalling that we are considering $\mathrm {Bi\,}\ge 0$:

Theorem 1

The alternating series

$$\begin{aligned} \sum _{n=0}^{\infty }\frac{\left( -\mathrm {Bi\,}/\sqrt{2}\right) ^{n}}{\varGamma \left( \frac{n+1}{2}\right) }\mathrm {Yu}_{n/2}^{\left( j\right) }\left( u\right) \end{aligned}$$

(126)

converges if and only if $\mathrm {Bi\,}<1$.

Proof

First, we prove the necessary condition. According to [34, theorem 10.6], if a series $\sum _{n=0}^{\infty }a_{n}$ converges, then $\underset{n\rightarrow \infty }{\lim }a_{n}=0$. Therefore, the series given in (126), converges if

$$\begin{aligned} \underset{n\rightarrow \infty }{\lim }\frac{\left( -\mathrm {Bi\,}/\sqrt{2} \right) ^{n}}{\varGamma \left( \frac{n+1}{2}\right) }\mathrm {Yu}_{n/2}^{\left( j\right) }\left( u\right) =0. \end{aligned}$$

(127)

Notice that, according to (125),

$$\begin{aligned} \mathrm {Yu}_{\nu }^{\left( j\right) }\left( u\right) =\int _{0}^{u}\mathrm{e}^{-t}t^{j}\left| t\right| ^{\nu }K_{\nu }\left( \left| t\right| \right) \mathrm {d}t, \end{aligned}$$

(128)

and, according to [23, Eq. 10.41.2],

$$\begin{aligned} K_{\nu }\left( z\right) \approx \sqrt{\frac{\pi }{2\nu }}\left( \frac{\mathrm{e}z}{ 2\nu }\right) ^{-\nu },\qquad \nu \rightarrow \infty , \end{aligned}$$

(129)

and thus,

$$\begin{aligned} \lim _{\nu \rightarrow \infty }\mathrm {Yu}_{\nu }^{\left( j\right) }\left( u\right) =\lim _{\nu \rightarrow \infty }\sqrt{\frac{\pi }{2\nu }}\left( \frac{\mathrm{e}}{ 2\nu }\right) ^{-\nu }\int _{0}^{u}\mathrm{e}^{-t}t^{j}\mathrm {d}t =\sqrt{\frac{\pi }{2}}\gamma \left( j+1,u\right) \lim _{\nu \rightarrow \infty }\sqrt{\frac{1}{\nu }}\left( \frac{\mathrm{e}}{2\nu }\right) ^{-\nu }, \end{aligned}$$

(130)

where $\gamma \left( a,x\right)$ denotes the lower incomplete gamma function [23, Eq. 8.2.1]. Notice as well that, according to Stirling’s formula [23, Eq. 5.11.3],

$$\begin{aligned} \varGamma \left( \nu \right) \approx \left( \frac{\nu }{\mathrm{e}}\right) ^{\nu }\sqrt{ \frac{2\pi }{\nu }},\qquad \nu \rightarrow \infty , \end{aligned}$$

(131)

so that, applying the duplication formula [23, Eq. 5.5.5],

$$\begin{aligned} \varGamma \left( 2z\right) =\frac{2^{2z-1}}{\sqrt{\pi }}\varGamma \left( z\right) \varGamma \left( z+\frac{1}{2}\right) ,\quad 2z\ne 0,-1,-2,\ldots , \end{aligned}$$

(132)

we obtain the following asymptotic formula:

$$\begin{aligned} \varGamma \left( \nu +\frac{1}{2}\right) \approx \sqrt{2\pi }\left( \frac{\nu }{\mathrm{e}}\right) ^{\nu },\quad \nu \rightarrow \infty . \end{aligned}$$

(133)

Therefore, from (130) and (133), we have

$$\begin{aligned} \underset{\nu \rightarrow \infty }{\lim }\frac{\mathrm {Yu}_{\nu }^{\left( j\right) }\left( u\right) }{\varGamma \left( \nu +\frac{1}{2}\right) }=\frac{1}{ 2}\gamma \left( j+1,u\right) \underset{\nu \rightarrow \infty }{\lim }\frac{ 2^{\nu }}{\sqrt{\nu }}. \end{aligned}$$

(134)

Therefore, taking $\nu =n/2$ in (134), we may calculate the following limit as

$$\begin{aligned} \underset{n\rightarrow \infty }{\lim }\frac{\left( -\mathrm {Bi\,}/\sqrt{2} \right) ^{n}}{\varGamma \left( \frac{n+1}{2}\right) }\mathrm {Yu}_{n/2}^{\left( j\right) }\left( u\right) =\frac{1}{\sqrt{2}}\gamma \left( j+1,u\right) \underset{n\rightarrow \infty }{\lim }\frac{\left( -\mathrm {Bi}\right) ^{n}}{ \sqrt{n}}. \end{aligned}$$

(135)

Thus, the convergence condition (127) is satisfied when $\mathrm {Bi}<1$, as we wanted to prove.

Next, we prove the sufficient condition. Note that (126) is an alternating series, and thus,

$$\begin{aligned} \sum _{n=0}^{\infty }\frac{\left( -\mathrm {Bi\,}/\sqrt{2}\right) ^{n}}{\varGamma \left( \frac{n+1}{2}\right) }\mathrm {Yu}_{n/2}^{\left( j\right) }\left( u\right) <\sum _{n=0}^{\infty }\frac{\left( \mathrm {Bi\,}/\sqrt{2}\right) ^{n} }{\varGamma \left( \frac{n+1}{2}\right) }\left| \mathrm {Yu}_{n/2}^{\left( j\right) }\left( u\right) \right| . \end{aligned}$$

(136)

According to (125), we have

$$\begin{aligned} \left| \mathrm {Yu}_{\nu }^{\left( j\right) }\left( u\right) \right|<\int _{0}^{\left| u\right| }\mathrm{e}^{-t}t^{j}t^{\nu }K_{\nu }\left( t\right) \mathrm {d}t<M\int _{0}^{\left| u\right| }t^{\nu }K_{\nu }\left( t\right) \mathrm {d}t<M\int _{0}^{\infty }t^{\nu }K_{\nu }\left( t\right) \mathrm {d}t, \end{aligned}$$

(137)

where we have set the finite bound

$$\begin{aligned} M=\max _{t\in \left( 0,\left| u\right| \right) }\left( \mathrm{e}^{-t}t^{j}\right) <\infty . \end{aligned}$$

(138)

Applying the following integral $\forall \mu =\nu$ [35, Eq. 6.561.16],

$$\begin{aligned} \int _{0}^{\infty }x^{\mu }K_{\nu }\left( x\right) \mathrm {d}x= & {} 2^{\mu -1}a^{-\mu -1}\varGamma \left( \frac{1+\mu +\nu }{2}\right) \varGamma \left( \frac{1+\mu -\nu }{2}\right) , \nonumber \\ \mathrm {Re}\left( \mu +1\pm \nu \right)> & {} 0,\quad \mathrm {Re\ }a>0, \end{aligned}$$

(139)

we obtain

$$\begin{aligned} \left| \mathrm {Yu}_{n/2}^{\left( j\right) }\left( u\right) \right| < \frac{M\sqrt{\pi }}{2}2^{n/2}\varGamma \left( \frac{n+1}{2}\right) . \end{aligned}$$

(140)

Inserting (140) in (136), we arrive at

$$\begin{aligned} \sum _{n=0}^{\infty }\frac{\left( -\mathrm {Bi\,}/\sqrt{2}\right) ^{n}}{\varGamma \left( \frac{n+1}{2}\right) }\mathrm {Yu}_{n/2}^{\left( j\right) }\left( u\right) <\frac{M\sqrt{\pi }}{2}\sum _{n=0}^{\infty }\mathrm {Bi\,}^{n}, \end{aligned}$$

(141)

which converges if $\mathrm {Bi}<1$, as we wanted to prove. $\square$

Appendix C: The Lambert W function

In order to solve x from

$$\begin{aligned} \exp \left( x^{a}\right) x^{b}=A, \end{aligned}$$

(142)

power to a / b both sides and multiply the resulting equation by a / b to obtain

$$\begin{aligned} \exp \left( \frac{a}{b}x^{a}\right) \frac{a}{b}x^{a}=\frac{a}{b}A^{a/b}. \end{aligned}$$

(143)

Performing the change $z=\frac{a}{b}x^{a}$, we have

$$\begin{aligned} \mathrm{e}^{z}z=\frac{a}{b}A^{a/b}. \end{aligned}$$

(144)

Knowing that the Lambert W function is the inverse function of $\mathrm{e}^{z}z$ [23, Sect. 4.13], we solve the above equation as

$$\begin{aligned} z=\mathrm {W}\left( \frac{a}{b}A^{a/b}\right) , \end{aligned}$$

(145)

and hence, undoing the change that was performed, we finally obtain

$$\begin{aligned} x=\left[ \frac{b}{a}\mathrm {W}\left( \frac{a}{b}A^{a/b}\right) \right] ^{1/a}. \end{aligned}$$

(146)