An analysis of the transient regime temperature field in wet grinding

Abstract

In this paper, the Samara–Valencia model for heat transfer in grinding is considered. This model is particularized to the case of wet grinding, assuming a constant heat transfer coefficient on the workpiece surface and a constant heat flux profile entering into the workpiece, obtaining a solution for the temperature field in the transient regime. Performing the limit $t\rightarrow \infty$ in this solution we get a formula analytically equivalent to the well-known solution given by DesRuisseaux for the steady-state temperature field. Also, we derive for the transient regime very simple formulas for relaxation times in wet and dry grinding.

Appendix A

1.1 A.1 Derivation of (5)

The heat equation for an instantaneous point heat source is

$$\begin{aligned} \frac{\partial G}{\partial t}-k\ \nabla ^{2}G=Q\ \delta \left( \vec {r}-\vec {r}^{\prime }\right) \ \delta \left( t-t^{\prime }\right) , \end{aligned}$$

(145)

subject to the boundary condition

$$\begin{aligned} \frac{\partial G}{\partial z}{\bigg \vert _{z=0}}=h_{0} G{\bigg \vert _{z=0}}, \end{aligned}$$

(146)

and the initial condition

$$\begin{aligned} \left. G\right| _{t=t^{\prime }}=0. \end{aligned}$$

We may split $G$ into two components:

$$\begin{aligned} G=G_{1}+G_{2}. \end{aligned}$$

(147)

On the one hand, $G_{1}$ satisfies the heat equation (145) for $z>0$, with a boundary condition as in (146) that is, however, homogeneous,

$$\begin{aligned} \frac{\partial G_{1}}{\partial z}{\bigg \vert _{z=0}}=0, \end{aligned}$$

(148)

and a homogeneous initial condition as well,

$$\begin{aligned} \left. G_{1}\right| _{t=t^{\prime }}=0. \end{aligned}$$

On the other hand, $G_{2}$ satisfies the heat equation (145), but without heat sources,

$$\begin{aligned} \frac{\partial G_{2}}{\partial t}-k\ \nabla ^{2}G_{2}=0,\quad z>0, \end{aligned}$$

(149)

with a homogeneous initial condition

$$\begin{aligned} \left. G_{2}\right| _{t=t^{\prime }}=0. \end{aligned}$$

(150)

The boundary condition that $G_{2}$ must satisfy can be obtained by finding the derivative with respect to $z$ in (147) and taking into account (148), (146), and (147), arriving at

$$\begin{aligned} \frac{\partial G_{2}}{\partial z}{\bigg \vert _{z=0}}=h_{0}\left[ G_{1}+G_{2}\right] _{z=0}. \end{aligned}$$

(151)

Since $G_{1}$ satisfies the heat equation for an instantaneous point source, we can apply the method of images to retain the boundary condition (148), using two point sources of the same strength $Q$, one located at $\left( x^{\prime },y^{\prime },z^{\prime }\right)$ and the other at $\left( x^{\prime },y^{\prime },-z^{\prime }\right)$. Since the Green function for an infinite solid $G_{\text {inf}}$ is [2, §10.2 (2)],

$$\begin{aligned} G_{\text {inf}}\left( \vec {r},t;\vec {r}^{\prime },t^{\prime }\right) =\frac{Q }{8\left[ \pi k\left( t-t^{\prime }\right) \right] ^{3/2}}\exp \left( -\frac{ \left( \vec {r}-\vec {r}^{\prime }\right) ^{2}}{4k\left( t-t^{\prime }\right) } \right) , \quad t>t^{\prime }, \end{aligned}$$

(152)

we have, for $t>t^{\prime }$,

$$\begin{aligned} G_{1}&=G_{\text {inf}}\left( \vec {r},t;x^{\prime },y^{\prime },z^{\prime },t^{\prime }\right) +G_{\text {inf}}\left( \vec {r},t;x^{\prime },y^{\prime },-z^{\prime },t^{\prime }\right) \nonumber \\&= \frac{Q}{8\left[ \pi k\left( t-t^{\prime }\right) \right] ^{3/2}}\exp \left( -\frac{\left( x-x^{\prime }\right) ^{2}+\left( y-y^{\prime }\right) ^{2}}{4k\left( t-t^{\prime }\right) }\right) \left[ \exp \left( -\frac{\left( z-z^{\prime }\right) ^{2}}{4k\left( t-t^{\prime }\right) }\right) +\exp \left( -\frac{\left( z+z^{\prime }\right) ^{2}}{4k\left( t-t^{\prime }\right) }\right) \right] . \end{aligned}$$

(153)

Once $G_{1}$ is calculated, substituting (153) into (151) yields the following boundary condition:

$$\begin{aligned} \frac{\partial G_{2}}{\partial z}\bigg \vert _{z=0}&= \frac{h_{0}Q}{4 \left[ \pi k\left( t-t^{\prime }\right) \right] ^{3/2}}\exp \left( -\frac{ \left( x-x^{\prime }\right) ^{2}+\left( y-y^{\prime }\right) ^{2}+z^{\prime 2}}{4k\left( t-t^{\prime }\right) }\right) +h_{0}\left. G_{2}\right| _{z=0}. \end{aligned}$$

(154)

Carrying out a change of variables

$$\begin{aligned} \tau =t-t^{\prime } \end{aligned}$$

(155)

in (149) and in (154), we obtain

$$\begin{aligned} \frac{\partial G_{2}}{\partial \tau }-k\ \nabla ^{2}G_{2}=0,\quad z>0, \end{aligned}$$

(156)

and

$$\begin{aligned} \frac{\partial G_{2}}{\partial z}\bigg \vert _{z=0}&= \frac{h_{0}Q}{ 4\left( \pi k\tau \right) ^{3/2}}\exp \left( -\frac{\left( x-x^{\prime }\right) ^{2}+\left( y-y^{\prime }\right) ^{2}+z^{\prime 2}}{4k\tau }\right) +h_{0}\left. G_{2}\right| _{z=0}, \end{aligned}$$

(157)

where we recall

$$\begin{aligned} G_{2}=G_{2}\left( x,y,z,\tau ;\vec {r}^{\prime }\right) . \end{aligned}$$

(158)

Since the solid is infinite in $x$, we may perform the Fourier transform in (158) on this variable $x$:

$$\begin{aligned} \hat{G}_{2}\left( \omega _{x},y,z,t;\vec {r}^{\prime }\right) =\mathcal {F}_{x} \left[ G_{2}\right] =\frac{1}{2\pi }\int _{-\infty }^{\infty }G_{2}\left( x,y,z,\tau ;\vec {r}^{\prime }\right) \ {\text {e}}^{\mathrm{i}\omega _{x}x}{\text {d}}x. \end{aligned}$$

Applying the Fourier transform properties [27, Eqns. 33.22; 33.40], we have

$$\begin{aligned} \mathcal {F}_{x}\left[ \exp \left( -\frac{\left( x-x^{\prime }\right) ^{2}}{ 4k\tau }\right) \right] =\frac{\sqrt{k\tau }}{\sqrt{\pi }}\exp \left( -k\tau \omega _{x}^{2}+{\text {i}}\omega _{x}x^{\prime }\right) . \end{aligned}$$

(159)

Thus, according to (159), the boundary condition (157) is transformed into

$$\begin{aligned} \frac{\partial \hat{G}_{2}}{\partial z}\bigg \vert _{z=0}&= \frac{h_{0}Q}{4\pi ^{2}k\tau }\exp \left( -\frac{\left( y-y^{\prime }\right) ^{2}+z^{\prime 2}}{4k\tau }\right) \exp \left( -k\tau \omega _{x}^{2}+{\text {i}}\omega _{x}x^{\prime }\right) +h_{0}\left. \hat{G}_{2}\right| _{z=0}. \end{aligned}$$

(160)

Similarly, performing again the Fourier transform on (160) but on the variable $y$, which is

$$\begin{aligned} \tilde{G}_{2}\left( \omega _{x},\omega _{y},z,\tau ;\vec {r}^{\prime }\right) =\mathcal {F}_{y}\left[ \hat{G}_{2}\right] =\frac{1}{2\pi }\int _{-\infty }^{\infty }\hat{G}_{2}\left( \omega _{x},y,z,\tau ;\vec {r}^{\prime }\right) \ {\text {e}}^{\mathrm{i}\omega _{y}y}\,{\text {d}}y, \end{aligned}$$

we obtain

$$\begin{aligned} \frac{\partial \tilde{G}_{2}}{\partial z}\bigg \vert _{z=0}&= \frac{ h_{0}Q}{4\pi ^{2}\sqrt{\pi k\tau }}\exp \left( -\frac{z^{\prime 2}}{4k\tau } -k\tau \left( \omega _{x}^{2}+\omega _{y}^{2}\right) \right) \exp \left[ {\text {i}}\left( \omega _{x}x^{\prime }+\omega _{y}y^{\prime }\right) \right] +h_{0}\left. \tilde{G}_{2}\right| _{z=0}. \end{aligned}$$

(161)

Last, we apply the Laplace transform on the variable $\tau$, which is

$$\begin{aligned} \bar{G}_{2}\left( \omega _{x},\omega _{y},z,s;\vec {r}^{\prime }\right) = \mathcal {L}\left[ \tilde{G}_{2}\right] =\int _{0}^{\infty }e_{2}^{-s\tau } \tilde{G}_{2}\left( \omega _{x},\omega _{y},z,\tau ;\vec {r}^{\prime }\right) {\text {d}}\tau . \end{aligned}$$

To do so, we may apply the Laplace properties [14, Eqn. 29.2.13; 29.3.84]; thus,

$$\begin{aligned} \mathcal {L}\left[ \frac{1}{\sqrt{\pi k\tau }}\exp \left( -\frac{z^{\prime 2} }{4k\tau }-k\tau \left( \omega _{x}^{2}+\omega _{y}^{2}\right) \right) \right] =\frac{\exp \left( -z^{\prime }\sqrt{\omega _{x}^{2}+\omega _{y}^{2}+s/k}\right) }{k\sqrt{\omega _{x}^{2}+\omega _{y}^{2}+s/k}}. \end{aligned}$$

(162)

Therefore, applying (162), the boundary condition (161) becomes

$$\begin{aligned} \frac{\partial \bar{G}_{2}}{\partial z}\bigg \vert _{z=0}&= \frac{h_{0}Q}{4\pi ^{2}k}\frac{\exp \left( -z^{\prime }\sqrt{\omega _{x}^{2}+\omega _{y}^{2}+s/k}\right) }{\sqrt{\omega _{x}^{2}+\omega _{y}^{2}+s/k}}\exp \Big ( {\text {i}}\left[ \omega _{x}x^{\prime }+\omega _{y}y^{\prime }\right] \Big ) +h_{0}\left. \bar{G}_{2}\right| _{z=0}. \end{aligned}$$

(163)

As we have done with the boundary condition, we may transform the heat equation for $G_{2}$, (156),

$$\begin{aligned} \frac{\partial ^{2}G_{2}}{\partial x^{2}}+\frac{\partial ^{2}G_{2}}{\partial y^{2}}+\frac{\partial ^{2}G_{2}}{\partial z^{2}}=\frac{1}{k}\frac{\partial G_{2}}{\partial \tau }. \end{aligned}$$

(164)

Applying the Fourier transform on the variables $x$ and $y$, taking into account the Fourier transform property for derivatives [27, Eq. 33.20], we obtain

$$\begin{aligned} -\omega _{x}^{2}\tilde{G}_{2}-\omega _{y}^{2}\tilde{G}_{2}+\frac{\partial ^{2}\tilde{G}_{2}}{\partial z^{2}}=\frac{1}{k}\frac{\partial \tilde{G}_{2}}{\partial \tau }. \end{aligned}$$

(165)

Performing now the Laplace transform on the variable $\tau$, applying the Laplace transform for derivatives [28, Eqn. 17.12.2], Eq. (165) becomes

$$\begin{aligned} k\left( -\omega _{x}^{2}\bar{G}_{2}-\omega _{y}^{2}\bar{G}_{2}+\frac{d^{2} \bar{G}_{2}}{dz^{2}}\right) =s\bar{G}_{2}-\left. \tilde{G}_{2}\right| _{\tau =0}. \end{aligned}$$

(166)

Notice that for $\tau =0$ (i.e., $t=t^{\prime }$), due to (150), we have

$$\begin{aligned} \left. \tilde{G}_{2}\right| _{\tau =0}=0, \end{aligned}$$

so (166) is rewritten as

$$\begin{aligned} \frac{d^{2}\bar{G}_{2}}{dz^{2}}=\left( \omega _{x}^{2}+\omega _{y}^{2}+\frac{s}{k}\right) \bar{G}_{2}, \end{aligned}$$

and the solution of this is

$$\begin{aligned} \bar{G}_{2}&= A\exp \left( -z\sqrt{\omega _{x}^{2}+\omega _{y}^{2}+s/k} \right) +B\exp \left( z\sqrt{\omega _{x}^{2}+\omega _{y}^{2}+s/k}\right) . \end{aligned}$$

(167)

To avoid a nondivergent solution for $\tilde{G}_{2}$ at $z\rightarrow \infty$ (recall that $z>0$), we must take $B=0$ in (167), so

$$\begin{aligned} \bar{G}_{2}=A\exp \left( -z\sqrt{\omega _{x}^{2}+\omega _{y}^{2}+s/k}\right) , \end{aligned}$$

(168)

and then

$$\begin{aligned} \left. \bar{G}_{2}\right| _{z=0}=A \end{aligned}$$

(169)

and

$$\begin{aligned} \frac{\partial \bar{G}_{2}}{\partial z}\bigg \vert _{z=0}=-A\sqrt{\omega _{x}^{2}+\omega _{y}^{2}+s/k}. \end{aligned}$$

(170)

Substituting (169) and (170) into (163) and solving, we arrive at

$$\begin{aligned} A=-\frac{h_{0}Q}{4\pi ^{2}k}\frac{\exp \left( -z^{\prime }\sqrt{\omega _{x}^{2}+\omega _{y}^{2}+s/k}\right) \exp \left( {\text {i}}\left[ \omega _{x}x^{\prime }+\omega _{y}y^{\prime }\right] \right) }{\sqrt{\omega _{x}^{2}+\omega _{y}^{2}+s/k}\left( \sqrt{\omega _{x}^{2}+\omega _{y}^{2}+s/k }+h_{0}\right) }. \end{aligned}$$

(171)

Substituting now (171) into (168), we obtain

$$\begin{aligned} \bar{G}_{2}=-\frac{h_{0}Q}{4\pi ^{2}}\frac{\exp \left( -\frac{z+z^{\prime }}{\sqrt{k}}\sqrt{k\left( \omega _{x}^{2}+\omega _{y}^{2}\right) +s}\right) \exp \Big ( {\text {i}}\left[ \omega _{x}x^{\prime }+\omega _{y}y^{\prime }\right] \Big ) }{\sqrt{k\left( \omega _{x}^{2}+\omega _{y}^{2}\right) +s}\left( \sqrt{k\left( \omega _{x}^{2}+\omega _{y}^{2}\right) +s}+h_{0}\sqrt{k}\right) }. \end{aligned}$$

(172)

To obtain $G_{2}$, we must inverse transform $\bar{G}_{2}$, first on variable $s$ to variable $\tau$, then on variable $\omega _{y}$ to variable $y$, and last on variable $\omega _{x}$ to variable $x$. From the Laplace transform properties [14, Eqns. 29.2.12; 29.3.90], we may inverse transform (172), obtaining

$$\begin{aligned} \tilde{G}_{2}&= -\frac{h_{0}Q}{4\pi ^{2}}\exp \left( {\text {i}}\left[ \omega _{x}x^{\prime }+\omega _{y}y^{\prime }\right] -k\tau \left[ \omega _{x}^{2}+\omega _{y}^{2}\right] \right) \exp \left( h_{0}\left[ z+z^{\prime }\right] +h_{0}^{2}k\tau \right) \ \mathrm {erfc}\left( h_{0}\sqrt{k\tau }+\frac{z+z^{\prime }}{2\sqrt{k\tau }}\right) . \end{aligned}$$

(173)

Now, from the Fourier transform properties [27, Eqns. 33.22; 33.41] we have

$$\begin{aligned} \mathcal {F}_{y}^{-1}\left[ \exp \left( {\text {i}}\omega _{y}y^{\prime }-k\tau \omega _{y}^{2}\right) \right] =\sqrt{\frac{\pi }{k\tau }}\exp \left( -\frac{\left( y-y^{\prime }\right) ^{2}}{4k\tau }\right) . \end{aligned}$$

(174)

Thus, performing the Fourier inverse transform on variable $\omega _y$ to variable $y$ in (173) and applying (174), we have

$$\begin{aligned} \hat{G}_{2}&= -\frac{h_{0}Q}{4\pi \sqrt{\pi k\tau }}\exp \left( -\frac{\left( y-y^{\prime }\right) ^{2}}{4k\tau }\right) \exp \left( {\text {i}}\omega _{x}x^{\prime }-k\tau \omega _{x}^{2}\right) \exp \left( h_{0}\left[ z+z^{\prime }\right] +h_{0}^{2}k\tau \right) \ \mathrm {erfc}\left( h_{0}\sqrt{k\tau }+\frac{z+z^{\prime }}{2\sqrt{k\tau }}\right) . \nonumber \\ \end{aligned}$$

(175)

Similarly, but performing now the Fourier inverse transform on variable $\omega _x$ to variable $x$ in (175), we arrive at

$$\begin{aligned} G_{2}&= -\frac{h_{0}Q}{4\pi k\left( t-t^{\prime }\right) }\exp \left( - \frac{\left( x-x^{\prime }\right) ^{2}+\left( y-y^{\prime }\right) ^{2}}{4k\left( t-t^{\prime }\right) }\right) \nonumber \\&\times \exp \left( h_{0}\left[ z+z^{\prime }\right] +h_{0}^{2}k\left[ t-t^{\prime }\right] \right) \ \mathrm {erfc}\left( h_{0}\sqrt{k\left( t-t^{\prime }\right) }+\frac{z+z^{\prime }}{2\sqrt{k\left( t-t^{\prime }\right) }}\right) , \end{aligned}$$

(176)

where we have taken (155) into account. Finally, substituting the results given in (153) and (176) into (147), we get

$$\begin{aligned} G&= G_{1}+G_{2} = \frac{Q}{4\pi k\left( t-t^{\prime }\right) }\exp \left( -\frac{\left( x-x^{\prime }\right) ^{2}+\left( y-y^{\prime }\right) ^{2}}{4k\left( t-t^{\prime }\right) }\right) \nonumber \\&\times \left\{ \frac{1}{2\sqrt{\pi k\left( t-t^{\prime }\right) }}\left[ \exp \left( -\frac{\left( z-z^{\prime }\right) ^{2}}{4k\left( t-t^{\prime }\right) }\right) +\exp \left( -\frac{\left( z+z^{\prime }\right) ^{2}}{ 4k\left( t-t^{\prime }\right) }\right) \right] \right. \nonumber \\&-\left. h_{0}\ {\text {e}}^{h_{0}\left( z+z^{\prime }\right) +h_{0}^{2}k\left( t-t^{\prime }\right) }\ \mathrm {erfc}\left( h_{0}\sqrt{ k\left( t-t^{\prime }\right) }+\frac{z+z^{\prime }}{2\sqrt{k\left( t-t^{\prime }\right) }}\right) \right\} . \end{aligned}$$

(177)

1.2 A.2 Derivation of (7)

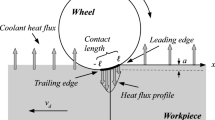
In the literature [12, Eq. 4–11], we find the following expression for the transient temperature distribution due to a continously acting band heat source on the surface of a moving body (Fig. 1) considering a constant heat band source strength $q$, a constant heat transfer coefficient $h$ on the surface, and a zero initial temperature, $T_{\text {r}}=0$,

$$\begin{aligned} T_{\text {wet}}\left( t,x,z\right) =T_{\text {dry}}\left( t,x,z\right) +\Delta T_{\text {wet}}\left( t,x,z\right) , \end{aligned}$$

where

$$\begin{aligned} T_{\text {dry}}\left( t,x,z\right)&= \frac{q}{2\pi k\rho c}\int _{-\ell }^{\ell }\int _{0}^{t}\frac{1}{t-t^{\prime }}\exp \left( -\frac{z^{2}+\left\{ x-x^{\prime }+v_{f}\left( t-t^{\prime }\right) \right\} ^{2}}{4k\left( t-t^{\prime }\right) }\right) \, {\text {d}}t^{\prime }\,{\text {d}}x^{\prime } \end{aligned}$$

(178)

and

$$\begin{aligned} \Delta T_{\text {wet}}\left( t,x,z\right)&= -\frac{qh_{0}{\text {e}}^{h_{0}z}}{2\rho c\sqrt{\pi k}}\int _{-\ell }^{\ell }\int _{0}^{t} \frac{1}{\sqrt{t-t^{\prime }}}\mathrm {erfc}\left( \frac{z}{2\sqrt{ k\left( t-t^{\prime }\right) }}+h_{0}\sqrt{k\left( t-t^{\prime }\right) } \right) \nonumber \\&\times \exp \left( kh_{0}^{2}\left( t-t^{\prime }\right) -\frac{\left\{ x-x^{\prime }+v_{f}\left( t-t^{\prime }\right) \right\} ^{2}}{4k\left( t-t^{\prime }\right) }\right) \, {\text {d}}t^{\prime }\,{\text {d}}x^{\prime }. \end{aligned}$$

(179)

Performing a change of variables $u=t-t^{\prime }$ in (178) and (179) and exchanging the integration order, we get

$$\begin{aligned} T_{\text {dry}}\left( t,x,z\right)&= \frac{q}{2\pi k\rho c} \int _{0}^{t}\int _{-\ell }^{\ell }\frac{1}{u}\exp \left( -\frac{z^{2}}{4ku}\right) \exp \left( -\frac{\left\{ x-x^{\prime }+v_{f}u\right\} ^{2}}{4ku} \right) \, {\text {d}}x^{\prime }{\text {d}}u \end{aligned}$$

(180)

and

$$\begin{aligned} \Delta T_{\text {wet}}\left( t,x,z\right)&= -\frac{qh_{0}{\text {e}}^{h_{0}z}}{2\rho c \sqrt{\pi k}}\int _{0}^{t}\int _{-\ell }^{\ell }\frac{{\text {e}}^{kh_{0}^{2}u}}{\sqrt{u} }\mathrm {erfc}\left( \frac{z}{2\sqrt{ku}}+h_{0}\sqrt{ku}\right) \exp \left( -\frac{\left\{ x-x^{\prime }+v_{f}u\right\} ^{2}}{4ku} \right) \, {\text {d}}x^{\prime }{\text {d}}u. \end{aligned}$$

(181)

Performing now a change of variables $\xi =\left\{ x-x^{\prime }+v_{f}u\right\} /( 2\sqrt{ku})$ in (180) and (181), we arrive at

$$\begin{aligned} \int _{-\ell }^{\ell }\exp \left( -\frac{\left\{ x-x^{\prime }+v_{f}u\right\} ^{2}}{4ku}\right) {\text {d}}x^{\prime }&= 2\sqrt{ku}\int _{\left( x-\ell +v_{f}u\right) /( 2\sqrt{ku}) }^{\left( x+\ell +v_{f}u\right) /( 2\sqrt{ku}) }\exp \left( -\xi ^{2}\right) {\text {d}}\xi \nonumber \\&= \sqrt{\pi ku}\left[ \mathrm {erf}\!\left( \frac{x+\ell +v_{f}u}{2\sqrt{ku}} \right) -\mathrm {erf}\!\left( \frac{x-\ell +v_{f}u}{2\sqrt{ku}}\right) \right] . \end{aligned}$$

(182)

Therefore, substituting (182) into (180) and (181), we finally obtain

$$\begin{aligned} T_{\text {dry}}\left( t,x,z\right)&= \frac{q}{2\rho c\sqrt{\pi k}} \int _{0}^{t}\exp \left( -\frac{z^{2}}{4ku}\right) \left[ \mathrm {erf}\!\left( \frac{x+\ell +v_{f}u}{2\sqrt{ku}}\right) - \mathrm {erf}\!\left( \frac{x-\ell +v_{f}u}{2\sqrt{ku}}\right) \right] \frac{\mathrm{d}u }{\sqrt{u}} \end{aligned}$$

and

$$\begin{aligned} \Delta T_{\text {wet}}\left( t,x,z\right)&= -\frac{qh_{0}{\text {e}}^{h_{0}z}}{2\rho c} \int _{0}^{t}{\text {e}}^{kh_{0}^{2}u}\mathrm {erfc}\left( \frac{z}{2\sqrt{ku}}+h_{0} \sqrt{ku}\right) \left[ \mathrm {erf}\!\left( \frac{x+\ell +v_{f}u}{2\sqrt{ku}}\right) - \mathrm {erf}\!\left( \frac{x-\ell +v_{f}u}{2\sqrt{ku}}\right) \right] {\text {d}}u, \end{aligned}$$

which correspond to (6) and (7), respectively.

1.3 A.3 Derivation of (9)

Indeed, straightforwardly from (3) and (7) we have

$$\begin{aligned} \underset{t\rightarrow \infty }{\lim }\Delta T_{\text {wet}}\left( x,z,t\right) =\Delta T_{\text {wet}}\left( x,z\right) . \end{aligned}$$

Thus, we must prove

$$\begin{aligned} \underset{t\rightarrow \infty }{\lim }T_{\text {dry}}\left( x,z,t\right) =T_{ \text {dry}}\left( x,z\right) . \end{aligned}$$

To do so, let us rewrite (7) as

$$\begin{aligned} \mathrm {erf}\!\left( \frac{x+\ell +v_{f}u}{2\sqrt{ku}}\right) -\mathrm {erf}\! \left( \frac{x-\ell +v_{f}u}{2\sqrt{ku}}\right)&= \frac{2}{\sqrt{\pi }}\int _{\left( x-\ell +v_{f}u\right) /( 2\sqrt{ku} ) }^{\left( x+\ell +v_{f}u\right) /( 2\sqrt{ku}) }\exp \left( -s^{2}\right) {\text {d}}s \nonumber \\&= \frac{1}{\sqrt{\pi ku}}\int _{-\ell }^{\ell }\exp \left( -\left[ \frac{ x-x^{\prime }+v_{f}u}{2\sqrt{ku}}\right] ^{2}\right) \, {\text {d}}x^{\prime }. \end{aligned}$$

(183)

Thus, substituting (183) into (7), exchanging the integration order, and taking the limit $t\rightarrow \infty$, we arrive at

$$\begin{aligned} \underset{t\rightarrow \infty }{\lim }T_{\text {dry}}\left( x,z,t\right)&= \frac{q}{2\rho c\sqrt{\pi k}}\int _{-\ell }^{\ell }\int _{0}^{\infty }\exp \left( -\frac{v_{f}\left( x-x^{\prime }\right) }{2k}\right) \frac{1}{u}\exp \left( -\frac{z^{2}+\left( x-x^{\prime }\right) ^{2} }{4ku}-\frac{v_{f}^{2}}{4k}u\right) \, {\text {d}}u\,{\text {d}}x^{\prime }. \end{aligned}$$

(184)

Using the integral representation [22, Eqn. 5.10.25],

$$\begin{aligned} K_{\nu }\left( z\right)&= \frac{1}{2}\left( \frac{z}{2}\right) ^{\nu }\int _{0}^{\infty }\exp \left( -t-\frac{z^{2}}{4t}\right) t^{-\nu -1}{\text {d}}t, \\ \left| \mathrm {arg}\,z\right|&< \frac{\pi }{4}, \end{aligned}$$

we may rewrite (184) as

$$\begin{aligned} \int _{0}^{\infty }\exp \left( -\frac{z^{2}+\left( x-x^{\prime }\right) ^{2}}{4ku}-\frac{v_{f}^{2}}{4k}u\right) \frac{{\text {d}}u}{u}=2K_{0}\left( \frac{\left| v_{f}\right| }{2k}\sqrt{\left( x-x^{\prime }\right) ^{2}+z^{2}}\right) . \end{aligned}$$

(185)

Inserting now (185) into (184), we finally get (1), as we wished to prove.