Abstract
The availability of technology in the mathematics classroom challenges the way teachers orchestrate student learning. Using the theory of instrumental orchestration as the main interpretative framework, this study investigates which types of orchestrations teachers develop when using technology and to what extent these are related to teachers’ views on mathematics education and the role of technology therein. Data consisted of videotapes of 38 lessons taught by three teachers, who also provided information on their views through questionnaires and interviews. Qualitative analysis of these data led to the identification of orchestration types and teacher profiles. The orchestration preferences of the three teachers proved to be related to their views. A detailed analysis of one exemplary episode suggests how other theoretical perspectives might complement the theory of instrumental orchestration.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In spite of technology’s recognised potential for teaching and learning, its integration into secondary mathematics education lags behind the high expectations that many researchers and educators had some decades ago (Lagrange, Artigue, Laborde & Trouche, 2003). The role of the teacher has been acknowledged as both a critical and a problematic factor in this integrative process (Artigue, Drijvers, Lagrange, Mariotti & Ruthven, 2009; Doerr & Zangor, 2000; Lagrange & Ozdemir Erdogan, 2009; Monaghan, 2004; Ruthven & Hennessy, 2002). It is critical in the sense that the way in which teachers approach the use of technology has major consequences for the effects of its use in the classroom (Kendal & Stacey, 2002). It is problematic, as teachers who do not perceive the use of technology in their teaching as valuable for their educational goals are able to avoid it, unless explicitly required to do so by institutional or curriculum constraints. Also, teachers often experience difficulties in adapting their teaching techniques (Sensevy, Schubauer-Leoni, Mercier, Ligozat & Perrot, 2005) to situations in which technology plays a role (Monaghan, 2004).
What is difficult from a teacher’s perspective in integrating technology into his or her mathematics teaching? Robert and Rogalski (2005) point out that teachers’ practices are both complex and stable. Building on this, Lagrange and Monaghan (2009) argue that the availability of technology amplifies the complexity and, as a consequence, challenges the stability of teaching practices: techniques that are used in ‘traditional’ settings can no longer be applied in a routine-like manner when technology is available. A new repertoire of teaching techniques, instrumented by the available tools, has to be developed. These new techniques are likely to be related to already existing ones as well as to the teachers’ underlying views on mathematics education (Pierce & Ball, 2009).
In order to help teachers to benefit from technology in everyday mathematics teaching, therefore, it is important to have more knowledge about the new teaching techniques that emerge in the technology-rich classroom and how these relate to teachers’ views on mathematics education and the role of technology therein.
2 Theoretical framework and research questions
The main theoretical perspective that informs our investigation of teacher behaviour in a technology-rich environment is the instrumental approach to tool use, and the notion of instrumental orchestration in particular.
The instrumental approach acknowledges the complexity of using technology within mathematics education (Artigue, 2002). According to this approach, the use of a technological tool involves a process of instrumental genesis, during which the object or artefact is turned into an instrument. This instrument is a psychological construct, which combines the artefact and the schemes (in the sense of Vergnaud, 1996) the user develops to use it for specific types of tasks. In such instrumentation schemes, technical knowledge about the artefact and domain-specific knowledge (in this case, mathematical knowledge) are intertwined. Instrumental genesis, therefore, is essentially the co-emergence of schemes and techniques for using the artefact.
Many studies focus on students’ instrumental genesis and its possible benefits for learning (e.g. see Kieran & Drijvers, 2006). However, it was acknowledged that students’ instrumental geneses need to be guided by the teacher through the orchestration (McKenzie, 2001) of mathematical situations (Mariotti, 2002). For example, Kendal and colleagues (Kendal & Stacey, 2002; Kendal, Stacey, & Pierce, 2004) showed that teachers privilege certain techniques for using technological tools over others and, in this way, guide the students’ acquisition of tool mastery and their learning processes. To describe how the teacher can fine-tune the students’ individual instruments and compose coherent sets of instruments within the classroom, thus enhancing both individual and collective geneses, Trouche (2004) introduced the metaphor of instrumental orchestration.
An instrumental orchestration is defined as the teacher’s intentional and systematic organisation and use of the various artefacts available in a—in this case computerised—learning environment in a given mathematical task situation, in order to guide students’ instrumental genesis (Trouche, 2004). We distinguish three elements within an instrumental orchestration: a didactic configuration, an exploitation mode and a didactical performance. These three elements are now described in more detail.
A didactical configuration is an arrangement of artefacts in the environment, or, in other words, a configuration of the teaching setting and the artefacts involved in it. In the musical metaphor of orchestration, setting up the didactical configuration can be compared with choosing musical instruments to be included in the band, and arranging them in space so that the different sounds result in polyphonic music, which in the mathematics classroom might come down to a sound and converging mathematical discourse.
An exploitation mode is the way the teacher decides to exploit a didactical configuration for the benefit of his or her didactical intentions. This includes decisions on the way a task is introduced and worked through, on the possible roles of the artefacts to be played, and on the schemes and techniques to be developed and established by the students. Decisions on the exploitation mode can be seen as part of the design of a Hypothetical Learning Trajectory (Simon, 1995). In terms of the metaphor of orchestration, setting up the exploitation mode can be compared with determining the partition for each of the musical instruments involved, bearing in mind the anticipated harmonies that will emerge.
A didactical performance involves the ad hoc decisions taken while teaching on how to actually perform in the chosen didactic configuration and exploitation mode: what question to pose now, how to do justice to (or to set aside) any particular student input, how to deal with an unexpected aspect of the mathematical task or the technological tool, or other emerging goals.
In the metaphor of orchestration, the didactical performance can be compared to a musical performance, in which the actual interplay between conductor and musicians reveals the feasibility of the intentions and the success of their realisation.
Didactical configurations and exploitation modes were introduced by Trouche (2004). As an instrumental orchestration is partially prepared beforehand and partially created ‘on the spot’ while teaching, we felt the need to add the actual didactical performance as a third component. Establishing the didactical configuration has a strong preparatory aspect: often, didactical configurations need to be thought of before the lesson and cannot easily be changed during it. Exploitation modes may be more flexible, while didactical performances have a strong ad hoc aspect. As such, the threefold model has a time dimension.
The model also has a global–local dimension. An instrumental orchestration has a global component, in that it is part of the teacher’s repertoire of teaching techniques. It also has an incidental, local actualisation appropriate for the specific didactical context and adapted to the target group and the didactical intentions.
Even if the metaphor of instrumental orchestration is appealing, it has its limitations like every metaphor. If we think of a teacher as a conductor of a symphony orchestra consisting of highly skilled musicians, who enters the concert hall with a clear idea on how to make the musicians play Mahler the way he himself reads the century-old partition, we might feel uneasy. However, if we think of the class as a jazz band, consisting of both novice and more advanced musicians, and the teacher being the band leader who prepared a global partition but is open for improvisation and interpretation by the students, and for doing justice to input at different levels, the metaphor makes more sense. It is in the latter way that we suggest to understand it.
Despite the potential of the instrumental orchestration model to help understand teachers’ practices in the technology-rich classroom, the number of elaborated examples of instrumental orchestrations described in the research literature to date is limited (Drijvers & Trouche, 2008; Trouche, 2004). Meanwhile, our goal formulated above is to find out which new teaching techniques emerge in the technology-rich classroom. In terms of the instrumental orchestration framework, one aim of this study is to identify different types of orchestrations. Therefore, the first research question is:
-
(1)
Which types of instrumental orchestration emerge in technology-rich classroom teaching?
As a means to make this research question feasible to deal with, we limit ourselves here to orchestrations in whole-class teaching. Of course, other organisations of the learning, such as individual student work and work in pairs or groups, are also important, but we address them elsewhere (Drijvers, submitted).
The process of a teacher developing instrumental orchestrations is guided by his or her knowledge of, experience with and views on mathematics education and the role of technology herein (Pierce & Ball, 2009). This includes the teachers’ own knowledge and skills concerning the integration of technology, and their concerns about time constraints and behavioural control. Gueudet and Trouche (2009) refer to these often implicit guidelines which drive a teacher’s choices as operational invariants. Such operational invariants can be very general, such as ‘learning takes place through interaction’, or more specific to the role of technology, for example ‘technology offers means to improve classroom interaction’. These operational invariants work out in types of invariant teacher behaviours, which are instrumented by the available tools. The notions of operational invariants and teachers’ views are used in this study to interpret the information from teachers in relation to their observed orchestrational behaviour. The second aim of this study, phrased in the introduction as the investigation of how teaching techniques relate to teachers’ views on mathematics education and the role of technology therein, is reformulated in terms of the instrumental orchestration framework as the following second research question:
-
(2)
To what extent are teachers’ repertoires of orchestrations related to their expressed views on mathematics education and the role of technology therein?
The way in which we answer these questions with instrumental orchestration as a framework can be considered as a test regarding the suitability and value of instrumental orchestration as an interpretative lens for research into teaching with technological tools. As such, our ‘hidden agenda’ is to contribute to the development of this model, its evaluation in terms of affordances and limitations, and its articulation with other theoretical approaches.
3 Research context
The research questions are addressed in the context of a research project on a technology-rich learning arrangement for the concept of functionFootnote 1. In this project, a learning arrangement for eighth-grade students as designed. The design was guided by Realistic Mathematics Education principles (Gravemeijer, 1994). The arrangement, which consisted of eight 50-min lessons, aimed at the development of a rich function concept, whereby functions are conceptualised as input–output assignments, as dynamic processes of co-variation and as mathematical objects with different representations (Drijvers, Doorman, Boon, Van Gisbergen & Gravemeijer, 2007; Slavit, 1997). The design of the learning materials was directed by a hypothetical learning trajectory, in which the expected conceptual development was guided and facilitated by means of activities carried out with a technological tool. An accompanying teacher guide contained suggestions and working formats for appropriate teaching techniques and included a planning scheme.
The main technological component of the learning arrangement is a Java applet called Algebra Arrows. The applet was embedded in an electronic learning environment called the Digital Mathematics Environment (DME). The applet allows for the construction and use of chains of operations (so-called arrow chains) and provides options for creating tables, graphs and formulae and for scrolling and tracing. The DME allows students to access their work from any location, and the teacher to access this work in order to monitor progress and track the conceptual development of the students. Figure 1 shows these digital tools. The right part is the Algebra Arrows window, in which students create and use their representations. At the left, the DME provides tasks and boxes in which the students type their answers. The numbered circles at the bottom of the screen allow for navigation through the tasks, the underlined one currently indicating task 2.
Besides teacher orchestration, other foci of this research project are students’ learning (Doorman, Boon, Drijvers, Van Gisbergen, Gravemeijer & Reed, 2009) and the relationships between learning outcomes and student attitudes and behaviours (Reed, Drijvers & Kirschner, 2010).
4 Method
The intervention consisted of the implementation of the above described learning arrangement in 29 eighth-grade classrooms in one Belgian and nine Dutch schools in three research cycles, each consisting of a (re)design phase, a teaching experiment phase and a phase of data analysis (Gravemeijer, 1994). In terms of the orchestration model, this learning arrangement offers tools and tasks, which are part of the didactical configuration, as well as suggestions in the teacher guide concerning exploitation modes. The teachers’ freedom, therefore, mainly concerned the configuration of the classroom setting, the exploitation mode and the didactical performance. The resulting orchestrations are the outcome of both the design by the researchers and the choices of the teachers themselves.
To investigate the first research question concerning the types of orchestration which emerge in technology-rich classroom teaching, video tapes were analysed of 38 lessons taught in five classes by three female mathematics teachers who volunteered to participate in the research project. The three were experienced teachers; however, the use of technology in this specific learning arrangement was new to them. One of these teachers taught the arrangement each of the three cycles, the others each taught it once. The three teachers were chosen so as to have some variety in their educational level (degree for upper secondary or lower secondary education, respectively) and school type (gymnasium or general secondary school).
For reasons mentioned above, data analysis focused on whole-class episodes in which technology was used. The unit of analysis was an episode, which was defined as the whole-class treatment of a single DME-task. If this treatment contained different orchestration types, the episode was cut into sub-episodes, each with a unique orchestration type. In this way, a corpus of 83 (sub-)episodes was identified. These were organised and analysed with the help of software for qualitative data analysisFootnote 2. The analysis was carried out in a bottom-up manner, though partly driven by theory (e.g. Kendal & Stacey, 2002; Pierce & Ball, 2009; Trouche, 2004). Six orchestration types were identified and the corpus was coded according to this categorization. A second coding of 24 episodes (29%) was done by a co-researcher and led to a good inter-rater reliability (a Cohen’s kappa of .72).
To investigate the second research question on the relationships between the types of orchestrations and teachers’ views on mathematical learning and teaching and the role of technology therein, each of the three teachers’ orchestrations were analysed on the basis of their observed teaching behaviours, and possible operational invariants were identified. Then, the teachers’ answers to an online questionnaire were used to obtain insight into their self-reported views. The questionnaire consisted of 40 items on a five-point rating scale, with the range of answers from ‘strongly agree’ to ‘strongly disagree’. Items were derived from previous research in this area and addressed the influence of technology on students’ learning and attitudes, on the lesson organisation, and on the role of the teacher (Drijvers et al., 2007; Reed et al., 2010). Teachers’ self-reported views and their observed orchestrations were then integrated to produce a profile for each of the three teachers, which was validated through a semi-structured post-intervention interview with the teacher concerned. To further explore the value of the instrumental orchestration framework, transcripts of a limited number of episodes were analysed in more detail.
5 Results
The results presented below consist of (1) a global inventory of observed orchestration types, (2) their frequency distribution over the three teachers involved, (3) profiles of three participating teachers with respect to their orchestrations and their views on mathematics education and the role of technology therein, and (4) an extended analysis of one exemplary episode.
5.1 A global inventory of orchestration types
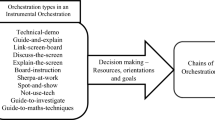
Six orchestration types were identified through a combination of theory-driven and data-driven analysis; these were termed Technical-demo, Explain-the-screen, Link-screen-board, Discuss-the-screen, Spot-and-show, and Sherpa-at-work. Each of these orchestration types is briefly described in terms of the first two elements of orchestration theory—i.e., didactical configuration and exploitation mode—and is illustrated by a short example. The localised, ad hoc nature of the third element of an instrumental orchestration—the didactical performance—makes it unsuitable for inclusion in this global inventory.
The Technical-demo orchestration concerns the demonstration of tool techniques by the teacher. It is recognised as an important aspect of technology-rich teaching (Monaghan, 2001, 2004). A didactical configuration for this orchestration includes access to the applet and the DME, facilities for projecting the computer screen, and a classroom arrangement that allows the students to follow the demonstration. As exploitation modes, teachers can demonstrate a technique in a new situation or task, or use student work to show new techniques in anticipation of what will follow. As an example, teachers exploited this orchestration type to demonstrate the technique of making an arrow chain of operations, or to draw a graph and scale it with the buttons above the graph window (see Fig. 1). Demonstration-like orchestrations are also well-known in non-technological teaching settings; however, the type of demonstration seen here is instrumented by the technical tools and also specific to the tool’s opportunities and constraints.
The Explain-the-screen orchestration concerns whole-class explanation by the teacher, guided by what happens on the computer screen. The explanation goes beyond techniques, and involves mathematical content. Didactical configurations can be similar to the Technical-demo ones. As exploitation modes, teachers may take student work as a point of departure for the explanation, or start with their own solution to a task. As an example, one teacher used the inverse arrow chain of the square chain to explain that square roots are always non-negative numbers. Explanatory orchestrations, of course, are also used in non-technological teaching settings, where they might be called Explain-the-board. The phenomena encountered in the technological environment, however, are often different from the ones faced at the traditional blackboard.
In the Link-screen-board orchestration, the teacher stresses the relationship between what happens in the technological environment and how this is represented in conventional mathematics of paper, book and blackboard. In addition to DME access and projection facilities, a didactical configuration includes a blackboard and a classroom setting such that both screen and board are visible. Similarly to the previously mentioned orchestration types, teachers’ exploitation modes may take student work as a point of departure or start with a task or problem situation they set themselves. As an example, teachers copied arrow chains from the screen to the board, often in abbreviated and more conventional mathematical forms. This orchestration type is specific to the technology used. Because transfer to paper-and-pencil is known to be a problematic issue (Billington, 2009; Bretscher, 2009; Kieran & Drijvers, 2006), this kind of orchestration was one of our a priori foci.
The Discuss-the-screen orchestration concerns a whole-class discussion about what happens on the computer screen. The goal is to enhance collective instrumental genesis. A didactical configuration includes DME access and projecting facilities, preferably access to student work, and a classroom setting favourable for discussion. As exploitation modes, student work, a task, or a problem or approach set by the teacher can serve as the point of departure for student reactions. As an example, one teacher used a screen similar to the one in Fig. 1 to discuss different ways of finding a break-even point. Of course, discussing results on the blackboard is a common teaching strategy. The advantage of discussion in a technological environment is that suggestions for different representations and techniques, as they emerge in the discussion, can be easily tried out, with fast and dynamic feedback on obtained outcomes.
In the Spot-and-show orchestration, student reasoning is brought to the fore through the identification of interesting DME student work during preparation of the lesson, and its deliberate use in a classroom discussion. Besides previously mentioned features, a didactical configuration includes access to the DME during lesson preparation. As exploitation modes, teachers may have the students whose work is shown explain their reasoning, and ask other students for reactions, or themselves provide feedback on the student work. An example of Spot-and-show is given in the episode elaborated below. In that episode the teacher spots an inappropriate answer in a student solution while preparing the lesson, and discusses it with the whole class during the lesson. As this orchestration depends on the facilities offered to the teacher to browse through the DME student work, it is technology-specific and instrumented by the DME.
In the Sherpa-at-work orchestration, a so-called Sherpa-student uses the technology to present his or her work, or to carry out actions the teacher requests. Didactical configurations are similar to the Discuss-the-screen orchestration type. The classroom setting should be such that the Sherpa-student can be in control of using the technology, with all students able to follow the actions of both Sherpa-student and teacher easily. As exploitation modes, teachers may have work presented or explained by the Sherpa-student, or may pose questions to the Sherpa-student and ask him/her to carry out specific actions in the technological environment. As an example, one teacher had students using the computer and data projector to show a family of graphs, explain their reasoning and change the screen as requested by the teacher. This orchestration type is described in the literature (Trouche, 2004) and was therefore derived a priori from theory rather than emerging from the data.
A reflection on this set of six identified orchestration types led to the distinction of a teacher-student dimension. In Technical-demo, Explain-the-screen and Link-screen-board, the teacher dominates the communication. Student input is restricted and the teacher guides the interactions in an Initiation-Response-Evaluation pattern. These orchestrations can be seen as teacher-centred.
In Discuss-the-screen, Spot-and-show and Sherpa-at-work orchestrations, students have the opportunity to react and have more input. Even though the teacher manages the orchestration, there is more interaction and students have more voice than in the first three orchestration types. These can therefore be seen as student-centred orchestrations.
Another remark on this inventory is that the orchestrations are not isolated, but part of orchestrational sequences, and play particular roles in such a sequence. For instance, Technical-demo was often observed to precede and prepare for a phase of individual student work, to improve the efficiency of the latter phase. Spot-and-show orchestrations, and to a lesser extent Sherpa-at-work and Discuss-the-screen orchestrations, often exploit previous student work, individually or in pairs.
In summary, six orchestration types were identified, which differ in their focus on the teacher or the student as driving the orchestration and in the degree of technological specificity: some can be seen as technological variants of regular teaching practices most teachers are familiar with, whereas others are more specific to the use of technology or to the use of the tools used in this study in particular.
5.2 Frequency distribution of types of orchestrations over three teachers
Table 1 shows the frequencies of the orchestration types for each of the three teachers and, for teacher A, for each of the three times she taught the lesson series. Technical-demo is the most frequently used orchestration type. In the post-intervention interviews, the three teachers said they felt the need to familiarise students with basic tool techniques, in order to prevent technical obstacles hindering the subsequent mathematical activities: some basic technical knowledge is needed and demonstrations can be an efficient means to provide it. This also avoided the teacher having to do too much “techno trouble shooting” (Monaghan, 2004, p. 346) or acting as “technical assistant” (Lagrange & Caliskan-Dedeoglu, 2009) during the work in pairs. In the interview, Teacher C explained the importance of Technical-demo as follows:
I want to prevent students from encountering technical difficulties while they are at work with the computer … and have to wait for my help, whereas it often concerns a minor issue.
The Spot-and-show orchestration also occurs frequently, but is unevenly spread over the three teachers. Although all three indicated in the post-intervention interview that they appreciated the facility to browse through the DME student work while preparing the next lesson, this orchestration type was mainly exploited by teacher B, who said:
The DME is practical for seeing what students do—you can use it to fine-tune your lesson.
The teacher guide, which the teachers received before the start of the teaching sequence, contained suggestions for teaching strategies which, in retrospect, match some of the identified orchestration types. A comparison of the suggested orchestrations in the teacher guide with the observed frequencies in Table 1 reveals that Link-screen-board and Discuss-the-screen were not suggested in the teacher guide, but were nevertheless quite frequently observed. Sherpa-at-work, on the contrary, was suggested several times in the teacher guide but was not popular with two of the three teachers. This shows that teachers felt free to adapt the suggestions in the teacher guide and make their own choices independently from it. We will come back to this in the discussion section that concludes this paper.
5.3 Teacher profiles of orchestrations and views on mathematics education and technology
Table 1 reveals a number of differences between the three teachers. In order to explain them, we related them to teachers’ answers to the questionnaire and the post-intervention interviews.
5.3.1 Teacher A
Table 1 shows that teacher A has slightly lower overall frequencies than teachers B and C. This corresponds to the observation that she takes time for her orchestrations to play out, and does not switch between orchestrations as fast as the other teachers. Apart from Technical-demo, which was discussed above, teacher A has relatively high frequencies for Discuss-the-screen and for Sherpa-at-work orchestrations. These are student-centred orchestration types, which teacher A used to evoke interaction between the students and herself. The underlying operational invariant is that students should be given a voice and that teaching should enable students to learn through interaction. In her classroom discussions, elements such as idea generation, comparison, evaluation and filtering (Sherin, 2002) can be traced.
Teacher A’s views on mathematics education and the role of technology, as she expressed it in the questionnaire and the post-intervention interview, stress the importance of interaction in the classroom. She sees technology as a means to stimulate this:
…so you can have discussions with the students using the images that you saw on the screen, … that makes it more lively.
Her observed orchestration behaviour can be related to these views. For example, her agreement with the questionnaire statement ‘As a teacher, one has to tell students clearly what they should do with ICT’ matches her use of Technical-demo orchestrations. She also agreed with the statements ‘The use of ICT gives the teacher more possibilities to build on students’ ideas during whole-class discussions’ and ‘The use of ICT creates shared images and experiences which one can discuss with the students', which explains her preference for student-centred orchestrations, in which discussion and interaction play important roles.
In the post-intervention interview, teacher A mentioned time constraints as the main reason not to use Sherpa-at-work in the third cycle. Technical constraints (e.g. slow internet connections during the first cycle or inappropriate classroom settings in the computer lab) also drove her choices for orchestrations, as well as practical issues such as the features of the classroom in which the lesson takes place: how are the tables arranged, how are the computers set up, is Internet access available, and so forth.
In short, the profile of teacher A is that of a teacher who prioritises student-centred orchestrations. This relates to her view on learning as an interactive process in which students should have a voice. Technology is a means to achieve this, and offers new possibilities for teaching mathematics in an interactive way.
5.3.2 Teacher B
Table 1 shows that teacher B has relatively high frequencies for Link-screen-board, and particularly for Spot-and-show. Technical-demo is not often used, possibly due to the fact that her class consisted of high-achieving students who are used to working independently and therefore might not need so much technical instruction. The Link-screen-board is used to establish links between the mathematics as it is represented in the technological environment and conventional mathematical representations and techniques. The Spot-and-show orchestration is used mainly to discuss either student inappropriate answers or original and insightful solutions.
Teacher B’s views on mathematics education and the role of technology, as expressed in the questionnaire and the post-intervention interview, stress the importance of establishing links between the DME-work and paper-and-pencil mathematics. She sees the use of technology as an effective means to achieve her mathematical teaching goals, while she recognises that knowledge thus obtained also needs to be transferred to the paper-and-pencil environment. In addition, she believes that discussing mistakes and original approaches is fruitful for learning, and that both of these are more visible within a technological environment.
Her observed orchestration behaviour can be related to these views. Her strong agreement with the statement ‘Compared with paper-and-pencil, ICT makes student work more visible for me’ matches with her frequent use of the DME’s facility to browse student work while preparing the Spot-and-show orchestrations. She also strongly agreed with the statement ‘ICT can help students to develop understanding’, which explains her interest in the use of ICT.
In the post-intervention interview, teacher B explained that she uses the Link-screen-board orchestration to
… take distance from the specific ICT-environment; otherwise the experience remains too much linked to the ICT.
Concerning Spot-and-show, Teacher B explained that many students in her class were eager to have their work shown, which was an extra incentive for her to use it. She did not use the other student-centred orchestration types, as she considered them too time-consuming and also thought they might bring about some loss of control.
In short, the profile of teacher B is a teacher who finds the mathematical content of the lesson to be paramount and uses technology as a means to teach this. This results in attention to the links between the DME-work and paper-and-pencil or blackboard mathematics. She likes to be in control of the situation, which made her choose mainly teacher-centred orchestration types. Even if her frequent use of Spot-and-show reflects the importance she accords to discussing misconceptions and original approaches with the students, she usually quite strongly guides the Spot-and-show orchestrations. This aspect of Teacher B’s profile is illustrated in the extended extract presented in the next section, which took place in teacher B’s class.
5.3.3 Teacher C
Table 1 shows that teacher C has relatively high frequencies for Technical-demo and Explain-the-screen, which are considered as teacher-centred orchestration types. The Technical-demo orchestration is used to show the students what is possible with the tool and how to use it. The Explain-the-screen orchestration is in some cases used to provide students with a good starting position for new tasks, and in some cases to explain how tasks could have been solved. The underlying operational invariants seem to include the desire to avoid technical obstacles during student computer work, and the belief that tasks should be clearly explained to the students, in order to foster more efficient learning activities.
In the post-intervention interview, teacher C described herself as a ‘typical teacher for mid-ability students’ who strongly believes that such students benefit from clear demonstrations and explanations in a structured and stepwise approach. Technology is a suitable and useful means to provide this kind of scaffolding. At the same time, she was aware that students may encounter difficulties while using technology, and wished to prevent these as much as possible. Furthermore, she wanted to be in control of what is happening in the classroom, and believed that more teacher-centred orchestrations support this.
Her observed orchestration behaviour can be related to these views. She strongly agreed with the statement ‘As a teacher, one has to tell students clearly what they should do with ICT’, which matches with her prioritising Technical-demo orchestrations. Teacher C was neutral on the statements ‘The use of ICT provides the teacher more possibilities to build on students’ ideas during whole-class discussions’ and ‘The use of ICT creates shared images and experiences which one can discuss with the students’. This might explain her preference for teacher-centred orchestrations. Her preference for a stepwise approach was reflected in her strong agreement with the statement ‘Students become more systematic in their approach through the work with ICT’. She explained that she focused Technical-demo orchestrations on obstacles she experienced herself when using the DME, and that time constraints made her avoid orchestrations such as Sherpa-at-work.
In short, teacher C’s profile shows a concern for difficulties which students may encounter when learning mathematics, particularly when using technology, and the conviction that clear explanations and instructions are suitable means to deal with this. This guides her choice for teacher-centred orchestrations. She wants technology to support a stepwise problem solving approach. Furthermore, time constraints and control are important factors for her in making her orchestrational choices.
From the profiles described here, we conclude that the three teachers differ in their preferences for orchestration types and that their preferences can be related to their views on mathematics education and the role of technology therein. In fact, their views on mathematics education and the opportunities technology offers can be seen as their theoretical discourse that justifies their orchestrational choices and guides their operational invariants. These choices were shown to be partially based on time constraints and concerns about control, which is in line with findings in other studies (Pierce & Ball, 2009). Finally, it is interesting to note that the profiles of teachers A and C reported here are close to similar profiles from two case studies (of teacher P1 and N, respectively) described by Ruthven, Hennessy, and Deaney (2008).
5.4 Extended analysis of one episode
So far, orchestrations have been described on a global level in order to draw up an inventory of orchestration types. However, more detailed issues, such as the teacher-student interaction during these orchestrations, remained unaddressed. To further investigate the explanatory power of the notion of instrumental orchestration and of its third element of didactical performance in particular, a number of episodes were analysed more extensively; one exemplary episode is presented here. As the Spot-and-show orchestration is highly instrumented by technology and offers interesting interaction potential, we chose a Spot-and-show episode, taught by teacher B.
During the first two lessons of the learning arrangement, the notion of arrow chains was introduced to the students after group work on diverse problem situations involving dependency and co-variation (see Doorman et al., 2009). In the third and fourth lessons, students worked in pairs with arrow chains in the DME. In task 8, one of the tasks of the fourth lesson, the designers filled the applet window with the start of a square and a square root chain and an empty graph window (see Fig. 2).
While preparing the fifth lesson, teacher B came upon the work of Florence (a pseudonym) and her classmate (see Fig. 3). These two students used a Table-Graph technique to solve this task: they added both tables and graphs in the applet window. As the tables provide integer input values and the students did not add an input variable in the input box, the graphs that appear are dot graphs. Then the students clicked on different input values in the table, and observed the effects on the two corresponding dots in the graph. This technique was used more often by these students as a means of investigating the function. In this case, this led them to think that it is ‘special’ that two points reflecting function values for the same input value are vertically aligned. Their reasoning, therefore, reads: ‘for the square they are all whole numbers, and for the square root they are whole numbers and fractions. And the square of a number is always right above the root?’. The question mark at the end indicates that the students were not sure about their findings. Teacher B decided to treat this task, and this inappropriate answer in particular, in a whole class discussion. The text frame below contains the verbatim transcript of this episode.


In analysing this episode from an instrumental orchestration perspective, it was recognised as a Spot-and-show orchestration: ‘Spot’ because the teacher, while preparing the lesson, spotted the inappropriate answer in the students’ DME-work, and ‘show’ referring to the teacher’s decision to display these students’ results as a starting point for whole-class discussion. The teacher’s phrase ‘Oh yes, I actually wanted to see quite a different one’ and her direct navigation to Florence's work reveal her deliberate intention to act the way she does.
The didactical configuration for the preparatory phase consists of the DME’s option for teachers to look at the students’ work at any time. As a result, the teacher notices the inappropriate answer and decides to deal with it in her lesson. Apparently, the teacher likes to use technology for “supporting learning through analysis of mathematical discrepancies” (Ruthven, Hennessy & Deaney, 2008, p. 312). The monitoring of students’ work is instrumented by DME-facilities that are not available to students. As the teacher finds the computer lab not to be appropriate for whole-class teaching, the lesson takes place in a regular classroom with a PC with DME access, connected to a data projector. The configuration includes putting the computer with the data projector in the centre of the classroom. This choice is driven by the constraints of one of the artefacts: if the projector was at the front, the projection would get too small for the students to read. The screen is projected on the wall above the blackboard, thus enabling the teacher to write on the board, which she regularly does—though not in the episode presented here. Both this way of preparing the lessons and the setting in the classroom are observed frequently in this teacher’s lessons.
The exploitation mode of this configuration includes the teacher’s choice to operate the PC herself. This, in combination with the computer being in the centre of the classroom, results in the teacher standing in the centre of the classroom, with the students closely around her, all focused on the projection on the wall. This exploitation mode enables classroom discussion and student involvement.
The didactical performance starts with the teacher displaying the student work she had selected to show and reading out their reasoning, while adding some minor comments (‘Look here, …’). Then she reformulates the answer and asks Florence for an explanation (‘What they say…’). When the explanation turns out to be inappropriate, she invites another student, Kay, to give his explanation, and checks whether Florence understands it. When this is not the case, the teacher rephrases Kay’s explanation and once more checks with Florence, who now says she understands, although she does not actually give evidence of this. Throughout the didactical performance, the teacher uses the mouse to relate her oral expressions to the phenomena on the screen.
The didactical performance is now considered in more detail. The starting point for the episode is Florence’s artefact-related notion: a dot graph in the applet window of the DME suggests to her a ‘special’ feature of dots being aligned vertically. This is related to the tool technique of creating a table of function values and a corresponding graph. An understanding of the underlying mathematical concepts and meaning seems to be lacking.
The mathematical meaning the teacher is aiming for is that the coordinates of a point of the graph of a function reflect the values of independent and dependent variables, conventionally represented on the horizontal and vertical axes, respectively. As a consequence, different functions with the same input value will result in points that are vertically aligned in the graph.
What does the teacher do to guide the learning process towards this meaning? Firstly, she reads the students’ written answer and approves parts of it that are not crucial to the targeted understanding. However, she does not comment on the final part of the answer and later says ‘I am not saying’ when asked if it is correct.
As a next step, she rephrases the students’ answer and illustrates it with mouse movements in the applet window, so that all students understand the conjecture made by Florence. Then the teacher brings the relevant question to the fore: ‘Why is it that these things are right above each other?’ This leads to a vague reaction from Florence. The teacher invites Kay to explain his reasoning, which indicates that his interpretation of the representation in the artefact is linked to his understanding of the meaning of the graph as a representation of a mathematical idea/concept. The teacher subsequently evokes a precision of the intended mathematical meaning by asking for the type of numbers that is represented on the horizontal axis. This raises awareness of the link between the arrow chain and the graph. As a final step, the teacher checks if Florence understands Kay’s explanation. As this does not seem to be the case, the teacher repeats and expands Kay’s reasoning in her own words, again supporting her explanation with mouse movements on the screen. Once more she checks this with Florence, who now says she understands. As a result, Florence and her classmate remove the remark on the vertically aligned dots after this classroom discussion and replace it by a remark on the increasing behaviour of the square function: “for the square they are always whole numbers, and for the square root they are whole numbers and fractions. The squares get higher with much bigger steps.”
This analysis reveals some important strategies this teacher applies in her didactical performance. Firstly, she evokes mathematical meaning in several ways, namely by posing open questions, by inviting students to explain their reasoning, and by giving her own explanations. Secondly, she uses revoicing techniques and thus ‘orchestrates multiple voices’ (Forman & Ansell, 2002), while she in some cases also improves the students’ formulations and privileges specific input. Thirdly, she gives mathematical meaning to tool techniques and mathematical representations by using the mouse to highlight parts of the screen during her explanations. Finally, she regularly checks students’ understanding. This approach is typical for teacher B, and is consistent with the profile presented above. She used Spot-and-show orchestration quite frequently, perceiving it as a means to enhance student involvement and discussion, which she believes contributes to the development of the mathematical meaning that she finds so important. Evoking mathematical meaning in classroom discussions based on student results seems to be one of her operational invariants.
But what about the link between instrumental orchestration and instrumental genesis? As the episode only shows the result of students using the artefact, we do not see direct traces of the students’ instrumental genesis. We argue, however, that Florence’s idea of two vertically aligned points being special is part of her scheme of using the Table-Graph technique to produce dot graphs. Even though her knowledge linked to this technique—the theorem-in-action, as it is called in instrumentation theory—is inappropriate, the episode indicates that the teacher can exploit the students’ experiences—in this case those of Florence and Kay in particular—for the purpose of attaching mathematical meaning to the technique used. The teacher privileges the epistemic value of the Table-Graph technique above its pragmatic value (Artigue, 2002). In her didactical performance of the Spot-and-show orchestration she put into action, she highlights the mathematical meaning of the concept of function as it emerges from the technique. This is exactly what instrumental genesis is about. In this sense, the lens of instrumentational orchestration has a great deal to offer in this analysis. However, our analysis also reveals the importance of the interplay between representations in the technological environment and mathematical meaning. This suggests that the analysis could benefit from notions from semiotic mediation theory, which stresses the mediation potential of artefacts between the learner and the mathematical knowledge (Bartolini Bussi & Mariotti, 2008). Analyses such as those by Maracci and Mariotti (2009) show that the semiotic mediation framework can complement theories on instrumentation and orchestration (Drijvers, Kieran & Mariotti, 2010).
6 Conclusions and discussion
6.1 Conclusions
The first research question of this study concerns the different types of instrumental orchestrations which emerge in technology-rich classroom teaching. The analysis revealed six orchestration types, which are different in their technological specificity. Discuss-the-screen and Explain-the-screen can be seen as technological variants of regular teaching practices most teachers are familiar with. More specific for the use of technology are Technical-demo, Sherpa-at-work and Link-screen-board. Specific for technological tools that provide the teacher with online monitoring of digital student work is the Spot-and-show orchestration. It can be concluded that the repertoire of orchestrations is diverse, that they differ in respect to whether the focus is on the teacher or the student, and that the orchestrations have different degrees of technological specificity. Technological and time constraints as well as control issues may influence the choice and exploitation of the orchestrations. Furthermore, a discrepancy was noticed between orchestrations that were suggested in the teacher guide and orchestrations that were actually observed.
The second research question concerns the relationships between these types of orchestrations and teachers’ expressed views on mathematical learning and teaching and the role of technology therein. The matching of observed orchestrations with data from questionnaires and interviews reveals considerable links between the three teachers’ preferences for orchestrations and their views on what is important to achieve during teaching and how technology can support this. We conclude that these three teachers’ choices for orchestrations are related to their expressed views.
6.2 Discussion
The above conclusions may inform mathematics teachers and teacher educators who are engaged in professional development on the issue of the integration of technological tools in teaching. With respect to these conclusions, three issues deserve further discussion: the inventory of the six orchestration types, including its generalizability and researchers’ expectations, the relationship between orchestrational choices and teachers’ expressed views, and the explanatory power of the instrumental orchestration framework, including its limitations and its articulation with other theoretical approaches.
With respect to the inventory of the six orchestration types, it is interesting to see that the identified orchestrations can to a certain extent be related to ‘traditional’ teaching techniques. This suggests an evolution of teaching techniques rather than a revolution. Also, the researchers’ expectations for the orchestrational opportunities the digital tools provide, as they were sketched in the teacher guide, were to a certain extent ignored by the teachers. They choose their orchestrations themselves, which led to discrepancies between the researchers’ prior expectations and the actual findings from observations, discrepancies that are also reported by Lagrange and Caliskan-Dedeoglu (2009). The data suggest that the teachers make their choices in line with their regular habits and their views on mathematics teaching, which underpins the remark on teachers’ practices as being stable, made by Robert and Rogalski (2005) and referred to in the introduction.
For the case of spreadsheet software, Lagrange and Ozdemir Erdogan (2009) report on the differences between teachers stressing the epistemological value of tool techniques, and students who primarily see the pragmatic value. Similar struggles were observed in this study, where teachers felt obliged to use technical-demo orchestrations relatively often, whereas their primary concern was in the mathematical meaning.
The method for identifying orchestration types has its limitations, which impact the generalizability of the results. First, the orchestration types were sometimes difficult to distinguish. Even if the inter-rater reliability of the codings was good, it was not always easy to decide, for example, if a Spot-and-show orchestration gradually turned into Discuss-the-screen or Explain-the-screen. Second, it is possible that other types of orchestrations might have emerged in a different learning arrangement or while observing other teachers. The observations took place during a specific intervention, consisting of a complex and innovative learning arrangement with which the three teachers were not familiar. This lack of familiarity, along with start-up problems, may have influenced their orchestration choices. Also, the time schedule for the learning arrangement was tight, which may also have affected the didactical performance and the decisions involved. And finally, the specific tool characteristics may have invited (or inhibited) specific types of orchestration. For example, Spot-and-show orchestrations clearly depend on the opportunity for the teacher to access student work while preparing the lesson.
Despite these limitations, we conjecture that the identified orchestration types also exist, maybe in adapted forms, outside the scope of this study. Therefore, it would be worthwhile investigating whether variants of the identified orchestration types can be recognised in other settings, such as group work or individual student–teacher interactions (Drijvers, submitted), and in learning arrangements with other types of technological tools.
Concerning the relationship between orchestrational choices and teachers’ expressed views, which was the second research focus, the data suggest that the teachers’ views on mathematics education and the opportunities technology offers can be seen as their theoretical discourse that justifies their orchestrational choices and guide their operational invariants. It is interesting to note that the teachers’ views as identified in this study correspond to findings reported elsewhere. We already mentioned the similarities between the profiles of teachers A and C and those of two teachers described by Ruthven, Hennessy & Deaney (2008). Lagrange and Caliskan-Dedeoglu (2009) also mention the relationship between teachers’ expectations towards technology and their general ideas on teaching and learning.
As a limitation of the study on the relationships between orchestrational choices and expressed views, however, we point out that the data in the study presented here are too limited to justify claims on the teachers’ operational invariants across other classes and other kinds of technological tools. Furthermore, the notion of operational invariants in itself might benefit from further elaboration and concretisation.
As a final point of discussion, we also wished to investigate what the framework of instrumental orchestration offers to the analysis of technology-rich classroom teaching. If we interpret the orchestration metaphor in terms of a jazz band with its band leader, as we suggested earlier, we experience this framework as a productive lens through which to view teacher behaviour. On the whole, it appears to do justice to the subtleties in the preparation and performance of teaching techniques. The first two dimensions of the model helped us to identify global patterns in teachers’ behaviours, while the third dimension of the model—the didactical performance—turned out to be more fruitful in the detailed analysis of a teaching episode. On a more critical note, however, one can wonder if similar results could have been obtained in our study without the somewhat difficult vocabulary of the theoretical framework. Furthermore, as with every metaphor, the musical metaphor has only a limited application to educational settings. Also, we perceived a danger of sticking too much to superficial aspects of teaching while describing didactical configurations and exploitation modes. That is why the extension with didactical performance as a third component was useful and allowed for more in-depth and domain-specific didactical analysis.
As an aside, it should also be noted that, while designing orchestrations, the teacher is also engaged in a process of instrumental genesis for accomplishing the intended teaching task (Bueno-Ravel & Gueudet, 2007). However, the data available here do not allow us to proceed beyond developing a state-of-the art inventory of orchestration types to observing this process of instrumental genesis over time.
At the global level of analysis, it is worthwhile to consider the integration of the orchestrational model with other theoretical approaches. As a first approach, Ruthven and colleagues (Ruthven, 2007, 2009; Ruthven, Deaney & Hennessy, 2009) designed a model with a focus on key structuring features that shape technology integration into classroom practice. Applications of this model (e.g. see Lagrange & Caliskan-Dedeoglu, 2009) show that it can complement and supplement the instrumental orchestration model, and may thereby contribute to further theoretical development. A second additional approach is Saxe’s (1991) four parameter model, which centres on emergent goals under the influence of activity structures, social interactions, prior understandings, and conventions and artefacts. Even if it was designed for completely different purposes, several studies successfully applied this model to frame teachers’ activities in technology-based mathematics lessons (Lagrange & Monaghan, 2009; Lagrange & Ozdemir Erdogan, 2009; Monaghan, 2004). In our own work, we used it as complementary to instrumentation and orchestration, to capture the changing meaning students attach to existing techniques (Doorman et al., 2009). Third, the recently developed notion of teacher resources and documents (Gueudet & Trouche, 2009) matches well with notions on instrumental genesis and orchestration and may be worth exploring further. Fourth and final, at a more detailed level of analysis—for example in the exemplary Spot-and-show episode—the interplay of tool techniques and mathematical meaning became more salient. It became clear that the analysis could benefit from the semiotic mediation perspective (Bartolini Bussi & Mariotti, 2008) as an additional theoretical lens. The articulation, integration and confrontation of these different models is a challenge for research in this domain and deserves further investigation.
Notes
For further information on the project, see the project website www.fi.uu.nl/tooluse/en/.
We use Atlas ti software, www.atlasti.com
References
Artigue, M. (2002). Learning mathematics in a CAS environment: The genesis of a reflection about instrumentation and the dialectics between technical and conceptual work. International Journal of Computers for Mathematical Learning, 7, 245–274.
Artigue, M., Drijvers, P., Lagrange, J-b, Mariotti, M. A., & Ruthven, K. (2009). Technologies numériques dans l'enseignement des mathématiques, où en est-on dans les recherches et dans leur intégration? [Technology in mathematics education: how about research and its integration?] In C. Ouvrier-Buffet & M.-J. Perrin-Glorian (Eds.), Approches plurielles en didactique des mathématiques; Apprendre à faire des mathématiques du primaire au supérieur: quoi de neuf? [Multiple approaches to the didactics of mathematics; learning mathematics from primary to tertiary level: what's new?] (pp. 185–207). Paris: Université Paris Diderot Paris 7.
Bartolini Bussi, M. G., & Mariotti, M. A. (2008). Semiotic mediation in the mathematics classroom: artefacts and signs after a Vygotskian perspective. In L. English, M. Bartolini Bussi, G. Jones, R. Lesh, & D. Tirosh (Eds.), Handbook of International Research in Mathematics Education (2nd ed., pp. 746–805). Mahwah: Lawrence Erlbaum.
Billington, M. (2009). Establishing didactical praxeologies: teachers using digital tools in upper secondary mathematics classrooms. Paper presented in WG9, Cerme6 conference, 28 January–1 February 2009, Lyon, France.
Bretscher, N. (2009). Dynamic geometry software: The teacher's role in facilitating instrumental genesis. Paper presented in WG9, Cerme6 conference, 28 January–1 February 2009, Lyon, France.
Bueno-Ravel, L., & Gueudet, G. (2007). Online resources in mathematics: teachers' genesis of use? In D. Pitta-Pantazi & G. Philippou (Eds.), Proceedings of the V Congress of the European Society for Research in Mathematics Education CERME5 (pp. 1369–1378). Cyprus: Larnaca.
Doerr, H. M., & Zangor, R. (2000). Creating meaning for and with the graphing calculator. Educational Studies in Mathematics, 41, 143–163.
Doorman, M., Boon, P., Drijvers, P., Van Gisbergen, S., Gravemeijer, K., & Reed, H. (2009). Tool use and functional thinking: An example of a form-function-shift. In M. Tzekaki, M. Kaldrimidou, & H. Sakonidis (Eds.), Proceedings of the 33rd Conference of the International Group for the Psychology of Mathematics Education (Vol. 2, pp. 449–456). Thessaloniki, Greece: PME.
Drijvers, P., & Trouche, L. (2008). From artefacts to instruments: A theoretical framework behind the orchestra metaphor. In G. W. Blume & M. K. Heid (Eds.), Research on technology and the teaching and learning of mathematics (Cases and perspectives, Vol. 2, pp. 363–392). Charlotte: Information Age.
Drijvers, P., Doorman, M., Boon, P., Van Gisbergen, S., & Gravemeijer, K. (2007). Tool use in a technology-rich learning arrangement for the concept of function. In D. Pitta-Pantazi & G. Philipou (Eds.), Proceedings of the V Congress of the European Society for Research in Mathematics Education CERME5 (pp. 1389–1398). Cyprus: Larnaca.
Drijvers, P., Kieran, C., & Mariotti, M. A. (2010). Integrating technology into mathematics education: Theoretical perspectives. In C. Hoyles & J.-B. Lagrange (Eds.), Mathematics education and technology—rethinking the terrain (pp. 89–132). New York: Springer.
Forman, E. A., & Ansell, E. (2002). Orchestrating the multiple voices and inscriptions of a mathematics classroom. Journal of the Learning Sciences, 11(2–3), 251–274.
Gravemeijer, K. (1994). Developing realistic mathematics education. Utrecht: CD-β Press.
Gueudet, G., & Trouche, L. (2009). Towards new documentation systems for mathematics teachers? Educational Studies in Mathematics, 71(3), 199–218.
Kendal, M., & Stacey, K. (2002). Teachers in transition: Moving towards CAS-supported classrooms. ZDM, The International Journal on Mathematics Education, 34(5), 196–203.
Kendal, M., Stacey, K., & Pierce, R. (2004). The influence of a computer algebra environment on teachers’ practice. In D. Guin, K. Ruthven, & L. Trouche (Eds.), The didactical challenge of symbolic calculators: Turning an computational device into a mathematical instrument (pp. 83–112). Dordrecht: Kluwer Academic Publishers.
Kieran, C., & Drijvers, P. (2006). The co-emergence of machine techniques, paper-and-pencil techniques, and theoretical reflection: A study of CAS use in secondary school algebra. International Journal of Computers for Mathematical Learning, 11, 205–263.
Lagrange, J. B., & Caliskan-Dedeoglu, N. (2009). Usages de la technologie dans des conditions ordinaires: le cas de la géométrie dynamique au collège. [The use of technology in ordinary conditions: the case of dynamic geometry in lower secondary education.] Recherches en Didactique des Mathématiques, 29(2), 189–226.
Lagrange, J.-B., & Monaghan, J. (2009). On the adoption of a model to interpret teachers’ use of technology in mathematics lessons. Paper presented in WG7, Cerme6 conference, 28 January–1 February 2009, Lyon, France.
Lagrange, J.-B., & Ozdemir Erdogan, E. (2009). Teachers’ emergent goals in spreadsheet-based lessons: analyzing the complexity of technology integration. Educational Studies in Mathematics, 71(1), 65–84.
Lagrange, J.-B., Artigue, M., Laborde, C., & Trouche, L. (2003). Technology and mathematics education: A multidimensional study of the evolution of research and innovation. In A. J. Bishop, M. A. Clements, C. Keitel, J. Kilpatrick, & F. K. S. Leung (Eds.), Second international handbook of mathematics education (Vol. 1, pp. 237–269). Dordrecht: Kluwer.
Maracci, M., & Mariotti, M.-A. (2009). The teacher’s use of ICT tools in the classroom after a semiotic mediation approach. Paper presented in WG9, Cerme6 conference, 28 January–1 February 2009, Lyon, France.
Mariotti, M. A. (2002). Influence of technologies advances in students’ math learning. In L. D. English (Ed.), Handbook of international research in mathematics education (pp. 757–786). Mahwah: Lawrence Erlbaum.
McKenzie, J. (2001). How teachers learn technology best. The Educational Technology Journal, 10(6). Available at: http://www.fno.org/mar01/howlearn.html. Accessed 20 Oct 2009.
Monaghan, J. (2001). Teachers’ classroom interactions in ICT-based mathematics lessons. In M. Van den Heuvel-Panhuizen (Ed.), Proceedings of the 25th Conference of the International Group for the Psychology of Mathematics Education (Vol. 3, pp. 383–390). Utrecht: Freudenthal Institute.
Monaghan, J. (2004). Teachers’ activities in technology-based mathematics lessons. International Journal of Computers for Mathematical Learning, 9, 327–357.
Pierce, R., & Ball, L. (2009). Perceptions that may affect teachers’ intention to use technology in secondary mathematics classes. Educational Studies in Mathematics, 71(3), 299–317.
Reed, H. C., Drijvers, P., & Kirschner, P. A. (2010). Effects of attitudes and behaviours on learning mathematics with computer tools. Computers and Education, 55(1), 1–15.
Robert, A., & Rogalski, J. (2005). A cross-analysis of the mathematics teacher’s activity. An example in a French 10th-grade class. Educational Studies in Mathematics, 59, 269–298.
Ruthven, K. (2007). Teachers, technologies and the structures of schooling. In D. Pitta-Pantazi & G. Philipou (Eds.), Proceedings of the V Congress of the European Society for Research in Mathematics Education CERME5 (pp. 52–67). Cyprus: Larnaca.
Ruthven, K. (2009). An investigative lesson with dynamic geometry: A case study of key structuring features of technology integration in classroom practice. Paper presented in WG9, Cerme6 conference, 28 January–1 February 2009, Lyon, France.
Ruthven, K., & Hennessy, S. (2002). A practitioner model of the use of computer-based tools and resources to support mathematics teaching and learning. Educational Studies in Mathematics, 49(1), 47–88.
Ruthven, K., Deaney, R., & Hennessy, S. (2009). Using graphing software to teach about algebraic forms: A study of technology-supported practice in secondary-school mathematics. Educational Studies in Mathematics, 71(3), 279–297.
Ruthven, K., Hennessy, S., & Deaney, R. (2008). Constructions of dynamic geometry: A study of the interpretative flexibility of educational software in classroom practice. Computers and Education, 51, 297–317.
Saxe, G. B. (1991). Culture and Cognitive Development: Studies in Mathematical Understanding. Hillsdale: Laurence Erlbaum Associates.
Sensevy, G., Schubauer-Leoni, M. L., Mercier, A., Ligozat, F., & Perrot, G. (2005). An Attempt to Model the Teacher’s Action in the Mathematics Class. Educational Studies in Mathematics, 59(1–3), 153–181.
Sherin, M. G. (2002). A balancing act: Developing a discourse community in a mathematics classroom. Journal of Mathematics Teacher Education, 5(3), 205–233.
Simon, M. A. (1995). Reconstructing mathematics pedagogy from a constructivist perspective. Journal for Research in Mathematics Education, 26, 114–145.
Slavit, D. (1997). An alternate route to the reification of function. Educational Studies in Mathematics, 33, 259–281.
Trouche, L. (2004). Managing complexity of human/machine interactions in computerized learning environments: Guiding students’ command process through instrumental orchestrations. International Journal of Computers for Mathematical Learning, 9, 281–307.
Vergnaud, G. (1996). Au fond de l'apprentissage, la conceptualisation. [At the basis of learning, the conceptualization.] In R. Noirfalise & M.-J. Perrin (Eds.), Actes de l'école d'été de didactique des mathématiques [Proceedings of the summer school on didactics of mathematics.] (pp. 174–185). Clermont-Ferrand: IREM.
Acknowledgement
We thank the teachers and students of the experimental sites for their collaboration, Sjef van Gisbergen for his work as second coder, and the Netherlands Organisation for Scientific Research (NWO) for supporting the research study (project no. 411-04-123).
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Drijvers, P., Doorman, M., Boon, P. et al. The teacher and the tool: instrumental orchestrations in the technology-rich mathematics classroom. Educ Stud Math 75, 213–234 (2010). https://doi.org/10.1007/s10649-010-9254-5
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10649-010-9254-5