Skip to main content
SpringerLink
Log in

Numerical treatment of nonlinear singular Flierl–Petviashivili systems using neural networks models

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

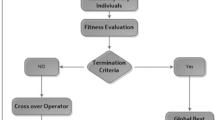
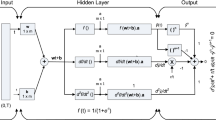
In this study, new intelligent computing methodologies have been developed for highly nonlinear singular Flierl–Petviashivili (FP) problem having boundary condition at infinity by exploiting three different neural network models integrated with active-set algorithm (ASA). A modification in the modeling is introduced to cater the singularity, avoid divergence in results for unbounded inputs and capable of dealing with strong nonlinearity. Three models have been constructed in an unsupervised manner for solving the FP equation using log-sigmoid, radial basis and tan-sigmoid transfer functions in the hidden layers of the network. The training of adaptive adjustable variables of each model is carried out with a constrained optimization technique based on ASA. The proposed models have been evaluated on three variants of the two FP equations. The designed models have been examined with respect to precision, stability and complexity through statistics.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Flierl GR (1979) Baroclinic solitary waves with radial symmetry. Dyn Atmos Oceans 3(1):15–38

    Article  Google Scholar 

  2. Petviashvili VI (1981) Red spot of Jupiter and the drift soliton in a plasma. JETP Lett 32:619–622

    Google Scholar 

  3. Boyd JP (1991) Monopolar and dipolar vortex solitons in two space dimensions. Wave Motion 13:223–241

    Article  MathSciNet  MATH  Google Scholar 

  4. Chandrasekhar S (1967) Introduction to the study of stellar structure. Dover Publications, New York

    Google Scholar 

  5. Shawagfeh NT (1993) Nonperturbative approximate solution for Lane-Emden equation. J Math Phys 34(9):4364–4369

    Article  MathSciNet  MATH  Google Scholar 

  6. Wazwaz AM (2001) A new method for solving differential equations of the Lane-Emden type. Appl Math Comput 118(2/3):287–310

    MathSciNet  MATH  Google Scholar 

  7. Wazwaz AM (2005) Analytical solution for the time-dependent Emden-Fowler type of equations by Adomian decomposition method. Appl Math Comput 166:638–651

    MathSciNet  MATH  Google Scholar 

  8. Wazwaz AM (2002) A new method for solving singular initial value problems in the second order ordinary differential equations. Appl Math Comput 128:47–57

    MathSciNet  Google Scholar 

  9. Wazwaz AM (1999) A reliable modification of Adomian’s decomposition method. Appl Math Comput 102:77–86

    MathSciNet  MATH  Google Scholar 

  10. Wazwaz AM (1999) The modified decomposition method and the Padé approximants for solving Thomas-Fermi equation. Appl Math Comput 105:11–19

    MathSciNet  MATH  Google Scholar 

  11. Wazwaz AM (1999) Analytical approximations and Padé approximants for Volterra’s population model. Appl Math Comput 100:13–25

    MathSciNet  MATH  Google Scholar 

  12. Wazwaz AM (2006) Pade approximants and Adomian decomposition method for solving the Flierl–Petviashivili equation and its variants. Appl Math Comput 182:1812–1818

    MathSciNet  MATH  Google Scholar 

  13. Mohyud-Din ST, Noor MA (2008) Homotopy perturbation method and Padé approximants for solving Flierl–Petviashivili equation. Appl Appl Math 3(2):224–234

    MathSciNet  MATH  Google Scholar 

  14. Momani S, Ertürk VS (2010) The solution of Flierl-Petviashivili equation and its variants using Dtm-Padé technique. World Appl Sci J 9((Special Issue of Applied Math)):32–38

    Google Scholar 

  15. Raja MAZ, Khan JA, Chaudhary NI, Shivanian E (2016) Reliable numerical treatment of nonlinear singular Flierl–Petviashivili equations for unbounded domain using ANN, GAs, and SQP. Appl Soft Comput 38:617–636

    Article  Google Scholar 

  16. Abu Arqub O, Maayah B (2016) Solutions of Bagley-Torvik and Painlevé equations of fractional order using iterative reproducing kernel algorithm. Neural Comput Appl. doi:10.1007/s00521-016-2484-4

    Google Scholar 

  17. Abu O (2015) Arqub, Adaptation of reproducing kernel algorithm for solving fuzzy Fredholm–Volterra integrodifferential equations. Neural Comput Appl. doi:10.1007/s00521-015-2110-x

    Google Scholar 

  18. Abu Arqub O, Al-Smadi M, Momani S, Hayat T (2016) Application of reproducing kernel algorithm for solving second-order, two-point fuzzy boundary value problems. Soft Comput. doi:10.1007/s00500-016-2262-3

    MATH  Google Scholar 

  19. Abu Arqub O, Al-Smadi M, Momani S, Hayat T (2016) Numerical solutions of fuzzy differential equations using reproducing kernel Hilbert space method. Soft Comput 20:3283–3302. doi:10.1007/s00500-015-1707-4

    Article  MATH  Google Scholar 

  20. Raja MAZ, Shah FH, Tariq M, Ahmad I (2016) Design of artificial neural network models optimized with sequential quadratic programming to study the dynamics of nonlinear Troesch’s problem arising in plasma physics. Neural Comput Appl. doi:10.1007/s00521-016-2530-2

    Google Scholar 

  21. Khan JA, Raja MAZ, Syam MI, Tanoli SAK, Awan SE (2015) Design and application of nature inspired computing approach for nonlinear stiff oscillatory problems. Neural Comput Appl 26(7):1763–1780. doi:10.1007/s00521-015-1841-z

    Article  Google Scholar 

  22. Baymani M, Effati S, Niazmand H, Kerayechian A (2015) Artificial neural network method for solving the Navier-Stokes equations. Neural Comput Appl 26(4):765–773

    Article  Google Scholar 

  23. Khan JA, Raja MAZ, Rashidi MM, Syam MI, Wazwaz AM (2015) Nature-inspired computing approach for solving non-linear singular Emden-Fowler problem arising in electromagnetic theory. Connect Sci 27(04):377–396

    Article  Google Scholar 

  24. Raja MAZ, Zameer A, Khan AU, Wazwaz AM (2016) A new numerical approach to solve Thomas-Fermi model of an atom using bio-inspired heuristics integrated with sequential quadratic programming. SpringerPlus 5(1):1400

    Article  Google Scholar 

  25. Raja MAZ (2014) Solution of the one-dimensional Bratu equation arising in the fuel ignition model using ANN optimised with PSO and SQP. Connect Sci 26(3):195–214

    Article  MathSciNet  Google Scholar 

  26. Jafarian A, Measoomy S, Abbasbandy S (2015) Artificial neural networks based modeling for solving Volterra integral equations system. Appl Soft Comput 27:391–398

    Article  Google Scholar 

  27. Ahmad I, Raja MAZ, Bilal M, Ashraf F (2016) Bio-inspired computational heuristics to study Lane-Emden systems arising in astrophysics model. SpringerPlus 5(1):1866

    Article  Google Scholar 

  28. Ahmad I, Raja MAZ, Bilal M, Ashraf F (2016) Neural network methods to solve the Lane-Emden type equations arsing in thermodynamic studies of the spherical gas cloud model. Neural Comput Appl. doi:10.1007/s00521-016-2400-y

    Google Scholar 

  29. Sabouri J, Effati S, Pakdaman M (2017) A neural network approach for solving a class of fractional optimal control problems. Neural Process Lett 45(1):59–74

    Article  Google Scholar 

  30. Raja MAZ, Khan JA, Haroon T (2014) Stochastic numerical treatment for thin film flow of third grade fluid using unsupervised neural networks. J Chem Inst Taiwan. doi:10.1016/j.jtice.2014.10.018

    Google Scholar 

  31. Raja MAZ (2014) Stochastic numerical techniques for solving Troesch’s Problem. Inf Sci 279:860–873

    Article  MATH  Google Scholar 

  32. Majeed K, Masood Z, Samar R, Raja MAZ (2017) A genetic algorithm optimized Morlet wavelet artificial neural network to study the dynamics of nonlinear Troesch’s system. Appl Soft Comput 56:420–435

    Article  Google Scholar 

  33. Raja MAZ, Samar R (2014) Numerical treatment for nonlinear MHD Jeffery–Hamel problem using neural networks optimized with interior point algorithm. Neurocomputing 124:178–193. doi:10.1016/j.neucom.2013.07.013

    Article  Google Scholar 

  34. Raja MAZ, Shah FH, Alaidarous ES, Syam MI (2017) Design of bio-inspired heuristic technique integrated with interior-point algorithm to analyze the dynamics of heartbeat model. Appl Soft Comput 52:605–629. doi:10.1016/j.asoc.2016.10.009

    Article  Google Scholar 

  35. Arqub OA, Abo-Hammour Z (2014) Numerical solution of systems of second-order boundary value problems using continuous genetic algorithm. Inf Sci 279:396–415

    Article  MathSciNet  MATH  Google Scholar 

  36. Raja MAZ, Khan JA, Shah SM, Samar R, Behloul D (2015) Comparison of three unsupervised neural network models for first Painlevé Transcendent. Neural Comput Appl 26(5):1055–1071. doi:10.1007/s00521-014-1774-y

    Article  Google Scholar 

  37. Momani S, Abo-Hammour ZS, Alsmadi OM (2016) Solution of inverse kinematics problem using genetic algorithms. Appl Math Inf Sci 10(1):225

    Article  Google Scholar 

  38. Raja MAZ (2014) Numerical treatment for boundary value problems of pantograph functional differential equation using computational intelligence algorithms. Appl Soft Comput 24:806–821

    Article  Google Scholar 

  39. Raja MAZ, Manzar MA, Samar R (2015) An efficient computational intelligence approach for solving fractional order Riccati equations using ANN and SQP. Appl Math Model 39(10):3075–3093. doi:10.1016/j.apm.2014.11.024

    Article  MathSciNet  Google Scholar 

  40. Masood Z, Majeed K, Samar R, Raja MAZ (2017) Design of Mexican Hat Wavelet neural networks for solving Bratu type nonlinear systems. Neurocomputing 221:1–14

    Article  Google Scholar 

  41. Raja MAZ, Niazi SA, Butt SA (2017) An intelligent computing technique to analyze the vibrational dynamics of rotating electrical machine. Neurocomputing 219:280–299

    Article  Google Scholar 

  42. Mohyud-Din ST, Noor MA, Noor KI (2009) Variational iteration method for solving Flierl–Petviashivili equation using He’s polynomials and Padé approximants. World Appl Sci J 6(9):1298–1303

    Google Scholar 

  43. Mohyud-Din ST, Noor MA, Noor KI (2010) Comparison and coupling of polynomials for Fierl–Petviashivili equation. Math Comput Appl 15(2):187–198

    MathSciNet  MATH  Google Scholar 

  44. Raja MAZ, Khan MAR, Mahmood T, Farooq U, Chaudhary NI (2016) Design of bio-inspired computing technique for nanofluidics based on nonlinear Jeffery–Hamel flow equations. Can J Phys 94(5):474–489

    Article  Google Scholar 

  45. Raja MAZ, Shah FH, Khan AA, Khan NA (2016) Design of bio-inspired computational intelligence technique for solving steady thin film flow of Johnson-Segalman fluid on vertical cylinder for drainage problem. Taiwan Inst Chem Eng 60:59–75. doi:10.1016/j.jtice.2015.10.020

    Article  Google Scholar 

  46. Raja MAZ, Shah FH, Syam MI (2017) Intelligent computing approach to solve the nonlinear Van der Pol system for heartbeat model. Neural Comput Appl. doi:10.1007/s00521-017-2949-0

    Google Scholar 

  47. Wang L (2005) Support vector machines: theory and application. Springer, Berlin

    Book  Google Scholar 

  48. Gill PE, Murray W, Saunders MA (2006) User’s guide for SNOPT Version 7: Software for large-scale nonlinear programming. Numerical Analysis Report 06-2, Department of Mathematics, University of California, San Diego, La Jolla, CA

  49. Gill PE, Murray W, Saunders MA (1995) User’s guide for QPOPT 1.0: a FORTRAN package for quadratic programming. Report SOL 95-4, Department of Operations Research, Stanford University, Stanford, CA

  50. Gill PE, Murray W, Saunders MA (2006) User’s guide for SQOPT Version 7: Software for large-scale linear and quadratic programming. Numerical Analysis Report 06-1, Department of Mathematics, University of California, San Diego, La Jolla, CA

  51. Gould NIM, Orban D, Toint PL (2003) GALAHAD, a library of thread-safe Fortran 90 packages for large-scale nonlinear optimization. ACM Trans Math Softw 29(4):353–372

    Article  MathSciNet  MATH  Google Scholar 

  52. Judice JJ, Sherali HD, Ribeiro IM, Faustino AM (2007) Complementarity active-set algorithm for mathematical programming problems with equilibrium constraints. J Optim Theory Appl 134(3):467–481

    Article  MathSciNet  MATH  Google Scholar 

  53. Hager WW, Zhang H (2006) A new active set algorithm for box constrained optimization. SIAM J Optim 17(2):526–557

    Article  MathSciNet  MATH  Google Scholar 

  54. Sloan SW (2005) A steepest edge active Set algorithm for solving sparse linear programming problems. Int J Numer Method Eng 26(12):2671–2685

    Article  MathSciNet  MATH  Google Scholar 

  55. Nocedal J, Wright ST (2006) Numerical optimization, 2nd edn. Springer, Berlin. ISBN 978-0-387-30303-1

    MATH  Google Scholar 

  56. Wong E (2011) Active-set methods for quadratic programming. Ph.D. Thesis, University of California, San Diego, USA

  57. Mohyud-Din ST, Yildirim A (2009) Solving nonlinear boundary value problems using He’s polynomials and Padé approximants. Math Probl Eng 2009. Article ID 690547

  58. Mohyud-Din ST, Usman M, Yildirim A (2010) An iterative algorithm for nonlinear BVPS using Pade approximants. World Appl Sci J 10(6):637–644

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Electrical Engineering, COMSATS Institute of Information Technology, Attock, Pakistan

    Muhammad Asif Zahoor Raja

  2. Department of Computer Science and Engineering, HITEC University Texila, Rawalpindi, Pakistan

    Junaid Ali Khan

  3. Department of Computer and Information Science, Pakistan Institute of Engineering and Applied Sciences, Nilore, Islamabad, Pakistan

    Aneela Zameer

  4. Department of Mathematical Sciences, University of Karachi, Karachi, 75270, Pakistan

    Najeeb Alam Khan

  5. Hamdard Institute of Engineering and Technology, Hamdard University, Islamabad, Pakistan

    Muhammad Anwaar Manzar

Authors
  1. Muhammad Asif Zahoor Raja
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Junaid Ali Khan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Aneela Zameer
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Najeeb Alam Khan
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Muhammad Anwaar Manzar
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Aneela Zameer.

Ethics declarations

Conflict of interest

The authors declare that they have no competing interests.

Appendix

Appendix

Complete expressions for the solution of the proposed scheme with fourteen places of decimal are provided here for the reproduction and verification of the results. Same equation numbers are referred here for better identification with the main manuscript text.

$$\hat{u}_{\text{LS}} \left( x \right) = \left( {\frac{{1 + x^{2} }}{{1 + x^{3} }} + \frac{{x^{2} }}{{1 + x^{3} }}\left( \begin{aligned} \frac{4.72632510851474}{{1 + {\text{e}}^{{ - \left( {1.65710173577515x + 2.27779096744896} \right)}} }} + \frac{ - 4.45031709267048}{{1 + {\text{e}}^{{ - \left( { - 3.56958568913710x + 6.62613183690404} \right)}} }} \hfill \\ + \frac{ - 2.23650019923638}{{1 + {\text{e}}^{{ - \left( { - 0.71859866765235x - 2.59945765214019} \right)}} }} + \frac{0.73190624969960}{{1 + {\text{e}}^{{ - \left( { - 1.91940354568530x - 3.61059364483905} \right)}} }} \hfill \\ + \frac{5.11507523597824}{{1 + {\text{e}}^{{ - \left( {0.89408386567960x + 2.28476124378728} \right)}} }} + \frac{3.83538037784671}{{1 + {\text{e}}^{{ - \left( { - 1.30345287906150x - 0.64487671895220} \right)}} }} \hfill \\ + \frac{1.84790897996908}{{1 + {\text{e}}^{{ - \left( {2.78382423750435x - 3.85784033875989} \right)}} }} + \frac{ - 0.52523154216449}{{1 + {\text{e}}^{{ - \left( { - 0.71294819225919x - 1.93880716849144} \right)}} }} \hfill \\ + \frac{6.53699521328446}{{1 + {\text{e}}^{{ - \left( {0.96411186775932x - 1.66126218702275} \right)}} }} + \frac{ - 7.18576280760247}{{1 + {\text{e}}^{{ - \left( { - 4.60722995331281x + 8.87260939644230} \right)}} }} \hfill \\ \end{aligned} \right)} \right)$$
(28)
$$\hat{u}_{\text{RB}} \left( r \right) = \left( {\frac{{1 + x^{2} }}{{1 + x^{3} }} + \frac{{x^{2} }}{{1 + x^{3} }}\left( \begin{aligned} - 0.72323894205343{\text{e}}^{{ - \left( {0.553303195007x + 1.77010552750341} \right)^{2} }} \hfill \\ - 2.91568268441046{\text{e}}^{{ - \left( {1.28822893617979x - 1.96477480403763} \right)^{2} }} \hfill \\ - 1.93226171990883{\text{e}}^{{ - \left( { - 0.70978529328024x - 0.41643049423644} \right)^{2} }} \hfill \\ - 0.02959622516246{\text{e}}^{{ - \left( {0.31583918575973x + 1.40299752833714} \right)^{2} }} \hfill \\ + 3.9872944467341{\text{e}}^{{ - \left( {0.62389115059975x - 0.6828302080878} \right)^{2} }} \hfill \\ + 3.84326621512007{\text{e}}^{{ - \left( { - 0.88728479960531x + 1.91402739675086} \right)^{2} }} \hfill \\ - 1.67692510938239{\text{e}}^{{ - \left( { - 1.48410653387875x + 1.98449500968432} \right)^{2} }} \hfill \\ - 2.28175466645687{\text{e}}^{{ - \left( {1.09978049675893x - 0.71425448496625} \right)^{2} }} \hfill \\ + 5.27367648116228{\text{e}}^{{ - \left( { - 1.73564376929631x + 3.8967359801976} \right)^{2} }} \hfill \\ + 2.25764575903348{\text{e}}^{{ - \left( { - 1.49851072245445x + 2.12478829653603} \right)^{2} }} \hfill \\ \end{aligned} \right)} \right)$$
(29)
$$u_{\text{TS}} \left( x \right) = \left( {\frac{{1 + x^{2} }}{{1 + x^{3} }} + \frac{{x^{2} }}{{1 + x^{3} }}\left( \begin{aligned} - 7.311383357855470 + \frac{1.29421376172621 \times 2}{{1 + {\text{e}}^{{ - 2\left( {1.51432531177837x - 1.94096678634061} \right)}} }} \hfill \\ + \frac{0.24564615594904 \times 2}{{1 + {\text{e}}^{{ - 2\left( {1.31335392628889x - 0.87050667836733} \right)}} }} + \frac{ - 1.78354087566988 \times 2}{{1 + {\text{e}}^{{ - 2\left( { - 0.2217120222215x - 0.6812838775957} \right)}} }} \hfill \\ + \frac{0.43104856261592 \times 2}{{1 + {\text{e}}^{{ - 2\left( {1.37969766064208x + 1.55574402348314} \right)}} }} + \frac{ - 1.46857857194636 \times 2}{{1 + {\text{e}}^{{ - 2\left( { - 0.62748038623427x - 1.69163507309337} \right)}} }} \hfill \\ + \frac{1.50311683748809 \times 2}{{1 + {\text{e}}^{{ - 2\left( {0.41140560603128x - 1.5791752769795} \right)}} }} + \frac{0.09619087525675 \times 2}{{1 + {\text{e}}^{{ - 2\left( {1.54023349256904x + 0.73179062527214} \right)}} }} \hfill \\ + \frac{ - 0.68343571033137 \times 2}{{1 + {\text{e}}^{{ - 2\left( { - 1.11310616902629x - 2.80171020977017} \right)}} }} + \frac{ - 1.82634479444537 \times 2}{{1 + {\text{e}}^{{ - 2\left( { - 3.7325288255196x - 5.72045675105031} \right)}} }} \hfill \\ + \frac{ - 3.09473729629636 \times 2}{{1 + {\text{e}}^{{ - 2\left( { - 2.36919201936288x + 4.01770385003562} \right)}} }} \hfill \\ \end{aligned} \right)} \right)$$
(30)
$$u_{\text{LS}} \left( x \right) = \left( {\frac{{1 + x^{2} }}{{1 + x^{3} }} + \frac{{x^{2} }}{{1 + x^{3} }}\left( \begin{aligned} \frac{15}{{1 + {\text{e}}^{{ - \left( {0.62787566019007x + 2.52838216054528} \right)}} }} + \frac{ - 10.7048232606873}{{1 + {\text{e}}^{{ - \left( { - 9.95405229455268x - 11.3180441306054} \right)}} }} \hfill \\ + \frac{ - 10.9204550541312}{{1 + {\text{e}}^{{ - \left( { - 2.18278617021429x - 7.17487716951065} \right)}} }} + \frac{ - 11.4985988300121}{{1 + {\text{e}}^{{ - \left( { - 8.41693250597733x - 10.205931560291} \right)}} }} \hfill \\ + \frac{ - 10.211941012151}{{1 + {\text{e}}^{{ - \left( { - 3.61662960636564x - 7.62440963072436} \right)}} }} + \frac{ - 10.855539537289}{{1 + {\text{e}}^{{ - \left( { - 9.4802032106731x - 10.3577493488161} \right)}} }} \hfill \\ + \frac{ - 12.7110988320754}{{1 + {\text{e}}^{{ - \left( { - 2.99868359771211x + 6.45601387989685} \right)}} }} + \frac{ - 1.98064169969149}{{1 + {\text{e}}^{{ - \left( { - 2.05876442801075x + 2.66747342710029} \right)}} }} \hfill \\ + \frac{ - 10.0881400939881}{{1 + {\text{e}}^{{ - \left( { - 10.6585383968093x - 10.6782642975707} \right)}} }} + \frac{ - 11.1082232011744}{{1 + {\text{e}}^{{ - \left( { - 6.33009565379611x - 9.63981989859923} \right)}} }} \hfill \\ \end{aligned} \right)} \right)$$
(38)
$$\hat{u}_{\text{RB}} \left( x \right) = \left( {\frac{{1 + x^{2} }}{{1 + x^{3} }} + \frac{{x^{2} }}{{1 + x^{3} }}\left( \begin{aligned} 1.68324391564392{\text{e}}^{{ - \left( { - 0.10712388714561x - 2.21511672890905} \right)^{2} }} \hfill \\ - 2.05499453801537{\text{e}}^{{ - \left( { - 0.52476179013829x - 3.37036767681847} \right)^{2} }} \hfill \\ + 1.55463824003447{\text{e}}^{{ - \left( {0.97423598176392x - 3.58266002843627} \right)^{2} }} \hfill \\ + 11.516335371765{\text{e}}^{{ - \left( { - 1.0850655003947x - 0.42130431141011} \right)^{2} }} \hfill \\ - 0.11796545133915{\text{e}}^{{ - \left( {1.2701966304861x + 4.66842062255857} \right)^{2} }} \hfill \\ - 0.41062548803041{\text{e}}^{{ - \left( {4.17183593775754x - 0.96015828675471} \right)^{2} }} \hfill \\ + 0.94786138308886{\text{e}}^{{ - \left( {2.84397615832785x + 0.74556129044324} \right)^{2} }} \hfill \\ + 0.21293802731812{\text{e}}^{{ - \left( { - 3.08518023831259x - 1.69573892787157} \right)^{2} }} \hfill \\ + 0.40985976734602{\text{e}}^{{ - \left( { - 1.63951673862173x + 2.04616296380706} \right)^{2} }} \hfill \\ + 2.13933788243694{\text{e}}^{{ - \left( { - 0.42594411510417x - 0.9319605433395} \right)^{2} }} \hfill \\ \end{aligned} \right)} \right)$$
(39)
$$\hat{u}_{\text{RB}} \left( x \right) = \left( {\frac{{1 + x^{2} }}{{1 + x^{3} }} + \frac{{x^{2} }}{{1 + x^{3} }}\left( \begin{aligned} - 7.311383357855470 + \frac{ - 1.99121552809285 \times 2}{{1 + {\text{e}}^{{ - 2\left( { - 0.85229344702745x + 1.36773934178084} \right)}} }} \hfill \\ + \frac{1.07500099939665 \times 2}{{1 + {\text{e}}^{{ - 2\left( { - 0.34902276066273x + 1.34857227942967} \right)}} }} + \frac{ - 0.59901142221974 \times 2}{{1 + {\text{e}}^{{ - 2\left( { - 1.03555424382006x - 2.12498182205873} \right)}} }} \hfill \\ + \frac{11.78812131451280 \times 2}{{1 + {\text{e}}^{{ - 2\left( {1.43933625849589x - 3.53689075669933} \right)}} }} + \frac{ - 0.46852496693387 \times 2}{{1 + {\text{e}}^{{ - 2\left( { - 1.26141785737207x - 3.63752443720412} \right)}} }} \hfill \\ + \frac{ - 8.10362905397083 \times 2}{{1 + {\text{e}}^{{ - 2\left( { - 0.40992951879207x - 1.50554728413777} \right)}} }} + \frac{1.54986401688038 \times 2}{{1 + {\text{e}}^{{ - 2\left( {5.94103063881747x + 4.32534775108113} \right)}} }} \hfill \\ + \frac{1.43825323424858 \times 2}{{1 + {\text{e}}^{{ - 2\left( { - 0.84887990769193x + 5.84607362112051} \right)}} }} + \frac{0.0302804784842 \times 2}{{1 + {\text{e}}^{{ - 2\left( {0.85893427468416x + 2.56877250502613} \right)}} }} \hfill \\ + \frac{0.50141177678916 \times 2}{{1 + {\text{e}}^{{ - 2\left( {4.44680325577113x + 3.20940133395529} \right)}} }} \hfill \\ \end{aligned} \right)} \right)$$
(40)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Raja, M.A.Z., Khan, J.A., Zameer, A. et al. Numerical treatment of nonlinear singular Flierl–Petviashivili systems using neural networks models. Neural Comput & Applic 31, 2371–2394 (2019). https://doi.org/10.1007/s00521-017-3193-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-017-3193-3

Keywords

Search

Navigation