Abstract
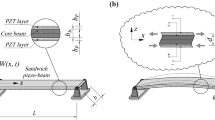
This paper addresses modeling and finite element analysis of the transient large-amplitude vibration response of thin rod-type structures (e.g., plane curved beams, arches, ring shells) and its control by integrated piezoelectric layers. A geometrically nonlinear finite beam element for the analysis of piezolaminated structures is developed that is based on the Bernoulli hypothesis and the assumptions of small strains and finite rotations of the normal. The finite element model can be applied to static, stability, and transient analysis of smart structures consisting of a master structure and integrated piezoelectric actuator layers or patches attached to the upper and lower surfaces. Two problems are studied extensively: (i) FE analyses of a clamped semicircular ring shell that has been used as a benchmark problem for linear vibration control in several recent papers are critically reviewed and extended to account for the effects of structural nonlinearity and (ii) a smart circular arch subjected to a hydrostatic pressure load is investigated statically and dynamically in order to study the shift of bifurcation and limit points, eigenfrequencies, and eigenvectors, as well as vibration control for loading conditions which may lead to dynamic loss of stability.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
Robbins, D.H., Reddy, J.N.: Analysis of piezoelectrically actuated beams using a layer-wise displacement theory. Comput. Struct. 41, 265–279 (1991)
Krommer, M.: On the correction of the Bernoulli–Euler beam theory for smart piezoelectric beams. Smart Mater. Struct. 10(4), 668 (2001)
Maurini, C., dell’Isola, F., Pouget, J.: On models of layered piezoelectric beams for passive vibration control. J. Phys. IV 115, 307–316 (2004)
Maurini, C., Pouget, J., dell’Isola, F.: On a model of layered piezoelectric beams including transverse stress effect. Int. J. Solids Struct. 41(16), 4473–4502 (2004)
dell’Isola, F., Rosa, L.: Almansi-type boundary conditions for electric potential inducing flexure in linear piezoelectric beams. Contin. Mech. Thermodyn. 9(2), 115–125 (1997)
Mindlin, R.D.: Forced thickness-shear and flexural vibrations of piezoelectric crystal plates. J. Appl. Phys. 23(1), 83–88 (1952)
Lee, C.-K.: Piezoelectric laminates: theory and experiments for distributed sensors and actuators. In: Tzou, H.S., Anderson, G.L. (eds.) Intelligent Structural Systems, pp. 75–167. Kluwer Academic Publishers, Dordrecht-Boston-London (1992)
Yang, J.S., Batra, R.C., Liang, X.Q.: The cylindrical bending vibration of a laminated elastic plate due to piezoelectric actuators. Smart Mater. Struct. 3, 1–9 (1994)
Ghosh, K., Batra, R.C.: Shape control of plates using piezoceramic elements. AIAA J. 33, 1354–1357 (1995)
Carrera, E.: An improved Reissner–Mindlin-type model for the electromechanical analysis of multilayered plates including piezo-layers. J. Intell. Mater. Syst. Struct. 8(3), 232–248 (1997)
Carrera, E., Boscolo, M.: Classical and mixed finite elements for static and dynamic analysis of piezoelectric plates. Int. J. Numer. Meth. Eng. 70, 1135–1181 (2007)
Maurini, C., Pouget, J., dell’Isola, F.: Extension of the Euler–Bernoulli model of piezoelectric laminates to include 3D effects via a mixed approach. Comput. Struct. 84(22), 1438–1458 (2006)
Alessandroni, S., Andreaus, U., dell’Isola, F., Porfiri, M.: Piezo-electromechanical (PEM) Kirchhoff–Love plates. Eur. J. Mech.-A/Solids 23(4), 689–702 (2004)
Rosi, G., Pouget, J., dell’Isola, F.: Control of sound radiation and transmission by a piezoelectric plate with an optimized resistive electrode. Eur. J. Mech.-A/Solids 29(5), 859–870 (2010)
Rogacheva, N.N.: Equations of state of piezoceramic shells. J. Appl. Math. Mech. 45(5), 677–684 (1981)
Rogacheva, N.: The Theory of Piezoelectric Plates and Shells, p. 260. CRC Press, Boca Raton (1994)
Le, K.C.: An asymptotically exact theory of functionally graded piezoelectric shells. Int. J. Eng. Sci. 112, 42–62 (2017)
Vetyukov, Y., Staudigl, E., Krommer, M.: Hybrid asymptotic–direct approach to finite deformations of electromechanically coupled piezoelectric shells. Acta Mech. 229(2), 953–974 (2018)
Kulikov, G.M., Plotnikova, S.V.: Exact electroelastic analysis of functionally graded piezoelectric shells. Int. J. Solids Struct. 51(1), 13–25 (2014)
Lammering, R.: The application of finite shell element for composites containing piezo-electric polymers in vibration control. Comput. Struct. 41, 1101–1109 (1991)
Tzou, H.S., Tseng, C.I.: Distributed vibration control and identification of coupled elastic/piezoelectric systems: Finite element formulation and application. Mech. Syst. Signal Process. 5, 215–231 (1991)
Tzou, H.S.: Piezoelectric Shells—Distributed Sensing and Control of Continua. Kluwer Academic Publishers, Dordrecht-Boston-London (1993)
Tzou, H.S., Ye, R.: Analysis of piezoelastic structures with laminated piezoelectric triangle shell elements. AIAA J. 34, 110–115 (1996)
Carrera, E.: Historical review of Zig-Zag theories for multilayered plates and shells. Appl. Mech. Rev. 56(2), 287–308 (2003)
Carrera, E., Giunta, G., Petrolo, M.: Beam Structures: Classical and Advanced Theories. Wiley, Chichester (2011)
Carrera, E., Brischetto, S., Nali, P.: Plates and Shells for Smart Structures: Classical and Advanced Theories for Modelling and Analysis. Wiley, Chichester (2011)
Naumenko, K., Eremeyev, V.A.: A layer-wise theory for laminated glass and photovoltaic panels. Compos. Struct. 112, 283–291 (2014)
Naumenko, K., Eremeyev, V.A.: A layer-wise theory of shallow shells with thin soft core for laminated glass and photovoltaic applications. Compos. Struct. 178, 434–446 (2017)
Icardi, U., Di Sciuva, M.: Large-deflection and stress analysis of multilayered plates with induced-strain actuators. Smart Mater. Struct. 5, 140–164 (1996)
Mukherjee, A., Chaudhuri, A.S.: Piezolaminated beams with large deformations. Int. J. Solids Struct. 39, 4567–4582 (2002)
Lentzen, S., Schmidt, R.: Nonlinear finite element modelling of composite structures with integrated piezoelectric layers. In: Brebbia, C.A., de Wilde, W.P. (eds.) High Performance Structures and Materials II, pp. 67–76. WIT Press, Southampton-Boston (2004)
Lentzen, S., Schmidt, R.: Simulation of sensor application and shape control of piezoelectric structures at large deflections. In: Atluri, S.N., Tadeu, A.J.B. (eds.) Advances in Computational & Experimental Engineering & Science, pp. 439–444. Tech Science Press, Encino (2004)
Lentzen, S., Schmidt, R.: Nonlinear shape control simulation of piezolaminated plates and shells. In: Yao, Z.H., Yuan, M.W., Zhong, W.X. (eds.) Computational Mechanics, Proceedings of the Sixth International Congress of Computational Mechanics, Beijing, China, vol. 2, paper R-304, Tsinghua University Press/Springer-Verlag (2004)
Lentzen, S., Schmidt, R.: On piezoelectric actuator layers in plates and shells at large deflections. In: Yang, W. (ed.) IUTAM Symposium “Mechanics and Reliability of Actuating Materials”, Beijing, China, 1–3 September 2004, 154–163. Springer, Dordrecht (2006)
Lentzen, S., Schmidt, R.: Nonlinear FE-simulation of piezolaminated plates and shells. In: Iyengar, N.G.R., Kumar, A. (eds.) Proceedings, International Congress on Computational Mechanics & Simulation, vol. I, pp. 77–85. Indian Institute of Technology Kanpur (2004)
Vu, T.D., Lentzen, S., Schmidt, R.: Geometrically nonlinear FE-analysis of piezolaminated plates based on first- and third-order shear deformation theory. In: Son, N.K., Cat, P.T., Tuan, P.A. (eds.) Proceedings of the 8 th International Conference on Mechatronics Technology, ICMT 2004, Hanoi, Vietnam, 8–12 November 2004, pp. 267–272. Vietnam National University Publisher, Hanoi (2004)
Nguyen, Q.D., Lentzen, S., Schmidt, R.: A geometrically nonlinear third-order shear deformation finite plate element incorporating piezoelectric layers. In: Son, N.K., Cat, P.T., Tuan, P.A. (eds.) Proceedings of the 8 th International Conference on Mechatronics Technology, ICMT 2004, Hanoi, Vietnam, 8–12 November 2004, pp. 303–308/ Vietnam National University Publisher, Hanoi (2004)
Zhang, S.Q., Chen, M., Zhao, G.Z., Wang, Z.X., Schmidt, R., Qin, X.S.: Modeling techniques for active shape and vibration control of macro-fiber composite laminated structures. Smart Struct. Syst. 19(6), 633–641 (2017)
Zhang, S.Q., Wang, Z.X., Qin, X.S., Zhao, G.Z., Schmidt, R.: Geometrically nonlinear analysis of composite laminated structures with multiple macro-fiber composite (MFC) actuators. Compos. Struct. 150, 62–72 (2016)
Zhang, S.Q., Schmidt, R., Müller, P.C., Qin, X.S.: Disturbance rejection control for vibration suppression of smart beams and plates under a high frequency excitation. J. Sound Vib. 353, 19–37 (2015)
Zhang, S.Q., Li, H.N., Schmidt, R., Müller, P.C.: Disturbance rejection control for vibration suppression of piezoelectric laminated thin-walled structures. J. Sound Vib. 333(5), 1209–1223 (2014)
Zhang, S.Q., Li, Y.X., Schmidt, R.: Active shape and vibration control for piezoelectric bonded composite structures using various geometric nonlinearities. Compos. Struct. 1(122), 239–249 (2015)
Krishna, M.R.M., Mei, C.: Finite element buckling and post-buckling analyses of a plate with piezoelectric actuator. In: Rogers, C.A., Rogers, R.C. (eds.) Proceedings of the Conference on Recent Advances in Adaptive and Sensory Materials and Their Applications, Virginia Polytechnic Institute and State University, Blacksburg, 1992, pp. 301–313. Technomic Publishing Company Inc, Lancaster, Pennsylvania (1992)
Chandrashekhara, K., Bhatia, K.: Active buckling control of smart composite plates—finite-element analysis. Smart Mater. Struct. 2, 31–39 (1993)
Wang, Q., Varadan, V.K.: Transition of the buckling load of beams by the use of piezoelectric layers. Smart Mater. Struct. 12, 696–702 (2003)
Chróscielewski, J., Klosowski, P., Schmidt, R.: Theory and numerical simulation of nonlinear vibration control of arches with piezoelectric distributed actuators. Mach. Dyn. Probl. 20, 73–90 (1998)
Lentzen, S., Schmidt, R.: Geometrically nonlinear composite shells with integrated piezoelectric layers. Proc. Appl. Math. Mech. 4, 63–66 (2004)
Tzou, H.S., Bao, Y., Ye, R.: In: Hagood, N.W. (ed.) Smart Structures and Materials 1994: Smart Structures and Intelligent Systems, Proceeding of SPIE, vol. 2190, pp. 206–214 (1994)
Pai, P.F., Nayfeh, A.H., Oh, K., Mook, D.T.: A refined nonlinear model of composite plates with integrated piezoelectric actuators and sensors. Int. J. Solids Struct. 30, 1603–1630 (1993)
Reddy, J.N.: On laminated composite plates with integrated sensors and actuators. Eng. Struct. 21, 568–593 (1999)
Oh, I.-K., Han, J.-H., Lee, I.: Postbuckling and vibration characteristics of piezolaminated composite plate subject to thermo-piezoelectic loads. J. Sound Vib. 233, 19–40 (2000)
Oh, I.-K., Han, J.-H., Lee, I.: Thermopiezoelastic snapping of piezolaminated plates using layerwise nonlinear finite elements. AIAA J. 39, 1188–1197 (2001)
Yi, S., Ling, S.F., Ying, M.: Large deformation finite element analyses of composite structures integrated with piezoelectric sensors and actuators. Finite Elem. Anal. Des. 35, 1–15 (2000)
Mukherjee, A., Chaudhuri, A.S.: Nonlinear dynamic response of piezolaminated smart beams. Comput. Struct. 83, 1289–1304 (2005)
Lentzen, S., Schmidt, R.: Nonlinear finite element modeling of vibration control of piezolaminated composite plates and shells. In: Wang, K.-W. (ed.) Smart Structures and Materials 2005: Damping and Isolation, Proceedings of SPIE, vol. 5760, Paper 5760-16, SPIE, Bellingham, WA, USA (2005)
Lentzen, S., Schmidt, R.: A geometrically nonlinear finite element for transient analysis of piezolaminated shells. In: van Campen, D.H., Lazurko, M.D., van den Oever, W.P.J.M. (eds.) Proceedings Fifth EUROMECH Nonlinear Dynamics Conference, Eindhoven, The Netherlands, 7–12 August 2005, pp. 2492–2500. Eindhoven University of Technology (2005)
Lentzen, S., Schmidt, R.: Large amplitude vibrations and modal sensing of intelligent thin piezolaminated structures. In: Soize, C., Schuëller, G.I. (eds.) EURODYN 2005, Proceedings of the 6th European Conference on Structural Dynamics, Paris, France, 4–7 September 2005, pp. 1569–1574, Millpress, Rotterdam (2005)
Lentzen, S., Schmidt, R.: Nonlinear transient analysis, vibration control and modal sensing of smart piezolaminated shells. In: Sivakumar, S.M., Meher Prasad, A., Dattaguru, B., Narayanan, S., Rajendran, A.M., Atluri, S.N. (eds.) Advances in Computational & Experimental Engineering and Science, pp. 2062–2067. Tech Science Press, Encino, California, USA (2005)
Zhang, S.Q., Schmidt, R.: Static and dynamic FE analysis of piezoelectric integrated thin-walled composite structures with large rotations. Compos. Struct. 112, 345–357 (2014)
Rao, J.N., Lentzen, S., Schmidt, R.: Genetically optimised placement of piezoelectric sensor arrays: linear and nonlinear transient analysis. In: Brebbia, C.A. (ed.) High-Performance Structures and Materials III, pp. 653–661. WIT Press, Southampton-Boston (2006)
Shi, G., Atluri, S.N.: Active control of nonlinear dynamic response of space-frames using piezo-electric actuators. Comput. Struct. 34, 549–564 (1990)
Lee, S.-W., Beale, D.G.: Active control of nonlinear oscillations in a flexible rod slider crank mechanism. In: Burdisso, R.A. (ed.) Proceedings of the Second Conference on Recent Advances in Active Control of Sound and Vibration, Virginia Polytechnic Institute and State University, Blacksburg, 1993, pp. 729–740. Technomic Publishing Company Inc, Lancaster, Pennsylvania (1993)
Zhou, Y.-H., Wang, J.: Vibration control of piezoelectric beam-type plates with geometrically nonlinear deformation. Int. J. Non-Linear Mech. 39, 909–920 (2004)
Chróscielewski, J., Klosowski, P., Schmidt, R.: Numerical simulation of geometrically nonlinear flexible beam control via piezoelectric layers. ZAMM 77(Supplement 1), S69–S70 (1997)
Chróscielewski, J., Klosowski, P., Schmidt, R.: Modelling and FE-analysis of large deflection shape and vibration control of structures via piezoelectric layers. In: Gabbert, U. (ed.) Smart Mechanical Systems—Adaptronics, Fortschritt-Berichte VDI, Series 11, No. 244, pp. 53–62. VDI-Verlag, Düsseldorf (1997)
Tzou, H.S., Zhou, Y.-H.: Dynamics and control of piezoelectric circular plates with geometrical nonlinearity. J. Sound Vib. 188, 189–207 (1995)
Tzou, H.S., Zhou, Y.-H.: Nonlinear piezothermoelasticity and multi-field actuation, part 2: control of nonlinear buckling and dynamics. ASME J. Vib. Acoust. 19, 382–389 (1997)
Zhou, Y.-H., Tzou, H.S.: Active control of nonlinear piezoelectric spherical shallow shells. Int. J. Solids Struct. 37, 1663–1677 (2000)
Batra, R.C., Liang, X.Q., Kachroo, P.: Shape control of a nonlinear smart plate. In: Varadan, V.V., Chandra, J. (eds.) Smart Structures and Materials 1997: Mathematics and Control in Smart Structures, Proceedings of SPIE, vol. 3039, pp. 518–525 (1997)
Batra, R.C., Liang, X.Q.: Finite dynamic deformations of smart structures. Comput. Mech. 20, 427–438 (1997)
Lai, Z., Xue, D.Y., Huang, J.-K., Mei, C.: Nonlinear panel flutter suppression with piezoelectric actuation. In: Burdisso, R.A. (ed.) Proceedings of the Second Conference on Recent Advances in Active Control of Sound and Vibration, Virginia Polytechnic Institute and State University, Blacksburg, 1993, pp. 863–874. Technomic Publishing Company Inc, Lancaster, Pennsylvania (1993)
Zhou, R.C., Lai, Z., Xue, D.Y., Huang, J.-K., Mei, C.: Suppression of nonlinear panel flutter with piezoelectric actuators using finite element method. AIAA J. 33, 1098–1105 (1995)
Zhou, R.C., Mei, C., Huang, J.-K.: Suppression of nonlinear panel flutter at supersonic speeds and elevated temperatures. AIAA J. 34, 347–354 (1996)
Shen, J.Y., Sharpe, L., Jr.: A finite element model for the aeroelasticity analysis of hypersonic panels, part III: flutter suppression. In: Varadan, V.V., Chandra, J. (eds.) Smart Structures and Materials 1997: Mathematics and Control in Smart Structures, Proceedings of SPIE, vol. 3039, pp. 315–323 (1997)
Zhang, S.Q., Zhao, G.Z., Zhang, S.Y., Schmidt, R., Qin, X.S.: Geometrically nonlinear FE analysis of piezoelectric laminated composite structures under strong driving electric field. Compos. Struct. 1(181), 112–120 (2017)
Rao, M.N., Tarun, S., Schmidt, R., Schröder, K.U.: Finite element modeling and analysis of piezo-integrated composite structures under large applied electric fields. Smart Mater. Struct. 25(5), 055044 (2016)
Xin, L., Hu, Z.: Free vibration of layered magneto-electro-elastic beams by SS-DSC approach. Compos. Struct. 125, 96–103 (2015)
Rao, M.N., Schmidt, R., Schröder, K.U.: Geometrically nonlinear static FE-simulation of multilayered magneto-electro-elastic composite structures. Compos. Struct. 127, 120–131 (2015)
Giorgio, I., Galantucci, L., Della, Corte A., Del Vescovo, D.: Piezo-electromechanical smart materials with distributed arrays of piezoelectric transducers: current and upcoming applications. Int. J. Appl. Electromagn. Mech. 47(4), 1051–1084 (2015)
Andreaus, U., dell’Isola, F., Porfiri, M.: Piezoelectric passive distributed controllers for beam flexural vibrations. JVC/J. Vib. Control, 10(5), 625–659 (2004) . https://doi.org/10.1177/1077546304038224
Alessandroni, S., Andreaus, U., dell’Isola, F., Porfiri, M.: A passive electric controller for multimodal vibrations of thin plates. Comput. Struct. 83(15–16), 1236–1250 (2005). https://doi.org/10.1016/j.compstruc.2004.08.028
Giorgio, I., Culla, A., Del Vescovo, D.: Multimode vibration control using several piezoelectric transducers shunted with a multiterminal network. Arch. Appl. Mech. 79, 859–879 (2009)
Pagnini, L.C., Piccardo, G.: The three-hinged arch as an example of piezomechanic passive controlled structure. Contin. Mech. Thermodyn. 28, 1247 (2016). https://doi.org/10.1007/s00161-015-0474-x
D’Annibale, F., Rosi, G., Luongo, A.: On the failure of the ‘similar piezoelectric control’ in preventing the loss of stability caused by nonconservative positional forces. Z. Angew. Math. Phys. 66(4), 1949–1968 (2015)
D’Annibale, F.: Piezoelectric control of the Hopf bifurcation of Ziegler’s column with nonlinear damping. Nonlinear Dyn. 86, 2179 (2016). https://doi.org/10.1007/s11071-016-2866-2
Šilhavý, M.: A direct approach to nonlinear shells with application to surface-substrate interactions. Math. Mech. Complex Syst. 1(2), 211–232 (2013). https://doi.org/10.2140/memocs.2013.1.211
Girchenko, A.A., Eremeyev, V.A., Altenbach, H.: Interaction of a helical shell with a nonlinear viscous fluid. Int. J. Eng. Sci. 61, 53–58 (2012)
Sze, K.Y., Yao, L.Q.: Modelling smart structures with segmented piezoelectric sensors and actuators. J. Sound Vib. 35, 495–520 (2000)
Sze, K.Y., Yao, L.Q., Yi, S.: A hybrid stress ANS solid-shell element and its generalization for smart structure modelling. Part II: smart structure modeling. Int. J. Numer. Meth. Eng. 48, 565–582 (2000)
Balamurugan, V., Nayaranan, S.: Active vibration control of smart shells using distributed piezoelectric sensors and actuators. Smart Mater. Struct. 10, 173–180 (2001)
Nardinocchi, P., Pezzulla, M., Placidi, L.: Thermodynamically based multiphysic modeling of ionic polymer metal composites. J. Intell. Mater. Syst. Struct. 22(16), 1887–1897 (2011)
Del Bufalo, G., Placidi, L., Porfiri, M.: A mixture theory framework for modeling the mechanical actuation of ionic polymer metal composites. Smart Mater. Struct. 17(4), 045010 (2008)
Tiersten, H.F.: Hamilton’s principle for linear piezoelectric media. Proc. IEEE 55(8), 1523–1526 (1967)
Allik, H., Hughes, T.J.: Finite element method for piezoelectric vibration. Int. J. Numer. Meth. Eng. 2(2), 151–158 (1970)
McMeeking, R.M., Landis, C.M., Jimenez, S.M.: A principle of virtual work for combined electrostatic and mechanical loading of materials. Int. J. Non-Linear Mech. 42(6), 831–838 (2007)
Abali, B.E.: Computational Reality: Solving Nonlinear and Coupled Problems in Continuum Mechanics. Springer, Singapore (2017)
Lammering, R., Mesecke-Rischmann, S.: Multi-field variational formulations and related finite elements for piezoelectric shells. Smart Mater. Struct. 12(6), 904–913 (2003)
Belokon, A.V., Eremeyev, V.A., Nasedkin, A.V., Solov’yev, A.N.: Partitioned schemes of the finite-element method for dynamic problems of acoustoelectroelasticity. J. Appl. Math. Mech. 64(3), 367–377 (2000)
Nasedkin, A.V., Eremeyev, V.A.: Harmonic vibrations of nanosized piezoelectric bodies with surface effects. ZAMM 94(10), 878–892 (2014)
Eremeyev, V.A., Nasedkin, A.V.: Mathematical models and finite element approaches for nanosized piezoelectric bodies with uncoulped and coupled surface effects. In: Wave Dynamics and Composite Mechanics for Microstructured Materials and Metamaterials, pp. 1–18. Springer, Singapore (2017)
Abali, B.E., Reich, F.A.: Thermodynamically consistent derivation and computation of electro–thermo–mechanical systems for solid bodies. Comput. Methods Appl. Mech. Eng. 319, 567–595 (2017)
Waszczyszyn, Z., Cichoń, Cz, Radwańska, M.: Stability of Structures by Finite Element Methods. Elsevier, Amsterdam (1994)
Riks, E.: On the Numerical Solution of Snapping Problems in the Theory of Elastic Stability, SUDAAR 401. Stanford University, Stanford (1970)
Riks, E.: The application of Newton’s method to the problem of elastic stability. Trans. ASME J. Appl. Mech. 39, 1060–1065 (1972)
Wempner, G.: Discrete approximations related to nonlinear theories of solids. Int. J. Solids Struct. 7, 1581–1599 (1971)
Chróścielewski, J., Nolte, L.-P.: Strategien zur Lösung nichtlinearer Probleme der Strukturmechanik und ihre modulare Aufbereitung im Konzept MESY, Mitt. Institut für Mechanik, 48, Ruhr-Universität, Bochum (1985)
Chróścielewski, J., Schmidt, R.: A solution control method for nonlinear finite element post-buckling analysis of structures. In: Szabó, J. (ed.) Post-Buckling of Elastic Structures, Proc. of the EUROMECH—Colloquium Nr. 200, Mátrafüred (Hungary), 1985, pp. 19–33. Elsevier Science Publisher B.V., Amsterdam (1986)
Cazzani, A., Stochino, F., Turco, E.: An analytical assessment of finite element and isogeometric analyses of the whole spectrum of Timoshenko beams. ZAMM, 96(10), 1220-1244 (2016). https://doi.org/10.1002/zamm.201500280
Cazzani, A., Malagu, M., Turco, E.: Isogeometric analysis of plane-curved beams. Math. Mech. Solids 21(5), 562–577 (2014). https://doi.org/10.1177/1081286514531265
Greco, L., Cuomo, M.: B-Spline interpolation of Kirchhoff–Love space rods. Comput. Methods Appl. Mech. Eng. 256, 251–269 (2013)
Alibert, J.-J., Della Corte, A., Giorgio, I., Battista, A.: Extensional Elastica in large deformation as \(\Gamma \)-limit of a discrete 1D mechanical system. ZAMP (2017). https://doi.org/10.1007/s00033-017-0785-9
Chróścielewski, J., Witkowski, W.: Discrepancies of energy values in dynamics of three intersecting plates. Int. J. Numer. Methods Biomed. Eng. 26(9), 1188–1202 (2010)
Witkowski, W., Rucka, M., Chróścielewski, J., Wilde, K.: On some properties of 2D spectral finite elements in problems of wave propagation. Finite Elem. Anal. Des. 55, 31–41 (2012)
Chróścielewski, J., Makowski, J., Stumpf, H.: Genuinely resultant shell finite elements accounting for geometric and material non-linearity. Int. J. Numer. Meth. Eng. 35, 63–94 (1992)
Chróścielewski, J., Makowski, J., Stumpf, H.: Finite element analysis of smooth, folded and multi-shell structures. Comput. Meth. Appl. Mech. Eng. 141, 1–46 (1997)
Kuhl, D., Crisfield, M.A.: Energy-conserving algorithms in non-linear structural dynamics. Int. J. Numer. Meth. Eng. 45, 569–599 (1999)
Chróścielewski, J., Lubowiecka, I., Witkowski, W.: Energy-conserving integration in six-field shell dynamics. In: ICTAM04 Abstract Book and CD-ROM Proceedings, 21st International Congress of Theoretical and Applied Mechanics, Warsaw, Poland, 337 (August 15–21, 2004)
Mukherjee, A., Joshi, S.P.: Gradientless technique for optimal distribution of piezoelectric material for structural control. Int. J. Numer. Meth. Eng. 57, 1737–1753 (2003)
Mukherjee, A., Joshi, S.P.: Piezoelectric sensor and actuator spatial design for shape control of piezolaminated plates. AIAA J. 40, 1204–1210 (2002)
Lentzen, S., Schmidt, R.: Nonlinear dynamics and control of smart piezolaminated plates and shells. In: Proceedings of ICDVC-2006, The Second International Conference on Dynamics, Vibration and Control, Beijing, China, 23–26 August 2006, Paper ICDVC2006-W42, Chinese Academy of Sciences, Beijing (2006)
Mukherjee, A., Saha Chaudhuri, A.: Active control of dynamic instability of piezo-laminated imperfect columns. Smart Mater. Struct. 11, 874–879 (2002)
Mukherjee, A., Saha Chaudhuri, A.: Exact solutions for instability control of piezolaminated imperfect struts. AIAA J. 14, 857–859 (2004)
Mukherjee, A., Saha Chaudhuri, A.: Active control of piezolaminated columns—exact solutions and experimental validation. Smart Mater. Struct. 14, 475–482 (2005)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Francesco dell’Isola.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
VAE acknowledges the support of the Ministry of Education and Science of the Russian Federation, Project No. 9.1001.2017/4.6.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Chróścielewski, J., Schmidt, R. & Eremeyev, V.A. Nonlinear finite element modeling of vibration control of plane rod-type structural members with integrated piezoelectric patches. Continuum Mech. Thermodyn. 31, 147–188 (2019). https://doi.org/10.1007/s00161-018-0672-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00161-018-0672-4