Abstract
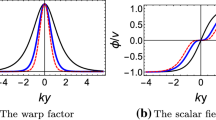
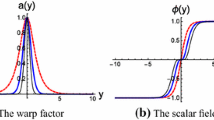
In this work, we investigate gravitational resonances in both single and double mimetic thick branes, which can provide a new way to detect the extra dimension. For the single brane model, we apply the relative probability proposed in [Phys. Rev.D 80 (2009) 065019]. For the double brane model, we investigate the resonances quasi-localized on the double brane, on the sub-branes and between the sub-branes, respectively. To investigate the resonances quasi-localized on the double brane, we introduce two different definitions of the relative probability and find that the corresponding mass spectra of gravitational resonances are almost the same. For the gravitational resonances quasi-localized on sub-branes and between the sub-branes, the influence of the distance between the two sub-branes and the thickness of the sub-branes are analyzed and new features are found in both cases.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
N. Arkani-Hamed, S. Dimopoulos and G.R. Dvali, The Hierarchy problem and new dimensions at a millimeter, Phys. Lett. B 429 (1998) 263 [hep-ph/9803315] [INSPIRE].
L. Randall and R. Sundrum, A Large mass hierarchy from a small extra dimension, Phys. Rev. Lett. 83 (1999) 3370 [hep-ph/9905221] [INSPIRE].
L. Randall and R. Sundrum, An Alternative to compactification, Phys. Rev. Lett. 83 (1999) 4690 [hep-th/9906064] [INSPIRE].
J.E. Kim, B. Kyae and H.M. Lee, Randall-Sundrum model for selftuning the cosmological constant, Phys. Rev. Lett. 86 (2001) 4223 [hep-th/0011118] [INSPIRE].
S. Kobayashi, K. Koyama and J. Soda, Thick brane worlds and their stability, Phys. Rev. D 65 (2002) 064014 [hep-th/0107025] [INSPIRE].
M. Giovannini, Gauge invariant fluctuations of scalar branes, Phys. Rev. D 64 (2001) 064023 [hep-th/0106041] [INSPIRE].
D. Bazeia, C. Furtado and A.R. Gomes, Brane structure from scalar field in warped space-time, JCAP 02 (2004) 002 [hep-th/0308034] [INSPIRE].
D. Bazeia and A.R. Gomes, Bloch brane, JHEP 05 (2004) 012 [hep-th/0403141] [INSPIRE].
C. Csáki, J. Erlich, T.J. Hollowood and Y. Shirman, Universal aspects of gravity localized on thick branes, Nucl. Phys. B 581 (2000) 309 [hep-th/0001033] [INSPIRE].
O. DeWolfe, D.Z. Freedman, S.S. Gubser and A. Karch, Modeling the fifth-dimension with scalars and gravity, Phys. Rev. D 62 (2000) 046008 [hep-th/9909134] [INSPIRE].
M. Gremm, Four-dimensional gravity on a thick domain wall, Phys. Lett. B 478 (2000) 434 [hep-th/9912060] [INSPIRE].
M. Gremm, Thick domain walls and singular spaces, Phys. Rev. D 62 (2000) 044017 [hep-th/0002040] [INSPIRE].
V.I. Afonso, D. Bazeia and L. Losano, First-order formalism for bent brane, Phys. Lett. B 634 (2006) 526 [hep-th/0601069] [INSPIRE].
D. Bazeia, L. Losano and C. Wotzasek, Domain walls in three field models, Phys. Rev. D 66 (2002) 105025 [hep-th/0206031] [INSPIRE].
V. Dzhunushaliev, V. Folomeev, S. Myrzakul and R. Myrzakulov, Phantom thick brane in 5D bulk, Mod. Phys. Lett. A 23 (2008) 2811 [arXiv:0804.0151] [INSPIRE].
I.P. Neupane, de Sitter brane-world, localization of gravity and the cosmological constant, Phys. Rev. D 83 (2011) 086004 [arXiv:1011.6357] [INSPIRE].
B. Bajc and G. Gabadadze, Localization of matter and cosmological constant on a brane in anti-de Sitter space, Phys. Lett. B 474 (2000) 282 [hep-th/9912232] [INSPIRE].
C. Ringeval, P. Peter and J.-P. Uzan, Localization of massive fermions on the brane, Phys. Rev. D 65 (2002) 044016 [hep-th/0109194] [INSPIRE].
J.A. Bagger and D.V. Belyaev, Brane-localized Goldstone fermions in bulk supergravity, Phys. Rev. D 72 (2005) 065007 [hep-th/0406126] [INSPIRE].
Y.-X. Liu, X.-H. Zhang, L.-D. Zhang and Y.-S. Duan, Localization of Matters on Pure Geometrical Thick Branes, JHEP 02 (2008) 067 [arXiv:0708.0065] [INSPIRE].
Y.-X. Liu, L.-D. Zhang, S.-W. Wei and Y.-S. Duan, Localization and Mass Spectrum of Matters on Weyl Thick Branes, JHEP 08 (2008) 041 [arXiv:0803.0098] [INSPIRE].
K. Ghoroku and A. Nakamura, Massive vector trapping as a gauge boson on a brane, Phys. Rev. D 65 (2002) 084017 [hep-th/0106145] [INSPIRE].
A. Kehagias and K. Tamvakis, Localized gravitons, gauge bosons and chiral fermions in smooth spaces generated by a bounce, Phys. Lett. B 504 (2001) 38 [hep-th/0010112] [INSPIRE].
W.T. Cruz, L.J.S. Sousa, R.V. Maluf and C.A.S. Almeida, Graviton resonances on two-field thick branes, Phys. Lett. B 730 (2014) 314 [arXiv:1310.4085] [INSPIRE].
Q.-Y. Xie, J. Yang and L. Zhao, Resonance Mass Spectra of Gravity and Fermion on Bloch Branes, Phys. Rev. D 88 (2013) 105014 [arXiv:1310.4585] [INSPIRE].
Z.-G. Xu, Y. Zhong, H. Yu and Y.-X. Liu, The structure of f (R)-brane model, Eur. Phys. J. C 75 (2015) 368 [arXiv:1405.6277] [INSPIRE].
C. Csáki, J. Erlich and T.J. Hollowood, Quasilocalization of gravity by resonant modes, Phys. Rev. Lett. 84 (2000) 5932 [hep-th/0002161] [INSPIRE].
H. Yu, Y. Zhong, B.-M. Gu and Y.-X. Liu, Gravitational resonances on f (R)-brane, Eur. Phys. J. C 76 (2016) 195 [arXiv:1506.06458] [INSPIRE].
H.-P. Nollert, Quasinormal modes: the characteristic ‘sound’ of black holes and neutron stars, Class. Quant. Grav. 16 (1999) R159 [INSPIRE].
Y.-X. Liu, Introduction to Extra Dimensions and Thick Braneworlds, in Memorial Volume for Yi-Shi Duan, M.L. Ge, R.G. Cai and Y.X. Liu eds., World Scientific (2018), pp. 211-275, [arXiv:1707.08541] [INSPIRE].
T.P. Sotiriou and V. Faraoni, f (R) Theories Of Gravity, Rev. Mod. Phys. 82 (2010) 451 [arXiv:0805.1726] [INSPIRE].
S. Nojiri and S.D. Odintsov, Introduction to modified gravity and gravitational alternative for dark energy, eConf C 0602061 (2006) 06 [hep-th/0601213] [INSPIRE].
S. Nojiri, S.D. Odintsov and V.K. Oikonomou, Modified Gravity Theories on a Nutshell: Inflation, Bounce and Late-time Evolution, Phys. Rept. 692 (2017) 1 [arXiv:1705.11098] [INSPIRE].
D. Kastor, S. Ray and J. Traschen, Lovelock Branes, Class. Quant. Grav. 34 (2017) 195005 [arXiv:1706.06684] [INSPIRE].
D. Bazeia, M.A. Marques and R. Menezes, Generalized Born-Infeld-like models for kinks and branes, EPL 118 (2017) 11001 [arXiv:1703.05848] [INSPIRE].
V.I. Afonso, D. Bazeia, R. Menezes and A.Y. Petrov, f (R)-Brane, Phys. Lett. B 658 (2007) 71 [arXiv:0710.3790] [INSPIRE].
B. Guo, Y.-X. Liu and K. Yang, Brane worlds in gravity with auxiliary fields, Eur. Phys. J. C 75 (2015) 63 [arXiv:1405.0074] [INSPIRE].
G. German, A. Herrera-Aguilar, D. Malagon-Morejon, I. Quiros and R. da Rocha, Study of field fluctuations and their localization in a thick braneworld generated by gravity nonminimally coupled to a scalar field with the Gauss-Bonnet term, Phys. Rev. D 89 (2014) 026004 [arXiv:1301.6444] [INSPIRE].
O. Arias, R. Cardenas and I. Quiros, Thick brane worlds arising from pure geometry, Nucl. Phys. B 643 (2002) 187 [hep-th/0202130] [INSPIRE].
Y. Zhong and Y.-X. Liu, Pure geometric thick f (R)-branes: stability and localization of gravity, Eur. Phys. J. C 76 (2016) 321 [arXiv:1507.00630] [INSPIRE].
J. Yang, Y.-L. Li, Y. Zhong and Y. Li, Thick Brane Split Caused by Spacetime Torsion, Phys. Rev. D 85 (2012) 084033 [arXiv:1202.0129] [INSPIRE].
P.M.L.T. da Silva and J.M. Hoff da Silva, f (R)-Einstein-Palatini formalism and smooth branes, Eur. Phys. J. Plus 132 (2017) 437 [arXiv:1603.04793] [INSPIRE].
K. Yang, W.-D. Guo, Z.-C. Lin and Y.-X. Liu, Domain wall brane in a reduced Born-Infeld-f (T ) theory, Phys. Lett. B 782 (2018) 170 [arXiv:1709.01047] [INSPIRE].
W.-D. Guo, Q.-M. Fu, Y.-P. Zhang and Y.-X. Liu, Tensor perturbations of f (T )-branes, Phys. Rev. D 93 (2016) 044002 [arXiv:1511.07143] [INSPIRE].
A. Karam, A. Lykkas and K. Tamvakis, Frame-invariant approach to higher-dimensional scalar-tensor gravity, Phys. Rev. D 97 (2018) 124036 [arXiv:1803.04960] [INSPIRE].
W.-D. Guo, Y. Zhong, K. Yang, T.-T. Sui and Y.-X. Liu, Thick brane in mimetic f (T ) gravity, arXiv:1805.05650 [INSPIRE].
A.H. Chamseddine and V. Mukhanov, Mimetic Dark Matter, JHEP 11 (2013) 135 [arXiv:1308.5410] [INSPIRE].
A.H. Chamseddine, V. Mukhanov and A. Vikman, Cosmology with Mimetic Matter, JCAP 06 (2014) 017 [arXiv:1403.3961] [INSPIRE].
J. Dutta, W. Khyllep, E.N. Saridakis, N. Tamanini and S. Vagnozzi, Cosmological dynamics of mimetic gravity, JCAP 02 (2018) 041 [arXiv:1711.07290] [INSPIRE].
J. Matsumoto, S.D. Odintsov and S.V. Sushkov, Cosmological perturbations in a mimetic matter model, Phys. Rev. D 91 (2015) 064062 [arXiv:1501.02149] [INSPIRE].
R. Myrzakulov, L. Sebastiani, S. Vagnozzi and S. Zerbini, Static spherically symmetric solutions in mimetic gravity: rotation curves and wormholes, Class. Quant. Grav. 33 (2016) 125005 [arXiv:1510.02284] [INSPIRE].
S. Vagnozzi, Recovering a MOND-like acceleration law in mimetic gravity, Class. Quant. Grav. 34 (2017) 185006 [arXiv:1708.00603] [INSPIRE].
S. Nojiri and S.D. Odintsov, Mimetic F (R) gravity: inflation, dark energy and bounce, Mod. Phys. Lett. A 29 (2014) 1450211 [Erratum ibid. A 29 (2014) 1450211] [arXiv:1408.3561] [INSPIRE].
A.V. Astashenok, S.D. Odintsov and V.K. Oikonomou, Modified Gauss-Bonnet gravity with the Lagrange multiplier constraint as mimetic theory, Class. Quant. Grav. 32 (2015) 185007 [arXiv:1504.04861] [INSPIRE].
S.D. Odintsov and V.K. Oikonomou, Mimetic F (R) inflation confronted with Planck and BICEP2/Keck Array data, Astrophys. Space Sci. 361 (2016) 174 [arXiv:1512.09275] [INSPIRE].
S.D. Odintsov and V.K. Oikonomou, Unimodular Mimetic F (R) Inflation, Astrophys. Space Sci. 361 (2016) 236 [arXiv:1602.05645] [INSPIRE].
S.D. Odintsov and V.K. Oikonomou, Dark Energy Oscillations in Mimetic F (R) Gravity, Phys. Rev. D 94 (2016) 044012 [arXiv:1608.00165] [INSPIRE].
S. Nojiri, S.D. Odintsov and V.K. Oikonomou, Viable Mimetic Completion of Unified Inflation-Dark Energy Evolution in Modified Gravity, Phys. Rev. D 94 (2016) 104050 [arXiv:1608.07806] [INSPIRE].
S.D. Odintsov and V.K. Oikonomou, The reconstruction of f (ϕ)R and mimetic gravity from viable slow-roll inflation, Nucl. Phys. B 929 (2018) 79 [arXiv:1801.10529] [INSPIRE].
N. Sadeghnezhad and K. Nozari, Braneworld Mimetic Cosmology, Phys. Lett. B 769 (2017) 134 [arXiv:1703.06269] [INSPIRE].
Y. Zhong, Y. Zhong, Y.-P. Zhang and Y.-X. Liu, Thick branes with inner structure in mimetic gravity, Eur. Phys. J. C 78 (2018) 45 [arXiv:1711.09413] [INSPIRE].
Y.-X. Liu, J. Yang, Z.-H. Zhao, C.-E. Fu and Y.-S. Duan, Fermion Localization and Resonances on A de Sitter Thick Brane, Phys. Rev. D 80 (2009) 065019 [arXiv:0904.1785] [INSPIRE].
C.A.S. Almeida, M.M. Ferreira Jr., A.R. Gomes and R. Casana, Fermion localization and resonances on two-field thick branes, Phys. Rev. D 79 (2009) 125022 [arXiv:0901.3543] [INSPIRE].
Y.-Z. Du, L. Zhao, Y. Zhong, C.-E. Fu and H. Guo, Resonances of Kalb-Ramond field on symmetric and asymmetric thick branes, Phys. Rev. D 88 (2013) 024009 [arXiv:1301.3204] [INSPIRE].
R.R. Landim, G. Alencar, M.O. Tahim and R.N. Costa Filho, A Transfer Matrix Method for Resonances in Randall-Sundrum Models, JHEP 08 (2011) 071 [arXiv:1105.5573] [INSPIRE].
R. Gregory, V.A. Rubakov and S.M. Sibiryakov, Opening up extra dimensions at ultra large scales, Phys. Rev. Lett. 84 (2000) 5928 [hep-th/0002072] [INSPIRE].
J.D. Lykken and L. Randall, The Shape of gravity, JHEP 06 (2000) 014 [hep-th/9908076] [INSPIRE].
W.-H. Tan et al., New Test of the Gravitational Inverse-Square Law at the Submillimeter Range with Dual Modulation and Compensation, Phys. Rev. Lett. 116 (2016) 131101 [INSPIRE].
Open Access
This article is distributed under the terms of the Creative Commons Attribution License (CC-BY 4.0), which permits any use, distribution and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Additional information
ArXiv ePrint: 1812.06453
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhong, Y., Zhang, YP., Guo, WD. et al. Gravitational resonances in mimetic thick branes. J. High Energ. Phys. 2019, 154 (2019). https://doi.org/10.1007/JHEP04(2019)154
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/JHEP04(2019)154