Thick branes with inner structure in mimetic f(R) gravity

Abstract

In this paper, we study the structure and gravitational resonances of thick branes generated by a mimetic scalar field in f(R) gravity. We obtain several typical thick brane solutions for $f(R)=R+\alpha R^2$. To study their stability, we analyze the tensor perturbation of the metric. It is shown that any thick brane model with $df/dR>0$ is stable and the graviton zero mode can be localized on the brane for each solution, which indicates that the four-dimensional Newtonian gravity can be restored. The effect of the parameter $\alpha$ on the gravitational resonances is studied. As a brane splits into multi sub-branes, the effective potential of the tensor perturbation will have an abundant inner structure with multi-wells, and this will lead to new phenomena of the gravitational resonances.

1 Introduction

In last 20 years, the brane world scenario has been an attractive topic and researched widely. Arkani-Hamed, Dimopoulos, and Dvali (ADD) provided an alternative solution to the gauge hierarchy problem [1]. In the ADD model, all matter fields are confined on a four-dimensional brane which is embedded in a higher-dimensional spacetime, only gravity can propagate in the bulk. After that, Randall and Sundrum proposed two different kinds of extra dimension models, RS-1 [2] and RS-2 [3]. In the RS-1 model the extra dimension is compact and warped but in the RS-2 model the scale of the warped extra dimension is infinite. In the RS-2 model, the four-dimensional Newtonian potential can be restored even if the scale of the extra dimension is infinite. However, the thicknesses of the brane of RS models are neglected, and this is the reason why we called them thin brane models. Combining the RS-2 model with the domain wall model [4] one can generalize the RS-2 model to a thick brane model [5,6,7]. The localization problem of matter fields on a thick brane was studied in Refs. [5, 7,8,9,10,11,12,13,14,15,16,17,18]. In the thick brane world scenario, the brane is usually generated by a canonical scalar field [19,20,21,22,23,24]. Furthermore, various kinds of thick branes generated by multi-scalar fields were also investigated widely [25,26,27,28,29]. For more details of thick brane worlds and extra dimensions, see the review papers [30,31,32].

On the other hand, physicists should answer what causes late-time universe acceleration and what dark matter is. To solve these issues indicated by astronomical observations, physicists provided two kinds of schemes, one assuming the existence of extra energy and matter, the other one modifying general relativity to match observations. Furthermore, renormalization of gravity is another motivation to modify general relativity. Mimetic gravity is a modified theory proposed by Chamseddine and Mukhanov [33]. In this theory the conformal degree of freedom of the background metric is isolated and it could mimic cold dark matter [34,35,36,37,38,39,40,41], or dark energy [42,43,44,45]. Barvinsky found that, for positive energy density of the mimetic fluid in cosmology, mimetic gravity is free of a ghost instability [35]. Then another paper confirmed that the original mimetic gravity theory suffers from ghost instability in all generality [46]. And using the extension of mimetic gravity the inflationary solution was studied in Ref. [47]. On the other hand, instead of cold dark matter this conformal degree of freedom can also mimic the scalar field which generates the thick brane. In the last few years, Zhong et al. investigated thick branes generated by the mimetic scalar field in Ref. [48]. It was found that one could construct some exact solutions of brane world, and some of them have inner structure. This inner structure in a thick brane can lead to new phenomena of the gravitational resonances, which was further investigated in Ref. [49]. Other recent research can be found in Refs. [50, 51].

As a simple interesting higher-order gravity [52], f(R) gravity has had great success in cosmology. For example, it can explain the inflation [53,54,55,56,57,58] and the late-time acceleration [59,60,61,62,63,64,65,66,67]. The ghost stability was also studied in detail (see Refs. [68, 69]). The mimetic method mentioned above was applied to f(R) gravity by Odintsov [70]. After that, Leon and Saridakis studied the dynamical behavior of mimetic f(R) gravity [71]. Odintsov and Oikonomou investigated dark energy oscillations in this gravity [72]. The stability of a de Sitter solution in this theory was studied [73]. Recently, other work confirmed that if the usual stability conditions of the standard f(R) gravity are assumed and the Lagrange multiplier $\lambda$ which is related to the mimetic field energy density is positive the mimetic f(R) gravity is stable [74].

The thick brane world in f(R) gravity has been studied widely [75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96]. The stability of the f(R) brane on the linear tensor perturbation was first investigated in Ref. [79] and then was further considered in Refs. [87,88,89,90,91]. In these models, the brane is generated by a background scalar field. In this paper, we would like to study the thick brane world in mimetic f(R) gravity. In this gravity theory the thick brane is generated by a mimetic scalar field coming from the conformal degree of freedom of the metric. In fact, such a thick brane model was studied in mimetic gravity [48] and mimetic f(T) gravity [97]. Meanwhile the thin brane scenario in mimetic f(R) gravity was investigated in Ref. [98]. Here, we focus on the thick brane model in mimetic f(R) gravity. We take $f(R) = R+\alpha R^2$ as an example, to study the effect of the higher-order term of the scalar curvature. We construct a series of thick branes with inner structure analytically by using the conformal degree of freedom of the mimetic f(R) theory. By analyzing the linear tensor perturbation of the metric, we study the stability and gravitational resonances of the system. The result shows that these thick branes are stable under the tensor perturbation, and the zero mode of graviton can be localized on the branes. Therefore, four-dimensional gravity can be recovered. Apart from the graviton zero mode, we also investigate the gravitational resonances, which stay on the brane for a long time. These resonances may lead to experimental signals in a high energy collider. The resonances on the f(R) brane were studied in Refs. [18, 20, 21]. Compared to this work, the branes here support more gravitational resonances thanks to their inner structure. The gravitational resonances on the sub-brane structure are also studied.

The organization of our work is as follows. In Sect. 2, we review mimetic f(R) theory and construct three flat thick brane models with $f(R)=R+\alpha R^2$. In Sect. 3, we investigate the tensor perturbation and the graviton zero mode in each brane model. In Sect. 4 we study the gravitational resonances, and show the abundant behavior of these resonances due to the inner structure of the branes. Finally, in Sect. 5 we present the conclusions and discussions.

2 Mimetic f(R) gravity and thick brane models

First, we give a brief review of thick branes in mimetic f(R) theory. The original mimetic scalar comes from the conformal degree freedom of the metric [33]. Later, it was found that this method is equivalent to the Lagrange multiplier method that was first investigated in Ref. [99]. In this paper, we will use the Lagrange multiplier method. The action of mimetic f(R) gravity in five-dimensional spacetime is

$$\begin{aligned} S=\int d^4xdy\sqrt{-g} \left[ {\frac{M_*^3}{2}} f(R)+L(\phi ) \right] , \end{aligned}$$

(1)

where $M_*$ is the fundamental mass scale, f(R) is a function of the scalar curvature R. In this paper, we set $M_*=1$. The Lagrangian of the mimetic scalar field is

$$\begin{aligned} L(\phi )=\lambda \left[ g^{MN}\partial _M\phi \partial _N\phi -U(\phi )\right] -V(\phi ), \end{aligned}$$

(2)

where $\lambda$ is the Lagrange multiplier, $U(\phi )$ and $V(\phi )$ are two scalar potentials, while the former is in fact determined by the kinetic term of the mimetic scalar field. The field equations can be obtained by varying the action (1) with respect to the metric $g_{MN}$, the scalar field $\phi$, and the Lagrange multiplier $\lambda$, respectively:

$$\begin{aligned}&f_R R_{MN}-\frac{1}{2}g_{MN}f +\left( g_{MN}\Box ^{(5)}-\nabla _M \nabla _N\right) f_R \nonumber \\&\quad = g_{MN}L(\phi )-2\lambda \partial _M \phi \partial _N \phi , \end{aligned}$$

(3)

$$\begin{aligned}&2\lambda \Box ^{(5)}\phi +2\nabla _M \lambda \nabla ^M\phi +\lambda \frac{\partial U}{\partial \phi }+\frac{\partial V}{\partial \phi }=0, \end{aligned}$$

(4)

$$\begin{aligned}&g^{MN}\partial _M \phi \partial _N \phi - U(\phi )=0&, \end{aligned}$$

(5)

where $\Box ^{(5)}=g^{MN}\nabla _M \nabla _N$ is the five-dimensional d’Alembert operator and $f_R\equiv df(R)/dR$. The indices $M,N,\cdots =0,1,2,3,5$ and $\mu ,\nu ,\cdots =0,1,2,3$ denote the bulk and brane coordinates, respectively. In the original mimetic gravity, $U(\phi )=-1$ [33]. Later, it was generated as $U(\phi )\ne -1$ by Astashenok, Odintsov and Oikonomou [100]. In order to generate a thick brane, the mimetic scalar field should be spacelike and only depend on the extra dimension y [48]. So from Eq. (5) we know that $U(\phi )=g^{MN}\partial _M \phi \partial _N \phi >0$.

In this paper we consider the four-dimensional flat brane with the metric

$$\begin{aligned} \mathrm{{d}}s^2=a^2(y)\eta _{\mu \nu } \mathrm{{d}}x^{\mu } \mathrm{{d}}x^{\nu }+\mathrm{{d}}y^2, \end{aligned}$$

(6)

where a(y) is the warp factor, y represents the extra dimension, and $\eta _{\mu \nu }$ is the four-dimensional Minkowski metric. With this metric, Eqs. (3)–(5) can be written as

$$\begin{aligned}&f+\frac{6a'^2}{a^2}f_R+\frac{2a''}{a}f_R-\frac{6a'}{a}f'_R-2f''_R-2V \nonumber \\&\quad -2\lambda \left( U-\phi '^2\right) =~0, \end{aligned}$$

(7)

$$\begin{aligned}&f+\frac{8a''}{a}f_R-\frac{8a'}{a}f'_R-2V-2\lambda \left( U+\phi '^2\right) =~0, \end{aligned}$$

(8)

$$\begin{aligned}&\frac{\partial V}{\partial \phi }+2\lambda '\phi '+\lambda \left( \frac{\partial U}{\partial \phi }+8\phi '\frac{a'}{a}+2\phi ''\right) =~0, \end{aligned}$$

(9)

$$\begin{aligned}&U(\phi )-\phi '^2=~0, \end{aligned}$$

(10)

and

$$\begin{aligned} R=-12\frac{a'^2}{a^2}-8\frac{a''}{a}, \end{aligned}$$

(11)

where the symbol prime denotes the derivative with respect to the extra dimension coordinate y. Combining Eqs. (7), (8), and (10), we can get

$$\begin{aligned}&\lambda =\frac{1}{\phi '^2}\left( \frac{3a''}{2a}f_R -\frac{3a'^2}{2a^2}f_R-\frac{a'}{2a}f'_R+\frac{1}{2}f''_R \right) , \end{aligned}$$

(12)

$$\begin{aligned}&V=\frac{f}{2}+\frac{3a'^2}{a^2}f_R+\frac{a''}{a}f_R-\frac{3a'}{a}f'_R-f''_R. \end{aligned}$$

(13)

Note that there are only three independent equations in Eqs. (7)–(10), because the left side of Eq. (3) is divergent-free [68]. Since there are six functions, f(R), a(y), $\phi (y)$, $\lambda (\phi )$, $V(\phi )$, and $U(\phi )$, we should fix three of them. In this paper, we will give f(R), a(y), and $\phi (y)$, and solve $\lambda (\phi )$, $V(\phi )$, and $U(\phi )$.

We consider $f(R)=R+\alpha R^2$ as an example, where $\alpha$ is the parameter which measures the degree of deviation from mimetic gravity. In this formula of f(R) we require

$$\begin{aligned} f_R > 0 \end{aligned}$$

(14)

in the whole extra dimension in order to guarantee that the graviton is not a ghost [68]. Then we will give three kinds of warp factors to study the behavior of gravitational resonances. There are several reasons why we choose these warp factors and mimetic scalar fields.

• First, usually gravity can be localized on the brane in a five-dimensional asymptotic AdS spacetime [32]. From Eq. (11) we know that, at infinity, that is, $y \rightarrow \pm \infty$, when $a(y) \rightarrow e^{-k|y|}$, the Ricci scalar approaches a negative constant, $-20 k^2$. So if the warp factor shows this kind of asymptotic behavior, the five-dimensional spacetime is an asymptotic AdS spacetime. The graviton zero mode of the tensor perturbation can be localized on the brane, which results in recovering of the four-dimensional Newtonian potential.

• Second, the localization of scalar field is another point that needs to be considered. It can be shown that the scalar field can also be localized on the brane embedded in a five-dimensional asymptotic AdS spacetime.

• Last, thanks to the conformal degree of freedom of mimetic f(R) theory, we could construct branes with inner structure analytically using different warp factors. We will construct three kinds of warp factor to get corresponding branes with inner structure next. On this basis, we can further study the new physics of brane with inner structure.

2.1 Model 1

In the first model, the warp factor and the scalar field are set as follows:

$$\begin{aligned}&a(y)=\text {sech}^{n} (ky), \end{aligned}$$

(15)

$$\begin{aligned}&\phi (y)=v\, \text {tanh}^n(ky), \end{aligned}$$

(16)

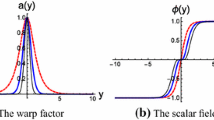
where the parameter k is usually taken as the order of $M_*$, n is a positive odd integer, and v is a positive parameter. Shapes of the warp factor and the scalar field for different n are depicted in Fig. 1a and b, respectively. From Fig. 1b, we can see that the scalar field is a single-kink and a double-kink for $n=1$ and $n\ge 3$, respectively. Besides, it can be noticed that as n increases the platform near $y=0$ of the double-kink scalar field becomes wider and the warp factor becomes more concentrated.

Fig. 1

Shapes of the warp factor a(y) and the scalar field $\phi (y)$ in model 1. The parameters are set as $n=1$ for the black lines, $n=3$ for the thick blue lines, and $n=5$ for the dashed red lines

We can solve U, V, and $\lambda$ from Eqs. (10)–(13) as a function of $\phi$,

$$\begin{aligned} U(\phi )=&~k^2 n^2 v^2 {\tilde{\phi }} ^{\frac{2(n-1)}{n}}\left( {\tilde{\phi }}^{\frac{2}{n}}-1 \right) ^2, \end{aligned}$$

(17)

$$\begin{aligned} V(\phi )=&~k^2 n\biggl (8 \alpha k^2 (n+1) (n+6) (5 n+2){\tilde{\phi }}^4\nonumber \\&~ - \left( 8 \alpha k^2 (n (37 n+56)+16)+6 n+3\right) {\tilde{\phi }}^2\nonumber \\&~ + 32 k^2 (\alpha +3 \alpha n)+3\biggr ), \end{aligned}$$

(18)

$$\begin{aligned} \lambda (\phi )=&~ \frac{{\tilde{\phi }}^{2-2 n}}{2 n v^2 \left( 1-{\tilde{\phi }}^2 \right) ^2} \biggl (8 \alpha k^2 (5 n+2) (n (3 n+2)-6) {\tilde{\phi }}^4\nonumber \\&~ + \left( 3-32 \alpha k^2 (n (4 n-9)-4)\right) {\tilde{\phi }} ^2 \nonumber \\&~ -\left( 16 \alpha k^2 (5 n+2)+3\right) \biggr ), \end{aligned}$$

(19)

where ${\tilde{\phi }}=\frac{\phi }{v}$.

Considering the condition (14) in this model, we obtain the range of $k^2 \alpha$:

$$\begin{aligned} -\frac{1}{16n}<k^2 \alpha <\frac{1}{40n^2}. \end{aligned}$$

(20)

Here we show the shapes of the dimensionless energy density $\rho /k^2$ in Fig. 2 for several situations. Besides, it is found that the brane will split into two sub-branes when $-\frac{1}{16n}<k^2 \alpha <-\frac{1}{8 n(4+5n)}$.

Fig. 2

The energy density of model 1 with $v=1$, and $n=1$ (the left panel) and $n=3$ (the right panel). In the left panel we set $k^2 \alpha =-0.06$ for the black line, $k^2 \alpha =-0.03$ for the thick blue line, and $k^2 \alpha =0.01$ for the dashed red line. In the right panel we set $k^2 \alpha =-0.018$ for the black line, $k^2 \alpha =-0.0073$ for the thick blue line, and $k^2 \alpha =0.00014$ for the dashed red line

Fig. 3

The warp factor of model 2. The parameter v is set to $v=1$, and $kb=5$ for the black line, $kb=15$ for the thick blue line, and $kb=30$ for the dashed red line

2.2 Model 2

Fig. 4

Plot of the range (the dark region) of $k^2 \alpha$ and kb in the condition of $f_R>0$ for model 2

Fig. 5

The energy density of model 2. The parameter v is set to $v=1$. In the left panel, we set $kb=7$, and $k^2 \alpha =-0.018$ for the black line, $k^2 \alpha =-0.008$ for the thick blue line, and $k^2 \alpha =0.006$ for the dashed red line. In the right panel, we set $k^2 \alpha =-0.008$, and $kb=5$ for the black line, $kb=10$ for the thick blue line, and $kb=15$ for the dashed red line

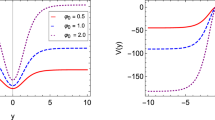
In the second model, the warp factor has a platform near the origin of the extra dimension, which can be seen from Fig. 3. The scalar field is a single-kink configuration. The expressions of the warp factor, the scalar field, and the scalar potential U are given by

$$\begin{aligned} a(y)&=\text {tanh} [k(y+b)]-\text {tanh} [k(y-b)], \end{aligned}$$

(21)

$$\begin{aligned} \phi (y)&=v\, \text {tanh}(ky), \end{aligned}$$

(22)

$$\begin{aligned} U(\phi )&=\frac{k^{2}}{v^{2}}\left( \phi ^{2}-v^{2}\right) ^{2}. \end{aligned}$$

(23)

Here we do not show the complicated $V(\phi )$ and $\lambda (\phi )$, which can be solved analytically. Note that the width of the platform of the warp factor is controlled by the parameter kb. Considering the condition (14), we can obtain the range of the parameter $k^2 \alpha$ numerically, which is shown in Fig. 4. From this figure, we can see that when $kb\gtrsim 2$ the range of $k^2 \alpha$ is about

$$\begin{aligned} -0.219<k^2 \alpha <0.00625. \end{aligned}$$

(24)

The dimensionless energy density $\rho /k^2$ in this model is shown in Fig. 5. The brane will split into multi-branes for $kb\gtrsim 2$ with $k^2 \alpha$ in the range of (24). When kb is close to zero the warp factor and the energy density will be close to model 1 with $n=1$. In other words, whether the brane splits or not depends on the value of $k^2 \alpha$; when $k^2 \alpha$ is smaller than some value the brane will split into two sub-branes.

We can also extend this warp factor to the form

$$\begin{aligned} a(y)=&~\text {tanh}[k(y-b-d)]-\text {tanh}[k(y+b+d)]\nonumber \\&-\text {tanh}[k(y+d)]+\text {tanh}[k(y-d)], \end{aligned}$$

(25)

where b and d are positive parameters. Using this warp factor one can construct a brane world with double number of sub-branes, which will be further investigated in Sect. 4.

2.3 Model 3

The third model is

$$\begin{aligned} a(y)=&~\text {sech}(k(y-b))+\text {sech}(ky)\nonumber \\&~+\text {sech}(k(y+b)), \end{aligned}$$

(26)

$$\begin{aligned} \phi (y)=&~v\, \text {tanh}(ky), \end{aligned}$$

(27)

$$\begin{aligned} U(\phi )=&~\frac{k^2}{v^2}(\phi ^2-v^2)^2. \end{aligned}$$

(28)

The scalar field is also a single-kink and the warp factor has peaks for large parameter kb, which can be seen from Fig. 6a. Here we also do not show the complicated expressions of $\lambda (\phi )$ and $V(\phi )$.

The range of $k^2 \alpha$ due to the condition $f_R>0$ is shown in Fig. 7. We can see that, for $kb\gtrsim 4$, the range of $k^2 \alpha$ is $-0.0625<k^2 \alpha <0.025$. The dimensionless energy density $\rho /k^2$ for $kb=5$ in this model is shown in Fig. 6b. In this situation, the sub-branes will always exist for $kb\gtrsim 4$ and $k^2 \alpha$ in the range we obtained. When kb is close to zero, the warp factor and the energy density will also close to model 1 with $n=1$. In other words, whether the brane split or not for the case of small kb depends on the value of $k^2 \alpha$. When $k^2 \alpha$ is less than some critical value the brane will split into two sub-branes.

Fig. 6

The warp factor and the energy density of model 3. The parameter v is set to $v=1$. In the left panel we set $kb=1$ for the black line, $kb=3$ for the thick blue line, and $kb=5$ for the dashed red line. In the right panel we set $kb=5$ and $k^2 \alpha =-0.06$ for the black line, $k^2 \alpha =-0.03$ for the thick blue line, and $k^2 \alpha =0.02$ for the dashed red line

Fig. 7

Plot of the range (the dark region) of $k^2 \alpha$ and kb in the condition of $f_R>0$ for model 3

We can also extend this three-peak model to multiple-peak model with the following warp factor:

$$\begin{aligned} a(y)=\sum ^{N}_{n=-N} \text {sech}(k(y+nb)), \end{aligned}$$

(29)

where N is an arbitrary positive integer.

3 Tensor perturbations and localization

In this section, we investigate the stability of the system by studying the tensor perturbation. The perturbed metric is given by

$$\begin{aligned} g_{MN}={\bar{g}}_{MN}+\delta g_{MN}, \end{aligned}$$

(30)

with

$$\begin{aligned} {\bar{g}}_{MN}= \begin{pmatrix} a^2(y) \eta _{\mu \nu } &{} 0 \\ 0 &{} 1 \end{pmatrix}, \quad \delta g_{MN}= \begin{pmatrix} a^2(y) h_{\mu \nu } &{} 0 \\ 0 &{} 0 \end{pmatrix}, \end{aligned}$$

(31)

where $h_{\mu \nu }=h_{\mu \nu }(x^{\rho },y)$ depends on all coordinates. Here, we only consider the tensor perturbation, so $\delta g_{5N}=0$. Using the relation $g^{NP}g_{PM}=\delta ^N_M$, one can obtain the inverse of $\delta g_{MN}$,

$$\begin{aligned} \delta g^{MN}= \begin{pmatrix} -a^{-2}(y)h^{\mu \nu } &{} 0 \\ 0 &{} 0 \end{pmatrix}, \end{aligned}$$

(32)

where $h^{\mu \nu }=\eta ^{\mu \lambda }\eta ^{\nu \rho }h_{\lambda \rho }$. Note that we only keep the first order. Then the following relations can be obtained:

$$\begin{aligned} \delta R_{\mu \nu }&=-\frac{1}{2}\left( \square ^{(4)}h_{\mu \nu }+\partial _{\mu }\partial _{\nu }h -\partial _{\nu }\partial _{\sigma }h^{\sigma }_{\mu }-\partial _{\mu }\partial _{\sigma }h^{\sigma }_{v} \right) \nonumber \\&\quad -2a a'h'_{\mu \nu } -3h_{\mu \nu }a'^2-a h_{\mu \nu }a''-\frac{1}{2}a^2 h''_{\mu \nu } \nonumber \\&\quad -\frac{1}{2}a\eta _{\mu \nu }a'h', \end{aligned}$$

(33)

$$\begin{aligned} \delta R_{\mu 5}&=\frac{1}{2}\partial _y \left( \partial _{\lambda } h^{\lambda }_{\mu }-\partial _{\mu }h \right) , \end{aligned}$$

(34)

$$\begin{aligned} \delta R_{55}&=-\frac{1}{2}\left( \frac{2a' h'}{a}+h'' \right) , \end{aligned}$$

(35)

$$\begin{aligned} \delta R&=-\frac{\square ^{(4)}h}{a^2}+\frac{\partial _{\mu }\partial _{\nu }h^{\mu \nu }}{a^2}-\frac{a'}{a}5h'-h''. \end{aligned}$$

(36)

Here $\square ^{(4)}=\eta ^{\mu \nu }\partial _{\mu }\partial _{\nu }$ is the four-dimensional d’Alembert operator, and $h=\eta ^{\mu \nu }h_{\mu \nu }$ is the trace of the tensor perturbation. Hereafter, we use the transverse-traceless gauge $h=0=\partial _{\mu }h^{\mu }_{\nu }$. Then Eqs. (33)–(36) can be simplified further. Using the above relations, we obtain the tensor perturbation equation

$$\begin{aligned}&-\frac{1}{4}a^{2}h_{\mu \nu }f(R)+\frac{1}{2}a^2 h_{\mu \nu }V-\frac{1}{2}\lambda a^2 h_{\mu \nu }\left[ \phi '^2-U(\phi ) \right] \nonumber \\&\qquad +\frac{1}{2}\left( -\frac{1}{2}\square ^{(4)}h_{\mu \nu }-3a'^2 h_{\mu \nu }-2aa'h'_{\mu \nu }-aa''h_{\mu \nu }\right. \nonumber \\&\qquad \left. -\frac{a^2}{2}h''_{\mu \nu } \right) f_R +a^2\left[ \frac{1}{2}h_{\mu \nu }\left( 3\frac{a'}{a}f'_R+f''_R \right) -\frac{1}{4}h'_{\mu \nu }f'_R \right] =0. \end{aligned}$$

(37)

Comparing with the Einstein equation (3), one can easily obtain

$$\begin{aligned} \left( a^{-2}\square ^{(4)}h_{\mu \nu }+4\frac{a'}{a}h'_{\mu \nu }+h''_{\mu \nu } \right) f_R+h'_{\mu \nu }f'_R=0. \end{aligned}$$

(38)

After the coordinate transformation $dz=a^{-1}dy$, we can rewrite the perturbed equation (38) as

$$\begin{aligned} \left[ \partial ^2_z+\left( 3\frac{\partial _z a}{a}+\frac{\partial _{z}f_R}{f_R} \right) \partial _z+\square ^{(4)} \right] h_{\mu \nu }=0. \end{aligned}$$

(39)

Considering the Kaluza–Klein (KK) decomposition $h_{\mu \nu }(x^{\rho },z)=\left( a^{-3/2}f_R^{-1/2} \right) \epsilon _{\mu \nu }(x^{\rho })\psi (z)$, where $\epsilon _{\mu \nu }(x^{\rho })$ satisfies the transverse and traceless conditions $\eta ^{\mu \nu }\epsilon _{\mu \nu }=0$ and $\partial _{\mu }\epsilon ^{\mu }_{\nu }=0$, we obtain the following Schrödinger-like equation for the extra-dimensional part $\psi (z)$:

$$\begin{aligned} \left[ - \partial ^2_z + W(z) \right] \psi (z)=m^2 \psi (z), \end{aligned}$$

(40)

where

$$\begin{aligned} W(z) =&~ \frac{3}{4}\frac{(\partial _z a)^2}{a^2}+\frac{3}{2}\frac{\partial _z a ~\partial _z f_R}{a f_R}\nonumber \\&-\frac{1}{4}\frac{(\partial _z f_R)^2}{f^2_R}+\frac{3}{2}\frac{\partial _z^2 a}{a}+\frac{1}{2}\frac{\partial _z^2 f_R}{f_R} \end{aligned}$$

(41)

is the effective potential of the gravitons. The effective potential (41) in y coordinate is

$$\begin{aligned} W(z(y))=\frac{9}{4}a'^2+2\frac{aa'f'_R}{f_R}-\frac{1}{4}a^2\frac{f'^2_R}{f^2_R}+\frac{3}{2}aa''+\frac{1}{2}\frac{a^2f''_R}{f_R}.\nonumber \\ \end{aligned}$$

(42)

It would be clearer if Eq. (40) is written in the following form:

$$\begin{aligned} QQ^{\dagger } \psi (z)=m^2 \psi (z), \end{aligned}$$

(43)

with

$$\begin{aligned}&Q=\partial _z+\left( \frac{3}{2}\frac{\partial _z a}{a}+\frac{1}{2}\frac{\partial _z f_R}{f_R} \right) , \end{aligned}$$

(44)

$$\begin{aligned}&Q^{\dagger }=-\partial _z + \left( \frac{3}{2}\frac{\partial _z a}{a}+\frac{1}{2}\frac{\partial _z f_R}{f_R} \right) . \end{aligned}$$

(45)

Equation (43) guarantees that there is no tachyonic KK graviton with $m^2<0$. So, the system is stable under the tensor perturbation.

The solution of the graviton zero mode is

$$\begin{aligned} \psi ^{(0)}(z)=\sqrt{N_0 a^{3}(z)f_R (z)} , \end{aligned}$$

(46)

where $N_0$ is the normalization constant. The zero mode $\psi ^{(0)}(z)$ is in fact the massless graviton. It should be normalizable in order to recover the four-dimensional Newtonian gravity. Thus, we should have the following normalization condition:

$$\begin{aligned} {\mathcal {I}}\equiv \int ^{\infty }_{-\infty }\left| \psi ^{(0)}(z) \right| ^2 \mathrm{{d}}z =1. \end{aligned}$$

(47)

Considering the solution (46) and the coordinate transformation $\mathrm{{d}}z=a^{-1}\mathrm{{d}}y$, the above condition reads

$$\begin{aligned} {\mathcal {I}} =&\int ^{\infty }_{-\infty }N_0 a^{2}(y)f_R (y) \mathrm{{d}}y \nonumber \\ =&\int ^{\infty }_{-\infty }N_0 \left[ a^2(y)-24 \alpha a'(y)^2 -16 \alpha a(y) a''(y) \right] \mathrm{{d}}y =1. \end{aligned}$$

(48)

For model 1, the graviton zero mode can be normalized and the normalization constant is given by

$$\begin{aligned} N_0=\frac{n(n+1)}{(8n^2 k^2 \alpha -2n -1){}_{2}F_1(1,-1-n;1+n;-1)}, \end{aligned}$$

(49)

where ${}_2F_1$ is the hypergeometric function. It can be seen that this value is positive and finite when n is a positive integer.

For models 2 and 3, we have, respectively,

$$\begin{aligned} N_0^{-1}&=~ 8kb \coth (2kb)-4 \!-\!\frac{16}{3}k^2 \alpha \text {csch}^3 (2kb) \Big [9\sinh (2kb) \nonumber \\&\quad +\sinh (6kb)-24 kb \cosh (2kb) \Big ], \end{aligned}$$

(50)

$$\begin{aligned} N_0^{-1}&=~ 6+4kb\text {csch}(kb)(2+\text {sech}(kb))-4k^2 \alpha \text {csch}^3(2kb)\nonumber \\&\quad \times \Big [-24kb -8kb \Big ( 22\cosh (kb)+9\cosh (3kb) \nonumber \\&\quad +\cosh (4kb)+\cosh (5kb)\Big )+\sinh (6kb) \nonumber \\&\quad +16\sinh (5kb)+8\sinh (4kb)+48 \sinh (3kb) \nonumber \\&\quad -3\sinh (2kb)+32\sinh (kb)\Big ]. \end{aligned}$$

(51)

This means that the graviton zero mode for each model considered in this paper can be localized near the brane¹ [6, 101]. The effective potentials and the graviton zero modes for the three models are shown in Fig. 8. From the analysis above of this section we notice that the tensor perturbation in mimetic f(R) gravity is the same as that in f(R) gravity [79]. The reason is that the tensor perturbation is independent of the mimetic scalar field. And this result is also consistent with the mimetic brane world [48]. But the mimetic scalar field gives a degree of freedom which could generate a more abundant inner structure.

Fig. 8

The effective potentials (the blue lines) and the corresponding graviton zero modes (the red dashed lines) for the three models. For model 1, we set $v=1$ and $k^2 \alpha =0.01$; for model 2, $v=1$, $kb=10$, and $k^2 \alpha =0.006$; and for model 3, $v=1$, $kb=5$, and $k^2 \alpha =0.02$

4 The gravitational resonances of mimetic f(R) brane

The abundant inner structure of the effective potential may lead to some interesting KK resonant behavior which will be studied in this section.

To get numerical solutions of Eq. (40), a convenient way is to impose the following boundary conditions for the KK modes:

$$\begin{aligned} \psi _{\text {even}}(0)=1,&\quad \partial _z \psi _{\text {even}}(0)=0; \end{aligned}$$

(52)

$$\begin{aligned} \psi _{\text {odd}}(0)=0,&\quad \partial _z \psi _{\text {odd}}(0)=1, \end{aligned}$$

(53)

where $\psi _{\text {even}}$ and $\psi _{\text {odd}}$ denote even and odd parity KK modes of $\psi (z)$, respectively. The integration of the function $\left| \psi (z) \right| ^2$ can be considered as the probability of finding massive KK gravitons along the extra dimension. In order to find gravitational KK resonances, one can define the relative probability [102]:

$$\begin{aligned} P(m^2)=\frac{\int ^{z_b}_{-z_b}|\psi (z)|^2 \mathrm{{d}}z}{\int ^{z_{\text {max}}}_{-z_{\text {max}}}|\psi (z)|^2 \mathrm{{d}}z}, \end{aligned}$$

(54)

where $2z_b$ is the approximate width of the brane and $z_{\text {max}}$ can be taken as $10z_b$. For a given $m^2$, using conditions (52) and (53), the even parity KK mode $\psi _\text {even}$ and the odd parity KK mode $\psi _\text {odd}$ can be solved numerically from the Schrödinger-like equation (40). In this case, the relative probability P corresponding to $\psi _{\text {even}}$ or $\psi _{\text {odd}}$ can be obtained. As a function of $m^2$, the relative probability will have a peak for some value of $m^2$. Then we may regard this mode as a gravitational KK resonance. Actually, we treat it as a KK resonance only when the corresponding peak has a full width at half maximum $\Gamma$, i.e., the width of the half height of the peak value. We can define the lifetime of the gravitational KK resonance as $\tau = \Gamma ^{-1}$.

Next, we will investigate gravitational KK resonances in three cases. Before that, in order to investigate conveniently we introduce some dimensionless parameters. Using the parameter k, we can define the dimensionless parameters ${\bar{y}}=ky$, ${\bar{z}}=kz$, ${\bar{b}}=kb$, ${\bar{\tau }}=k\tau$, ${\bar{\Gamma }}=\Gamma /k$, ${\bar{m}}=m/k$, ${\bar{W}}=W/k^2$, and ${\bar{\alpha }}=k^2 \alpha$. In our system, both parameters ${\bar{b}}$ and ${\bar{\alpha }}$ can affect the KK resonance behavior. The effect of the parameter ${\bar{b}}$ has been investigated in Refs. [49, 103, 104], so in this paper, we will focus on the effects of the parameter ${\bar{\alpha }}$, which can measure the deviation from mimetic gravity.

4.1 Case 1

We begin with the following warp factor:

$$\begin{aligned} a({\bar{y}})=\tanh ({\bar{y}}+{\bar{b}})-\tanh ({\bar{y}}-{\bar{b}}). \end{aligned}$$

(55)

In this case we choose ${\bar{b}}=10$ as a specific example to investigate gravitational KK resonances. So from Eq. (24) we know that ${\bar{\alpha }}$ has two bounds. The effects of the parameter ${\bar{\alpha }}$ on the effective potential can be seen from Fig. 9. From this figure we can see that the height of the two big barriers decreases rapidly with ${\bar{\alpha }}$. When ${\bar{\alpha }}$ approaches zero, the barriers will disappear. Besides, the depth of the effective potential will decrease first and then increase with ${\bar{\alpha }}$. It is worth to note that in Ref. [20] the KK resonances were found when ${\bar{\alpha }}$ is out of the range of Eq. (14).

Fig. 9

The effect of the parameter ${\bar{\alpha }}$ on the effective potential with ${\bar{b}}=10$ for case 1

In this case we set ${\bar{z}}_b$ in the relative probability (54) as ${\bar{z}}_b=6.5$. For ${\bar{\alpha }}=-0.19$, $-0.14$, and $-0.0012$ we can obtain the relative probabilities. Then the corresponding effective potentials, the relative probabilities, and the wave functions of the first odd and even KK resonances are shown in Figs. 10, 11, and 12. From Figs. 10a, 11a, and 12a, we can see that the height of the effective potential barrier decreases with the parameter ${\bar{\alpha }}$. Besides, from Figs. 10b and 11b we can see that the peak values do not decrease with ${\bar{m}}^2$ monotonously, which is an unusual phenomenon.

Fig. 10

The effective potential, the relative probability, and the wave functions of the first odd and even KK resonances with ${\bar{b}}=10$ and ${\bar{\alpha }}=-0.19$ for case 1

Fig. 11

The effective potential, the relative probability, and the wave functions of the first odd and even KK resonances with ${\bar{b}}=10$ and ${\bar{\alpha }}=-0.14$ for case 1

Fig. 12

The effective potential, the relative probability, and the wave functions of the first odd and even KK resonances with ${\bar{b}}=10$ and ${\bar{\alpha }}=-0.0012$ for case 1

We are also interested in the first gravitational KK resonance, its lifetime ${\bar{\tau }}_1$ and the mass square ${\bar{m}}^2$ for different values of ${\bar{\alpha }}$ are shown in Fig. 13. They can be fitted as the following two functions:

$$\begin{aligned} {\bar{m}}^2&=0.102 {\bar{\alpha }}+0.109, \end{aligned}$$

(56)

$$\begin{aligned} {\bar{\tau }}_1&=\frac{1}{0.00335 -0.447 {\bar{\alpha }}}+132. \end{aligned}$$

(57)

Fig. 13

The effects of the parameter ${\bar{\alpha }}$ on the mass square ${\bar{m}}^2$ and the lifetime ${\bar{\tau }}$ of the first KK resonance for case 1. Red dots are numerical results, blue solid lines are fit functions. In the left panel the fit function is ${\bar{m}}^2=0.102 {\bar{\alpha }}+0.109$, in the right panel the fit function is ${\bar{\tau }}_1=\frac{1}{0.00335 -0.447 {\bar{\alpha }}}+131.621$

From Eq. (56) we can see that the mass square ${\bar{m}}^2$ of the first KK resonance linearly increases with the parameter ${\bar{\alpha }}$. From Eq. (57) we can see that the lifetime of the first KK resonance increases with ${\bar{\alpha }}$ slowly first and then rapidly when ${\bar{\alpha }}$ closes to the upper bound.

4.2 Case 2

In this case, we investigate the brane world with three sub-branes, for which the warp factor is

$$\begin{aligned} a({\bar{y}})=\text {sech}({\bar{y}}-{\bar{b}})+\text {sech}({\bar{y}})+\text {sech}({\bar{y}}+{\bar{b}}). \end{aligned}$$

(58)

Without loss of generality we choose ${\bar{b}}=5$ as a specific example, and the corresponding range of ${\bar{\alpha }}$ is $-0.0642<{\bar{\alpha }}<0.025$. Gravitational KK resonances also exist in this kind of warp factor, but the situation will be different from case 1. The effective potential for different values of ${\bar{\alpha }}$ can be seen in Fig. 14. From this figure we can see that there are three sub-wells, and the effect of ${\bar{\alpha }}$ to the effective potential is similar to that in case 1. We fix ${\bar{z}}_b=12$ and set ${\bar{\alpha }}$ as $-$ 0.0581, $-$ 0.0373, and 0.0161 as examples to study the gravitational KK resonances.

Fig. 14

The effect of the parameter ${\bar{\alpha }}$ on the effective potential with ${\bar{b}}=5$ for case 2

Fig. 15

The effective potential, the relative probability, and wave functions of the first odd and even KK resonance with ${\bar{b}}=5$ and ${\bar{\alpha }}=-0.0581$ for case 2

Fig. 16

The effective potential, the relative probability, and wave functions of the first odd and even KK resonance with ${\bar{b}}=5$ and ${\bar{\alpha }}=-0.0373$ for case 2

Fig. 17

The effective potential, the relative probability, and wave functions of the first odd and even KK resonance with ${\bar{b}}=5$ and ${\bar{\alpha }}=0.016$ for case 2

The shapes of the effective potential, the relative probability and the wave functions of the first odd and even KK resonances are shown in Figs. 15, 16, and 17. We can see that, for some values of ${\bar{\alpha }}$, the relative probabilities of the KK resonances do not decrease with their masses ${\bar{m}}^2$ monotonously, which is similar to case 1. Besides, Figs. 15 and 17 show that the masses of some KK resonances are very close, which is similar to the result in [29], where the doubly degenerate phenomenon happens. Comparing the effective potential with that in Ref. [29], we can see that they both have sub-structure, and this sub-structure is the main reason of this phenomenon.

We also investigate the lifetime ${\bar{\tau }}_1$ and the mass square ${\bar{m}}^2$ of the first resonance for different values of ${\bar{\alpha }}$. The results are shown in Fig. 18 and we also get the following fit functions:

$$\begin{aligned} {\bar{m}}^2&=0.00373-0.0557{\bar{\alpha }}, \end{aligned}$$

(59)

$$\begin{aligned} {\bar{\tau }}_1&=\frac{10000}{14.3-540{\bar{\alpha }}}+238. \end{aligned}$$

(60)

From Eq. (59), one can see that the mass square ${\bar{m}}^2$ of the first KK resonance linearly decreases with the parameter ${\bar{\alpha }}$, which is different from case 1. Equation (60) shows that the lifetime increases with ${\bar{\alpha }}$ slowly first and then rapidly, just like the case 1.

Fig. 18

The effects of ${\bar{\alpha }}$ to the scaled mass ${\bar{m}}^2$ and the scaled lifetime ${\bar{\tau }}_1$ of the first KK resonance for case 2. Red dots are numerical results and solid blue lines are fit functions. In the left panel the fit function is ${\bar{m}}^2=0.00373-0.0557{\bar{\alpha }}$, in the right panel the fit function is ${\bar{\tau }}_1=\frac{1}{14.3-540{\bar{\alpha }}}+0.0238$

From case 1 and case 2, we find that, when ${\bar{\alpha }}$ is small, there is an unusual phenomenon, i.e., the peak values of the relative probability of the KK resonances do not decrease monotonously with ${\bar{m}}^2$. This phenomenon appears when ${\bar{\alpha }} \lesssim -0.024$ for case 1 and ${\bar{\alpha }} \lesssim -0.014$ for case 2.

4.3 Case 3

In this case, we will focus on the gravitational KK resonances quasi-localized in sub-wells and between sub-wells. The warp factor is

$$\begin{aligned} a({\bar{y}})&=\text {tanh}({\bar{y}}-{\bar{b}}-{\bar{d}})-\text {tanh}({\bar{y}}+{\bar{b}}+{\bar{d}})\nonumber \\&\quad -\text {tanh}({\bar{y}}+{\bar{d}})+\text {tanh}({\bar{y}}-{\bar{d}}). \end{aligned}$$

(61)

Compared with case 1, this warp factor has two platforms and the effective potential has more abundant sub-structure, which can be seen in Fig. 19.

From case 1 we have found that for large ${\bar{b}}$ the range of ${\bar{\alpha }}$ is $-0.219<{\bar{\alpha }}<0.00625$. In the current case we set ${\bar{b}}=13$ and ${\bar{d}}=2.3$, for which the range of ${\bar{\alpha }}$ is still $-0.219<{\bar{\alpha }}<0.00625$.

The effective potential for different values of ${\bar{\alpha }}$ is shown in Fig. 20. In order to investigate the KK resonances only quasi-localized in sub-wells, we need to redefine the corresponding relative probability $P_s$ [49]:

$$\begin{aligned} P_{s}=\left\{ \begin{array}{cl} \frac{\int _{{\bar{z}}_{1}}^{{\bar{z}}_{2}}|\psi ({\bar{z}})|^{2} d {\bar{z}}}{\int _{{\bar{z}}_{m}-5\left( {\bar{z}}_{2}-{\bar{z}}_{1}\right) }^{{\bar{z}}_{m}+5\left( {\bar{z}}_{2}-{\bar{z}}_{1}\right) }|\psi ({\bar{z}})|^{2} d {\bar{z}}}, &{} {\bar{z}}_{m} \ge 5\left( {\bar{z}}_{2}-{\bar{z}}_{1}\right) \\ &{} \\ \frac{\int _{{\bar{z}}_{1}}^{{\bar{z}}_{2}}|\psi ({\bar{z}})|^{2} d {\bar{z}}}{\int _{0}^{10\left( {\bar{z}}_{2}-{\bar{z}}_{1}\right) }|\psi ({\bar{z}})|^{2} d {\bar{z}}}, &{} {\bar{z}}_{m}<5\left( {\bar{z}}_{2}-{\bar{z}}_{1}\right) \end{array}\right. \end{aligned}$$

(62)

where ${\bar{z}}_1$ and ${\bar{z}}_2$ are the left and right edges of the right sub-well, respectively (as Fig. 19b shows), and ${\bar{z}}_m=\frac{{\bar{z}}_1 + {\bar{z}}_2}{2}$. Besides, between two sub-wells there is also a potential well, and KK resonances can also be quasi-localized in it. We also need to redefine the relative probability in this region [49]:

$$\begin{aligned} P_{m}=\frac{\int ^{{\bar{z}}_1}_{-{\bar{z}}_1}|\psi ({\bar{z}})|^2\mathrm{{d}}{\bar{z}}}{\int ^{10{\bar{z}}_1}_{-10{\bar{z}}_1}|\psi ({\bar{z}})|^2\mathrm{{d}}{\bar{z}}}. \end{aligned}$$

(63)

Fig. 19

The warp factor and the effective potential $W({\bar{z}})$ for case 3. The parameters are set as ${\bar{b}}=13$, ${\bar{d}}=2.3$, and ${\bar{\alpha }}=-0.00126$

Fig. 20

The effect of the parameter ${\bar{\alpha }}$ on the effective potential with ${\bar{b}}=13$ and ${\bar{d}}=2.3$ for case 3

We solve the Schrödinger-like equation (40) numerically with the boundary conditions (52) and (53). Using the redefined relative probabilities (62) and (63), one can get the gravitational KK resonances. Figures 21, 23, and 25 show the effective potential and the corresponding relative probability for ${\bar{\alpha }}=-0.189$, ${\bar{\alpha }}=-0.0838$, and ${\bar{\alpha }}=-0.00126$, respectively. Through these figures we can see that the effects of ${\bar{\alpha }}$ on the effective potentials and relative probability are very considerable. Compared with the results of mimetic gravity brane world (see Fig. 11(c) in Ref. [49]), we find that relative probabilities of KK resonances in sub-wells for small ${\bar{\alpha }}$ are much larger, which can be seen in Fig. 21b. As ${\bar{\alpha }}$ approaches zero, mimetic f(R) gravity goes back to mimetic gravity and the results of gravitational KK resonances also recover that of mimetic gravity [49].

From Figs. 21b, 23b, and 25b we can see that the peaks of relative probabilities of gravitational KK resonances in the sub-wells appear in clusters. And the main peak value of each cluster does not monotonically decrease with ${\bar{m}}^2$ when ${\bar{\alpha }}$ is small, this is because the sub-wells also have their sub-structure changing with ${\bar{\alpha }}$. From Figs. 21a, 23a, and 25a we can also see that the peak values of relative probabilities of gravitational KK resonances quasi-localized between sub-wells will not monotonically decrease with ${\bar{m}}^2$. Besides, comparing the above two cases, we see that there are no corresponding KK resonances with large relative probabilities $P_m$ at the locations of the main peaks of clusters in $P_s$. This is caused by the existence of the sub-structure of the effective potential. The wave functions of KK resonances quasi-localized both between sub-wells and in sub-wells are shown in Figs. 22, 24, and 26 for corresponding ${\bar{\alpha }}$.

On the other hand, from Figs. 21b, 23b, and 25b we find that the mass square ${\bar{m}}^2$ of the first odd parity KK resonance and the first even parity KK resonance are very close. One could also regard this as doubly degenerate [29].

Fig. 21

The effective potential, the relative probabilities of the even parity KK mode $\psi _e$ (dashed blue lines) and the odd parity KK mode $\psi _o$ (solid red lines) quasi-localized between the sub-wells $P_m$ and in the sub-wells $P_s$ with ${\bar{b}}=13$, ${\bar{d}}=2.3$, and ${\bar{\alpha }}=-0.189$ for case 3

Fig. 22

Resonances quasi-localized between sub-wells and in sub-wells with ${\bar{b}}=13$, ${\bar{d}}=2.3$, and ${\bar{\alpha }}=-0.189$ for case 3

Fig. 23

The effective potential, the relative probabilities of the even parity KK mode $\psi _e$ (dashed blue lines) and the odd parity KK mode $\psi _o$ (solid red lines) quasi-localized between the sub-wells $P_m$ and in the sub-wells $P_s$ with ${\bar{b}}=13$, ${\bar{d}}=2.3$, and ${\bar{\alpha }}=-0.0838$ for case 3

Fig. 24

The KK resonances between sub-wells and in a sub-well with ${\bar{b}}=13$, ${\bar{d}}=2.3$, and ${\bar{\alpha }}=-0.0838$ for case 3

Fig. 25

The effective potential, the relative probabilities of the even parity KK mode $\psi _e$ (dashed blue lines) and the odd parity KK mode $\psi _o$ (solid red lines) quasi-localized between the sub-wells $P_m$ and in the sub-wells $P_s$ with ${\bar{b}}=13$, ${\bar{d}}=2.3$, and ${\bar{\alpha }}=-0.00126$ for case 3

5 Conclusions and discussions

In this work, we studied the brane world system in mimetic f(R) gravity. Due to the existence of the mimetic scalar field, we can get thick branes with abundant inner structure. We gave three kinds of solutions of the thick brane model for $f(R)=R+\alpha R^2$.

Then we investigated the stability of mimetic f(R) brane world, and found that the system is stable under the tensor perturbation. The existence of the normalized graviton zero mode indicates that four-dimensional gravity can be restored. The result is the same as the tensor perturbation of f(R)-branes in Ref. [79]; this is because the tensor perturbation is independent of the mimetic scalar field.

After that, we studied the gravitational KK resonances, which are quasi-localized on the brane. We only studied the effects of the parameter $\alpha$ on the behavior of the KK resonances. We found that, for a small $\alpha$, the effective potential has a sub-structure which leads to an unusual phenomenon in the KK resonance spectrum. The lifetime of the first KK resonance increases rapidly, while $\alpha$ is close to its upper bound. In case 3 we focused on gravitational KK resonances quasi-localized in sub-wells and between sub-wells. We found that KK resonances can be quasi-localized both in sub-wells and between sub-wells. If $\alpha$ tends to zero the result would tend to the mimetic gravity brane world in Ref. [49]. Compared with Ref. [49], the relative probabilities of KK resonances in the sub-wells are more obvious and the main peak values of the clusters do not monotonically decrease with ${\bar{m}}^2$ for a small $\alpha$. Besides, the phenomenon of gravitational KK resonance being doubly degenerate also appears when we study KK resonances quasi-localized in a sub-well.

Fig. 26

The KK resonances between sub-wells and in a sub-well with ${\bar{b}}=13$, ${\bar{d}}=2.3$, and ${\bar{\alpha }}=-0.00126$ for case 3

We note that it is proper to set the five-dimensional fundamental mass scale $M_*$ as unity rather than the Planck mass. In this model the relation between the four-dimensional spacetime mass scale $M_{\text {Pl}}$ and five-dimensional spacetime fundamental mass scale $M_*$ is as follows:

$$\begin{aligned} M^2_{\text {Pl}}=M_*^3 \int ^{\infty }_{-\infty }a(z)^3 f_R \mathrm{{d}}z, \end{aligned}$$

(64)

which means the four-dimensional mass scale is effective. The five-dimensional fundamental scale is determined by the warp factor and f(R). We use the parameter k to recover the dimensions of the parameters y, z, b, d, $\tau$, $\Gamma$, m, W, and $\alpha$. For example, if we set $k=M_*$, for model 2, we have

$$\begin{aligned} M_{\text {Pl}}^2&=M_*^3 \Bigg ( \frac{2}{3 k} \text {csch}^2(2 b k) \Big (-\left( 16 \alpha k^2+3\right) \cosh (4 b k) \nonumber \\&\quad +6 b k \big (16 \alpha k^2 \tanh (b k) \left( \coth ^2(b k)+1\right) +\sinh (4 b k)\big )\nonumber \\&\quad -80 \alpha k^2+3 \Big ) \Bigg ). \end{aligned}$$

(65)

If we set the parameters $kb=10$ and $k^2 \alpha =-0.008$ then the five-dimensional spacetime fundamental mass scale can be obtained: $M_*=M_{\text {Pl}}/8.73=1.40 \times 10^{15}~\text {TeV}$ from Eq. (65). We have the parameter $b= 1.41 \times 10^{-33}~ \text {m}$. When the energy of a particle approaches the fundamental mass scale the effect of quantum gravity will become obvious. In this model the effect of quantum gravity is not considered. From Fig. 10 the mass of the first massive graviton is $m=\sqrt{0.0831} \times 1.40 \times 10^{15}~\text {TeV}=1.16 \times 10^{14}~\text {TeV}$, which is less than the fundamental mass scale. So the massive graviton can be produced in a collider even if its energy is lower than the fundamental mass scale.

At last, we discuss briefly the correction of the four-dimensional Newtonian potential from the gravitational KK modes. For the brane located around $z=z_0$, the four-dimensional Newtonian potential correction of a mass point M is given by [6]

$$\begin{aligned} U_{N}(r) \sim G_{N} \frac{M}{r}\left[ 1+\int _{0}^{\infty } \mathrm{{d}} m~ \mathrm {e}^{-m r} \psi _{m}^{2}\left( z_{0}\right) \right] , \end{aligned}$$

(66)

where r is the distance to the mass point on the brane, and $\psi _m(z)$ is the normalized wave function with mass m and the normalized constant $N_m$. In this paper if the brane is located around $z=0$, the contribution to the four-dimensional Newtonian potential is only from even KK modes. For the brane with inner structure the KK resonances that can be quasi-located at a sub-brane also make a contribution to the four-dimensional Newtonian potential. From Ref. [6] we know that the normalization constant $N_m$ is determined by the asymptotic behavior of the effective potential W(z) at the boundary of the extra dimension. For the solutions considered in this paper, if we assume that $W(z)\propto \frac{\beta (\beta +1)}{z^2}$ and $\psi _m(0)\sim (m/k)^{\beta -1}$ at $z\gg 1/k$, we find $\beta =\frac{3}{2}$, which is not associated with $\alpha$. Hence, for the brane located around $z=0$ the correction to the four-dimensional Newtonian potential is

$$\begin{aligned} U_{N}(r) \sim G_{N} \frac{M}{r}\left[ 1+\frac{C}{(kr)^2}\right] , \end{aligned}$$

(67)

where C is a dimensionless constant determined by the structure of brane. Here, we only consider the asymptotic behavior of the effective potential W(z) at the boundary of the extra dimension. The inner structure of the effective potential around $z=0$ should have an effect on this result. This is a difficult issue and it will be studied in our future work.

In the model of mimetic brane world with abundant inner structure, it is also interesting to investigate localization of various kinds of matter fields and the corresponding KK resonance structures, which will also be studied in our future work.