A few remarks on spatial interference in visual stimuli

Abstract

Many vision experiments, e.g., tests of masking and visual crowding, involve the effect of adding a second stimulus to an initial one. The effects of such additions are generally considered in terms of physiological mechanisms and the possibility of interference in the stimuli is generally not considered. In the present study, interference between two stimuli was assessed by comparing the sum of amplitudes in the combined stimulus to the sums of the amplitudes in the two stimuli determined separately. With this approach, evidence for interference was found. It was also found that adding a second stimulus may alter the phase angles. These observations mean that the same stimulus presented together with other stimuli may have less stimulus power than when presented by itself. Thus, it is necessary to take account of the possibility of interference when interpreting results from experiments in which the effect of one stimulus element upon another is explored.

Introduction

There can be little doubt that the “stimulus power” of one stimulus element in a visual stimulus display can be reduced by the introduction of other elements. To take an obvious example, consider the simple case of a stimulus consisting of a bright dot presented on a dark background. Were one to add a surrounding field matching the dot in brightness one would have created a uniform field which would have reduced (if not altogether abolished) the stimulus power of the initial dot. In this case when a subject is no longer able to see the dot one would explain this by a change in the stimulus and not in terms of physiological mechanisms. Another example involving the same bright dot would be to simply add uniform luminance to the whole stimulus display. In which case one would have reduced the contrast of the bright dot.¹ Also in this case, an explanation of any change in response resulting from the change in the stimulus would (presumably) primarily be in terms of the stimulus and only secondarily, if at all, in terms of physiological mechanisms. These examples describe, of course, very simple cases, and it seems unlikely that anyone would dispute that the stimulus power of the initial stimulus is reduced by the additions in these instances. Yet, in the case of more subtle, or smaller additions, such as, e.g., the addition of a masking stimulus to a target stimulus, the possibility that the additional stimulus reduces the power of the target stimulus is rarely, if ever, considered. Rather, the results of such experiments are almost invariably discussed exclusively in terms of mechanisms in the visual system. The present report seeks to analyze the effect upon the stimulus power of a given stimulus element of introducing an additional element into the stimulus display. The report also seeks to provide a mathematical framework for understanding and quantifying such effects. These analyses, it should be emphasized, deal with visual stimuli and do not involve the visual system or visual perception (i.e., they do not deal with responses to the stimuli).

The present report seeks to explore interactions between visual stimuli or between visual stimulus elements within the framework of interference. “Interference” refers to an interaction between two or more signals. It can be easily explained in terms of two sinusoidal signals of equal frequency and amplitude. This is illustrated in Fig. 1. If two such signals are added in the way so that the peaks and troughs in one signal coincide, respectively, with the peaks and troughs in the other, i.e., if the two signals are in-phase, the amplitude of the resulting signal will correspond to the sum of the two amplitudes. This is termed “constructive interference” and is illustrated in Fig. 1a. On the other hand, if the peaks in one signal coincide with the troughs in the other, i.e., if the two signals are out of phase, they will annihilate each other. In this case, if the two signals have equal amplitudes, the resulting signal will have zero amplitude. This is known as “destructive interference” and is shown in Fig. 1b. The sum of two signals may fall anywhere between these extremes. What is important in the present context is that the amplitude of the combined signal may not be larger than the sum of the two amplitudes, and, most importantly, the amplitude of the combined signal will be smaller than the sum of the individual amplitudes whenever the two signals have different phases.

Fig. 1

Interference between two sinusoidal signals. a The two signals are in phase, causing the amplitude of their sum to equal the sum of their individual amplitudes. Since the amplitudes of the two signals in this case were equal, the amplitude of the sum becomes twice that of each of the initial signals. b The two signals are out of phase, causing them to cancel. Since the two signals have equal amplitudes, their sum becomes zero in this case

Combinations of stimulus elements can be found in stimuli designed to investigate visual masking (e.g., Breitmeyer & Ogmen, 2000), lateral masking (e.g., Kurylo, Yeturo, Lanza, & Bukhari, 2017) and visual crowding (e.g., Levi, 2008; Whitney & Levi, 2011). However, in these investigations it is generally assumed (typically tacitly) that adding a second stimulus element to an initial one does not reduce the stimulus power of the initial element and, consequently, that any perceptual effects must be attributed to factors in the visual system (e.g., Clarke, Herzog, & Francis, 2014; Hermens, Luksys, Gerstner, Herzog, & Ernst, 2008; Manassi, Lonchampt, Clarke, & Herzog, 2016; Shin, Chung, & Tjan, 2017).² The present investigation examines this assumption.

In a discrete Fourier transform of a spatial signal, each component is calculated as $\sum f[x] e^{i \omega x}$, where x denotes position, f[x] the signal as a function of position (square brackets indicate that the signal is sampled at discrete intervals), ω gives the spatial frequency of the component, and $i = \sqrt {-1}$ . Thus, each element in the Fourier spectrum is a sine function with a given amplitude and phase and is expressed by a complex number, i.e., has the form d + i e where d and e are real numbers. A complex number can be represented by a vector in the complex plane. (The complex plane is the plane which has a real and an imaginary axis. The real axis has 1 as its unit and the imaginary axis has $i = \sqrt {-1}$ as its unit.) In this representation, the length of the vector gives the amplitude of the component whereas the angle of the vector denotes the phase, i.e., phase angle. In Fig. 2a are shown two vectors of equal length (i.e., equal amplitude) but with different phase angles: 𝜃 _a and 𝜃 _b . In Fig. 2b is shown the addition of these two vectors. As should be apparent, the length of the sum of the two vectors is shorter than the sum of the lengths of the two vectors determined separately. If we denote the vectors by a and b, we get that a + b, is shorter than the sum of the lengths of the individual vectors a and b. (This is an example of what is known as the “triangle inequality”.) Mathematically, this can be expressed as |a + b| < |a| + |b| when a and b have different phase angles. (This notation is based on the fact that for a complex number z = x + i y, with x and y being real numbers and $i = \sqrt {-1}$, the absolute, i.e., the amplitude, is $|z| = \sqrt {x^{2} + y^{2}}$.)

Fig. 2

Vector representations in the complex plane of the adding of Fourier components. a Two components of equal amplitudes but different phase angles, i.e., the vectors have equal lengths but different directions as indicated by 𝜃 _a and 𝜃 _b . b Addition of the two vectors in (a). As can be seen, the length of the sum (a + b) is shorter than the length of a plus the length of b. Panels c and d give the vector representations of the adding of the signals depicted in Fig. 1a and b, respectively. In (c) the two vectors have the same direction (𝜃 _a = 𝜃 _b ) making |a + b| = |a| + |b| whereas in (c) the vectors point in opposite directions (𝜃 _a = 𝜃 _b + π) making their sum equal 0 (i.e., |a + b| = 0). “Re” and “Im” denote the real and imaginary axes, respectively

In Fig. 1 interference was illustrated in terms of summation of sine functions. As already mentioned, the Fourier transform represents a signal as a series of such functions. Such a series is known as a Fourier series in which each component is represented by a sine function of a particular frequency having a particular amplitude and phase. Since it is easy to understand interference in terms of sine functions, Fourier series provide a convenient framework for exploring interference effects.

That sine functions are relevant for vision is indicated by both psychophysical and neurophysiological evidence. In the case of psychophysical data, it has been found that complex waveforms are detected when the fundamental component reaches threshold (Campbell & Robson, 1968). This implies that stimuli are analyzed into separate Fourier components and that detection depends on the amplitudes of these components.

In relation to visual neurons, there are data to indicate that neurons in the visual cortex respond selectively to particular spatio-temporal Fourier components in the stimuli (De Valois, Albrecht, & Thorell, 1982). De Valois, De Valois, and Yund (1979) recorded responses from single neurons in cortical Area V1 to drifting checkerboard patterns and found that the responses are determined by the Fourier components and not the edges in the patterns. Skottun, Zhang, and Grosof (1994) found that the bifurcation of the directional response of cortical cells to rapidly drifting patterns of random dots, something which is very difficult to understand in terms of time and space, can be understood in terms of the spatio-temporal frequency content of the stimuli. Also, Jones and Palmer (1987) have suggested that cortical simple cells may be modeled as 2-D Gabor functions. This would make these cells responsive to sine grating over limited ranges of spatial frequencies. Together, these findings suggest that Fourier transforms provide a reasonable framework for understanding visual stimuli (De Valois & De Valois, 1990).

As should be clear from the above, one effect of interference is to reduce the amplitudes in stimuli. That this is relevant is indicated by the fact that the responses of visual neurons depend fundamentally upon stimulus amplitude (see, e.g., Sclar, Maunsell, & Lennie, 1990) (stimulus amplitude in visual stimuli is usually referred to as “contrast”). Typically, the responses of these neurons increase with increasing amplitude. Thus, it would seem reasonable to assume that anything that reduces the effective amplitudes in visual stimuli would be relevant for neuronal responses as well as for visual perception.

Methods

Interference was explored numerically by 2D-Fourier transforms of stimuli on a computer using Mathematica (Wolfram Research, Inc.). Stimuli were generated as 64 × 255 element arrays with bright elements (value 1.0) on a dark background (value 0.0). The target stimuli were uppercase letters 22–26 elements wide and 31 elements high. With the exception of the stimulus shown in Fig. 4a the interfering stimuli were rectangles five elements wide and 33 elements tall. An example of a target stimulus along with a interfering stimulus on each side is shown in Fig. 3a. The value given for the separation between the target and the interfering stimuli was between the outer edge of the target and the inner edge of the interfering stimulus (measured along the horizontal dimension). The various steps in the procedures are described in connection with the corresponding results.

Fig. 3

a A target stimulus, letter “X”, along with two interfering stimuli consisting of vertical bars. The separation between the target and the interfering stimuli is two picture elements in this image. (The separation is along the horizontal dimension.) b Same as in A with the exception that the stimuli have been multiplied with a 2-D Gaussian window with standard deviation of 20 picture elements along both dimensions. c Relative amplitude sum as a function of separation between the target and each of the interfering stimuli for the case where there was no Gaussian window (i.e., for the case shown in (a)). d Same as in c with the exception that the Gaussian window was applied (i.e., the stimuli were of the form shown in (b)). In (c) and (d), a relative amplitude sum of 1.0 indicates no interference (dashed horizontal line) and values less than this indicate the presence of interference

Fig. 4

a A target stimulus consisting of an “X” flanked by an “X” on either side, i.e., the target stimulus and the interfering stimuli were identical. b Relative amplitude sum for the stimuli in a as a function of separation between the target stimuli and each of the flanking stimuli. The upper trace shows results obtained with a Gaussian window and the lower trace shows data when no window was applied. For the Gaussian window, σ was 40 elements

Results

As was pointed out above, the Fourier transform analyses signals into series of sinusoidal components each defined by a complex number. As illustrated in Fig. 2b, when adding two Fourier components, the sum of the amplitudes determined together will be smaller than the sum of the two amplitudes determined separately unless the phases of the two components are identical. This reduction is interference.

We will denote one stimulus as the target stimulus and another as the interfering stimulus (or stimuli). Further, we will denote each component in the 2D-Fourier spectrum of the target stimulus by t(ω _x ,ω _y ) and the corresponding components in the interfering stimulus by i(ω _x ,ω _y ), where ω _x and ω _y denote the spatial frequency of the given component along the x- and y-dimensions, respectively. (The component i must not be confused with the imaginary unit $i = \sqrt -1$.) The amplitudes of the two components then become |t(ω _x ,ω _y )| and |i(ω _x ,ω _y )|, respectively, and that of their sum becomes |t(ω _x ,ω _y ) + i(ω _x ,ω _y )|. Since each component can be represented as a vector (as was explained above and illustrated in Fig. 2b), we get that |t(ω _x ,ω _y ) + i(ω _x ,ω _y )| < |t(ω _x ,ω _y )| + |i(ω _x ,ω _y )| when the phases of the two components differ (i.e., the transformation of a signal into its Fourier spectrum is linear but the transformation into the amplitude spectrum is not). That is, when the phases differ, the amplitude of the target and interfering stimuli assessed together will be smaller than the sum of the amplitudes of the two stimuli assessed separately. Consequently, when the phases differ, the full amplitudes (for a given ω _x and ω _y ) of both stimuli cannot be contained in the amplitude of the combined stimulus.

In order to obtain a single measure of interference, the sum of amplitudes in the combined stimulus was divided by the sum of amplitudes in the target plus the sum of amplitudes in the interfering stimulus: $\sum |\textbf {t} (\omega _{x}, \omega _{y}) + \textbf {i} (\omega _{x} , \omega _{y}) |/(\sum |\mathbf {t}(\omega _{{x}} , \omega _{y})| + \sum |\mathbf {i}(\omega _{{x}} , \omega _{y})|)$. This ratio is denoted the Relative Amplitude Sum.

In Fig. 3c is shown the relative amplitude sum of a target stimulus consisting of the letter “X” flanked on either side by an interfering stimulus made up of a vertical rectangle (as shown in Fig. 3a). The results are given as a function of separation between the target stimulus and each of the interfering stimuli. The horizontal dashed line marking a relative amplitude sum of 1.0 indicates no interference and the vertical distance from this line indicates the magnitude of the interference. As can be seen, the addition of the interfering stimuli reduces the relative amplitude sum to about 0.8 (i.e., an approximately 20% reduction). Thus, in this case, we shall have to conclude that there is interference between the target and the interfering stimuli.

In order for there to be interference between two spatially separate elements, it is required that they both fall inside the area from which stimulation is integrated. It has been suggested that Fourier transforms in the visual system are localized (De Valois & De Valois, 1990). If so, it may be that interference effects only occur for stimuli close together in space. In order to simulate interference effects under such conditions, the stimuli were windowed by a 2D-Gaussian (σ = 20 elements along both dimensions). The stimuli in Fig. 3a after they have been windowed in this manner are shown in Fig. 3b. In Fig. 3d is shown the relative amplitude sum as a function of separation between target and interfering stimuli under these conditions. As can be seen, windowing the stimuli reduces the amount of interference and limits the spatial extent of the interference but does not abolish it. It should in this connection be emphasized that even though the extent of the Fourier transform has been reduced in order to simulate a limited extent of spatial summation in the visual system, the interference still takes place in the stimuli.

The average relative amplitude sum in Fig. 3a (for data with no window) is 0.80 (SD = 0.004; average of 48 separations). This may create the impression that the reduction in stimulus power caused by interference is relatively modest. However, other stimulus configurations have the ability to cause larger interference effects. In Fig. 4 is shown the case where the central stimulus element was an X flanked by an identical X on either side. The relative amplitude sum as a function of separation is shown in Fig. 4b. The lower trace gives the results for no window whereas the upper trace gives results for when a Gaussian window with σ = 40 elements was imposed. In the “un-windowed” case, the average relative amplitude sum was 0.63 (SD = 0.006), which means that interference caused a 37% reduction in the amplitudes.

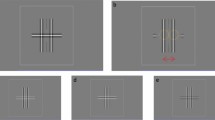
The relative amplitude sum gives a measure of how much the amplitudes in the combined stimulus differ from the amplitudes in the target and mask. However, it does not tell us specifically how much the amplitudes in the target are affected. If we assumed that the target and masking stimuli are equally influenced the residual amplitude sum would provide an appropriate measure of the amplitudes of the target stimulus in the combined stimulus relative to when presented alone. In an attempt to illustrate the potential interference effect exerted by interfering stimuli upon a target stimulus, a target stimulus (exemplified by the letter “H”) was re-generated from the amplitude spectrum of t and the phase spectrum of t + i. That is to say, each component in the Fourier series was set to |t|(c o s 𝜃 _{t + i} + i s i n 𝜃 _{t + i} ), where 𝜃 _{t + i} denotes the phase angle of the combined stimulus t + i and |t| gives the target amplitude for the given component. The result is shown in Fig. 5c. (For comparison, in Fig. 5a is shown the original target and in Fig. 5b is shown the target along with the flanking interfering stimuli.) As can be seen, the target stimulus is somewhat degraded relative to the original stimulus (i.e., relative to Fig. 5a). In order to illustrate the interference effect more clearly, the difference (simple subtraction) between the original stimulus (Fig. 5a) and the re-generated one (Fig. 5c) is shown in Fig. 5d. Together, Fig. 5c and d illustrate that interference from flanking stimulus elements has the potential to degrade a target stimulus.

Fig. 5

a A target stimulus in the form of letter “H”. b The target stimulus in a flanked by a bar stimulus on either side. The separation between the target and each of the bars was two elements. c The target stimulus generated (using the inverse Fourier transform) from the amplitudes of the target stimulus and the phases of the combined stimulus, i.e., from the amplitudes of (a) and the phases of (b). d The difference between (a) and (c)

A word of clarification may be needed at this point. The image of the target in Fig. 5b (i.e., the letter “H”) is physically identical to the image of the target in Fig. 5a. Obviously, the adding of two nearby rectangles does not change the target. What is changed is its stimulus power.

Up until this point, only the effect of interference upon the amplitudes has been considered. However, from Fig. 2 it ought to be clear that also the phases may be affected by interference. This is further underscored by Fig. 5c in which the image of the target is reconstructed from the phases of the combined target and interfering stimuli, i.e., from the stimuli shown in Fig. 5b, and the amplitudes of the target alone, shown in Fig. 5a. Since the difference between Fig. 5a and c is only in the phase spectra and since Fig. 5a and c are clearly different, this indicates that interfering stimuli have the ability to not only alter the amplitudes in visual stimuli but also their phases. In order to explore the effect of interference upon phase spectra, the average difference between the phase spectrum of the target by itself (t) and that of the combined stimulus (t + i) was calculated.

Phase angle is a cyclical variable with a period of 2π. This means that in the case of an absolute phase angle difference that is larger than π, the actual difference is 2π minus the angle. Thus, if we calculate the difference by simple subtraction, i.e., as 𝜃 _{t−(t + i)} = 𝜃 _t − 𝜃 _{t + i} , we need to “adjust” the result as:

$$\theta = \left\{ \begin{array}{ll} 2 \pi - |\theta_{t - (t+i)}|, & \quad \text{if } |\theta_{t - (t+i)}| > \pi;\\ | \theta_{t - (t+i)}|, & \quad \text{otherwise}. \end{array} \right. $$

Note that this gives 𝜃 as the absolute of the difference between 𝜃 _t and 𝜃 _{t + i} so that when computing the average difference we get the average of the absolute difference (i.e., $1/n \sum | \theta |$, where n is the number of components in the image).

The average absolute phase difference between the target stimulus and the target stimulus combined with the interfering stimulus is shown in Fig. 6 as a function of the separation between the target stimulus and the flanking interfering stimuli. The upper trace shows the effects when there is no spatial restriction on the extent of the interference. The lower trace shows the case where a Gaussian window (σ = 20 elements) has been imposed. As should be apparent from these plots (as well as from Fig. 5c and d), adding interfering stimuli can alter the phase spectra.

Fig. 6

The change in phase spectra as a result of adding interfering stimuli. The results show the average absolute phase difference between t + i and t as a function of separation. The lower trace is for a windowed transform using a 2-D Gaussian with σ = 20. The stimuli were the ones shown in Fig. 3a and b

Discussion

The present analyses have demonstrated that the amplitudes in a target and masking stimulus combined may be smaller than the sum of the amplitudes in the two stimuli determined separately. They have also shown that adding a masking stimulus to a target can alter its phase angles. It should be emphasized that these effects are in the stimuli. That is to say, the interference effects described here exist independently of whether or not the stimuli are actually being perceived or stimulate any visual system.

The effects of introducing additional stimulus elements upon perception or neuronal responses have largely been interpreted in terms of interactions in the visual system. The present demonstrations show that it may also be necessary to take account of interactions in the stimuli and that one cannot assume that a stimulus element has the same stimulus power when presented together with other elements as when presented by itself. The present analyses have sought to provide a mathematical framework for estimating such differences.

In this connection, it should be emphasized that the example stimuli shown here are just that, examples. This means that the values given here cannot be applied directly to other stimuli and other conditions. Rather, interference effects need to be estimated with regard to the particular stimuli made use of in a given case. Also, the method presented here is only one method for demonstrating interference between elements in visual stimuli. It represents an example of how interference can be demonstrated in a quantitative manner. The present method was chosen because of its relative simplicity. However, different methods may give different magnitudes of the interference effects. Thus, one ought to exercise caution when making interpretations based on the specific quantitative estimates of interference presented here.

It was pointed out above that the stimuli examined here are of the kinds employed in experiments on masking and crowding. The terms “masking” and “crowding” refer to certain kinds of responses to stimuli (stimuli similar to the ones shown here). Because they involve only stimuli, and not responses, the present analyses, although they may have relevance for masking and crowding, should not be understood as attempts to explain these phenomena. Also, since the analyses only deal with stimuli the results from psychophysical experiments, which deal with responses to visual stimuli, are not in a position to invalidate the present observations. In other words, the present observations hold irrespective of psychophysical results.

The present analyses have focused on spatial interactions. This may make it seem the interactions are limited to those between simultaneously presented stimuli. However, given the temporal integration of the visual system (full temporal integration–Bloch’s law–extends up to about 100 ms, Hart, 1992, and partial temporal summation may extend to as much as 1000 ms, Legge, 1978) it is possible that interference effects may occur between stimuli presented at somewhat different times.

In conclusion, the amplitudes that can be attributed to a given stimulus element may be smaller when this element is presented together with other stimuli than when presented in isolation. Also, the phases linked to the stimulus may be different in the two cases. Consequently, even though a target stimulus is physically identical when it is presented by itself and when presented together with other stimuli, it cannot be counted on to have the same stimulus power in the two instances.