Abstract
Nowadays, China BeiDou Navigation Satellite System (BDS) has been developed well and provided global services with highly precise positioning, navigation and timing (PNT) as well as unique short-message communication, particularly global system (BDS-3) with higher precision multi-frequency signals. The precise point positioning (PPP) can provide the precise position, receiver clock, and zenith tropospheric delay (ZTD) with a stand-alone receiver compared to the traditional double differenced relative positioning mode, which has been widely used in PNT, geodesy, meteorology and so on. However, it has a lot of challenges for multi-frequency BDS PPP with different strategies and more unknown parameters. In this paper, the detailed PPP models using the single-, dual-, triple-, and quad-frequency BDS observations are presented and evaluated. Firstly, BDS system and PPP method are introduced. Secondly, the stochastic models of time delay bias in BDS-2/BDS-3 PPP including the neglection, random constant, random walk and white noise are presented. Then, three single-frequency, four dual-frequency, four triple-frequency and four quad-frequency BDS PPP models are provided. Finally, the BDS PPP models progress and performances including theoretical comparison of the models, positioning performances, precise time and frequency transfer, ZTD, inter-frequency bias (IFB) and differential code bias (DCB) are presented and evaluated as well as future challenges. The results show that the multi-frequency BDS observations will greatly improve the PPP performances.
Similar content being viewed by others
Introduction
Global Positioning System (GPS) has been widely used in positioning, navigation, timing (PNT) services and sciences related to positioning on Earth’s surface with an unprecedented high precision and accuracy, since it became full operation in 1993 (Jin et al. 2011). With decades of GPS developments, numerous achievements and applications have been obtained from ground-based and spaceborne GPS observations. For example, detailed regional and global crustal deformation and plate motions were precisely measured by ground-based GPS observations (e.g., Jin and Park 2006). The tropospheric and ionospheric delays can be precisely extracted from continuous, all-weather and real-time GPS measurements, which have been used in meteorology (e.g., Jin et al. 2019) and space weather (Jin et al. 2017a) as well as lithospheric-atmospheric coupling (e.g., Jin et al. 2015). In addition, GPS multipath is one of main errors. Nowadays, the GPS-Reflected signals can be used in various environmental remote sensing (Jin et al. 2017c), e.g., soil moisture (Jia et al. 2019), water storage (Jin and Zhang 2016), snow depth (Qian and Jin 2016; Jin et al. 2016), sea level change (Jin et al. 2017b) and ocean wave wind speed (Dong and Jin 2019).
Furthermore, more next generation Global Navigation Satellite Systems (GNSS) are being upgraded and developed, e.g., China’s BeiDou Navigation Satellite System (BDS), US’s modernized GPS-IIF and GPS-III, Russia’s restored GLONASS and European Union’s Galileo systems as well as India’s Regional Navigation Satellite Systems (IRNSS) and Japan’s Quasi-Zenith Satellite System (QZSS). Higher positioning accuracy and more applications are expected in coming years. China has been developing the independent BeiDou Navigation Satellite System (BDS) since 1994, which is similar in principle to GPS and compatible with other GNSS. The BDS will provide highly reliable and precise PNT services as well as unique short-message communication under all-weather, all-time and worldwide conditions. On December 27, 2018, BDS-3 preliminary system provide global services officially. A number of BDS positioning algorithms and models have been developed, particularly precise point positioning (PPP) with a stand-alone receiver, which have been widely used in PNT and geodesy (e.g., Li et al. 2014; Jin and Su 2019). BDS observations together with other GNSS will provide the higher-precision PPP solutions. The BDS/GNSS PPP techniques have advantages for the applications of the seismology without effects of reference stations (Benedetti et al. 2014; Bilich et al. 2008; Colosimo et al. 2011; Tu 2013). Furthermore, BDS can also be used as a remotely sensing tool. The zenith tropospheric delay (ZTD) can be estimated from BDS PPP, which can be used in meteorology (Dong and Jin 2018; Su and Jin 2018). Since BDS/GNSS and time are mutually linked, the high-precision time and frequency can be realized by the BDS/GNSS carrier phase time transfer technique, which is a common all in view (AV) technique. Qin et al. (2020a) showed the BDS-3 clock stability and prediction accuracy compared with the BDS-2 satellites. Zhang et al. (2020b) obtained and assessed the BDS-3 precise time transfer performances.
With available BDS-3 B1I, B3I, B1C and B2a signals, the BDS PPP solutions can be achieved using the single-, dual-, triple- and quad-frequency observations. However, the BDS PPP models are complex for different frequencies and strategies. Therefore, how to construct a precise and suitable PPP model is a key issue. In this paper, detailed PPP models from single- to quad-frequency BDS observations are presented as well as their progress and performances. In the second section, BDS system and PPP method are introduced. The stochastic models of time delay bias (TDB) in BDS-2/BDS-3 PPP are showed in the third section. The single-, dual-, triple- and quad-frequency BDS PPP models are presented in the fourth section. The progress and performances of various BDS PPP models are showed in the fifth section. Finally, summary and future challenges are given in the sixth section.
BDS system and PPP
The development of BDS system has planned three steps, namely demonstration system (BDS-1), regional system (BDS-2) and global system (BDS-3), respectively (Yang et al. 2018). Until the end of 2019, 24 BDS-3 satellites in Medium Earth Orbit (MEO), 3 satellites in Inclined Geo-Synchronous Orbit (IGSO) and 1 Geostationary Earth Orbit (GEO) satellites have been launched, indicating that the deployment of the core BDS constellation will be finished soon. The construction of BDS-3 with global coverage will be completed in 2020 (Yang et al. 2019). Figure 1 shows the position dilution of precision (PDOP) values distribution for BDS-2 and BDS (BDS-2/BDS-3) constellation at 12:00 Coordinated Universal Time (UTC), day of year (DOY) 20, 2019. Combining the BDS-3 satellites, the BDS service areas have been widely expanded.
Distribution of PDOP values for BDS-2 (left) and BDS (right) constellation at 12:00 UTC, DOY 20, 2019
The main functions of BDS are the PNT services, augmentation service capabilities and short message communication services (http://www.beidou.gov.cn). The accuracy of the BDS signal-in-space (SIS) is higher than 0.5 m and the accuracy of standard point positioning (SPP) is better than 10 m in three dimensions. Besides, the BDS velocity determination accuracy is better than 0.2 m/s and the corresponding timing accuracy is better than 20 ns (CSNO 2019). The new structure of BDS signals makes it possible with multi-frequency observations. Table 1 shows the detailed information for the signals of BDS (BDS-2/BDS-3). Nowadays, the BDS services are available to global users and the increasing frequency signals have the potential to expand service functions and improve service performances. Combining with the US’s GPS, Russia’s GLONASS and European Union’s Galileo system as well as other regional systems, more challenge, opportunities and applications of multi-frequency and multi-system GNSS constellation are being carried out and exploited in the following years.
Since the introduction of PPP by Zumberge et al. (1997), it has been popular and of great interest in the GNSS community. Other than the traditional double differenced relative positioning mode, PPP can provide the precise position, receiver clock, and ZTD with a stand-alone receiver. As an extension of GNSS pseudorange positioning, the addition of carrier phase observations causes the initial dozens of convergence time for ambiguities. PPP has the popularity for many applications including the meteorology, geodesy, geodynamics and so on. For instance, BDS/GNSS PPP can provide an alternative tool for survey receiver operation without the need of reference stations. Over the past years, great developments and progress have evolved for GNSS surveying (Hofmann-Wellenhof et al. 2007; Leick et al. 2015). The BDS development can benefit the geodetic surveying and facilitate positioning techniques into the applications including the mapping, navigation, machine guidance and automation. BDS PPP can acquire the position with the millimeter-level accuracy for the positioning science and georeferencing applications.
Stochastic models of time delay bias in BDS PPP
As shown in Table 1, the signal modulation modes of BDS-2 and BDS-3 are different although they have the same B1I and B3I signals. In general, the new processing or receiving unit is adding on BDS-2 receiver for BDS-3 observing. Owing to the different processing or receiving unit for BDS-2 and BDS-3 observations, a systematic delay called time delay bias (TDB) exists between the BDS-2 and BDS-3 B1I and B3I observations. Some processing strategies can be applied for BDS-2 and BDS-3 combined PPP solutions and the corresponding TDB stochastic models can be expressed as follows.
Neglection
The neglection of TDB parameters in BDS PPP will change the estimable parameters including receiver clock and carrier phase ambiguities. This operation will apply the BDS-2 and BDS-3 observations to one common system. The stochastic model for neglection of TDB can be expressed as:
where k denotes the epoch number. Neglection of the existing TDB will cause the BDS pseudorange observations to have great residuals.
Random constant
The random constant assumes that the TDB retains the estimated values of the last epoch without process noise, which can be expressed as:
Random walk
The random walk process assumes that the TDB retains the estimated values of the last epoch with a process noise. Random constant is a special case of random walk and can be described as:
where \(\sigma_{TDB}^{2}\) denotes the process noise.
White noise
The TDB with the white noise stochastic model is regarded as independent and unrelated over the time, which can be expressed as:
Obvious TDB parameters exist between BDS-2 and BDS-3 for the JAVAD TRE_3, CETC-54-GMR-4016 and GNSS_GGR receivers (Jiao et al. 2019b). The characteristics of TDB are attributed to the receiver itself without external frequency source. It is recommended to estimate the TDB with random constant and walk models for the strong correlation among time series of TDB (Qin et al. 2020b). Also, neglection of TDB parameters and giving the BDS-2 observations a weak weight are also a great choice in BDS PPP, which has been taken by Su and Jin (2019).
BDS PPP models
Figure 2 shows the multipath combination (MPC) amplitudes for the BDS C01, C06, C12, C19 and C20 satellites, representing the BDS-2 GEO, BDS-2 IGSO, BDS-2 MEO, BDS-3 MEO and BDS-3 MEO, respectively, observed at station XIA3 during the DOY 9–14, 2019 from international GNSS Monitoring and Assessment System (iGMAS) (http://www.igmas.org). The MPC formulas can refer to Hauschild et al. (2012). The differences between the MPCs at different signals are not obvious. Hence, we will assume that the observation weight ratio of BDS B1I, B3I, B1C and B2a signals is 1:1:1:1 in this study. Besides, the TDB existing between BDS-2 and BDS-3 is neglected for all following PPP models. The introduced PPP models are also suitable when applying other TDB stochastic models.
MPCs of BDS B1I, B3I, B1C and B2a signals at iGMAS station XIA3 during DOY 9–14, 2019
Single-frequency PPP
Standard uncombined single-frequency PPP
In the standard uncombined single-frequency PPP (SF1) model, the receiver uncalibrated code delay (UCD) will be absorbed by the receiver clock or ionospheric delay. With m available satellites observed, the SF1 model for BDS B1I (B3I or B1C or B2a) single-frequency signals can be written as (Lou et al. 2016):
where \(\varvec{P}\) and \({\varvec{\Phi}}\) denote the vector of the pseudorange and carrier phase observed minus computed values; \(d\varvec{x}\) denotes the vector of receiver position increments and the zenith wet delay (ZWD) values; \(\varvec{B}\) denotes the corresponding design matrix; \(d\bar{t}_{r}\) denotes the vector of the estimated receiver clock offset; \(\varvec{e}_{m}\) is the m-row vector in which all values are 1; \(\varvec{\tau}\) denotes the estimated slant ionospheric parameters vector; \(\varvec{I}_{m}\) denotes the m-dimension identity matrix; \(a\) denotes the vector of the float ambiguities; \(\lambda\) denotes the carrier phase wavelengths; \(\varvec{\varepsilon}_{\varvec{P}}\) and \(\varvec{\varepsilon}_{{\varvec{\Phi}}}\) denote the vector of pseudorange and carrier phase observation noises; \(\varvec{c}_{\varvec{P}}\) and \(\varvec{c}_{{\varvec{\Phi}}}\) denote the pseudorange and carrier phase variance factor matrix; \(\varvec{Q}_{0} = {\text{diag}}(1/\sin^{2} (E_{1} ),1/\sin^{2} (E_{2} ), \ldots ,1/\sin^{2} (E_{m} ))\) denotes the cofactor matrix, where E is the satellite elevation angle; and \(\otimes\) denotes the Kronecker product operation.
GRAPHIC single-frequency PPP
In GRoup And PHase Ionospheric Correction (GRAPHIC) single-frequency PPP (SF2) model, the first order ionospheric delay is mitigated using the arithmetic mean of pseudorange and carrier phase observations, and the SF2 model with m satellites can be written as (Cai et al. 2017):
Ionosphere-constrained single-frequency PPP
Adding virtual ionospheric observations from the external ionospheric model such as global ionospheric maps (GIMs), the ionosphere-constrained single-frequency PPP (SF3) model can be described as (Gao et al. 2017):
where \(\varvec{\tau}_{0}\) denotes ionospheric prior observations vector, \(\varvec{\varepsilon}_{\tau }\) denotes the ionosphere observations precision vector, and \(\varvec{c}_{\varvec{\tau}}\) denotes the ionosphere prior observations variance factor matrix.
Dual-frequency PPP
Standard uncombined dual-frequency PPP
In the standard uncombined dual-frequency PPP (DF1) model, the receiver UCD will be absorbed by the receiver clock and ionospheric parameters at the same time. The DF1 model with m satellites for B1I and B3I signals can be written as (Odijk et al. 2016):
where \(\varvec{u}_{2} = \left[ {\begin{array}{*{20}c} 1 & {u_{2} } \\ \end{array} } \right]^{T}\), \(u_{k} = f_{1}^{2} /f_{k}^{2} ,k = 2,3,4\) denotes the frequency-dependent multiplier factors, f denotes the carrier phase frequency; \({\varvec{\Lambda}}_{2} = {\text{diag}}(\lambda_{1} ,\lambda_{2} )\); \(\varvec{a^{\prime}}^{T} \varvec{ = }\left[ {\begin{array}{*{20}c} {\varvec{a}_{1}^{T} } & {\varvec{a}_{2}^{T} } \\ \end{array} } \right]\).
IF dual-frequency PPP
In IF dual-frequency PPP (DF2) model, the first-order ionospheric delay can be eliminated. The DF2 model with m satellites for B1I and B3I signals can be expressed as (Cai 2009):
where \(\varvec{f}^{T} = \left[ {\begin{array}{*{20}c} {\alpha_{m,n} } & {\beta_{m,n} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {f_{m}^{2} }-{f_{n}^{2} } \\ \end{array} } \right]/(f_{m}^{2} - f_{n}^{2} )\), m, n = 1, 2, 3 and 4.
UofC dual-frequency PPP
The UofC dual-frequency PPP (DF3) model applies the dual-frequency IF observations and arithmetic mean of pseudorange and carrier phase observations. With m satellites available, the DF3 model for B1I and B3I signals can be described as (Xiang et al. 2019):
Ionosphere-constrained dual-frequency PPP
In the ionosphere-constrained dual-frequency PPP (DF4) model, an additional receiver differential code bias (DCB) parameter is needed to separate the pure slant ionospheric delay parameters. The DF4 model with m satellites can be written as (Li et al. 2015):
where \(\varvec{n}_{2} = \left[ {\begin{array}{*{20}c} {\beta_{1,2} } & { - \alpha_{1,2} } \\ \end{array} } \right]^{T}\); DCB denotes the vector of the DCB between B1I and B3I signals.
Triple-frequency PPP
Standard uncombined triple-frequency PPP
In standard uncombined triple-frequency PPP (TF1) model, the receiver B1I/B3I UCD will be absorbed by the receiver clock and ionospheric parameters. Besides, an additional inter-frequency bias (IFB) parameter is needed to compensate the effects of the DCB on the third pseudoranges. The TF1 model for B1I, B3I and B2a signals with m satellites can be expressed as (Guo et al. 2016):
where \(\varvec{v}_{ 3} = \left[ {\begin{array}{*{20}c} 0 & 0 & 1 \\ \end{array} } \right]^{T}\); \(ifb_{TF 1}\) denotes the IFB vector in TF1 model; \(\varvec{u}_{ 3} = \left[ {\begin{array}{*{20}c} 1& {u_{2} } & {u_{3} } \\ \end{array} } \right]^{T}\); \({\varvec{\Lambda}}_{ 3} = {\text{diag}}(\lambda_{1} ,\lambda_{2} ,\lambda_{ 3} )\); \(\varvec{a^{\prime\prime}}^{T} \varvec{ = }\left[ {\begin{array}{*{20}c} {\varvec{a}_{1}^{T} } & {\varvec{a}_{2}^{T} } & {\varvec{a}_{ 3}^{T} } \\ \end{array} } \right]\).
IF triple-frequency PPP with two combinations
The triple-frequency PPP (TF2) models using B1I, B3I and B2a signals can be formed by two IF combinations (B1I/B3I and B1I/B2a). An estimable IFB parameter is necessary to mitigate the receiver UCDs inconsistency between the B1I/B3I and B1I/B2a combinations. The TF2 model can be expressed as (Su et al. 2020):
where \(\varvec{v}_{2} = \left[ {\begin{array}{*{20}c} 0 & 1 \\ \end{array} } \right]^{T}\); \(\varvec{C} = \left[ {\begin{array}{*{20}c} {\alpha_{1,2} } & {\beta_{1,2} } & 0 \\ {\alpha_{1,3} } & 0 & {\beta_{1,3} } \\ \end{array} } \right]\); \(ifb_{TF 2}\) denotes the IFB vector in TF2 model.
IF triple-frequency PPP with one combination
The triple-frequency PPP (TF3) models with one IF combination integrate the B1I, B3I and B2a signals to one combined observation. Particularly for BDS-2, the BDS-2 B1I/B3I IF combination is also applied so that combined BDS-2/BDS-3 PPP can be conducted. An estimable IFB existing between the B1I/B3I/B2a and B1I/B3I pseudorange is also needed to be estimated. With m1 BDS-3 satellites and m2 BDS-2 satellites, the TF3 model can be expressed as (Tu et al. 2018):
where \(\varvec{C^{\prime}} = \left[ {\begin{array}{*{20}c} {e_{1} } & {e_{2} } & {e_{3} } \\ \end{array} } \right]\), in which e1, e2 and e3 denote the triple-frequency combination coefficients with the criteria that are IF and geometry-free and have the least noise (Pan et al. 2017). \(\varvec{\bar{C^{\prime}} = }\left[ {\begin{array}{*{20}c} {\alpha_{1,2} } & {\beta_{1,2} } & 0 \\ \end{array} } \right]\).\(ifb_{TF 3}\) denotes the IFB vector in TF3 model;
Ionosphere-constrained triple-frequency PPP
Similar to DF4 model, the ionosphere-constrained triple-frequency PPP (TF4) model with B1I, B3I and B2a signals needs an additional receiver DCB parameter in addition to the IFB parameter. The TF4 model with m BDS satellites can be written as (Su et al. 2020):
where \(\varvec{n}_{3} = \left[ {\begin{array}{*{20}c} {\beta_{1,2} } & {-\alpha_{1,2} } & {u_{3} \cdot \beta_{1,2} } \\ \end{array} } \right]^{T}\), and \(ifb_{TF 4}\) denotes the IFB vector in TF4 model.
Quad-frequency PPP
Standard uncombined quad-frequency PPP
In the standard uncombined quad-frequency PPP (QF1) model using B1I, B3I B1C and B2a raw observations, two IFB parameters are needed for the DCB effects of B1C and B2a signals. The QF1 model with m satellites can be written as (Zhang et al. 2020a):
where \(\varvec{v}_{ 4} = \left[ {\begin{array}{*{20}c} 0& 0& 1& 0\\ 0& 0& 0& 1\\ \end{array} } \right]^{T}\); \(\varvec{u}_{ 4} = \left[ {\begin{array}{*{20}c} 1& {u_{2} } & {u_{3} } & {u_{ 4} } \\ \end{array} } \right]^{T}\); \({\varvec{\Lambda}}_{4} = {\text{diag}}(\lambda_{1} ,\lambda_{2} ,\lambda_{ 3} ,\lambda_{4} )\); \(\varvec{a^{\prime\prime\prime}}^{T} \varvec{ = }\left[ {\begin{array}{*{20}c} {\varvec{a}_{1}^{T} } & {\varvec{a}_{2}^{T} } & {\varvec{a}_{ 3}^{T} } & {\varvec{a}_{ 4}^{T} } \\ \end{array} } \right]\). \(ifb_{QF1}\) denotes the IFBs matrix in QF1 model.
IF quad-frequency PPP with two combinations
The quad-frequency PPP (QF2) models can also be formed by the B1I/B3I and B1C/B2a IF combinations, respectively. In this situation, an IFB parameter for the inconsistency between the B1I/B3I and B1C/B2a is generated. The QF2 model with m satellites can be expressed as:
where \(\varvec{C^{\prime\prime}} = \left[ {\begin{array}{*{20}c} {\alpha_{1,2} } & {\beta_{1,2} } & 0& 0\\ 0& 0& {\alpha_{3,4} } & {\beta_{3,4} } \\ \end{array} } \right]\), and \(ifb_{QF 2}\) denotes the IFB vector in QF2 model.
IF quad-frequency PPP with one combination
The quad-frequency PPP (QF3) models can be formed by a quad-frequency IF combination, which is similar to the TF3 model. The B1I/B3I IF combination is also applied for BDS-2 observations. Hence, the QF3 model with m1 BDS-3 satellites and m2 BDS-2 satellites can be described as:
where \(\varvec{C^{\prime\prime\prime}} = \left[ {\begin{array}{*{20}c} {e^{\prime}_{1} } & {e^{\prime}_{2} } & {e^{\prime}_{3} } & {e^{\prime}_{4} } \\ \end{array} } \right]\), in which \(e^{\prime}_{1}\), \(e^{\prime}_{ 2}\), \(e^{\prime}_{ 3}\) and \(e^{\prime}_{ 4}\) denote the quad-frequency combination coefficients with the same criteria of TF3 model. \(\varvec{\bar{C^{\prime\prime\prime}} = }\left[ {\begin{array}{*{20}c} {\alpha_{1,2} } & {\beta_{1,2} } & 0& 0\\ \end{array} } \right]\).
Ionosphere-constrained quad-frequency PPP
Similar to the TF4 model, two IFB parameters and a receiver DCB parameter are also necessary in the ionosphere-constrained quad-frequency PPP (QF4) model, which can be expressed as (Su et al. 2019):
where \(\varvec{n}_{4} = \left[ {\begin{array}{*{20}c} {\beta_{1,2} } & {-\alpha_{1,2} } & {u_{3} \cdot \beta_{1,2} } & {u_{4} \cdot \beta_{1,2} } \\ \end{array} } \right]^{T}\), \(ifb_{QF 4}\) denotes the IFBs matrix in QF4 model.
Progress and performances
Nowadays, most previous studies related to BDS PPP mainly focused on BDS-2 solutions (e.g., Chen et al. 2016; Li et al. 2019; Liu et al. 2017). Since the BDS-3 began to offer global PNT services at end of year 2018, some studies related to the BDS-3 PPP have been investigated. For instance, Zhang et al. (2019) conducted a comprehensive assessment of the BDS-3 signal quality, real-time kinematic (RTK) and PPP performances. Jiao et al. (2019a) assessed the BDS-2, BDS-2/BDS-3, GPS, GLONASS, and Galileo PPP using the iGMAS stations in term of static and kinematic aspects. Su and Jin (2019) showed the PPP time transfer using the stations from iGMAS and demonstrated that the triple-frequency PPP time transfer performances are identical to dual-frequency PPP solution.
With the available BDS-3 orbit and clock products provided by Deutsches GeoForschungsZentrum (GFZ) or GNSS Research Center of Wuhan university (WHU) (Deng et al. 2014; Wang et al. 2019b), the BDS-3 PPP solutions can be achieved. The B1I/B3I IF combination is used for precise orbit determination (POD) of the BDS satellites using the network stations (Wang et al. 2019a). Besides, China Academy Science (CAS) has begun to provide the BDS-3 B1I, B3I, B1C, B2a and B2b DCB products available at ftp://gipp.org.cn/product/dcb/mgex/2019 (Wang et al. 2016). The BDS applications will receive more attentions with development of BDS. The main performances of various BDS PPP models are shown as follows.
Theoretical comparison of BDS PPP models
Table 2 provides the characteristics of the BDS PPP models including the selected signals, combination coefficients, ionospheric coefficients and noise amplification. The single-frequency SF1 and SF2 PPP models are equivalent since they have the relationship of linear transformation for the mathematical and stochastic models (Xu and Xu 2016). It also applies equally to dual-frequency PPP models (DF1, DF2 and DF3), triple-frequency PPP models (TF1, TF2 and TF3), and quad-frequency PPP models (QF1, QF2 and QF3). To compare those BDS PPP models, the estimated parameters including the receiver clock, DCB, IFB, and ionospheric delay are provided in Table 3. The receiver position increments, the ZWD and float ambiguities are not shown although they are also needed to be considered in the PPP models.
Positioning performances
BDS single-frequency PPP can achieve the precise position with the centimeter–decimeter accuracy level and multi-frequency BDS PPP has the millimeter–centimeter level when the estimable carrier phase ambiguities converge. The positioning error is estimated as constant for static PPP and white noise in kinematic PPP mode. Figure 3 shows the static positioning errors of BDS single-, dual-, triple- and quad-frequency PPP at the iGMAS station KUN1 in the north, east and up components on DOY 16, 2019. The positioning performance is compared with the iGMAS reference value. The result has shown that the multi-frequency signals will greatly improve the BDS positioning performance, particularly triple-frequency and quad-frequency BDS observations. Furthermore, the receiver positioning errors have an accuracy of few centimeters after convergence in BDS dual-, triple-, quad-frequency PPP models.
Positioning errors of BDS single-, dual-, triple- and quad-frequency PPP at the iGMAS station KUN1 in the north, east and up components on DOY 16, 2019
Precise time and frequency transfer
BDS PPP can also be applied for precise time transfer when the two stations are connected to the time laboratory. Figure 4 shows the clock differences of the BDS single-, dual-, triple- and quad-frequency PPP for the time-link BRCH–XIA3 on DOY 17, 2019. As shown, the time series of the BDS multi-frequency PPP clock differences are smoother than the single-frequency solutions. To assess how well the frequency stability of the BDS PPP models, Figure 5 shows the corresponding Allan deviation (ADEV) of the BDS PPP time transfer using the time-link BRCH-XIA3 on DOY 17, 2019, in which the ADEV is calculated by the Stable32 software (http://www.wriley.com/). The results indicate that the frequency stabilities of 10,000 s for BDS single-, dual-, triple- and quad-frequency PPP time transfer are better than 1.6 × 10−14.
Clock differences of the BDS single-, dual-, triple- and quad-frequency PPP for the time-link BRCH–XIA3 on DOY 17, 2019
ADEV of the BDS single-, dual-, triple- and quad-frequency PPP time transfer using the time-link BRCH–XIA3 on DOY 17, 2019
ZTD estimation
The tropospheric delay can be estimated as the random walk in the PPP processing. Figure 6 shows the time series of the ZTD in BDS single-, dual-, triple- and quad-frequency PPP models at iGMAS station XIA3 on DOY 17, 2019. The root mean squares (RMS) of ZTD errors at station XIA3 are (6.8, 6.8, 5.2) cm, (2.1, 2.2, 2.1, 2.1) cm, (2.0, 2.0, 2.0, 2.0) cm and (1.6, 1.6, 1.6, 1.6) cm for BDS single-, dual-, triple- and quad-frequency PPP models, respectively, in which the ZTDs from iGMAS products are regarded as a reference value. No significant difference was found for the accuracy of the estimated tropospheric delay within the dual-, triple- and quad-frequency PPP models.
Time series of the ZTD in BDS single-, dual-, triple- and quad-frequency PPP models at stations XIA3 on DOY 17, 2019
IFB and DCB
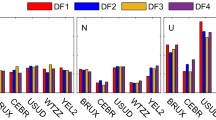
The receiver hardware delays can be estimated as the random walk or constant in the BDS multi-frequency PPP models. Take the BDS quad-frequency PPP models as the examples, Figure 7 shows the estimated IFB time series of BDS QF1, QF2 and QF3 models at iGMAS stations XIA1 and BRCH and Figure 8 provides the estimated DCB time series in BDS QF4 model on DOY 14, 2019. The IFB and DCB values are estimated as the random walk in the BDS PPP models. We can see that the IFB and DCB time series are stable over time and it’s reasonable to model the hardware delays as the constants within one day in the BDS multi-frequency PPP models.
Time series of IFB in BDS QF1, QF2 and QF3 models at iGMAS stations XIA1 and BRCH on DOY 14, 2019
Time series of DCB in QF4 PPP model at iGMAS stations XIA1 and BRCH on DOY 14, 2019
To check the possible systematic bias between the BDS-2 and BDS-3 receiver DCB and evaluate the effects of combining BDS-2 and BDS-3 observations on receiver DCB, BDS-2-only and BDS-2 + BDS-3 solutions with lower computation loads by taking advantage of GIMs are used to estimate the receiver DCBs from over 100 stations with BDS C2I and C6I observations from multi-GNSS Experiment (MGEX) (http://www.igs.org), respectively. The standard deviation (STD) distribution of receiver C2I–C6I DCBs with geomagnetic latitudes is shown in Fig. 9. The results indicate that the STDs of receiver DCB are less than 0.4 ns and no obvious systematic bias exists in the BDS-2 and BDS-3 receiver DCB. Furthermore, the stability of receiver DCB is better when combining BDS-3 observations (Wang et al. 2020).
Distribution of receiver C2I–C6I DCBs STD with geomagnetic latitudes
Summary and challenges
With the rapid development of BDS regional navigation satellite system (BDS-2) and global navigation satellite system (BDS-3), BDS provides global services with highly precise PNT as well as short-message communication and augment service. Compared to the traditional double differenced relative positioning model, BDS PPP can provide precise position, receiver clock, ZTD, IFB and DCB with a stand-alone receiver, which has wide applications. Particularly with the available BDS B1I, B3I, B1C and B2a signals, the BDS single-, dual-, triple and quad-frequency PPP solutions can be achieved. In this paper, BDS PPP models from single- to quad-frequency observations are presented in details. BDS-2 and BDS-3 systems are introduced and the TDB is shown. Three single-frequency, four dual-frequency, four triple-frequency and four quad-frequency BDS PPP models are provided. The progress and performances of various BDS PPP models are presented and evaluated, including the theoretical comparison of the models, positioning performances, precise time transfer, ZTD, IFB and DCB. The results have shown that the multi-frequency BDS signals will greatly improve the PPP performances.
Although a number of achievements of BDS PPP models have been obtained and applied, but it still needs some improvements or developments. For example, more BDS combination strategies and PPP models for different frequencies and systems are still challenging and need to be further investigated in the future, including the weights of different frequencies signals and systems, and the rapid ambiguity resolution of BDS multi-frequency PPP. The development of BDS PPP models should be further improved when the BDS system is fully constructed. Together with multi-GNSS systems, it should further develop and improve multi-GNSS PPP performances.
Availability of data and materials
The used data showed in this study are obtained from iGMAS (http://www.igmas.org) and International GNSS Service (IGS) (http://www.igs.org), which are referenced in the text.
References
Benedetti, E., Branzanti, M., Biagi, L., Colosimo, G., Mazzoni, A., & Crespi, M. (2014). Global Navigation Satellite Systems seismology for the 2012 Mw 6.1 Emilia earthquake: exploiting the VADASE algorithm. Seismological Research Letters,85, 649–656.
Bilich, A., Cassidy, J. F., & Larson, K. M. (2008). GPS Seismology: Application to the 2002 Mw 7.9 Denali fault earthquake. Bulletin of the Seismological Society of America,98, 593–606.
Cai, C. (2009). Precise point positioning using dual-frequency GPS and GLONASS measurements. In Masters Abstracts International (Vol. 03, p. 172).
Cai, C., Gong, Y., Gao, Y., & Kuang, C. (2017). An approach to speed up single-frequency PPP convergence with quad-constellation GNSS and GIM. Sensors,17, 1302.
Chen, J., Wang, J., Zhang, Y., Yang, S., Chen, Q., & Gong, X. (2016). Modeling and assessment of GPS/BDS combined precise point positioning. Sensors,16, 1151.
Colosimo, G., Crespi, M., & Mazzoni, A. (2011). Real-time GPS seismology with a stand-alone receiver: A preliminary feasibility demonstration. Journal of Geophysical Research: Solid Earth. https://doi.org/10.1029/2010JB007941.
CSNO. (2019). BeiDou navigation satellite system signal in space interface control document open service signal B1I (Version 1.0). China Satellite Navigation Office.
Deng, Z., Ge, M., Uhlemann, M., & Zhao, Q. (2014). Precise orbit determination of BeiDou satellites at GFZ. In Proceedings of IGS workshop (pp. 23–27).
Dong, Z., & Jin, S. (2018). 3-D water vapor tomography in Wuhan from GPS, BDS and GLONASS observations. Remote Sensing,10, 62.
Dong, Z., & Jin, S. G. (2019). Evaluation of spaceborne GNSS-R retrieved ocean surface wind speed with multiple datasets. Remote Sensing, 11(23), 2747. https://doi.org/10.3390/rs11232747.
Gao, Z., Ge, M., Shen, W., Zhang, H., & Niu, X. (2017). Ionospheric and receiver DCB-constrained multi-GNSS single-frequency PPP integrated with MEMS inertial measurements. Journal of Geodesy,91, 1351–1366.
Guo, F., Zhang, X., Wang, J., & Ren, X. (2016). Modeling and assessment of triple-frequency BDS precise point positioning. Journal of Geodesy,90, 1223–1235.
Hauschild, A., Montenbruck, O., Sleewaegen, J.-M., Huisman, L., & Teunissen, P. J. (2012). Characterization of compass M-1 signals. GPS Solutions,16, 117–126.
Hofmann-Wellenhof, B., Lichtenegger, H., & Wasle, E. (2007). GNSS–global navigation satellite systems: GPS, GLONASS, Galileo, and more. Berlin: Springer.
Jia, Y., Jin, S. G., Savi, P., Gao, Y., Tang, J., Chen, Y., et al. (2019). GNSS-R soil moisture retrieval based on a XGboost machine learning aided method: Performance and validation. Remote Sensing,11(14), 1655. https://doi.org/10.3390/rs11141655.
Jiao, G., Song, S., Ge, Y., Su, K., & Liu, Y. (2019a). Assessment of BeiDou-3 and multi-GNSS precise point positioning performance. Sensors,19, 2496.
Jiao, G., Song, S., & Jiao, W. (2019b). Improving BDS-2 and BDS-3 joint precise point positioning with time delay bias estimation. Measurement Science & Technology,31, 025001.
Jin, S. G., Feng, G. P., & Gleason, S. (2011). Remote sensing using GNSS signals: Current status and future directions. Advances in Space Research,47(10), 1645–1653. https://doi.org/10.1016/j.asr.2011.01.036.
Jin, S. G., Jin, R., & Kutoglu, H. (2017a). Positive and negative ionospheric responses to the March 2015 geomagnetic storm from BDS observations. Journal of Geodesy,91(6), 613–626. https://doi.org/10.1007/s00190-016-0988-4.
Jin, S. G., Li, J. H., & Gao, C. (2019). Atmospheric sounding from FY-3C GPS radio occultation observations: First results and validation. Advances in Meteorology.,9, 9. https://doi.org/10.1155/2019/4780143.
Jin, S. G., Occhipinti, G., & Jin, R. (2015). GNSS ionospheric seismology: Recent observation evidences and characteristics. Earth-Science Reviews,147, 54–64. https://doi.org/10.1016/j.earscirev.2015.05.003.
Jin, S. G., & Park, P. H. (2006). Strain accumulation in South Korea inferred from GPS measurements. Earth Planets and Space,58(5), 529–534. https://doi.org/10.1186/BF03351950.
Jin, S. G., Qian, X. D., & Kutoglu, H. (2016). Snow depth variations estimated from GPS-Reflectometry: A case study in Alaska from L2P SNR data. Remote Sensing,8(1), 63. https://doi.org/10.3390/rs8010063.
Jin, S. G., Qian, X., & Wu, X. (2017b). Sea level change from BeiDou Navigation Satellite System-Reflectometry (BDS-R): First results and evaluation. Global and Planetary Change,149, 20–25. https://doi.org/10.1016/j.gloplacha.2016.12.010.
Jin, S. G., & Su, K. (2019). Co-seismic displacement and waveforms of the 2018 Alaska earthquake from high-rate GPS PPP velocity estimation. Journal of Geodesy,93, 1559–1569.
Jin, S. G., Zhang, Q. Y., & Qian, X. (2017c). New progress and application prospects of Global Navigation Satellite System Reflectometry (GNSS + R). Acta Geodaetica et Cartographica Sinica,46(10), 1389–1398. https://doi.org/10.11947/j.AGCS.2017.20170282.
Jin, S. G., & Zhang, T. Y. (2016). Terrestrial water storage anomalies associated with drought in Southwestern USA derived from GPS observations. Surveys in Geophysics,37(6), 1139–1156. https://doi.org/10.1007/s10712-016-9385-z.
Leick, A., Rapoport, L., & Tatarnikov, D. (2015). GPS satellite surveying. Hoboken: Wiley.
Li, B., Ge, H., & Shen, Y. (2015). Comparison of ionosphere-free, UofC and uncombined PPP observation models. Acta Geodaetica et Cartographica Sinica,44, 734–740.
Li, X., Ge, M., Lu, C., Zhang, Y., Wang, R., Wickert, J., et al. (2014). High-rate GPS seismology using real-time precise point positioning with ambiguity resolution. IEEE Transactions on Geoscience and Remote Sensing,52, 6165–6180.
Li, X., Li, X., Liu, G., Feng, G., Yuan, Y., Zhang, K., et al. (2019). Triple-frequency PPP ambiguity resolution with multi-constellation GNSS: BDS and Galileo. Journal of Geodesy,93, 1105–1122.
Liu, Y., Ye, S., Song, W., Lou, Y., & Chen, D. (2017). Integrating GPS and BDS to shorten the initialization time for ambiguity-fixed PPP. GPS Solutions,21, 333–343.
Lou, Y., Zheng, F., Gu, S., Wang, C., Guo, H., & Feng, Y. (2016). Multi-GNSS precise point positioning with raw single-frequency and dual-frequency measurement models. GPS Solutions,20, 849–862.
Odijk, D., Zhang, B., Khodabandeh, A., Odolinski, R., & Teunissen, P. J. (2016). On the estimability of parameters in undifferenced, uncombined GN network and PPP-RTK user models by means of S-system theory. Journal of Geodesy,90, 15–44.
Pan, L., Zhang, X., Li, X., Liu, J., & Li, X. (2017). Characteristics of inter-frequency clock bias for block IIF satellites and its effect on triple-frequency GPS precise point positioning. GPS Solutions,21, 811–822.
Qian, X. D., & Jin, S. G. (2016). Estimation of snow depth from GLONASS SNR and phase-based multipath reflectometry. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing,9(10), 4817–4823. https://doi.org/10.1109/jstars.2016.2560763.
Qin, W., Ge, Y., Wei, P., Dai, P., & Yang, X. (2020a). Assessment of the BDS-3 on-board clocks and their impact on the PPP time transfer performance. Measurement,153, 107356.
Qin, W., Ge, Y., Zhang, Z., Su, H., Wei, P., & Yang, X. (2020b). Accounting BDS3–BDS2 inter-system biases for precise time transfer. Measurement,156, 107566.
Su, K., & Jin, S. (2018). Improvement of multi-GNSS precise point positioning performances with real meteorological data. Journal of Navigation,71(6), 1363–1380. https://doi.org/10.1017/S0373463318000462.
Su, K., & Jin, S. (2019). Triple-frequency carrier phase precise time and frequency transfer models for BDS-3. GPS Solutions,23, 86.
Su, K., Jin, S., & Jiao, G. (2020). Assessment of multi-frequency GNSS PPP models using GPS, Beidou, GLONASS, Galileo and QZSS. Measurement Science & Technology. https://doi.org/10.1088/1361-6501/ab69d5.
Su, K., Jin, S. G., & Hoque, M. M. (2019). Evaluation of ionospheric delay effects on multi-GNSS positioning performance. Remote Sensing,11(2), 171. https://doi.org/10.3390/rs11020171.
Tu, R. (2013). Fast determination of displacement by PPP velocity estimation. Geophysical Journal International,196, 1397–1401.
Tu, R., Zhang, P., Zhang, R., Liu, J., & Lu, X. (2018). Modeling and assessment of precise time transfer by using BeiDou navigation satellite system triple-frequency signals. Sensors,18, 1017.
Wang, C., Guo, J., Zhao, Q., & Liu, J. (2019a). Empirically derived model of solar radiation pressure for BeiDou GEO satellites. Journal of Geodesy,93, 791–807.
Wang, C., Zhao, Q., Guo, J., Liu, J., & Chen, G. (2019b). The contribution of intersatellite links to BDS-3 orbit determination: Model refinement and comparisons. Navigation,66, 71–82.
Wang, Q., Jin, S. G., Yuan, L., Hu, Y., Chen, J., & Guo, J. (2020). Estimation and analysis of BDS-3 differential code biases from MGEX observations. Remote Sensing,12(1), 68. https://doi.org/10.3390/rs12010068.
Wang, N., Yuan, Y., Li, Z., Montenbruck, O., & Tan, B. (2016). Determination of differential code biases with multi-GNSS observations. Journal of Geodesy,90, 209–228.
Xiang, Y., Gao, Y., Shi, J., & Xu, C. (2019). Consistency and analysis of ionospheric observables obtained from three precise point positioning models. Journal of Geodesy,93, 1161–1170.
Xu, G., & Xu, Y. (2016). GPS: Theory, algorithms and applications. Berlin: Springer.
Yang, Y., Gao, W., Guo, S., Mao, Y., & Yang, Y. (2019). Introduction to BeiDou-3 navigation satellite system. Navigation,66, 7–18.
Yang, Y., Xu, Y., Li, J., & Yang, C. (2018). Progress and performance evaluation of BeiDou global navigation satellite system: Data analysis based on BDS-3 demonstration system. Science China Earth Sciences,61, 614–624.
Zhang, P., Tu, R., Gao, Y., Zhang, R., & Han, J. (2020a). Performance of Galileo precise time and frequency transfer models using quad-frequency carrier phase observations. GPS Solutions,24, 40.
Zhang, P., Tu, R., Wu, W., Liu, J., Wang, X., & Zhang, R. (2020b). Initial accuracy and reliability of current BDS-3 precise positioning, velocity estimation, and time transfer (PVT). Advances in Space Research,65(4), 1225–1234.
Zhang, Z., Li, B., Nie, L., Wei, C., Jia, S., & Jiang, S. (2019). Initial assessment of BeiDou-3 global navigation satellite system: signal quality, RTK and PPP. GPS Solutions,23(111), 156.
Zumberge, J., Heflin, M., Jefferson, D., Watkins, M., & Webb, F. (1997). Precise point positioning for the efficient and robust analysis of GPS data from large networks. Journal of Geophysical Research: Solid Earth,102, 5005–5017.
Acknowledgements
The authors would like to thank editor and reviewers for construction comments to improve our manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (NSFC) Project (Grant No. 41761134092), Jiangsu Province Distinguished Professor Project (Grant No. R2018T20) and Startup Foundation for Introducing Talent of NUIST (Grant No. 2243141801036).
Author information
Authors and Affiliations
Contributions
SJ and KS conceived the idea and contributed to the writing of the paper. Both authors read and approved the final manuscript.
Authors’ Information
Shuanggen Jin received the B.Sc. degree in Geodesy from Wuhan University, China in 1999 and the Ph.D. degree in Geodesy from the University of Chinese Academy of Sciences, China in 2003. He is currently a Professor and Dean at Nanjing University of Information Science and Technology, China and Professor at Shanghai Astronomical Observatory, CAS, China. His main research areas include Satellite Navigation, Remote Sensing, and Space/Planetary Exploration. He has over 400 papers in international peer-reviewed journals and Proceedings, 10 patents/software copyrights and 10 books/monographs with more than 5000 citations and H-index > 40. Prof. Jin has been President of International Association of Planetary Sciences (IAPS) (2015–2019), President of the International Association of CPGPS (2016–2017), Chair of IUGG Union Commission on Planetary Sciences (UCPS) (2015–2023), Vice-President of the IAG Commission (2015–2019). He has received one first-class and four second-class Prizes of Provincial Awards, 100-Talent Program of CAS, IAG Fellow, IUGG Fellow, Member of Russian Academy of Natural Sciences, Member of European Academy of Sciences and Member of Academia Europaea etc.
Ke Su received B.S. degree in geomatics from Shandong University of Science and Technology, Qingdao, China, in 2017. He is currently working toward the Ph.D. degree in Shanghai Astronomical Observatory, CAS, Shanghai, China. His research focuses on GNSS Precise Point Positioning and its Applications. He has published about 10 SCI papers.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Consent for publication
Not applicable.
Ethics approval and consent to participate
Not applicable.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
