Abstract
The flow regime of micro flow varies from collisionless regime to hydrodynamic regime according to the Knudsen number Kn, which is defined as the ratio of the mean free path over the local characteristic length. On the kinetic scale, the dynamics of a small-perturbed micro flow can be described by the linearized kinetic equation. In the continuum regime, according to the Chapman-Enskog theory, hydrodynamic equations such as linearized Euler equations and Navier-Stokes equations can be derived from the linearized kinetic equation. In this paper, we are going to propose a unified gas kinetic scheme (UGKS) based on the linearized kinetic equation. For the simulation of small-perturbed micro flow, the linearized scheme is more efficient than the nonlinear one. In the continuum regime, the cell size and time step of UGKS are not restricted to be less than the particle mean free path and collision time, and the UGKS becomes much more efficient than the traditional upwind-flux-based operator-splitting kinetic solvers. The important methodology of UGKS is the following. Firstly, the evolution of microscopic distribution function is coupled with the evolution of macroscopic flow quantities. Secondly, the numerical flux of UGKS is constructed based on the integral solution of kinetic equation, which provides a genuinely multiscale and multidimensional numerical flux. The UGKS recovers the solution of linear kinetic equation in the rarefied regime, and converges to the solution of the linear hydrodynamic equations in the continuum regime. An outstanding feature of UGKS is its capability of capturing the accurate viscous solution in bulk flow region once the hydrodynamic flow structure can be resolved by the cell size even when the cell size is much larger than the kinetic length scale, such as the capturing of the viscous boundary layer with a cell size being much larger than the particle mean free path. Such a multiscale property is called unified preserving (UP) which has been studied in (Guo, et al. arXiv preprint arXiv:1909.04923, 2019). In this paper, a mathematical proof of the UP property for UGKS will be presented and this property is applicable to UGKS for solving both linear and nonlinear kinetic equations.
Similar content being viewed by others
1 Introduction
The Boltzmann equation is a fundamental equation in kinetic theory, and it is widely applied in the fields of aerospace engineering, chemical industry, as well as the microelectromechanical systems (MEMS). The modeling scale of the Boltzmann equation is on the kinetic scale, namely the particle mean free path and collision time scale. Such small modeling scale makes the Boltzmann equation reliable but on the other hand quite complicated, comparing to the hydrodynamic scale Navier-Stokes (NS) and Euler equations. The complication of the Boltzmann equation comes from its high dimension and stiff collision operator. The asymptotic theories, such as the Hilbert expansion and Chapman-Enskog theory, have been developed to bridge the Boltzmann equation and the hydrodynamic equations, and connect the kinetic parameters to the hydrodynamic ones [1–3]. Similar to the asymptotic theories, the linearized Boltzmann equation has also been studied when dealing with the small perturbed flow field in MEMS and porous media. For such a small perturbed flow field, the linearized Boltzmann equation can faithfully recover the physical solution in a much effective way [3]. As shown in Fig. 1, the asymptotic analysis can also be applied on the linearized kinetic equation, which means the linearized kinetic equation corresponds to the linearized NS and Euler equations in the hydrodynamic scale. In many applications, the flow regime or the local Knudsen number varies several order of magnitude in a single computation, and therefore an effective multiscale numerical scheme is highly demanded.
For the last several decades, researchers have been trying to develop effective multiscale numerical schemes [4–9]. In 2010, Xu, et al. proposed the unified gas-kinetic scheme (UGKS), which is the first genuine multiscale scheme being able to capture the viscous effect with cell size much larger than the kinetic scale. The direct modeling methodology of UGKS are: firstly, the evolution of microscopic distribution function is coupled with the evolution of macroscopic flow quantities; secondly, the numerical flux of UGKS is constructed based on the evolution solution of kinetic equation, which provides a genuinely multiscale numerical flux [10]. The UGKS has been successfully applied in radiation and neutron transport [11–15], plasma physics [16], and multiphase flow [17], etc. In order to reduce the computational cost, the unified gas-kinetic wave-particle (UGKWP) method, i.e. a stochastic version of UGKS has been proposed by Liu, et al. [18]. The UGKWP method is a multiscale method that has the asymptotic complexity diminishing (ACD) property [19]. The UGKWP is effective in the simulation of three dimensional hypersonic flow problems in all regimes. The discrete unified gas-kinetic scheme (DUGKS) developed by Guo, et al. is also a multiscale scheme [5, 20], and has been successfully applied in the field of micro flow [21, 22], gas mixture [23], gas-particle multiphase flow [24], phonon transport [25], radiation [26], etc. The general synthetic iteration scheme was first proposed by Wu, et al. for the steady state solution of the linearized kinetic equation [6], and is recently extended to the simulation of nonlinear kinetic equation and diatomic gas [27, 28].
In order to measure the capability of numerical schemes in capturing the multiscale flow physics, Guo, et al. proposes the concept of unified preserving (UP) property [1]. The definition of UP is for a consistent numerical scheme of the kinetic equation, if the scheme satisfies:
-
1.
it is uniformly stable for all Knudsen number;
-
2.
for Kn≪1, two parameters α,β∈(0,1) exist, such that as Δt=O(Knα), Δx=O(Knβ), the asymptotic expansion of the numerical scheme is identical to the Chapman-Enskog expansion of the kinetic equation up to the order of n;
Then, the scheme is called a n-th order UP scheme. From the above definition, one finds that the UP capability of a scheme can be measured by three parameters n and α, β. A higher n and lower α, β indicates a better multiscale scheme.
In this paper, we extend UGKS to the micro flow simulation and propose a linearized version of UGKS. The advantage of the linearized UGKS in comparison with the nonlinear UGKS is that it is much more efficient and accurate in the micro flow simulation. However, the drawback is that the application of linearized version of UGKS is limited to the small perturbed flow problems, but there are still wide applications. The rest of this paper is organised as following. In Section 2, we are going to specify the linearized kinetic equation and propose the unified gas-kinetic scheme for linearized system. In Section 3, we are going to analyze the unified preserving property of UGKS. The numerical tests are shown in Section 4. And Section 5 will be the conclusion.
2 Unified gas-kinetic scheme for linearized kinetic equation
2.1 Linearized kinetic equation
In this work, the kinetic BGK equation is considered [29],
where \(f(\vec {x},t,\vec {v})\) is the velocity distribution function of gas particle, τ is the local relaxation parameter which is determined by τ=μ/p with the gas pressure p and dynamic viscosity μ. The local equilibrium Maxwellian distribution \(g\left (\vec {x},t,\vec {v}\right)\) has the form
with density ρ, velocity \(\vec {U}\), temperature T, Boltzmann constant kB, molecular mass m. For the study of micro flow, assume that the unperturbed velocity \(\vec {U}_{0}=0\), and the following dimensionless is used,
where the reference density ρ0 and temperature T0 are the unperturbed density and temperature, the reference velocity is the most probable speed \(\left |\vec {U}_{ref}\right |=\sqrt {2k_{B}T_{0}/m}\). The distribution function \(\tilde {f}\left (\vec {x},t,\tilde {\vec {v}}\right)\) can be linearized with respect to the small perturbation δ [30],
where the small perturbation δ can be a small pressure gradient, small temperature difference, small external force, etc. The linearized moments can be obtained by taking moments to the above distribution function,
where
The linearized BGK equation can be written as
where the linearized equilibrium distribution function \(\tilde {g}_{\delta } \) is
In this paper, the variable hard sphere model of argon gas is considered, and the dimensionless dynamic viscosity coefficient is related to the Knudsen number as
where the parameter α=1.0, ω=0.72, and the Knudsen number defined as Kn=λ/L0, which is the dimensionless form of particle mean free path λ. According to the asymptotic analysis, the relaxation time \(\tilde {\tau }\) is related to the dynamic viscosity \(\tilde {\mu }\) as \(\tilde {\tau }=\tilde {\mu }/\tilde {p}\) [4]. For a small perturbed flow with a small variation of pressure, the asymptotic behavior as \(\tilde {\tau }\to 0\) is the same as the asymptotic behavior as Kn→0. For the sake of simple notation, the tilde and subscript δ is omitted in the rest of this paper, and no confusion will be caused.
Analogy to the Chapman-Enskog theory, the linearized hydrodynamic equations can be derived from the above linearized kinetic equation in continuum regime [1, 2]. We perform asymptotic analysis to Eq. (7) with respect to τ, and the distribution function can be expanded as
and correspondingly the time derivative is also expanded as
where \(\partial _{t_{k}}\) stands for the contribution to ∂t from the spatial gradients of the (k+1)−th order hydrodynamic variables. Substitute the expansion of the distribution function (10) and time derivative (11) into the linearized kinetic Eq. (7), and the following hierarchy can be obtained
where \(D_{0}=\partial _{t_{0}}+\vec {v}\cdot \nabla \). The conservative constraint of collision operator gives
where \(\psi =\left (1,\vec {v},\vec {v}^{2}/2\right)\) is the collision invariants. Consider the two dimensional case, the second order hierarchy gives the linearized Euler equations
where U, V are the macroscopic x-directional velocity and y-directional velocity. The second and third order hierarchies give the linearized Navier-Stokes equations
where the viscous coefficient \(\mu =\frac {\tau }{2}\), heat conduction coefficient \(\kappa =\frac {5\tau }{8}\), and the Prandtl number is \(\frac {c_{p}\mu }{\kappa }=1\).
2.2 Unified gas-kinetic scheme
Consider two dimensional flow, the following reduced distribution functions are introduced to reduce the computational cost,
The moments of the reduced distribution function are
The reduced distribution functions follow the kinetic equations
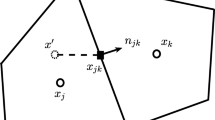
where \(g_{h}=\rho +2\vec {v}\cdot \vec {U}+T\left (\vec {v}^{2}-1\right)\) and \(g_{b}=\frac 12T\) are the reduced equilibrium distribution function. The finite volume evolution equation of UGKS is obtained by integrating Eq. (22) with respect to space and time. Consider space control volume Ωi and velocity control volume Ωj, and the cell averaged quantities are defined as
where Ωij=Ωi⊗Ωj is the control volume in the phase space. The UGKS evolution equations of the distribution functions are
which are coupled with the evolution equations of the macroscopic conservative variables.
Assume that tn=0, the center of cell interface \(\vec {x}_{\partial \Omega _{j}}=0\), the projection of velocity on the outer normal vector \(\vec {n}_{\partial \Omega _{j}}\) is u, and the UGKS multiscale numerical flux is
where \(\vec {\psi }=\left (1,\vec {v},\frac 12\vec {v}^{2}\right)\) is the conservative moments. The key ingredient of UGKS is the use of integral solution \(f\left (0,t,\vec {v}\right)\) in the construction of numerical flux,
where \(f_{0}\left (\vec {x},\vec {v}\right)\) is the initial distribution at t=0, and
where H[x] is the Heaviside function, and the least squares method is used for spatial reconstruction. The time derivative is approximated by the first order Chapman-Enskog expansion,
Substitute the integral solution Eq. (27) into the numerical flux Eq. (26), and we have
and
where the time integration coefficients are
The evolution equations Eqs. (24),(25) and multiscale fluxes (30),(31) close the UGKS formulation. In the next section we are going to analyse the unified preserving property of UGKS.
3 Unified preserving property of UGKS
The concept of unified preserving (UP) property was proposed by Guo, et al. to measure capability of the schemes in capturing the multiscale flow physics [1]. The definition of UP is for a consistent numerical scheme of the kinetic Eq. (1), if the scheme satisfies:
-
1.
it is uniformly stable for all Knudsen number;
-
2.
for τ≪1, two parameters α,β∈(0,1) exist, such that as Δt=O(τα), Δx=O(τβ), the asymptotic expansion of the numerical scheme is identical to the Chapman-Enskog expansion of the kinetic equation up to the order of n;
Then the scheme is called a n-th order UP scheme. In this section, we are going to prove that the UGKS is a second order UP scheme with α=β=1/2.
Theorem 1.
Consider a UGKS with spatial and temporal accuracy on the order of 2 or higher. If Δt≤O(τ1/2) and Δx≤O(τ1/2), the Chapman-Enskog expansion coefficients of f obtained from the UGKS satisfy
for n=2, if the relaxation time τ is a constant.
Proof Without loss of generality, consider the one dimensional case. The numerical flux of UGKS at cell interface xi−1/2 can be written as
For 0≤Δt≤τ, 0≤Δx≤τ namely Δt=τα with α>1, Δx=τβ with β>1. The coefficients c1−5 can be expanded up to \(\left (\frac {\Delta t}{\tau }\right)^{2}=O\left (\tau ^{2\alpha -2}\right)\) as
and therefore, we have
where \(\mathcal {L}\) notates for a generalized linearized operator, and Q=(g−f)/τ is the collision operator. We can obtain the modified equation of UGKS as
The underbraced term \(\mathcal {A}\) can be estimated as
which gives
and the modified UGKS equation can be written as
As shown in Fig. 2, the first three order terms in \(\mathcal {L}_{0}\) and the first order term in \(\mathcal {L}_{1}\) need to be included in the calculation of the first three asymptotic expansions of the modified equation. And the Chapman-Enskog hierarchy can be obtained as following
Order sequence of the modified Eq. 40. L0 axis shows the order sequence of the top three order terms in \(\mathcal {L}_{0}\), L1 axis shows the order sequence of the top three order terms in \(\mathcal {L}_{1}\). Terms that have a higher order than τ need to be included in the calculation of the first three asymptotic expansions of the modified equation
For τ<Δt≤τ0.5, τ<Δx≤τ0.5 namely Δt=τα with 0.5≤α<1, Δx=τβ with 0.5≤β<1. The coefficients c1−5 can be estimated as
and we can obtain the modified equation of UGKS as
where
As shown in Fig.3, the first three order terms in \(\mathcal {L}_{0}\), the first two order terms in \(\mathcal {L}_{1,2}\), and the first order term in \(\mathcal {L}_{3}\) need to be included in the calculation of the first three asymptotic expansions of the modified equation. After some calculations, one can get the Chapman-Enskog hierarchy as following
Order sequence of the modified Eq. 43. L0 axis shows the order sequence of the top three order terms in \(\mathcal {L}_{0}\), L1 axis shows the order sequence of the top three order terms in \(\mathcal {L}_{1}\), L2 axis shows the order sequence of the top three order terms in \(\mathcal {L}_{2}\), L3 axis shows the order sequence of the top three order terms in \(\mathcal {L}_{3}\). Terms that have a higher order than τ need to be included in the calculation of the first three asymptotic expansions of the modified equation
Based on the above analysis, it is shown that for Δt≤O(τ1/2) and Δx≤O(τ1/2), the UGKS exactly preserves the second order Chapman-Enskog expansion. Therefore the UGKS is a second order unified preserving scheme.
Note that Theorem 1 holds for both linear and nonlinear UGKS. The conventional way to analyze the multiscale property of UGKS is to perform discrete asymptotic analysis to the discrete governing equations of UGKS, and then compare the discrete asymptotic analysis to the continuous Chapman-Enskog solution, which has been done by Liu et al. [31]. As shown in Fig. 4, the conventional analysis and current UP analysis are equivalent, and both show that the UGKS preserves the NS solution in bulk flow region in continuum regime even when the cell size and time step are much larger than the kinetic particle mean free path and collision time.
4 Numerical tests
We perform six numerical tests to verify the accuracy and multiscale property of UGKS, including two 1D test cases and four 2D test cases. The Knudsen number of the numerical tests varies from 10 to 10−4, covering the flow regime from highly rarefied to Navier-Stokes regimes. It can be observed from the comparison that the UGKS well captures the kinetic solution in rarefied regime, and is able to capture NS solution with cell size being much larger than the particle mean free path.
4.1 Poiseuille flow
The first test case is the one dimensional poiseuille flow. The argon gas is confined between two isothermal walls located at x=0 and x=1. The y-directional external force \(\vec {F}=F_{\delta } \vec {y}\) is small, and all flow quantities are expanded with respect to the small force Fδ. Two cases with different Knudsen numbers are calculated. For the first test case, the Knudsen number is 1.0, the physical space is divided into 40 equally distributed cells and the velocity space [−5,5] is divided into 32 equally distributed velocity points. The second case is in the continuum regime with Knudsen number 10−4, and a 4th order spatial reconstruction is used in physical space with 20 equally distributed cells, and in velocity space 8 Gauss-Hermite quadrature points is used. Specifically, the 4th order spatial reconstruction interpolates the cell interface value fi+1/2 from its 4 neighbour cells fi−1,fi,fi+1,fi+2. The point value is interpolated as
and the spatial derivative is interpolated as
The convergence criterion for both cases is Res<10−7, with \(\text {Res}=\max \left (\vec {W}^{n+1}-\vec {W}^{n}\right)/\Delta t\). The UGKS solution is compared with the kinetic reference solution in rarefied regime and analytic NS solution in the continuum regime. As shown in Fig. 5, the UGKS solution well agrees with the reference solution. For the Knudsen number 10−4 case, the time step is about 400 times of the relaxation time, and in such a case, the traditional upwind flux based DVM solution significantly deviates from the analytical one due to large numerical dissipation [32]. However, the integral solution based multiscale flux of UGKS accurately recovers the NS dynamics.
4.2 Couette flow
The Couette flow is a steady flow driven by the surface shear stresses of two infinite parallel plates moving oppositely along their own planes. The two plates locate at y=−h/2 and y=h/2, and the Knudsen number is defined as Kn=λ/h. Three Knudsen numbers \(0.2/\sqrt {\pi }\), \(2/\sqrt {\pi }\), and \(0.2/\sqrt {\pi }\) are used to calculate the solutions in the transitional regime in order to demonstrate the capability of UGKS in capturing the physical structure of Knudsen layer. The molecular model used is the VHS model Eq. (9), with parameter α=1.0, ω=0.72, recovering the argon gas with viscosity coefficient 2.117×10−5 Pa·s. The physical space is divided into 30 cells, and 64×64 velocity grids are used to cover [−3,3]×[−3,3] velocity space, and the computational time is 40 seconds to obtain a converged solution. We compare the UGKS solution with the linearized Boltzmann solution by Sone, et al. [33] and NS solution with slip boundary condition. It can be observed in Fig. 6 that the UGKS can capture the non-equilibrium structure of the gas flow that locates within several mean free paths close to a wall boundary.
Couette flow velocity profile in the upper half channel with Knudsen number \(\text {Kn}_{s}=0.2/\sqrt {\pi }\), \(\text {Kn}_{m}=2/\sqrt {\pi }\), \(\text {Kn}_{l}=20/\sqrt {\pi }\). UGKS solution is shown in symbol, the linear Boltzmann solution is shown in solid line, and the NS solution with slip boundary condition is shown in dashed line
4.3 Micro flow through periodic square cylinders
In the second test case, we simulate the micro flow through porous media, with a similar numerical set up as Wu et al. [34]. We study a pressure gradient driven flow passing through an array of square cylinders. One replicated square is picked as our computational domain. Periodic boundary condition is used for the computational domain boundary, and the solid boundary with accommodation α=1 is used for the cylinder boundary. Two types of solid squares are considered, namely a solid square and a caved square. For the solid square case, three Knudsen numbers Kn=10−1,10−2,10−4 are calculated. The size of spatial cell is Δx=1/120. For Kn=10−1,10−2 the velocity space [−5,5]×[−5,5] is equally divided into 32×32 points, and for Kn=10−4, the 8×8 Gauss-Hermite quadrature is used in the velocity space. Our code is operated on one i7-8700K CPU. The computational time for Kn=10−4 is 5 minutes, and the computational times for Kn=10−2 and Kn=10−1 are 20 minutes and 25 minutes respectively. For this test case, the explicit scheme is used, and the computational efficiency can be improved by 2-3 magnitudes by implementing the LU-SGS and multigrid iteration technique [35]. The UGKS results are shown in Figs. 7 to 9. For the Kn=10−4 case, the numerical cell size is 83 times of the particle mean free path. We compare the streamline and the velocity profile along y=0.25 of UGKS and NS solution as shown in Figs. 8 and 9. It can be observed that the NS solutions are well captured even with a cell size much larger than the kinetic length scale. Similar to the solid square, for the caved square case, three Knudsen numbers Kn=10−1,10−2,10−4 are calculated and the results are shown in Figs. 10 to 12. In continuum regime, the UGKS well agrees with NS solution as shown in Figs. 11 to 12. The computational time for Kn=10−4 is 6 minutes, and the computational times for Kn=10−2 and Kn=10−1 are 24 minutes and 30 minutes respectively.
4.4 Thermal creep micro flow
In the third test case, we study the micro flow driven by a small temperature gradient. Consider a 1.0×0.25 rectangular cavity. The temperature of the left and right wall is Tl=0 and Tr=1.0. The temperature distribution of the top and bottom wall is Tt,b=x. We consider two flow regimes with Kn=10 and Kn=10−2. The spatial cell size is set as Δx=1/120. For Kn=10−2, the velocity space [−5,5]×[−5,5] is equally divided into 64×64 points. For Kn=10, a 90×90 nonuniform distributed velocity space is applied, where the velocity point distribution is
where
with a1=5.56×10−3 and q=1.1. Similar to the nonlinear case [36], counterclockwise and clockwise streamlines are formed on the top and bottom regions of the cavity for the rarefied case, while a reversed streamline is formed in the continuum regime, as shown in Fig. 13. We also compare the UGKS solution to the NS solution with slip boundary condition in Fig. 14. It can be observed that the UGKS solution agrees well with NS solution for density, velocity and temperature distribution. The thermal creep phenomenon in a NS system is caused due to the slip boundary condition. The explicit scheme computational time is 23 minutes for Kn=10−2 and 180 minutes for Kn=10 to reach a residue of 10−7.
4.5 Flow induced by a hot microbeam
We study the flow induced by a hot microbeam in the transitional flow regime. The numerical setup is the same as Zhu, et al. [21]. A cavity with isothermal boundary is located at [0,10]×[0,8], inside which a hot microbeam is located at [1,5]×[1,3]. The temperature of the cavity boundary is T=0 and the temperature of the microbeam boundary is T=1. The transitional flow regime with Knudsen number Kn=5×10−3 is simulated, and the 8×8 Gauss-Hermite quadrature is used for velocity space. After reaching the steady state, two thermal gradient induced vertexes will be formed at each corner of the microbeam. Two sets of meshes have been used for UGKS calculation, a uniform mesh with Δx=0.1λ, and a nonuniform mesh with boundary cell size Δx=0.5λ. The cell size near boundary is set to be less than the mean free path λ to resolve the physical structure of Knudsen layer. The linearized UGKS is implemented on the uniform mesh and the nonlinear UGKS is implemented on the nonuniform mesh. The multigrid LU-SGS iteration technique is used and a convergence solution can be obtained within 10 hours with a convergence criterion 10−7. The velocity magnitude and temperature distribution of UGKS are shown in Fig. 15, and the streamline and heat flux are shown in Fig. 16. We compare the x-velocity profile along x=0.5 and y-velocity profile along y=0.5 to the general synthetic iteration scheme (GSIS) proposed by Wu et al. [27, 28]. As shown in Fig. 17, the results of UGKS agree well with the GSIS results.
4.6 Lid-driven cavity flow
The last test case is the simulation of the lid-driven cavity flow. The cavity is located at [0,1]×[0,1], and the top lid is moving towards positive x direction with a small velocity \(\vec {U}=U_{\delta }\vec {x}\). Two Knudsen numbers are considered, namely Kn=10−1 and Kn=10−4. The spatial cell size for both cases is Δx=0.01, and the velocity space for Kn=10−1 is [−5,5]×[−5,5] divided by 32×32 velocity points, and 8×8 Gauss-Hermite quadrature is used for Kn=10−4 case. The results of UGKS are compared to NS solution as shown in Figs. 18, 19, 20 and 21. For the rarefied case, it can be observed that the NS equations break down, especially for the heat flux calculation. The special heat transfer from cold to hot region is not captured by NS solution, while the velocity profile doesn’t deviate that far. In the continuum regime, the UGKS recovers the NS solution. Especially for the velocity field, the UGKS and NS solutions are identical, even with the UGKS cell size being 100 times larger than the particle mean free path. For this test case, the linearized UGKS is about 2.5 times faster than the nonlinear UGKS under the same cell size and velocity points, while the flux calculation of linearized UGKS is about 3.5 times faster than nonlinear UGKS.
5 Conclusion
In this paper, we extend the UGKS to the micro flow simulation. In comparison with the nonlinear UGKS, the linearized UGKS is faster and more accurate for the micro flow simulation. The multiscale property of UGKS is inherited by the linearized UGKS. In the rarefied regime, the linearized UGKS well captures the solution of linear kinetic equation. In the continuum regime, the viscous solution can be accurately captured by UGKS even with cell size and time step being much larger than the particle mean free path and collision time. Theoretically, we prove the unified preserving property of UGKS, which shows that UGKS is a second order UP scheme. The proof holds for both the linearized UGKS and nonlinear UGKS. In term of flux calculation, the linearized UGKS is more than three times faster than the nonlinear UGKS. Combining the linearized UGKS and implicit technique, such as LU-SGS and multigrid [37, 38], the UGKS will be a powerful numerical tool for the study of micro flow in the fields of porous media and MEMS.
Availability of data and materials
All data and materials are available upon request.
References
Guo Z, Li J, Xu K (2019) On unified preserving properties of kinetic schemes. arXiv preprint arXiv:1909.04923.
Chapman S, Cowling TG, Burnett D (1990) The mathematical theory of non-uniform gases: an account of the kinetic theory of viscosity, thermal conduction and diffusion in gases. Cambridge university press.
Cercignani C (1969) Mathematical methods in kinetic theory. Springer.
Xu K, Huang J-C (2010) A unified gas-kinetic scheme for continuum and rarefied flows. J Comput Phys 229(20):7747–7764.
Guo Z, Xu K, Wang R (2013) Discrete unified gas kinetic scheme for all Knudsen number flows: Low-speed isothermal case. Phys Rev E 88(3):033305.
Su W, Zhu L, Wang P, Zhang Y, Wu L (2020) Can we find steady-state solutions to multiscale rarefied gas flows within dozens of iterations?J Comput Phys 407:109245.
Yuan R, Liu S, Zhong C (2020) A multi-prediction implicit scheme for steady state solutions of gas flow in all flow regimes. Commun Nonlinear Sci:105470.
Jenny P, Torrilhon M, Heinz S (2010) A solution algorithm for the fluid dynamic equations based on a stochastic model for molecular motion. J Comput Phys 229(4):1077–1098.
Fei F, Zhang J, Li J, Liu Z (2020) A unified stochastic particle Bhatnagar-Gross-Krook method for multiscale gas flows. J Comput Phys 400:108972.
Xu K (2015) Direct modeling for computational fluid dynamics: construction and application of unified gas-kinetic schemes. World Scientific.
Sun W, Jiang S, Xu K, Li S (2015) An asymptotic preserving unified gas kinetic scheme for frequency-dependent radiative transfer equations. J Comput Phys 302:222–238.
Sun W, Jiang S, Xu K (2017) A multidimensional unified gas-kinetic scheme for radiative transfer equations on unstructured mesh. J Comput Phys 351:455–472.
Sun W, Jiang S, Xu K (2018) An asymptotic preserving implicit unified gas kinetic scheme for frequency-dependent radiative transfer equations. Int J Numer Anal Model 15:134–153.
Li W, Liu C, Zhu Y, Zhang J, Xu K (2020) Unified gas-kinetic wave-particle methods III: Multiscale photon transport. J Comput Phys 408:109280.
Shuang T, Wenjun S, Junxia W, Guoxi N (2019) A parallel unified gas kinetic scheme for three-dimensional multi-group neutron transport. J Comput Phys 391:37–58.
Liu C, Xu K (2017) A unified gas kinetic scheme for continuum and rarefied flows V: Multiscale and multi-component plasma transport. Commun Comput Phys 22(5):1175–1223.
Liu C, Wang Z, Xu K (2019) A unified gas-kinetic scheme for continuum and rarefied flows VI: Dilute disperse gas-particle multiphase system. J Comput Phys 386:264–295.
Liu C, Zhu Y, Xu K (2020) Unified gas-kinetic wave-particle methods I: Continuum and rarefied gas flow. J Comput Phys 401:108977.
Crestetto A, Crouseilles N, Dimarco G, Lemou M (2019) Asymptotically complexity diminishing schemes (ACDS) for kinetic equations in the diffusive scaling. J Comput Phys 394:243–262.
Guo Z, Wang R, Xu K (2015) Discrete unified gas kinetic scheme for all Knudsen number flows. II. thermal compressible case. Phys Rev E 91(3):033313.
Zhu L, Guo Z (2019) Application of discrete unified gas kinetic scheme to thermally induced nonequilibrium flows. Comput Fluids 193:103613.
Wang P, Su W, Zhang Y (2018) Oscillatory rarefied gas flow inside a three dimensional rectangular cavity. Phys Fluids 30(10):102002.
Zhang Y, Zhu L, Wang R, Guo Z (2018) Discrete unified gas kinetic scheme for all Knudsen number flows. III. Binary gas mixtures of Maxwell molecules. Phys Rev E 97(5):053306.
Tao S, Zhang H, Guo Z, Wang L-P (2018) A combined immersed boundary and discrete unified gas kinetic scheme for particle–fluid flows. J Comput Phys 375:498–518.
Zhang C, Guo Z, Chen S (2017) Unified implicit kinetic scheme for steady multiscale heat transfer based on the phonon Boltzmann transport equation. Phys Rev E 96(6):063311.
Luo X-P, Wang C-H, Zhang Y, Yi H-L, Tan H-P (2018) Multiscale solutions of radiative heat transfer by the discrete unified gas kinetic scheme. Phys Rev E 97(6):063302.
Su W, Zhu L, Wu L (2020) Fast convergence and asymptotic preserving of the General Synthetic Iterative Scheme. arXiv preprint arXiv:2003.09958.
Zhu L, Pi X, Su W, Li Z-H, Zhang Y, Wu L (2020) General synthetic iteration scheme for non-linear gas kinetic simulation of multi-scale rarefied gas flows. arXiv preprint arXiv:2004.10530.
Bhatnagar PL, Gross EP, Krook M (1954) A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component systems. Phys Rev 94(3):511–525.
Sharipov F, Graur IA (2012) Rarefied gas flow through a zigzag channel. Vacuum 86(11):1778–1782.
Liu C, Xu K, Sun Q, Cai Q (2016) A unified gas-kinetic scheme for continuum and rarefied flows IV: Full Boltzmann and model equations. J Comput Phys 314:305–340.
Chen S, Xu K (2015) A comparative study of an asymptotic preserving scheme and unified gas-kinetic scheme in continuum flow limit. J Comput Phys 288:52–65.
Sone Y, Takata S, Ohwada T (1990) Numerical analysis of the plane Couette flow of a rarefied gas on the basis of the linearized Boltzmann equation for hard-sphere molecules. EJMF 9(3):273–288.
Wu L, Ho MT, Germanou L, Gu X-J, Liu C, Xu K, Zhang Y (2017) On the apparent permeability of porous media in rarefied gas flows. J Fluid Mech 822:398–417.
Zhu Y, Zhong C, Xu K (2017) Unified gas-kinetic scheme with multigrid convergence for rarefied flow study. Phys Fluids 29(9):096102.
Huang J-C, Xu K, Yu P (2013) A unified gas-kinetic scheme for continuum and rarefied flows III: Microflow simulations. Commun Comput Phys 14(5):1147–1173.
Zhu Y, Zhong C, Xu K (2016) Implicit unified gas-kinetic scheme for steady state solutions in all flow regimes. J Comput Phys 315:16–38.
Zhu Y, Zhong C, Xu K (2017) Unified gas-kinetic scheme with multigrid convergence for rarefied flow study. Phys Fluids 29(9):096102.
Acknowledgements
The authors would like to thank Dr. Yajun Zhu for his advice on the construction of implicit scheme, as well as providing the nonlinear UGKS results. The authors would also like to thank Professor Lei Wu and Dr Wei Su for fruitful discussions and sharing the GSIS data. Specially thanks goes to Professor Zhaoli Guo for the discussion and professional advice on the unified preserving property.
Funding
The current research is supported by Hong Kong research grant council (16206617) and National Science Foundation of China (11772281, 91852114), and the National Numerical Windtunnel project.
Author information
Authors and Affiliations
Contributions
Our group has been working on the topic for a long time. The research output is coming from our joint effort. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Liu, C., Xu, K. A unified gas-kinetic scheme for micro flow simulation based on linearized kinetic equation. Adv. Aerodyn. 2, 21 (2020). https://doi.org/10.1186/s42774-020-00045-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s42774-020-00045-8