Introduction

Expiratory time constant (τ) is an important, yet not widely used parameter providing information about the mechanical properties of the respiratory system. Although not routinely used in clinical practice, τ can be used to optimize mechanical ventilation by predicting time for complete exhalation, optimizing the respiratory rate, calculating common inspiratory variables without end-expiratory pause or assessing the response to bronchodilators [1,2,3]. Further, it has been integrated into complex algorithms of supported modes of ventilation to achieve optimal targeting schemes, such as adaptive support ventilation and adaptive mechanical ventilation [4, 5].

Commonly studied parameters of lung mechanics, such as respiratory system compliance (CRS), resistance (RRS), driving pressure (dP) or plateau pressure (PPLAT), are routinely obtained during inspiration. However, such parameters are influenced by ventilator settings (i.e., inspiratory flow, pressure, tidal volume [VT], and inspiratory time). Exhalation, on the other hand, is usually passive and therefore expiratory variables, such as τ, provide a more independent measure of lung mechanics compared to inspiratory parameters.

τ has been traditionally defined as the product of CRS and RRS in a single compartment lung model during passive deflation [6, 7]. However, it is better defined as the amount of time that an exponentially decaying quantity takes to decay by a factor of 1/e, where the first τ represents 63% of exhaled VT, 2τ 86%, 3τ 95%, 4τ 98% and 5τ represent 99% of the exhaled VT etc. Accordingly, all time constants should be of equal duration in an exponentially decaying flow [8].

Several authors have studied τ in heterogenous patient populations using different methodologies [7,8,9,10,11,12,13]. For example, calculated τ may adopt either dynamic or static CRS and inspiratory or expiratory airway resistance. On the other hand, some authors do not use quasi-static variables and rely on direct measurements of τ from the expiratory flow curve [10, 13]. Therefore, different formulations are often used interchangeably in clinical practice and may be a source of imprecision when interpreting results.

Comparisons of these different methods of τ determination had not been performed. Therefore, the aim of this prospective observational study was to compare measured τ from the expiratory flow waveform (i.e., representing the gold standard), with five alternative methods of τ calculation under variable flow and constant flow ventilation (i.e., pressure-controlled ventilation [PCV] and in volume-controlled ventilation [VCV]) in routine clinical care of patients following cardiac surgery. This study tested whether lung emptying can be accurately described (and also predicted) by a single τ value (i.e., explored whether the time constant can be used to characterize the exponentially decaying flow during passive exhalation). Comparison of the six methods of τ determination would enable identifying the most reliable approach for assessing τ at the bedside and making more informed decisions on setting mechanical ventilation parameters based on τ.

Materials and methods

Study design and participants

This prospective observational study was performed in a tertiary referral university hospital (East Slovak Institute for Cardiovascular Diseases, Kosice, Slovakia) from December 2022 to February 2023 and conforms to the relevant STROBE reporting guidelines. The institutional ethics committee approved the study (IEC N.A3112022) and informed consent was obtained from all patients prior to enrollment. The study was retrospectively registered at ClinicalTrials.gov (NCT05827640). Institutional ethics committee also confirms that all methods and experimental protocols were carried out in accordance with relevant guidelines and regulations.

Thirty adult patients undergoing elective cardiac surgery with extracorporeal circulation were included. Patients were excluded from the study if they had any known lung disease or previous thoracic surgery. After surgery, all patients were transferred to the intensive care unit (ICU) and supported with mechanical ventilation (Servo-U, Maquet, Getinge AB, Solna, Sweden).

Mechanical ventilation parameters and data acquisition

First, the ventilation mode was set to mandatory VCV for 15 min. Next, mandatory PCV was set for another 15 min. All patients were in the supine position, sedated and paralyzed using continuous infusion of propofol and atracurium with no spontaneous breathing efforts. During VCV, an end-inspiratory pause (TPAUSE 10%) had been added to obtain inspiratory PPLAT under static conditions. ARDSNet tables were used to determine predicted body weight (PBW) for all patients [14].

Respiratory variables in VCV for all patients were set as follows: positive end-expiratory pressure (PEEP) of 6–9 cmH2O depending on the local protocol, protective VT of 7 mL/kg PBW, TPAUSE as 10%, I:E ratio of 1:2, rise time 5% and the respiratory rate of 14 breaths/min. After 15 min, VCV was changed to PCV with the same ventilator settings and inspiratory pressure was set in a way to best match the VT during VCV.

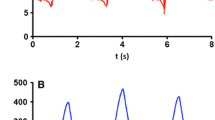
Pressure, flow, and volume data were recorded at 20 ms sampling rate after admission to the ICU using a data acquisition device (DR WAVE®, Quadrus Medical Technologies, NY, USA) connected to the Servo-U ventilator using Servo-U flow sensor. All results in the study were derived from waveforms recorded by the device and extracted measurements and calculations included: peak inspiratory pressure (PIP), PPLAT, PEEP, exhaled VT, inspiratory airway resistance (RI), expiratory airway resistance (RE), CRS, peak inspiratory flow, peak expiratory flow rate (PEFR), and expiratory flow at 50% and 75% of the exhaled VT as appropriate. Data were visualized and analyzed using Matlab® R2021b. An example of the pressure and flow waveforms for a single breath in PCV and VCV is depicted in Fig. 1.

Fig. 1
figure 1

Pressure and flow waveforms during A pressure-controlled ventilation (PCV) and B volume-controlled ventilation (VCV). Measurements extracted from the waveforms and used in calculations of the expiratory time constant (τ) are highlighted. EOE end of exhalation (0.04 L/s), PEEP positive end-expiratory pressure, PEFR peak expiratory flow rate, PIP peak inspiratory pressure, PPLAT plateau pressure, VTe exhaled tidal volume

Full size image

Methods of τ calculation and measurement

Six different methods were used to evaluate the expiratory τ. We have defined the start of exhalation (SOE) using the breath phase flag from the Servo-U ventilator, which corresponded to the first zero-flow crossing, and the end of exhalation (EOE) as the first time when the expiratory flow decreased to 0.04 L/s from PEFR, which also reduced the signal noise and artifacts caused by cardiac oscillations [13].

Exhaled VT was used in all formulae. Expiratory flows were treated as positive values throughout. τ was measured, calculated or derived from expiratory flow curves as follows:

1. Measured τ was derived from the expiratory flow waveform [1, 9]. Flow was integrated from SOE to EOE using the trapezoidal rule to obtain volume expired in time. A mathematical algorithm was created to measure time from SOE until 63% of the exhaled VT was reached (τ1). Similarly, to obtain the second τ (τ2) and the third τ (τ3), the time durations from 63 to 86% of the exhaled VT and from 86 to 95% of the exhaled VT were measured, respectively.

2. Calculated τ as the product of compliance and resistance [7]. Compliance and RE were calculated using the respective formulas for PCV and VCV. RE was calculated as proposed by Jonson [8]:

$$\tau ={R}_{E}\cdot {C}_{RS}$$

For PCV: \({R}_{E}=\frac{PIP- PEEP}{PEFR}\),\({C}_{DYN}=\frac{{V}_{T}}{PIP-PEEP}\)

For VCV: \({R}_{E}=\frac{{P}_{PLAT} -PEEP}{PEFR}\),\({C}_{STAT}=\frac{{V}_{T}}{{P}_{PLAT}-PEEP}\) where CSTAT is static compliance and CDYN is dynamic compliance, and PEFR is peak expiratory flow rate.

3. \(\tau\) calculated with the Aerts formula [10].

\(\tau =\frac{{0.5 \cdot V}_{T}}{{\dot{V}}_{50}- {\dot{V}}_{end-exp}}\), where \({\dot{V}}_{50}\) is expiratory flow at 50% of expired VT and \({\dot{V}}_{end-exp}\) expiratory flow at end-expiration.

4. \(\tau\) calculated with the Brunner formula [11].

$$\tau =\frac{{V}_{T}}{PEFR}$$

5. \(\tau\) calculated with the Guttmann formula [12]. The expiratory volume versus flow curve was divided into five equal volume slices from the maximum slope in the expiratory flow curve following the PEFR, to the end of exhalation (Fig. 2). τ was calculated for each slice of the volume versus flow curve using the least squares fitting method. Final τ was then obtained as the average of the τ from all five slices.

Fig. 2
figure 2

Guttmann’s method for determining the expiratory time constant (τ) in A pressure-controlled ventilation (PCV) and B volume-controlled ventilation (VCV)

Full size image

6. \(\tau\) calculated with the Lourens formula [13].

\(\tau =\frac{{0.75 \cdot V}_{T}}{{\dot{V}}_{75}- {\dot{V}}_{end-exp}}\), where \({\dot{V}}_{75}\) is expiratory flow at 75% of the exhaled VT (i.e., 25% expired volume, or 75% of the volume remaining to be exhaled), \({\dot{V}}_{end-exp}\) is expiratory flow at end expiration.

The details of τ determination as per each method are also shown graphically in Figs. 1, 2, 3.

Fig. 3
figure 3

Flow waveform during A pressure-controlled ventilation (PCV) and B volume-controlled ventilation (VCV) highlighting points used in different methods to obtain the expiratory time constant (τ). EOE end of exhalation, Meas. measured, VTe exhaled tidal volume

Full size image

The τ by each method was computed for each patient-breath and averaged over all PCV or VCV breaths. The mean τ was then taken across all patients. Measured τ was taken as the reference for comparison with each of the other five methods.

Outcomes and definitions

The primary outcome of this study was to compare the differences between measured τ1 and five different methods of calculating τ in passive, mechanically ventilated patients under variable flow (PCV) and constant flow (VCV) conditions.

The secondary outcomes were: (1) comparison of the τ between PCV and VCV for each method of τ determination; (2) comparison of the predicted time to exhale 95% of the expired VT using the first measured τ multiplied by 3 (i.e., 95% of the exhaled VT = 3*τ1) with the measured time to exhale 95% of the VT; (3) comparing the duration of the first, the second and the third measured τ (i.e., τ1, τ2, and τ3, respectively), as per exponentially decaying τ equation.

Statistical analysis

Categorical data are expressed as n (%), continuous data are expressed as mean or median with 95% confidence intervals (95% CI). The distributions were tested for normality using Kolmogorov–Smirnov test and for skewness and kurtosis. Comparison of the six τ means over all breaths and patients was performed using one-way ANOVA. Here, each method of τ determination was considered independent, as the statistical tests are more robust in this case (i.e., larger differences between means are needed when compared with repeated measures t-tests for the same level of statistical significance). If significant, then Dunnett’s post hoc test was used to compare each of the five methods of τ determination with the measured τ as the reference. Student’s t test was used to compare mean τ between PCV and VCV within each method of τ determination. Student’s t test was also used to compare the first measured τ multiplied by 3 with the measured time required to expire 95% of the exhaled VT. In comparing the first, the second, and the third mean measured τ, the Welch’s one-way ANOVA was followed by the Games–Howell post hoc test. P values lower than 0.05 were considered statistically significant. Statistical tests were run using Python 3.11.0 SciPy version 1.10.0 and R (The R-foundation for Statistical Computing, Vienna, Austria), and visualizations were performed using graphical user interface for R (RStudio version 4.3.2).

Results

Thirty patients were included in this prospective observational study. Their median (IQR) age was 65 (62–68) years, BMI was 29 (28–30) kg/m2 and 23 (67%) was male. Other patient characteristics are summarized in Additional file 1: Table S1. The respiratory variables are presented in Table 1. The mean number of recorded breaths per patient was 215 (95% CI 209–221) for PCV mode and 211 (95% CI 203–219) for VCV mode and they were analyzed via six different methods to obtain the τ.

Table 1 Respiratory variables before the beginning of the 15-min ventilation recordings, means with 95%CI are presented
Full size table

Mean values of τ for each method are shown in Table 2 where the τ as determined by each method during PCV versus VCV was compared, with no significant differences between the modes. The comparison of each τ method to the first measured value of τ (τ1) as the "gold standard" was then performed and is presented in Fig. 4 for each ventilation mode. Brunner, Calculated as CRS*RE, and Guttmann τ were all significantly different from the measured τ1 in both ventilation modes (overall ANOVA: p < 0.001, for PCV and p < 0.0001 for VCV). Mean differences between measured τ1 and other 5 methods to determine τ in PCV and VCV for each individual patient are available in the Additional file 2: Table S2 and Additional file 3: Table S3.

Table 2 Six methods to determine the expiratory time constant (τ) in pressure-controlled ventilation (PCV) and volume-controlled ventilation (VCV)
Full size table
Fig. 4
figure 4

Boxplots showing comparison of measured first expiratory time constant (τ1) with each of the other five methods of τ calculation in: A pressure-controlled ventilation (PCV) and B volume-controlled ventilation (VCV). Values are displayed as means, IQRs and 95% confidence intervals (black cursors within the boxplots). Mean of the measured τ1 is represented as the dashed red line. The five methods of τ determination were compared with the measured τ1 as the reference using the Dunnett’s post hoc test, displaying adjusted p values

Full size image

To test the assumption of the time constants’ equalities, the time required to exhale 95% of the expired VT was compared with the first τ multiplied by three (i.e., 95% of the expired VT = 3*τ1). Predicted time to exhale 95% of the expired VT was significantly different from the measured value (p < 0.0001). All methods overestimated the time needed to exhale 95% of the expired VT (Fig. 5).

Fig. 5
figure 5

Measured time to reach the 95% of the exhaled VT (red dotted line) compared with predicted times to reach 95% of the exhaled VT according to each of the six methods of the expiratory time constant (τ) determination (3* τ). The τ as determined by each method was multiplied by 3 in: A pressure-controlled ventilation (PCV) and B volume-controlled ventilation (VCV). Values are displayed as means with 95% confidence intervals

Full size image

The absolute difference between predicted and measured time to exhale 95% VTe was 0.5 s for both ventilation modes (95% CI 0.48–0.52 s, p < 0.0001 for PCV and 0.48– 0.53 s, p < 0.0001 for VCV) (Table 3). The time difference between predicted and measured time to exhale 95% of VTe (0.5 s for both modes) represents 18% of total expiratory phase of respiratory cycle. We found that 2.2*τ1, rather than 3*τ1 are needed to exhale 95% of the VTe.

Table 3 Measured and predicted time for complete exhalation
Full size table

Time constant inequalities

The computer algorithm measured the first τ (τ1), the second τ (τ2), and the third τ (τ3) corresponding to the time needed from 0 to 63%, from 63 to 86% and from 86 to 95% of the exhaled VT, respectively. These three time constants were significantly different from each other (ANOVA; p < 0.0001, for both modes of ventilation) (Table 4).

Table 4 The first, the second, and the third measured expiratory time constants (τ1, τ2, and τ3, respectively) in pressure-controlled ventilation (PCV) and volume-controlled ventilation (VCV)
Full size table

Individual per-patient differences in τ1, τ2, and τ3 for both modes are shown in Additional file 4: Table S4.

Discussion

The main result of this study is that measured τ, as well as the other five methods, reliably determines the expiratory time constant in postoperative patients under constant or variable flow ventilation. Regardless of ventilation mode, τ calculated as the product of RE * CRS, Brunner, and Guttman were all significantly longer than measured τ, while Aerts was shorter. Furthermore, the first, the second, and the third measured τ differ significantly in duration. Predicted values extrapolated from the first τ (3*τ) overestimated measured time to exhale 95% of the VTe in all six methods in both ventilation modes. Moreover, we found that instead of 3*τ1, only 2.2*τ are needed to exhale 95% of VTe.

The expiratory time constant describes ideal lung emptying in a single compartment model with exponentially decreasing flow, where all time constants (equal in duration) are responsible for different volumes of exhaled air. Using the model definition, most authors have proposed to calculate the time constant instead of measuring it [6,7,8]. However, this model oversimplifies lung dynamics, which vary greatly in clinical practice due to complexity of the respiratory system under mechanical ventilation, especially in the presence of diverse underlying lung pathology. With changes in airway resistance during tidal ventilation and the presence of fixed additional resistances (such as the endotracheal tube—ETT), lung emptying is heavily modified compared to the simple one-compartment model. As a result, the time constants (first, second, third, etc.) can hardly be of equal duration. In our study on postoperative patients with generally favorable lung mechanics, we confirmed that the first three time constants do not equal but differ significantly indicating the single compartment model may not best represent passive exhalation in this patient group. Differences between consequent time constants can be even more pronounced in acute respiratory failure with time constant inequalities [15].

Brunner’s, Aerts’, and Lourens’ methods all use ratio of exhaled volume to either PEFR or a two-point difference of the expiratory flow waveform during later stages of exhalation, assuming a linear flow–volume relationship. However, exhalation was later found to be a rather dynamic process in mechanically ventilated patients with changing resistance [16]. Aerts’, as well as Lourens’ formulae, does not consider the early (most dynamic and resistance-dependent) part of exhalation, but only considers the more linear portion, where the single compartment model assumptions could hold and the flow-dependent resistance of the ETT was less important. Despite these physiological differences in the methods, our results show that all methods yield very similar τ in postoperative patients without prior lung disease. Further studies are needed to confirm our findings in ventilated patients with obstructive lung disease.

Lourens et al. also compared calculated τ multiplied by 3 with the measured time to reach complete exhalation as dictated by the 0.04 L/s cutoff of exhaled flow and found that mean calculated τ correlated well with real measured time to reach complete exhalation in chronic obstructive pulmonary disease (COPD) patients. We did not confirm these findings in postoperative patients without expiratory flow limitation, which is the hallmark of patients with severe COPD. This is also supported by significantly shorter τ in our cohort (τ = 0.59 s) versus COPD patients (τ = 2.8 s) [13]. Patients with expiratory flow limitation tend to have more linear decay of expiratory flow. It is therefore probable that Lourens’ method to determine τ may be more appropriate in patients with COPD.

Guttmann et al. proposed to calculate τ for each of five equal volume slices with the least square fitting method and found that consecutive volume portions were exhaled at nearly identical time constants in ARDS patients. Guttmann also found that resistance of the ETT represents the major resistance responsible for longer τ compared to the time constants of the pure respiratory system alone [12]. While Guttmann looks at five discrete windows of exhalation, measured τ differs in that it measures time until a certain volume is exhaled, which implicitly includes the dynamics of the flow. Measured τ were significantly shorter toward the end of exhalation (progressive shortening of subsequent τ), perhaps in part due to negligible resistance of the ETT in the later parts of the flow curve [18, 19].

While τ can also be calculated as a product of CRS and RRS, the resulting τ depends greatly on the type of compliance (CDYN or CSTAT) and resistance (RI or RE) being used in calculations. It was proposed that at least six methods exist to determine RE, producing significantly different results [22]. Therefore, resultant τ will also be different. In this study, we achieved the most consistent results with RE calculation using Jonson formula [22] for both modes of ventilation, where difference in pressure (PPLAT—PEEP in VCV or PIP-PEEP in PCV) was calculated and then divided by PEFR. Interestingly, τ calculated as the product of CRS (using expiratory volume) and RE using Jonson’s formula reduces to Brunner (VTe/PEFR). Hence, these two methods then yield the same results. Mean values for measured and calculated τ in our study differed by around 50 ms in PCV and 60 ms in VCV. Calculating τ reliably usually necessitates obtaining quasi-static variables (i.e., end inspiratory and end expiratory hold), while measuring τ directly does not. Therefore, measuring τ eliminates the need for such maneuvers, while still providing consistent results that are clinically acceptable.

Only one (or the first) τ is measured or calculated in clinical practice and routinely displayed on modern mechanical ventilators. This means that prediction of near-complete exhalation and therefore the respiratory rate is dependent on a single variable. Based on our data, the τ definition is not upheld in postoperative mechanically ventilated patients because the first τ multiplied by 3 does not equal complete exhalation but overestimates it significantly. Despite our findings contradicting the predictions based on exponential decay in flow, τ seems to remain the only variable objectively assessing the speed of exhalation in clinical practice. Significant differences between measured, calculated, or derived τ found in this study may be of clinical importance to properly set the respiratory rate [1]. This is likely clinically negligible in healthy lungs or at low respiratory rates, but may become significant with high respiratory rates needed to maintain adequate gas exchange. In the era of protective low tidal volume, high respiratory rates are often needed. Therefore, a correction factor is probably required if the first measured τ is used to predict the respiratory rate because we found the first τ to be the longest, while the second and the third τ are progressively shorter.

This physiologic study has several limitations. The main limitation is the patient selection. We have studied the τ in passive patients following cardiac surgery without known previous lung disease. Therefore, the extrapolation of our findings to other groups of patients with lung disease might not be appropriate. It is imperative that further studies on τ focus on patients presenting with restrictive and obstructive exhalation patterns. To best reflect routine clinical care at the bedside, PPLAT was determined using only brief end-expiratory pause (i.e., TPAUSE = 10%). By study design, we decided to average τ in all 200 breaths and therefore proper end inspiratory pause (i.e., 4 s) that is conventionally used to reliably determine PPLAT could not be applied for each breath. It can therefore be assumed that calculated time constants using CRS may have been slightly different if longer end-inspiratory pause was used. Similarly, equations to determine CDYN and RE in PCV provide only a rough estimation of pulmonary mechanics. Nonetheless, calculated τ in both ventilation modes are in good agreement with the other five methods.

To conclude, although differences between measured and calculated/derived τ were found, all six methods seem to reliably determine τ in postoperative patients under constant and variable mechanical ventilation. Our results challenge the time constant concept of equal τ of an exponentially decaying flow in a single compartment model. Alternatively, a search for a new variable to objectively assess the speed of exhalation with the general aim of accurately predicting time for complete exhalation is warranted. This would in turn contribute to more personalized setting of the respiratory rate consequently minimizing dynamic hyperinflation and possibly protect the lungs from injurious mechanical ventilation.