Introduction

In recent years, due to the complexity of the systems, it may not be possible to evaluate the work of the real system. The complete study of the complex systems may increase the time and cost. When it is not possible to study the system directly, the decision-makers from various fields of science depend on simulation. According to Jdid et al. [12] “The simulation depends on the application of the study on systems similar to the real systems and then projecting these results if they are appropriate on the real system. The simulation is based on generating a series of random numbers that are subject to a uniform probability distribution”. Jdid et al. [11] suggested using probability distribution to generate random numbers for the required system. Random numbers are generated through a well-planned generator using the probability distribution. The random number generators are run using the algorithm designed keeping the mind the target to study the system. A physical or computer method that generates random numbers is called the random number generator. A random number generator generates random numbers using the statistical distribution and has no specific pattern. Due to high-speed computers, mathematical algorithms are designed and implemented to generate random numbers, see [24]. Accept-reject simulation method has been widely used to generate random numbers using a suitable underlying distribution. In this simulation method, two uniform numbers are generated and applied to calculate the probability using the underlying distribution. The ratio of probabilities obtained using the first uniform number and the mode are compared with the second uniform number in generating the random numbers. Devroye [9] suggested the approach for generating random numbers using log-concave probability densities. Hurtado and Barbat [10] used the Monte Carlo simulation to generate random numbers. Ridout [19] engaged in the development of a random number generation technique employing Laplace transformation. Martino and Miguez [16] introduced accept/reject sampling to generate random numbers. Stein and Keblis [23] introduced the method of simulation for triangular distribution. Wang et al. [25] introduced the accept-reject technique for generating random variates. Martino et al. [15] worked on accept-reject simulation and presented an algorithm to generate random numbers. Mohazzabi and Connolly [17] proposed the simulation criteria for normal distribution. Luengo et al. [14] demonstrated parameter estimation through the utilization of Monte Carlo simulation methods. Schinazi [20] proposed the method to generate discrete random numbers. Álvarez et al. [2] improved the statistical qualities of a random number generator.

Recently, neutrosophic statistics have gotten attention due to many applications for the data recorded from the complex process or when the data has neutrosophic numbers, [22]. Many studies including [3, 7, 8] discussed the efficiency of neutrosophic statistics over classical statistics. Alhabib et al. [1] introduced the fundamentals of neutrosophic methods for generating uniform random numbers. Aslam [4] introduced the Weibull distribution under indeterminacy as the generalization of classical Weibull distribution. Khan et al. [13] explored the gamma distribution within the framework of neutrosophic statistics and applied it to analyze complex data. Sherwani et al. [21] presented the concept of work distributions under neutrosophic statistics. By following Aslam [4] and Nayana et al. [18] proposed DUS-Weibull distribution under indeterminacy. Aslam [6] presented the truncated variable algorithm for generating random variates from the neutrosophic DUS-Weibull distribution. Second, [5] introduced novel approaches involving sine–cosine and convolution techniques to generate random numbers within the neutrosophic framework.

After a comprehensive review of the existing literature and to the best of our understanding, no prior research has been conducted on the utilization of the accept-reject simulation method within the framework of neutrosophic statistics. This paper aims to address this gap by introducing the accept-reject simulation technique tailored for neutrosophic uniform distribution (NUD) and neutrosophic Weibull distribution (NWD). The following sections will detail the algorithms employed for implementing the accept-reject simulation method and will provide comprehensive tables of random variates across a spectrum of uncertainty levels.

Preliminaries

In this section, we will introduce the neutrosophic uniform distribution and neutrosophic Weibull distribution briefly.

Neutrosophic uniform distribution (NUD)

Consider the neutrosophic uniform random variable denoted as \({x}_{NU}\), which exhibits a degree of uncertainty \({I}_{{x}_{NU}}\) within the range \(\left[{I}_{{x}_{LU}},{I}_{{x}_{UU}}\right]\). This variable follows a probability distribution function (pdf) characterized by indeterminacy, with parameters \({a}_{N}\) and \({b}_{N}\) representing the uniform distribution, as detailed in the work of Aslam [4].

$$f\left({x}_{NU}\right)=\left(\frac{1}{\left({b}_{L}-{a}_{L}\right)}\right)+\left(\frac{1}{\left({b}_{U}-{a}_{U}\right)}\right){I}_{{x}_{NU}};{I}_{{x}_{NU}}\epsilon \left[{I}_{{x}_{LU}},{I}_{{x}_{UU}}\right],{a}_{N}\le {x}_{NU}\le {b}_{N}$$
(1)

Note that the first part denotes the pdf of the uniform distribution under classical statistics and the second part denotes the indeterminate part. The corresponding cumulative distribution function (cdf), say \(F\left({x}_{NU}\right)\) under indeterminacy can be given as

$$F\left({x}_{NU}\right)=\left(\frac{{x}_{NL}-{a}_{L}}{\left({b}_{L}-{a}_{L}\right)}\right)+\left(\frac{{x}_{NU}-{a}_{U}}{\left({b}_{U}-{a}_{U}\right)}\right){I}_{{x}_{NU}};{I}_{{x}_{NU}}\epsilon \left[{I}_{{x}_{LU}},{I}_{{x}_{UU}}\right], {a}_{N}\le {x}_{NU}\le {b}_{N}$$
(2)

The probability density function, denoted as \(f\left({x}_{N{S}_{U}}\right)\), for the case when \({a}_{L}={a}_{U}={a}_{NS}\) and \({b}_{L}={b}_{U}={b}_{NS}\), and with the degree of indeterminacy \({I}_{NS}\), can be expressed as follows:

$$f\left({x}_{N{S}_{U}}\right)=\left(\frac{1}{\left({b}_{NS}-{a}_{NS}\right)}\right)\left(1+{I}_{NS}\right);{I}_{NS}\epsilon \left[{I}_{LS},{I}_{US}\right], {a}_{N}\le {x}_{NU}\le {b}_{N}$$
(3)

The streamlined expression for the cumulative distribution function, denoted as \(F\left({x}_{N{S}_{U}}\right)\), when \({a}_{L}={a}_{U}={a}_{NS}\) and \({b}_{L}={b}_{U}={b}_{NS}\) under conditions of indeterminacy, can be presented as follows:

$$F\left({x}_{N{S}_{U}}\right)=\left(\frac{{x}_{NS}-{a}_{NS}}{\left({b}_{NS}-{a}_{NS}\right)}\right)\left(1+{I}_{NS}\right);{I}_{NS}\epsilon \left[{I}_{LS},{I}_{US}\right], {a}_{N}\le {x}_{NU}\le {b}_{N}$$
(4)

Note the pdf and cdf under indeterminacy reduces to pdf and cdf under classical statistics when no indeterminacy is found that is \({I}_{{x}_{NU}}={I}_{NS}=0\).

Neutrosophic weibull distribution

Aslam [4] introduced the concept of the neutrosophic Weibull distribution (NWD) for the first time. Let \({x}_{LW}\) represent a neutrosophic random variable following the Weibull distribution under indeterminacy, characterized by the scale parameter \(\alpha\), shape parameter \(\beta\), and the measure of indeterminacy \({I}_{NW}\) within the range \(\left[{I}_{LW},{I}_{UW}\right]\). The probability density function (pdf) for this indeterminate Weibull distribution, as derived in [4], is expressed as follows:

$$f\left({x}_{NW}\right)=\left\{\left(\frac{\beta }{\alpha }\right){\left(\frac{{x}_{L}}{\alpha }\right)}^{\beta -1}{e}^{-{\left(\frac{{x}_{L}}{\alpha }\right)}^{\beta }}\right\}+\left\{\left(\frac{\beta }{\alpha }\right){\left(\frac{{x}_{U}}{\alpha }\right)}^{\beta -1}{e}^{-{\left(\frac{{x}_{U}}{\alpha }\right)}^{\beta }}\right\}{I}_{NW};{I}_{NW}\epsilon \left[{I}_{LW},{I}_{UW}\right]$$
(5)

The modified version of the probability density function, denoted as \(f\left({x}_{N{S}_{W}}\right)\), for the scenario where \({x}_{L}={x}_{U}={x}_{S}\) and the measure of indeterminacy is \({I}_{NS}\), can be formulated as follows:

$$f\left({x}_{N{S}_{W}}\right)=\left\{\left(\frac{\beta }{\alpha }\right){\left(\frac{{x}_{S}}{\alpha }\right)}^{\beta -1}{e}^{-{\left(\frac{{x}_{S}}{\alpha }\right)}^{\beta }}\right\}\left(1+{I}_{NS}\right);{I}_{NS}\epsilon \left[{I}_{LS},{I}_{US}\right]$$
(6)

The cdf corresponding to the Weibull distribution is represented as \(F\left({x}_{N{S}_{W}}\right)\), and it can be expressed as follows:

$$F\left({x}_{N{S}_{W}}\right)=1-\left\{{e}^{-{\left(\frac{{x}_{S}}{\alpha }\right)}^{\beta }}\left(1+{I}_{NS}\right)\right\}+{I}_{NS}; {I}_{NS}\epsilon \left[{I}_{LS},{I}_{US}\right]$$
(7)

The mode of the Weibull distribution is represented as \(f\left({\widehat{x}}_{NW}\right)\) is given by

$$f\left({\widehat{x}}_{NW}\right)=\alpha {\left(\frac{\beta -1}{\beta }\right)}^{\frac{1}{\beta }}\left(1+{I}_{NS}\right); {I}_{NS}\epsilon \left[{I}_{LS},{I}_{US}\right]$$
(8)

The NWD reduces to the Weibull distribution under classical statistics when \({I}_{NS}={I}_{NW}=0\).

Neutrosophic accept-reject simulation method

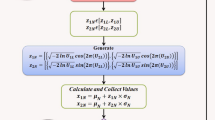
We present the neutrosophic accept-reject simulation method in the section. In this section, we will present the routine to generate random variate from the NUD and NWD. Suppose that \({u}_{N1}\sim {U}_{N1}\left(\left[\mathrm{0,0}\right],\left[\mathrm{1,1}\right]\right)\) and \({u}_{N2}\sim {U}_{N2}\left(\left[\mathrm{0,0}\right],\left[\mathrm{1,1}\right]\right)\) be two random numbers follow the NUD. Suppose that \({x}_{N{S}_{U}}\) and \({x}_{N{S}_{W}}\) are neutrosophic random variables following the NWD and NUD, respectively. Let \({\widehat{x}}_{NW}\) and \({\widehat{x}}_{NU}\) be the mode of \({x}_{NW}\) and \({x}_{NU}\), respectively. The random variate \({x}_{NU}\) will be obtained from the following expression.

$${x}_{N{S}_{U}}={a}_{NS}+\left(\frac{{u}_{N}}{\left(1+{I}_{NS}\right)}\right)\left({b}_{NS}-{a}_{NS}\right);{u}_{N}\epsilon \left[{u}_{L},{u}_{U}\right],{I}_{NS}\epsilon \left[{I}_{LS},{I}_{US}\right]$$
(9)

The random variate \({x}_{NW}\) will be obtained from the following expression.

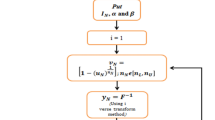
$${x}_{N{S}_{W}}=\alpha {\left[-\mathrm{ln}\left(\frac{1-\left({u}_{N}-{I}_{NS}\right)}{1+{I}_{NS}}\right)\right]}^{\frac{1}{\beta }};{I}_{NS}\epsilon \left[{I}_{LS},{I}_{US}\right],{u}_{N}\epsilon \left[{u}_{L},{u}_{U}\right]$$
(10)

Based on the above-mentioned information, the following accept-reject routine under indeterminacy will be implemented to generate \(n\) random variate \({x}_{N{S}_{U}}\) from NUD.

Step-1: pre-specified \({I}_{NS}\), \({a}_{NS}\) and \({b}_{NS}\).

Step-2: Generate two NUD random numbers, say \({u}_{N1}\sim {U}_{N1}\left(\left[\mathrm{0,0}\right],\left[\mathrm{1,1}\right]\right)\) and \({u}_{N2}\sim {U}_{N2}\left(\left[\mathrm{0,0}\right],\left[\mathrm{1,1}\right]\right)\).

Step-3: Find \({x}_{N{S}_{U}}\) using \({x}_{N{S}_{U}}={a}_{NS}+\left(\frac{{u}_{N1}}{\left(1+{I}_{NS}\right)}\right)\left({b}_{NS}-{a}_{NS}\right)\)

Step-4: Compute \(f\left({x}_{N{S}_{U}}\right)\) using \(f\left({x}_{N{S}_{U}}\right)=\left(\frac{1}{\left({b}_{NS}-{a}_{NS}\right)}\right)\left(1+{I}_{NS}\right)\).

Step-5: Compute \(f\left({\widehat{x}}_{N{S}_{U}}\right)\) at any value between \({a}_{NS}\) and \({b}_{NS}\).

Step-6: If \({u}_{N2}<f\left({x}_{N{S}_{U}}\right)/f\left({\widehat{x}}_{N{S}_{U}}\right)\), then record \({x}_{NU}\) and go to step-7, otherwise, repeat the previous steps.

Step-7: Return \({x}_{N{S}_{U}}\) and repeat the process to generate \(n\) variate of \({x}_{N{S}_{U}}\).

The algorithm to generate random variate from the NUD is depicted in Fig. 1.

Fig. 1
figure 1

Accept-reject routine for NUD

Full size image

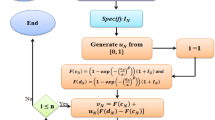
The following accept-reject routine will be implemented to generate \(n\) random variate \({x}_{N{S}_{W}}\) from NWD.

Step-1: pre-specified \({I}_{NS}\), \({a}_{NS}\) and \({b}_{NS}\).

Step-2: Generate two NUD random numbers, say \({u}_{N1}\sim {U}_{N1}\left(\left[\mathrm{0,0}\right],\left[\mathrm{1,1}\right]\right)\) and \({u}_{N2}\sim {U}_{N2}\left(\left[\mathrm{0,0}\right],\left[\mathrm{1,1}\right]\right)\).

Step-3: Find \({x}_{N{S}_{W}}\) using \({x}_{N{S}_{W}}=\alpha {\left[-\mathrm{ln}\left(\frac{1-\left({u}_{N1}-{I}_{NS}\right)}{1+{I}_{NS}}\right)\right]}^{\frac{1}{\beta }}\)

Step-4: Compute \(f\left({x}_{N{S}_{W}}\right)\) using \(f\left({x}_{N{S}_{W}}\right)=\left\{\left(\frac{\beta }{\alpha }\right){\left(\frac{{x}_{S}}{\alpha }\right)}^{\beta -1}{e}^{-{\left(\frac{{x}_{S}}{\alpha }\right)}^{\beta }}\right\}\left(1+{I}_{NS}\right)\).

Step-5: Compute mode \(f\left({\widehat{x}}_{N{S}_{W}}\right)\) and compute \(f\left({\widehat{x}}_{N{S}_{W}}\right)=\left\{\left(\frac{\beta }{\alpha }\right){\left(\frac{{\widehat{x}}_{S}}{\alpha }\right)}^{\beta -1}{e}^{-{\left(\frac{{\widehat{x}}_{S}}{\alpha }\right)}^{\beta }}\right\}\left(1+{I}_{NS}\right)\)

Step-6: If \({u}_{N2}<f\left({x}_{N{S}_{W}}\right)/f\left({\widehat{x}}_{N{S}_{W}}\right)\), then record \({x}_{NW}\) and go to step-7, otherwise, repeat the previous steps.

Step-7: Return \({x}_{N{S}_{W}}\) and repeat the process to generate \(n\) variate of \({x}_{N{S}_{W}}\).

The algorithm to generate random variate from the NWD is depicted in Fig. 2.

Fig. 2
figure 2

Accept-reject routine for NWD

Full size image

Note that the proposed neutrosophic accept-reject algorithms are an extension of accept-reject algorithms under classical statistics. The proposed simulation methods under neutrosophic statistics are reduced to the simulation methods under classical statistics when no indeterminacy is found in the data.

Simulation studies

An extensive simulation study has been carried out to investigate the behavior of random variates generated by the developed algorithms across a range of parameters for NUD and NWD. In this section, we will present and analyze the simulation tables obtained through the accept-reject simulation method and the repetitive simulation method. A wide simulation study is conducted to see the behavior of random variate obtained from the developed algorithms at various values of parameters of NUD and NWD. In this section, the simulation tables obtained from the accept-reject simulation method and repetitive simulation method will be given and discussed.

Accept-reject simulation method

The random variate from the accept-reject method for the NUD is obtained for various values of \({a}_{NS}\) and \({b}_{NS}\) is reported in Tables 1, 2. To see the effect of intermediacy on these random variate, various values of \({I}_{NS}\) are considered in the generation of random variates from NUD and NWD. The random variate obtained from NUD using the values of \({u}_{N1}\), \({u}_{N2}\), \({a}_{NS}\)=10 and \({b}_{NS}\)=20 are reported in Table 1. The random variate obtained from NUD using the values of \({u}_{N1}\), \({u}_{N2}\), \({a}_{NS}\)=15 and \({b}_{NS}\)=20 are reported in Table 2. From Tables 1, 2, it can be noted that for the fixed values of \({a}_{NS}\)=15, \({b}_{NS}\)=20 and \({I}_{NS}\), there is an increase in random variate. The random variate decreases as the values of \({I}_{NS}\) increases from 0 to 1. Note that the values of random variate \({I}_{NS}\)=0 presents the values of random variate for classical statistics. From Tables 1, 2, it can be noted that indeterminacy plays a significant role in decreasing the random variate. It's worth emphasizing that computer-based uniform random variate generation is commonly employed to simulate random numbers. However, this simulation approach often overlooks the influence of the measure of indeterminacy when generating random numbers in the computer. Our analysis underscores that, in the presence of uncertainty, the resulting random numbers differ from those generated in a deterministic setting. Therefore, when faced with uncertainty, depending on uniformly distributed random variables generated using traditional simulation methods could result in erroneous conclusions.

Table 1 Random numbers from NUD when \({a}_{NS}\)=10 and \({b}_{NS}\)=20
Full size table
Table 2 Random numbers from NUD when \({a}_{NS}\)=15 and \({b}_{NS}\)=20
Full size table

The random variate from NWD for various values of \({I}_{NS}\) and parameters are shown in Tables 3, 4, 5, 6. Table 3 is presented for \(\alpha =2\) and \(\beta =0.50\). The random variate for \(\alpha =2\) and \(\beta =1\) (exponential distribution) is shown in Table 4. The random variate for \(\alpha =2\) and \(\beta =1.5\) is shown in Table 5. The random variate for \(\alpha =2\) and \(\beta =1.5\) is shown in Table 5. The random variate for \(\alpha =2\) and \(\beta =2\) is shown in Table 5. From Tables 3, 4, 5, 6, there is a decreasing trend in random variate as the values of \({I}_{NS}\) increase. For example, for the exponential distribution, when \({u}_{N1}=0.6724\) and \({u}_{N2}=0.3931\), the value of random variate is 1.2212 when \({I}_{NS}\)=0 and the value of random variate is 2.000.

Table 3 Random numbers from NWD when \(\alpha =2\) and \(\beta =0.50\)
Full size table
Table 4 Random numbers from NWD when \(\alpha =2\) and \(\beta =1.0\)
Full size table
Table 5 Random numbers from NWD when \(\alpha =2\) and \(\beta =1.50\)
Full size table
Table 6 Random numbers from NWD when \(\alpha =2\) and \(\beta =2.0\)
Full size table

Concluding remarks

This paper has introduced two simulation methods for generating random variates using NUD and NWD. The paper presented the essential computational procedures, simulation techniques, and algorithms necessary for these methods. Random variates derived from NUD and NWD were generated under various parameter settings and indeterminacy levels. The analysis reveals that the measure of indeterminacy significantly influences the random variates, with a decrease observed as the level of indeterminacy increases. It’s important to highlight that computer-based uniform random variate generation is a prevalent method for simulating random numbers. Nonetheless, this simulation approach frequently disregards the impact of the measure of indeterminacy when generating random numbers in the computer. Our analysis underscores that in the presence of uncertainty, the resulting random numbers deviate from those generated in a deterministic environment. Therefore, depending on uniform random variables generated through traditional simulation methods can potentially lead to erroneous decisions. These proposed simulation methods have versatile applications in fields such as education, medicine, computer science, and engineering. Furthermore, the potential for extending these methods to handle other distributions is a promising avenue for future research.