Introduction

In the classical theory of statistics, the data are formed in crisp numbers and analyzed. Since one cannot always compute or offer exact values for statistical traits in real life, it is quite desirable to approximate them. Making the transition from classical to neutrosophic statistics is one technique; depending on the types of indeterminacies, however, numerous approaches may be available. Several advances have been made in recent years to model such inaccurate situations using fuzzy logic and neutrosophy [5, 9, 34, 36, 39, 40]. In addition, according to neutrosophic logic, the parameters take undetermined values which arise while working with statistical data, particularly when working with vague and inaccurate statistical data [5]. Smarandache [33, 36] proposed that a logical statement can be represented in a 3D Neutrosophic Space, where each dimension of the space represents the statement's Truth (T), Falsehood (F), and Indeterminacy (I). Several studies have been conducted using neutrosophic probability distributions to calculate indeterminacy in real-world scenarios, with better results than classical statistics. The concepts of probability distribution in crisp logic were generalized to neutrosophic logic with applications. In terms of neutrosophic statistics, Alhasan and Smarandache [3] proposed the Neutrosophic Weibull distribution. Similarly, distributions like neutrosophic-Poisson, neutrosophic-Uniform, neutrosophic-Exponential are available in the literature. A neutrosophic-Beta distribution for the data is in interval form was developed by Sherwani et al. [32]. Patro and Samarande [28] introduced Neutrosophic Binomial and Neutrosophic Normal distributions. These distributions are provided with an additional room in the relevant area, allowing it to solve more problems that were previously neglected in classical statistics due to indeterminacy and aberrant values [34]. Neutrosophic time series prediction [30] and modelling were also examined in a variety of scenarios, including neutrosophic moving averages, neutrosophic logarithmic models, neutrosophic linear models, and so on, see Guan et al. [13]. Neutrosophic logic has successfully solved a variety of decision-making challenges, such as examining green credit ratings and personnel selection, see Nabeeh et Al. [24,25,26]. Aslam et al. [2, 4, 6,7,8] extended the idea of control charts and sampling plans with the presence of indeterminacy and presented various neutrosophic control charts and sampling plans, as well as discussed applying the neutrosophic theory to engineering systems.

The Weibull model is one among the few essential distributions used in reliability theory that are crucial to understanding dependability applications. Many of the analyses using the Weibull model are now available across the engineering literature [18, 22, 27]. Fisher and Tippett [31] proposed a basic theory of the Weibull distribution as one of three types of extreme value distributions. Grabner et al. [12] used the complex combination of Weibull density for wind speed data. The effect of the shape and scale parameters on distribution characteristics such as the reliability, hazard rate etc. is a key feature of the Weibull distribution. The discrete additive Weibull distribution is proposed by Unnikrishnan et al. [31]. An extended version and modified version of Weibull distribution were studied in reliability engineering systems by Yong [39] and Hong [15], respectively. Kundu and Ganguly [20] initiated a cumulative exposure model using Weibull distribution. Wirwicki [38] developed a two-parameter Weibull distribution and studied the strength of ceramic materials like Zirconium dioxide and Wais [37] applied Weibull distribution in the wind sector. Hangal [14] studied the use of generalized Weibull distribution in public health and disease modelling. Quinn and Quinn [29] have reviewed Weibull statistics in reporting strengths of dental materials. Lai et al. [21] prepared a monograph on the Weibull distribution and its extensions that cover practically every aspect.

The paper proposed a new life distribution using the DUS transformation of Neutrosophic Weibull distribution. In the literature of statistics, there are various DUS transformed distributions proposed with some well-known baseline distributions. An approach for proposing new distributions with the DUS transform is found to be effective for modelling. A DUS transformation method has been used to analyze patient information on bladder cancer by Kumar et al. [19]. Kavya and Manoharan [17] introduced the Generalized DUS (GDUS) transformation of Weibull distribution. Deepthi and Chacko [10] studied the properties of DUS-Lomax distribution for survival data analysis. Tripathi et al. [36] studied the inferences for the DUS-Exponential Distribution based on upper record values. Maurya et al. [23] worked with Lindley distribution. AbuJarad et al. [1] developed Bayesian survival analysis on generalized DUS-exponential. Gauthami and Chacko [11] proposed an upside-down failure rate model using DUS-inverse Weibull distribution. Karakaya et al. [16] developed DUS-Kumaraswamy distribution with applications in biomedical and epidemiological research.

The paper is organized into seven sections. The next section describes the probability density (pdf) function, cumulative density function (cdf), and hazard rate function. The statistical properties are studied in the subsequent section followed by which the parameter estimation using the method of maximum likelihood is discussed. Then a simulation study to check the flexibility of the estimates is explained. In the penultimate section, real-life data analysis is presented and a conclusion is given in the final section.

DUS-neutrosophic Weibull

Let \(f\left( x \right)\) and \(F\left( X \right)\) be the pdf and cdf of the baseline distribution respectively, we consider the DUS transformed distribution with pdf

$$ g\left( x \right) = \frac{1}{e - 1}f(x)e^{F(x)} . $$
(1)

The cdf of DUS transformation is given as

$$ G\left( x \right) = \frac{1}{e - 1}\left[ {e^{F\left( x \right)} - 1} \right]. $$
(2)

The hazard rate function is

$$ h\left( x \right) = \frac{1}{{e - e^{F\left( x \right)} }}f\left( x \right)e^{F\left( X \right)} . $$
(3)

Suppose \(I_{N} \in \left( {I_{L} ,I_{U} } \right)\) is an indeterminacy interval, where N is the neutrosophic statistical number and let \(X_{N} = X_{L} + X_{U} I_{N}\) be a random variable following neutrosophic Weibull distribution with scale parameter, \(\alpha\) and shape parameter,\(\beta\). The neutrosophic distribution tends to the classical distribution when \(I_{N} = 0\). Therefore, consider neutrosophic Weibull distribution of a random variable (r.v) \(X_{N}\) with neutrosophic probability distribution function (npdf) as

$$ \begin{aligned} f\left( {x_{N} } \right) & = \left( {\frac{\beta }{{\alpha^{\beta } }}x_{N}^{\beta - 1} e^{{ - \left( {\frac{{x_{N} }}{\alpha }} \right)^{\beta } }} } \right) + \left( {\frac{\beta }{{\alpha^{\beta } }}x_{N}^{\beta - 1} e^{{ - \left( {\frac{{x_{N} }}{\alpha }} \right)^{\beta } }} } \right)I_{N} \\ & = \left( {\frac{\beta }{{\alpha^{\beta } }}x_{N}^{\beta - 1} e^{{ - \left( {\frac{{x_{N} }}{\alpha }} \right)^{\beta } }} } \right)\left( {1 + I_{N} } \right) \\ & \quad I_{N} \in \left( {I_{L} ,I_{U} } \right),\;x_{N} \in \left( {x_{L} ,x_{U} } \right) > 0 \\ & \quad x_{N} > 0 ,\alpha > 0, \beta > 0. \\ \end{aligned} $$
(4)

The corresponding neutrosophic cumulative distribution (ncdf) is

$$ F\left( {x_{N} } \right) = \left( {1 - e^{{ - \left( {\frac{{x_{N} }}{\alpha }} \right)^{\beta } }} } \right)\left( {1 + I_{N} } \right),\quad x_{N} > 0 ,\alpha > 0, \beta > 0. $$
(5)

Using Eqs. (1), (2), and (3), DUS-neutrosophic Weibull (DUS-NW) distribution is proposed below with two parameters such as \(\alpha\), the scale parameter and \(\beta\), the shape parameter. The npdf and ncdf of the proposed distribution, respectively, are

$$ g\left( {x_{N} } \right) = \left( {\frac{1}{e - 1}\frac{\beta }{{\alpha^{\beta } }}X_{N}^{\beta - 1} e^{{ - \left( {\frac{{X_{N} }}{\alpha }} \right)^{\beta } }} e^{{\left( {1 - e^{{ - \left( {\frac{{X_{N} }}{\alpha }} \right)^{\beta } }} } \right)\left( {1 + I_{N} } \right)}} } \right)\left( {1 + I_{N} } \right),\quad x_{N} > 0 ,\alpha > 0, \beta > 0, $$
(6)

and

$$ G\left( {x_{N} } \right) = \frac{1}{e - 1}e^{{\left( {1 - e^{{ - \left( {\frac{{X_{N} }}{\alpha }} \right)^{\beta } }} } \right)\left( {1 + I_{N} } \right)}} ;\quad x_{N} > 0 ,\alpha > 0, \beta > 0. $$
(7)

Also, the hazard rate function is

$$ h_{N} \left( {x_{N} } \right) = \frac{{\left( {\frac{1}{e - 1}\frac{\beta }{{\alpha^{\beta } }}X_{N}^{\beta - 1} e^{{ - \left( {\frac{{X_{N} }}{\alpha }} \right)^{\beta } }} e^{{\left( {1 - e^{{ - \left( {\frac{{X_{N} }}{\alpha }} \right)^{\beta } }} } \right)\left( {1 + I_{N} } \right)}} } \right)\left( {1 + I_{N} } \right)}}{{1 - \frac{1}{e - 1}e^{{\left( {1 - e^{{ - \left( {\frac{{X_{N} }}{\alpha }} \right)^{\beta } }} } \right)\left( {1 + I_{N} } \right)}} }};\quad x_{N} { > 0 , }\alpha { > 0, }\beta { > 0}. $$
(8)

From Eq. (4), the DUS-neutrosophic Weibull becomes the DUS-Weibull model when \(I_{N} = 0\) and it is a special case of a generalized DUS-exponential model studied by Kavya and Manoharan [17].

Shape of the density curve

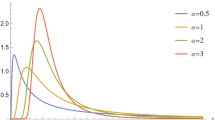
From Fig. 1, it can observe the following properties of the npdf of \(DUS - NW\left( {\alpha ,\beta } \right)\).

  1. (i)

    \(\alpha <1, \beta \ge 1\), \(g(x)\) is decreasing

  2. (ii)

    \(\alpha \ge 1, \beta >1\), \(g(x)\) is unimodal

  3. (iii)

    \(\alpha <1, \beta <1\), \(g(x)\) is decreasing

  4. (iv)

    \(\alpha \ge 1, \beta \le 1\), \(g(x)\) is decreasing

Fig. 1
figure 1

npdf of DUS-NW

Full size image

Figure 2 represents the plot of ncdf of \(DUS - NW\left( {\alpha ,\beta } \right)\).

Fig. 2
figure 2

ncdf of DUS-NW

Full size image

The plot of hazard function rate is shown in Fig. 3 which has upside-down bathtub shaped and decreasing shapes.

Fig. 3
figure 3

nhrf of DUS-NW

Full size image

Statistical properties of DUS-neutrosophic Weibull

The main statistical properties like moments, generating functions, quantile function, order statistics and entropy have been studied in this section.

Moments

The \(r^{th}\) moment of the distribution, for \(r \in N,\mu^{\prime}_{r}\) is given as

$$ \begin{aligned} \mu^{\prime}_{r} & = E\left[ {X^{r} } \right] \\ & = \int\limits_{0}^{\infty } {x^{r} \left( {\frac{1}{e - 1}\frac{\beta }{{\alpha^{\beta } }}X_{N}^{\beta - 1} e^{{ - \left( {\frac{{X_{N} }}{\alpha }} \right)^{\beta } }} e^{{\left( {1 - e^{{ - \left( {\frac{{X_{N} }}{\alpha }} \right)^{\beta } }} } \right)\left( {1 + I_{N} } \right)}} } \right)\left( {1 + I_{N} } \right){\text{d}}x} . \\ \end{aligned} $$
(9)

Using exponential expansion \(e^{x} = \sum\nolimits_{i = 0}^{\infty } {\frac{{x^{i} }}{i!}}\) and binomial series of expansion \(\left( {1 - y} \right)^{b} = \sum\nolimits_{i = 0}^{\infty } {\left( { - 1} \right)} \left( {\mathop {}\limits_{i}^{b} } \right)y^{i}\), Eq. (9) becomes

$$ \mu^{\prime}_{r} = \left( {\frac{\beta }{{\left( {e - 1} \right)\alpha^{\beta } }}e^{{\left( {1 + I_{N} } \right)}} \sum\limits_{l = 0}^{\infty } {\sum\limits_{i = 0}^{\infty } {\frac{{\left( { - 1} \right)^{i} }}{l!}\left( {\mathop {}\limits_{i}^{l} } \right)} \frac{{\Gamma \left( {\frac{r}{\beta } + 1} \right)}}{{\left( {\frac{i + 1}{{\alpha^{\beta } }}} \right)^{{\frac{r}{\beta } + 1}} }}} } \right)\left( {1 + I_{N} } \right). $$
(10)

The higher order moments can be found similarly. Hence, the mean and variance is given by:

$$ E\left[ {X_{N} } \right] = \left( {\frac{\beta }{{\left( {e - 1} \right)\alpha^{\beta } }}e^{{\left( {1 + I_{N} } \right)}} \sum\limits_{l = 0}^{\infty } {\sum\limits_{i = 0}^{\infty } {\frac{{\left( { - 1} \right)^{i} }}{l!}\left( {\mathop {}\limits_{i}^{l} } \right)} \frac{{\Gamma \left( {\frac{1}{\beta } + 1} \right)}}{{\left( {\frac{i + 1}{{\alpha^{\beta } }}} \right)^{{\frac{1}{\beta } + 1}} }}} } \right)\left( {1 + I_{N} } \right). $$
(11)
$$ \begin{aligned} V\left[ {X_{N} } \right] = & \left( {\frac{\beta }{{\left( {e - 1} \right)\alpha^{\beta } }}e^{{\left( {1 + I_{N} } \right)}} \sum\limits_{l = 0}^{\infty } {\sum\limits_{i = 0}^{\infty } {\frac{{\left( { - 1} \right)^{i} }}{l!}\left( {\mathop {}\limits_{i}^{l} } \right)} \frac{{\Gamma \left( {\frac{2}{\beta } + 1} \right)}}{{\left( {\frac{i + 1}{{\alpha^{\beta } }}} \right)^{{\frac{1}{\beta } + 1}} }}} } \right)\left( {1 + I_{N} } \right) \\ & \quad - \left\{ {\left( {\frac{\beta }{{\left( {e - 1} \right)\alpha^{\beta } }}e^{{\left( {1 + I_{N} } \right)}} \sum\limits_{l = 0}^{\infty } {\sum\limits_{i = 0}^{\infty } {\frac{{\left( { - 1} \right)^{i} }}{l!}\left( {\mathop {}\limits_{i}^{l} } \right)} \frac{{\Gamma \left( {\frac{2}{\beta } + 1} \right)}}{{\left( {\frac{i + 1}{{\alpha^{\beta } }}} \right)^{{\frac{1}{\beta } + 1}} }}} } \right)\left( {1 + I_{N} } \right)} \right\}^{2} . \\ \end{aligned} $$
(12)

Moment generating function

As \({X}_{N}\sim DUS-NW\left(\alpha ,\beta \right)\), the moment generating function is given as

$$ \begin{aligned} M_{{X_{N} }} \left( t \right) &= E\left( {e^{{tX_{N} }} } \right) \\ & = \left( {\frac{\beta }{{\left( {e - 1} \right)\alpha^{\beta } }}e^{{\left( {1 + I_{N} } \right)}} \sum\limits_{l = 0}^{\infty } {\sum\limits_{i = 0}^{\infty } {\frac{{\left( { - 1} \right)^{i} }}{l!}\left( {\mathop {}\limits_{i}^{l} } \right)} \sum\limits_{k = 0}^{\infty } {\frac{{t^{k} }}{k!}} \frac{{\Gamma \left( {\frac{k}{\beta } + 1} \right)}}{{\left( {\frac{i + 1}{{\alpha^{\beta } }}} \right)^{{\frac{k}{\beta } + 1}} }}} } \right)\left( {1 + I_{N} } \right). \\ \end{aligned} $$
(13)

Characteristic function

The characteristic function of \({X}_{N}\sim DUS-NW\left(\alpha ,\beta \right)\) is given as

$$ \begin{aligned} &\phi_{{X_{N} }} \left( t \right)\\ &\quad = E\left[ {e^{{itX_{N} }} } \right] \\ &\quad = \left( {\frac{\beta }{{\left( {e - 1} \right)\alpha^{\beta } }}e^{{\left( {1 + I_{N} } \right)}} \sum\limits_{l = 0}^{\infty } {\sum\limits_{i = 0}^{\infty } {\frac{{\left( { - 1} \right)^{i} }}{l!}\left( {\mathop {}\limits_{i}^{l} } \right)} \sum\limits_{k = 0}^{\infty } {\frac{{\left( {it} \right)^{k} }}{k!}} \frac{{\Gamma \left( {\frac{k}{\beta } + 1} \right)}}{{\left( {\frac{i + 1}{{\alpha^{\beta } }}} \right)^{{\frac{k}{\beta } + 1}} }}} } \right)\left( {1 + I_{N} } \right), \\ &\quad \quad \;{\text{where}}\;i = \sqrt { - 1} . \\ \end{aligned} $$
(14)

Cumulant generating function

The cumulant generating function \({X}_{N}\sim DUS-NW\left(\alpha ,\beta \right)\) is as follows:

$$ \begin{aligned} K_{{X_{N} }} \left( t \right) &= \log \phi_{{X_{N} }} \left( t \right) \\ & = \left( {\log \frac{\beta }{{\left( {e - 1} \right)\alpha^{\beta } }}e^{{\left( {1 + I_{N} } \right)}} \sum\limits_{l = 0}^{\infty } {\sum\limits_{i = 0}^{\infty } {\frac{{\left( { - 1} \right)^{i} }}{l!}\left( {\mathop {}\limits_{i}^{l} } \right)}}}\right. \\ & \quad \times\left.{{\sum\limits_{k = 0}^{\infty } {\frac{{\left( {it} \right)^{k} }}{k!}} \frac{{\Gamma \left( {\frac{k}{\beta } + 1} \right)}}{{\left( {\frac{i + 1}{{\alpha^{\beta } }}} \right)^{{\frac{k}{\beta } + 1}} }}} } \right)\left( {1 + I_{N} } \right). \\ \end{aligned} $$
(15)

Quantile function

The quantile function specifies the value of a random variable so that the probability of the variable being less than or equal to that value equals the specified probability. Suppose is \({X}_{N}\sim DUS-NW\left(\alpha ,\beta \right)\) a neutrosophic random variable with a distribution function \(F\left( {X_{N} } \right)\) such that

$$F\left[{Q}_{{X}_{N}}\left(p\right)\right]=p.$$

Hence, the quantile function is given by

$$ Q\left( p \right) = \left[ { - \alpha^{\beta } \log \left( {1 - \log \left( {\frac{{p\left( {e - 1} \right)}}{{1 + I_{N} }}} \right)} \right)} \right]^{{\frac{1}{\beta }}} . $$
(16)

While setting \(p = \frac{1}{2}\) in Eq. (16), we get the median of \(DUS - NW\left( {\alpha ,\beta } \right)\) as

$$ {\text{Median}} = \left[ { - \alpha^{\beta } \log \left( {1 - \log \left( {\frac{1}{2}\frac{{\left( {e - 1} \right)}}{{1 + I_{N} }}} \right)} \right)} \right]^{{\frac{1}{\beta }}} . $$
(17)

Order statistics

Order statistics are highly pertinent in reliability theory and survival analysis because of the significance of the hazard rate function in these domains. Let \(X_{N1} ,X_{N2} ,...X_{Nn}\) be the n independent and identically distributed (i.i.d) random variable with corresponding order statistics \(X_{N\left( 1 \right)} ,X_{N\left( 2 \right)} ,...X_{N\left( n \right)}\) derived from DUS-NW with density function \(g\left( {x_{N} } \right)\) and distribution function \(G\left( {x_{N} } \right)\). Hence the \(r^{th}\) order statistics for pdf and the cdf is given as

$$ \begin{aligned} g_{r} \left( {x_{N} } \right) & = \frac{n!}{{\left( {r - 1} \right)!\left( {n - r} \right)!}}G^{r - 1} \left( x \right)\left[ {1 - G\left( x \right)} \right]^{n - r} g\left( x \right) \\ & = \frac{n!}{{\left( {r - 1} \right)!\left( {n - r} \right)!}}\frac{1}{{\left( {e - 1} \right)^{n} }}\frac{\beta }{{\alpha^{\beta } }}X_{N}^{\beta - 1} e^{{^{{ - \left( {\frac{{X_{N} }}{\alpha }} \right)^{\beta } }} }} \\ & \quad \times\left( {e^{{^{{\left( {1 - e^{{ - \left( {\frac{{X_{N} }}{\alpha }} \right)^{\beta } }} } \right)\left( {1 + I_{N} } \right)}} }} } \right)^{r - 1} \\ & \quad\times\left( {e - e^{{^{{\left( {1 - e^{{ - \left( {\frac{{X_{N} }}{\alpha }} \right)^{\beta } }} } \right)\left( {1 + I_{N} } \right)}} }} } \right)^{n - r} \left( {1 + I_{N} } \right) \\ \end{aligned} $$
(18)
$$ \begin{aligned} G_{r} \left( x \right) & = \sum\limits_{j = r}^{n} {\left( {\mathop {}\limits_{j}^{n} } \right)G^{j} \left( x \right)\left[ {1 - G\left( x \right)} \right]^{n - j} } \\ & = \sum\limits_{j = r}^{n} {\left( {\mathop {}\limits_{j}^{n} } \right)\left( {\frac{{e^{{^{{^{{\left( {1 - e^{{ - \left( {\frac{{X_{N} }}{{\alpha_{N} }}} \right)^{{\beta_{N} }} }} } \right)\left( {1 + I_{N} } \right)}} }} }} }}{e - 1}} \right)}^{j} \\ & \quad \times \left( {\frac{{e - e^{{^{{^{{\left( {1 - e^{{ - \left( {\frac{{X_{N} }}{{\alpha_{N} }}} \right)^{{\beta_{N} }} }} } \right)\left( {1 + I_{N} } \right)}} }} }} }}{e - 1}} \right)^{n - j} \\ \end{aligned} $$
(19)

Entropy

The entropy function is used to investigate system reliability and repairability in many engineering systems. Renyi (1961) introduced the quantum form of the classical Rényi entropy. Let \({X}_{N}\sim DUS-NW\left(\alpha ,\beta \right)\) and \(\gamma\) is the order \(\left( {\gamma \ne 1,\gamma \ge 0} \right)\).

$$ \begin{aligned} \tau_{r} \left( \gamma \right) & = \frac{1}{1 - \gamma }\log \left[ {\int {\tau^{\gamma } \left( {x_{N} } \right){\text{d}}x} } \right] \\ & = \left( {\frac{1}{1 - \gamma }\log \left( {\frac{{\beta_{N} }}{{\left( {e - 1} \right)\left( {\alpha_{N} } \right)^{{\beta_{N} }} }}} \right)^{\gamma } \sum\limits_{i = 0}^{\infty } }\right. \\ & \quad \times \left.{ {\sum\limits_{l = 0}^{\infty } {\frac{{\left( { - 1} \right)^{i + l} }}{l!}\gamma^{i} \left( {\mathop {}\limits_{i}^{l} } \right)\frac{{\Gamma \left( {\gamma + \frac{\gamma + 1}{{\beta_{N} }}} \right)}}{{\left( {\frac{l + \gamma }{{\left( {\alpha_{N} } \right)^{{\beta_{N} }} }}} \right)^{{\gamma + \frac{\gamma + 1}{{\beta_{N} }}}} }}} } } \right)\left( {1 + I_{N} } \right), \\ \end{aligned} $$
(20)

where \(\tau_{\gamma } \left( \gamma \right)\) is a non-decreasing function of \(\gamma\).

Estimation of parameters

The method of the maximum likelihood function for parameter estimation is discussed in this section.

Maximum likelihood function

For a given n observation \(x_{N1} ,x_{N2} ,....x_{Nn}\), the likelihood function of \({X}_{N}\sim DUS-NW\left(\alpha ,\beta \right)\) is given as

$$ \begin{aligned} &L\left( {x_{Ni} ,\alpha_{N} ,\beta_{N} } \right) = \coprod\limits_{i = 1}^{n} {f\left( {x_{Ni} ,\alpha_{N} ,\beta_{N} } \right)} \\ & = \left( {\frac{1}{{\left( {e - 1} \right)^{n} }}\frac{{\beta^{n} }}{{\alpha^{n\beta } }}\coprod\limits_{i = 1}^{n} {X_{Ni}^{\beta - 1} } e^{{ - \sum\limits_{i = 1}^{n} {\left( {\frac{{X_{Ni} }}{\alpha }} \right)^{\beta } } }} e^{{\sum\limits_{i = 1}^{n} {\left( {1 - e^{{ - \left( {\frac{{X_{Ni} }}{\alpha }} \right)^{\beta } }} } \right)} }} } \right)\\ & \quad \times\left( {1 + I_{N} } \right). \\ \end{aligned} $$
(21)

The corresponding log-likelihood is obtained as

$$\begin{aligned} &\log L_{{}} \left( {x_{Ni} ,\alpha ,\beta } \right) \\& \quad= \left( \begin{gathered} - n\log (e - 1) + n\log \beta - n\beta \log \alpha \hfill \\ + \left( {\beta - 1} \right)\sum\limits_{i = 1}^{n} {\log X_{Ni} } - \sum\limits_{i = 1}^{n} {\left( {\frac{{X_{Ni} }}{\alpha }} \right)^{\beta } } \hfill \\ + \sum\limits_{i = 1}^{n} {\left( {\left( {1 - e^{{ - \left( {\frac{{X_{Ni} }}{\alpha }} \right)^{\beta } }} } \right)\left( {1 + I_{N} } \right)} \right)} \hfill \\ \end{gathered} \right) \\&\quad + n\log \left( {1 + I_{N} } \right).\end{aligned} $$
(22)

The maximum likelihood estimator (MLE) for the parameters \(\alpha \) and \(\beta \) can be obtained by maximizing the log-likelihood function. The derivatives corresponding to the parameters \(\alpha \) and \(\beta \) are given by

$$ \frac{\partial \log L}{{\partial \alpha }} = \frac{ - n\beta }{\alpha } + \sum\limits_{i = 1}^{n} {\frac{{X_{i}^{\beta } }}{{\alpha^{\beta + 1} }} + \sum\limits_{i = 1}^{n} {e^{{ - \left( {\frac{{X_{i} }}{\alpha }} \right)^{\beta } }} } \frac{{X_{i}^{\beta } }}{{\alpha^{\beta + 1} }}\left( {1 + I_{N} } \right)} , $$
(23)
$$ \begin{aligned}\frac{\partial \log L}{{\partial \beta }} &= \frac{n}{\beta } - n\log \alpha + \sum\limits_{i = 1}^{n} {\log X_{i} - } \sum\limits_{i = 1}^{n} {\left( {\frac{{X_{i} }}{\alpha }} \right)}^{\beta } \\ & \log \left( {\frac{{X_{i} }}{\alpha }} \right) + \sum\limits_{i = 1}^{n} {e^{{ - \left( {\frac{{X_{i} }}{\alpha }} \right)^{\beta } }} } \left( {\frac{{X_{i} }}{\alpha }} \right)^{\beta } \log \frac{{X_{i} }}{\alpha }\left( {1 + I_{N} } \right).\end{aligned} $$
(24)

With the difficulty in the computation of the non-linear equations, Eqs. (23) and (24) can be solved by the inversion method using statistical software R. This yields the ML estimates of \(\alpha \) and \(\beta \) for a chosen initial value.

Simulation studies

To evaluate the performance of MLE of the DUS-NW, an extensive examination has been done. This is compared with the flexibility of the proposed distribution with two indeterminacy measures, i.e. \({I}_{N}=(0.2, 0.5)\) and \({I}_{N}=(0.6, 0.8)\) with classical DUS-Weibull distribution \(({I}_{N}=0)\). Bias and mean square error (MSE) are calculated for different values \(\alpha \) and \(\beta \) for assorted sample sizes \(n=100, 250, 500, 1000\). The results are given below.

The samples are generated using the inversion method for different values of parameters and for two interval measures with \({I}_{N}=(0.2, 0.5)\) and \({I}_{N}=(0.6, 0.8)\). From Tables 1, 2, 3, it can be observed that the Bias and MSE results of DUS-NW (\(\alpha ,\beta )\) are lower compared to classical DUS-Weibull distribution for increasing values of sample size with the different parameter sets for \(\alpha \) and \(\beta \). Here the indeterminacy parameter \({I}_{N}\) plays a crucial role in reducing the error for the estimates.

Table 1 Bias and MSE for estimates (\(\widehat{\alpha },\widehat{\beta }\) ̂) for \({I}_{N}\)= (0.2, 0.5)
Full size table
Table 2 Bias and MSE for estimates (\(\widehat{\alpha },\widehat{\beta }\) ̂) for \({I}_{N}\)= (0.6, 0.8)
Full size table
Table 3 Bias and MSE for estimates (\(\widehat{\alpha },\widehat{\beta }\) ̂) for \({I}_{N}\)=0 (Classical DUS-Weibull)
Full size table

Application

In this section, the parameters of the proposed distribution is computed using real-life data examples, and the goodness of fit of the proposed distribution is verified using the AIC (Akaike's Information criteria) and BIC (Bayesian Information criteria) values. The real-life neutrosophic data (see Table 4) of population density of some villages in the USA are considered, see Albassam et al. [2].

Table 4 Population density of villages in the USA
Full size table

The MLE approaches are used to determine the parameters of the DUS-NW(\(\alpha ,\beta )\) distribution, and the goodness of fit is used to assess the performance of the models. The estimates are shown in Table 5.

Table 5 Estimation of parameters and goodness of fit the distribution
Full size table

In terms of neutrosophy, it can be demonstrated that given results of DUS-NW(\(\alpha ,\beta )\) in terms of imprecision and uncertainty are more accurate and flexible, rather than ignoring imprecision and uncertainty that of DUS-Weibull. As a result, when the data have an interval measure \(({I}_{N})\) and contains some indeterminacy, the recommended DUS-NW((\(\alpha ,\beta )\) distribution has more accurate results than the standard DUS-Weibull distribution. Moreover, DUS-NW(\(\alpha ,\beta )\) has a better-fit and contending results among all other distributions mentioned in the study.

Conclusion

Unlike classical probability distributions, which accept a specific value, neutrosophic probability distributions adopt an intrusive approach to explaining and solving a wide range of real-world situations. This explains why neutrosophic statistics take into account aberrant and imprecise values that classical logic ignores. The Weibull distribution has a wide range of applications in several disciplines such as engineering system, reliability, and sampling plans so that by considering the interval form of data that have imprecisions and arises in many real-life scenarios, thus a DUS-transformation on Neutrosophic Weibull distribution have been proposed. It has been established with several properties of the proposed distribution such as shape, the measure of spread r-th moment, hazard rate function, generating functions, and order statistics. An MLE approach was performed for estimating the parameters. The efficiency of the distribution was investigated by a simulation study. The flexibility of the proposed distribution is driven with an application to a real-life data set with comparison to the classical distributions and Neutrosophic Weibull. It has been concluded that the proposed DUS-NW offers reliable results even by dealing with data's indeterminacy and uncertainty. The study can be further extended to neutrosophic multivariate statistics considering many parameters. Furthermore, future research can be made to plithogenic statistics [35] which is a generalization of classical multivariate statistics.