Introduction

Order statistics has been playing important role in many areas including quality control and inference. It is used in ordering the data and used to deal with the application of these ordered data and their related functions. In acceptance sampling plans, the order statistics is used to shorten the failure data and use to improve the robustness of sampling plans [15]. Evans et al. [9] applied the discrete random variable from order statistics in bootstrapping. Shi et al. [16] studied the application of correlated random variables from order statistics at-speed testing. Chen [5] discussed the use of order statistics in various statistical tests and in clinical studies. The order statistics is applied in statistical tests to give minimum variance unbiased estimators. Dytso et al. [8] discussed the application of order statistics in image denoising. Bhoj and Chandra [4] applied the order statistics for skewed distribution. More applications of order statistics can be seen in [1, 10, 12,13,14, 20] discussed that the measurement quantities are not always imprecise. Classical statistics cannot be applied in the presence of imprecise data. Neutrosophic statistics is an extension of classical statistics and is applied when imprecise data is presented [17]. Chen et al. [6, 7] discussed the methods to analyze the neutrosophic data. Aslam [3] proposed an algorithm to generate random variables from the DUS-neutrosophic Weibull distribution. Recently, Florentin [18] proved the efficiency of neutrosophic statistics over interval statistics and classical statistics. Jdid et al. [11] presented generating the random variable method from the uniform distribution.

The existing order statistics methods cannot be applied when imprecise data is presented. According to the best of our knowledge, there is no work on order statistics under neutrosophic statistics. We will introduce neutrosophic order statistics first and then we will design algorithms to generate neutrosophic random numbers. In this paper, we will propose a generator to generate random numbers from neutrosophic statistics. We will present the algorithms to generate minimum neutrosophic data and maximum neutrosophic data from the Weibull distribution. The neutrosophic data will be presented for various measures of indeterminacy to see its effect on neutrosophic data. Based on the simulation study, it is expected the reduction in neutrosophic data as the degree of indeterminacy is increased.

Neutrosophic order statistics

Let \({x}_{N}={x}_{L}+{x}_{U}{I}_{N};{I}_{N}\epsilon \left[{I}_{L},{I}_{U}\right]\) and \({n}_{nN}={n}_{L}+{n}_{U}{I}_{N};{I}_{N}\epsilon \left[{I}_{L},{I}_{U}\right]\) be neutrosophic random variable and neutrosophic sample size, respectively. Note that the first values in both neutrosophic forms present the determinate value (classical statistics) and the second values present the indeterminate part. Rearranging \({n}_{nN}\) neutrosophic sample in ascending order \({x}_{\left(1N\right)},{x}_{\left(2N\right)},{x}_{\left(3N\right)},\dots ,{x}_{\left(nN\right)}\), where \({x}_{\left(iN\right)}\) be the \(ith\) smaller value in \({n}_{nN}\). Let \({y}_{N}\) presents \(ith\) neutrosophic shorted values from \({x}_{\left(1N\right)},{x}_{\left(2N\right)},{x}_{\left(3N\right)},\dots ,{x}_{\left(nN\right)}\) with the following neutrosophic probability density function (npdf):

$$g\left({y}_{N}\right)=g\left({y}_{L}\right)+g\left({y}_{U}\right){I}_{N{y}_{N}};{I}_{N{y}_{N}};{I}_{N{y}_{N}}\epsilon \left[{I}_{L{y}_{L}},{I}_{U{y}_{U}}\right]$$
(1)
$$\mathrm{where}\,g\left({y}_{N}\right)\epsilon \left[\left(\frac{{n}_{L}!}{\left[\left({i}_{L}-1\right)!\left({n}_{L}-{i}_{L}\right)!\right]f\left({y}_{L}\right)F{\left({y}_{L}\right)}^{{i}_{L}-1}{\left[1-F\left({y}_{L}\right)\right]}^{{n}_{L}-{i}_{L}}}\right),\left(\frac{{n}_{U}!}{\left[\left({i}_{U}-1\right)!\left({n}_{U}-{i}_{U}\right)!\right]f\left({y}_{U}\right)F{\left({y}_{U}\right)}^{{i}_{U}-1}{\left[1-F\left({y}_{U}\right)\right]}^{{n}_{u}-{i}_{U}}}\right)\right]$$
(2)

Let \({y}_{N}\) be a minimum value of the data \({y}_{N}=min\left({x}_{1N},{x}_{2N},{x}_{3N},\dots ,{x}_{nN}\right)\). The npdf of \({y}_{N}\) by following [19] is given by

$$g\left({y}_{N}\right)={n}_{N}f\left({y}_{N}\right){\left[1-F\left({y}_{N}\right)\right]}^{{n}_{N}-1};{n}_{N}\epsilon \left[{n}_{L},{n}_{U}\right]$$
(3)

The ncdf of \({y}_{N}\) is given by:

$$G\left({y}_{N}\right)={\left[1-F\left({y}_{N}\right)\right]}^{{n}_{N}};{n}_{N}\epsilon \left[{n}_{L},{n}_{U}\right]$$
(4)

Suppose that \({w}_{N}\) be the maximum value of the data from NWD. By following [19], the npdf of \({w}_{N}={\text{max}}({x}_{1N},{x}_{2N},{x}_{3N},\dots ,{x}_{nN})\) is given by:

$$g\left({w}_{N}\right)={n}_{N}f\left({w}_{N}\right){\left[F\left({w}_{N}\right)\right]}^{{n}_{N}-1};{n}_{N}\epsilon \left[{n}_{L},{n}_{U}\right]$$
(5)

The ncdf of \({w}_{N}\) is given by:

$$G\left({w}_{N}\right)={\left[F\left({w}_{N}\right)\right]}^{{n}_{N}};{n}_{N}\epsilon \left[{n}_{L},{n}_{U}\right]$$
(6)

Algorithm to generate minimum neutrosophic value

From [2], the npdf of the neutrosophic Weibull distribution (NWD) is given by.

$$f\left({x}_{N}\right)=\left\{\left(\frac{\beta }{\alpha }\right){\left(\frac{{x}_{N}}{\alpha }\right)}^{\beta -1}{e}^{-{\left(\frac{{x}_{N}}{\alpha }\right)}^{\beta }}\right\}+\left\{\left(\frac{\beta }{\alpha }\right){\left(\frac{{x}_{N}}{\alpha }\right)}^{\beta -1}{e}^{-{\left(\frac{{x}_{N}}{\alpha }\right)}^{\beta }}\right\}{I}_{N}; {I}_{N}\epsilon \left[{I}_{L},{I}_{U}\right]$$
(7)

The neutrosophic cumulative distribution function (ncdf) of the NWD is given by:

$$F\left({x}_{N}\right)=1-\left\{{e}^{-{\left(\frac{{x}_{N}}{\alpha }\right)}^{\beta }}\left(1+{I}_{N}\right)\right\}+{I}_{N}; {I}_{N}\epsilon \left[{I}_{L},{I}_{U}\right]$$
(8)

Let \(G\left({y}_{N}\right)={u}_{N}\) and \(F\left({y}_{N}\right)={v}_{N}\) in Eq. (4), we have

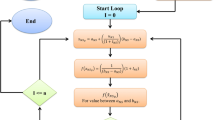
$${v}_{N}=\left[1-{\left({u}_{N}\right)}^{\frac{1}{{n}_{N}}}\right];{n}_{N}\epsilon \left[{n}_{L},{n}_{U}\right]$$
(9)

To generate the neutrosophic minimum data of \({n}_{N}\) from \({x}_{N}\) follows NWD, the following routine will be run:

Step-1: Generate a uniform random number between 0 and 1 that is \({u}_{N}\sim U(\mathrm{0,1})\).

Step-2: Specify \({I}_{N}\), \(\alpha\) and \(\beta\).

Step-3: Compute the values of \({v}_{N}\) using Eq. (9).

Step-4: Use the inverse transform method, compute \({y}_{N}={F}^{-1}\left({v}_{N}\right)\)

Step-5: Return \({y}_{N}\)

The operational process to generate the minimum neutrosophic value is shown in Fig. 1.

Fig. 1
figure 1

Algorithm to generate minimum value

Full size image

The minimum neutrosophic values are generated using the above-mentioned algorithm and are shown in Tables 1, 2, 3, 4 and 5. Tables 1, 2, 3, 4 and 5 present these values for various values of measure of indeterminacy \({I}_{N}\) \(\alpha ,\) \(\beta\) and \(n\). From Tables 1, 2, 3, 4 and 5, it is clear for other same values, as \({I}_{N}\) increases, we note the decreasing trend in minimum neutrosophic values. We also note that for other same parameters, when \(\alpha\) increases, the values of minimum neutrosophic values are increased.

Table 1 Random variate when \(\alpha =0.5\), \(\beta =0.5\) and \(n\) = 15
Full size table
Table 2 Random variate when \(\alpha =1\), \(\beta =0.5\) and \(n\) = 15
Full size table
Table 3 Random variate when \(\alpha =1\), \(\beta =1\) and \(n\) = 15
Full size table
Table 4 Random variate when \(\alpha =2\), \(\beta =0.5\) and \(n\) = 15
Full size table
Table 5 Random variate when \(\alpha =2\), \(\beta =1\) and \(n\) = 15
Full size table

Comparative analyses of minimum neutrosophic values

As discussed before that neutrosophic statistics is an extension of classical statistics. Neutrosophic statistics reduces to classical statistics when \({I}_{L}=0\). In this section, we will compare the results of minimum neutrosophic values with the minimum values obtained under classical statistics. The minimum values under classical statistics are shown in Tables 1, 2, 3, 4 and 5. Figure 2 shows the behavior of minimum neutrosophic values for exponential distribution \(\left(\alpha =1,\beta =1\right)\) for various values of \({I}_{N}\). Figure 2 depicts that there is no specific trend in minimum neutrosophic values. But, it is interesting to be noted that the curve of minimum values from the exponential distribution under classical statistics is higher than the other minimum neutrosophic values of \({I}_{N}>0\). From this study, it is concluded that under uncertainty, the minimum random variate is smaller than the minimum random variate under classical statistics.

Fig. 2
figure 2

Minimum neutrosophic values for various \({I}_{N}\)

Full size image

Effect of parameters on random variates

In this section, we will explore how the parameters of the Weibull distribution impact the generation of minimum random variate values. We present Tables 1, 2, 3, 4 and 5, each showcasing various combinations of \(\alpha\) and \(\beta\) values. Specifically, Table 1 displays results for \(\alpha\)=0.5, \(\beta\)=0.5, and \(n\)=15. Table 2 features data for \(\alpha\)=1, \(\beta\)=0.5, and \(n\)=15. Table 3 presents results for \(\alpha\)=1, \(\beta\)=1, and \(n\)=15. Additionally, Table 4 shows outcomes for \(\alpha\)=2, \(\beta\)=0.5, and \(n\)=15, while Table 5 reveals data for \(\alpha\)=2, \(\beta\)=1, and \(n\)=15. To investigate how these parameters influence the generation of random variates, we introduce Figs. 3 and 4. Figure 3 is presented with \(\alpha\)=0.5, 0.10, and \(\beta\)=0.5, shedding light on the effect of \(\alpha\) on random variates while keeping \(\beta\) constant. Notably, Fig. 3 demonstrates an increasing trend in random variate values as \(\mathrm{\alpha }\) progresses from 0.5 to 1, for the same \(\beta\) value of 0.5. In Fig. 4, we examine the behavior of random variates when α remains the same but \(\upbeta\) varies. This figure showcases the impact of different \(\beta\) values (0.5 and 1.0) on random variates when \(\alpha\)=2. It is evident from Fig. 4 that as \(\beta\) increases, the values of random variates also show an increase. Therefore, Fig. 4 illustrates the rising trend in random variates as \(\beta\) changes from 0.5 to 1 when \(\mathrm{\alpha }\) is set to 2.

Fig. 3
figure 3

Minimum neutrosophic values when \({I}_{N}\) = 0.4

Full size image
Fig. 4
figure 4

Minimum neutrosophic values when \({I}_{N}\) = 0.4

Full size image

Algorithm to generate maximum neutrosophic value

Let \(G\left({w}_{N}\right)={u}_{N}\) and \(F\left({w}_{N}\right)={v}_{N}\) in Eq. (4), we have

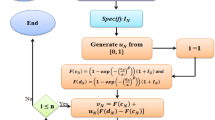
$${v}_{N}=\left[{\left({u}_{N}\right)}^{\frac{1}{{n}_{N}}}\right];{n}_{N}\epsilon \left[{n}_{L},{n}_{U}\right]$$
(10)

To generate the neutrosophic minimum data of \({n}_{N}\) from \({x}_{N}\) follows NWD, the following routine will be run:

Step-1: Generate a uniform random number between 0 and 1 that is \({u}_{N}\sim U(\mathrm{0,1})\).

Step-2: Specify \({I}_{N}\), \(\alpha\) and \(\beta\).

Step-3: Compute the values of \({v}_{N}\) using Eq. (10).

Step-4: Use the inverse transform method, compute \({w}_{N}={F}^{-1}\left({v}_{N}\right)\)

Step-5: Return \({w}_{N}\)

The operational process to generate the maximum neutrosophic value is shown in Fig. 5.

Fig. 5
figure 5

Algorithm to generate maximum value

Full size image

The maximum neutrosophic values are generated using the above-mentioned algorithm and are shown in Tables 6, 7, 8, 9 and 10. Tables 6, 7, 8, 9 and 10 present these values for various values of measure of indeterminacy \({I}_{N}\) \(\alpha ,\) \(\beta\) and \(n\). From Tables 1, 2, 3, 4 and 5, it is clear for other same values, as \({I}_{N}\) increases, we note the decreasing trend in maximum neutrosophic values. We also note that for other same parameters, when \(\alpha\) increases, the values of maximum neutrosophic values are increased.

Table 6 Maximum Random variate when \(\alpha =0.5\), \(\beta =0.5\) and \(n\)= 15
Full size table
Table 7 Maximum Random variate when \(\alpha =1\), \(\beta =0.5\) and \(n\)= 15
Full size table
Table 8 Maximum Random variate when \(\alpha =1\), \(\beta =1\) and \(n\) = 15
Full size table
Table 9 Maximum Random variate when \(\alpha =2\), \(\beta =0.5\) and \(n\) = 15
Full size table
Table 10 Maximum Random variate when \(\alpha =2\), \(\beta =1\) and \(n\) = 15
Full size table

Comparative analyses of maximum neutrosophic values

As discussed before that neutrosophic statistics is an extension of classical statistics. Neutrosophic statistics reduces to classical statistics when \({I}_{L}=0\). In this section, we will compare the results of maximum neutrosophic values with the maximum values obtained under classical statistics. The maximum values under classical statistics are shown in Tables 1, 2, 3, 4 and 5. Figure 6 shows the behavior of maximum neutrosophic values for exponential distribution \(\left(\alpha =1,\beta =1\right)\) for various values of \({I}_{N}\). Figure 6 depicts that there is no specific trend in maximum neutrosophic values. But, it is interesting to be noted that the curve of maximum values from the exponential distribution under classical statistics is higher than the other maximum neutrosophic values of \({I}_{N}>0\). From this study, it is concluded that under uncertainty, the maximum random variate is smaller than the maximum random variate under classical statistics.

Fig. 6
figure 6

Maximum neutrosophic values for various \({I}_{N}\)

Full size image

Discussion

We have introduced algorithms designed to compute both the minimum and maximum values from a Weibull distribution. Random number generation plays a ubiquitous role in computing. Simulated data proves invaluable when obtaining the original data is challenging or impossible. Simulated data finds application across a multitude of fields, such as medical science, survey research, reliability analysis, machine learning, and computer science. However, the algorithms currently used in computer systems for generating simulated data often overlook the consideration of the measure of indeterminacy in generating random variates. The adoption of our proposed algorithms allows for the generation of minimum and maximum values from the Weibull distribution under conditions of uncertainty.

Concluding remarks

New algorithms to generate minimum and maximum neutrosophic data were generated using the Weibull distribution in the paper. The neutrosophic random variate was presented for various values of shape and scale parameters of the Weibull distribution. From the study, it was observed that the measure of indeterminacy affected the random variate significantly. From the tables, it was noted that as the measure of indeterminacy increases, the minimum and maximum values of neutrosophic data decrease. The neutrosophic data presented in the paper can be applied where it is difficult to record the original data under complexity. The algorithms we've proposed for various statistical distributions hold promise for future research applications. Furthermore, there is potential for future research to delve into the development of statistical tests tailored to fit neutrosophic ordered statistics. Additionally, the exploration of computer software for generating random variates through our proposed methodology stands as a viable avenue for future research.