Introduction

The Poisson distribution is a popular model for count data. However its use is restricted by the equality of its mean and variance (equi-dispersion). Many models with the ability to represent under-, equi- and over- dispersion have been proposed in the research literature to overcome this restriction. Notable among these distributions are the hyper-Poisson (HP) of Bardwell and Crow (1964), generalized Poisson of Consul (1989), double-Poisson of Efron (1986), Poisson polynomial of Cameron and Johansson (1997), weighted Poisson of Castillo and Pérez-Casany (2005) and COM-Poisson of Conway and Maxwell (1962) (see also Shmueli et al., 2005).

Of these models the HP distribution was first proposed by Bardwell and Crow (1964) and Crow and Bardwell (1965). The probability mass function (pmf) of the HP with parameters (λ, β) distribution is given by

$$ P\left( X= k\right)=\frac{\varGamma \left(\beta \right)}{\varGamma \left( k+\beta \right)}\frac{\lambda^k}{\varphi \left(1,\beta; \lambda \right)}, k=0,1,2,\cdots; \lambda >0 $$
(1)

where \( \varphi \left(1,\beta; \lambda \right)={\displaystyle \sum_{j=0}^{\infty}\frac{(1)_j}{{\left(\beta \right)}_j}\frac{\lambda^j}{j!}}, \) is the confluent hypergeometric function and (β) j  = β(β + 1) ⋯ (β + j − 1).

The pmf has a simple recurrence relation, that is,

$$ \left(\beta + k\right) P\left( X= k+1\right)=\lambda P\left( X= k\right),\kern0.48em k=1,2,3,.... $$

The probability generating function (pgf) is given by

$$ P(s)=\varphi \left(1,\beta; \lambda s\right)/\varphi \left(1,\beta; \lambda \right). $$

Staff (1964) studied a displaced Poisson distribution which is the HP distribution with the parameter β restricted to be a positive integer. The case when β is negative was investigated later by Staff (1967). The HP distribution attracted the attention of many researchers of late. Kemp (2002) dealt with a q-analogue of the distribution and Ahmad (2007) proposed a Conway-Maxwell-HP distribution. Roohi and Ahmad (2003a, 2003b) investigated moments of the HP distribution. Kumar and Nair (2011, 2012, 2013, 2015) studied various extensions and alternatives of the HP distribution. Sáez-Castillo and Conde-Sánchez (2013) studied a HP regression model for over-dispersed and under-dispersed count data. Best (2001) and Antic et al. (2006) considered the HP distribution in word length and text length research. Khazraee et al. (2015) investigated the application of the HP generalized linear model for analyzing motor vehicle crashes.

Since the HP distribution is an important model for applications and is able to handle under- and over- dispersion, where there are relatively fewer models with this feature, it is of interest to add further flexibility to the HP distribution especially for empirical modeling. Another advantage of such a generalization is that it will result in representing a larger family of distributions and avoids piecemeal analysis. In this paper we propose a new generalization of the HP distribution by replacing Γ(k + β) in (1) with Γ(α k + β), α > 0 and the normalization constant becomes E α, β (λ) which is the generalized Mittag-Leffler function defined by

$$ {E}_{\alpha, \beta}\left(\lambda \right)={\displaystyle \sum_{j=0}^{\infty }{\lambda}^j/\varGamma \left(\alpha j+\beta \right)} $$
(2)

Consequently the proposed distribution is called the Mittag-Leffler function distribution (MLFD). In general adding an extra parameter increases the complexity. However, for the MLFD, the extra parameter α adds flexibility but retains computational tractability since computation of E α, β (λ) does not pose a problem due to many software packages (example MATLAB) which offered routines for its quick computation. When α = β = 1, the MLFD is the Poisson distribution which is equi-dispersed. However for α, β ≠ 1, the MLFD still can be equi-dispersed and this characteristic allows more flexibility in modeling of equi-dispersion by a non-Poisson multi-parameter model compared to the single parameter Poisson model. The MLFD is shown to be log-concave and this confers a number of attractive properties for modeling and inference; see Walther (2009) for a good review of statistical modeling and inference with log-concave distributions. The proposed MLFD should not be confused with a class of discrete Mittag-Leffler distributions proposed by Pillai and Jayakumar (1995). It is pertinent to give a brief review of some developments in statistical models involving the Mittag-Leffler function.

The Mittag-Leffler function (with β = 1 in (2) and is denoted by E α (z)) was first introduced by Swedish mathematician Gosta Mittag-Leffler (1903; 1905) and it arises as the solution of a fractional differential equation. This function and its many extended versions were studied by many mathematicians over the years. Haubold et al. (2011) have given a good survey on the Mittag-Leffler function. Recently, this function has also been explored for applications in statistics. Pillai (1990) showed that 1 − E α (−z α), 0 < α ≤ 1 are valid cumulative distribution functions (cdf) and named it as Mittag-Leffler distribution with cdf and pdf respectively given by

$$ \begin{array}{l} F\left( x;\alpha \right)={\displaystyle \sum_{j=1}^{\infty }{\left(-1\right)}^{j-1}{x}^{j\;\alpha}/\varGamma \left(\alpha j+1\right)}, x>0,0<\alpha \le 1\kern0.6em \mathrm{and}\\ {} f\left( x;\alpha \right)={\displaystyle \sum_{j=1}^{\infty }{\left(-1\right)}^{j-1}\left( j\alpha \right){x}^{j\;\alpha -1}/\varGamma \left(\alpha j+1\right)}, x>0,0<\alpha \le 1\end{array} $$
(3)

Since for α = 1 this distribution reduces to the exponential distribution with mean 1, it can be treated as a generalization of the exponential distribution. Pillai (1990) studied different properties of this distribution. Jose and Pillai (1986), Jayakumar and Pillai (1993), Lin (1998), Jayakumar (2003), Jose et al. (2010) studied different aspects of this distribution.

Pillai and Jayakumar (1995) proposed a class of discrete Mittag-Leffler (DML) distributions having pgf P(z) = E(z X) = 1/[1 + c(1 − z)α]. The DML distribution arises as a mixture of the Poisson distribution with parameter θλ, where θ is a constant and λ follows the Mittag-Leffler distribution in (3). They have studied different properties of the DML distribution, gave a probabilistic derivation and an application in a first order autoregressive discrete process. The DML is also a particular case of the discrete Linnik distribution (Devroye, 1990).

Jose and Abraham (2011) introduced another discrete distribution based on the Mittag-Leffler function which arises when the exponential waiting time distribution in the usual Poisson process is replaced by the Mittag-Leffler distribution. The pmf of this distribution is

$$ P\left( X= k\right)={\displaystyle \sum_{i= k}^{\infty}\left(\begin{array}{l} i\\ {} k\end{array}\right)\;{\left(-1\right)}^{\left( i- k\right)}{z}^{i\;\alpha}/\varGamma \left(\alpha\;i+1\right)}, k=0,1,\cdots; 0<\alpha \le 1. $$
(4)

In this article we have taken a completely different route to propose a discrete distribution based on the Mittag-Leffler function. The proposed distribution, which under certain conditions also arises from a queuing theory setup, is simple and extremely flexible in its shape and modality and it can model under-, equi- and over- dispersed count data. Section 2 defines the MLFD and basic structural properties are given. MLFD as a distribution in a queuing system is given in Section 3. Reliability and stochastic ordering properties are discussed in Section 4. Section 5 deals with parameter estimation and examples of applications of MLFD. The conclusion is given in Section 6.

Mittag-Leffler Function Distribution: Definition and Properties

In this section we define the proposed MLFD and investigate its main distributional, reliability and ordering properties.

Definition 1. A discrete random variable X is said to follow the MLFD with parameters (λ, α, β) if its pmf is defined by

$$ P\left( X= k\right)={\lambda}^k/\left\{\varGamma \left(\alpha k+\beta \right)\;{E}_{\alpha, \beta}\left(\lambda \right)\right\}, k=0,1,2,\cdots; \lambda, \alpha, \beta >0 $$
(5)

where \( {E}_{\alpha, \beta}\left(\lambda \right)={\displaystyle \sum_{j=0}^{\infty }{\lambda}^j/\varGamma \left(\alpha j+\beta \right)} \) is the generalized Mittag-Leffler function. The distribution henceforth will be denoted by MLFD (λ, α, β).

Remark 1: The MLFD pmf (5) may be obtained by replacing k ! in the Poisson pmf e − λ λ k/k ! with Γ(αk + β), and the normalization constant e − λ is now 1/E α, β (λ).

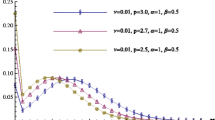
It may be noted that the proportion of zeros given by P(X = 0) = 1/{Γ(β) E α, β (λ)}, increases with increase in β (see Fig. 1(b)) when (λ, α) are fixed; increases with decrease in λ (see Fig. 1(c) and (d)) for fixed (α, β); and increases (decreases) with α > (<) 1 (see Fig. 1(e) and (f)) for fixed (λ, β). Whereas when β → 0+ the proportion of zeros decreases (see Fig. 1(b)) with the pmf proportional to λ k/Γ(αk) , k = 0, 1, 2, ⋯.

Fig. 1
figure 1

Plots of MLFD (λ, α, β) pmf for some values of the parameters

Full size image

Recurrence relation between probabilities

The MLFD (λ, α, β) pmf in (5) has a simple recurrence relation given by

$$ \varGamma \left(\alpha\;k+\alpha +\beta \right)\; P\left( X= k+1\right)=\lambda \kern0.24em \varGamma \left(\alpha\;k+\beta \right)\; P\left( X= k\right), k\ge 1 $$
(6)

with P(X = 0) = 1/{Γ(β) E α, β (λ)}.

When α is a positive integer, (6) can be expressed as (αk + β) α P(X = k + 1) = λP(X = k).

The distribution exhibits long tailedness for 0 < α < 1 as the ratio of successive probabilities varies slowly (this corresponds to over-dispersion) as k tends to infinity while for α ≥ 1 this ratio tends to zero faster implying presence of a Poisson-type tail.

The recurrence relation in (6) facilitates easy computation of the probabilities. The computation of the normalizing constant E α, β (λ) is only required for P(X = 0).

Note that the recurrence relation (or the difference equation) in (6) reduces to that of HP (λ, β) distribution for α = 1 and displaced Poisson distribution when α = 1 and β is an integer (further discussed in Section 2.5.1).

Computation of the generalized Mittag-Leffler function Eαβ(λ)

For statistical inference and applications it is necessary to compute the generalized Mittag-Leffler function E α, β (λ), which is the normalizing constant, where

$$ {E}_{\alpha, \beta}\left(\lambda \right)={\displaystyle \sum_{j=0}^{\infty }{\lambda}^j/\varGamma \left(\alpha j+\beta \right)}. $$

Numerical computation of the generalized Mittag-Leffler function is well-researched. Seybold and Hilfer (2008) gave a numerical algorithm for calculating the generalized Mittag-Leffler function for arbitrary complex argument z and real parameters α and β based on a Taylor series, exponentially improved asymptotics and integral representation. If |λ| ≤ 1, a simple way to compute E α, β (λ) is to calculate the terms a j  = λ j/Γ(αj + β) in the infinite series E α, β (λ) by employing the recurrence relation a j + 1/a j  = λ/(αj + β) with a 0 = 1/Γ(β) (see Lee et al., 2001). This avoids the computation of the gamma function Γ(x). The summation is terminated when a j is very small. The error estimate is given by Theorem 4.1 of Seybold and Hilfer (2008) which determines the number of terms N such that

$$ {E}_{\alpha, \beta}\left(\lambda \right)\approx {\displaystyle \sum_{j=0}^N{\lambda}^j/\varGamma \left(\alpha j+\beta \right)}. $$

For other values of λ, asymptotic series and integral representation (see equations (2.3), (2.4) and (2.7) of Seybold and Hilfer, 2008) are employed. Error estimates are also given for these cases. The computation of the Mittag-Leffler function is given by many software packages like Matlab (MLF (alpha, Z, P)) and Mathematica (MittagLefflerE [a, b, z]). (See also Gorenflo et al., 2002.) See also Garrappa (2015) for a recent contribution towards numerical evaluation of Mittag-Leffler function.

Shapes of pmf

The pmf of MLFD (λ, α, β) is plotted for a number of combinations of parameters to study the different shapes of the distribution.

From the plots of the pmf it is seen that the distribution can be unimodal with nonzero mode (see Fig. 1(a)) or it can have nonzero modes at two points (see Fig. 1(h)) or non-increasing with the mode at 0 (see Fig. 1(g)). See Section 4.3 item (i) for further discussion on the modes.

Cumulative distribution function and generating functions

The cumulative distribution function (cdf) of X ~ MLFD (λ, α, β) is seen to be

$$ P\left( X\le r\right)=1-{\lambda}^{r+1}\;\left[{E}_{\alpha, \beta +\left( r+1\right)\alpha}\left(\lambda \right)/{E}_{\alpha, \beta}\left(\lambda \right)\right] $$

by using the known relation \( {\lambda}^r{E}_{\alpha, \beta + r\;\alpha}\left(\lambda \right)={E}_{\alpha, \beta}\left(\lambda \right)-{\displaystyle \sum_{j=0}^{r-1}{\lambda}^j/\varGamma \left(\alpha j+\beta \right)} \) (Haubold et al., 2011).

The pgf is given in terms of E α,β (λ) as

$$ P(s)= E\left({s}^X\right)={E}_{\alpha, \beta}\left(\lambda\;s\right)/{E}_{\alpha, \beta}\left(\lambda \right),0<\lambda s $$

The moment generating function (mgf) and the factorial moment generating function (fmgf) are obtained from the pgf as

$$ {E}_{\alpha, \beta}\left(\lambda\;{e}^s\right)/{E}_{\alpha, \beta}\left(\lambda \right)\kern0.37em \mathrm{and}\;{E}_{\alpha, \beta}\left(\lambda\;\left(1+ s\right)\right)/{E}_{\alpha, \beta}\left(\lambda \right)\;\mathrm{respectively}. $$

Related distributions and connections with other families of distributions

Particular cases of MLFD (λ, α, β)

The MLFD (λ, α, β) includes a number of well-known distributions as particular cases:

  1. (i)

    When α = β = 1, MLFD (λ, α, β) reduces to the Poisson distribution with parameter λ.

  2. (ii)

    When α = 0, β (≥0) MLFD (λ, α, β) becomes the geometric distribution with parameter λ provided 0 < λ < 1. Since for α → 0+, \( \underset{\alpha \to {0}^{+}}{ \lim }{E}_{\alpha, \beta}\left(\lambda \right)\to {\displaystyle \sum_{j=0}^{\infty}\frac{\lambda^j}{\varGamma \left(\beta \right)}}=\frac{1}{\left(1-\lambda \right)\varGamma \left(\beta \right)},0<\lambda <1 \) (Hanneken et al., 2009).

  3. (iii)

    When α = 1, β (≥0) MLFD (λ, α, β) reduces to the HP (λ, β) distribution (Bardwell and Crow, 1964; Johnson et al., 2005, p. 200).

Proof: \( P\left( X= k\right)=\frac{\lambda^k}{\varGamma \left( k+\beta \right){E}_{1,\beta}\left(\lambda \right)}, k=0,1,2,\cdots; \lambda >0 \) where \( {E}_{1,\beta}\left(\lambda \right)={\displaystyle \sum_{j=0}^{\infty }{\lambda}^j/\varGamma \left( j+\beta \right)=}{\displaystyle \sum_{j=0}^{\infty }{\lambda}^j/\left\{{\left(\beta \right)}_j\varGamma \left(\beta \right)\right\}} \) \( =\frac{1}{\varGamma \left(\beta \right)}{\displaystyle \sum_{j=0}^{\infty}\frac{(1)_j}{{\left(\beta \right)}_j}\frac{\lambda^j}{j!}}=\frac{\varphi \left(1,\beta; \lambda \right)}{\varGamma \left(\beta \right)} \).

Hence P(X = k) reduces to the pmf of HP (λ, β) distribution given in Eq. (1).

An alternative form of the pmf of the HP (λ, β) distribution when β > 1 can be seen as

$$ P\left( X= k\right)=\frac{\varGamma \left(\beta -1\right)}{\varGamma \left( k+\beta \right)}\frac{e^{-\lambda}{\lambda}^{k+\beta -1}}{\gamma \left(\beta -1,\lambda \right)}, k=0,\, 1,\, 2,\cdots; \, \lambda >0,\, \beta >1, $$

since \( {E}_{1,\beta}\left(\lambda \right)=\frac{\lambda^{1-\beta}\;{e}^{\lambda}\;\gamma \left(\beta -1,\lambda \right)}{\varGamma \left(\beta -1\right)} \) (see Simon, 2013), where \( \gamma \left( u,\lambda \right)={\displaystyle \underset{0}{\overset{\lambda}{\int }}{e}^{- y}\;{y}^{u-1}\; dy} \) is the incomplete gamma function.

  1. (iv)

    When α = 1 and β (=t + 1) is a positive integer, MLFD (λ, α, β) reduces to the displaced Poisson distribution (see Staff, 1964; Johnson et al., 2005, p. 200) with parameter λ and t.

In addition, the following new distributions involving hyperbolic and error functions are also seen as particular cases.

  1. (v)

    When α = 2 and β = 2, MLFD (λ, α, β) reduces to a new discrete distribution with parameter λ and pmf

    $$ P\left( X= k\right)=\frac{\lambda^{k+\left(1/2\right)}}{\varGamma \left(2\left( k+1\right)\right)}\frac{\kern0.24em 1}{ \sinh \left(\sqrt{\lambda}\right)}=\frac{{\left(\sqrt{\lambda}\right)}^{2 k+1}}{\left(2 k+1\right)!}\frac{\kern0.24em 1}{ \sinh \left(\sqrt{\lambda}\right)}, k=0,1,2,\cdots; \lambda >0, $$

since \( {E}_{2,2}\left(\lambda \right)= \sinh \left(\sqrt{\lambda}\right)/\sqrt{\lambda} \) (Haubold et al., 2011).

  1. (vi)

    When α = 2 and β = 1, MLFD (λ, α, β) reduces to a new distribution with parameter λ and pmf

    $$ P\left( X= k\right)=\frac{\lambda^k}{\varGamma \left(2 k+1\right)}\frac{\kern0.24em 1}{ \cosh \left(\sqrt{\lambda}\right)}=\frac{{\left(\sqrt{\lambda}\right)}^{2 k}}{\left(2 k\right)!}\frac{\kern0.24em 1}{ \cosh \left(\sqrt{\lambda}\right)}, k=0,1,2,\cdots; \lambda >0 $$

since \( {E}_{2,1}\left(\lambda \right)= \cosh \left(\sqrt{\lambda}\right) \) (Haubold et al., 2011).

  1. (vii)

    When α = 1/2 and β = 1, MLFD (λ, α, β) reduces to a new distribution with parameter λ and pmf

    $$ P\left( X= k\right)=\frac{ \exp \left(-{\lambda}^2\right)\kern0.24em {\lambda}^k}{\left( k/2\right)!\kern0.36em erfc\;\left(-\lambda \right)}, k=0,1,2,\cdots; \lambda >0 $$

    since \( {E}_{1/2,1}\left(\sqrt{\lambda}\right)= \exp \left(\lambda \right)\; erfc\;\left(-\sqrt{\lambda}\right) \) (Haubold et al., 2011) where erfc (λ) is the

    complementary error function defined as \( erfc\;\left(\lambda \right)=1- e r f\left(\lambda \right)=1-\frac{2}{\sqrt{\pi}}{\displaystyle \underset{0}{\overset{\lambda}{\int }} \exp \left(-{t}^2\right)\; dt} \).

Also \( erfc\;\left(\lambda \right)=2\;\left[\frac{1}{\sqrt{2\pi}}{\displaystyle \underset{-\infty }{\overset{-\sqrt{2}\lambda}{\int }} \exp \left(-{t}^2/2\right)\; dt}\right]=2\varPhi \left(-\sqrt{2}\lambda \right) \), Φ(.) being the cdf of the standard normal distribution.

  1. (viii)

    MLFD (λ, α, β) degenerates with mass only at zero for either α → ∞ or β → ∞ or both and also when λ → 0+.

Remark 2. For 0 ≤ α ≤ 1, the MLFD (λ, α, β) can be viewed as a continuous bridge between the geometric (α = 0) and HP (α = 1) distributions in the range of the parameter α; in particular, the MLFD (λ, α, 1) can be viewed as a continuous bridge between the geometric (α = 0) and Poisson (α = 1) distributions in the range of the parameter α, a property also shared by the COM-Poisson distribution.

MLFD as weighted Poisson distribution

The MLFD (λ, α, β) is seen as a weighted Poisson distribution as follows: If X ~ Poisson (λ) having pmf

$$ P\left( X= k\right)={e}^{-\lambda}{\lambda}^k/ k!, k=0,1,2,\cdots; \lambda >0, $$

then for integer α and β it can be shown that weighted distribution with weight function 1/(k + 1)(α − 1)k + β − 1 gives the pmf of MLFD (λ, α, β). Since the weight function 1/(k + 1)(α − 1)k + β − 1 is monotonically decreasing in k for α, β > 1, MLFD (λ, α, β) is stochastically smaller than the Poisson distribution when α, β > 1. (See Patil et al. 1986; Ross, 1983; Castillo and Pérez-Casany, 2005)

MLFD as member of some families of discrete distributions

  1. i.

    MLFD (λ, α, β) is a member of the generalized hypergeometric family (Kemp 1968a, b). This can be checked by comparing the recurrence relation in Eq. (6) with that of the generalized hypergeometric distributions (see equation (2.63) in page 91 of Johnson et al., 2005).

  2. ii.

    MLFD (λ, α, β) is a member of the generalized power series distribution (Patil 1962, 1964) when λ is the primary parameter.

  3. iii.

    For fixed values of the parameters α and β, the MLFD (λ, α, β) is also a member of the exponential family of distributions.

Moments and related results

Denoting \( E\left({X}^r\right)={\mu}_r^{/} \), E(X [r]) = μ [r] and E[{X − E(X)}r] = μ r , x [r] = x (x − 1) ⋯ (x − r + 1) and using the relation \( E\left({X}_{\left[ r\right]}\right)={\mu}_r^{/}=\frac{d^r}{d{ s}^r}{\left. P(s)\right|}_{s=1} \), where P(s) is the pgf of MLFD (λ, α, β) mentioned in Section 2.4, and along with a result for the derivative of E α, β (λ) with respect to λ given by

$$ \frac{d}{ d\lambda}\;{E}_{\alpha, \beta}\left(\lambda \right)=\frac{E_{\alpha, \beta -1}\left(\lambda \right)-\left(\beta -1\right){E}_{\alpha, \beta}\left(\lambda \right)}{\alpha\;\lambda}, $$

we can derive the following formulas:

\( {\mu}_1^{/}=\lambda \frac{d}{ d\lambda} \log \left[{E}_{\alpha, \beta}\left(\lambda \right)\right]=\frac{E_{\alpha, \beta -1}\left(\lambda \right)}{\;\alpha\;{E}_{\alpha, \beta}\left(\lambda \right)}-\frac{1-\beta}{\alpha} \), provided α > 0 and β > 1.

$$ {\mu}_2^{/}=\frac{1}{\alpha^2}\frac{E_{\alpha, \beta -2}\left(\lambda \right)}{\;{E}_{\alpha, \beta}\left(\lambda \right)}-\frac{2\beta -3}{\alpha^2}\frac{E_{\alpha, \beta -1}\left(\lambda \right)}{\;{E}_{\alpha, \beta}\left(\lambda \right)}+{\left(\frac{\beta -1}{\alpha}\right)}^2 $$

\( {\mu}_2=\frac{1}{\alpha^2}\left\{\frac{E_{\alpha, \beta -2}\left(\lambda \right)}{\;{E}_{\alpha, \beta}\left(\lambda \right)}-{\left(\frac{E_{\alpha, \beta -1}\left(\lambda \right)}{\;{E}_{\alpha, \beta}\left(\lambda \right)}\right)}^2+\frac{E_{\alpha, \beta -1}\left(\lambda \right)}{\;{E}_{\alpha, \beta}\left(\lambda \right)}\right\} \), provided α > 0 and β > 2.

The variance can also be expressed as

$$ {\mu}_2=\lambda \frac{d}{d\lambda}{\mu}_1^{/}=\lambda \frac{d}{d\lambda}\left[\lambda \frac{d}{d\lambda} \log \left[{E}_{\alpha, \beta}\left(\lambda \right)\right]\right]=\lambda \frac{d}{d\lambda} \log \left[{E}_{\alpha, \beta}\left(\lambda \right)\right]+{\lambda}^2\frac{d^2}{d{\lambda}^2} \log \left[{E}_{\alpha, \beta}\left(\lambda \right)\right] $$

The above results can alternatively be derived easily by first deriving E(αX + β)[r], r = 1, 2 and then simplifying.

In all the above expressions there is restriction on the values of β. This situation may be overcome by using the following relation repeatedly till the conditions are satisfied:

$$ {E}_{\alpha, \beta}\left(\lambda \right)=\left(1/\varGamma \left(\beta \right)\right)+\lambda\;{E}_{\alpha, \alpha +\beta}\left(\lambda \right) $$

(see Erdelyi 1955; Hanneken et al., 2009).

The gamma function for negative argument can be computed using the formula (Fisher and Kilicman, 2012)

$$ \varGamma \left(- n\right)=\left\{\begin{array}{l}-\varGamma \left(- n+1\right)/ n,\mathrm{when}\; n\ne 1,2,\cdots \\ {}{\left(-1\right)}^n/ n!\left\{\rho (n)-\gamma \right\}, n=1,2,\cdots \end{array}\right. $$

where \( \rho (n)={\displaystyle \sum_{i=1}^n\frac{1}{i}} \) and γ = − Γ /(1) is the Euler’s constant.

Recurrence relations of moments

The following recurrence relations hold:

  1. (i)
    $$ {\mu}_{r+1}^{/}=\lambda\;\frac{d}{ d\lambda}\;{\mu}_r^{/}+{\mu}_r^{/}\kern0.24em {\mu}_1^{/} $$
  2. (ii)
    $$ {\mu}_{r+1}=\lambda\;\frac{d}{ d\lambda}\;{\mu}_r+ r{\mu}_{r-1}\;{\mu}_2 $$
  3. (iii)
    $$ {\mu}_{{}^{\left[ r+1\right]}}=\lambda\;\frac{d}{ d\lambda}\;{\mu}_{{}^{\left[ r\right]}}+\left({\mu}_1^{/}- r\;\right){\mu}_{{}^{\left[ r\right]}} $$
  4. (iv)
    $$ E{\left(\alpha \left( X-1\right)+\beta \right)}_{\alpha}=\lambda +{\left(\beta -\alpha \right)}_{\alpha} P\left( X=0\right) $$

The relations (i) to (iii) can be proved by using the general relations for GPSD or by direct manipulation while (iv) follows from the difference equation in (6).

Since μ 2 > 0 and λ ≠ 0, \( {\mu}_2=\lambda\;\frac{d}{ d\lambda}\;{\mu}_1^{/}>0 \) implies \( \frac{d}{ d\lambda}\;{\mu}_1^{/}>0 \). Hence \( {\mu}_1^{/} \) is a monotonically increasing function of λ.

Alternative formulae for moments

An alternative formula for moments is given by

\( E\left[{\left( X+1\right)}_r\right]= r!{E}_{\alpha, \beta}^{r+1}\left(\lambda \right)/{E}_{\alpha, \beta}\left(\lambda \right) \),

where \( {E}_{\alpha, \beta}^{\rho}\left(\lambda \right)={\displaystyle \sum_{k=0}^{\infty}\frac{{\left(\rho \right)}_k}{k!}\frac{\lambda^k}{\varGamma \left(\alpha k+\beta \right)}} \) is the generalized Mittag-Leffler function (Prabhakar, 1971).

Proof: \( E\left[{\left( X+1\right)}_r\right]={\displaystyle \sum_{k=0}^{\infty}\frac{{\left( k+1\right)}_r{\lambda}^k}{\varGamma \left(\alpha k+\beta \right){E}_{\alpha, \beta}\left(\lambda \right)}} \) \( =\frac{r!}{E_{\alpha, \beta}\left(\lambda \right)}\;{\displaystyle \sum_{k=0}^{\infty}\frac{{\left( r+1\right)}_k}{k!}\frac{\lambda^k}{\varGamma \left(\alpha k+\beta \right)}} \)

$$ = r!{E}_{\alpha, \beta}^{r+1}\left(\lambda \right)/{E}_{\alpha, \beta}\left(\lambda \right) $$

since k ! (k + 1) r  = r ! (r + 1) k .

Approximation of the mean and variance for large values of λ

Using the result that for large values of λ, E α,β (λ) → {λ (1 − β)/α exp(λ 1/α)}/α (see Gerhold, 2012) we can derive approximations for the mean and variance of MLFD (λ, α, β) as (1 − β + λ 1/α)/α and λ 1/α/α 2 respectively. The expression for the mean follows from either \( {\mu}_1^{/}=\frac{E_{\alpha, \beta -1}\left(\lambda \right)}{\;\alpha\;{E}_{\alpha, \beta}\left(\lambda \right)}+\frac{1-\beta}{\alpha} \) or directly from \( {\mu}_1^{/}=\lambda \frac{d}{ d\lambda} \log \left[{E}_{\alpha, \beta}\left(\lambda \right)\right] \). Then variance can be obtained by using the relation \( {\mu}_2=\lambda\;\frac{d}{ d\lambda}\;{\mu}_1^{/} \).

In particular for MLFD (λ, α, 1) the approximate mean and variance will be λ 1/α/α and λ 1/α/α 2. These approximations are good when α ∈ (0, 2] (see Simon, 2013) and may be useful in a regression formulation where the covariates are linked through the mean and variance.

Index of dispersion

The index of dispersion (ID) is given by ID = Variance/Mean. Contour plots of ID for different choices of parameters (α, β) keeping λ = 0.25 and λ = 5 fixed are presented in Fig. 2(a) and (b) respectively to depict the contours of ID. Labels on a given line indicate the value of ID on that line. In these figures, the ID of the region on the left (right) of a given line is more (less) than the ID value on that given line.

Fig. 2
figure 2

ID of MLFD (λ, α, β) for some values of the parameters

Full size image

From Fig. 2 (a) and (b), it is obvious that the MLFD (λ, α, β) is very flexible with respect to the ID and is able to accommodate under-, equi- and over- dispersion in count data. Interestingly, this family includes a non-Poisson distribution with equi-dispersion when λ is kept fixed. Some such pairs of values for (α, β) can be easily taken from line of equi-dispersion in the contour plots in Fig. 2(a) when λ = 0.25 and from Fig. 2(b) when λ = 5.

Using results of the Section 2.6.3 for large values of λ it can be stated that the ID of MLFD (λ, α, β) is approximately given by λ 1/α/α((1 − β) + λ 1/α) which reduces to 1/α for MLFD. (λ, α, 1). Thus for large λ MLFD (λ, α, 1) expected to be over (under)- dispersed depending on α < (>)1, while MLFD (λ, α, β) will be under-dispersed in the region α > 1, β < 1.

MLFD (z, α, 1) as a distribution in a queuing system

MLFD (z, α, 1), like the COM-Poisson distribution, can be derived as the probability of the system being in the k-th state for a queuing system with state dependent service rate.

Consider a queuing system with Poisson inter arrival times with parameter λ, first-come- first-served policy, and exponential service times that depend on the system state (n-th state means n number of units in the system). The mean service time in the n-th state is μ n  = μ (n α)[α], n ≥ 1 and μ n  = μ for α = 0, where, 1/μ is the normal mean service time for a unit when that unit is the only one in the system and α is the pressure coefficient, a constant reflecting the degree to which the service rate of the system is affected by the system. For the sake of completeness, the proof that the probability is the pmf of MLFD (z, α, 1) where z = λ/μ is given as follows:

Following Conway and Maxwell (1962, p. 134–35), the system of differential difference equations are

$$ {P}_0\left( t+\varDelta \right)=\left(1-\lambda\;\varDelta \right){P}_0(t)+{\mu}_1\;\varDelta {P}_1(t) $$
(7)

and

$$ {P}_n\left( t+\varDelta \right)=\left(1-\lambda\;\varDelta -{\left( n\alpha \right)}_{\left[\alpha \right]}\mu\;\varDelta \right){P}_n(t)+\lambda\;\varDelta\;{P}_{n-1}(t)+{\left(\left( n+1\right)\alpha \right)}_{\left[\alpha \right]}\mu\;\varDelta {P}_{n+1}(t), n=1,2,\cdots $$
(8)

From (7) we get P 0(t + Δ) − P 0(t) = − λ ΔP 0(t) + μ α ! ΔP 1(t) since μ 1 = μ(α) α  = μα !. This implies, \( \underset{\varDelta \to 0}{ \lim}\frac{P_0\left( t+\varDelta \right)-{P}_0(t)}{\varDelta}=-\lambda\;{P}_0(t)+\mu\;\alpha !{P}_1(t) \)

or \( {P}_0^{/}(t)=-\lambda\;{P}_0(t)+\mu\;\alpha !{P}_1(t) \).

Assuming a steady state (i.e. \( {P}_n^{/}(t)=0 \) for all n), we get P 1(t) = zP 0(t)/α ! where λ/μ = z. Similarly, from (8), we get

\( \underset{\varDelta \to 0}{ \lim}\frac{P_n\left( t+\varDelta \right)-{P}_n(t)}{\varDelta}=-\left(\lambda +{\left( n\alpha \right)}_{\left[\alpha \right]}\mu\;\right){P}_n(t)+\lambda \kern0.24em {P}_{n-1}(t)+{\left(\left( n+1\right)\alpha \right)}_{\left[\alpha \right]}\mu\;{P}_{n+1}(t) \).

It follows that

$$ {P}_n^{/}(t)=-\left(\lambda +{\left( n\alpha \right)}_{\left[\alpha \right]}\mu\;\right){P}_n(t)+\mu z\kern0.24em {P}_{n-1}(t)+{\left(\left( n+1\right)\alpha \right)}_{\left[\alpha \right]}\mu\;{P}_{n+1}(t)=0 $$

because \( {P}_n^{/}(t)=0 \) for all n and λ/μ = z.

This implies that (z + (nα)[α] )P n (t) = z P n − 1(t) + ((n + 1)α)[α]  P n + 1(t) since μ ≠ 0.

Putting n = 1 we get

(z + α !)P 1(t) = zP 0(t) + (2α)[α]  P 2(t),

P 2(t) = {z 2/(2α) ! }P 0(t). Since α ! (2α)[α] = (2α) !

Similarly, for n = 2 we get

$$ \left( z+{\left(2\alpha \right)}_{\left[\alpha \right]}\right){P}_2(t)= z{P}_1(t)+{\left(3\alpha \right)}_{\left[\alpha \right]}\;{P}_3(t) $$

P 2(t) = {z 3/(3α) ! }P 0(t),

since (3α ! )(3α)[α] = (3α) !

In general, P n (t) = {z n/(nα) ! }P 0(t),

where \( {P}_0(t)=1/{\displaystyle \sum_{n=0}^{\infty}\left\{{z}^n/\left( n\alpha \right)!\right\}} \). This is the pmf of MLFD (z, α, 1).

In the case when α is not an integer one can use α ! = Γ(α + 1).

Reliability, stochastic ordering and log concavity

Discrete life time models have lately been a favorite subject of many studies since in many situations the life of a system may be observed as counts, and even when the life is measured in a continuous scale the actual observations may be recorded in a way making a discrete model more appropriate. It is therefore important to study the reliability properties of the proposed discrete distribution. Stochastic ordering is a closely related important area that has found applications in many diverse areas such as economics, reliability, survival analysis, insurance, finance, actuarial and management sciences (see Shaked and Shanthikumar, 2007). In this section we study the reliability properties and stochastic ordering of the MLFD (λ, α, β) distribution.

Survival and failure rate function

The survival and failure rate function for MLFD (λ, α, β) are respectively given by

$$ \begin{array}{c}\hfill S(t)= P\left( X> t\right)={\lambda}^{t+1}\;{E}_{\alpha, \beta +\left( t+1\right)\alpha}\left(\lambda \right)/{E}_{\alpha, \beta}\left(\lambda \right)\;\mathrm{and}\hfill \\ {}\hfill r(t)= P\left( X= t\right)/ P\left( X\ge t\right)=1/\varGamma \left(\alpha t+\beta \right){E}_{\alpha, \beta + t\alpha}\left(\lambda \right).\hfill \end{array} $$

This distribution has non decreasing failure rate function which we have shown later in section 4.3. The failure rate function r(t) is plotted in Fig. 3 for some choices of parameters to see how it behaves with changing parameter values. The values of r(t) tend to increase with α or β but decrease with increase in λ when other two parameters are kept fixed.

Fig. 3
figure 3

Failure rate of MLFD (λ, α, β) for some values of the parameters

Full size image

Stochastic ordering with HP

The following result stochastically compares the MLFD (λ, α, β) with the HP (λ, β) by using the likelihood ratio order.

Definitions: Let X and Y be two discrete random variables with pmfs f(x) and g(x). Then X is said to be smaller than Y in the likelihood ratio order denoted by X ≤  lr   Y if g(x)/f(x) increases in x over the union of the supports of X and Y; X is smaller than Y in the hazard rate order X ≤  hr   Y if r X (t) ≥ r Y (t) for all t; X is smaller than Y in the mean residual life order X ≤  MRL Y if μ X (t) ≤ μ Y (t) for all t, where r X (.) and μ X (.) are respectively the hazard rate and mean residual life (MRL) functions of X.

Theorem 1. For α > 1, X ~ MLFD (λ, α, β) is smaller than Y ~ HP (λ, β) distribution in the likelihood ratio order i.e. X ≤  lr   Y, while for 0 < α < 1, HP (λ, β) is greater than MLFD (λ, α, β) distribution in the likelihood ratio order i.e. Y ≤  lr   X.

Proof: If X ~ MLFD (λ, α, β) and Y ~ HP (λ, β) then

$$ \frac{P\left( Y= n\right)}{P\left( X= n\right)}=\frac{\varGamma \left( n\alpha +\beta \right)}{\varGamma \left( n+\beta \right)}\frac{E_{1,\beta}\left(\lambda \right)}{E_{\alpha, \beta}\left(\lambda \right)} $$

For α > 1 this ratio is clearly increasing in n (see Shaked and Shanthikumar, 2007 and Gupta et al., 2014). Hence X ≤  lr   Y is proved. While for 0 < α < 1, the ratio is decreasing in n which proves that Y ≤  lr   X.

Corollary 1. For α > 1, X ~ MLFD (λ, α, β) is smaller than Y ~ HP (λ, β) distribution in the MRL life order that is X ≤  MRL   Y.

Proof. The result follows since X ≤  lr   Y ⇒ X ≤  hr   Y ⇒ X ≤  MRL   Y. (see Gupta et al., 2014).

Log-concavity

The log-concavity of any probability distribution has important implications on its reliability function, failure rate function, tail probabilities and moments. The MLFD (λ, α, β) has a log-concave pmf since for this distribution (Gupta et al., 1997)

\( \varDelta\;\eta (t)=\frac{P\left( t+1\right)}{P(t)}-\frac{P\left( t+2\right)}{P\left( t+1\right)}=\lambda \frac{\varGamma \left(\alpha\; t+\beta \right)\varGamma \left(\alpha\; t+2\;\alpha +\beta \right)-{\left\{\varGamma \left(\alpha\; t+\alpha +\beta \right)\right\}}^2}{\varGamma \left(\alpha\; t+\alpha +\beta \right)\varGamma \left(\alpha\; t+2\;\alpha +\beta \right)} \) > 0.

The following results are direct consequence of log-concavity (Mark, 1996):

  1. i.

    MLFD (λ, α, β) is a strongly unimodal distribution due to the log-concavity of its pmf (see Steutel 1985).

    • ➢ MLFD (λ, α, β) has a unique mode at X = k if

    • $$ \varGamma \left(\alpha k+\beta \right)/\varGamma \left(\alpha k-\alpha +\beta \right)<\lambda <\varGamma \left(\alpha k+\alpha +\beta \right)/\varGamma \left(\alpha k+\beta \right) $$

    • Proof: This follows easily from the probability recurrence relation given in (5).

    • ➢ MLFD (λ, α, β) has a non increasing pmf with a unique mode at X = 0 if λ < Γ(α + β)/Γ(β) (See the pmf plots in Fig. 1(g) for some choices of (λ, α, β) satisfying the condition.)

    • ➢ MLFD (λ, α, β) has two modes at X = k and X = k + 1 if

    • $$ \lambda =\varGamma \left(\alpha k+\alpha +\beta \right)/\varGamma \left(\alpha k+\beta \right) $$

    • (See the pmf plot in Fig. 1(h) for some (λ, α, β) satisfying the condition.)

  1. ii.

    MLFD (λ, α, β) has non decreasing failure rate function.

  2. iii.

    MLFD (λ, α, β) has at most an exponential tail.

  3. iv.

    MLFD (λ, α, β) remains log-concave if truncated.

  4. v.

    \( \frac{P\left( X= i+ k\right)}{P\left( X= i\right)}\ge \frac{P\left( X= j+ k\right)}{P\left( X= j\right)}\;\mathrm{f}\mathrm{o}\mathrm{r}\kern0.24em i< j \).

Data Fitting

Parameter estimation

Suppose that we have a sample of size n from MLFD (λ, α, β) reported as grouped frequencies in k classes, like (X, f) = {(x 1, f 1), (x 2, f 2,), . . . , (x k , f k )}, where f i is the frequency of i-th observed value x i and n = ∑f i is the sample size. Then the log-likelihood function is given by

\( \log L\left(\left.{x}_1,{x}_2,\cdots, {x}_k\right|\;\lambda, \alpha, \beta \right)=\left({\displaystyle \sum_{i=1}^k{f}_i\;{x}_i}\right) \log \lambda -{\displaystyle \sum_{i=1}^k{f}_i \log \varGamma \left(\alpha\;{x}_i+\beta \right)}- n \log {E}_{\alpha, \beta}\left(\lambda \right) \).

Numerical optimization method is used to obtain the maximum likelihood estimates (MLE) of the parameters required for the data fitting and the likelihood ratio test.

Numerical examples

Here we have considered two frequency data sets. The first data set in Table 1 is about trips made by Dutch households owning at least one car during a particular survey week in 1989 (van Ophem, 2000). This data is slightly over-dispersed with Mean = 3.038, Variance = 3.410 and index of dispersion (ID) = 1.123. The second data set in Table 2 is the frequency distribution of the α - particles emitted by a radioactive substance in 2608 periods, each of 7.5 sec (Rutherford and Geiger, 1910). This data is slightly under-dispersed with Mean = 3.872, Variance = 3.695 and index of ID = 0.9543

Table 1 Observed and expected frequencies of trips made by Dutch households owning at least one car during a particular survey week in 1989(van Ophem, 2000)
Full size table
Table 2 Frequency distribution of the α- particles emitted by a radioactive substance in 2608 periods (Rutherford and Geiger, 1910)
Full size table

The MLFD (λ, α, β) model is a generalization/extension of the HP (λ, β) and MLFD (λ, α, 1). Therefore the MLFD (λ, α, β) model has been fitted and compared with the HP (λ, β), MLFD (λ, α, 1) to ascertain the benefits accrued through the proposed generalization. In addition, we have also considered a recently introduced three-parameter distribution namely the COM-Poisson type negative binomial [COMNB (λ, α, β)] distribution having pmf P(X = k) = (λ) k α k/{(k !)β  S β,λ (α)}, k = 0, 1, 2, ⋯ where S β,λ (α) is the normalizing constant (Chakraborty and Ong, 2016) for comparative data fitting. The performances of various distributions are compared using the AIC (Akaike Information Criterion) defined as AIC = −2 log L + 2 k, where k is the number of parameter(s) and log L is the maximum of log-likelihood for a given data set (Burnham and Anderson, 2004). We also provide chi-square goodness of fit statistics with p-values. In Tables 1 and 2 the degrees of freedoms for χ 2 are given alongside its value and the standard errors for parameter estimates are given within parentheses.

From Table 1 it can be seen that the MLFD (λ, α, β) gives the best fit since it has the lowest χ 2 value and is also the first choice in model selection with lowest AIC value. Moreover MLFD (λ, α, β) is the only distribution with good fit at 1% since its p-value is more than 0.01 while for the rest the p-values are less than 0.01.

From Table 2 considering the χ 2 values together with p-values it can be seen that all the distributions except the COMNB (λ, α, β) give adequate fits. But among them the MLFD (λ, α, β) gives the best fit since it has the lowest value of χ 2 with the highest p-value. It is also the selected model because it has the lowest AIC value.

Conclusion

A new generalization of the HP distribution which is a continuous bridge between the geometric and HP is derived using the generalized Mittag-Leffler function. Some known and new distributions are seen as particular cases of this distribution. This new generalization belongs to the generalized power series, generalized hypergeometric families and also arises as weighted Poisson distributions. Like the HP, COM-Poisson and generalized Poisson distributions, this distribution is also able to cater for under-, equi- and over- dispersion. Although the new generalization of the HP distribution has an extra parameter, it is computationally not more complicated than the HP since it retains the two-term probability recurrence formula and the normalizing constant, in terms of the generalized Mittag-Leffler function, is readily computed. It has many interesting probabilistic and reliability properties and is found to be a better empirical model than the HP distribution.