Introduction

Nanotechnology refers to the science of using nano in the field of various sciences and techniques, which is widely used in many branches of science today, and researchers are seriously researching it [1,2,3,4,5,6,7]. Today, nanofluids (NFs) have shown an important role in the development of industry and technological progress in various fields of industry. The idea of using nanoparticles was proposed for the first time in 1904 by Maxwell [8] and an important evolution occurred in the field of fluid heat transfer. Murshed et al. [9] first introduced this suspended particle–fluid mixture as NF, then Choi [10] developed this concept widely. Conventional fluids have focused researchers' attention on NFs due to their performance and properties with lower thermophysical properties than the new class of smart fluids. The distribution of nanoparticles (NPs) in the base fluid due to the high thermal conductivity (TC) and also the change in mass transfer improves the thermophysical properties such as density, viscosity, and TC [11,12,13,14]. Viscosity is one of the most efficient thermophysical properties of lubricants, and the study of rheological properties of lubricants has been one of the most attractive topics for researchers [15,16,17,18,19,20,21,22,23]. Oils are used as a coolant and lubricant in various industrial systems to reduce friction between parts and their wear. They have various other uses, some of which are shown in Fig. 1. In a study, the effect of the addition of Al2O3-Fe2O3 NPs on the thermal properties of 10W40 engine oil was studied [24]. In this study, the effect of SVF (0, 0.25, 0.5, 1, 2 and 4%) was investigated. The experiments were performed in the temperature range of 25–65 °C. The results show that even the lowest TC (at SVF = 4%, about 33% improved the TC) of the NF. The percentage of this increase depends on various factors including the SVF, NP properties, base fluid properties, and temperature. NFs have found many applications due to their properties, which has made the study of these properties of particular importance. Also, because these properties depend on the SVF, the properties of the NF can be adjusted by changing the SVF. In 2003, the results of an experimental study of a cooling system report an increase in the cooling rate in the cooling system [25]. In another study, Wu et al. [26] investigated the potential of water/aluminum oxide NFs in cooling systems. Their results indicate an increase in the freezing rate of NFs. By adding 2% alumina NPs to the water, they reduced the solidification time by about 20.5% and increase the efficiency of the system. The results of research in this field indicate the improvement of the performance of cooling systems using NFs. Compared to the frequency of research in the field of TC, less research was done in the field of dynamic viscosity of NFs. A research team of Iranian experts tried to evaluate a wide range of behavioral issues of viscosity with changes in the factors of composition ratio, base fluid (oil/water/ethylene glycol, etc.), and the diversity of NPs [27,28,29,30,31,32,33,34]. In a study by Hemmat et al. [30], the rheological behavior of Al2O3-MWCNT (65%-35%)/5W50 HNLs was evaluated to facilitate its applications in the automotive industry. Dynamic viscosity of HNLs was measured in SVF = 0 to 1% at temperatures between 5 and 55 °C and SR between SR = 666.5 to 10,664 s−1. Their findings distinguish the behavior of the HNLs from the non-Newtonian type. It was also observed that with increasing SVF, the non-Newtonian behavior of HNLs was intensified. Conversely, increasing the temperature had the opposite effect. They also presented a new correlation based on temperature and SVF with a correlation accuracy of 0.9923 to predict the viscosity of HNLs. In a study in 2021 [35], the researchers experimentally investigated the rheological behavior of MWCNT-TiO2 nanoparticles mixed in 5W40 base oil. They showed that the rheological behavior of base oil and HNL correspond to the classification of Newtonian and non-Newtonian fluids. The viscosity of HNL also increases with decreasing SR and temperature and increasing SVF, and the presence of NPs enhances the viscosity of the HNL by up to 790%. In 2019 [36], the viscosity behavior of MWCNT-Al2O3 (30:70)/5W50 HNL in the temperature range of 5–55 °C, SVF = 0.05 to 1%, and SR range of 666.5–11,997 s−1 were investigated. Viscosity measurements show pseudo-plastic behavior at all temperatures and SVFs. The results show that the viscosity of HNL decreases with increasing temperature and increases with increasing SVF. In addition, this study proposes an optimized NP ratio as an oil additive to eliminate the unwanted viscosity reduction after the addition of NPs for thermal recovery purposes. A group of Chinese researchers conducted various studies using the properties of nanofluids in their new and practical studies. They improved the performance of the heat exchanger by introducing a new heat exchange medium and reinforcing structure [37,38,39]. In another study, they addressed the issue of thermal management of electronic components based on structures and nanofluids inspired by the new wave [40], also the effect of bionic channel structure and nanofluids on the characteristics of electricity generation of waste heat utilization equipment has been the title of another study of this group [41]. What is investigated in this article is to focus on the comparative analysis of the rheological behavior of HNLs to select the optimal HNL. The target NFs in this study have different composition ratios of NP but the same base fluid. The effect of the ratio of different compounds on the behavior of viscosity and improvement of the desired nanofluid was compared with each other. By using different theoretical methods, the classification of flow type was determined. Finally, using RSM, an empirical model was presented to predict viscosity data with acceptable accuracy (validated using R-Squared and MOD). At the end of the analysis, the viscosity sensitivity was plotted for six different SVFs. The results of this study, which is the result of a detailed and comprehensive comparison of the rheology and viscosity properties of the desired nanofluid, will introduce the optimal nanofluid to industrialists. Also, studying with the RSM method will save researchers from spending exorbitant laboratory costs in the future.

Fig. 1
figure 1

Applications of NF in various industries

Full size image

Experimental

Preparation of HNLs

HNLs require NPs and base oil. For this purpose, Al2O3 and MWCNT NPs and 10W40 base oil were used to make HNLs with different ratios of 25:75 and 30:70 (Fig. 2). The physical properties and strength properties of NPs are described in Table 1.

Fig. 2
figure 2

NPs used in this study

Full size image
Table 1 Specifications of MWCNT and Al2O3 NPs
Full size table

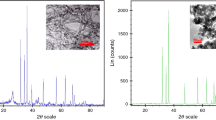
To determine the morphology (size and shape of NPs), surface properties (surface details of NPs), the crystal structure of NPs as well as NP identification, advanced scanning electron microscope (SEM) and transmission electron microscope (TEM) imaging methods and X-ray diffraction analysis (XRD) were used. The details are taken in Figs. 3, 4 and 5 with high magnification and accuracy.

Fig. 3
figure 3

TEM pictures of used NPs

Full size image
Fig. 4
figure 4

SEM pictures of used NPs

Full size image
Fig. 5
figure 5

XRD analysis for used NPs

Full size image

Equation 1 was used to determine the amount of required nanomaterials in the preparation of HNLs with different SVFs. Also, for weighing nanomaterials, a digital scale with an accuracy of 0.001 gr was used.

$$SVF= \left(\frac{{0.75\left(\frac{w}{\rho }\right)}_{Al2O3}+{0.25\left(\frac{w}{\rho }\right)}_{MWCNT}}{{0.25\left(\frac{w}{\rho }\right)}_{MWCNT}+{0.75\left(\frac{w}{\rho }\right)}_{Al2O3}+{\left(\frac{w}{\rho }\right)}_{10W40}+}\right)\times100$$
(1)

A magnetic stirrer is required to mix the weighed NPs in the base fluid. This device was used for 1 h for the initial uniformity of the HNLs. Then, to increase the stability and break the NP clusters and prevent the formation of sediment, an ultrasonic vibrator was used for 1 h). As a result, it was observed that the prepared NFs in different SVFs were stable after three weeks. Figure 6 shows images of stabilized HNLs for different SVFs.

Fig. 6
figure 6

HNL samples prepared at different SVFs

Full size image

Measurement of dynamic viscosity

One way to obtain information about the rheological behavior of NFs is to use a Brookfield viscometer. The viscometer is used to determine the viscosity of fluids. Technical specifications and operating environment conditions are stated in Table 2. Prior to measurement, a calibration test was performed to prevent measurement errors. The range of conditions for measuring the viscosity of HNLs is shown in Table 3. To reduce the effect of viscometer measurement error, all experiments were measured twice and then the average data were recorded. Some of the measured viscosity data are reported in Table 4.

Table 2 Viscometer technical specifications
Full size table
Table 3 Laboratory conditions for measuring HNL viscosity
Full size table
Table 4 Some results measured with CAP2000 + viscometer
Full size table

Comparison and discussion

Rheological behavior

Shear stress-SR

One of the methods to evaluate the rheological behavior of HNLs is to investigate the shear stress at different SRs. In general, the slope of these curves is equal to the viscosity of HNLs. In the curves of Fig. 7, the shear stress versus the SR for two similar HNLs with the same base fluid with different percentages in the lowest and highest SVFs is shown. According to Eq. 2, for Newtonian fluid, there is a linear relationship between SR and shear stress. In the case of fluids with non-Newtonian behavior, the shear stress is a nonlinear function of the SR. According to the curves of Fig. 7, the behavior of HNLs in different temperatures and SVFs will be non-Newtonian.

Fig. 7
figure 7

Curve of changes in shear stress-SR at different laboratory conditions

Full size image
$$\uptau =\mu *\mathrm{SR}$$
(2)

Power-law index

To ensure the non-Newtonian behavior of HNLs, the power-law model method was used. For this purpose, the power-law index curves according to Eq. 3, are plotted in Fig. 8 for both HNLs relative to temperature in different SVFs.

Fig. 8
figure 8

Effect of main parameters (temperature and SVF) on power-law index

Full size image
$$\uptau =m{*\mathrm{SR}}^{n}$$
(3)

According to Fig. 8, both HNLs can be classified as non-Newtonian fluids because they are lower than the index line with a certainty of n values in all SVFs. However, more precisely in Table 4, the values of n in several SVFs and at all studied temperatures are reported. Table 5 shows that at T = 55 °C, the behavior of these HNLs tends to be non-Newtonian fluids even more than other temperatures. As a result, HNLs can show a suitable reaction to enhance lubrication in different engine operating conditions.

Table 5 Power law index values at different laboratory conditions
Full size table

To make a more accurate and statistical comparison of the behavior of the two HNLs under comparison, the results of the power-law index values are reported in Table 5. The results show that both HNLs have a value of n less than 1 at all temperatures. MWCNT-Al2O3 (25–75%)/10W40 HNL at T = 55 °C and SVF = 0.05% shows stronger non-Newtonian behavior. On the other hand, both HNLs are more prone to non-Newtonian behavior at higher temperatures and SVFs.

Viscosity-SR

Investigating the effect of SR on viscosity can be introduced as the next method to describe the rheological behavior of HNLs. In Fig. 9 as an example, the viscosity curve in terms of SR in the temperature range of T = 5–55 °C and SVF = 0.05% for the MWCNT-Al2O3 (25–75%) /10W40 and MWCNT-Al2O3 (30–70%)/10W40 HNLs was compared versus the 10W40 base fluid. According to the obvious principles in fluid mechanics, the dependence of the viscosity on SR indicates that the behavior of the HNL is close to that of the non-Newtonian fluid. Therefore, the dependence of the viscosity of HNLs on SR in Fig. 9 indicates that the HNLs are non-Newtonian. Also, for more reliability and observation of changes in viscosity, magnification was done at T = 5 °C and 55 °C. As can be seen, the viscosity was decreased with respect to the temperature with a significant slope. Of course, the slope of changes at low temperatures is greater.

Fig. 9
figure 9

Viscosity-SR at different laboratory conditions

Full size image

Viscosity comparison

Viscosity enhancement

After investigating the rheological behavior of HNLs, the viscosity of HNLs was compared. The curves shown in Figs. 10 and 11 show the changes in viscosity enhancement to SVF for HNLs at SR = 3999 and 6665 s−1 and different temperatures. According to Eq. 4, viscosity enhancement is obtained from the difference between the viscosity of the HNL and the base fluid divided by the base fluid, which is reported as a percentage.

Fig. 10
figure 10

Relative viscosity in terms of SVF at different temperatures at SR = 3999 s−1

Full size image
Fig. 11
figure 11

Relative viscosity in terms of SVF at different temperatures at SR = 6665 s−1

Full size image
$$\mathrm{Viscosity \,enhancement }\,(\mathrm{\%})=\frac{{\mu }_{nf}-{\mu }_{bf}}{{\mu }_{bf}}\times 100$$
(4)

According to Table 6, the maximum viscosity reduction belonged to MWCNT-Al2O3 (25–75%)/10W40 HNL in SVF = 0.05% and T = 5 °C, which is equal to − 1.85%. On the other hand, the maximum increase in viscosity at T = 55 °C and SVF = 1% belonged to MWCNT-Al2O3 (30%-70%) / 10W40 HNL and was equal to 34.97%.

Table 6 Statistical data on the percentage change of viscosity enhancement of HNLs
Full size table

Figure 12 schematically shows the rheological performance of the studied HNLs in the present study in industrial applications.

Fig. 12
figure 12

The rheological performance of studied HNLs in the present study in industrial applications

Full size image

The effect of temperature on viscosity

After dispersion NPs into the oil, the viscosity was calculated at all temperatures and quantitatively reported in SVF = 0.05% in Table 7. Figure 13 compares the viscosity-temperature curves at SVF = 0.05% and SR = 3999 and 6665 s−1. According to the results, the addition of MWCNT and Al2O3 NPs with the ratio of (25:75) only at T = 5 °C reduces the viscosity of HNLs by − 1.85%. In this sense, this HNL can be considered by craftsmen.

Table 7 Comparative study of the effect of temperature on the viscosity of HNLs relative to the base fluid at SVF = 0.05%
Full size table
Fig. 13
figure 13

Comparison of the effect of temperature on the viscosity of the studied HNLs in SVF = 0.05%

Full size image

Figure 14 and Table 8 compare and analyze the viscosity results of HNLs in SVF = 0.1%. Unfortunately, at SVF = 0.1%, at no temperature, the desired viscosity behavior was not observed for any of the HNLs.

Fig. 14
figure 14

Comparison of the effect of temperature on the viscosity of the studied HNLs in SVF = 0.1%

Full size image
Table 8 Comparative study of the effect of temperature on the viscosity of HNLs relative to the base fluid at SVF = 0.1%
Full size table

Impractical results

RSM method

The purpose of using the RSM in this study is to determine the relationship between the target response and the variables affecting it in the form of providing a predictive relationship as well as modeling experimental data. For this purpose, laboratory data were normalized with the Quartic model due to statistical inadequacy and then the results were extracted. Laboratory data including temperature, SR and SVF were introduced as input and viscosity data (target response) as output to Design of expert (DOE) software. Tables 9 and 10 show the statistical outputs of the normalized data using the quadratic model.

Table 9 Optimized modeling accuracy
Full size table
Table 10 ANOVA for Response surface quartic model
Full size table

New correlation

To predict the experimental data of the selected HNL as well as how the interaction between the target response and the independent variables, a nonlinear three-variable-quadratic relationship was used. The condition for using Eq. 5 is to observe the range of test conditions, which is unacceptable outside this range.

$$\begin{aligned} {\left( {\text{Viscosity}} \right)^{0.55}} &= \, + 39.87127 - 1.45299\text{T} - 1.69500\text{E} - 003 + 7.37688\text{E}-005 \, \text{T}{\dot{\gamma}} \\ &\quad + 0.030075{\text{T}^2} + 18.30736SV{F^2} + 9.14611E - 004 \, {\text{T}^2}*SVF - 0.22282TSV{F^2} \\ &\quad- 8.86737\text{E}-009 \, {T^2} - 3.11056\text{E}-010SVF*\text{SR}^{2} - 4.15818\text{E}-004{\text{T}^3} - 29.23742SV{F^3} \\ &\quad + 2.28810\text{E}-{011^3} + 4.04801\text{E}-011 \, {\text{T}^2}^2 + 0.12543 \, \text{T}*SV{F^3} + 2.22791\text{E}-006{\text{T}^4} + {14.64807^4} - 5.14218\text{E}-{016^4} \\ \end{aligned}$$
(5)

In Fig. 15, the modeled data have an acceptable correlation with the experimental data on the criterion line.

Fig. 15
figure 15

Correlation of predicted data with actual data

Full size image

Margin of deviation (MOD)

The standard MOD method is used to determine the degree of scattering and deviation of the data relative to the zero standard line. Equation 6 was used to calculate the MOD.

$$MOD=\frac{{\mu }_{{rel}_{exp}}-{\mu }_{{rel}_{pre}}}{{\mu }_{{rel}_{exp}}}\times 100$$
(6)

Figure 16 shows the range of MOD values for all laboratory data. The allowable range of MOD values for the selected HNL was set at − 3.43% < MOD < 4.75.

Fig. 16
figure 16

Range of MOD values in all laboratory data

Full size image

Viscosity sensitivity

Sensitivity analysis is a method to determine the effect of different effective parameters on the target response. In this study, only the effect of SVF change on viscosity was investigated. Equation 7 was used to calculate the viscosity sensitivity to calculate.

$$Viscosity \,sensitivity =\frac{{\left({Viscosity}_{{ }_{after \,change}}\right)}_{Pre}-{\left({Viscosity}_{{ }_{before \,change}}\right)}_{Pre}}{{\left({Viscosity}_{{ }_{before \,change}}\right)}_{Pre}}\times 100$$
(7)

Figure 17 shows the viscosity sensitivity for 6 different SVFs with + 10% variations. Observations show that the highest sensitivity was occurred in high SVFs.

Fig. 17
figure 17

Viscosity sensitivity analysis for all data in different laboratory conditions

Full size image

Conclusion

In this study, the rheological behavior of hybrid nano-lubricants (HNLs) is compared that differ in the ratio of components in the base oil. The purpose of the comparison is to determine the HNL with the best lubrication performance at the start of the vehicle. The results of this study are summarized in the following cases:

  • Observing the pseudo-plastic non-Newtonian fluid.

  • Observing more viscous HNLs with a composition ratio of 30:70 compared to HNLs with a composition ratio of 25:75 in equal conditions with an increase in SVF.

  • Observing the decrease in viscosity in low SVFs due to the presence of NPs in the layers between the HNL and facilitating the sliding of the layers on top of each other.

  • Optimal efficiency of the RSM in predicting viscosity values and constructing an experimental model

  • Observing the greatest sensitivity to changes in high SVFs