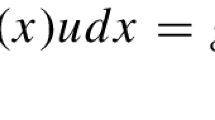1 Introduction

Fixed point theory has been an important tool in the study of differential and integral equations [1, 2], economics [3], optimization and game theory [4] among others. The simplest theorem from elementary calculus considers the existence of positive roots for the equation: \(f(x)=x\) on \(\mathbb{R}_{+}=[0, +\infty)\). Clearly, if there exist \(b>a>0\) such that \(f\in C[a,b]\) and either \(f(a)\leq a\) and \(f(b)\geq b\) or \(f(a)\geq a\) and \(f(b)\leq b\), then there exists a \(x^{\star}\in [ a,b]\) such that \(x^{\star}=f(x^{\star})\), that is: the function \(f(x)\) has a fixed point \(x^{\star}\in[ a,b]\). Such result had been expanded to an abstract operator equation to obtain the Guo-Krasnoselskiĭ fixed point theorem concerning cone expansion and compression of norm type as follows (see [5] and [6]).

Lemma 1.1

Let X be a Banach space and P be a cone in X. Assume that \(\Omega_{1}\) and \(\Omega_{2}\) are open subsets of X with \(0\in\Omega_{1}\) and \(\overline{\Omega}_{1}\subset\Omega_{2}\). Let \(T:P\cap(\overline{\Omega}_{2}\setminus\Omega_{1})\rightarrow P\) be completely continuous operator. If either \(\Vert Tu\Vert\leq\Vert u\Vert\) for \(u\in P\cap\partial\Omega_{1}\) and \(\Vert Tu\Vert\geq\Vert u\Vert\) for \(u\in P\cap\partial\Omega_{2}\) or \(\Vert Tu\Vert\leq\Vert u\Vert\) for \(u\in P\cap\partial\Omega_{2}\) and \(\Vert Tu\Vert\geq\Vert u\Vert\) for \(u\in P\cap\partial\Omega_{1}\) holds, then T has a fixed point in \(P\cap(\overline{\Omega}_{2}\setminus\Omega_{1})\).

It is well-known that this abstract result can be applied to obtain an abundance of concrete results for some special problems [1, 7–10], for example, (a) Hammerstein integral equations, (b) boundary value problems for semilinear ordinary differential equations, (c) boundary value problems for semilinear elliptic differential equations, (d) initial-value problems for semilinear parabolic differential equations, (e) discrete boundary value problems or the nonlinear algebraic equations systems, (f) boundary value problems for semilinear fractional differential equations, (g) boundary value problems for semilinear time scale differential equations, (h) existence of periodic solutions for some functional differential equations, etc. Because these problems can be regarded as abstract operator equations.

Let X be an ordered Banach space with the cone \(X_{+}\). We found that many problems depend on properly constructing subcones of \(X_{+}\). For example, the following well-known subcones of \(X_{+}\) have been extensively applied. First, let \(P_{1}\) be defined as

$$ P_{1} = \bigl\{ u\in C[0,1]: u(t) \geq c\|u\| \bigr\} , $$
(1.1)

where \(X=C[0, 1]\), \(X_{+} = \{u\in X, u(t)\geq0 \mbox{ for } t\in [0,1]\}\) and

$$\|u\|=\|u\|_{\infty}=\max_{0\leq t \leq1}\bigl|u(t)\bigr|. $$

The cone \(P_{1}\) was first used in [11] and then in [5], followed by many authors in studying boundary value problems, for instance, [8, 12–14]. Recently, in [14], the authors proved results on the existence of positive solutions for singular fractional differential equations with integral boundary conditions. \(P_{1}\) was applied with the constant c defined as \(c=\frac{k_{2} (1-M_{0})}{k_{1}}\), where \(M_{0}\), \(k_{1}\) and \(k_{2}\) are determined by the associated Green’s function.

Second, let \(P_{2}\) be defined as

$$ P_{2} = \biggl\{ u\in C^{1} [0,1]: u(t) \geq \frac{b}{a+b}\Vert c\Vert _{\infty}, u(0) \geq\frac{b}{a} \bigl\Vert u'\bigr\Vert _{\infty}, u'(t) \geq c\Vert u\Vert _{\infty} \mbox{ on } [0, 1] \biggr\} , $$
(1.2)

where

$$\|u\| = \max\bigl\{ \|u\|_{\infty}, \bigl\| u'\bigr\| _{\infty} \bigr\} , $$

a, b, c are positive constants used for the boundary conditions. The cone \(P_{2}\) was most recently used in [10] to prove the existence of positive solutions for second-order non-local boundary value problems with singularities in space variables.

Third, let \(P_{3}\) be defined as

$$ P_{3} = \bigl\{ u\in C[0,1]: u(t) \geq q(t) \|u\|, t \in[0,1]\bigr\} , $$
(1.3)

where \(X=C[0,1]\), \(2<\alpha<3\), \(q(t)=t^{\alpha-1}\), \(\|u\| =\|u\|_{\infty } \). The cone \(P_{3}\) was applied in [15] to prove the existence of solutions for fractional boundary value problems.

Last, define \(P_{4}\) as

$$ P_{4}=\bigl\{ x\in\mathbb{R}^{n}: x_{i}\geq\gamma|x|, i\in[1, n] \bigr\} , $$
(1.4)

where \(X=\mathbb{R}^{n}\), \(|x| = \max_{1\leq i \leq n} |x_{i}|\), \(1>\gamma >0\). The cone \(P_{4}\) was used in [9, 16] to prove the existence of positive solutions for a class of nonlinear algebraic systems.

As a generalization to some subcones applied previously, we introduce the following unified subcone \(P_{u_{0}}\) on the abstract ordered Banach space X. Letting \(u_{0}\in X_{+} \) with \(\Vert u_{0}\Vert\leq1\), define

$$ P_{u_{0}}=\bigl\{ x\in X_{+},x\geq \Vert x\Vert u_{0} \bigr\} . $$
(1.5)

For \(a,b\geq0\) and \(x,y\in P_{u_{0}}\), we have

$$ ax+by\geq \bigl( a\Vert x\Vert +b\Vert y\Vert \bigr) u_{0} \geq \Vert ax+by\Vert u_{0}. $$

It can be verified that \(P_{u_{0}}\) is a cone, which is a subcone of \(X_{+}\).

In this paper, we will consider the existence of solutions for the operator equation

$$ T ( x ) = x,\quad x\in P_{u_{0}}. $$
(1.6)

When \(T=Kf\), where K is a linear operator and f is nonlinear, we can obtain an abstract Hammerstein equation:

$$ x=Kf ( x ) ,\quad x\in P_{u_{0}}. $$
(1.7)

\(P_{u_{0}}\) is a new and general cone. When we choose different \(u_{0}\), some known cones such as (1.1)-(1.4) can be obtained. When the obtained abstract results are applied to concrete cases (a)-(h), new results can be naturally obtained. Compared to the Guo-Krasnoselskiĭ’s result, our abstract results are established on order intervals rather than an annular region of the cone. Therefore, no conditions for the operator T outside the interval are necessary. This expands the recent idea in [9].

2 Main results

Let X be an ordered Banach space defined with the cone \(X_{+}\). An ordered interval is defined as

$$[x, y] = \{z\in X: x\leq z\leq y \}. $$

For any \(r>0\), we denote \(\Omega_{r}= \{ x\in X:\Vert x\Vert < r \} \) and \(\partial\Omega_{r}= \{ x\in X:\Vert x\Vert =r \} \).

Theorem 2.1

Assume that X is an ordered Banach space with the order cone \(X_{+}\). Let \(0\leq u_{0}\leq\varphi\) be such that \(\|u_{0}\| \leq1\), \(\| \varphi\| =1\) satisfying the condition:

$$ \textit{if } x\in X_{+},\Vert x\Vert\leq1, \textit{then } x\leq \varphi. $$

If there exist positive numbers \(0< a< b\) such that \(T: P_{u_{0} }\cap( \overline{\Omega}_{b}\setminus\Omega_{a}) \rightarrow P_{u_{0} }\) is a completely continuous operator and the conditions:

$$ \bigl\Vert T(x) \bigr\Vert _{x\in[a u_{0}, a \varphi]} \leq a \quad \textit{and} \quad \bigl\Vert T(x) \bigr\Vert _{x \in[b u_{0}, b \varphi] }\geq b $$
(2.1)

or

$$ \bigl\Vert T(x)\bigr\Vert _{x \in[a u_{0}, a \varphi]} \geq a \quad \textit{and} \quad \bigl\Vert T(x) \bigr\Vert _{x\in[b u_{0}, b \varphi]} \leq b $$
(2.2)

are satisfied, then T has a fixed point \(x_{0}\in[a u_{0}, b\varphi]\).

Proof

Assume that condition (2.1) is satisfied. For \(x\in P_{u_{0} }\cap \partial\Omega_{a}\), we have \(\| x \| =a\) and \(\frac{x}{\|x\|} \leq \varphi\), hence \(x\leq\|x\| \varphi= a\varphi\). Since \(x\in P_{u_{0} }\), we have

$$ x\geq \|x\| u_{0}= a u_{0}. $$

Therefore \(x\in[a u_{0}, a\varphi]\). Condition (2.1) ensures that \(\| T(x) \| \leq a= \| x \| \).

On the other hand, for \(x\in P_{u_{0} }\cap\partial\Omega_{b}\), we have \(\| x \| =b\) and \(\frac{x}{\|x\|}\leq\varphi\), hence \(x\leq\| x\| \varphi= b\varphi\). Again, \(x\in P_{u_{0} } \) implies that

$$ x \geq \|x\| u_{0} = b u_{0}. $$

Therefore \(x\in[b u_{0}, b \varphi]\). By condition (2.1), we obtain \(\|T(x)\| \geq b= \| x \|\). Applying Lemma 1.1, we obtain that T has at least one fixed point \(x_{0} \in P_{u_{0}} \cap(\overline{\Omega}_{b}\setminus \Omega _{a})\). Obviously, \(x_{0}\in\overline{ \Omega}_{b}\) implies \(x\leq\|x\| \varphi\leq b\varphi\) and \(x_{0}\in P_{u_{0}}\) ensures that \(x\geq\| x \| u_{0} \geq a u_{0}\). So \(x_{0}\in[ a u_{0} , b\varphi]\).

The proof is similar if condition (2.2) holds. □

As a special case of Theorem 2.1, let \(0<\delta\leq1\) and \(u_{0}= \delta\varphi\), we have

$$ P_{u_{0}}=P_{ \delta\varphi}=\bigl\{ x\in X_{+}, x\geq\delta \Vert x\Vert \varphi\bigr\} . $$

Therefore, we obtain the following theorem by applying Theorem 2.1.

Theorem 2.2

If there exist positive numbers \(a< b\) such that \(T: P_{\delta \varphi}\cap(\overline{\Omega}_{b}\setminus\Omega_{a})\rightarrow P_{\delta\varphi}\) is a completely continuous operator and the conditions

$$ \bigl\Vert T(x)\bigr\Vert _{x\in[ \delta a\varphi,a\varphi]}\leq a \quad \textit{and} \quad \bigl\Vert T(x)\bigr\Vert _{x\in[ \delta b\varphi ,b\varphi]}\geq b $$
(2.3)

or

$$ \bigl\Vert T(x)\bigr\Vert _{x\in[ \delta a\varphi,a\varphi]}\geq a \quad \textit{and} \quad \bigl\Vert T(x)\bigr\Vert _{x\in[ \delta b\varphi ,b\varphi]}\leq b $$
(2.4)

are satisfied, then T has a fixed point \(x_{0}\in[ \delta a\varphi, b\varphi]\).

In Theorem 2.2, let \(\delta=1\), we obtain the following corollary, which is a generalization of the fixed point theorem in finite dimensional spaces recently obtained in [9].

Corollary 2.3

If there exist positive numbers \(a< b\) such that \(T: P_{\varphi}\cap (\overline{\Omega}_{b}\setminus\Omega_{a})\rightarrow P_{\varphi}\) is completely continuous and the conditions

$$ \bigl\Vert T(a\varphi)\bigr\Vert \leq a \quad \textit{and} \quad \bigl\Vert T(b \varphi)\bigr\Vert \geq b $$
(2.5)

or

$$ \bigl\Vert T( a\varphi)\bigr\Vert \geq a \quad \textit{and} \quad \bigl\Vert T(b \varphi)\bigr\Vert \leq b $$
(2.6)

are satisfied, then T has a fixed point \(x_{0}\in[ a\varphi ,b\varphi]\).

Example 1

Consider the equation: \(x=x^{2}-1=f ( x ) \). Clearly, there exist the positive numbers 1 and 2 such that \(x^{2}-1\geq 0\) for \(x\in [ 1,2 ] \), \(f ( 1 ) =0\leq1\), and \(f ( 2 ) =3\geq2\). Thus, in view of Corollary 2.3, there exists \(\xi\in [1,2 ] \) such that \(\xi=\xi^{2}-1\). In fact, we have

$$ \xi=\frac{1+\sqrt{5}}{2}\approx1. 618. $$

However, \(f ( x ) \leq0\) for \(x\in [ 0,1 ] \).

We now consider the semilinear operator equation (1.7).

Theorem 2.4

Let \(f: X_{+} \to X \) be nonlinear and \(K: X\to X\) be a linear operator. Assume that \(u_{0}\) and φ are the same as in Theorem  2.1. If there exist positive numbers \(m\leq M\) and \(a< b\) such that

$$ m\bigl\Vert f ( x ) \bigr\Vert \leq\bigl\| K f( x) \bigr\| \leq M\bigl\Vert f ( x ) \bigr\Vert \quad \textit{for } x\in P_{u_{0} }\cap( \overline{\Omega}_{b}\setminus\Omega_{a}), $$
(2.7)

where \(Kf: P_{u_{0}}\cap(\overline{\Omega} _{b}\setminus\Omega_{a})\rightarrow P_{u_{0}} \) is completely continuous and, in addition, the conditions

$$ \bigl\Vert f(x)\bigr\Vert _{x\in[ a u_{0} ,a\varphi]}\leq\frac{a}{M}\quad \textit{and}\quad \bigl\Vert f(x)\bigr\Vert _{x\in[ b u_{0} ,b\varphi]}\geq \frac{b}{m} $$
(2.8)

or

$$ \bigl\Vert f(x)\bigr\Vert _{x\in[ a u_{0},a\varphi]}\geq\frac{a}{m} \quad \textit{and} \quad \bigl\Vert f(x)\bigr\Vert _{x\in[ b u_{0},b\varphi]}\leq \frac{b}{M} $$
(2.9)

are satisfied, then the operator equation (1.7) has a solution \(x_{0}\in[ a u_{0}, b\varphi]\).

Proof

As in the proof of Theorem 2.1, it can be shown that condition (2.8) ensures the following conditions:

$$x\in P_{u_{0}}\cap\partial \Omega_{a} \subset[au_{0}, a \varphi]\quad \mbox{and} \quad x\in P_{u_{0}}\cap\partial \Omega_{b} \subset[bu_{0}, b \varphi]. $$

Therefore,

$$\bigl\Vert Kf(x)\bigr\Vert \leq M \bigl\Vert f(x)\bigr\Vert \leq a \quad \mbox{for } x\in P_{u_{0}}\cap \partial \Omega_{a} $$

and

$$\bigl\Vert Kf(x)\bigr\Vert \geq m \bigl\Vert f(x)\bigr\Vert \geq b \quad \mbox{for } x\in P_{u_{0}} \cap \partial \Omega_{b} . $$

The rest of the proof is similar to that of Theorem 2.1. □

Remark 2.5

In Theorem 2.4, let \(u_{0}= \delta\varphi\), we can obtain the parallel theorem of Theorem 2.2 for the semilinear case.

Remark 2.6

Condition (2.7) is always true when K is bounded and invertible. For a bounded linear operator, \(M=\|K\|\). If K is invertible, \(m=\frac{1}{\|K^{-1}\|}\).

For a Banach space with a normal cone, the norm condition (2.7) can be reduced to an order condition. The definition of a normal cone is given below [6].

Definition 2.7

The order cone \(X_{+}\) is called normal iff there is a number \(c>0\) such that, for all \(x, y \in X\):

$$\mbox{if } 0\leq x\leq y, \mbox{then } \|x\| \leq c \|y\|. $$

The following result for a Banach space with a normal cone can be easily applied in many cases.

Theorem 2.8

Let X be an ordered Banach space with the normal cone \(X_{+}\) and the normal parameter c. Let \(f: X_{+} \to X \) be nonlinear and \(K: X \to X\) be a linear operator. Assume that there exist positive numbers \(m\leq M\) and \(a< b\) such that

$$ m\bigl\Vert f ( x ) \bigr\Vert \varphi\leq K f ( x ) \leq M \bigl\Vert f ( x ) \bigr\Vert \varphi\quad \textit{for } x\in P_{\delta\varphi} \cap(\overline{\Omega}_{b}\setminus\Omega_{a}), $$
(2.10)

\(Kf: P_{\delta\varphi}\cap(\overline{\Omega} _{b}\setminus\Omega_{a})\rightarrow P_{\delta\varphi} \) is a completely continuous operator, and that the conditions

$$ \bigl\Vert f(x)\bigr\Vert _{x\in[ \delta a\varphi,a\varphi]}\leq\frac {a}{cM} \quad \textit{and} \quad \bigl\Vert f(x)\bigr\Vert _{x\in[ \delta b\varphi,b\varphi]}\geq \frac{cb}{m} $$
(2.11)

or

$$ \bigl\Vert f(x)\bigr\Vert _{x\in[ \delta a\varphi,a\varphi]}\geq\frac {ca}{m} \quad \textit{and} \quad \bigl\Vert f(x)\bigr\Vert _{x\in[ \delta b\varphi,b\varphi]}\leq \frac{b}{cM} $$
(2.12)

are satisfied; then the operator equation (1.7) has a solution \(x_{0}\in[ \delta a\varphi, b\varphi]\).

The proof of Theorem 2.8 follows directly from Theorem 2.4 (\(u_{0}= \delta\varphi\)) and the fact that condition (2.10) implies

$$\frac{m}{c}\bigl\Vert f(x)\bigr\Vert \leq\bigl\Vert Kf(x) \bigr\Vert \leq cM \bigl\Vert f(x) \bigr\Vert \quad \mbox{for } x\in P_{\delta\varphi}\cap(\overline{\Omega}_{b}\setminus \Omega_{a}). $$

In the following example, we use the notation \(\operatorname{col}(x_{1}, x_{2})\) to denote the column vector \((x_{1}, x_{2})^{\bot} \in\mathbb{R}^{2}\).

Example 2

Let \(f(x) = x^{2} -1\), \(x\in\mathbb{R}_{+}= [0, \infty)\). Consider the system of equation:

$$ \left ( \textstyle\begin{array}{@{}c@{\quad}c@{}} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\displaystyle \right ) f(x) =x, $$
(2.13)

where \(a_{ij} >0\), \(x=\operatorname{col}(x_{1}, x_{2}) \in\mathbb{R}^{2}\), \(f(x) = \operatorname{col}(f(x_{1}), f(x_{2}))\). Let the norm of \(\mathbb {R}^{2}\) be defined as \(\|x\|= \max\{ |x_{1}|, |x_{2}| \}\) and denote

$$\mathbb{R}^{2}_{+}=\bigl\{ \operatorname{col}(x_{1}, x_{2}): x_{i}\geq0, i=1,2 \bigr\} . $$

Obviously \(\mathbb{R}^{2}_{+}\) is a normal cone of \(\mathbb{R}^{2}\) with the normal parameter \(c=1\).

System (2.13) can be written as \(Kf(x) =x\), where \(K: \mathbb{R}^{2}\to\mathbb{R}^{2}\) is the linear operator

$$K(x) = \left ( \textstyle\begin{array}{@{}c@{\quad}c@{}} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\displaystyle \right ) x, \quad x= \operatorname{col}(x_{1}, x_{2}) \in\mathbb{R}^{2}. $$

Assume that

$$m=2\min(a_{ij}) =1 \quad \mbox{and} \quad M=2\max(a_{ij}) =2. $$

Let \(\varphi= \operatorname{col}(1, 1)\), \(\delta= \frac{m}{M}\), \(a=\frac{6}{5}\), \(b=5\). It can be verified that conditions (2.10) and (2.11) are satisfied. Therefore, (2.13) has at least one solution \(x=\operatorname{col}(x_{1}, x_{2})\) and \(\frac{3}{5}\leq x_{i} \leq5\), \(i=1,2\). In fact, if \(a_{11}=a_{12}=1\), \(a_{21}=a_{22}=\frac{1}{2}\), we can find that \(x = \operatorname{col}(\frac{2(1+\sqrt{11})}{5}, \frac {1+\sqrt{11}}{5} )\) is a solution of (2.13).

It can be seen that Example 2 is true for any finite dimensional space with the dimension \(n> 2\).

Remark 2.9

If there exist \(\{a_{k}\}\) and \(\{b_{k}\}\) such that \(a_{k}\) and \(b_{k}\) (\(k=1, 2, \ldots, n\)) satisfy all conditions of Theorem 2.1, and

$$[a_{i} u_{0}, b_{i}\varphi] \cap[a_{j} u_{0}, b_{j} \varphi] = \phi \quad \mbox{for } i\neq j, $$

then we can obtain n fixed points of T with \(a_{k}\), \(b_{k}\) (\(k=1, 2, \ldots, n\)) as an ordered sequence. The same results on multiple fixed points can be derived from other theorems.

Remark 2.10

Theorems proved in this section can also be extended to negative intervals to prove the existence of negative solutions.

3 Applications

The results obtained in Section 2 can be applied to existence of solutions for differential and difference equations. We will show some examples.

Example 3

Consider the discrete Dirichlet boundary value problem [9]:

$$ \left \{ \textstyle\begin{array}{l} \bigtriangleup^{2} x_{i-1} + f(x_{i}) =0, \quad i\in[1, n], \\ x_{0} =0 = x_{n+1}, \end{array}\displaystyle \right . $$
(3.1)

where n is a positive integer, \([1, n] = \{1, 2, \ldots, n \}\), \(f: \mathbb{R}_{+} \to\mathbb{R}_{+} \), △ is the forward difference operator,

$$ \bigtriangleup x_{i-1}=x_{i} - x_{i-1}, \qquad \bigtriangleup^{2} x_{i-1} = \bigtriangleup( \bigtriangleup x_{i-1} ) . $$

Let

$$ g_{ij} = \left \{ \textstyle\begin{array}{l@{\quad}l} \frac{(n-i+1)j}{n+1}, & 1\leq j \leq i \leq n, \\ \frac{(n-j+1)i}{n+1}, & 1\leq i \leq j \leq n.\end{array}\displaystyle \right . $$

BVP (3.1) can be rewritten as

$$ x_{i} = \sum_{j=1}^{n} g_{ij}f(x_{j})\quad \mbox{for } i\in[1, n], $$
(3.2)

where \(x=\operatorname{col}(x_{1}, x_{2}, \ldots, x_{n})\), \(f(x) = \operatorname{col} (f(x_{1}), f(x_{2}), \ldots,f(x_{n})) \). The same as shown in Example 2, (3.2) can be written as \(x=Kf(x)\) for \(x\in\mathbb{R}^{n} _{+}\), where \(K: \mathbb {R}^{n}\to\mathbb{R}^{n} \) is a linear operator. Let

$$\begin{aligned}& \|x\| = \max\bigl\{ \vert x_{i} \vert \bigr\} ,\qquad \varphi= \{1, 1, \ldots, 1\}, \\& m= n \min_{i,j \in[1, n]}\{g_{ij}\},\qquad M= n \max _{i,j\in[1, n]}\{ g_{ij}\}. \end{aligned}$$

Let \(\delta=\frac{m}{M}\). Applying Theorem 2.8, we obtain the results that were obtained in [9] most recently.

The following definition of a fractional derivative is related to our next example on fractional boundary value problem.

Definition 3.1

The Riemann-Liouvillle fractional derivative of order \(\alpha> 0\) of a continuous function \(u: [0, \infty) \to\mathbb{R} \) is defined to be

$$ D_{0+}^{\alpha} u(t) = \frac{1}{\Gamma(n-\alpha )} \biggl( \frac{d}{dt} \biggr)^{n} \int_{0} ^{t} \frac {u(s)}{ (t-s)^{\alpha-n +1}}\, ds, \quad n= \lceil{\alpha} \rceil, $$

where \(\lceil{\alpha} \rceil\) denotes the ceiling function that returns the smallest integer greater than or equal to α.

Example 4

Consider the fractional boundary value problem [15]:

$$\begin{aligned}& D_{0+}^{\alpha} u(t) + \lambda h(t) f\bigl(u(t)\bigr) =0, \quad 0< t< 1, 2< \alpha< 3, \end{aligned}$$
(3.3)
$$\begin{aligned}& u(0)=u^{\prime}(0)=u^{\prime}(1) =0, \end{aligned}$$
(3.4)

where \(\lambda>0\) is a parameter, \(h :(0, 1) \to(0, \infty)\), and \(f:[0, \infty) \to\mathbb{R}^{+}\) are nonnegative and continuous.

Let \(X=C[0, 1]\) with the standard norm \(\|u\| = \max_{0\leq t\leq 1}|u(t)|\), \(u\in X\). Let \(X_{+} = \{u\in C[0,1], u(t) \geq0 \mbox{ for } t\in[0,1] \} \). Define the Hammerstein operator \(N: X \to X\):

$$ N (u) (t) = \lambda \int_{0}^{1} G(t, s)a(s)f\bigl(u(s)\bigr)\, ds, \quad t\in[0, 1], u\in X, $$
(3.5)

where

$$ G(t, s) = \left \{ \textstyle\begin{array}{l@{\quad}l} \frac{ (1-s)^{\alpha-2} t^{\alpha-1} }{ \Gamma (\alpha)} & \mbox{if } 0 \leq t \leq s \leq1, \\ \frac{ (1-s)^{\alpha-2} t^{\alpha-1} }{ \Gamma(\alpha )} - \frac{ (t-s)^{\alpha-1} }{\Gamma(\alpha)} & \mbox{if } 0\leq s\leq t\leq1. \end{array}\displaystyle \right . $$

It is well-known that \(u\in X\) is a solution of (3.3)-(3.4) if and only if \(N(u)=u\) [15].

System (3.3)-(3.4) was recently studied in [17]. Applying Theorem 2.1, the following new result on the existence of a positive solution is obtained.

Theorem 3.2

Assume that \(h(s) \geq0 \) for \(s>0\) and \(f(x)> 0\) for \(x>0\). Denote

$$\begin{aligned}& {f}_{0}=\lim_{x\to0^{+}} \frac{f(x)}{x}, \qquad f_{\infty} = \lim_{x\to\infty} \frac{f(x)}{x}, \\& A= \int_{0}^{1} G(1,s)h(s) \, ds, \qquad B = \int _{0}^{1} G(1,s)h(s)q(s) \, ds, \end{aligned}$$

where \(q(s) =s^{\alpha-1}\). Assume that \(0< f_{0}, f_{\infty}<\infty \). If \(A f_{0} < B f_{\infty}\), then the BVP (3.3)-(3.4) has at least one positive solution for \(\lambda\in ( \frac{1}{ B f_{\infty}}, \frac{1}{A f_{0} } )\).

Proof

Let \(u_{0}=q(t) \), \(\varphi= 1\). It was shown that, for any \(\lambda >0\), \(N: P_{u_{0}} \to P_{u_{0}} \) is completely continuous [15]. For \(u\in P_{u_{0}}\), \(\|u\| = u(1)\). So \(u_{0}\) and φ satisfy the conditions of Theorem 2.1.

Since \(\lambda< \frac{1}{A f_{0}}\), we select \(\varepsilon_{1} >0\) small enough such that \(\lambda(f_{0}+ \varepsilon_{1} )A < 1\). Let \(\delta>0\) such that \(\frac{f(x)}{x}< f_{0} + \varepsilon_{1} \) for \(x\in(0, \delta)\) and \(a=\frac{\delta}{2}\). Then, for \(u \in C[0, 1]\), \(u\in[a q(t), a] \), we have

$$\begin{aligned} \|N(u)\| =& N(u) (1) = \lambda \int_{0}^{1} G(1, s) h(s) f\bigl(u(s)\bigr) \, ds \\ \leq& \lambda( f_{0}+ \varepsilon_{1} ) \int_{0}^{1} G(1, s) h(s) u(s)\, ds \leq a . \end{aligned}$$

Since \(\lambda> \frac{1}{Bf_{\infty}}\), there exist \(c>0\) and \(\varepsilon_{2}>0\) such that

$$\lambda(f_{\infty} -\varepsilon_{2} ) \int_{c}^{1} G(1, s) h(s) q(s)\, ds >1. $$

Let \(N >0\) such that \(\frac{f(x)}{x} > f_{\infty} - \varepsilon_{2} \) for \(x\geq N\). Assume that \(N> c^{\alpha-1} \delta\). Let \(b= \frac{N}{c^{\alpha-1}}\). For \(u \in C[0, 1]\), \(b t^{\alpha -1} \leq u \leq b \), \(u(t) \geq N \) for \(t \in[c, 1]\). Therefore

$$\begin{aligned} \|N(u)\| =& N(u) (1) = \lambda \int_{0}^{1} G(1, s) h(s) f\bigl(u(s)\bigr)\, ds \\ \geq& \lambda(f_{\infty}- \varepsilon_{2}) \int_{c}^{1} G(1, s) h(s) u(s)\, ds \\ \geq & \lambda(f_{\infty}- \varepsilon_{2}) b \int_{c}^{1} G(1, s) h(s) q(s) \, ds \geq b. \end{aligned}$$

By Theorem 2.1, N has a fixed point \(u_{\lambda} \in[a q(t), b]\). It is a positive solution of (3.3)-(3.4). □