Impact of the fear and Allee effect on a Holling type II prey–predator model

Abstract

In this paper, we propose and investigate a prey–predator model with Holling type II response function incorporating Allee and fear effect in the prey. First of all, we obtain all possible equilibria of the model and discuss their stability by analyzing the eigenvalues of Jacobian matrix around the equilibria. Secondly, it can be observed that the model undergoes Hopf bifurcation at the positive equilibrium by taking the level of fear as bifurcation parameter. Moreover, through the analysis of Allee and fear effect, we find that: (i) the fear effect can enhance the stability of the positive equilibrium of the system by excluding periodic solutions; (ii) increasing the level of fear and Allee can reduce the final number of predators; (iii) the Allee effect also has important influence on the permanence of the predator. Finally, numerical simulations are provided to check the validity of the theoretical results.

1 Introduction

Predator–prey model has always been a hot research topic in biological mathematics [1–16]. Mastering the dynamic behavior between predators and bait can further understand the relationship between the two and balance the ecosystem. However, for some populations, when their density is reduced to a certain extent, the population will maintain at a very low level or tend to extinction. Biologist Allee summarized this phenomenon as Allee effect [17]. Allee effect is caused by many reasons, including inbreeding, depression [18], mating difficulty [19], low density social disorder [20] and so on. More and more scholars have studied Allee effect in recent years due to its biological significance [21–29]. For some endangered species, Allee effect is more likely to occur, so Allee effect is very important for the management of endangered species conservation, population development and utilization, as well as the introduction of species are very important. Zu et al. [30] proposed a prey–predator system with Holling II type response function incorporating Allee effect in prey as follows:

$$ \textstyle\begin{cases} \frac{dx}{dt}=x (\frac{rx}{a+x}-d_{1}-kx )-\frac{exy}{1+bx}, \\ \frac{dy}{dt}=-d_{2}y+\frac{cexy}{1+bx}. \end{cases} $$

(1.1)

The meaning of all parameters of model (1.1) is shown in Table 1. In the model, authors consider that it is difficult for the prey population to find a mate to reproduce because of the small population, that is, Allee effect affects the birth rate of the prey population. Here, the birth rate of the prey population is expressed as $A(a,x)=\frac{rx}{a+x}$, where r denotes the maximum birth rate of prey population and x is the prey population density at time t, $a>0$ presents the level of Allee which can measure the degree of Allee effect on the prey. $A(a,x)$ satisfied $\lim_{a\rightarrow +\infty }A(a,x)=0$, $\lim_{x\rightarrow 0}A(a,x)=0$, $\lim_{a\rightarrow 0}A(a,x)=r$, $\lim_{x\rightarrow +\infty }A(a,x)=r$, $\frac{\partial A(a,x)}{\partial a}<0$.

Table 1 Meaning of parameters in model (1.1) and (1.3)

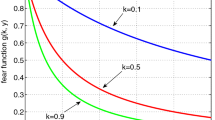
However, in nature, fear of predators also has a variety of effects on animals, such as habitat use, foraging behavior, reproduction and physiological changes. In recent years, many experts began to study the predator model with fear effect; see [31–36]. In order to study the effect of fear on free-living songbird population, Zanette et al. [31] used the play of predator’s call to control the fear factor, and eliminated the effect of direct predation on the experiment by blocking. The results show that the number of offspring of sparrow will be reduced by 40% only by adding fear effect to the prey, and the predation risk itself is enough to affect the change of wild animal population. In order to establish a model to simulate the impact of fear on species reduction, we use a function $K(f,y)$ to indicate the fear factor which is used to measure the consumption of anti-predator defense owing to the fear on the system. From the biological viewpoint and experimental results, the fear factor $K(f,y)$ should meet [27] $K(0,y)=1$, $K(f,0)=1$, $\lim_{f\rightarrow +\infty }K(f,y)=0$, $\lim_{y\rightarrow +\infty }K(f,y)=0$, $\frac{\partial K(f,y)}{\partial f}<0$ and $\frac{\partial K(f,y)}{\partial y}<0$. Wang et al. [32] introduced a simple function $K(f,y)=\frac{1}{1+fy}$ as the fear factor where $f>0$ presents the level of fear induced by predators and y is the predator population density at time t, and studied the prey–predator system with Holling II type response function incorporating fear effect in prey as follows:

$$ \textstyle\begin{cases} \frac{dx}{dt}=x (\frac{r}{1+fy}-d_{1}-kx )-\frac{exy}{1+bx}, \\ \frac{dy}{dt}=-d_{2}y+\frac{cexy}{1+bx}. \end{cases} $$

(1.2)

Inspired by the previous articles, we wonder what the dynamic behavior of the system will be if Allee effect and fear effect appear in the prey population at the same time? Since both Allee effect and fear effect affect the birth rate of the population, we express the birth rate of the prey in terms of $A(a,x)K(f,y)=\frac{rx}{(a+x)(1+fy)}$, which describe the impact of Allee and fear effect on the system. Then we obtain a Holling II type predator–prey model with Allee effect and fear effect in prey as follows:

$$ \textstyle\begin{cases} \frac{dx}{dt}=x (\frac{rx}{(a+x)(1+fy)}-d_{1}-kx )- \frac{exy}{1+bx}, \\ \frac{dy}{dt}=-d_{2}y+\frac{cexy}{1+bx}. \end{cases} $$

(1.3)

The meaning of all parameters of model (1.3) is shown in Table 1. Considering the practical significance of the model, we assume $r>d_{1}$, $ce>bd_{2}$ always hold in this paper.

The rest of the article is arranged as follows: In Sect. 2, we provide a qualitative analysis of the system, which include the stability of the equilibria and the sufficient condition for Hopf bifurcation at positive equilibrium and the corresponding biological interpretation. We analyze the influence of dread and Allee effect on the system in Sect. 3. We do numerical simulation to verify the rationality of the results in Sect. 4. In Sect. 5, we end up this paper with a short conclusion.

2 Stability analysis of the model

In this part, the existence and stability of equilibria of the model (1.3) are discussed.

2.1 Equilibria and their existence condition

The biological equilibria in the model (1.3) are as below:

• (i) The extinction equilibrium $B_{0}(0,0)$, which invariably exists with no restrictions.

• (ii) If $0< a< a_{1}$ holds, the model (1.3) has two predator free equilibria $B_{1}(x_{1},0)$ and $B_{2}(x_{2},0)$, where $a_{1}=\frac{(\sqrt{r}-\sqrt{d_{1}})^{2}}{k}$.Obviously $x_{1}$ and $x_{2}$ satisfy equation as follows:

  $$ kx^{2}+(d_{1}+ak-r)x+d_{1}a=0. $$

  Set

  $$ \Delta _{1}=(d_{1}+ak-r)^{2}-4akd_{1}. $$

  When $\Delta _{1}>0$ and $d_{1}+ak-r<0$ i.e., $0< a< a_{1}$ holds, then the model (1.3) has two predator free equilibria, and

  $$ x_{1,2}=\frac{r-d_{1}-ak\mp \sqrt{\Delta _{1}}}{2k}. $$

  (2.1)

• (iii) If $r>r_{1}$ and $ce>bd_{2}$ hold, the model (1.3) has unique coexistence equilibrium $B^{*}(x^{*},y^{*})$, where $x^{*}= \frac{d_{2}}{ce-bd_{2}}$, $r_{1}=\frac{(a+x^{*})(d_{1}+kx^{*})}{x^{*}}>d_{1}$, and $y^{*}$ is the positive solution of the equation as follows:

  $$ A_{1}y^{2}+A_{2}y+A_{3}=0, $$

  where

  $$ A_{1}=\frac{ef}{1+bx^{*}}, \quad\quad A_{2}=d_{1}f+fkx^{*}+ \frac{e}{1+bx^{*}}, \quad\quad A_{3}=d_{1}+kx^{*}- \frac{rx^{*}}{a+x^{*}}. $$

  Let

  $$ \Delta _{2}=A_{2}^{2}-4A_{1}A_{3}, $$

  when $A_{3}<0$ i.e., $r>r_{1}$ holds, then the equation has unique positive solution, that is, the model (1.3) has unique positive equilibrium $B^{*}(x^{*},y^{*})$, and

  $$ y^{*}=\frac{-A_{2}+\sqrt{\Delta _{2}}}{2A_{1}}. $$

  (2.2)

2.2 Local stability of the equilibria

The local stability of the model (1.3) near each equilibrium point refers to the behavior of the solution of the system (1.3) under small disturbance near each equilibrium point. We study the stability of the model (1.3) near each equilibrium point. First, we derive the Jacobian matrix of the model (1.3) as follows:

$$ J(x,y)= \begin{pmatrix} \frac{rx(2a+x)}{(a+x)^{2}(1+fy)}-d_{1}-2kx-\frac{ey}{(1+bx)^{2}} & - \frac{frx^{2}}{(a+x)(1+fy)^{2}}-\frac{ex}{1+bx} \\ \frac{cey}{(1+bx)^{2}} & \frac{cex}{1+bx}-d_{2} \end{pmatrix}. $$

Now, let us give the dynamic behavior of the model system near each steady state one by one in the form of the following theorems.

Theorem 2.1

$B_{0}(0,0)$ is always a locally asymptotically stable node.

Proof

The Jacobian matrix of model (1.3) around $B_{0}$ is

$$ J(0,0)= \begin{pmatrix} -d_{1} & 0 \\ 0 & -d_{2} \end{pmatrix}, $$

its eigenvalues are $\lambda _{1}=-d_{1}<0$ and $\lambda _{2}=-d_{2}<0$, so the extinction equilibrium $B_{0}(0,0)$ is always a locally asymptotically stable node. □

Remark 2.1

According to Theorem 2.1, the extinction equilibrium $B_{0}$ is always locally asymptotically stable, which means that when the population density of predator and prey is located in the attractive region of $B_{0}$, they will die out. Especially, as the population density of the prey decreases, both populations will eventually die out.

Theorem 2.2

Suppose $0< a< a_{1}$ holds, then

• (i) $B_{1}(x_{1},0)$ is a unstable node, if $0< b< b_{1}$ holds; and $B_{1}(x_{1},0)$ is a saddle point, if $b>b_{1}$ holds, where $b_{1}=\frac{ce}{d_{2}}-\frac{1}{x_{1}}$.

• (ii) $B_{2}(x_{2},0)$ is a saddle point, if $0< b< b_{2}$ holds; and $B_{2}(x_{2},0)$ is a stable node, if $b>b_{2}$ holds, where $b_{2}=\frac{ce}{d_{2}}-\frac{1}{x_{2}}$.

Proof

(i) Note that $\frac{rx_{1}}{a+x_{1}}-d_{1}-kx_{1}=0$, then Jacobian matrix of model (1.3) around $B_{1}$ is

$$ J(x_{1},0)= \begin{pmatrix} \frac{x_{1}\sqrt{\Delta _{1}}}{a+x_{1}} & - \frac{frx_{1}^{2}}{(a+x_{1})}-\frac{ex_{1}}{1+bx_{1}} \\ 0 & \frac{cex_{1}}{1+bx_{1}}-d_{2} \end{pmatrix}, $$

its eigenvalues are $\lambda _{1}=\frac{x_{1}\sqrt{\Delta _{1}}}{a+x_{1}}>0$ and $\lambda _{2}=\frac{cex_{1}}{1+bx_{1}}-d_{2}$, then, if $\lambda _{2}>0$ i.e., $0< b< b_{1}$ holds, $B_{1}(x_{1},0)$ is a unstable node; and, if $\lambda _{2}<0$ i.e., $b>b_{1}$ holds, $B_{1}(x_{1},0)$ is a saddle point.

Similarly, it can be proved that (ii) is true. □

Remark 2.2

If there is no positive equilibrium in the model (1.3), the local stability of equilibria $B_{0}$, $B_{1}$ and $B_{2}$ determines its asymptotic dynamic behavior. According to Theorem 2.1 and Theorem 2.2, If the Allee effect of prey is very weak, that is, the parameter a is smaller and the predator’s processing time b is rather long, then $B_{1}$ is the saddle and $B_{2}$ is locally asymptotically stable. The steady trajectory of $B_{1}$ is the boundary owing to Allee effect. It separates quadrant I into two areas (see Fig. 3), the attraction regions of $B_{0}$ and $B_{2}$, respectively. If the number of prey is lower, both predator and prey population will die out. Instead, if the Allee factor on prey is rather strong and the predator’s processing time b is rather short, then $B_{1}$ is unstable and $B_{2}$ is saddle. When t tends to infinity, any normal trajectory tends to $B_{0}$, that is, $B_{0}$ is a globally asymptotically steady node, and both predator and prey population will die out, independent of the initial population density. Hence, if there is no positive equilibrium in the model (1.3), according to the intensity of Allee factor, the processing time of predator and the initial value of population density, either the predator population is die out or both the predator and the prey are die out.

Theorem 2.3

$B^{*}(x^{*},y^{*})$ is locally asymptotically stable if $0< a< a_{2}$ and $r_{1}< r\leq r_{2}$ or $0< a< a_{2}$ and $r>r_{2}$ and $f>f_{1}$ hold; $B^{*}(x^{*},y^{*})$ is unstable if $a\geq a_{2}$ and $r>r_{1}$ or $0< a< a_{2}$ and $r>r_{2}$ and $0< f< f_{1}$ hold, where

$$\begin{aligned}& a_{2}=\frac{k(x^{*})^{2}}{d_{1}}, \\& r_{2}=\frac{a+x^{*}}{x^{*}} \biggl(d_{1}+kx^{*}+ \frac{(k(x^{*})^{2}-ad_{1})(1+bx^{*})}{b(x^{*})^{2}+2abx^{*}+a} \biggr), \\& \begin{aligned} f_{1}&= \frac{e(b(x^{*})^{2}+2abx^{*}+a)^{2}}{(k(x^{*})^{2}-ad_{1})(1+bx^{*})^{2}((k(x^{*})^{2}-ad_{1})(1+bx^{*})+ (d_{1}+kx^{*})(b(x^{*})^{2}+2abx^{*}+a))} \\ & \quad{} \cdot \biggl(\frac{rx^{*}}{a+x^{*}}-d_{1}-kx^{*}- \frac{(k(x^{*})^{2}-ad_{1})(1+bx^{*})}{b(x^{*})^{2}+2abx^{*}+a} \biggr). \end{aligned} \end{aligned}$$

Proof

Note that $\frac{rx^{*}}{(a+x^{*})(1+fy^{*})}-d_{1}-kx^{*}- \frac{ey^{*}}{1+bx^{*}}=0$ and $r>r_{1}$ hold, then Jacobian matrix of model (1.3) at $B^{*}$ is

$$ J\bigl(x^{*},y^{*}\bigr)= \begin{pmatrix} J_{11} & J_{12} \\ J_{21} & 0 \end{pmatrix}, $$

where

$$ \begin{aligned} J_{11}&=x^{*} \biggl( \frac{ra}{(a+x^{*})^{2}(1+fy^{*})}-k- \frac{bey^{*}}{(1+bx^{*})^{2}} \biggr), \\ J_{12}&=-\frac{fr(x^{*})^{2}}{(a+x^{*})(1+fy^{*})^{2}}- \frac{ex^{*}}{1+bx^{*}}< 0, \\ J_{21}&=\frac{cey^{*}}{(1+bx^{*})^{2}}>0, \end{aligned} $$

the secular equation is $\lambda ^{2}-J_{11}\lambda -J_{12}J_{21}=0$, and the two eigenvalues meet $\lambda _{1}\lambda _{2}=\det (J(x^{*},y^{*}))=-J_{12}J_{21}>0$, $\lambda _{1}+\lambda _{2}=\operatorname{tr}(J(x^{*},y^{*}))=J_{11}$. Then the two eigenvalues have the same sign. Thus $B^{*}$ is locally asymptotically stable if $J_{11}<0$, and unstable if $J_{11}>0$.

By a simple computation, $J_{11}<0$ is equivalent to

$$ \biggl(\frac{bex^{*}}{(1+bx^{*})^{2}}+\frac{ae}{(a+x^{*})(1+bx^{*})} \biggr)y^{*}< \frac{k(x^{*})^{2}-ad_{1}}{a+x^{*}}. $$

(2.3)

If $k(x^{*})^{2}-ad_{1}\leq 0$, i.e. $a\geq a_{2}$ holds, then the inequality (2.3) does not hold because the left side of the inequality is positive, that is, $B^{*}(x^{*},y^{*})$ is unstable if $a\geq a_{2}$ and $r>r_{1}$ hold.

If $k(x^{*})^{2}-ad_{1}>0$, i.e. $0< a< a_{2}$ holds, we substitute (2.2) into the inequality (2.3) and obtain

$$\begin{aligned} \begin{aligned}[b] f&> \frac{e(b(x^{*})^{2}+2abx^{*}+a)^{2}}{(k(x^{*})^{2}-ad_{1})(1+bx^{*})^{2}((k(x^{*})^{2}-ad_{1})(1+bx^{*})+ (d_{1}+kx^{*})(b(x^{*})^{2}+2abx^{*}+a))} \\ &\quad{} \cdot \biggl(\frac{rx^{*}}{a+x^{*}}-d_{1}-kx^{*}- \frac{(k(x^{*})^{2}-ad_{1})(1+bx^{*})}{b(x^{*})^{2}+2abx^{*}+a} \biggr) \doteq f_{1}. \end{aligned} \end{aligned}$$

(2.4)

If $\frac{rx^{*}}{a+x^{*}}-d_{1}-kx^{*}- \frac{(k(x^{*})^{2}-ad_{1})(1+bx^{*})}{b(x^{*})^{2}+2abx^{*}+a}\leq 0$, i.e., $r_{1}< r\leq r_{2}$ holds, the inequality (2.4) clearly holds because the left side of the inequality is positive, Hence $B^{*}(x^{*},y^{*})$ is stable if $0< a< a_{2}$ and $r_{1}< r\leq r_{2}$.

If $r>r_{2}$, at this case $J_{11}<0$ i.e., $f>f_{1}$. Hence $B^{*}(x^{*},y^{*})$ is stable $0< a< a_{2}$ and $r>r_{2}$ and $f>f_{1}$ hold; otherwise $E^{*}(x^{*},y^{*})$ is unstable if $0< a< a_{2}$ and $r>r_{2}$ and $0< f< f_{1}$ hold.

In conclusion, the theorem holds. □

Remark 2.3

When the Allee factor intensity of the predator is strong enough, the model tends to unstable, at this case, fear effect cannot change the stability of the system. When the Allee factor intensity of the prey is weak enough and the fear caused by predator is at low level, the model shows unstable dynamic behavior (see Fig. 5), When the fear caused by predator is at a high level, the model shows stable behavior (see Fig. 6). A possible biological explanation for this appearance is that when prey population are very dread of predators, they will reduce their feeding activities and fit to various defense mechanisms to rescue themselves from predators. This appearance greatly assists prey species to increase its biomass, so in a long run, it also contributes to the persistence of the prey species and enhances the stability and persistence of the whole system.

Theorem 2.4

$B_{0}(0,0)$ is always a locally asymptotically stable node, if $a>\max \{a_{1},a_{3}\}$ holds, where $a_{3}=\frac{(r-d_{1})x^{*}-k(x^{*})^{2}}{d_{1}+kx^{*}}$.

Proof

From the previous discussion on the existence of equilibrium points, we know that when $a>a_{1}$ the boundary equilibrium points do not exist, and when $a>a_{3}$ i.e., $r>r_{1}$ the positive equilibrium point does not exist. Then when $a>\max \{a_{1},a_{3}\}$ holds, the model (1.3) only exist extinction equilibrium which is locally asymptotically stable, correspondingly is a globally asymptotically stable node. □

Remark 2.4

According to Theorem 2.4, we know that Allee effect increases the risk of population death. As Allee effect is very strong and satisfies $a>\max \{a_{1},a_{3}\}$, the model (1.3) has no positive equilibrium and other boundary equilibrium, at this case $B_{0}$ will become globally asymptotically stable (see Fig. 2). Any normal trajectory tends to $B_{0}$, as t goes to infinity. No matter what the initial population density of prey is, prey and predator cannot coexist.

We can use Table 2 show the occurrence and behavior of all equilibria of model (1.3). Then, we will investigate the occurrence of Hopf bifurcation around the positive equilibrium point and the existence of limit cycle emerging across Hopf bifurcation.

Table 2 Stationary states and their stability in model (1.3)

2.3 Hopf bifurcation

Theorem 2.5

Suppose $0< a< a_{2}$ and $r>r_{2}$, then model (1.3) experiences a Hopf bifurcation nearby $B^{*}$ at $f=f_{1}$.

Proof

the secular equation is $\lambda ^{2}-J_{11}\lambda -J_{12}J_{21}=0$, and the two eigenvalues meet $\lambda _{1}\lambda _{2}=\det (J(x^{*},y^{*}))=-J_{12}J_{21}>0$ $\operatorname{tr}(J(x^{*},y^{*}))=J_{11}$, then

$$\begin{aligned}& \det \bigl(J\bigl(x^{*},y^{*}\bigr)\bigr)\big| _{f=f_{1}}>0. \end{aligned}$$

(2.5)

$$\begin{aligned}& \operatorname{tr}\bigl(J\bigl(x^{*},y^{*}\bigr)\bigr)\big| _{f=f_{1}}=J_{11}| _{f=f_{1}}=0. \end{aligned}$$

(2.6)

By simple computation, we obtain

$$ \begin{aligned} \frac{d}{df}\bigl[\operatorname{tr}\bigl(J \bigl(x^{*},y^{*}\bigr)\bigr)\bigr]\bigg| _{f=f_{1}}&= \frac{d}{df}(J_{11})\bigg| _{f=f_{1}} \\ &= \biggl(\frac{bex^{*}}{(1+bx^{*})^{2}}+\frac{ae}{(a+x^{*})(1+bx^{*})} \biggr)\frac{dy^{*}}{df}\bigg| _{f=f_{1}}. \end{aligned} $$

Obviously $B^{*}$ satisfies

$$ \frac{rx^{*}}{(a+x^{*})(1+fy^{*})}-d_{1}-kx^{*}- \frac{ey^{*}}{1+bx^{*}}=0. $$

(2.7)

By deriving both sides of (2.7) with respect to f at the same time, we have

$$ \frac{dy^{*}}{df}\bigg| _{f=f_{1}}=- \frac{\frac{rx^{*}y^{*}| _{f=f_{1}}}{(a+x^{*})(1+fy^{*}| _{f=f_{1}})^{2}}}{\frac{frx^{*}}{(a+x^{*})(1+fy^{*}| _{f=f_{1}})^{2}}+\frac{e}{1+bx^{*}}}< 0, $$

hence

$$ \frac{d}{df}\bigl[\operatorname{tr}\bigl(J\bigl(x^{*},y^{*} \bigr)\bigr)\bigr]\big| _{f=f_{1}}\neq 0. $$

(2.8)

From (2.5), (2.6) and (2.8), we know that model (1.3) experiences Hopf bifurcation nearby $B^{*}$ at $f=f_{1}$. It should be noted that when the value of fear parameter f exceeds the threshold value $f_{1}$, the transition from unstable state to stable state occurs through Hopf bifurcation (see Fig. 7), that means the fear factor can enhance the stability of the system by preventing the limit cycle oscillation. □

3 The synthetical impact of fear and Allee effect on predator–prey species

In this part, the influence of fear and Allee effect on each of population when the positive equilibrium exist and is locally asymptotically stable will be discussed in three situations as follows.

3.1 Without Allee effect

If the model (1.3) has no Allee effect in prey species, i.e., $a=0$, model (1.3) becomes model (1.2). It is similar to Theorem 2.3, we find that $B^{*}(x^{*},y^{*})$ is locally asymptotically stable if $r_{1}< r\leq r_{2}$ or $r>r_{2}$ and $f>f_{1}$ hold; $B^{*}(x^{*},y^{*})$ is unstable if $r>r_{2}$ and $0< f< f_{1}$ hold. In this case, the stability of positive equilibrium is relate with the growth rate of prey species and the level of fear. Furthermore, model (1.3) also experiences a Hopf bifurcation around $B^{*}$ at $f=f_{1}$. It should be noted that when the value of fear parameter f exceeds the threshold value $f_{1}$, the transition from unstable state to stable state occurs through Hopf bifurcation.

3.2 Without fear effect

If the model (1.3) has no Allee effect in prey species, i.e., $f=0$, model (1.3) becomes model (1.1). In this case, the model has a unique positive $B(x^{*},y^{*})$, if $r>r_{1}$ and

$$ x^{*}=\frac{d_{2}}{ce-bd_{2}}, \quad\quad y^{*}= \frac{1+bx^{*}}{e} \biggl( \frac{rx^{*}}{a+x^{*}}-d_{1}-kx^{*} \biggr), $$

then the derivatives of $x^{*}$ and $y^{*}$ with respect to the level of Allee a are

$$ \frac{dx^{*}}{da}=0, \quad\quad \frac{dy^{*}}{da}=- \frac{rx^{*}(1+bx^{*})}{e(a+x^{*})^{2}}< 0. $$

Hence, the prey population $x^{*}$ is unconcerned with the level of Allee a, and the increase of a can decrease predator population. When $a=0$, the predator population $y^{*}$ achieves the maximum value $\frac{(1+bx^{*})(r-d_{1}-kx^{*})}{e}$. when $a=\frac{(r-d_{1}-kx^{*})x^{*}}{d_{1}+kx^{*}}$, i.e., $y^{*}=0$, the predator species goes to extinction.

3.3 Incorporate fear and Allee effect

Because final density of the prey species $x^{*}= \frac{d_{2}}{ce-bd_{2}}$ is unconcerned with the fear and Allee effect, we just talk about the influence of fear factor on predator species. $y^{*}=\frac{-A_{2}+\sqrt{\Delta _{2}}}{2A_{1}}$ is a continuous function of f and a, and satisfies

$$ \frac{rx^{*}}{(a+x^{*})(1+fy^{*})}-d_{1}-kx^{*}- \frac{ey^{*}}{1+bx^{*}}=0. $$

We can get the following result by taking derivatives to f and a, respectively, from both sides of the above formula:

$$\begin{aligned}& \frac{\partial y^{*}}{\partial f}=- \frac{\frac{rx^{*}y^{*}}{(a+x^{*})(1+fy^{*})^{2}}}{\frac{frx^{*}}{(a+x^{*})(1+fy^{*})^{2}}+\frac{e}{1+bx^{*}}}< 0, \\& \frac{\partial y^{*}}{\partial a}=- \frac{\frac{rx^{*}}{(a+x^{*})^{2}(1+fy^{*})}}{\frac{frx^{*}}{(a+x^{*})(1+fy^{*})^{2}}+\frac{e}{1+bx^{*}}}< 0. \end{aligned}$$

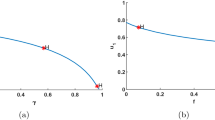
Hence, the predator population density $y^{*}$ decreases with the increase of the level of Allee a and the fear level f, respectively. The predator population density $y^{*}$ achieves the maximum value $\frac{(1+bx^{*})(r-d_{1}-kx^{*})}{e}$, when there is no fear and Allee effect in the system, i.e., $a=0$, $f=0$. The relationship between $y^{*}$ and f is shown in Fig. 1 (a), and the relationship between $y^{*}$ and a is shown in Fig. 1 (b).

Figure 1

(a) The relationship between $y^{*}$ and f; (b) the relationship between $y^{*}$ and a

We also find that $\lim_{f\rightarrow +\infty }y^{*}=0$, $\lim_{a\rightarrow a^{*}}y^{*}=0$, where $a^{*}=\frac{(r-d_{1}-kx^{*})x^{*}}{d_{1}+kx^{*}}$.

That is, the predator species will approach extinction as the increase of fear level, or as the Allee level trends to $a^{*}$.

4 Numerical simulation

In this section, we provide some numerical simulations to confirm the theoretical analysis and explain the dynamics behavior of model (1.3). We investigated the dynamical behavior of model (1.3) for varying values of three parameters: the growth rate of prey species r, the level of fear f and the level of Allee a. We fix the other parameter values as

$$ d_{1}=0.9, \quad\quad k=0.6, \quad\quad e=0.7, \quad\quad b=0.8, \quad \quad c=0.8, \quad\quad d_{2}=0.5. $$

Example 4.1

Set $r=1.1$, $a=2$, $f=0.5$, then the model (1.3) has a unique equilibrium $B_{0}=(0,0)$, which is locally asymptotically stable, at the same time, from Theorem 2.4, it is also globally asymptotically stable, that means the predator and prey species will die out, independence on initial value of population density. The simulation results are shown in Fig. 2.

Figure 2

(a) The phase diagram of model (1.3) for $r=1.1$, $a=2$, $f=0.5$; (b) solution curves for $r=1.1$, $a=2$, $f=0.5$. The initial values are $(4,0.5)$, $(4,1)$, $(4,1.5)$

Example 4.2

Set $r=2$, $a=0.1$, $f=1$, then the model (1.3) has a extinct equilibrium $B_{0}=(0,0)$, which is locally asymptotically stable, and two predator free equilibria $B_{1}=(0.0914,0)$ and $B_{2}=(1.642,0)$ which are saddle and locally asymptotically stable, respectively. From Theorem 2.2, the steady trajectory of $B_{1}$ is the boundary owing to Allee effect. It separates quadrant I into two areas (see Fig. 3), the attraction regions of $B_{0}$ and $B_{2}$, respectively. when the initial value of population density of prey falls in the attraction regions of $B_{0}$, both predator and prey population will die out as t tends to infinity; when the initial value of population density of prey falls in the attraction regions of $B_{2}$, the predator population will die out as t approaches infinity. The simulation results are shown in Fig. 3.

Figure 3

(a) The phase diagram of model (1.3) for $r=2$, $a=0.1$, $f=1$; (b) solution curves for $r=2$, $a=0.1$, $f=1$. The initial values are $(4,0.5)$, $(4,1)$, $(4,1.5)$

Example 4.3

Set $r=3$, $a=0.1$, $f=1$, then $a_{2}=6.5104$, $r_{1}=2.8638$, $r_{2}=5.3409$ and $0< a< a_{2}$ and $r_{1}< r\leq r_{2}$. From Theorem 2.3, the model (1.3) gets unique coexistence equilibrium $B^{*}=(3.125,0.0423)$, which is locally asymptotically stable, The simulation results are shown in Fig. 4.

Figure 4

(a) The phase diagram of model (1.3) for $r=3$, $a=0.1$, $f=1$; (b) solution curves for $r=3$, $a=0.1$, $f=1$. The initial values are $(4,0.5)$, $(4,1)$, $(4,1.5)$

Example 4.4

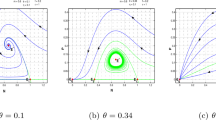
Set $r=6$, $a=0.1$, $f=0.008$, then $a_{2}=6.5104$, $r_{1}=2.8638$, $r_{2}=5.3409$, $f_{1}=0.0103$ and $0< a< a_{2}$, $r> r_{2}$ and $0< f< f_{1}$. From Theorem 2.3, The model (1.3) gets unique coexistence equilibrium $B^{*}=(3.125,9.5959)$, which is a unstable source point of spiral state and the model exist one limit cycle. We can clearly observe that the trajectories of an initial value inside and outside the limit cycle approach the limit cycle. The simulation results are shown in Fig. 5.

Figure 5

(a) The phase diagram of model (1.3) for $r=6$, $a=0.1$, $f=0.008$; (b) solution curves for $r=6$, $a=0.1$, $f=0.008$. The initial values are $(3,12)$, $(9,5)$

Example 4.5

Set $r=6$, $a=0.1$, $f=1$, then $a_{2}=6.5104$, $r_{1}=2.8638$, $r_{2}=5.3409$, $f_{1}=0.0103$ and $0< a< a_{2}$, $r> r_{2}$ and $f>f_{1}$. From Theorem 2.3, the model (1.3) has a unique coexistence equilibrium $B^{*}=(3.125,9.5959)$, which is locally asymptotically stable. Compared with Fig. 6, we know that increase the fear effect reduces the final number of predators $y^{*}$, and transition from unstable to stable state occurs at $B^{*}$. At this time, the fear factor can exclude the limit cycle oscillation and enhance the steadiness of the model. The simulation results are shown in Fig. 6.

Figure 6

(a) The phase diagram of model (1.3) for $r=6$, $a=0.1$, $f=1$; (b) solution curves for $r=6$, $a=0.1$, $f=1$. The initial values are $(0.1,0.5)$, $(9,1)$, $(9,1.5)$

Example 4.6

Set $r=6$, $a=0.1$, then $a_{2}=6.5104$, $r_{1}=2.8638$, $r_{2}=5.3409$, $f_{1}=0.0103$. From Theorem 2.5, the model (1.3) experiences a Hopf bifurcation nearby $B^{*}$ at $f=0.0103$. Obviously, the fear factor f plays an important role managing the populations. For a small fear factor, prey and predator exhibit periodic oscillation. The population remains stable when $f>f_{1}$, with the increase of fear factor, the population of predator becomes smaller and smaller and tends to zero, but it is still greater than zero. So the increase of fear level will not lead to the extinction of prey and predator population. The Hopf bifurcation diagrams taking f as bifurcation parameter are shown in Fig. 7.

Figure 7

Bifurcation diagrams with parameter n for $r=6$, $a=0.1$. (a) The variation of x with f; (b) variation of y with f

Example 4.7

Set $r=6$, $a=0$, $f=0.008$, then $a_{2}=6.5104$, $r_{1}=2.7750$, $r_{2}=5.4$, $f_{1}=0.0085$ and $0\leq a< a_{2}$, $r> r_{2}$ and $0< f< f_{1}$. The model becomes a model without Allee effect, in this case, similar to Example 4.4, the model (1.3) gets unique coexistence equilibrium $B^{*}=(3.125,13.250)$, which is a unstable source point of spiral state and the system exist one limit cycle. We can clearly observe that the trajectories of an initial value inside and outside the limit cycle approach the limit cycle. The simulation results are shown in Fig. 8.

Figure 8

(a) The phase diagram of model (1.3) for $r=6$, $a=0$, $f=0.008$; (b) solution curves for $r=6$, $a=0$, $f=0.008$. The initial values are $(3,13)$, $(9,5)$

Example 4.8

Set $r=6$, $a=0$, $f=1$, then $a_{2}=6.5104$, $r_{1}=2.7750$, $r_{2}=5.4$, $f_{1}=0.0085$ and $0\leq a< a_{2}$, $r> r_{2}$ and $f>f_{1}$. The model becomes model (1.2) without Allee effect, in this case, similar to Example 4.5, the model (1.3) gets unique coexistence equilibrium $B^{*}=(3.125,1.0148)$, which is locally asymptotically stable. Compared with Fig. 9, we know that increase the fear effect not only reduces the final number of predators $y^{*}$, but also transforms $B^{*}$ from unstable to stable state. At this time, the fear factor can exclude the limit cycle oscillation and enhance the stability of the system. The simulation results are shown in Fig. 9.

Figure 9

(a) The phase diagram of model (1.3) for $r=6$, $a=0$, $f=1$; (b) solution curves for $r=6$, $a=0$, $f=1$. The initial values are $(0.1,0.5)$, $(9,1)$, $(9,5)$

Example 4.9

Set $r=6$, $a=0.1$, $f=0$, then $a_{2}=6.5104$, $r_{1}=2.8638$, $r_{2}=5.3409$. The model (1.3) becomes model (1.1) without fear effect, in this case, the model (1.1) has a unique coexistence equilibrium $B^{*}=(3.125,15.1948)$, which is unstable. Compared with Example 4.5, we know that the decrease of the level of fear not only increases final number of predators $y^{*}$, but also changes $B^{*}$ from stable to unstable. The simulation results are shown in Fig. 10.

Figure 10

(a) The phase diagram of model (1.3) for $r=6$, $a=0.1$, $f=0$; (b) solution curves for $r=6$, $a=0.1$, $f=0$. The initial values are $(3,14)$, $(10,20)$

Example 4.10

Set $r=6$, $a=0$, $f=0$, then $a_{2}=6.5104$, $r_{1}=2.7750$, $r_{2}=5.4$, $f_{1}=0.0085$. The model becomes a model without Allee and fear effect, in this case, similar to Example 4.4, the model (1.3) gets unique coexistence equilibrium $B^{*}=(3.125,16.125)$, which is a unstable source point of spiral state and the model exist one limit cycle. We can clearly observe that the trajectories of an initial value inside and outside the limit cycle approach the limit cycle. Compared with Examples 4.5, 4.8 and 4.9, we know that reducing the fear and Allee effect not only increases the final number of predators $y^{*}$, but also changes $B^{*}$ from stable to unstable. At this time, the final number of predators $y^{*}$ obtains the maximum value and the decrease of fear and Allee effect can emerge the limit cycle oscillation and destroy the stability of the system. The simulation results are shown in Fig. 11.

Figure 11

(a) The phase diagram of model (1.3) for $r=6$, $a=0$, $f=0$; (b) solution curves for $r=6$, $a=0$, $f=0$. The initial values are $(3,14)$, $(9,15)$

5 Conclusion

In this article, we have studied the impact of the fear and Allee effect on a prey–predator model with Holling type II response function. We analyze the dynamic behavior of the model mathematically, including existence and stability of equilibria, the occurrence of Hopf bifurcation around the positive equilibrium point and the existence of limit cycle emerging through Hopf bifurcation. We find that the increase the level of fear effect can stabilize the system by excluding periodic solutions and decrease the final number of predators at the positive equilibrium, but not lead to the extinction of the predator population, which is different from the system without fear factor. We also find that the Allee effect has big influence on the permanence of the predator, the final prey population $x^{*}$ is unconcerned with fear and Allee effect, and the final predator population $y^{*}$ decreases with the increase of the Allee level a and the fear level f. When there is no fear and Allee effect in the system, i.e., $a=0$, $f=0$, the predator population $y^{*}$ achieves the maximum value $\frac{(1+bx^{*})(r-d_{1}-kx^{*})}{e}$. When $a=\frac{(r-d_{1}-kx^{*})x^{*}}{d_{1}+kx^{*}}$, the predator species goes to extinction. The extinction equilibrium $B_{0}$ is locally stable, which means that when the population density of prey and predator is located in the attractive region of $B_{0}$, they will die out. By comparison, we know that the Allee effect increases the risk of population death. Furthermore, if the model (1.3) has no positive equilibrium and other boundary equilibrium, in this case, the Allee effect is very strong, and $B_{0}$ will become globally asymptotically stable. Any normal trajectory tends to $B_{0}$, as t goes to infinity. No matter what the initial value of population density of prey is, prey and predator species cannot coexist. The system in this paper has complex dynamic behavior, which enrich the dynamic behavior of predator–prey system. The research in this paper is of great significance for the study of the complex dynamic behavior of the ecosystem with Allee effect on predator species.