Abstract
In this paper, we prpose a single-species stage structure model with Michaelis–Menten-type harvesting for mature population. We investigate the existence of all possible equilibria of the system and discuss the stability of equilibria. We use Sotomayor’s theorem to derive the conditions for the existence of saddle-node and transcritical bifurcations. From the ecological point of view, we analyze the effect of harvesting on the model of mature population and consider it as a bifurcation parameter, giving the maximum threshold of continuous harvesting. By constructing a Lyapunov function and Bendixson–Dulac discriminant, we give sufficient conditions for the global stability of boundary equilibrium and positive equilibrium, respectively. Our study shows that nonlinear harvesting may lead to a complex dynamic behavior of the system, which is quite different from linear harvesting. We carry out numeric simulations to verify the feasibility of the main results.
Similar content being viewed by others
1 Introduction
In nature world, the growth of species experiences different stages. For example, the growth of frogs can be divided into fertilized eggs, tadpoles, and adult frogs; the growth of silkworm can be divided into eggs, larvae, pupae, and adults. At different stages, species exhibit vastly different characteristics and habits. Therefore it is more practical to study stage structure ecology modeling.
During the last decade, many scholars have studied the stage structure model of species (see [1–15] and references therein), and many interesting characteristic features of the stage structure model were obtained.
Recently, Lei [8] proposed a stage structure amensalism system with a cover for the first species:
where \(x_{1}(t)\) and \(x_{2}(t)\) represent the densities of the juvenile and adult populations of the first species at time t, respectively, \(y(t)\) represents the density of the second species at time t and \(k\in (0,1)\) represents the cover of the first species. Sufficient conditions are obtained ensuring the global attractivity of the positive equilibrium and the boundary equilibrium of the system. Their study shows that the first species may still be driven to extinction due to the influence of the second species.
In ecosystems, maturation, pregnancy, and hunting always occur. Therefore, considering the time delay due to pregnancy effect on the growth of the predator, Zhang and Zhang [6] studied the stage structure model with time delay and density-dependent juvenile birth rate, and they gave conditions for uniform persistence and extinction of the system in the following model:
where \(x_{1}(t)\) and \(x_{2}(t)\) represent the densities of the juvenile and adult prey species at time t, respectively, and \(y(t)\) represents the density of the predator species at time t, respectively. Then Yue [12] found that in the proof of their main result, Zhang and Zhang had made some mistake and their result is incorrect. By establishing some new lemmas and applying the differential inequality theory Yue finally obtained a set of sufficient conditions ensuring the permanence of the system.
On the other hand, human beings get what they need to live by exploiting natural resources, which may lead to the harvesting ecological modeling, and already many scholars [16–26] obtained interesting results in this direction. Xiao and Lei [16] investigated the following single-species stage structure model of nonselective harvesting:
where \(x_{1}\) and \(x_{2}\) indicate the densities of juvenile and adult species at time t, respectively. They showed that system (1.3) has two possible equilibria. The boundary equilibrium \(O(0,0)\) is globally asymptotically stable if \(\alpha <(\delta _{2}+q_{2}Em) (1+ \frac{\delta _{1}+q_{1}Em}{\beta } )\), that is, when the birth rate of the juvenile species is small enough, the species will be driven to extinction. The unique positive equilibrium \(A(x_{1}^{*},x_{2}^{*})\) is globally asymptotically stable if \(\alpha >(\delta _{2}+q_{2}Em) (1+ \frac{\delta _{1}+q_{1}Em}{\beta } )\), which means that when the birth rate of juvenile species is large enough, the system is persistent. Meanwhile, with the increase of harvesting, the extinction rate of species will accelerate, and the final density of species will decrease, which indicates that harvesting plays an important role on the persistent or extinction of the species.
With more works on the harvesting model published, some scholars began to focus their attention to the so called Michaelis–Menten-type harvesting [27–33]. The harvesting term takes the form of \(H=\frac{hEx}{mE+nx}\), which was first proposed by Clark [34]. Such a kind of harvesting is more realistic and practical than linear harvesting in ecosystem. Since the form of linear harvest is \(H=qEx\), we get that \(\lim_{E\rightarrow +\infty }H=\infty \) and \(\lim_{x\rightarrow +\infty }H=\infty \), so that if the fishing effort or the population is large, then the harvested species can be unlimited, obviously, which is against the facts. For the Michaelis–Menten- type harvesting, \(\lim_{E\rightarrow +\infty }H=\frac{hx}{m}\), which is equivalent to assuming that when the fishing effort is large, then the final harvest is determined by the population size. At the same time, \(\lim_{x\rightarrow +\infty }H=\frac{hE}{n}\), that is, although the population is very large with the limited fishing capacity, we can only harvest a limited number of organisms, which is more consistent with the actual situation. Chen [29] incorporated Michaelis–Menten-type harvesting to the first species of the Lotka–Volterra commensal symbiosis model, which leads to the following model:
The author analyzed and studied the local and global dynamic behavior of the system. Compared with the system without harvesting, his study indicates that despite the cooperation of the second species, the first species may still be driven to extinction due to the overharvesting.
In 2018, Liu, Zhao, Huang, and Deng [31] proposed a two-species amensalism model with Michaelis–Menten-type harvesting and a cover for the first species:
The authors discussed the existence and stability of all possible equilibria of the system and found an interesting phenomenon: Under certain conditions, the system can exhibits saddle-node bifurcation and transcritical bifurcation. However, for the system without harvesting, the dynamic behavior is very simple: two species may coexist, or the first one is driven to extinction while the second one is permanent. The study of Liu et al. [31] shows that Michaelis–Menten-type harvesting can make the dynamic behavior of the system more complex.
Up to now, to the best of our knowledge, still no scholars proposed and investigated the dynamic behavior of the single-species stage structure model with Michaelis–Menten-type harvesting. This motivated us to propose the following system:
where α, β, \(\delta _{1}\), \(\delta _{2}\), γ, h, E, m, and n are positive constants, where α represents the the birth rate of the immature species, β indicates the surviving rate of immaturity to reach maturity, \(\delta _{1}\) and \(\delta _{2}\) represent the death rates of immature and mature species, respectively, γ represents the intraspecific competition of mature species, h represents the harvesting coefficient of mature species, and E represents the combined harvesting effort of mature species.
We take the following transformations to simplify system (1.6):
for which we reserve t, x, y to express τ, x̄, ȳ, respectively. Then we obtain
where
and the initial conditions
From the ecological point of view, we only discuss the dynamic behavior of the system in the first quadrant.
The purpose of this paper is studying the stability of equilibria and the bifurcation phenomenon of system (1.7). The paper is arranged as follows: in the next section, we study the existence and local stability of the equilibria of system (1.7). In Sect. 3, we investigate saddle-node bifurcation and transcritical bifurcation of system (1.7). In Sect. 4, we discuss the global asymptotic stability of positive equilibrium of system (1.7). The numerical simulations in Sect. 5 show the feasibility of the main results. We end the paper with a brief discussion.
2 Equilibria and their stability
2.1 The existence of equilibria
The equilibria of the system are given by the system
Obviously, there always exists a boundary equilibrium \(E_{0}(0,0)\). To obtain the positive equilibria for the system, we consider the following equations:
Theorem 1
There exists a unique boundary equilibrium\(E_{0}(0,0)\). For the possible positive equilibria, we have:
-
(1)
When\(0< c< c^{**}\), the system has a unique positive equilibrium\(E_{1}^{*}(x_{1}^{*},y_{1}^{*})\).
-
(2)
When\(c=c^{**}\)and\(\frac{b}{a}-e-1>0\), the system has a unique positive equilibrium\(E_{1}^{*}(x_{1}^{*},y_{1}^{*})\).
-
(3)
When\(c^{**}< c< c^{*}\)and\(\frac{b}{a}-e-1>0\), the system has two positive equilibria\(E_{1}^{*}(x_{1}^{*},y_{1}^{*})\)and\(E_{2}^{*}(x_{2}^{*},y_{2}^{*})\).
-
(4)
When\(c=c^{*}\)and\(\frac{b}{a}-e-1>0\), the system has a unique positive equilibrium\(E_{3}^{*}(x_{3}^{*},y_{3}^{*})\).
-
(5)
When\(c>c^{*}\), the system has no positive equilibrium.
Here
Proof
For the second equation of (2.2), let Δ denote its discriminant and express Δ in terms of c:
If \(\Delta \geq 0\), then the equilibria exists, that is,
and then
When \(({\frac{b}{a}-e-1 )^{2}}=\Delta \), we can calculate that
Thus we can conclude that
-
(i)
if \(0< c< c^{**}\), rhen \(({\frac{b}{a}-e-1 )^{2}}<\Delta \);
-
(ii)
if \(c=c^{**}\) then \(({\frac{b}{a}-e-1 )^{2}}=\Delta \);
-
(iii)
if \(c>c^{**}\) then \(({\frac{b}{a}-e-1 )^{2}}>\Delta \).
In addition, we easily get that \(c^{**}\leq c^{*}\) and \(c^{**}=c^{*}\) if and only if \(\frac{b}{a}-e-1=0\). For the above conditions, we can conclude that:
-
(1)
when \(0< c< c^{**}\), \(y_{1}^{*}>0\), \(y_{2}^{*}<0\);
-
(2)
when \(c=c^{**}\), \(y_{1}^{*}>0\) and \(y_{2}^{*}=0\) if \(\frac{b}{a}-e-1>0\); \(y_{1}^{*}=0\) and \(y_{2}^{*}<0\) if \(\frac{b}{a}-e-1<0\); in addition, if \(\frac{b}{a}-e-1=0\), then \(c^{**}=c^{*}\), and \(y_{1}^{*}=y_{2}^{*}=0\).
-
(3)
when \(c^{**}< c< c^{*}\), \(y_{1}^{*}>0\) and \(y_{2}^{*}>0\) if \(\frac{b}{a}-e-1>0\); \(y_{1}^{*}<0\) and \(y_{2}^{*}<0\) if \(\frac{b}{a}-e-1<0\).
-
(4)
when \(c=c^{*}\), \(y_{3}^{*}>0\) if \(\frac{b}{a}-e-1>0\).
-
(5)
when \(c>c^{*}\), the system has no positive equilibria.
This completes the proof. □
2.2 Stability of the equilibria
To investigate the stability property of the equilibria of system (1.7), we calculate the Jacobian matrix of system (1.7):
So the trace and determinant of the Jacobian matrix (2.3) are given by
Obviously, \(\operatorname{tr} J<0\) for all \(y\geq 0\), so we just have to decide on the sign of the determinant.
2.2.1 Stability of the boundary equilibrium \(E_{0}(0,0)\)
Theorem 2
For all positive parameters, there is a boundary equilibrium\(E_{0}(0,0)\).
-
(1)
If\(c< e (\frac{b}{a}-1 )\), then\(E_{0}(0,0)\)is a saddle.
-
(2)
If\(c>e (\frac{b}{a}-1 )\), then\(E_{0}(0,0)\)is a stable node.
-
(3)
In the case\(c=e (\frac{b}{a}-1 )\), if\(\frac{a^{2}(b-a-ae)}{e(a^{2}+b)^{2}}\neq 0\),then\(E_{0}(0,0)\)is a saddle node, and if\(\frac{a^{2}(b-a-ae)}{e(a^{2}+b)^{2}}=0\), then\(E_{0}(0,0)\)is a stable node.
Proof
The Jacobian matrix of system (1.7) at \(E_{0}\) is
The determinant of the Jacobian matrix of system (1.7) at \(E_{0}\) is
Let \(\lambda _{1}\) and \(\lambda _{2}\) be the eigenvalues of \(\operatorname{Det}J(E_{0})\). When \(\operatorname{Det}J(E_{0})<0\), \(E_{0}\) is a saddle. When \(\operatorname{Det}J(E_{0})>0\), it is easy to figure out that \([\operatorname{tr} J(E_{0})]^{2}-4\operatorname{Det}J(E_{0})= [a-(1+\frac{c}{e}) ]^{2}+4b \geq 0\), so \(E_{0}\) is a stable node. When \(\operatorname{Det}J(E_{0})=0\), \(\lambda _{1}=0\) and \(\lambda _{2}<0\). To investigate the stability property of the equilibrium \(E_{0}\), we introduce the new time variable \(d\tau =\frac{dt}{e+y}\), and then we have
The linear part of system (2.5) is transformed into the normal form by the linear transformation
under which system (2.5) can be rewritten as
where
and \(P_{1}(u,v)\) and \(Q_{1}(u,v)\) are power series in \((u,v)\) with terms \(u^{i}v^{j}\) satisfying \(i+j\geq 4\).
Letting \(ds=b_{01}\, d\tau \), we have
where \(c_{0i}=\frac{a_{0i}}{b_{01}}\), \(d_{0i}=\frac{b_{0i+1}}{b_{01}}\), and \(P_{2}(u,v)\) and \(Q_{2}(u,v)\) are power series in \((u,v)\) with terms \(u^{i}v^{j}\) satisfying \(i+j\geq 4\).
By the implicit function theorem there exists a unique function \(v=\varphi (u)\) in the first quadrant such that \(\varphi (0)=0\) and \(P(u,\varphi (u))=0\). From the second equation of (2.8) we obtain
Then substituting (2.9) into the first equation of (2.8), we get that
By Theorem 7.1 in Chap. 2 in [34], if the coefficient of \(u^{2}\) is \(\frac{a^{3}(ae+a-b)}{a^{4}+2a^{2}b+b^{2}}\neq 0\), that is, \(m=2\), then \(E_{0}(0,0)\) is a saddle node. If \(\frac{a^{3}(ae+a-b)}{a^{4}+2a^{2}b+b^{2}}=0\), then we have \(m=3\) and \(a_{m}=\frac{a^{4}e}{a^{4}+2a^{2}b+b^{2}}>0\), so \(E_{0}(0,0)\) is an unstable node. Since we used the transformation \(ds=b_{01}d\tau \) and \(b_{01}<0\), the orbits with time go in the opposite direction, so \(E_{0}(0,0)\) is a stable node.
This completes the proof. □
2.2.2 Stability of the positive equilibria \(E_{i}^{*}(x_{i}^{*},y_{i}^{*})\) (\(i=1,2,3\))
To discuss the stability of \(E_{i}^{*}(x_{i}^{*},y_{i}^{*})\) (\(i=1,2,3\)), we simplify the determinant of \(E_{i}^{*}\):
Theorem 3
For system (1.7), when the equilibrium\(E_{1}^{*}(x_{1}^{*},y_{1}^{*})\)exists, it is a stable node.
Proof
The determinant of system (1.7) about the equilibrium \(E_{1}^{*}(x_{1}^{*},y_{1}^{*})\) is
Obviously,
and
so \(E_{1}^{*}(x_{1}^{*},y_{1}^{*})\) is a stable node. □
Theorem 4
For system (1.7), when the equilibrium\(E_{2}^{*}(x_{2}^{*},y_{2}^{*})\)exists, it is a saddle.
Proof
The determinant of system (1.7) about the equilibrium \(E_{2}^{*}(x_{2}^{*},y_{2}^{*})\) is
so \(E_{2}^{*}(x_{2}^{*},y_{2}^{*})\) is a saddle. □
Theorem 5
For system (1.7), when the equilibrium\(E_{3}^{*}(x_{3}^{*},y_{3}^{*})\)exists, it is a saddle node.
Proof
The determinant of system (1.7) about the equilibrium \(E_{3}^{*}(x_{3}^{*},y_{3}^{*})\) is
So the determinant of \(\operatorname{Det}J (E_{3}^{*}(x_{3}^{*},y_{3}^{*}) )\) has an eigenvalue 0. To analyze the stability of \(E_{3}^{*}(x_{3}^{*},y_{3}^{*})\), we move \(E_{3}^{*}(x_{3}^{*},y_{3}^{*})\) to the origin by the translation \((X,Y)=(x-x_{3}^{*},y-y_{3}^{*})\) and expand in power series around the origin. Then system (1.7) becomes
where
The linear part of system (2.10) is transformed into the normal form by the linear transformation
under which system (2.10) becomes
where
and \(P_{3}(U,V)\) and \(Q_{3}(U,V)\) are power series in \((U,V)\) with terms \(U^{i}V^{j}\) satisfying \(i+j\geq 4\).
Let \(d\tau =g_{01}dt \), where τ is a new time variable. Then we have
and \(P_{4}(U,V)\) and \(Q_{4}(U,V)\) are power series in \((U,V)\) with terms \(U^{i}V^{j}\) satisfying \(i+j\geq 4\).
According to the implicit function theorem, there is a unique function \(V=\varphi (U)\) in the first quadrant such that \(\varphi (0)=0\) and \(Q(U,\varphi (U))=0\). From the second equation of (2.13) we obtain
Then substituting (2.14) into the first equation of (2.13), we get that
From Theorem 7.1 in Chap. 2 iof [35] we obtain \(m=2\), \(a_{m}=\frac{f_{02}}{g_{01}}\neq 0\), so \(E_{3}^{*}(x_{3}^{*},y_{3}^{*})\) is a saddle node.
This completes the proof. □
For more detail about the nonnegative equilibria of system (1.7), one could refer to Table 1.
3 Bifurcation analysis
In this section, we will analyze the bifurcations of system (1.7) and derive conditions for saddle-node bifurcation and transcritical bifurcation.
3.1 Saddle-node bifurcation
In Sect. 2.1, we have given conditions for the existence of interior equilibria. We find that system (1.7) has two different equilibria (\(E_{1}^{*}\) and \(E_{2}^{*}\)) if \(c^{**}< c< c^{*}\) and \(\frac{b}{a}-e-1>0\); \(E_{1}^{*}\) and \(E_{2}^{*}\) coincide with \(E_{3}^{*}\) if \(c=c^{*}\) and \(\frac{b}{a}-e-1>0\), and there is only one unique positive equilibrium \(E_{3}^{*}\); \(E_{1}^{*}\) and \(E_{2}^{*}\) disappear if \(c>c^{*}\), and the system has no positive equilibrium point. This phenomenon is due to saddle-node bifurcation at \(E_{3}^{*}\), which exists when \(c=c_{SN}=\frac{1}{4}(\frac{b}{a}+e-1)^{2}\) and \(\frac{b}{a}-e-1>0 \).
Theorem 6
System (1.7) undergoes a saddle-node bifurcation around\(E_{3}^{*}(x_{3}^{*},y_{3}^{*})\)with respect to bifurcation parametercif\(c=c_{SN}\)and\(\frac{b}{a}-e-1>0\).
Proof
Now we use Sotomayor’s theorem to prove the transversality condition of saddle-node bifurcation at \(c=c_{SN}\). From Theorem 4 we can easily obtain that \(\operatorname{Det}J(E_{3}^{*})=0\), \(\operatorname{tr} J(E_{3}^{*})<0\), so \(J(E_{3}^{*})\) has a zero eigenvalue and a negative eigenvalue. Let the eigenvectors corresponding to the zero eigenvalues of matrices \(J(E_{3}^{*},c_{SN})\) and \(J(E_{3}^{*},c_{SN})^{T}\) be V and W. Then we have
Moreover,
We can easily see that V and W satisfy
Therefore we can conclude that with the change of parameter \(c=c_{SN}\), the number of interior equilibria of system (1.7) changes from zero to two.
The proof of Theorem 6 is finished. □
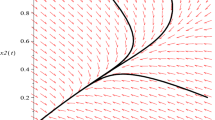
For \(a=1\), \(e=0.5\) and \(b=2\), we get \(c_{SN}=0.5625\), \(c^{**}=0.5\) and \(\frac{b}{a}-e-1=0.5>0\). For \(c=0.52\), \(c^{**}< c< c_{SN}\), system (1.7) has two different boundary equilibria \(E_{1}^{*}\) and \(E_{2}^{*}\) (Fig. 1(d)), which coincide with each other when \(c=c_{SN}=0.5625\) (Fig. 1(e)). There is no positive equilibrium when \(0.6=c>c_{SN}\) (Fig. 1(f)).
Dynamics behaviors of the system (5.1)
3.2 Transcritical bifurcation
Through the discussion of the existence of the internal equilibria in the second section, we find an interesting phenomenon: when \(c=c^{**}=\frac{be}{a}-e\), \(E_{2}^{*}\) coincides with \(E_{0}\) if \(\frac{b}{a}-e-1>0\); and \(E_{1}^{*}\) coincides with \(E_{0}\) if \(\frac{b}{a}-e-1<0\). This phenomenon is due to the occurrence of transcritical bifurcation at \(E_{0}\).
Theorem 7
System (1.7) undergoes a transcritical bifurcation when the parameters satisfy\(c=c_{TC}=c^{**}\), wherecis taken as the bifurcation parameter.
Proof
Now we use Sotomayor’s theorem to prove the transversality condition of transcritical bifurcation at \(c=c_{TC}\). From Theorem 2 we get \(\operatorname{Det}J(E_{0})=0\) and \(\operatorname{tr} J(E_{0})<0\), so \(J(E_{0})\) has a zero eigenvalue. Let the eigenvectors corresponding to the zero eigenvalues of matrices \(J({E_{0}},c_{TC})\) and \(J({E_{0}},c_{TC})^{T}\) be V and W. Then we have
Moreover,
Thus we have
The proof of Theorem 7 is finished. □
For \(a=1\) and \(e=0.5\), we get \(c=c_{TC}=0.4\), \(\frac{b}{a}-e-1=0.3>0\) if \(b=1.8\), and then \(E_{2}^{*}\) coincides with \(E_{0}\) (Fig. 2(a)); we get \(c=c_{TC}=0.25\), \(\frac{b}{a}-e-1=0\) if \(b=1.5\), and then there is only the boundary equilibrium \(E_{0}\) (Fig. 2(b)); we get \(c=c_{TC}=0.1\), \(\frac{b}{a}-e-1=-0.3<0\) if \(b=1.2\), and then \(E_{1}^{*}\) coincides with \(E_{0}\) (Fig. 2(c)).
The phase portraits of transcritical bifurcation of system (1.7) when \(c=c_{TC}\)
4 Global stability of equilibria
In this section, we consider the global stability of equilibria of system (1.7).
Theorem 8
If\(b< a\), then\(E_{0}(0,0)\)is globally asymptotically stable.
Proof
Consider a Lyapunov function of the form
Obviously, the function \(V(x,y)\) is zero at the equilibrium \(E_{0}(0,0)\) and is positive in the first quadrant. Calculating the derivative of \(V(x,y)\) along the solution of system (1.7), we have
Since \(b< a\), \(D^{+}V(t)<0\) for all \(x,y>0\) except the boundary equilibrium \(E_{0}(0,0)\), where \(D^{+}V(t)=0\). Therefore \(V(x,y)\) satisfies Lyapunov’s asymptotic stability theorem, so the boundary equilibrium \(E_{0}(0,0)\) of system (1.7) is globally asymptotically stable.
The proof of Theorem 8 is finished. □
For \(a=1\), \(b=0.8\), \(c=0.4\) and \(e=0.5\), we get \(c>e(\frac{b}{a}-1)=-0.2\) and \(b< a\). By Theorems 2 and 8 the boundary equilibrium \(E_{0}(0,0)\) is a stable node and globally asymptotically stable (Fig. 3).
Theorem 9
If\(0< c< c^{**}\), then system (1.7) has a unique positive equilibrium\(E_{1}^{*}\), which is globally asymptotically stable.
Proof
Too prove that \(E_{1}^{*}\) is globally asymptotically stable in the first quadrant, we consider the Dulac function \(u(x,y)=1\). Then
where
According to the Bendixson–Dulac discriminant, the system has no limit cycle in the first quadrant, so \(E_{1}^{*}\) is globally asymptotically stable.
The proof of Theorem 9 is finished. □
For \(a=1\), \(b=2\), \(c=0.4\), and \(e=0.5\), we get \(0< c< c^{**}=0.5\). By Theorems 3 and 8 the only positive equilibrium \(E_{1}^{*}(0.5,0.5)\) is a stable node and globally asymptotically stable (Fig. 1(a)).
5 Numeric simulations
Example 5.1
Consider the following system:
In this system, corresponding to system (1.7), we choose \(a=1\) and \(e=0.5\), so \(c^{*}=\frac{1}{4}(b-0.5)^{2}\), \(c^{**}=0.5(b-1)\). By Theorem 1 system (1.7) has a unique boundary equilibrium \(E_{0}(0,0)\) for all positive parameters.
-
(1)
Take \(b=2\), \(c=0.4\). Then \(0< c< c^{**}=0.5\). By Theorems 2, 3, and 9, the boundary equilibrium \(E_{0}(0,0)\) of the system is a saddle. The only positive equilibrium \(E_{1}^{*}(0.5,0.5)\) is a stable node and globally asymptotically stable (Fig. 1(a)).
-
(2)
Take \(b=2\), \(c=0.5\). Then \(c=c^{**}\), \(a_{m}=-\frac{1}{18}\neq 0\), \(\frac{b}{a}-e-1=0.5>0\). By Theorems 2 and 3 the boundary equilibrium \(E_{0}(0,0)\) of the system is a saddle node. The only positive equilibrium \(E_{1}^{*}(0.5,0.5)\) is a stable node (Fig. 1(b)).
-
(3)
Take \(b=1.5\), \(c=0.25\). Then \(c=c^{**}\), \(a_{m}=-\frac{1}{18}=0\), \(\frac{b}{a}-e-1=0\). By Theorem 2 the boundary equilibrium \(E_{0}(0,0)\) of the system is a stable node (Fig. 1(c)).
-
(4)
Take \(b=2\), \(c=0.52\). Then \(0.5=c^{**}< c< c^{*}=0.5625\), \(\frac{b}{a}-e-1=0.5>0\). By Theorems 2, 3, and 4 the boundary equilibrium \(E_{0}(0,0)\) of the system is a stable node. The positive equilibrium \(E_{1}^{*}(0.456,0.456)\) is a stable node, and \(E_{2}^{*}(0.0438,0.0438)\) is a saddle (Fig. 1(d)).
-
(5)
Take \(b=2\), \(c=0.5625\). Then \(c=c^{*}\), \(\frac{b}{a}-e-1=0.5>0\). By Theorems 2 and 5 the boundary equilibrium \(E_{0}(0,0)\) of the system is a stable node. The only positive equilibrium \(E_{3}^{*}(0.25,0.25)\) is a saddle node (Fig. 1(e)).
-
(6)
Take \(b = 2\), \(c = 0.6\). Then \(c>c^{*}=0.5625\). By Theorems 1 and 2 the boundary equilibrium \(E_{0}(0, 0)\) of the system is a stable node, and there is no positive equilibrium (Fig. 1(f)).
6 Conclusion
In this paper, we investigate a single-species system with stage structure and harvesting for the mature population. We discuss the local and global stability of the possible equilibria of the system. Furthermore, we find some interesting dynamical phenomenon of the model. When \(b< a\), that is, \(\alpha <\delta _{2} (1+\frac{\delta _{1}}{\beta } )\), the boundary equilibrium of the system is globally asymptotically stable. This means that when the birth rate of the immature population is too low, the species drives to extinction. When \(c< c^{*}\), that is, \(\alpha > (\delta _{2}+\frac{hr}{m^{2}\delta _{2}} ) (1+ \frac{\delta _{1}}{\beta } )\), the system has a unique positive equilibrium \(E_{1}^{*}\) and is globally asymptotically stable. This shows that when the birth rate of the immature population is large enough, harvesting has no effect on the persistence of the system.
Qualitative analysis shows that Michaelis–Menten-type harvesting term plays a crucial role in studying the dynamics and bifurcations of the system. The saddle-node bifurcation can make the dynamics of the system change significantly. When the bifurcation parameters pass the threshold, the number of internal equilibria will change by 0, 1, 2. If \(c>c^{*}\) and \(c=\frac{hE\alpha }{\delta _{2}^{2}}\), then c is proportional to E, that is, overfishing can lead to species extinction. Ecologically, the saddle-node bifurcation and the transcritical bifurcation give the maximum threshold for continuous harvesting, and there is no risk of extinction of mature species. In practice, this allows decision makers to make the best harvesting strategy to ensure the sustainable development of ecosystem.
References
Lei, C.: Dynamic behaviors of a stage structured commensalism system. Adv. Differ. Equ. 2018(1), Article ID 301 (2018)
Chen, F., Xie, X., Li, Z.: Partial survival and extinction of a delayed predator–prey model with stage structure. Appl. Math. Comput. 219(8), 4157–4162 (2012)
Li, T., Chen, F., et al.: Stability of a mutualism model in plant-pollinator system with stage-structure and the Beddington–DeAngelis functional response. J. Nonlinear Funct. Anal. 2017, Article ID 50 (2017)
Chen, F., Xie, X., Chen, X.: Dynamic behaviors of a stage-structured cooperation model. Commun. Math. Biol. Neurosci. 2015, Article ID 4 (2015)
Lin, X., Xie, X., et al.: Convergences of a stage-structured predator–prey model with modified Leslie–Gower and Holling-type II schemes. Adv. Differ. Equ. 2016(1), Article ID 181 (2016)
Zhang, L., Zhang, C.: Uniform persistence, periodicity and extinction in a delayed biological system with stage structure and density-dependent juvenile birth rate. Am. J. Comput. Math. 6(2), 130–140 (2016)
Xiao, Z., Li, Z., Zhu, Z., et al.: Hopf bifurcation and stability in a Beddington–DeAngelis predator–prey model with stage structure for predator and time delay incorporating prey refuge. Open Math. 17(1), 141–159 (2019)
Lei, C.: Dynamic behaviors of a stage structure amensalism system with a cover for the first species. Adv. Differ. Equ. 2018(1), Article ID 272 (2018)
Xue, Y., Pu, L., Yang, L.: Global stability of a predator–prey system with stage structure of distributed-delay type. Commun. Math. Biol. Neurosci. 2015, Article ID 12 (2015)
Zhang, F., Chen, Y., Li, J.: Dynamical analysis of a stage-structured predator–prey model with cannibalism. Math. Biosci. 307, 33–41 (2019)
Li, Z., Han, M., Chen, F.: Global stability of a stage-structured predator–prey model with modified Leslie–Gower and Holling-type II schemes. Int. J. Biomath. 5(6), 1250057 (2012)
Yue, Q.: Permanence of a delayed biological system with stage structure and density-dependent juvenile birth rate. Eng. Lett. 27(2), 263–268 (2019)
Pu, L., Miao, Z., et al.: Global stability of a stage-structured predator–prey model. Commun. Math. Biol. Neurosci. 2015, Article ID 5 (2015)
Li, Z., Han, M., Chen, F.: Global stability of a predator–prey system with stage structure and mutual interference. Discrete Contin. Dyn. Syst., Ser. B 19(1), 173–187 (2014)
Chen, F., Chen, W., et al.: Permanence of a stage-structured predator–prey system. Appl. Math. Comput. 219(17), 8856–8862 (2013)
Xiao, A., Lei, C.: Dynamic behaviors of a non-selective harvesting single species stage structure system incorporating partial closure for the populations. Adv. Differ. Equ. 2018(1), Article ID 245 (2018)
Huang, X., Chen, F., Xie, X., et al.: Extinction of a two species competitive stage-structured system with the effect of toxic substance and harvesting. Open Math. 17(1), 856–873 (2019)
Li, T., Huang, X., Xie, X.: Stability of a stage-structured predator–prey model with Allee effect and harvesting. Commun. Math. Biol. Neurosci. 2019, Article ID 13 (2019)
Chen, F., Wu, H., Xie, X.: Global attractivity of a discrete cooperative system incorporating harvesting. Adv. Differ. Equ. 2016(1), Article ID 268 (2016)
Lin, Q.: Dynamic behaviors of a commensal symbiosis model with non-monotonic functional response and non-selective harvesting in a partial closure. Commun. Math. Biol. Neurosci. 2018, Article ID 4 (2018)
Lei, C.: Dynamic behaviors of a non-selective harvesting May cooperative system incorporating partial closure for the populations. Commun. Math. Biol. Neurosci. 2018, Article ID 12 (2018)
Lin, Q., Xie, X., Chen, F., et al.: Dynamical analysis of a logistic model with impulsive Holling type-II harvesting. Adv. Differ. Equ. 2018(1), Article ID 192 (2018)
Liu, Y., Xie, X., et al.: Permanence, partial survival, extinction and global attractivity of a non-autonomous harvesting Lotka–Volterra commensalism model incorporating partial closure for the populations. Adv. Differ. Equ. 2018(1), Article ID 211 (2018)
Xie, X., Chen, F., Xue, Y.: Note on the stability property of a cooperative system incorporating harvesting. Discrete Dyn. Nat. Soc. 2014, Article ID 327823 (2014)
Chen, B.: Dynamic behaviors of a non-selective harvesting Lotka–Volterra amensalism model incorporating partial closure for the populations. Adv. Differ. Equ. 2008(1), Article ID 111 (2008)
Su, Q., Chen, F.: The influence of partial closure for the populations to a non-selective harvesting Lotka–Volterra discrete amensalism model. Adv. Differ. Equ. 2019(1), Article ID 281 (2019)
Yuan, R., Wang, Z., Jiang, W.: Global Hopf bifurcation of a delayed diffusive predator–prey model with Michaelis–Menten type prey harvesting. Appl. Anal. 95(2), 444–466 (2016)
Liu, Y., Guan, X., et al.: On the existence and stability of positive periodic solution of a nonautonomous commensal symbiosis model with Michaelis–Menten type harvesting. Commun. Math. Biol. Neurosci. 2019, Article ID 2 (2019)
Chen, B.: The influence of commensalism on a Lotka–Volterra commensal symbiosis model with Michaelis–Menten type harvesting. Adv. Differ. Equ. 2019(1), Article ID 43 (2019)
Hu, D., Cao, H.: Stability and bifurcation analysis in a predator–prey system with Michaelis–Menten type predator harvesting. Nonlinear Anal., Real World Appl. 33(1), 58–82 (2017)
Liu, Y., Zhao, L., Huang, X., Deng, H.: Stability and bifurcation analysis of two species amensalism model with Michaelis–Menten type harvesting and a cover for the first species. Adv. Differ. Equ. 2018(1), Article ID 295 (2018)
Song, Q., Yang, R., Zhang, C., et al.: Bifurcation analysis in a diffusive predator–prey system with Michaelis–Menten type predator harvesting. Adv. Differ. Equ. 2018(1), Article ID 329 (2018)
Kong, L., Zhu, C.: Bogdanov–Takens bifurcations of codimensions 2 and 3 in a Leslie–Gower predator–prey model with Michaelis-Menten type prey harvesting. Math. Methods Appl. Sci. 40(18), 6715–6731 (2017)
Clark, C.W., Mangel, M.: Aggregation and fishery dynamics: a theoretic study of schooling and the purse seine tuna fisheries. Fish. Bull. 77(2), 317–337 (1979)
Zhang, Z., Ding, T., Huang, W., Dong, Z.: Qualitative Theory of Differential Equation. Science Press, Beijing (1992)
Acknowledgements
The authors would like to thank Dr. Xiaofeng Chen for useful discussion on mathematical modeling.
Availability of data and materials
Not applicable.
Funding
The research was supported by the Natural Science Foundation of Fujian Province (2019J01783).
Author information
Authors and Affiliations
Contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Competing interests
The authors declare that there is no conflict of interests.
Consent for publication
Not applicable.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yu, X., Zhu, Z., Lai, L. et al. Stability and bifurcation analysis in a single-species stage structure system with Michaelis–Menten-type harvesting. Adv Differ Equ 2020, 238 (2020). https://doi.org/10.1186/s13662-020-02652-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-020-02652-7