1 Introduction

During the past few decades, several physical models have been developed in the form of fractional differential equations. They can be used to modeling certain phenomena in fractal networks, signal processing, turbulent flows, wave propagation, etc. Compared with a classical integral-order equation, the main advantage of the fractional order equation is that it provides an excellent instrument for the description of memory and hereditary properties of various physical models.

In this paper, we consider the following time-fractional initial-boundary value problems (IBVPs):

$$\begin{aligned} &D_{t}^{\alpha } u-\nabla \cdot \bigl(a(x,t)\nabla u\bigr) =f(x,t)\quad \text{on } Q:= \Omega \times (0,T], \end{aligned}$$
(1a)
$$\begin{aligned} &u(x,0)=u_{0}(x) \quad\text{for } x\in {\bar{\Omega }} \end{aligned}$$
(1b)

with \(u|_{\partial \Omega } =0 \text{ for } {t\in [0,T]}\). Here we assume that the spatial domain \(\Omega \subset \mathbb{R}^{2}\) is a convex polyhedral domain. We assume that \(u_{0}\in C(\bar{\Omega })\), \(f\in C(\bar{Q})\), and the diffusivity coefficient \(a(x,t)\) satisfies

$$ \lambda ^{-1}\leq a(x,t)\leq \lambda\quad \text{for a fixed constant } \lambda \geq 1. $$
(2)

In (1a), \(D_{t}^{\alpha }\) is the Caputo fractional derivative operator defined by

$$ D_{t}^{\alpha }v(x,t) =\frac{1}{\Gamma (1-\alpha )} \int _{0}^{t}(t-s)^{- \alpha }\frac{\partial v(x,s)}{\partial s} \,ds. $$
(3)

The time-fractional diffusion equation (1a)–(1b) has been proved to be a very valuable tool in modeling complex systems, for example, charge carrier transport in amorphous semiconductors [8], nuclear magnetic resonance (NMR) diffusometry in percolative structures [18], rouse or reptation dynamics in polymeric systems [40], transport on fractal geometries [33], etc. The analytical solution of some fractional partial differential equations can be obtained by Laplace transform, differential transform method, and fractional complex transform, etc. [1, 25, 28–30]. But most of the equations have no analytical solution, so it is very important to solve them numerically.

Numerical methods for time-fractional IBVPs with constant or time-independent diffusion parameter have received a huge amount of attention over the last decade. For such problems, several numerical methods have been proposed and analyzed, such as finite difference method [7, 19–21, 27, 36, 38], finite element method [6, 32, 39, 41, 43, 44, 48], discontinuous Galerkin (DG) methods [3, 4, 9–11, 31, 34], spectral method [23], and finite volume method [15, 46], etc. The time-fractional IBVPs (1a)–(1b) with time-space dependent diffusivity is indeed very interesting and also practically important, and the numerical solutions of this problems were considered by a few authors only. Alikhanov [2] constructed an L2-\(1_{\sigma }\) scheme for problem (1a)–(1b), and the error analysis of this scheme was based on the sufficient smoothness assumption of the solution. Mustapha [17] studied a semidiscrete Galerkin finite element method for time-fractional diffusion equations with time-space dependent diffusivity, and the optimal error bounds in spatial \(L^{2}\)- and \(H^{1}\)-norms were derived for smooth and nonsmooth initial data by using novel energy arguments. The regularity result about the solutions of the subdiffusion model was proved for both nonsmooth initial data and incompatible source term by Jin [16], and a complete error analysis was presented for a fully discrete conforming FEM. Zhang and Shi [45] proposed a fully discrete L1 mixed finite element method for time fractional diffusion equation with a smooth solution, and a novel result of the consistency error estimate with order \(O(h^{2})\) of the bilinear element was obtained. Zhao et al. [47] presented a fully discrete L1 finite element method for multiterm time fractional diffusion equation with constant diffusivity, and a superconvergence result for \(H^{1}\)-norm estimate was obtained. Yin et al. [42] presented two families of novel fractional θ-methods to solve the fractional cable model, and an optimal convergence result with O\((\tau ^{2}+h^{k+1})\) for smooth solutions was obtained. Syed et al. [26] proposed a homotopy analysis method for the space-time fractional Korteweg–de Vries (KdV) equation. Huang and Stynes [13] proposed a fully discrete finite element method for the multiterm time fractional diffusion equation with a weak singularity solution, and a simple postprocessing of the computed solution yielded a higher order of convergence in the spatial direction.

Imitating [16, Sect. 2], we derive that the solution of (1a)–(1b) satisfies

$$ \bigl\Vert u(\cdot, t) \bigr\Vert _{2} \leq C, \qquad\bigl\Vert \partial _{t}^{l} u( \cdot, t) \bigr\Vert _{2} \leq C\bigl(1+t^{\alpha -l}\bigr),\qquad \bigl\Vert D_{t}^{\alpha }u( \cdot, t) \bigr\Vert _{2} \leq C $$
(4)

for \(l=0,1,2\) and \(0< t\leq T\). The aim of this paper is constructing a fully discrete conforming finite element method for time-fractional IBVPs (1a)–(1b) with a weak singularity solution (4), and then the superconvergence result in \(H^{1}\)-norm of this method will be analyzed.

The paper is structured as follows. In Sect. 2, several operators are introduced. In Sect. 3 the L1 discretization on a graded temporal mesh of the Caputo temporal derivative is presented, and then the finite element discretization of the spatial component of the differential operator is described. In Sect. 4 an optimal \(H^{1}(\Omega )\) convergence bound for the computed solution is derived, and a simple postprocessing of the computed solution will yield a higher order of convergence in the spatial direction. Finally, numerical results in Sect. 5 show that our theoretical results are optimal.

Notation. C and K are generic constants that are independent of the mesh parameters N and h. We write \(\|\cdot \|\) for the norm in \(L^{2}(\Omega )\). For each \(q\in \mathbb{N}\), the notation \(H^{q}(\Omega )\) is used for the standard Sobolev space with its associated norm \(\|\cdot \|_{q}\) and seminorm \(|\cdot |_{q}\).

2 Preliminaries

Let \(\mathcal{T}_{h}\) be a quasiuniform partition of Ω into element \(K_{m}\) for \(m=1,\ldots, M\), and \(h=\max_{1\le m\le M} \{\operatorname{diam}(K_{m})\}\) be the mesh size. Then we define the following bilinear finite element spaces:

$$ V_{h}:= \bigl\{ v_{h}\in H_{0}^{1}( \Omega ): v_{h}| _{K_{m}} \in \operatorname{span}\{1,x,y,xy\} \text{ for } m=1,2,\ldots, M \bigr\} $$

and

$$ V_{0h}:= \{ v_{h}\in V_{h}: v_{h}| _{\partial \Omega }=0 \}. $$

Next, we will introduce three operators, which are used in finite element analyses of time-dependent problems [37]. First, we define the \(L^{2}\)projector \(P_{h}: L^{2}(\Omega ) \to V_{0h}\) by \((P_{h}w, v_{h}) = (w,v_{h}) \ \forall v_{h}\in V_{0h}\). By [5, (1.2)], one has

$$ \Vert \nabla P_{h} v \Vert \leq K \Vert \nabla v \Vert \quad\text{for all } v\in H_{0}^{1}( \Omega ). $$
(5)

Next we need a time-dependent Ritz projector \(R_{h}(t): H_{0}^{1}(\Omega )\rightarrow V_{0h}\) defined by \((a(\cdot,t)\times \nabla R_{h}(t)w,\nabla v_{h} )= (a( \cdot,t)\nabla w,\nabla v_{h} ) \ \forall v_{h}\in V_{0h}\). For a fixed \(k\geq 0\), since \(V_{0h} \subset H_{0}^{1}(\Omega )\) is the space of piecewise polynomials of degree at most k, it is well known [24, (3.2)] that

$$ \bigl\Vert w-R_{h}(t)w \bigr\Vert +h \bigl\Vert w-R_{h}(t)w \bigr\Vert _{1}\leq Ch^{k+1} \vert w \vert _{k+1} \quad\forall w \in H^{k+1}(\Omega ) \cap H_{0}^{1}(\Omega ). $$
(6)

In order to obtain our optimal \(H^{1}\)-norm convergence and superconvergence results given in Sect. 4, we introduce a time-dependent discrete Laplacian \(\Delta _{h}(t): V_{0h}\rightarrow V_{0h}\) defined by

$$ \bigl(\Delta _{h}(t) v, w \bigr)=- \bigl(a(\cdot,t) \nabla v, \nabla w \bigr) \quad\forall v,w \in V_{0h}, $$
(7)

which will be used to convert the integral form L1 FEM (16) to the differential form scheme (17). According to [16, p. 12], we have that \(\Delta _{h}(t): V_{0h}\rightarrow V_{0h}\) is bounded and invertible on \(V_{0h}\) under condition (2). Imitating [37, p. 11], one has

$$\begin{aligned} \bigl(\Delta _{h}(t) R_{h}(t) v,\chi \bigr)&=- \bigl(a( \cdot,t)\nabla R_{h}(t)v, \nabla \chi \bigr)=- \bigl(a(\cdot,t)\nabla v,\nabla \chi \bigr) \\ &= \bigl(\nabla \cdot \bigl(a(\cdot,t)\nabla v \bigr), \chi \bigr) \\ &= \bigl( P_{h}\nabla \cdot \bigl(a(\cdot,t)\nabla v \bigr){ ,} \chi \bigr), \quad\forall \chi \in V_{0h}. \end{aligned}$$

Thus these three operators are related by

$$ \Delta _{h}(t) R_{h}(t) v = P_{h}\nabla \cdot \bigl(a(\cdot,t)\nabla v \bigr),\quad \forall v\in H^{2}(\Omega ). $$
(8)

3 Temporal graded meshes; the L1 FEM

In this section, the well-known L1 scheme on graded meshes will be introduced, and then we present a fully discrete conforming finite element method.

Let N be a positive integer. Set \(t_{n}=T(n/N)^{r}\) for \(n=0,1,\dots,N\), where the mesh grading constant \(r\geq 1\) is chosen by the user. Set \(\tau _{n}=t_{n}-t_{n-1}\) for \(n=0,1,\dots,N\).

For \(n\ge 1\), the Caputo fractional derivative \(D_{t}^{\alpha }u(x,t_{n})\) of (3) can be approximated by the well-known L1 formula:

$$ D_{t}^{\alpha }u(x,t_{n}) \approx D_{N}^{\alpha }u^{n}:= \frac{d_{n,1}}{\Gamma (2-\alpha )}u^{n}- \frac{d_{n,n}}{\Gamma (2-\alpha )}u^{0}+\frac{1}{\Gamma (2-\alpha )} \sum _{i=1}^{n-1}u^{n-i}(d_{n,i+1}-d_{n,i}), $$
(9)

where \(d_{n,i}:= [(t_{n}-t_{n-i})^{1-\alpha }-(t_{n}-t_{n-i+1})^{1- \alpha } ]/\tau _{n-i+1}\) for \(i=1,\dots,n\). Note that \(d_{n,1}=\tau _{n}^{-\alpha }\). It is easily to see that

$$ d_{n,i+1} < d_{n,i}\quad\text{for } 0\le i \le n-1 \le N-1. $$
(10)

Imitating [36, Lemma 5.2], we derive the following truncation error of the L1 scheme (9).

Lemma 3.1

Assume the solution of (1a)–(1b) satisfies (4). For all \((x, t_{n})\in Q\), one has

$$ \bigl\Vert D_{t}^{\alpha }u(x,t_{n})-D_{N}^{\alpha }u(x,t_{n}) \bigr\Vert _{1}\leq Cn^{- \min \{2-\alpha, r\alpha \}}. $$

As in [36, (4.6)], define the positive real numbers \(\theta _{n,j}\), for \(n=1,2,\dots, N\) and \(j=1,2,\dots, n-1\), by

$$ \theta _{n,n}=1,\qquad \theta _{n,j}=\sum _{k=1}^{n-j}\tau _{n-k}^{\alpha }(d_{n,k}-d_{n,k+1}) \theta _{n-k,j}. $$
(11)

Observe that (10) implies \(\theta _{n,j}>0\) for all \(n,j\). Furthermore, as in [36, Lemma 4.3], for \(n=1,2,\dots, N\), one has

$$ \tau ^{\alpha }_{n} \sum _{j=1}^{n}j^{-\beta }\theta _{n,j}\leq \frac{T^{\alpha } N^{-\beta }}{1-\alpha }, \quad\text{provided that } \beta \le r\alpha. $$
(12)

Next, we will state a nonstandard Gronwall inequality, which is given in [12, Lemma 4.4].

Lemma 3.2

Assume that sequences \(\{\xi ^{n}\}_{n=1}^{\infty }, \{\eta ^{n}\}_{n=1}^{\infty }\)are nonnegative and the grid function \(\{ v^{n}: n=0,1,\dots, N\}\)satisfies \(v^{0} \geq 0\)and

$$ \bigl(D_{N}^{\alpha } v^{n}\bigr) v^{n} \leq \xi ^{n} v^{n}+\bigl(\eta ^{n}\bigr)^{2}\quad \textit{for } n=1,2,\dots,N. $$
(13)

Then

$$ v^{n}\leq v^{0}+\tau _{n}^{\alpha } \Gamma (2-\alpha )\sum_{j=1}^{n} \theta _{n,j}\xi ^{j}+\sqrt{T^{\alpha }\Gamma (1-\alpha )}\max _{1 \leq j\leq n}\eta ^{j} \quad\textit{for } n=1,2,\dots,N, $$
(14)

where \(\theta _{n,j}\)is defined by (11).

Imitating the proof of [14, Lemma 4.2], we derive the following property of the L1 scheme, which will be used in our later analysis.

Lemma 3.3

Let the functions \(v^{j} = v(\cdot, t^{j})\)be in \(L^{2}(\Omega )\)for \(j=0,1,\dots, N\). Then the discrete L1 scheme satisfies

$$ \bigl( a(\cdot, t_{n})D_{N}^{\alpha } v^{n},v^{n} \bigr)\geq \bigl( D_{N}^{ \alpha } \bigl\Vert \sqrt{a(\cdot, t_{n})}v^{n} \bigr\Vert \bigr) \bigl\Vert \sqrt{a(\cdot, t_{n})}v^{n} \bigr\Vert \quad \textit{for }n=1,2,\ldots,N. $$

Proof

Let \(n\in \{1,2,\ldots,N\}\). Applying \(a(x,t)> 0\) and Cauchy–Schwarz inequality, one has

$$\begin{aligned} \bigl(a(\cdot, t_{n})D_{N}^{\alpha }v^{n},v^{n} \bigr)={}& \frac{d_{n,1}}{\Gamma (2-\alpha )} \bigl(a(\cdot, t_{n})v^{n}, v^{n} \bigr) -\frac{d_{n,n}}{\Gamma (2-\alpha )} \bigl(a(\cdot, t_{n})v^{0}, v^{n} \bigr) \\ &{} -\frac{1}{\Gamma (2-\alpha )}\sum_{i=1}^{n-1} (d_{n,i}-d_{n,i+1}) \bigl(a(\cdot, t_{n})v^{n-i}, v^{n} \bigr) \\ \ge{}& \frac{d_{n,1}}{\Gamma (2-\alpha )} \bigl\Vert \sqrt{a(\cdot, t_{n})}v^{n} \bigr\Vert ^{2} -\frac{d_{n,n}}{\Gamma (2-\alpha )} \bigl\Vert \sqrt{a(\cdot, t_{n})}v^{0} \bigr\Vert \bigl\Vert \sqrt{a(\cdot, t_{n})}v^{n} \bigr\Vert \\ &{} -\frac{1}{\Gamma (2-\alpha )}\sum_{i=1}^{n-1} (d_{n,i}-d_{n,i+1}) \bigl\Vert \sqrt{a(\cdot, t_{n})}v^{n-i} \bigr\Vert \bigl\Vert \sqrt{a(\cdot, t_{n})}v^{n} \bigr\Vert \\ ={}& \bigl(D_{N}^{\alpha } \bigl\Vert \sqrt{a(\cdot, t_{n})}v^{n} \bigr\Vert \bigr) \bigl\Vert \sqrt{a( \cdot, t_{n})}v^{n} \bigr\Vert , \end{aligned}$$

where we used \(d_{n,i} >d_{n,i+1} >0\). □

3.1 The L1 FEM

To begin, our problem (1a)–(1b) will be discretized only in space applying a conforming finite element method. Then the semidiscrete FEM reads: seek \(u_{h}(\cdot, t) \in V_{0h}\) for each \(t\in (0,T]\) such that

$$ \bigl(D_{t}^{\alpha } u_{h}, v_{h} \bigr)+ \bigl(a(x,t)\nabla u_{h}, \nabla v_{h} \bigr)=(f,v_{h}) \quad\text{with } u_{h}^{0}=R_{h}(t_{0})u_{0} \text{ and all } v_{h}\in V_{0h}.$$
(15)

Applying the L1 scheme (9) to discretize (15) in the temporal domain, the fully discrete L1 FEM is: seek \(u_{h}^{n} \in V_{0h}\) such that

$$ \bigl(D_{N}^{\alpha } u_{h}^{n}, v_{h}\bigr)+ \bigl(a(x,t_{n})\nabla u_{h}^{n}, \nabla v_{h} \bigr)=\bigl(f^{n},v_{h}\bigr) \quad\text{for }n=1,\dots, N \text{ and all } v_{h}\in V_{0h}. $$
(16)

Invoking (7), the L1 FEM (16) takes the form: find \(u_{h}^{n} \in V_{0h}\) for \(n=0,1,\dots,N\) such that

$$ \bigl(D_{N}^{\alpha } u_{h}^{n},v_{h} \bigr)- \bigl(\Delta _{h}(t_{n}) u_{h}^{n},v_{h} \bigr)=\bigl(P_{h}f^{n},v_{h}\bigr)\quad \text{for }n=1,\dots, N \text{ and all } v_{h}\in V_{0h} $$

with \(u_{h}^{0}=R_{h}(t_{0})u_{0}\). This formulation of our L1 FEM can be written as: find \(u_{h}^{n} \in V_{0h}\) for \(n=0,1,\dots,N\) such that

$$ D_{N}^{\alpha } u_{h}^{n} - \Delta _{h}(t_{n}) u_{h}^{n}=P_{h}f^{n} \quad\text{with } u_{h}^{0}=R_{h}(t_{0})u_{0} \text{ and } n=1,\dots, N, $$
(17)

where \(D_{N}^{\alpha } u_{h}^{n}, \Delta _{h}(t_{n}) u_{h}^{n}\) and \(P_{h}f^{n}\) all lie in \(V_{0h}\) are used.

4 Superconvergence of the L1 FEM

In this section, a superconvergence bound for \(\|\nabla R_{h}u^{n}-\nabla u^{n}_{h}\|\) will be presented, and then a superconvergence result of the L1 FEM (17) will be derived.

Let \(u^{n}\) and \(u^{n}_{h}\) be the solutions of (1a)–(1b) and (16), respectively, at time \(t=t_{n}\) for \(n = 0,1,\dots, N\). In order to facilitate the error analysis, denote \(\zeta ^{n}:=R_{h}(t_{n})u^{n}-u^{n}_{h}\) and \(\rho ^{n}:=R_{h}(t_{n})u^{n}-u^{n}\). Then we write

$$ u^{n}-u_{h}^{n}= \bigl(R_{h}(t_{n})u^{n}-u^{n}_{h} \bigr)-\bigl(R_{h}(t_{n})u^{n}-u^{n} \bigr)= \zeta ^{n}-\rho ^{n}, $$
(18)

The error of \(\rho ^{n}\) can be approximated immediately applying (6), but the approximation of \(\zeta ^{n}\) is difficult, and we estimate it now. From (1a), (8), and (17), one has

$$\begin{aligned} D_{N}^{\alpha } \zeta ^{n}-\Delta _{h}(t_{n})\zeta ^{n}&= \bigl[R_{h}(t_{n})D_{N}^{\alpha }u^{n}- \Delta _{h}(t_{n})R_{h}(t_{n})u^{n} \bigr]- \bigl(D_{N}^{\alpha }u_{h}^{n} - \Delta _{h}(t_{n}) u_{h}^{n} \bigr) \\ &=\bigl(R_{h}(t_{n})-P_{h}\bigr) D_{N}^{\alpha } u^{n}+P_{h} \bigl( D_{N}^{ \alpha } u^{n}-\nabla \cdot \bigl(a( \cdot,t_{n})\nabla u^{n}\bigr) \bigr)-P_{h}f^{n} \\ &=P_{h}\bigl(R_{h}(t_{n})-I\bigr) D_{N}^{\alpha } u^{n}+P_{h} \bigl(f^{n}-\varphi ^{n}\bigr)-P_{h}f^{n} \\ &=P_{h}\bigl( D_{N}^{\alpha } \rho ^{n}- \varphi ^{n}\bigr), \end{aligned}$$
(19)

where \(\varphi ^{n}:=D_{t}^{\alpha } u(x,t_{n})-D_{N}^{\alpha } u(x,t_{n})\).

Now the optimal-rate convergence of our method in \(L^{\infty }(H^{1})\) and a superconvergence bound for \(\|\nabla R_{h}u^{n}-\nabla u^{n}_{h}\|\) will be stated in the following theorem.

Theorem 4.1

(Error estimate for the L1 FEM)

Assume \(\|u\|_{L^{\infty }(H^{2})}\)and \(\|D_{t}^{\alpha }u\|_{L^{\infty }(H^{2})}\)are finite. Let \(u^{n}\)and \(u_{h}^{n}\)be the solutions of (1a)–(1b) and (16), respectively. Then for \(n=1,2,\dots,N\), there exists a constant C such that

$$\begin{aligned} &\bigl\Vert \nabla u^{n}-\nabla u^{n}_{h} \bigr\Vert \leq C \bigl(h+ N^{-\min \{2- \alpha, r\alpha \}} \bigr), \end{aligned}$$
(20)
$$\begin{aligned} &\bigl\Vert \nabla R_{h}(t_{n})u^{n}-\nabla u^{n}_{h} \bigr\Vert \leq C \bigl(h^{2}+ N^{- \min \{2-\alpha, r\alpha \}} \bigr). \end{aligned}$$
(21)

Proof

Fix \(n\in \{1,2,\ldots, N\}\). Multiplying (19) by \(-\Delta _{h}(t_{n}) \zeta ^{n}\) and integrating over Ω, one has

$$ - \bigl(D_{N}^{\alpha } \zeta ^{n}, \Delta _{h} (t_{n})\zeta ^{n} \bigr)+ \bigl\Vert \Delta _{h}(t_{n}) \zeta ^{n} \bigr\Vert ^{2}=- \bigl(P_{h}\bigl(D_{N}^{\alpha } \rho ^{n}{-}\varphi ^{n}\bigr),\Delta _{h}(t_{n}) \zeta ^{n} \bigr). $$
(22)

It is obvious that

$$ D _{N}^{\alpha } \rho ^{n}= D_{N}^{\alpha } \rho ^{n}- D_{t}^{\alpha } \rho ^{n}+ D_{t}^{\alpha } \rho ^{n}= \bigl(D_{t}^{\alpha }u^{n}-D_{N}^{\alpha }u^{n} \bigr)- R_{h}(t_{n}) \bigl(D_{t}^{\alpha }u^{n}-D_{N}^{\alpha }u^{n} \bigr)+ D_{t}^{\alpha }\rho ^{n}. $$
(23)

Inserting (23) into (22) and recalling the definition (7) of \(\Delta _{h}(t_{n})\) yields

$$\begin{aligned} &\bigl( a(\cdot,t_{n})D_{N}^{\alpha } \bigl(\nabla \zeta ^{n}\bigr), \nabla \zeta ^{n} \bigr)+ \bigl\Vert \Delta _{h}(t_{n}) \zeta ^{n} \bigr\Vert ^{2}\\ &\quad=- \bigl( D_{t}^{ \alpha } \rho ^{n}, \Delta _{h}(t_{n}) \zeta ^{n} \bigr)+ \bigl( a( \cdot,t_{n})\nabla P_{h}\bigl(-R_{h}(t_{n}) \varphi ^{n}\bigr), \nabla \zeta ^{n} \bigr). \end{aligned}$$

Applying Lemma 3.3 and Cauchy–Schwarz inequality, one has

$$\begin{aligned} &D_{N}^{\alpha } \bigl\Vert \sqrt{a(\cdot,t_{n})} \nabla \zeta ^{n} \bigr\Vert \bigl\Vert \sqrt{a( \cdot,t_{n})}\nabla \zeta ^{n} \bigr\Vert \\ &\quad \leq \frac{1}{4} \bigl\Vert D_{t}^{\alpha } \rho ^{n} \bigr\Vert ^{2}+ \bigl\Vert \sqrt{a(\cdot,t_{n})}\nabla P_{h}\bigl(R_{h}(t _{n}) \varphi ^{n} \bigr) \bigr\Vert \bigl\Vert \sqrt{a(\cdot,t_{n})}\nabla \zeta ^{n} \bigr\Vert . \end{aligned}$$

Invoking (5), (6), and (2), we get

$$ D_{N}^{\alpha } \bigl\Vert \sqrt{a( \cdot,t_{n})}\nabla \zeta ^{n} \bigr\Vert \bigl\Vert \sqrt{a( \cdot,t_{n})}\nabla \zeta ^{n} \bigr\Vert \leq Ch^{4}+\sqrt{\lambda }K \bigl\Vert \nabla \bigl(R_{h}(t_{n}) \varphi ^{n}\bigr) \bigr\Vert \bigl\Vert \sqrt{a( \cdot,t_{n})}\nabla \zeta ^{n} \bigr\Vert . $$
(24)

Observe that (24) is a particular case of (13). Thus we can invoke Lemma 3.2 to get

$$\begin{aligned} \bigl\Vert \sqrt{a(\cdot,t_{n})}\nabla \zeta ^{n} \bigr\Vert \leq{} & \bigl\Vert \sqrt{a(\cdot,t_{n})} \nabla \zeta ^{0} \bigr\Vert +\sqrt{\lambda }K\tau _{n}^{\alpha } \Gamma (2-\alpha ) \sum_{j=1}^{n}\theta _{n,j} \bigl\Vert \nabla \bigl(R_{h}(t_{j}) \varphi ^{j}\bigr) \bigr\Vert \\ &{}+\sqrt{T^{\alpha }\Gamma (1-\alpha )}\max_{1\leq j\leq n}Ch^{2}. \end{aligned}$$

Inequality \(\|\nabla R_{h}(t) w\|\leq \lambda \|\nabla w\|\ \forall w\in H_{0}^{1}( \Omega )\) follows easily from the definition of \(R_{h}(t)\). Hence

$$\begin{aligned} &\bigl\Vert \sqrt{a(\cdot,t_{n})}\nabla \zeta ^{n} \bigr\Vert \\ &\quad \leq \bigl\Vert \sqrt{a(\cdot,t_{n})} \nabla \zeta ^{0} \bigr\Vert +\lambda \sqrt{\lambda }K \tau _{n}^{\alpha }\Gamma (2- \alpha )\sum _{j=1}^{n}\theta _{n,j} \bigl\Vert \nabla \varphi ^{j} \bigr\Vert +C\sqrt{T^{ \alpha }\Gamma (1-\alpha )}h^{2}. \end{aligned}$$
(25)

By Lemma 3.1, we get \(\|\varphi ^{j}\|_{1}\leq Cj^{-\min \{2-\alpha,r\alpha \}}\). Substituting this inequality into (25) and recalling (12) yields

$$\begin{aligned} \bigl\Vert \nabla \zeta ^{n} \bigr\Vert \leq{}& \lambda \bigl\Vert \nabla \zeta ^{0} \bigr\Vert +C\lambda ^{2}K \tau _{n}^{\alpha }\Gamma (2-\alpha )\sum_{j=1}^{n} \theta _{n,j}j^{- \min \{2-\alpha,r\alpha \}} \\ &{} +C\sqrt{\lambda }\sqrt{T^{\alpha }\Gamma (1-\alpha )}h^{2} \\ \leq{}& C\lambda ^{2}KT^{\alpha }\Gamma (1-\alpha )N^{-\min \{2-\alpha,r \alpha \}}+C\sqrt{\lambda T^{\alpha }\Gamma (1-\alpha )}h^{2}, \end{aligned}$$

where we used \(\|\nabla \zeta ^{0}\|=\|\nabla (R_{h} u^{0}-u_{h}^{0})\|=0\), then invoked (12) with \(\eta =\min \{2-\alpha, r\alpha \}\) for the \(j^{-\min \{2-\alpha, r\alpha \}}\) term. Combining this bound and (6) with (18), we get (20). □

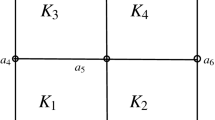
Let \(I_{h}:H^{2}(\Omega )\rightarrow V_{0h}\) be the associated interpolation operator satisfying \(I_{h}u(a_{i})=u(a_{i})\), where \(a_{i}, (i=1,2,3,4)\) are the four vertices of \(K_{m}\). Imitating the proof given for [35, Lemma 2] yields

$$ \bigl\Vert R_{h}(t)w-I_{h}w \bigr\Vert _{1}\leq Ch^{2} \Vert u \Vert _{3}, \quad\forall w \in H_{0}^{1}( \Omega )\cap H^{3}(\Omega ). $$
(26)

In order to derive the global superconvergence result, we adopt the same interpolation postprocessing operator \(I_{2h}\) as in [22], which satisfies

$$\begin{aligned} &I_{2h}I_{h}w=I_{2h}w,\quad \forall w\in H^{2}(\Omega ), \end{aligned}$$
(27a)
$$\begin{aligned} & \Vert w-I_{2h}w \Vert _{1}\leq Ch^{2} \vert w \vert _{3}, \quad\forall w\in H^{3}(\Omega ), \end{aligned}$$
(27b)
$$\begin{aligned} & \Vert I_{2h}w_{h} \Vert _{1}\leq C \Vert w_{h} \Vert _{1}, \quad\forall w_{h}\in V_{0h}. \end{aligned}$$
(27c)

Corollary 4.2

Under the conditions of Theorem 4.1and assuming \(\|u\|_{L^{\infty }(H^{3})}\)is finite, let the finite element space be the conforming rectangular bilinear element space, then the following superconvergence estimates hold:

$$\begin{aligned} &\bigl\Vert I_{h}u^{n}-u_{h}^{n} \bigr\Vert _{1}\leq C \bigl(h^{2}+ N^{-\min \{2-\alpha, r\alpha \}} \bigr), \\ &\bigl\Vert u^{n}-I_{2h}u_{h}^{n} \bigr\Vert _{1}\leq C \bigl(h^{2}+ N^{-\min \{2- \alpha, r\alpha \}} \bigr). \end{aligned}$$

Proof

Applying (26) and (21), one has

$$\begin{aligned} \bigl\Vert I_{h}u^{n}-u_{h}^{n} \bigr\Vert _{1}&\leq \bigl\Vert I_{h}u^{n}-R_{h}(t_{n})u^{n} \bigr\Vert _{1}+ \bigl\Vert R_{h}(t_{n})u^{n}-u_{h}^{n} \bigr\Vert _{1} \\ &\leq Ch^{2}+ C \bigl(h^{2}+ N^{-\min \{2-\alpha, r\alpha \}} \bigr) \\ &\leq C \bigl(h^{2}+ N^{-\min \{2-\alpha, r\alpha \}} \bigr). \end{aligned}$$

Furthermore, combining this result with (27a)–(27c) yields

$$\begin{aligned} \bigl\Vert u^{n}-I_{2h}u_{h}^{n} \bigr\Vert _{1}&\leq \bigl\Vert u^{n}-I_{2h}I_{h}u^{n} \bigr\Vert _{1}+ \bigl\Vert I_{2h}I_{h}u^{n}-I_{2h}u_{h}^{n} \bigr\Vert _{1} \\ &= \bigl\Vert u^{n}-I_{2h}u^{n} \bigr\Vert _{1}+ \bigl\Vert I_{2h}\bigl(I_{h}u^{n}-u_{h}^{n} \bigr) \bigr\Vert _{1} \\ &\leq Ch^{2}+C \bigl\Vert I_{h}u^{n}-u_{h}^{n} \bigr\Vert _{1} \\ &\leq C \bigl(h^{2}+ N^{-\min \{2-\alpha, r\alpha \}} \bigr). \end{aligned}$$

Thus the proof is complete. □

5 Numerical experiments

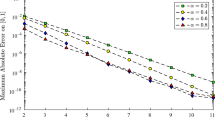
We compute numerical solutions for an example of problem (1a)–(1b) that near \(t=0\) behaves as described in (4). The \(E_{1}^{M,N}\) and \(E_{2}^{M,N}\) errors in the computed solutions are defined by

$$ E_{1}^{M,N}:=\max_{0\leq n\leq N} \bigl\Vert I_{h}u^{n}-u_{h}^{n} \bigr\Vert _{1}, \qquad E_{2}^{M,N}:= \max_{0\leq n\leq N} \bigl\Vert u^{n}-I_{2h}u_{h}^{n} \bigr\Vert _{1}. $$

Example 5.1

Consider the two-dimensional time-fractional diffusion problem (1a)–(1b) with \(\Omega =(0,\pi )\times (0,\pi )\), \(a(x,y,t)=t\cos (t)xy/\pi ^{2}\), \(T=1\). The function f is chosen such that the exact solution of the problem (1a)–(1b) is \(u(x,y,t)=(t^{\alpha }+t^{3})\sin x\sin y\).

Corollary 4.2 predicts the rate of convergence \(O(h^{2}+N^{-\min \{2-\alpha,r\alpha \}})\) for \(E_{1}^{M,N}\) and \(E_{2}^{M,N}\). We choose a uniform rectangular partition of Ω with \(M+1\) nodes in each spatial direction. Tables 1 and 2 show the \(E_{1}^{M,N}\) and \(E_{2}^{M,N}\) errors for \(\alpha =0.4, 0.6, 0.8\) with \(r= (2-\alpha )/\alpha \). We take \(M=N\) so that the temporal error dominates the spatial error in the bound of Corollary 4.2. The orders of convergence displayed indicate that the rate of convergence is \(N^{-(2-\alpha )}\), as predicted by Corollary 4.2. Table 3 shows the spatial errors and the associated orders of convergence for \(\alpha =0.4\) and \(r=(2-\alpha )/\alpha \). Here we take \(N=2000\) so that the spatial error dominates the results, and we observe \(O(h^{2})\) convergence, as predicted by Corollary 4.2.

Table 1 \(E_{1}^{M,N}\) errors and orders of convergence for L1 FEM with \(r=(2-\alpha )/\alpha \)
Full size table
Table 2 \(E_{2}^{M,N}\) errors and orders of convergence for L1 FEM with \(r=(2-\alpha )/\alpha \)
Full size table
Table 3 \(E_{1}^{M,N}\) and \(E_{2}^{M,N}\) convergent results on spatial direction for L1 FEM with \(\alpha =0.4\)
Full size table