1 Introduction

For single species model, especially the logistic model, the dynamical behaviors, such as the stability, persistence, permanence, extinction, and existence of positive periodic solutions, have been extensively studied during the last decades. Also, feedback control of species in ecosystem has become a focus of intense research for the ecological balance. It is well known that when a certain component of an ecosystem changes, it inevitably causes a series of corresponding changes in other components, which in turn affects the component that originally changed. This process is called feedback control [3]. Its function is to enable the ecosystem to reach and maintain the steady state. By applying the feedback control method to the population ecosystem, a large number of scholars have extensively investigated the logistic model, and many interesting results have been obtained. For example, Gopalsamy and Weng [4] firstly introduced a feedback control variable into the delay logistic model and proposed the following ecosystem:

$$ \begin{gathered} \frac{\mathrm{d}n}{\mathrm{d}t} =rn(t) \biggl[1- \biggl( \frac{a_{1}n(t)+a_{2}n(t-\tau )}{K}-bu(t) \biggr) \biggr], \\ \frac{\mathrm{d}u}{\mathrm{d}t} =-au(t)+cn(t-\tau ). \end{gathered} $$
(1.1)

By constructing some suitable Lyapunov functional, the authors [4] obtained the global stability under certain condition. Subsequently, Fan and Wang [1] considered the global asymptotical stability of the following logistic equation with feedback control:

$$ \begin{gathered} \frac{\mathrm{d}x}{\mathrm{d}t} =x \biggl(1-\frac{x}{K} \biggr)-xu, \\ \frac{\mathrm{d}u}{\mathrm{d}t} =-\eta u+ax. \end{gathered} $$
(1.2)

By use of a new method combined with the upper and lower solution technique, which is different from the Lyapunov function method, the authors in [1] proved that system (1.2) has a unique positive equilibrium \(E^{*}(x^{*},u^{*})\) which is globally asymptotically stable. In addition, the single species with pure delay or distributed delay, the mutualism system, the epidemic model, the discrete Lotka–Volterra competitive system, and the cooperative system with feedback control were investigated in [5–10], and [11], respectively. Very recently, in [12] the author considered a logistic model with feedback of fractional order.

On the other hand, in this vast world, the relationship of species is complex and diverse. Allee [13] pointed out that if the population is too sparse, mating between the populations will be more difficult, and then the ability to cope with predators will be weakened, which in turn will lead to lower birth rates and higher death rates. This phenomenon is called the Allee effect [14]. In recent years, the ecological model with Allee effect has been extensively studied. For example, Conway and Smoller [15], Bazykin [16] proposed the following single species model with Allee effect through incorporating a continuous growth function:

$$ \frac{\mathrm{d}x}{\mathrm{d}t}=r \biggl(1-\frac{x}{K} \biggr) (x-m)x. $$
(1.3)

Here r denotes the intrinsic per capita growth rate of the population and K is the carrying capacity. If \(m\leq 0\), it shows the weak Allee effect, while if \(0< m< K\), it shows the strong Allee effect. As was pointed out in [17] and [18], the strong Allee effect introduces a population threshold, below which the species may be extinct, and above which it survives. In contrast, a population with weak Allee effect does not have such threshold. For more details on the Allee effect, please see [19–21].

Furthermore, Dennis [22] firstly deduced the additive Allee effect in the following equation:

$$ \frac{\mathrm{d}x}{\mathrm{d}t}=r \biggl[ \biggl(1-\frac{x}{K} \biggr)- \frac{m}{x+a} \biggr]x. $$
(1.4)

Here, \(\frac{m}{x+a}\) is the term of additive Allee effect. m and a are constants which indicate the severity of the Allee effect. Moreover, the criteria of the additive Allee effect are as follows:

  1. (a)

    If \(0< m< a\), then the Allee effect in (1.4) is weak;

  2. (b)

    If \(m>a\), then the Allee effect in (1.4) is strong.

Consequently, an increasing number of researchers have taken into account the additive Allee effect when analyzing the rich phenomenon in ecology and biology. For example, in [23], the authors presented the Hopf bifurcation and stability analysis for a delayed logistic equation with additive Allee effect. Moreover, the predator-prey model, the diffusive or the impulsive ecological model, the fractional order Leslie–Gower model, and the hybrid bioeconomic system with the additive Allee effect were investigated in [24–31], and [32], respectively.

Recently, Lin [2] proposed a single species logistic model with Allee effect and feedback control

$$ \begin{gathered} \frac{\mathrm{d}x}{\mathrm{d}t}=rx(1-x) \frac{x}{\beta +x}-axu, \\ \frac{\mathrm{d}u}{\mathrm{d}t}=-bu+cx. \end{gathered} $$
(1.5)

The author in [2] shows that the species may be extinct when the Allee effect is large. As we know, the traditional logistic system with feedback control always admits a unique positive equilibrium which is globally attractive. In other words, the Allee effect makes system (1.5) become unstable, i.e., the system could collapse under large perturbation. Also, the latest papers on population models have inspired us a lot, see for instance [33–36]. Hence, one can naturally propose the following interesting and meaningful question: How can the additive Allee effect influence the logistic system with feedback control? Does the logistic system with additive Allee effect and feedback control still admit a unique positive equilibrium? Motivated by the above, in this paper, we shall investigate the following single species logistic model with additive Allee effect and feedback control:

$$ \begin{gathered} \frac{\mathrm{d}x}{\mathrm{d}t}=x \biggl(1-x-\frac{m}{x+a} \biggr)-bxu, \\ \frac{\mathrm{d}u}{\mathrm{d}t}=-u+cx, \end{gathered} $$
(1.6)

where x and u represent the density of the population and feedback control variable, respectively. Here a, b, c, and m are all positive constants. The biological meaning of m and a in (1.6) is the same as that in system (1.4). For system (1.6), we shall present the stability and bifurcation analysis. Moreover, the impact of the additive Allee effect and feedback control on the dynamical behaviors will be discussed in this paper.

Thus far, to the best of the authors’ knowledge, this paper is the first work which proposes and investigates the logistic model with additive Allee effect and feedback control. The detailed contribution is in two aspects. One is to discuss the existence and stability for the above system under three different Allee effect cases, i.e., \(m< a\), \(m>a\), and \(m=a\). The other is to propose the bifurcation phenomenon under the strong Allee effect case (\(m>a\)). Compared with [1] and [2], the differences are listed as follows. Firstly, the system in [1] and [2] admits at most one positive equilibrium. However, system (1.6) can admit one or two positive equilibria when the additive Allee effect constants m and a satisfy certain condition. The above shows that the additive Allee effect can have a direct impact on the species’ permanence and extinction. Secondly, the system in [1] and [2] has a trivial equilibrium which is always unstable. However, for system (1.6), in order to decide whether the trivial equilibrium is stable or not, one should compare the size of m with a. In other words, comparing with [1] and [2], system (1.6) is experiencing more complex dynamics such as the transcritical bifurcation and saddle-node bifurcation when incorporating the additive Allee effect and feedback control.

The rest of the paper is organized as follows. In Sect. 2, we discuss the existence and stability of equilibrium for system (1.6). In Sect. 3, we present certain condition under which the saddle-node bifurcation and transcritical bifurcation occur. We also carry out some numerical simulations to verify the main results. In Sect. 4, we discuss and give a conclusion to end this paper.

2 Existence and stability of equilibria

In this section, we discuss the existence and stability of the equilibria for system (1.6). By simple computation, we obtain that system (1.6) always has a trivial equilibrium \(E_{0}(0,0)\), and other interior equilibria shall be investigated as follows.

2.1 The existence of positive equilibria

The equilibria of system (1.6) are determined by the following equation:

$$ \textstyle\begin{cases} x (1-x-\frac{m}{x+a} )-bxu=0, \\ -u+cx=0. \end{cases} $$
(2.1)

Easily one can find that the system always admits the trivial equilibrium \(E_{0}(0,0)\). From the view of biology, we only consider the positive equilibria, and so we pay attention to the positive solution of the following equation:

$$ (1+bc)x^{2}+\bigl[a(1+bc)-1\bigr]x+m-a=0. $$
(2.2)

Let the discriminant of equation (2.2) denoted by \(\triangle (m)\) be as follows:

$$ \triangle (m)=(1+a+abc)^{2}-4m(1+bc), $$
(2.3)

and let \(m^{\ast }\) be the unique root of \(\triangle (m)=0\). Through simple calculation, we have

$$ m^{\ast }=\frac{(1+a+abc)^{2}}{4(1+bc)}. $$
(2.4)

System always has a trivial equilibrium \(E_{0}(x_{0},u_{0})\). If \(m< m^{*}\), then \(\bigtriangleup (m)>0\). So (1.6) has two different equilibria, i.e., \(E_{1}(x_{1},u_{1})\), \(E_{2}(x_{1},u_{1})\). Here \(x_{1}=\frac{1-a-abc-\sqrt{\bigtriangleup (m)}}{2(1+bc)}\), \(u_{1}=cx_{1}\), \(x_{2}=\frac{1-a-abc+\sqrt{\bigtriangleup (m)}}{2(1+bc)}\), and \(u_{2}=cx_{2}\). However, if \(m>m^{*}\), then \(\bigtriangleup (m)<0\). So (1.6) has no equilibria. Also, if \(m=m^{*}\), \(\bigtriangleup (m)=0\), then (1.6) has a unique equilibrium \(E_{3}(x_{3},u_{3})\) where \(x_{3}=\frac{1-a-abc}{2(1+bc)}\) and \(u_{3}=cx_{3}\). Through the above analysis, we can obtain the existence of the positive equilibria in the case of weak Allee effect, strong Allee effect, and \(m=a\) as follows.

Theorem 2.1

(The case of weak Allee effect, i.e., \(m< a\))

System (1.6) has a unique positive equilibrium\(E_{2}(x_{2},u_{2})\).

Theorem 2.2

(The case of strong Allee effect, i.e., \(m>a\))

  1. (i)

    If \(a(1+bc)<1\) and

    1. (a)

      If\(a< m< m^{\ast }\), then system (1.6) has two distinct positive equilibria\(E_{1}(x_{1},u_{1})\)and\(E_{2}(x_{2},u_{2})\).

    2. (b)

      If\(m=m^{\ast }\), then system (1.6) has a unique positive equilibrium\(E_{3}(x_{3},u_{3})\).

    3. (c)

      If\(m>m^{\ast }\), then system (1.6) has no positive equilibria.

  2. (ii)

    If\(a(1+bc)\geq 1\), then system (1.6) has no positive equilibria.

Theorem 2.3

(The case of \(m=a\))

  1. (i)

    If\(a(1+bc)<1\), then system (1.6) has a unique positive equilibrium\(E_{2}(x_{2},u_{2})\).

  2. (ii)

    If\(a(1+bc)\geq 1\), then system (1.6) has no positive equilibria.

2.2 Stability of the equilibria \(E_{0}\), \(E_{1}\), \(E_{2}\), and \(E_{3}\)

Firstly, we investigate the stability of the trivial equilibrium \(E_{0}\). The Jacobian matrix of system (1.6) is calculated as follows:

$$ J= \begin{bmatrix} 1-2x-\frac{ma}{(x+a)^{2}}-bu& -bx \\ c & -1 \end{bmatrix}. $$
(2.5)

So the Jacobin matrix at \(E_{0}(0,0)\) is

$$ J_{E_{0}}= \begin{bmatrix} 1-\frac{m}{a}& 0 \\ c & -1 \end{bmatrix}. $$
(2.6)

By direct calculation, we can obtain two eigenvalues of \(J_{E_{0}}\), i.e., \(\lambda _{1}=1-\frac{m}{a}\) and \(\lambda _{2}=-1<0\). So, if \(0< m< a\), we have \(\lambda _{1}>0\), then \(E_{0}(0,0)\) is a hyperbolic saddle. If \(m>a\), we have \(\lambda _{1}<0\), then \(E_{0}(0,0)\) is a hyperbolic stable node.

Secondly, as was pointed out in Theorem 2.2, when \(a(1+bc)<1\) and \(a< m< m^{*}\), there exist two positive equilibria \(E_{1}(x_{1},u_{1})\) and \(E_{2}(x_{2},u_{2})\). The Jacobian matrix about the equilibria \(E_{i}(x_{i},u_{i})\), \(i=1,2\), is given by

$$ J_{E_{i}}= \begin{bmatrix} 1-2x_{i}-\frac{ma}{(x_{i}+a)^{2}}-bu_{i}& -bx_{i} \\ c & -1 \end{bmatrix}. $$
(2.7)

Combining with (2.1), the determinant and the trace of the Jacobian matrix are given by

$$\begin{aligned}& \operatorname{Det}[J_{E_{i}}]=x_{i}+\frac{ma}{(x_{i}+a)^{2}}- \frac{m}{x_{i}+a}+bcx_{i}, \\& \operatorname{Tr}[J_{E_{i}}]=-2x_{i}-\frac{ma}{(x_{i}+a)^{2}}-bu_{i}< 0. \end{aligned}$$

After straightforward computation, we have

$$\begin{aligned}& \operatorname{Det}[J_{E_{1}}]=\frac{x_{1}}{2(x_{1}+a)^{2}(1+bc)} \bigl[ \bigtriangleup (m)-(1+a+abc)\sqrt{\bigtriangleup (m)} \bigr]< 0, \\& \operatorname{Det}[J_{E_{2}}]=\frac{x_{2}}{2(x_{2}+a)^{2}(1+bc)} \bigl[ \bigtriangleup (m)+(1+a+abc)\sqrt{\bigtriangleup (m)} \bigr]>0. \end{aligned}$$

Therefore, \(E_{1}\) is always a saddle and \(E_{2}\) is a hyperbolic stable node.

In all, in the following, the stability of the equilibria in the case of weak Allee effect, strong Allee effect, and \(m=a\) is discussed in Theorems 2.4, 2.5, and 2.6, respectively.

Theorem 2.4

(The case of weak Allee effect, i.e., \(m< a\))

  1. (1)

    \(E_{0}(0,0)\)is a hyperbolic saddle.

  2. (2)

    \(E_{2}(x_{2},u_{2})\)is a hyperbolic stable node.

Corollary 2.1

When\(m< a\), for system (1.6), the unique positive equilibrium\(E_{2}(x_{2},u_{2})\)is globally asymptotically stable.

Proof

As was mentioned before, \(E_{2}\) is locally asymptotically stable. So we only need to prove that \(E_{2}\) is attractive. Define the Lyapunov function \(V(x,u)=x-x_{2}-x_{2}\ln \frac{x}{x_{2}}+\frac{b}{2c}(u-u_{2})^{2}\). Obviously, \(V(x,u)\) is positive definite. By use of \(1-x_{2}-\frac{m}{x_{2}+a}-bu_{2}=0\) and \(u_{2}=cx_{2}\), we can obtain the derivative of \(V(x,u)\) along the positive solution of (1.6) as follows:

$$ \begin{aligned} \dot{V}(x,u)&=x-x_{2}-x_{2}\ln \frac{x}{x_{2}}+\frac{b}{2c}(u-u_{2})^{2} \\ &=\dot{x}-\frac{x_{2}}{x}\dot{x}+\frac{b}{c}(u-u_{2})\dot{u} \\ &=(x-x_{2}) \biggl(1-x-\frac{m}{x+a} \biggr)-b(x-x_{2})u_{2}- \frac{b}{c}(u-u_{2})^{2} \\ &=- \biggl(1-\frac{m}{(x_{2}+a)(x+a)} \biggr) (x-x_{2})^{2}- \frac{b}{c}(u-u_{2})^{2} \\ &\leq - \biggl(1-\frac{m}{(x_{2}+a)(1+a)} \biggr) (x-x_{2})^{2}- \frac{b}{c}(u-u_{2})^{2} \\ &\leq - \biggl(1-\frac{m}{a} \biggr) (x-x_{2})^{2}- \frac{b}{c}(u-u_{2})^{2}. \end{aligned} $$

We can conclude that \(\dot{V}(x,u)\leq 0\) since \(m< a\) and \(\limsup_{t\rightarrow \infty } x(t)\leq 1\). Also \(\dot{V}(x,u)=0\) if and only if \(x=x_{2}\), \(u=u_{2}\). Thus one can deduce that \(E_{2}(x_{2},u_{2})\) is globally asymptotically stable. The proof of Corollary 2.1 is finished. □

Theorem 2.5

(The case of strong Allee effect, i.e., \(m>a\))

\(E_{0}(0,0)\)is always a hyperbolic stable node. Suppose that\(a(1+bc)<1\),

  1. (1)

    If\(a< m< m^{*}\), then\(E_{1}\)is a saddle and\(E_{2}\)is a hyperbolic stable node.

  2. (2)

    If\(m=m^{*}\), then\(E_{3}\)is an attracting saddle-node.

Proof

In what follows, we only prove that \(E_{3}\) is a saddle-node when \(m=m^{*}\). Let \(X=x-x_{3}\), \(U=u-u_{3}\), we transform system (1.6) to the following system:

$$ \textstyle\begin{cases} \dot{X}=(X_{3}+x_{3}) [1-X-x_{3}-\frac{m}{X+x_{3}+a} ]-b(X+x_{3})(U+u_{3}) , \\ \dot{U} = -U+cX. \end{cases} $$
(2.8)

Applying the Taylor expansion of \(\frac{m}{X+x_{3}+a}\), system (2.8) can be rewritten as

$$ \textstyle\begin{cases} \dot{X}=bcx_{3}X-bx_{3}U+ [-1+ \frac{m}{(x_{3}+a)^{2}}-\frac{mx_{3}}{(x_{3}+a)^{3}} ]X^{2} \\ \hphantom{\dot{X}=} {}-\frac{m}{(x_{3}+a)^{3}}X^{3}-bXU+P(X), \\ \dot{U}=-U+cX, \end{cases} $$
(2.9)

where \(P(X)\) denotes the power series with term \(X^{i}\) satisfying \(i\geq 4\). The Jacobian matrix of system (2.9) evaluated at the origin, i.e., the Jacobian matrix of system (1.6) at \(E_{3}\), can be calculated as follows:

$$ J_{E_{3}}= \begin{bmatrix} bcx_{3}&-bx_{{3}} \\ c&-1 \end{bmatrix}, $$
(2.10)

then the eigenvalues of \(J_{E_{3}}\) are \(\lambda _{1}=0\), \(\lambda _{2}=bcx_{3}-1\). Under the transformation

$$ \begin{pmatrix} X \\ U \end{pmatrix} = \begin{pmatrix} 1&bx_{3} \\ c&1 \end{pmatrix} \begin{pmatrix} x \\ u \end{pmatrix}, $$
(2.11)

system (2.9) can be rewritten as

$$ \textstyle\begin{cases} \dot{x}=c_{20}x^{2}+c_{11}xu+c_{02}u^{2}+c_{30}x^{3}+c_{12}xu^{2}+c_{21}x^{2}u+c_{03}u^{3}+P_{1}(x,u), \\ \dot{u}=d_{01}u+d_{02}u^{2}+d_{11}xu+d_{20}x^{2}+d_{21}x^{2}u+d_{12}xu^{2}+d_{03}u^{3}+d_{30}x^{3}+P_{2}(x,u), \end{cases} $$
(2.12)

where \(P_{1}(x,u)\), \(P_{2}(x,u)\) denote the power series with term \(x^{i}u^{j}\) satisfying \(i+j\geq 4\) and

$$\begin{aligned}& c_{20}=\frac{ma-(1+bc)(x_{3}+a)^{3}}{(1-bcx_{3})(x_{3}+a)^{3}},\qquad c_{11}= \frac{2mabx_{3}-(b+2bx_{3}+b^{2}cx_{3})(x_{3}+a)^{3}}{(1-bcx_{3})(x_{3}+a)^{3}}, \\& c_{02}= \frac{mab^{2}x_{3}^{2}-(b^{2}x_{3}+b^{2}x_{3}^{2})(x_{3}+a)^{3}}{(1-bcx_{3})(x_{3}+a)^{3}},\qquad c_{30}=\frac{-m}{(1-bcx_{3})(x_{3}+a)^{3}}, \\& c_{12}=\frac{-3mb^{2}x_{3}^{2}}{(1-bcx_{3})(x_{3}+a)^{3}},\qquad c_{21}=\frac{-3mbx_{3}}{(1-bcx_{3})(x_{3}+a)^{3}},\qquad c_{03}=\frac{-mb^{3}x_{3}^{3}}{(1-bcx_{3})(x_{3}+a)^{3}}, \\& d_{01}=bcx_{3}-1,\qquad d_{02}= \frac{(b^{2}cx_{3}^{2}+b^{2}cx_{3})(x_{3}+a)^{3}-mab^{2}x_{3}^{2}}{(1-bcx_{3})(x_{3}+a)^{3}}, \\& d_{11}= \frac{(b^{2}c^{2}x_{3}+2bcx_{3}+bc)(x_{3}+a)^{3}-2mabcx_{3}}{(1-bcx_{3})(x_{3}+a)^{3}}, \\& d_{20}=\frac{(c+bc^{2})(x_{3}+a)^{3}-mac}{(1-bcx_{3})(x_{3}+a)^{3}},\qquad d_{21}=\frac{3mbcx_{3}}{(1-bcx_{3})(x_{3}+a)^{3}}, \\& d_{12}=\frac{3mb^{2}cx_{3}^{2}}{(1-bcx_{3})(x_{3}+a)^{3}},\qquad d_{03}=\frac{mb^{3}cx_{3}^{3}}{(1-bcx_{3})(x_{3}+a)^{3}},\qquad d_{30}=\frac{mc}{(1-bcx_{3})(x_{3}+a)^{3}}. \end{aligned}$$

Introducing a new time variable \(\tau =(bcx_{3}-1)t\), for notational simplicity, we still retain t to denote τ and obtain

$$ \textstyle\begin{cases} \dot{x}=e_{20}x^{2}+e_{11}xu+e_{02}u^{2}+e_{30}x^{3}+e_{12}xu^{2}+e_{21}x^{2}u+e_{03}u^{3}+Q_{1}(x,u), \\ \dot{u}=u+f_{02}u^{2}+f_{11}xu+f_{20}x^{2}+f_{21}x^{2}u+f_{12}xu^{2}+f_{03}u^{3}+f_{30}x^{3}+Q_{2}(x,u), \end{cases} $$
(2.13)

where \(e_{ij}=\frac{c_{ij}}{bcx_{3}-1}\), \(f_{ij}=\frac{d_{ij}}{bcx_{3}-1}\), \(c_{ij}\), \(d_{ij}\) (\(i+j= 2,3\)) are the same as those in (2.12). When \(m=m^{\ast }\), the coefficient of \(x^{2}\) can be simplified as \(e_{20}= \frac{(1-a-abc)(1+a+abc)^{2}}{8(1+bc)^{2}(1-bcx_{3})(x_{3}+a)^{3}}>0\). Considering the new time variable τ and using Theorem 7.1 in [37], we can conclude that the equilibrium \(E_{3}\) is an attracting saddle-node. This completes the proof. □

Remark 2.1

When \(a(1+bc)<1\), \(m>m^{\ast }\) or \(a(1+bc)\geq 1\), we can conclude that \(E_{0}(0,0)\) is globally asymptotically stable. The detailed reason is as follows. If \(a(1+bc)<1\), \(m>m^{\ast }\), or \(a(1+bc)\geq 1\), system (1.6) has a unique stable equilibrium \(E_{0}(0,0)\). And the solution of system (1.6) is bounded, so the solution cannot extend to the infinity. Also, there exists no limit cycle since system (1.6) has no interior equilibria. Thus \(E_{0}(0,0)\) is global asymptotically stable.

Theorem 2.6

(The case of \(m=a\))

  1. (1)

    \(E_{0}(0,0)\)is an attracting saddle-node.

  2. (2)

    \(E_{2}\)is locally asymptotically stable.

Proof

Here we only need to prove that \(E_{0}(0,0)\) is a saddle-node. If \(m=a\), (2.6) can be rewritten as

$$ J_{E_{0}}= \begin{bmatrix} 0& 0 \\ c & -1 \end{bmatrix}, $$
(2.14)

then the eigenvalues of \(J_{E_{0}}\) are \(\lambda _{1}=0\), \(\lambda _{2}=-1\). So \({E_{0}}\) is a non-hyperbolic equilibrium, we shall analyze the stability of \(E_{0}\) by use of Theorem 7.1 in [37]. Let

$$ \begin{pmatrix} x \\ u \end{pmatrix} = \begin{pmatrix} 1&0 \\ c&1 \end{pmatrix} \begin{pmatrix} x_{1} \\ u_{1} \end{pmatrix}. $$
(2.15)

System (1.6) can be changed as follows:

$$ \textstyle\begin{cases} \dot{x_{1}} = x_{1}-x_{1}^{2}- \frac{ax_{1}}{x_{1}+a}-bcx_{1}^{2}-bx_{1}u_{1}, \\ \dot{u_{1}} = -u_{1}-cx_{1}+cx_{1}^{2}+ \frac{acx_{1}}{x_{1}+a}+bc^{2}x_{1}^{2}+bcx_{1}u_{1}. \end{cases} $$
(2.16)

Introducing a new time variable \(\tau =-t\), for notational simplicity, we still retain to denote τ and have

$$ \textstyle\begin{cases} \dot{x_{1}} = -x_{1}+x_{1}^{2}+ \frac{ax_{1}}{x_{1}+a}+bcx_{1}^{2}+bx_{1}u_{1}, \\ \dot{u_{1}} = u_{1}+cx_{1}-cx_{1}^{2}- \frac{acx_{1}}{x_{1}+a}-bc^{2}x_{1}^{2}-bcx_{1}u_{1}. \end{cases} $$
(2.17)

Applying the Taylor expansion of \(\frac{1}{x_{1}+a}\), we can obtain

$$ \textstyle\begin{cases} \dot{x_{1}} = (1-\frac{1}{a}+bc )x_{1}^{2}+ \frac{x_{1}^{3}}{a^{2}}+bx_{1}u_{1}+R_{1}(x_{1}, u_{1})\triangleq \bar{P}(x_{1},u_{1}), \\ \dot{u_{1}} = u_{1}+ (-c+\frac{c}{a}-bc^{2} )x_{1}^{2}-\frac{cx_{1}^{3}}{a^{2}}-bcx_{1}u_{1}+R_{2}(x_{1}, u_{1}) \triangleq u_{1}+\bar{Q}(x_{1},u_{1}). \end{cases} $$
(2.18)

Here \(R_{1}(x_{1},u_{1})\) and \(R_{2}(x_{1},u_{1})\) denote the power series with term \(x_{1}^{i}u_{1}^{j}\) satisfying \(i+j\geq 4\). Let \(u_{1}+\bar{Q}(x_{1},u_{1})=0\), we can get the implicit function \(u_{1}=\phi (x_{1})=(c-\frac{c}{a}+bc^{2})x_{1}^{2}+M(x_{1})\), and then \(\bar{P}(x_{1},u_{1})=\bar{P}(x_{1},\phi (x_{1}))=\frac{a+abc-1}{a}x_{1}^{2}+T(x_{1})\). Here \(M(x_{1})\) and \(T(x_{1})\) denote the power series with term \(x_{1}^{i}\) satisfying \(i\geq 3\) and \(i\geq 4\), respectively. Considering the new time variable τ and using Theorem 7.1 in [37], we can conclude that the equilibrium \(E_{0}\) is an attracting saddle-node. The proof is complete. □

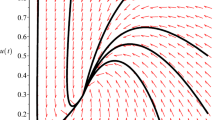
The corresponding illustrative phase portraits in Theorems 2.4–2.6 are shown in Figs. 1–3, respectively.

Figure 1
figure 1

The phase portraits of system (1.6) when \(m< a\). Here \(E_{0}(0,0)\) is a hyperbolic saddle and \(E_{2}(x_{2},u_{2})\) is a stable node

Full size image
Figure 2
figure 2

The phase portraits of system (1.6) when \(m>a\): (a) Two distinct positive equilibria \(E_{1}\) and \(E_{2}\). \(E_{1}\) is a saddle and \(E_{2}\) is locally asymptotically stable. (b) Unique positive equilibrium \(E_{3}\) which is a saddle-node. (c), (d), (e) No positive equilibria

Full size image
Figure 3
figure 3

The phase portraits of system (1.6) when \(m=a\): (a) Two equilibria \(E_{0}\) and \(E_{2}\). \(E_{0}\) is a saddle-node and \(E_{2}\) is a stable node. (b), (c) A trivial equilibrium \(E_{0}\) which is a saddle-node

Full size image

3 Bifurcation

For the case of weak Allee effect, the unique positive equilibrium is globally asymptotically stable. Thus there exist no bifurcation phenomena. In the following, we discuss the occurrence of the saddle-node bifurcation and transcritical bifurcation under the cases of strong Allee effect and the critical case when \(m=a\).

3.1 Saddle-node bifurcation

From Sect. 2, we have analyzed the existence of the equilibria \(E_{1}\), \(E_{2}\), \(E_{3}\). In other words, if \(0< m< m^{\ast }\), then system (1.6) has two positive equilibria, i.e., \(E_{1}(x_{1},u_{1})\) and \(E_{2}(x_{2},u_{2})\). If \(m=m^{\ast }\), the system has a unique equilibrium \(E_{3}(x_{3},u_{3})\). If \(m>m^{\ast }\), the system has no positive equilibria. The appearance or annihilation of equilibria may lead to the occurrence of saddle-node bifurcation which exists when \(m=m_{\mathrm{SN}}\triangleq \frac{(1+a+abc)^{2}}{4(1+bc)}\). We will prove the existence of saddle-node bifurcation as follows.

Theorem 3.1

System (1.6) undergoes the saddle-node bifurcation when\(m=m_{\mathrm{SN}}\).

Proof

In order to prove the occurrence of saddle-node bifurcation at \(m=m_{\mathrm{SN}}\), we use Sotomayor’s theorem in [38] to verify the transversality condition when \(m=m_{\mathrm{SN}}\). The Jacobian matrix at \(E_{3}\) is given by

$$ J_{E_{3}}= \begin{bmatrix} 1-2x_{3}-\frac{ma}{(x_{3}+a)^{2}}-bu_{3}& -bx_{3} \\ c & -1 \end{bmatrix}, $$
(3.1)

and combining with (2.1), the determinant and the trace of the Jacobian matrix are given by

$$\begin{aligned}& \operatorname{Det}[J_{E_{3}}]=x_{3}+\frac{ma}{(x_{3}+a)^{2}}- \frac{m}{x_{3}+a}+bcx_{3}, \\& \operatorname{Tr}[J_{E_{3}}]=-2x_{3}-\frac{ma}{(x_{3}+a)^{2}}-bu_{3}< 0. \end{aligned}$$

Obviously \(\operatorname{Det}[J_{E_{3}}]=0\), then \(J_{E_{3}}\) has a unique zero eigenvalue, named \(\lambda _{1}\).

Let V and W be two eigenvectors respectively corresponding to the eigenvalue \(\lambda _{1}\) for the matrices \(J(E_{3})\) and \(J(E_{3})^{T}\). After simple calculation, we have

$$ V={ \begin{pmatrix} V_{1} \\ V_{2} \end{pmatrix}}={ \begin{pmatrix} 1 \\ c \end{pmatrix}}, \qquad W={ \begin{pmatrix} W_{1} \\ W_{2} \end{pmatrix}}={ \begin{pmatrix} 1 \\ \frac{-b(1-a-abc)}{2(1+bc)} \end{pmatrix}}. $$

Moreover,

$$\begin{aligned}& F_{m}(E_{3};m_{\mathrm{SN}})={ \begin{pmatrix} \frac{1-a-abc}{1+a+abc} \\ 0 \end{pmatrix}} , \\& \begin{aligned} D^{2}F(E_{3};m_{\mathrm{SN}}) (V,V)&={ \begin{pmatrix} \frac{\partial ^{2}F_{1}}{\partial x^{2}}V_{1}^{2}+2 \frac{\partial ^{2}F_{1}}{\partial x \partial u}V_{1}V_{2}+ \frac{\partial ^{2}F_{1}}{\partial u^{2}}V_{2}^{2} \\ \frac{\partial ^{2}F_{2}}{\partial x^{2}}V_{1}^{2}+2 \frac{\partial ^{2}F_{2}}{\partial x \partial u}V_{1}V_{2}+ \frac{\partial ^{2}F_{2}}{\partial u^{2}}V_{2}^{2} \end{pmatrix}_{(E_{3};m_{\mathrm{SN}})}} \\ &={ \begin{pmatrix} \frac{2(1+bc)(a+abc-1)}{1+a+abc} \\ 0 \end{pmatrix}}. \end{aligned} \end{aligned}$$

Here \(F_{1}=x(1-x-\frac{m}{x+a})-bxu\) and \(F_{2}=-u+cx\). One could easily see that V and W satisfy the transversality condition

$$ \begin{aligned} &W^{T}F_{m}(E_{3};m_{\mathrm{SN}})= \frac{1-a-abc}{1+a+abc}\neq0, \\ &W^{T}\bigl[D^{2}F(E_{3};m_{\mathrm{SN}}) (V,V) \bigr]=\frac{2(1+bc)(a+abc-1)}{1+a+abc} \neq0, \end{aligned} $$

which means that the saddle-node bifurcation occurs at \(E_{3}\) when \(m=m_{\mathrm{SN}}\). Thus we complete the proof. □

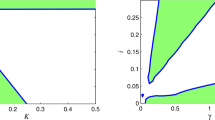
As was mentioned before, the number of interior equilibria of system (1.6) changes from zero to two when m passes from one side of \(m=m_{\mathrm{SN}}\) to the other side. For \(a= 0.5\), \(b = 1\), \(c = 0.25\), we get \(m _{\mathrm{SN}} = 0.528125\). For \(m< m_{\mathrm{SN}}\), system (1.6) has two distinct interior equilibria \(E_{1}(x_{1}, u_{1} )\) and \(E_{2}(x_{2}, u_{2})\), which collided with each other if \(m=m_{\mathrm{SN}}\), and no interior equilibria if \(m>m_{\mathrm{SN}}\). The above result is shown in Fig. 4.

Figure 4
figure 4

The saddle-node bifurcation of system (1.6)

Full size image

3.2 Transcritical bifurcation

As was mentioned before, system (1.6) has a boundary equilibrium \(E_{0}\). Moreover, we find that \(E_{0}\) coincides with \(E_{1}\) when \(m=a\). And the stability of \(E_{0}\) changes when m varies from \(m< a\) to \(m>a\). Hence, the appearance or annihilation of equilibria may lead to the occurrence of transcritical bifurcation which exists when

$$ m=m_{\mathrm{TC}}\triangleq a. $$

We obtain the occurrence of transcritical bifurcation as follows.

Theorem 3.2

System (1.6) undergoes the transcritical bifurcation when\(m=m_{\mathrm{TC}}\).

Proof

We still use Sotomayor’s theorem in [38] to verify the occurrence of the transcritical bifurcation when \(m=a\). The Jacobian matrix at \(E_{0}\) is given by

$$ J_{E_{0}}= \begin{bmatrix} 0& 0 \\ c & -1 \end{bmatrix}. $$
(3.2)

Obviously \(J_{E_{0}}\) has a unique zero eigenvalue, named \(\lambda _{1}\).

Let V and W be two eigenvectors respectively corresponding to the eigenvalue \(\lambda _{1}\) for the matrices \(J(E_{0})\) and \(J(E_{0})^{T}\), after simple calculation, we have

$$ V={ \begin{pmatrix} V_{1} \\ V_{2} \end{pmatrix}}={ \begin{pmatrix} 1 \\ c \end{pmatrix}}, \qquad W={ \begin{pmatrix} W_{1} \\ W_{2} \end{pmatrix}}={ \begin{pmatrix} 1 \\ 0 \end{pmatrix}}. $$

Moreover,

$$\begin{aligned}& F_{m}(E_{0};m_{\mathrm{TC}})={ \begin{pmatrix} 0 \\ 0 \end{pmatrix}}, \\& DF_{m}(E_{0};m_{\mathrm{TC}})V={ \begin{pmatrix} -\frac{1}{a}&0 \\ 0&0 \end{pmatrix}_{(E_{0};m_{\mathrm{TC}})}} { \begin{pmatrix} 1 \\ c \end{pmatrix}}={ \begin{pmatrix} -\frac{1}{a} \\ 0 \end{pmatrix}}, \\& \begin{aligned} D^{2}F(E_{0};m_{\mathrm{TC}}) (V,V)&={ \begin{pmatrix} \frac{\partial ^{2}F_{1}}{\partial x^{2}}V_{1}^{2}+2 \frac{\partial ^{2}F_{1}}{\partial x \partial u}V_{1}V_{2}+ \frac{\partial ^{2}F_{1}}{\partial u^{2}}V_{2}^{2} \\ \frac{\partial ^{2}F_{2}}{\partial x^{2}}V_{1}^{2}+2 \frac{\partial ^{2}F_{2}}{\partial x \partial u}V_{1}V_{2}+ \frac{\partial ^{2}F_{2}}{\partial u^{2}}V_{2}^{2} \end{pmatrix}_{(E_{0};m_{\mathrm{TC}})}} \\ &={ \begin{pmatrix} \frac{2(1-a(bc+1))}{a} \\ 0 \end{pmatrix}}. \end{aligned} \end{aligned}$$

Therefore, V and W satisfy the transversality condition

$$ \begin{aligned} &W^{T}F_{m}(E_{0};m_{\mathrm{TC}})=0, \\ &W^{T}\bigl[DF_{m}(E_{0};m_{\mathrm{TC}})V \bigr]=-\frac{1}{a}\neq0, \\ &W^{T}\bigl[D^{2}F(E_{0};m_{\mathrm{TC}}) (V,V) \bigr]=\frac{2(1-a(bc+1))}{a}\neq0, \end{aligned} $$

which means that when \(m=a\), the transcritical bifurcation occurs at \(E_{0}\). This completes the proof of Theorem 3.2. □

The above result is shown in Fig. 5.

Figure 5
figure 5

The transcritical bifurcation of system (1.6)

Full size image

4 Conclusion

In this paper, different from [1] and [2], we have paid attention to the impact of the additive Allee effect and feedback control on the logistic model. We have obtained the dynamic behaviors under three different Allee effect cases, i.e., \(m< a\), \(m>a\), and \(m=a\).

For the case \(m< a\), besides a trivial equilibrium which is a saddle, system (1.6) also has a unique positive equilibrium which is globally asymptotically stable. The above is stated in Theorem 2.1 and Theorem 2.4. In other words, the additive Allee effect has no impact on the species if the Allee effect is weak. The obtained results coincide with those in [1] and [2].

For the case \(m>a\), the detailed results are divided into two cases. When \(a\geq \frac{1}{1+bc}\) or \(a< \frac{1}{1+bc}\), \(m>m^{*}\), system (1.6) has no positive equilibrium. If \(a<\frac{1}{1+bc}\) and \(a< m< m^{*}\), system (1.6) has a trivial equilibrium \(E_{0}\) and two positive equilibria \(E_{1}\) and \(E_{2}\). Here \(E_{0}\), \(E_{1}\) are stable nodes and \(E_{2}\) is a saddle. When \(a<\frac{1}{1+bc}\) and \(m=m^{*}\), system (1.6) has a unique positive equilibrium \(E_{3}\) which is an attracting saddle-node. All the above shows that whether the species can survive or not depends on the additive Allee effect constants m and a. The smaller these two parameters, the better the survival of the population. Furthermore, in Theorem 3.1 and Theorem 3.2, we have revealed that the system undergoes the saddle-node bifurcation around the equilibrium \(E_{3}\) and the transcritical bifurcation around \(E_{0}\).

For the critical case \(m=a\), if \(a<\frac{1}{1+bc}\), system (1.6) has a trivial equilibrium \(E_{0}\) which is a saddle-node and a unique positive equilibrium \(E_{2}\) which is globally asymptotically stable. However, if \(a\geq \frac{1}{1+bc}\), system (1.6) has no positive equilibrium, which is presented in Theorem 2.3 and Theorem 2.6. All the above shows that if \(m=a\), whether the species can survive or not depends on the feedback control constants b and c. The feedback control increases the species’ extinction probability.

To sum up, the obtained results have revealed that both the additive Allee effect and feedback control have a vital influence on the species’ permanence, extinction, and stability. In detail, the species can survive when the additive Allee effect is weak. However, when the additive Allee effect and feedback control is strong, the risk of extinction of the species will be greater. Especially, from Theorems 2.2–2.3 and Theorems 2.5–2.6, one can conclude that the feedback control strength also has a great effect on the dynamic behaviors. The above is completely different from the corresponding results in [1] and [2]. In fact, both [1] and [2] conclude that the feedback control variable cannot alter the species’ permanence or extinction. Interestingly, Theorems 2.2–2.3 and Theorems 2.5–2.6 tell us that not only the Allee effect but also feedback control can make system (1.6) become “unstable”. The main results in this paper are a good extension and supplement to those in [1] and [2].