Second-order numerical methods for the tempered fractional diffusion equations

Abstract

In this paper, a class of second-order tempered difference operators for the left and right Riemann–Liouville tempered fractional derivatives is constructed. And a class of second-order numerical methods is presented for solving the space tempered fractional diffusion equations, where the space tempered fractional derivatives are evaluated by the proposed tempered difference operators, and in the time direction is discreted by the Crank–Nicolson method. Numerical schemes are proved to be unconditionally stable and convergent with order $O(h^{2}+\tau ^{2})$. Numerical experiments demonstrate the effectiveness of the numerical schemes.

1 Introduction

In recent years, many fractional models [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18, 21, 22, 24,25,26,27] with (tempered) fractional derivatives have been widely applied in many fields of science and technology, a lot of research results have been obtained. Among them, Li and Deng [14] constructed a class of second-order tempered weighted and shifted Grünwald difference operators (abbr. TWSGD) for the Riemann–Liouville tempered fractional derivatives, and then a class of second-order numerical schemes was proposed for solving a two-sided space tempered fractional diffusion equation. Numerical schemes are unconditionally stable and convergent with order $O(h^{2}+\tau ^{2})$. Dehghan et al. [6] developed a high-order numerical scheme for the space-time tempered fractional diffusion-wave equation, the numerical scheme was proved to be unconditionally stable and convergent with order $O(h^{4}+\tau ^{2})$. Qu and Liang [18] used the Crank–Nicolson method and TWSGD method [14] to solve a class of variable-coefficient tempered fractional diffusion equations and proved that the numerical schemes are unconditionally stable and convergent with order $O(h^{2}+\tau ^{2})$. Yu et al. [24] extended quasi-compact discretizations to Riemann–Liouville tempered fractional derivatives and derived the numerical scheme for solving a tempered fractional diffusion equation. Yu et al. [25] constructed a numerical scheme for one-sided space tempered fractional diffusion equation, and the numerical scheme was shown to be stable and convergent with order $O(h^{3}+\tau )$. Çelik and Duman [2] solved the symmetric space tempered fractional diffusion equation by the finite element method and achieved convergence order $O(h^{2}+\tau ^{2})$. Zhang et al. [27] proposed a modified second-order Lubich tempered difference operator for the Riemann–Liouville tempered fractional derivatives and constructed a numerical scheme for solving the normalized Riesz space tempered fractional diffusion equation. The stability and convergence of the numerical scheme have been proved. Hu and Cao [12] combined the implicit midpoint method and the modified second-order Lubich tempered difference operator to derive a numerical scheme for solving the normalized Riesz space tempered fractional diffusion equation with a nonlinear source term and discussed the stability and convergence of the numerical scheme.

In this paper, we consider the following space tempered fractional diffusion equation [14]:

$$ \textstyle\begin{cases} \frac{{\partial }u(x,t)}{\partial t}=l\frac{{\partial }^{\alpha , \lambda }_{-}u(x,t)}{\partial x^{\alpha }}+r\frac{{\partial }^{\alpha ,\lambda }_{+}u(x,t)}{\partial x^{\alpha }}+f(x,t), &(x,t)\in (a,b)\times (0,T], \\ u(x,0)=\varphi (x), &x\in [a,b], \\ u(a,t)=\psi _{l}(t),\qquad u(b,t)=\psi _{r}(t), &t\in [0,T], \end{cases} $$

(1)

where $1<\alpha <2$ and $\lambda \geq 0$, $f(x,t)$ is the linear source term, diffusion coefficients l and r are nonnegative constants with $l+r\neq 0$, and if $l\neq 0$, then $\psi _{l}(t)\equiv 0$, if $r \neq 0$, then $\psi _{r}(t)\equiv 0$. The normalized left and right Riemann–Liouville tempered fractional derivatives $\frac{{\partial } ^{\alpha ,\lambda }_{-}u(x,t)}{\partial x^{\alpha }}$ and $\frac{ {\partial }^{\alpha ,\lambda }_{+}u(x,t)}{\partial x^{\alpha }}$ are defined as follows [1, 14]:

$$\begin{aligned}& \frac{{\partial }^{\alpha ,\lambda }_{-}u(x,t)}{\partial x^{\alpha }}= {}_{a}D^{\alpha ,\lambda }_{x}u(x,t)- \lambda ^{\alpha }u(x,t)-\alpha \lambda ^{\alpha -1}\frac{{\partial }u(x,t)}{\partial x}, \\& \frac{{\partial }^{\alpha ,\lambda }_{+}u(x,t)}{\partial x^{\alpha }}= {}_{x}D^{\alpha ,\lambda }_{b}u(x,t)- \lambda ^{\alpha }u(x,t)+\alpha \lambda ^{\alpha -1}\frac{{\partial }u(x,t)}{\partial x}, \end{aligned}$$

here the left and right Riemann–Liouville tempered fractional derivatives ${}_{a}D^{\alpha ,\lambda }_{x}u(x,t)$ and ${}_{x}D^{\alpha , \lambda }_{b}u(x,t)$ are defined by

$$\begin{aligned}& {}_{a}D^{\alpha ,\lambda }_{x}u(x,t)=\frac{e^{-\lambda x}}{\varGamma (2- \alpha )} \frac{\partial ^{2}}{\partial x^{2}}\biggl( \int _{a}^{x}\frac{e^{ \lambda \tau }u(\tau ,t)}{(x-\tau )^{\alpha -1}}\,d\tau \biggr), \\& {}_{x}D^{\alpha ,\lambda }_{b}u(x,t)=\frac{e^{\lambda x}}{\varGamma (2- \alpha )} \frac{\partial ^{2}}{\partial x^{2}}\biggl( \int _{x}^{b}\frac{e^{- \lambda \tau }u(\tau ,t)}{(\tau -x)^{\alpha -1}}\,d\tau \biggr), \end{aligned}$$

where $\varGamma (\cdot )$ is the gamma function.

Obviously, when $\lambda = 0$, the left and right Riemann–Liouville tempered fractional derivatives degenerate to the left and right Riemann–Liouville fractional derivatives, respectively. When $l=r=-\frac{1}{2\cos (\frac{\alpha \pi }{2})}$, the two-sided tempered fractional diffusion equation degenerates to the normalized Riesz tempered fractional diffusion equation.

Considering these existing works in the literature, the aim of this paper is to try to give a class of new second-order tempered difference operators; then, using the Crank–Nicolson method and the proposed difference operators, to construct a class of second-order numerical methods for solving problem (1) and give the theoretical analysis of the numerical methods.

The outline of this paper is arranged as follows. In Sect. 2, new second-order tempered difference operators are introduced. In Sect. 3, numerical schemes for problem (1) are derived. In Sect. 4, the stability and convergence of the numerical schemes are obtained. In Sect. 5, some numerical examples are given to verify the theoretical results. In Sect. 6, we summarize the work of this paper.

2 Second-order tempered difference operators

In this section, we first introduce a fractional Sobolev space $S_{\lambda }^{n+\alpha }(\mathbb{R})$ defined as follows [27]:

$$ S_{\lambda }^{n+\alpha }(\mathbb{R})=\biggl\{ \nu \Bigm| \nu \in L_{1}( \mathbb{R}),\mbox{and } \int _{\mathbb{R}}\bigl(\lambda ^{2}+w^{2} \bigr)^{\frac{n+\alpha }{2}} \bigl\vert \hat{\nu }(w) \bigr\vert \,dw< \infty\biggr\} , $$

(2)

where ${\hat{\nu }}(w)=\int _{\mathbb{R}}\nu (x)e^{-iwx}\,dx$ is the Fourier transform of $\nu (x)$.

Lemma 2.1

([27])

Let $\nu (x) \in L_{1}(\mathbb{R})$, $1<\alpha <2$, and $\lambda \geq 0$. Then the Fourier transforms of the left and right Riemann–Liouville tempered fractional derivatives are

$$ \mathcal{F}\bigl[{}_{-\infty }D^{\alpha ,\lambda }_{x}\nu \bigr](w)=( \lambda +iw)^{ \alpha }\hat{\nu }(w) $$

and

$$ \mathcal{F}\bigl[{}_{x}D^{\alpha ,\lambda }_{+\infty }\nu \bigr](w)=( \lambda -iw)^{ \alpha }\hat{\nu }(w). $$

Lemma 2.2

([1, 14])

Let $1<\alpha <2$, $\lambda \geq 0$, the shift numberpis an integer, his the step size, $\nu (x)$is defined on the bounded interval $[a, b]$and belongs to $S_{\lambda }^{2+\alpha }(\mathbb{R})$after zero extension on the interval $x\in (-\infty ,a)\cup (b,+\infty )$. The shifted Grünwald type difference operators are defined as follows:

$$\begin{aligned} &A_{h,p}^{\alpha ,\lambda }\nu (x)=\frac{1}{h^{\alpha }}\sum _{k=0} ^{[\frac{x-a}{h}]+p}w_{k}^{\alpha }e^{-(k-p)\lambda h} \nu \bigl(x-(k-p)h\bigr)-\frac{1}{h ^{\alpha }}G_{p}(1)\nu (x), \end{aligned}$$

(3)

$$\begin{aligned} &\hat{A}_{h,p}^{\alpha ,\lambda }\nu (x)=\frac{1}{h^{\alpha }}\sum _{k=0}^{[\frac{b-x}{h}]+p}w_{k}^{\alpha }e^{-(k-p)\lambda h} \nu \bigl(x+(k-p)h\bigr)-\frac{1}{h ^{\alpha }}G_{p}(1)\nu (x), \end{aligned}$$

(4)

then

$$\begin{aligned}& A_{h,p}^{\alpha ,\lambda }\nu (x)={}_{a}D^{\alpha ,\lambda }_{x} \nu (x)-\lambda ^{\alpha }\nu (x)+O(h), \end{aligned}$$

(5)

$$\begin{aligned}& \hat{A}_{h,p}^{\alpha ,\lambda }\nu (x)={}_{x}D^{\alpha ,\lambda } _{b}\nu (x)-\lambda ^{\alpha }\nu (x)+O(h), \end{aligned}$$

(6)

where $w_{k}^{\alpha }=(-1)^{k}(_{k}^{\alpha })$ ($k\geq 0$) denotes the normalized Grünwald weights,

$$ G_{p}(s)=e^{p\lambda h}\bigl(1-e^{-\lambda h}s \bigr)^{\alpha }=\sum_{k=0}^{+ \infty }w_{k}^{\alpha }e^{-(k-p)\lambda h}s^{k}. $$

Meanwhile, denote

$$ W_{p}(s)=e^{ps}\biggl(\frac{1-e^{-s}}{s} \biggr)^{\alpha }=1+\biggl(p-\frac{\alpha }{2}\biggr)s+\biggl( \frac{p ^{2}}{2}-\frac{p\alpha }{2}+\frac{\alpha }{6}+ \frac{\alpha (\alpha -1)}{8} \biggr)s^{2}+O\bigl( \vert s \vert ^{3}\bigr) $$

with $s=(\lambda+iw)h$, $(\lambda-iw)h$, orλh, $i^{2}=-1$.

Lemma 2.3

Let $1<\alpha <2$, $\lambda \geq 0$, the shift numberpis an integer, his the step size, $\nu (x)$is defined on the bounded interval $[a, b]$and belongs to $S_{\lambda }^{2+\alpha }(\mathbb{R})$after zero extension on the interval $x\in (-\infty ,a)\cup (b,+\infty )$. The new difference operators are presented by

$$\begin{aligned} &B_{h,p}^{\alpha ,\lambda }\nu (x)=\frac{1}{h^{\alpha }}\sum _{k=0} ^{[\frac{x-a}{h}]+p}\hat{w}_{k}^{\alpha }e^{-(k-p)\lambda h} \nu \bigl(x-(k-p)h\bigr)-\frac{1}{h ^{\alpha }}\hat{G}_{p}(1)\nu (x), \end{aligned}$$

(7)

$$\begin{aligned} &\hat{B}_{h,p}^{\alpha ,\lambda }\nu (x)=\frac{1}{h^{\alpha }}\sum _{k=0}^{[\frac{b-x}{h}]+p}\hat{w}_{k}^{\alpha }e^{-(k-p)\lambda h} \nu \bigl(x+(k-p)h\bigr)-\frac{1}{h^{\alpha }}\hat{G}_{p}(1)\nu (x), \end{aligned}$$

(8)

then

$$\begin{aligned}& B_{h,p}^{\alpha ,\lambda }\nu (x)={}_{a}D^{\alpha ,\lambda }_{x} \nu (x)-\lambda ^{\alpha }\nu (x)+O(h), \end{aligned}$$

(9)

$$\begin{aligned}& \hat{B}_{h,p}^{\alpha ,\lambda }\nu (x)={}_{x}D^{\alpha ,\lambda } _{b}\nu (x)-\lambda ^{\alpha }\nu (x)+O(h), \end{aligned}$$

(10)

where

$$\begin{aligned}& \hat{w}_{k}^{\alpha }=\biggl(\frac{1}{2} \biggr)^{\alpha } \sum_{m=0} ^{k}(-1)^{m}w_{m}^{\alpha }w_{k-m}^{\alpha },\quad k\geq 0, \\& \hat{G}_{p}(s)=e^{p\lambda h}\biggl(\frac{1-e^{-2\lambda h}s^{2}}{2} \biggr)^{ \alpha }=\sum_{k=0}^{+\infty } \hat{w}_{k}^{\alpha }e^{-(k-p)\lambda h}s ^{k}. \end{aligned}$$

Proof

Taking the Fourier transform on both sides of (7) and (8), we obtain

$$\begin{aligned} \mathcal{F}\bigl[B_{h,p}^{\alpha ,\lambda }\nu \bigr](w) &= \frac{1}{h^{\alpha }} \sum_{k=0}^{+\infty } \hat{w}_{k}^{\alpha }e^{-(k-p)(\lambda +iw) h} \hat{\nu }(w)- \frac{1}{h^{\alpha }}\biggl(e^{p\lambda h}\biggl(\frac{1-e^{-2 \lambda h}}{2} \biggr)^{\alpha }\biggr)\hat{\nu }(w) \\ &=e^{ph(\lambda +iw)}\biggl(\frac{1-e^{-2(\lambda +iw) h}}{2h}\biggr)^{\alpha } \hat{\nu }(w)-e^{ph\lambda }\biggl(\frac{1-e^{-2\lambda h}}{2h}\biggr)^{\alpha } \hat{\nu }(w) \\ &=\bigl[(\lambda +iw)^{\alpha }\hat{W}_{p}\bigl((\lambda +iw)h \bigr)-\lambda ^{ \alpha }\hat{W}_{p}(\lambda h)\bigr]\hat{\nu }(w), \end{aligned}$$

where $\hat{W}_{p}(s)=e^{ps}(\frac{1-e^{-2s}}{2s})^{\alpha }=1+(p- \alpha )s+(\frac{p^{2}}{2}-p\alpha +\frac{2}{3}\alpha +\frac{\alpha ( \alpha -1)}{2})s^{2}+O(|s|^{3})$ with $s=(\lambda +iw)h$ or λh, $i^{2}=-1$.

$$\begin{aligned} \mathcal{F}\bigl[\hat{B}_{h,p}^{\alpha ,\lambda }\nu \bigr](w) &= \frac{1}{h^{ \alpha }}\sum_{k=0}^{+\infty } \hat{w}_{k}^{\alpha }e^{-(k-p)(\lambda -iw) h}\hat{\nu }(w)- \frac{1}{h^{\alpha }}\biggl(e^{p\lambda h}\biggl(\frac{1-e ^{-2\lambda h}}{2} \biggr)^{\alpha }\biggr)\hat{\nu }(w) \\ &=e^{ph(\lambda -iw)}\biggl(\frac{1-e^{-2(\lambda -iw) h}}{2h}\biggr)^{\alpha } \hat{\nu }(w)-e^{ph\lambda }\biggl(\frac{1-e^{-2\lambda h}}{2h}\biggr)^{\alpha } \hat{\nu }(w) \\ &=\bigl[(\lambda -iw)^{\alpha }\hat{W}_{p}\bigl((\lambda -iw)h \bigr)-\lambda ^{ \alpha }\hat{W}_{p}(\lambda h)\bigr]\hat{\nu }(w), \end{aligned}$$

where $\hat{W}_{p}(s)$ with $s=(\lambda -iw)h$ or λh, $i^{2}=-1$.

Denote

$$\begin{aligned}& \begin{aligned} \phi (w) &=\mathcal{F}\bigl[B_{h,p}^{\alpha ,\lambda }\nu \bigr](w)- \mathcal{F}\bigl[_{- \infty }D^{\alpha ,\lambda }_{x}\nu -\lambda ^{\alpha }\nu \bigr](w) \\ &=\bigl[(\lambda +iw)^{\alpha }\bigl(\hat{W}_{p}\bigl((\lambda +iw)h\bigr)-1\bigr)- \lambda ^{\alpha }\bigl(\hat{W}_{p}(\lambda h)-1\bigr)\bigr]\hat{\nu }(w), \end{aligned} \\& \begin{aligned} \hat{\phi }(w) &=\mathcal{F}\bigl[\hat{B}_{h,p}^{\alpha ,\lambda }\nu \bigr](w)- \mathcal{F}\bigl[{}_{x}D^{\alpha ,\lambda }_{+\infty }\nu - \lambda ^{\alpha } \nu \bigr](w) \\ &=\bigl[(\lambda -iw)^{\alpha }\bigl(\hat{W}_{p}\bigl((\lambda -iw)h\bigr)-1\bigr)- \lambda ^{\alpha }\bigl(\hat{W}_{p}(\lambda h)-1\bigr)\bigr]\hat{\nu }(w), \end{aligned} \end{aligned}$$

and there exist two positive constants C and Ĉ such that

$$\begin{aligned}& \bigl\vert \phi (w) \bigr\vert \leq C\bigl[h \vert \lambda +iw \vert ^{\alpha +1}+h \vert \lambda \vert ^{\alpha +1}\bigr] \bigl\vert \hat{\nu }(w) \bigr\vert , \\& \bigl\vert \hat{\phi }(w) \bigr\vert \leq \hat{C}\bigl[h \vert \lambda -iw \vert ^{\alpha +1}+h \vert \lambda \vert ^{ \alpha +1}\bigr] \bigl\vert \hat{\nu }(w) \bigr\vert . \end{aligned}$$

Taking the inverse Fourier transform of $\phi (w)$ and utilizing known conditions $\nu (x)\in S_{\lambda }^{2+\alpha }(\mathbb{R})$, we can obtain

$$\begin{aligned} \bigl\vert B_{h,p}^{\alpha ,\lambda }\nu (x)-{_{-\infty }}D^{\alpha ,\lambda } _{x}\nu (x)+\lambda ^{\alpha }\nu (x) \bigr\vert &\leq \frac{1}{2\pi } \int _{ \mathbb{R}} \bigl\vert \phi (w) \bigr\vert \,dw \\ &\leq Ch \int _{\mathbb{R}}\bigl( \vert \lambda +iw \vert ^{ \alpha +1}+ \vert \lambda \vert ^{\alpha +1}\bigr) \bigl\vert \hat{\nu }(w) \bigr\vert \,dw=O(h). \end{aligned}$$

Similar provability

$$\begin{aligned} \bigl\vert \hat{B}_{h,p}^{\alpha ,\lambda }\nu (x){-{}_{x}}D^{\alpha ,\lambda } _{+\infty }\nu (x)+\lambda ^{\alpha }\nu (x) \bigr\vert &\leq \frac{1}{2\pi } \int _{\mathbb{R}} \bigl\vert \hat{\phi }(w) \bigr\vert \,dw \\ &\leq \hat{C}h \int _{\mathbb{R}}\bigl( \vert \lambda -iw \vert ^{\alpha +1}+ \vert \lambda \vert ^{\alpha +1}\bigr) \bigl\vert \hat{\nu }(w) \bigr\vert \,dw=O(h). \end{aligned}$$

The proof is completed. □

Lemma 2.4

Let $1<\alpha <2$, $\lambda \geq 0$, his the step size, $\nu (x)$is defined on the bounded interval $[a, b]$and belongs to $S_{\lambda }^{2+\alpha }(\mathbb{R})$after zero extension on the interval $x\in (-\infty ,a)\cup (b,+\infty )$. The new second-order tempered difference operators are given as follows:

$$\begin{aligned}& C_{h}^{\alpha ,\lambda }\nu (x) =\gamma _{1}A_{h,1}^{\alpha ,\lambda } \nu (x)+\gamma _{2}B_{h,1}^{\alpha ,\lambda }\nu (x)+\gamma _{3}B_{h,-1} ^{\alpha ,\lambda }\nu (x) \\& \hphantom{C_{h}^{\alpha ,\lambda }\nu (x) }=\frac{1}{h^{\alpha }}\sum_{k=0}^{[\frac{x-a}{h}]+1}\bigl( \gamma _{1}w _{k}^{\alpha }+\gamma _{2} \hat{w}_{k}^{\alpha }+\gamma _{3}\hat{w}_{k-2} ^{\alpha }\bigr) e^{-(k-1)\lambda h}\nu \bigl(x-(k-1)h\bigr) \\& \hphantom{C_{h}^{\alpha ,\lambda }\nu (x) ={}}{}-\frac{1}{h^{\alpha }}\biggl(\gamma _{1}e^{\lambda h} \bigl(1-e^{-\lambda h}\bigr)^{ \alpha }+\gamma _{2}e^{\lambda h} \biggl(\frac{1-e^{-2\lambda h}}{2}\biggr)^{\alpha} \\& \hphantom{C_{h}^{\alpha ,\lambda }\nu (x) ={}} {}+\gamma _{3}e^{-\lambda h}\biggl(\frac{1-e^{-2\lambda h}}{2} \biggr)^{\alpha }\biggr) \nu (x) \\& \hphantom{C_{h}^{\alpha ,\lambda }\nu (x)}=\frac{1}{h^{\alpha }}\sum_{k=0}^{[\frac{x-a}{h}]+1} g_{k}^{\alpha }\nu \bigl(x-(k-1)h\bigr)-\frac{1}{h^{\alpha }} \tilde{G}_{1}(1)\nu (x), \end{aligned}$$

(11)

$$\begin{aligned}& \hat{C}_{h}^{\alpha ,\lambda }\nu (x) =\gamma _{1}\hat{A}_{h,1}^{ \alpha ,\lambda }\nu (x)+\gamma _{2}\hat{B}_{h,1}^{\alpha ,\lambda } \nu (x)+\gamma _{3} \hat{B}_{h,-1}^{\alpha ,\lambda }\nu (x) \\& \hphantom{\hat{C}_{h}^{\alpha ,\lambda }\nu (x)}=\frac{1}{h^{\alpha }}\sum_{k=0}^{[\frac{b-x}{h}]+1}\bigl( \gamma _{1}w _{k}^{\alpha }+\gamma _{2} \hat{w}_{k}^{\alpha }+\gamma _{3}\hat{w}_{k} ^{\alpha }\bigr) e^{-(k-1)\lambda h}\nu \bigl(x+(k-1)h\bigr) \\& \hphantom{\hat{C}_{h}^{\alpha ,\lambda }\nu (x)={}} {}-\frac{1}{h^{\alpha }}\biggl(\gamma _{1}e^{\lambda h} \bigl(1-e^{-\lambda h}\bigr)^{ \alpha }+\gamma _{2}e^{\lambda h} \biggl(\frac{1-e^{-2\lambda h}}{2}\biggr)^{\alpha} \\& \hphantom{\hat{C}_{h}^{\alpha ,\lambda }\nu (x)={}} {}+\gamma _{3}e^{-\lambda h}\biggl(\frac{1-e^{-2\lambda h}}{2} \biggr)^{\alpha }\biggr) \nu (x) \\& \hphantom{\hat{C}_{h}^{\alpha ,\lambda }\nu (x)}=\frac{1}{h^{\alpha }}\sum_{k=0}^{[\frac{b-x}{h}]+1} g_{k}^{\alpha }\nu \bigl(x+(k-1)h\bigr)-\frac{1}{h^{\alpha }} \tilde{G}_{1}(1)\nu (x), \end{aligned}$$

(12)

then

$$\begin{aligned}& C_{h}^{\alpha ,\lambda }\nu (x)={}_{a}D^{\alpha ,\lambda }_{x} \nu (x)- \lambda ^{\alpha }\nu (x)+O\bigl(h^{2}\bigr), \end{aligned}$$

(13)

$$\begin{aligned}& \hat{C}_{h}^{\alpha ,\lambda }\nu (x)={}_{x}D^{\alpha ,\lambda }_{b} \nu (x)-\lambda ^{\alpha }\nu (x)+O\bigl(h^{2}\bigr), \end{aligned}$$

(14)

where

$$\begin{aligned}& g_{k}^{\alpha }=\bigl(\gamma _{1}w_{k}^{\alpha }+ \gamma _{2}\hat{w}_{k}^{ \alpha }+\gamma _{3} \hat{w}_{k-2}^{\alpha }\bigr) e^{-(k-1)\lambda h},\quad k \geq 0\ \bigl( \hat{w}_{-1}^{\alpha },\hat{w}_{-2}^{\alpha }=0 \bigr), \\& \tilde{G}_{1}(1)=\gamma _{1}G_{1}(1)+\gamma _{2}\hat{G}_{1}(1)+\gamma _{3} \hat{G}_{-1}(1), \\& \gamma _{1}=\frac{2\alpha -2}{\alpha }+\frac{4}{\alpha }\gamma _{3}, \qquad \gamma _{2}=\frac{2-\alpha }{\alpha }-\frac{4+\alpha }{\alpha }\gamma_{3}. \end{aligned}$$

Proof

Taking the Fourier transform on both sides of (11) and (12), we obtain

$$\begin{aligned} \mathcal{F}\bigl[C_{h}^{\alpha ,\lambda }\nu \bigr](w) =&\gamma _{1}\mathcal{F}\bigl[A _{h,1}^{\alpha ,\lambda }\nu \bigr](w)+ \gamma _{2}\mathcal{F}\bigl[B_{h,1}^{ \alpha ,\lambda }\nu \bigr](w)++\gamma _{3}\mathcal{F}\bigl[B_{h,-1}^{\alpha , \lambda } \nu \bigr](w) \\ =&\frac{1}{h^{\alpha }}\sum_{k=0}^{+\infty }\bigl( \gamma _{1}w_{k}^{\alpha }+\gamma _{2} \hat{w}_{k}^{\alpha }+\gamma _{3}\hat{w}_{k-2}^{\alpha } \bigr)e ^{-(k-1)(\lambda +iw) h}\hat{\nu }(w) \\ &{}-\frac{1}{h^{\alpha }}\biggl(\gamma _{1}e^{\lambda h} \bigl(1-e^{-\lambda h}\bigr)^{ \alpha }+\gamma _{2}e^{\lambda h} \biggl(\frac{1-e^{-2\lambda h}}{2}\biggr)^{\alpha} \\ &{}+\gamma _{3}e^{-\lambda h}\biggl(\frac{1-e^{-2\lambda h}}{2} \biggr)^{\alpha }\biggr) \hat{\nu }(w) \\ =&e^{h(\lambda +iw)}\biggl(\gamma _{1}\biggl(\frac{1-e^{-(\lambda +iw)h}}{h} \biggr)^{ \alpha }+\gamma _{2}\biggl(\frac{1-e^{-2(\lambda +iw) h}}{2h} \biggr)^{\alpha }\biggr) \hat{\nu }(w) \\ &{}+\gamma _{3}e^{-h(\lambda +iw)}\biggl(\frac{1-e^{-2(\lambda +iw) h}}{2h} \biggr)^{ \alpha }\hat{\nu }(w) -\biggl(\gamma _{1}e^{\lambda h} \biggl( \frac{1-e^{-\lambda h}}{h}\biggr)^{\alpha } \\ &{}+\gamma _{2}e^{\lambda h}\biggl(\frac{1-e^{-2\lambda h}}{2h} \biggr)^{\alpha }+ \gamma _{3}e^{-\lambda h}\biggl( \frac{1-e^{-2\lambda h}}{2h}\biggr)^{\alpha }\biggr) \hat{\nu }(w) \\ =&\bigl[(\lambda +iw)^{\alpha }\tilde{W}\bigl((\lambda +iw)h\bigr)-\lambda ^{\alpha }\tilde{W}(\lambda h)\bigr]\hat{\nu }(w), \end{aligned}$$

where

$$\begin{aligned} \tilde{W}(s)&=\gamma _{1}W_{1}(s)+\gamma _{2}\hat{W}_{1}(s)+\gamma _{3} \hat{W}_{-1}(s) \\ &=\gamma _{1}+\gamma _{2}+\gamma _{3}+\biggl[\gamma _{1}\biggl(1-\frac{ \alpha }{2}\biggr)+\gamma _{2}(1-\alpha )+\gamma _{3}(-1-\alpha )\biggr]s+O\bigl(\vert s\vert ^{2}\bigr) \end{aligned}$$

with $s=(\lambda +iw)h$ or λh, $i^{2}=-1$.

$$\begin{aligned} \mathcal{F}\bigl[\hat{C}_{h}^{\alpha ,\lambda }\nu \bigr](w) =&\gamma _{1} \mathcal{F}\bigl[\hat{A}_{h,1}^{\alpha ,\lambda }\nu \bigr](w)+\gamma _{2} \mathcal{F}\bigl[\hat{B}_{h,1}^{\alpha ,\lambda } \nu \bigr](w)+\gamma _{3} \mathcal{F}\bigl[\hat{B}_{h,-1}^{\alpha ,\lambda } \nu \bigr](w) \\ =&\frac{1}{h^{\alpha }}\sum_{k=0}^{+\infty }\bigl( \gamma _{1}w_{k}^{\alpha }+\gamma _{2} \hat{w}_{k}^{\alpha }+\gamma _{3}\hat{w}_{k-2}^{\alpha } \bigr)e ^{-(k-1)(\lambda -iw) h}\hat{\nu }(w) \\ &{}-\frac{1}{h^{\alpha }}\biggl(\gamma _{1}e^{\lambda h} \bigl(1-e^{-\lambda h}\bigr)^{ \alpha }+\gamma _{2}e^{\lambda h} \biggl(\frac{1-e^{-2\lambda h}}{2}\biggr)^{\alpha} \\ &{}+\gamma _{3}e^{-\lambda h}\biggl(\frac{1-e^{-2\lambda h}}{2} \biggr)^{\alpha }\biggr) \hat{\nu }(w) \\ =&e^{h(\lambda -iw)}\biggl(\gamma _{1}\biggl(\frac{1-e^{-(\lambda -iw)h}}{h} \biggr)^{ \alpha }+\gamma _{2}\biggl(\frac{1-e^{-2(\lambda -iw) h}}{2h} \biggr)^{\alpha }\biggr) \hat{\nu }(w) \\ &{}+\gamma _{3}e^{-h(\lambda -iw)}\biggl(\frac{1-e^{-2(\lambda -iw) h}}{2h} \biggr)^{ \alpha }\hat{\nu }(w) -\biggl(\gamma _{1}e^{\lambda h} \biggl( \frac{1-e^{-\lambda h}}{h}\biggr)^{\alpha } \\ &{}+\gamma _{2}e^{\lambda h}\biggl(\frac{1-e^{-2\lambda h}}{2h} \biggr)^{\alpha }+ \gamma _{3}e^{-\lambda h}\biggl( \frac{1-e^{-2\lambda h}}{2h}\biggr)^{\alpha }\biggr) \hat{\nu }(w) \\ =&\bigl[(\lambda -iw)^{\alpha }\tilde{W}\bigl((\lambda -iw)h\bigr)-\lambda ^{\alpha}\tilde{W}(\lambda h)\bigr]\hat{\nu }(w), \end{aligned}$$

where $\tilde{W}(s)$ with $s=(\lambda -iw)h$ or λh, $i^{2}=-1$.

And then making

$$ \textstyle\begin{cases} \gamma _{1}+\gamma _{2}+\gamma _{3}=1, \\ \gamma _{1}(1-\frac{\alpha }{2})+\gamma _{2}(1-\alpha )+\gamma _{3}(-1- \alpha )=0, \end{cases} $$

we get

$$ \gamma _{1}=\frac{2\alpha -2}{\alpha }+\frac{4}{\alpha }\gamma _{3},\qquad \gamma _{2}=\frac{2-\alpha }{\alpha }-\frac{4+\alpha }{\alpha }\gamma _{3}. $$

Denote

$$\begin{aligned}& \begin{aligned} \phi (w) &=\mathcal{F}\bigl[C_{h}^{\alpha ,\lambda }\nu \bigr](w)- \mathcal{F}\bigl[_{- \infty }D^{\alpha ,\lambda }_{x}\nu -\lambda ^{\alpha }\nu \bigr](w) \\ &=\bigl[(\lambda +iw)^{\alpha }\bigl(\tilde{W}\bigl((\lambda +iw)h\bigr)-1 \bigr)-\lambda ^{ \alpha }\bigl(\tilde{W}(\lambda h)-1\bigr)\bigr]\hat{\nu }(w), \end{aligned} \\& \begin{aligned} \hat{\phi }(w) &=\mathcal{F}\bigl[C_{h}^{\alpha ,\lambda }\nu \bigr](w)- \mathcal{F}\bigl[{}_{x}D^{\alpha ,\lambda }_{+\infty }\nu -\lambda ^{\alpha } \nu \bigr](w) \\ &=\bigl[(\lambda -iw)^{\alpha }\bigl(\tilde{W}\bigl((\lambda -iw)h\bigr)-1 \bigr)-\lambda ^{ \alpha }\bigl(\tilde{W}(\lambda h)-1\bigr)\bigr]\hat{\nu }(w), \end{aligned} \end{aligned}$$

and there exist two positive constants C and Ĉ such that

$$\begin{aligned}& \bigl\vert \phi (w) \bigr\vert \leq C\bigl[h^{2} \vert \lambda +iw \vert ^{\alpha +2}+h^{2} \vert \lambda \vert ^{\alpha +2}\bigr] \bigl\vert \hat{\nu }(w) \bigr\vert , \\& \bigl\vert \hat{\phi }(w) \bigr\vert \leq \hat{C}\bigl[h^{2} \vert \lambda -iw \vert ^{\alpha +2}+h^{2} \vert \lambda \vert ^{\alpha +2}\bigr] \bigl\vert \hat{\nu }(w) \bigr\vert . \end{aligned}$$

Taking the inverse Fourier transform of $\phi (w)$ and utilizing known conditions $\nu (x)\in S_{\lambda }^{2+\alpha }(\mathbb{R})$, we can obtain

$$\begin{aligned} \bigl\vert C_{h}^{\alpha ,\lambda }\nu (x)-{_{-\infty }}D^{\alpha ,\lambda } _{x}\nu (x)+\lambda ^{\alpha }\nu (x) \bigr\vert &\leq \frac{1}{2\pi } \int _{\mathbb{R}} \bigl\vert \phi (w) \bigr\vert \,dw \\ &\leq Ch^{2} \int _{\mathbb{R}}\bigl( \vert \lambda +iw \vert ^{\alpha +2}+ \vert \lambda \vert ^{ \alpha +2}\bigr) \bigl\vert \hat{\nu }(w) \bigr\vert \,dw \\ &=O\bigl(h^{2}\bigr). \end{aligned}$$

Similar provability

$$\begin{aligned} \bigl\vert \hat{C}_{h}^{\alpha ,\lambda }\nu (x)-{}_{x}D^{\alpha ,\lambda }_{+ \infty } \nu (x)+\lambda ^{\alpha }\nu (x) \bigr\vert &\leq \frac{1}{2\pi } \int _{\mathbb{R}} \bigl\vert \hat{\phi }(w) \bigr\vert \,dw \\ &\leq \hat{C}h^{2} \int _{\mathbb{R}}\bigl( \vert \lambda -iw \vert ^{\alpha +2}+ \vert \lambda \vert ^{\alpha +2}\bigr) \bigl\vert \hat{\nu }(w) \bigr\vert \,dw \\ &=O\bigl(h^{2}\bigr). \end{aligned}$$

The proof is completed. □

In this part, because of the selectivity of $\gamma _{3}$, a class of approximation operators with second-order accuracy for the Riemann–Liouville tempered fractional derivatives is given.

3 Numerical schemes

For the space interval $[a,b]$ and the time interval $[0,T]$, we choose the grid points $x_{i} = a+ih$, $0\leq i\leq N$, $t_{n} = n\tau$, $0\leq n\leq M$, where $h=(b-a)/N$ is the space stepsize, $\tau = T/M$ denotes the time stepsize. The exact solution and numerical solution at the point $(x_{i},t_{n})$ are denoted by $u_{i}^{n}=u(x_{i},t_{n})$ and $U_{i}^{n}$, respectively. Denoting $t_{n+1/2}=(t_{n}+t_{n+1})/2$, $f_{i}^{n}=f(x_{i},t_{n})$. In this paper, $u(x,\cdot )$ is defined on the bounded interval $[a, b]$ and $u(x,\cdot )$ belongs to $S_{\lambda }^{2+\alpha }(\mathbb{R})$ after zero extension on the interval $x\in (-\infty ,a)\cup (b,+\infty )$.

Using the Crank–Nicolson method to discrete time for problem (1) at point $(x_{i},t_{n})$, we get

$$\begin{aligned}& \frac{u_{i}^{n+1}-u_{i}^{n}}{\tau }=l\biggl(\frac{{\partial }^{\alpha , \lambda }_{-}u}{\partial x^{\alpha }}\biggr)_{i}^{n+1/2}+ r\biggl(\frac{{\partial }^{\alpha ,\lambda }_{+}u}{\partial x^{\alpha }}\biggr)_{i}^{n+1/2}+f_{i} ^{n+1/2}+O\bigl(\tau ^{2}\bigr), \\& \quad 1 \leq i\leq N-1, 0\leq n\leq M-1. \end{aligned}$$

(15)

From Lemma 2.4, we obtain

$$\begin{aligned} \frac{u_{i}^{n+1}-u_{i}^{n}}{\tau } =&l\bigl(C_{h}^{\alpha ,\lambda }u_{i} ^{n+1/2}-\alpha \lambda ^{\alpha -1}\delta _{x}u_{i}^{n+1/2} \bigr) \\ &{}+r\bigl(\hat{C}_{h}^{\alpha ,\lambda }u_{i}^{n+1/2}+ \alpha \lambda ^{\alpha -1}\delta _{x}u_{i}^{n+1/2} \bigr)+f_{i}^{n+1/2}+O\bigl(\tau ^{2}+h ^{2} \bigr), \end{aligned}$$

(16)

where $\delta _{x}u_{i}^{n}=\frac{u_{i+1}^{n}-u_{i-1}^{n}}{2h}$, $u_{i}^{n+1/2}=(u_{i}^{n}+u_{i}^{n+1})/2$.

Rearrange (16) to get

$$\begin{aligned} u_{i}^{n+1}-u_{i}^{n} =&\tau lC_{h}^{\alpha ,\lambda }u_{i}^{n+1/2}+ \tau r \hat{C}_{h}^{\alpha ,\lambda }u_{i}^{n+1/2} -\tau \alpha \lambda ^{\alpha -1}(l-r)\delta _{x}u_{i}^{n+1/2} \\ &{}+\tau f_{i}^{n+1/2}+O\bigl(\tau ^{3}+h^{2} \tau \bigr). \end{aligned}$$

(17)

Furthermore, (17) can be written as

$$\begin{aligned} u_{i}^{n+1}-u_{i}^{n} =&\tau l \frac{1}{h^{\alpha }}\sum_{k=0}^{i+1}g _{k}^{\alpha }u_{i-k+1}^{n+1/2}-\tau (l+r) \frac{1}{h^{\alpha }} \tilde{G}(1)u_{i}^{n+1/2} \\ &{}+\tau r\frac{1}{h^{\alpha }}\sum_{k=0}^{N-i+1}g_{k}^{\alpha }u_{i+k-1} ^{n+1/2}-\tau \alpha \lambda ^{\alpha -1}(l-r)\frac{u_{i+1}^{n+1/2}-u _{i-1}^{n+1/2}}{2h} \\ &{}+\tau f_{i}^{n+1/2}+O\bigl(\tau ^{3}+h^{2} \tau \bigr). \end{aligned}$$

(18)

Eliminating the local truncation error, we obtain the numerical scheme as follows:

$$\begin{aligned} U_{i}^{n+1}-U_{i}^{n} =&\tau l \frac{1}{h^{\alpha }}\sum_{k=0}^{i+1}g _{k}^{\alpha }U_{i-k+1}^{n+1/2}-\tau (l+r) \frac{1}{h^{\alpha }} \tilde{G}(1)U_{i}^{n+1/2} \\ &{}+\tau r\frac{1}{h^{\alpha }}\sum_{k=0}^{N-i+1}g_{k}^{\alpha }U_{i+k-1} ^{n+1/2}-\tau \alpha \lambda ^{\alpha -1}(l-r)\frac{U_{i+1}^{n+1/2}-U _{i-1}^{n+1/2}}{2h} \\ &{}+\tau f_{i}^{n+1/2}. \end{aligned}$$

(19)

That is,

$$\begin{aligned} U_{i}^{n+1} =&U_{i}^{n}+\tau l \frac{1}{h^{\alpha }}\sum_{k=0}^{i+1}g _{k}^{\alpha }\frac{U_{i-k+1}^{n}+U_{i-k+1}^{n+1}}{2} \\ &{}-\tau (l+r)\frac{1}{h^{\alpha }}\tilde{G}(1)\frac{U_{i}^{n}+U_{i} ^{n+1}}{2}+\tau r \frac{1}{h^{\alpha }}\sum_{k=0}^{N-i+1}g_{k}^{\alpha} \frac{U_{i+k-1}^{n}+U_{i+k-1}^{n+1}}{2} \\ &{}-\tau \alpha \lambda ^{\alpha -1}(l-r)\frac{U_{i+1}^{n+1}+U_{i+1} ^{n}-U_{i-1}^{n+1}-U_{i-1}^{n}}{4h}+\tau f_{i}^{n+1/2}. \end{aligned}$$

(20)

Furthermore, the matrix form of (20) can be written as follows:

$$\begin{aligned} \biggl(I-\frac{\tau (lA+rA^{T})}{2h^{\alpha }}+\frac{\tau \alpha \lambda ^{\alpha -1}(l-r)}{4h}B\biggr)U^{n+1} =& \biggl(I+\frac{\tau (lA+rA^{T})}{2h ^{\alpha }} \\ &{}-\frac{\tau \alpha \lambda ^{\alpha -1}(l-r)}{4h}B\biggr)U^{n} \\ &{}+\tau F^{n+1/2}, \end{aligned}$$

(21)

where $U^{n}=(U_{1}^{n},U_{2}^{n},\ldots,U_{N-2}^{n},U_{N-1}^{n})^{T}$, A is the following $(N-1)$ order Toeplitz matrix:

$$ A= \begin{pmatrix} g_{1}^{\alpha }-\tilde{G}_{1}(1)& g_{0}^{\alpha }& & & & \\ & & & & & \\ g_{2}^{\alpha }&g_{1}^{\alpha }-\tilde{G}_{1}(1)&g_{0}^{\alpha }& & & \\ & & & & & \\ \vdots &\vdots &\ddots &\ddots & & \\ & & & & & \\ \vdots &\vdots &\vdots &\ddots &\ddots & \\ & & & & & \\ g_{N-2}^{\alpha }&g_{N-3}^{\alpha }& g_{N-4}^{\alpha }&\cdots & g_{1}^{\alpha }-\tilde{G}_{1}(1) & g_{0}^{\alpha } \\ & & & & & \\ g_{N-1}^{\alpha }&g_{N-2}^{\alpha }& g_{N-3}^{\alpha } &\cdots & g_{2}^{\alpha } & g_{1}^{\alpha }-\tilde{G}_{1}(1) \end{pmatrix}, $$

(22)

and $B=\operatorname{tridiag}{\{-1,0,1\}}$ is $(N-1)$ order tridiagonal matrix, the term $F^{n+1/2}$ is given by

$$\begin{aligned} F^{n+1/2} =&\bigl(f_{1}^{n+1/2},f_{2}^{n+1/2}, \ldots,f_{N-2}^{n+1/2},f_{N-1} ^{n+1/2} \bigr)^{T} \\ &{}+\frac{U_{0}^{n+1/2}}{h^{\alpha }}\bigl(\lg _{2}^{\alpha }+rg_{0}^{\alpha }, \lg _{3}^{\alpha },\ldots,\lg _{N-1}^{\alpha },\lg _{N}^{\alpha }\bigr)^{T} \\ &{}+\frac{U_{N}^{n+1/2}}{h^{\alpha }}\bigl(rg_{N}^{\alpha },rg_{N-1}^{\alpha }, \ldots,rg_{3}^{\alpha },rg_{2}^{\alpha }+\lg _{0}^{\alpha }\bigr)^{T} \\ &{}-\frac{(l-r)\alpha \lambda ^{\alpha -1}}{2h}\bigl(-U_{0}^{n+1/2},0,\ldots,0,U _{N}^{n+1/2}\bigr)^{T}. \end{aligned}$$

4 Stability and convergence of the numerical schemes

In order to analyze the stability and convergence of the numerical schemes, we give some lemmas.

Lemma 4.1

([19])

A real matrixAof orderNis negative definite if and only if $D=\frac{A+A^{T}}{2}$is negative definite.

Lemma 4.2

For $1<\alpha <2$, $\lambda \geq 0$, $h>0$, if any one of the following three conditions is satisfied:

• (1) $\alpha \in (1,\frac{\sqrt{57}-5}{2}]$and $\frac{(2\alpha ^{2}-\alpha +2)(1-\alpha )}{5\alpha ^{2}+4}\leq \gamma _{3}\leq \frac{(2-\alpha )(\alpha -1)}{\alpha ^{2}+5\alpha -4}$;

• (2) $\alpha \in (\frac{\sqrt{57}-5}{2},\frac{\sqrt{73}-5}{2})$and $\max\{ \frac{(2\alpha ^{2}-\alpha +2)(1-\alpha )}{5\alpha ^{2}+4},\frac{(2-\alpha )^{2}}{8-\alpha ^{2}-5\alpha } \} \leq \gamma _{3}\leq \frac{(2-\alpha )(\alpha -1)}{\alpha ^{2}+5\alpha -4}$;

• (3) $\alpha \in [\frac{\sqrt{73}-5}{2},2)$and $\frac{(2-\alpha )^{2}}{8-\alpha ^{2}-5\alpha } \leq \gamma _{3}\leq \frac{(2-\alpha )(\alpha -1)}{\alpha ^{2}+5 \alpha -4}$,

then we have

$$ g_{1}^{\alpha }< 0, \qquad g_{0}^{\alpha }+g_{2}^{\alpha }>0,\qquad g_{k} ^{\alpha }>0,\quad k\geq 3. $$

(23)

Proof

It is easy to know from the expression of $w_{k}^{\alpha }$ that

$$ w_{0}^{\alpha }=1,\qquad w_{1}^{\alpha }=-\alpha ,\qquad w_{k}^{\alpha}>0,\quad k\geq 2. $$

(24)

Utilizing automatic differentiation techniques [20], and from the expression of $\hat{w}_{k}^{\alpha }$, we know

$$ \hat{w}_{0}^{\alpha }=\biggl(\frac{1}{2} \biggr)^{\alpha }, \qquad \hat{w}_{1}^{ \alpha }=0,\qquad \hat{w}_{k}^{\alpha }=\frac{1}{k}(k-2\alpha -2) \hat{w}_{k-2}^{\alpha }\quad (k\geq 2), $$

(25)

which leads to

$$ \hat{w}_{2}^{\alpha }< 0, \qquad \hat{w}_{k}^{\alpha }=0\quad (k \mbox{ is odd, and }k\geq 3),\qquad \hat{w}_{k}^{\alpha }>0\quad (k\mbox{ is even and }k\geq 4). $$

(26)

Note that

$$\begin{aligned}& g_{k}^{\alpha }=\biggl(\biggl(\frac{2\alpha -2}{\alpha }+ \frac{4}{\alpha }\gamma _{3} \biggr)w_{k}^{\alpha }+ \biggl(\frac{2-\alpha }{\alpha }-\frac{4+\alpha }{ \alpha }\gamma _{3}\biggr) \hat{w}_{k}^{\alpha } +\gamma _{3}\hat{w}_{k-2}^{ \alpha } \biggr)e^{-(k-1)\lambda h} \\& \quad \bigl(k\geq 0, \hat{w}_{-1}^{\alpha }, \hat{w}_{-2}^{\alpha } \bigr), \end{aligned}$$

then

$$\begin{aligned}& \begin{aligned}[b] g_{0}^{\alpha }+g_{2}^{\alpha } &=\biggl(\biggl( \frac{2\alpha -2}{\alpha }+\frac{4}{ \alpha }\gamma _{3} \biggr)w_{0}^{\alpha }+ \biggl(\frac{2-\alpha }{\alpha }-\frac{4+ \alpha }{\alpha }\gamma _{3}\biggr) \hat{w}_{0}^{\alpha }\biggr)e^{\lambda h} \\ &\quad {}+\biggl(\biggl(\frac{2\alpha -2}{\alpha }+\frac{4}{\alpha }\gamma _{3} \biggr)w_{2} ^{\alpha }+\biggl(\frac{2-\alpha }{\alpha }-\frac{4+\alpha }{\alpha } \gamma _{3}\biggr)\hat{w}_{2}^{\alpha }+\gamma _{3}\hat{w}_{0}^{\alpha }\biggr)e^{-\lambda h}, \end{aligned} \end{aligned}$$

(27)

$$\begin{aligned}& g_{k}^{\alpha }=\biggl(\frac{2\alpha -2}{\alpha }+\frac{4}{\alpha } \gamma _{3} \biggr)w_{k}^{\alpha }e^{-(k-1)\lambda h}\quad (k\mbox{ is odd and }k \geq 1), \end{aligned}$$

(28)

$$\begin{aligned}& \begin{aligned}[b] g_{k}^{\alpha } &=\biggl(\biggl(\frac{2\alpha -2}{\alpha }+ \frac{4}{\alpha }\gamma _{3} \biggr)w_{k}^{\alpha }+ \biggl(\biggl(\frac{2-\alpha }{\alpha }-\frac{4+\alpha }{ \alpha }\gamma _{3}\biggr) \frac{k-2\alpha -2}{k} \\ &\quad {}+\gamma _{3}\biggr)\hat{w}_{k-2}^{\alpha } \biggr)e^{-(k-1)\lambda h} \quad (k\mbox{ is even and }k\geq 4). \end{aligned} \end{aligned}$$

(29)

If $\gamma _{3}>\frac{1-\alpha }{2}$, then

$$ \frac{2\alpha -2}{\alpha }+\frac{4}{\alpha }\gamma _{3}>0. $$

(30)

Combining (24) and (30), we obtain from (28)

$$ g_{1}^{\alpha }< 0,\qquad g_{k}^{\alpha }>0\quad (k\mbox{ is odd and } k\geq 3). $$

If $\gamma _{3}\leq \frac{(2-\alpha )(\alpha -1)}{\alpha ^{2}+5\alpha -4}$, then we have

$$\begin{aligned}& \frac{2-\alpha }{\alpha }-\frac{4+\alpha }{\alpha }\gamma _{3}>0, \end{aligned}$$

(31)

$$\begin{aligned}& \biggl(\frac{2-\alpha }{\alpha }-\frac{4+\alpha }{\alpha }\gamma _{3}\biggr) \frac{4-2\alpha -2}{4}+\gamma _{3}\leq 0. \end{aligned}$$

(32)

Based on inequalities (30)–(32), and if $\frac{(2\alpha ^{2}-\alpha +2)(1-\alpha )}{5\alpha ^{2}+4}\leq \gamma _{3}\leq \frac{(2-\alpha )(\alpha -1)}{\alpha ^{2}+5\alpha -4}$, then we can get from (27)

$$\begin{aligned} g_{0}^{\alpha }+g_{2}^{\alpha } \geq& \biggl( \biggl(\frac{2\alpha -2}{\alpha }+\frac{4}{\alpha }\gamma _{3}\biggr) \frac{\alpha ^{2}-\alpha +2}{2} \\ &{} +\biggl(\frac{1}{2}\biggr)^{\alpha }\biggl(\biggl( \frac{2-\alpha }{\alpha }-\frac{4+\alpha }{\alpha }\gamma _{3}\biggr) (1-\alpha )+ \gamma _{3}\biggr)\biggr)e^{-\lambda h} \\ >&\biggl(\biggl(\frac{2\alpha -2}{\alpha }+\frac{4}{\alpha }\gamma _{3} \biggr)\frac{\alpha ^{2}-\alpha +2}{2} \\ &{} +\biggl(\frac{1}{2}\biggr) \biggl(\biggl(\frac{2-\alpha }{\alpha }- \frac{4+\alpha }{\alpha }\gamma _{3}\biggr) (1-\alpha )+\gamma _{3} \biggr)\biggr)e^{-\lambda h}\geq 0. \end{aligned}$$

And if $\frac{1-\alpha }{2}<\gamma _{3}\leq \frac{(2-\alpha )(\alpha -1)}{\alpha ^{2}+5\alpha -4}$, then we can obtain from (29)

$$ g_{4}^{\alpha }=\biggl(\biggl(\frac{2\alpha -2}{\alpha }+ \frac{4}{\alpha }\gamma _{3} \biggr)w_{4}^{\alpha }+ \biggl(\biggl(\frac{2-\alpha }{\alpha }-\frac{4+\alpha }{\alpha }\gamma _{3}\biggr) \frac{4-2\alpha -2}{4}+\gamma _{3}\biggr)\hat{w}_{2}^{\alpha } \biggr)e^{-3\lambda h}>0. $$

If $\alpha \in (1,\frac{\sqrt{57}-5}{2})$ and $\gamma _{3}\leq \frac{(2-\alpha )^{2}}{8-\alpha ^{2}-5\alpha }$, or $\alpha \in (\frac{\sqrt{57}-5}{2},2)$ and $\gamma _{3}\geq \frac{(2-\alpha )^{2}}{8-\alpha ^{2}-5\alpha }$, or $\alpha =\frac{\sqrt{57}-5}{2}$, then

$$ \biggl(\frac{2-\alpha }{\alpha }-\frac{4+\alpha }{\alpha }\gamma _{3}\biggr) \frac{6-2\alpha -2}{6}+\gamma _{3}\geq 0. $$

(33)

Combining (30) and (33), and if $\alpha \in (1,\frac{\sqrt{57}-5}{2})$ and $\frac{1-\alpha }{2}<\gamma _{3}\leq \frac{(2-\alpha )^{2}}{8-\alpha ^{2}-5\alpha }$, or $\alpha \in (\frac{\sqrt{57}-5}{2},2)$ and $\gamma _{3}>\max \{\frac{1-\alpha }{2}, \frac{(2-\alpha )^{2}}{8-\alpha ^{2}-5\alpha }\}$, or $\alpha =\frac{\sqrt{57}-5}{2}$ and $\gamma _{3}>\frac{1-\alpha }{2}$, then

$$ g_{6}^{\alpha }=\biggl(\biggl(\frac{2\alpha -2}{\alpha }+ \frac{4}{\alpha }\gamma _{3} \biggr)w_{6}^{\alpha }+ \biggl(\biggl(\frac{2-\alpha }{\alpha }-\frac{4+\alpha }{\alpha }\gamma _{3}\biggr) \frac{6-2\alpha -2}{6}+\gamma _{3}\biggr)\hat{w}_{4}^{\alpha } \biggr)e^{-5\lambda h}>0. $$

If $\alpha \in (1,\frac{\sqrt{73}-5}{2})$ and $\gamma _{3}\leq \frac{(2-\alpha )(3-\alpha )}{12-\alpha ^{2}-5\alpha }$, or $\alpha \in (\frac{\sqrt{73}-5}{2},2)$ and $\gamma _{3}\geq \frac{(2-\alpha )(3-\alpha )}{12-\alpha ^{2}-5\alpha }$, or $\alpha =\frac{\sqrt{73}-5}{2}$, then

$$ \biggl(\frac{2-\alpha }{\alpha }-\frac{4+\alpha }{\alpha }\gamma _{3}\biggr) \frac{8-2\alpha -2}{8}+\gamma _{3}\geq 0. $$

(34)

From (30) and (34), and if $\alpha \in (1,\frac{\sqrt{73}-5}{2})$ and $\frac{1-\alpha }{2}<\gamma _{3}\leq \frac{(2-\alpha )(3-\alpha )}{12-\alpha ^{2}-5\alpha }$, or $\alpha \in (\frac{\sqrt{73}-5}{2},2)$ and $\gamma _{3}>\max \{\frac{1-\alpha }{2}, \frac{(2-\alpha )(3-\alpha )}{12-\alpha ^{2}-5\alpha }\}$, or $\alpha =\frac{\sqrt{73}-5}{2}$ and $\gamma _{3}>\frac{1-\alpha }{2}$, then

$$ g_{8}^{\alpha }=\biggl(\biggl(\frac{2\alpha -2}{\alpha }+ \frac{4}{\alpha }\gamma _{3} \biggr)w_{8}^{\alpha }+ \biggl(\biggl(\frac{2-\alpha }{\alpha }-\frac{4+\alpha }{\alpha }\gamma _{3}\biggr) \frac{8-2\alpha -2}{8}+\gamma _{3}\biggr)\hat{w}_{6}^{\alpha } \biggr)e^{-7\lambda h}>0. $$

If $\gamma _{3}\leq \frac{2-\alpha }{4}$, then

$$ \biggl(\frac{2-\alpha }{\alpha }-\frac{4+\alpha }{\alpha }\gamma _{3}\biggr) \frac{k-2\alpha -2}{k}+\gamma _{3}\geq 0\quad (k\mbox{ is even and }k\geq 10). $$

(35)

Combining (30) and (35), and if $\frac{1-\alpha }{2}<\gamma _{3}\leq \frac{2-\alpha }{4}$, then

$$\begin{aligned} g_{k}^{\alpha } =&\biggl(\biggl(\frac{2\alpha -2}{\alpha }+ \frac{4}{\alpha }\gamma _{3} \biggr)w_{k}^{\alpha }+ \biggl(\biggl(\frac{2-\alpha }{\alpha }-\frac{4+\alpha }{\alpha }\gamma _{3}\biggr) \frac{k-2\alpha -2}{k} \\ &{}+\gamma _{3}\biggr)\hat{w}_{k-2}^{\alpha } \biggr)e^{-(k-1)\lambda h}>0\quad (k\mbox{ is even and }k\geq 10). \end{aligned}$$

Summarizing the above relationships, we find that if any one of the following three conditions is satisfied:

• (1) $\alpha \in (1,\frac{\sqrt{57}-5}{2}]$ and $\frac{(2\alpha ^{2}-\alpha +2)(1-\alpha )}{5\alpha ^{2}+4}\leq \gamma _{3}\leq \frac{(2-\alpha )(\alpha -1)}{\alpha ^{2}+5\alpha -4}$;

• (2) $\alpha \in (\frac{\sqrt{57}-5}{2},\frac{\sqrt{73}-5}{2})$ and $\max \{ \frac{(2\alpha ^{2}-\alpha +2)(1-\alpha )}{5\alpha ^{2}+4}, \frac{(2-\alpha )^{2}}{8-\alpha ^{2}-5\alpha } \} \leq \gamma _{3}\leq \frac{(2-\alpha )(\alpha -1)}{\alpha ^{2}+5\alpha -4}$;

• (3) $\alpha \in [\frac{\sqrt{73}-5}{2},2)$ and $\frac{(2-\alpha )^{2}}{8-\alpha ^{2}-5\alpha }\leq \gamma _{3}\leq \frac{(2-\alpha )(\alpha -1)}{\alpha ^{2}+5\alpha -4}$,

then the results of (23) hold.

The proof is completed. □

Theorem 4.1

If matrix A is defined by (22), then $D=\frac{A+A^{T}}{2}$is strictly diagonally dominant and negative definite.

Proof

Denoting $D=\frac{A+A^{T}}{2}=(d_{i,j})_{(N-1)\times (N-1)}$, we have

$$ D= \begin{pmatrix} g_{1}^{\alpha }-\tilde{G}_{1}(1)&\frac{1}{2}(g_{0}^{\alpha }+g_{2} ^{\alpha })&\frac{1}{2}g_{3}^{\alpha }&\cdots &\frac{1}{2}g_{N-2}^{ \alpha }&\frac{1}{2}g_{N-1}^{\alpha } \\ & & & & & \\ \frac{1}{2}(g_{2}^{\alpha }+g_{0}^{\alpha })&g_{1}^{\alpha }- \tilde{G}_{1}(1)&\frac{1}{2}(g_{0}^{\alpha }+g_{2}^{\alpha })&\cdots &\frac{1}{2}g_{N-3}^{\alpha }&\frac{1}{2}g_{N-2}^{\alpha } \\ & & & & & \\ \vdots &\ddots &\ddots &\ddots &\vdots &\vdots \\ & & & & & \\ \vdots &\vdots &\ddots &\ddots &\ddots &\vdots \\ & & & & & \\ \frac{1}{2}g_{N-2}^{\alpha }&\frac{1}{2}g_{N-3}^{\alpha }&\frac{1}{2}g _{N-4}^{\alpha }&\cdots &g_{1}^{\alpha }-\tilde{G}_{1}(1) & \frac{1}{2}(g_{0}^{\alpha }+g_{2}^{\alpha }) \\ & & & & & \\ \frac{1}{2}g_{N-1}^{\alpha }&\frac{1}{2}g_{N-2}^{\alpha }&\frac{1}{2}g _{N-3}^{\alpha }&\cdots &\frac{1}{2}(g_{2}^{\alpha }+g_{0}^{\alpha }) &g_{1}^{\alpha }-\tilde{G}_{1}(1) \end{pmatrix}. $$

Because the following relationships are established:

$$\begin{aligned} &\sum_{k=0}^{+\infty }w_{k}^{\alpha }e^{-k\lambda h}= \bigl(1-e^{-\lambda h}\bigr)^{ \alpha }, \\ &\sum_{k=0}^{+\infty }\hat{w}_{k}^{\alpha }e^{-k\lambda h}= \biggl(\frac{1-e ^{-2\lambda h}}{2}\biggr)^{\alpha }, \end{aligned}$$

we know

$$\begin{aligned} \sum_{k=0}^{+\infty }g_{k}^{\alpha } &=\sum_{k=0}^{+\infty }\biggl(\biggl( \frac{2 \alpha -2}{\alpha }+\frac{4}{\alpha }\gamma _{3} \biggr)w_{k}^{\alpha }+ \biggl(\frac{2- \alpha }{\alpha }-\frac{4+\alpha }{\alpha }\gamma _{3}\biggr) \hat{w}_{k}^{ \alpha }+\gamma _{3}\hat{w}_{k-2}^{\alpha } \biggr)e^{-(k-1)\lambda h} \\ &=\gamma _{1}G_{1}(1)+\gamma _{2} \hat{G}_{1}(1)+\gamma _{3}\hat{G}_{-1}(1) \\ &=\tilde{G}_{1}(1). \end{aligned}$$

That is,

$$ \sum_{k=0}^{+\infty }g_{k}^{\alpha }- \tilde{G}_{1}(1)=0. $$

(36)

From Lemma 4.2 and (36), we know

$$\begin{aligned}& \sum_{j=1}^{N-1}d_{i,j}< 0, \\& -d_{i,i}> \sum_{j\neq i}^{N-1}d_{i,j},\quad i=1,2,\ldots,N-1. \end{aligned}$$

Thus, matrix D is strictly diagonally dominant. Utilizing the Gershgorin theorem [23], we know that the eigenvalues of matrix D are all negative. That is, matrix D is negative definite.

The proof is completed. □

Theorem 4.2

The numerical scheme (20) is unconditionally stable.

Proof

Denoting $M=\frac{\tau (lA+rA^{T})}{2h^{\alpha }}-\frac{ \tau \alpha \lambda ^{\alpha -1}(l-r)}{4h}B$, then the matrix form (21) becomes

$$ (I-M)U^{n+1}=(I+M)U^{n}+\tau F^{n+1/2}. $$

(37)

Let $\lambda (M)$ represent the eigenvalue of matrix M, then the eigenvalue of matrix $(I-M)^{-1}(I+M)$ is $\frac{1+\lambda (M)}{1- \lambda (M)}$. Because $\frac{M+M^{T}}{2}=\frac{\tau (l+r)(A+A^{T})}{4h ^{\alpha }}=\frac{\tau (l+r)}{2h^{\alpha }}D$, from Lemma 4.1 and Theorem 4.1, we know $\lambda (M)<0$, then $|\frac{1+\lambda (M)}{1- \lambda (M)}|<1$. Thus the spectral radius of matrix $(I-M)^{-1}(I+M)$ is less than one.

The proof is completed. □

Define $\mathbf{U}_{h}$ = {$\mathbf{u}\mid \mathbf{u}=\{\mathbf{u}_{i}\}$ is a grid function defined on $\{x_{i}=a+ih\}_{i=1}^{N-1}$ and $\mathbf{u}_{0}=\mathbf{u}_{N}=0$}. And we define the corresponding discrete $L_{2}$-norm $\|\mathbf{u}\|_{L_{2}}=(h\sum_{i=1}^{N-1} \mathbf{u}_{i}^{2})^{1/2}$ for all $\mathbf{u}\in \mathbf{U}_{h}$.

Lemma 4.3

([14])

For matrixMin (37), there exists

$$ \bigl\Vert (I-M)^{-1} \bigr\Vert _{2}\leq 1,\qquad \bigl\Vert (I-M)^{-1}(I+M) \bigr\Vert _{2}\leq 1, $$

where $\|\cdot \|_{2}$denotes 2-norm (spectral norm).

Theorem 4.3

The numerical scheme (20) is convergent, i.e., there is a constantCsuch that

$$ \bigl\Vert e^{n} \bigr\Vert _{L_{2}}\leq C\bigl(\tau ^{2}+h^{2}\bigr),\quad n=1,2,\ldots,M, $$

where $e^{n}=(e_{1}^{n},e_{2}^{n},\ldots,e_{N-1}^{n})^{T}$, $e_{i}^{n}=u _{i}^{n}-U_{i}^{n}$.

Proof

The proof is similar [14]. Combining (18) and (19), we obtain

$$ (I-M)e^{n+1}=(I+M)e^{n}+R^{n}, $$

(38)

where $R^{n}=(R_{1}^{n},R_{2}^{n},\ldots,R_{N-1}^{n})^{T}$, and $R_{i}^{n}=O(\tau ^{3}+\tau h^{2})$ is the local truncation error. Equation (38) can be rewritten as

$$ e^{n+1}=(I-M)^{-1}(I+M)e^{n}+(I-M)^{-1}R^{n}. $$

By taking the Euclidean norm $\|\cdot \|_{2}$ at the same time on both sides of the upper form, we get

$$\begin{aligned} \bigl\Vert e^{n} \bigr\Vert _{2} &\leq \bigl\Vert (I-M)^{-1}(I+M)e^{n-1} \bigr\Vert _{2}+ \bigl\Vert (I-M)^{-1}R^{n-1} \bigr\Vert _{2} \\ &\leq \bigl\Vert (I-M)^{-1}(I+M) \bigr\Vert _{2} \bigl\Vert e^{n-1} \bigr\Vert _{2}+ \bigl\Vert (I-M)^{-1} \bigr\Vert _{2} \bigl\Vert R ^{n-1} \bigr\Vert _{2}. \end{aligned}$$

Noting that $\|\cdot \|_{L_{2}}=h^{1/2}\|\cdot \|_{2}$ and from Lemma 4.3, we can get

$$\begin{aligned} \bigl\Vert e^{n} \bigr\Vert _{L_{2}} &\leq \bigl\Vert (I-M)^{-1}(I+M) \bigr\Vert _{2} \bigl\Vert e^{n-1} \bigr\Vert _{L_{2}}+ \bigl\Vert (I-M)^{-1} \bigr\Vert _{2} \bigl\Vert R^{n-1} \bigr\Vert _{L_{2}} \\ &\leq \bigl\Vert e^{n-1} \bigr\Vert _{L_{2}}+ \bigl\Vert R^{n-1} \bigr\Vert _{L_{2}}. \end{aligned}$$

Because the local truncation error is given as $|R_{i}^{k}|\leq C(\tau ^{3}+\tau h^{2})$, and noticing that $\|e^{0}\|_{L_{2}}=0$, we have

$$\begin{aligned} \bigl\Vert e^{n} \bigr\Vert _{L_{2}} &\leq \bigl\Vert e^{n-1} \bigr\Vert _{L_{2}}+ \bigl\Vert R^{n-1} \bigr\Vert _{L_{2}}\leq \bigl\Vert e ^{n-2} \bigr\Vert _{L_{2}}+ \bigl\Vert R^{n-2} \bigr\Vert _{L_{2}}+ \bigl\Vert R^{n-1} \bigr\Vert _{L_{2}} \\ &\leq \bigl\Vert e^{0} \bigr\Vert _{L_{2}}+\sum _{k=0}^{n-1} \bigl\Vert R^{k} \bigr\Vert _{L_{2}}\leq C\bigl(\tau ^{2}+h^{2}\bigr). \end{aligned}$$

The proof is completed. □

5 Numerical experiments

The observation order is defined as

$$ \mathrm{Order}=\log _{2} \biggl(\frac{ \Vert e \Vert _{L_{2},h}}{ \Vert e \Vert _{L_{2},h/2}} \biggr). $$

We give four examples to verify the effectiveness of the numerical schemes and compare the numerical results of our method with those of the CN-TWSGD method [14] ($\max\{ \frac{(2- \alpha )(\alpha ^{2}+\alpha -8)}{\alpha ^{2}+3\alpha +2},\frac{(1- \alpha )(\alpha ^{2}+2\alpha )}{2(\alpha ^{2}+3\alpha +4)} \} \leq \beta _{3}\leq \frac{(2-\alpha )(\alpha ^{2}+2\alpha -3)}{2(\alpha ^{2}+3\alpha +2)}$, $\beta _{1}=\frac{\alpha }{2}+\beta _{3}$, $\beta _{2}=\frac{2- \alpha }{2}-2\beta _{3}$) for Example 2.

Example 1

([14])

Consider the initial-boundary value problem of tempered fractional diffusion equation

$$ \textstyle\begin{cases} \frac{\partial u(x,t)}{\partial t}=\frac{{\partial }^{\alpha ,\lambda }_{-}u(x,t)}{\partial x^{\alpha }}+e^{-\lambda x+t}((\lambda ^{\alpha }-\alpha \lambda ^{\alpha }+1)x^{2+\alpha } \\ \hphantom{\frac{\partial u(x,t)}{\partial t}={}}{} -\frac{\varGamma (3+\alpha )}{\varGamma (3)}x^{2}+\alpha (\alpha +2) \lambda ^{\alpha -1}x^{\alpha +1}),& (x,t)\in (0,1)\times (0,1], \\ u(0,t)=0,\qquad u(1,t)=e^{-\lambda +t},& t\in [0,1], \\ u(x,0)=e^{-\lambda x}x^{2+\alpha }, &x\in [0,1], \end{cases} $$

where $1<\alpha <2$.

The exact solution is $u(x,t)=e^{-\lambda x+t}x^{2+\alpha }$.

Choosing different α, λ, and $\gamma _{3}$, we use the proposed method to solve Example 1, the errors and observation orders are displayed in Tables 1, 2, and 3. From Tables 1–3, we find that the numerical schemes are second-order accuracy both in time and space, which is a match with theoretical results.

Table 1 Errors and corresponding observation orders at $t=1$, $\alpha =1.2$

Table 2 Errors and corresponding observation orders at $t=1$, $\alpha =1.5$

Table 3 Errors and corresponding observation orders at $t=1$, $\alpha =1.8$

Example 2

([14])

Consider the initial-boundary value problem of tempered fractional diffusion equation

$$ \textstyle\begin{cases} \frac{\partial u(x,t)}{\partial t}=\frac{{\partial }^{\alpha ,\lambda }_{+}u(x,t)}{\partial x^{\alpha }}+e^{\lambda x+t}((\lambda ^{\alpha }- \alpha \lambda ^{\alpha }+1)(1-x)^{2+\alpha } \\ \hphantom{\frac{\partial u(x,t)}{\partial t}={}}{}-\frac{\varGamma (3+\alpha )}{\varGamma (3)}(1-x)^{2}+\alpha (\alpha +2) \lambda ^{\alpha -1}(1-x)^{\alpha +1}), & (x,t)\in (0,1)\times (0,1], \\ u(0,t)=e^{t},\qquad u(1,t)=0,& t\in [0,1], \\ u(x,0)=e^{\lambda x}(1-x)^{2+\alpha },& x\in [0,1], \end{cases} $$

where $1<\alpha <2$.

The exact solution is $u(x,t)=e^{\lambda x+t}(1-x)^{2+\alpha }$.

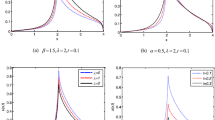
In order to compare the CN-TWSGD method with the proposed method in this paper, we choose different α, λ, $\beta _{3}$, and $\gamma _{3}$ to solve Example 2, the errors, observation orders, and CPU times are displayed in Tables 4–9. From Tables 4–9, we see that both the CN-TWSGD method and our method are effective.

Table 4 Errors and corresponding observation orders at $t=1$, $\lambda =1/50$

Table 5 Errors and corresponding observation orders at $t=1$, $\lambda =1/50$

Table 6 Errors and corresponding observation orders at $t=1$, $\lambda =0$

Table 7 Errors and corresponding observation orders at $t=1$, $\lambda =0$

Table 8 Errors and corresponding observation orders at $t=1$, $\lambda =2$

Table 9 Errors and corresponding observation orders at $t=1$, $\lambda =2$

Example 3

(cf. [27])

Consider the initial-boundary value problem of tempered fractional diffusion equation

$$ \textstyle\begin{cases} \frac{\partial u(x,t)}{\partial t}=l\frac{{\partial }^{\alpha ,\lambda }_{-}u(x,t)}{\partial x^{\alpha }}+r\frac{{\partial }^{\alpha ,\lambda }_{+}u(x,t)}{\partial x^{\alpha }}+f(x,t), &(x,t)\in (0,1)\times (0,1], \\ u(0,t)=0,\qquad u(1,t)=0, &t\in [0,1], \\ u(x,0)=e^{-\lambda x}x^{4}(1-x)^{4}, & x\in [0,1], \end{cases} $$

where $1<\alpha <2$, $l=1$, $r=2$, and the linear source term is

$$\begin{aligned} f(x,t) =&\alpha e^{\alpha t-\lambda x}x^{4}(1-x)^{4}-e^{\alpha t} \Biggl[e ^{-\lambda x}\sum_{k=0}^{4}(-1) \bigl(_{k}^{4}\bigr)\frac{\varGamma (5+k)}{\varGamma (5+k- \alpha )}x^{4+k-\alpha } \\ &{}+2e^{\lambda (x-2)}\sum_{i=0}^{+\infty } \frac{(2\lambda )^{i}}{i!} \sum_{k=0}^{4}(-1) \bigl(_{k}^{4}\bigr)\frac{\varGamma (5+k+i)}{\varGamma (5+k+i- \alpha )}(1-x)^{4+k+i-\alpha } \\ &{}-3\lambda ^{\alpha }e^{-\lambda x}x^{4}(1-x)^{4}+ \alpha \lambda ^{\alpha -1}e^{-\lambda x}\bigl(-\lambda x^{4}(1-x)^{4}+4 \bigl(x-x^{2}\bigr)^{3}(1-2x)\bigr)\Biggr]. \end{aligned}$$

The exact solution is $u(x,t)=e^{\alpha t-\lambda x}x^{4}(1-x)^{4}$.

Choosing different α and λ, we use the proposed method to solve Example 3, the errors and observation orders are displayed in Table 10. From Table 10, we find that the numerical scheme is second-order accuracy both in time and space, which is in line with our convergence analysis.

Table 10 Errors and corresponding observation orders at $t=1$, $\gamma _{3}=0$

Example 4

Consider the initial-boundary value problem of tempered fractional diffusion equation:

$$ \textstyle\begin{cases} \frac{\partial u(x,t)}{\partial t}=\frac{{\partial }^{\alpha ,\lambda }_{-}u(x,t)}{\partial x^{\alpha }} +\frac{{\partial }^{\alpha ,\lambda }_{+}u(x,t)}{\partial x^{\alpha }},& (x,t)\in (0,1)\times (0,1], \\ u(0,t)=0,\qquad u(1,t)=0,& t\in [0,1], \\ u(x,0)=x^{2}(1-x)^{2}, & x\in [0,1], \end{cases} $$

where $1<\alpha <2$.

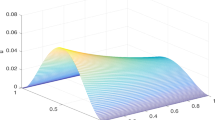
Using the proposed method to take the step size $h=\tau =1/400$, the result obtained in solving Example 4 is taken as the true solution. Choosing different α and λ, we use the proposed method to solve Example 4, the errors and observation orders are displayed in Table 11. Figure 1 shows the particle concentration of the solution of the tempered fractional diffusion equation with $\alpha =1.5$ and $\lambda =3$ at different times. Figure 2 shows the particle concentration of the solution of the classical ($\lambda =0$) fractional diffusion equation with $\alpha =1.5$ at different times. It can be seen from Fig. 1 and Fig. 2 that the tempered fractional diffusion equation governs the transition densities, which become slower in progress.

Figure 1

$\gamma _{3}=0$, $\alpha =1.5$, $\lambda =3$, the change in particle concentration $u(x,t)$ at different times

Figure 2

$\gamma _{3}=0$, $\alpha =1.5$, $\lambda =0$, the change in particle concentration $u(x,t)$ at different times

Table 11 Errors and corresponding observation orders at $t=1$, $\gamma _{3}=0$

6 Conclusion

In this paper, a class of second-order tempered difference operators for the left and right Riemann–Liouville tempered fractional derivatives is constructed, and then a class of second-order numerical methods is presented for solving the space tempered fractional diffusion equation. Numerical schemes are proved to be unconditionally stable and convergent theoretically and are verified to be effective by numerical experiments.