1 Introduction

This paper is concerned with numerical methods for solving the following initial-boundary value problem of tempered fractional diffusion equations (tempered-FDEs):

$$ \begin{gathered} {\frac{\partial u(x, t)}{\partial t}=d(x) \bigl( \kappa_{1} {_{a}} {\mathbf {D}}_{x}^{{\alpha},\lambda}+ \kappa_{2} {_{x}} {\mathbf {D}} _{b}^{{\alpha},\lambda} \bigr)u(x,t)+f(x,t)}, \\ u(a,t)=0,\quad \quad u(b,t)=0, \quad t\in[0,T], \\ u(x,0)=u_{0}(x),\quad x\in[a,b], \end{gathered} $$
(1)

where \(f(x, t)\) is the source term, \(d(x)\geq0\) is the diffusion coefficient functions, the parameters \(\kappa_{1}\geq0\), \(\kappa_{2} \geq0\) are skewed parameters that control the bias of the dispersion, see Benson et al. [1], and λ is non-negative. Here, the \({_{a}}{\mathbf {D}}_{x}^{{\alpha},\lambda}u(x,t)\) and \({_{x}} {\mathbf {D}}_{b}^{{\alpha},\lambda}u(x,t)\) represent the left and right Riemann-Liouville tempered fractional derivatives of the function \(u(x,t)\) with order α (\(1<\alpha<2\)), respectively, defined by (see Baeumera and Meerschaert [2])

$$ {_{a}}\mathbf{D}_{x}^{\alpha,\lambda}u(x)= {_{a}}D_{x}^{\alpha,\lambda }u(x)-\alpha\lambda^{\alpha-1} \,\partial_{x}u(x)-\lambda^{\alpha}u(x) $$

and

$$ {_{x}}\mathbf{D}_{b}^{\alpha,\lambda}u(x)= {_{x}}D_{b}^{\alpha,\lambda }u(x)+\alpha\lambda^{\alpha-1} \,\partial_{x}u(x)-\lambda^{\alpha}u(x), $$

where

$${ {_{a}}D_{x}^{{\alpha},{\lambda}}u(x)=e^{-\lambda x} {_{a}}D_{x}^{\alpha} \bigl(e^{\lambda x}u(x) \bigr)=\frac{e^{-\lambda x}}{\Gamma(n-\alpha)}\frac{\partial^{n}}{\partial x^{n}} \int_{a}^{x} \frac{e^{\lambda\xi}u(\xi)}{(x-\xi)^{\alpha-n+1}} \,\mathrm{d}\xi} $$

and

$${ {_{x}}D_{b}^{{\alpha},\lambda}u(x)=e^{\lambda x} {_{x}}D_{b}^{\alpha} \bigl(e^{-\lambda x}u(x) \bigr)= \frac{(-1)^{n}e^{\lambda x}}{\Gamma(n-\alpha)}\frac{\partial^{n}}{\partial x^{n}} \int_{x}^{b} \frac{e^{-\lambda\xi}u(\xi)}{(\xi-x)^{\alpha-n+1}} \,\mathrm{d}\xi}, $$

where \(\Gamma(\cdot)\) denotes the gamma function, and \(\partial_{x}\) is the first order partial differential operator with respect to x. Truly, when \(\lambda=0\), it reduces to the αth order left and right Riemann-Liouville fractional derivatives of \(u(x)\), respectively, then the above equation (1) reduces to fractional diffusion equations (FDEs).

From the existing literature, tempered-FDEs (1) is an exponentially-tempered extension of FDEs, which has proven to be an excellent tool in capturing some rare or extreme events in geophysics [2–4] and finance [5, 6]. For the FDEs problems, there are a variety of numerical schemes, and their fast algorithms developed extensively in the past decades. We refer readers to [7–16] and the references therein for the recent progress in these problems. In recent years, Deng’s group have further derived some high order difference approximations for the left and right Riemann-Liouville tempered fractional derivatives in [17], and their results have been an interest in the numerical simulation of the tempered fractional Black-Scholes equation for European double barrier option [18]. Moreover, the tempered fractional diffusion models are also used to simulate exponential tempering of the power-law jump length of the continuous time random walk and the Fokker-Planck equation of the new stochastic process, see [19, 20]. However, in these cases, the diffusion coefficients are usually constants, few papers have focused on the tempered fractional diffusion model with variable coefficients. Therefore, it is the aim of this paper to derive a class of variable-coefficient tempered fractional diffusion models.

The paper is organized as follows. In Section 2, we apply the Crank-Nicolson discretization for the tempered-FDEs, and the desired order in space and time is obtained. In Section 3, it is shown that the method is unconditionally stable and convergent. Numerical examples are presented in Section 4 to verify our theoretical analysis. Finally, Section 5 presents the conclusion.

2 The Crank-Nicolson discretization for the tempered fractional diffusion equations

To develop the Crank-Nicolson scheme for problem (1), we let \(h = \frac{b-a}{N+1}\) and \(\tau= \frac{T}{M}\) be the space step and time step respectively, where N, M are some given positive integers. Then the spatial and temporal partitions can be defined by \(x_{i} = a + i h\), \(i=0, 1, \ldots, N+1\) and \(t_{m} = m\tau\), \(m = 0, 1 , \ldots, M\). Next, for convenience, we introduce the following notation:

$$t_{m+\frac{1}{2}}=\frac{1}{2}(t_{m}+t_{m+1}),\quad \quad f^{m+\frac {1}{2}}_{i}=f(x_{i},t_{m+\frac{1}{2}}), \quad \quad d_{i}=d(x_{i}). $$

Note that Li and Deng [17] have established a second order tempered-WSGD operators \({_{a}}\mathfrak{D}_{x}^{\alpha,\lambda}\) and \({_{x}}\mathfrak{D}_{b}^{\alpha,\lambda}\) to approximate the left and right Riemann-Liouville tempered fractional derivatives of \(u(x)\) at point \(x_{i}\), respectively, which gives

$$\begin{aligned} {_{a}}D_{x}^{\alpha,\lambda}u(x_{i})- \alpha\lambda^{\alpha }u(x_{i}) =&{_{a}} \mathfrak{D}_{x}^{\alpha,\lambda}u(x_{i})+{\mathcal {O}} \bigl(h^{2}\bigr) \\ =&\frac{1}{h^{\alpha}}\sum_{k=0}^{i+1}g_{k}^{(\alpha )}u(x_{i-k+1})- \frac{1}{h^{\alpha}}\phi({\lambda})u(x_{i})+{\mathcal {O}} \bigl(h^{2}\bigr) \end{aligned}$$

and

$$\begin{aligned} {_{x}}D_{b}^{\alpha,\lambda}u(x_{i})-\alpha \lambda^{\alpha }u(x_{i}) =&{_{x}}\mathfrak{D}_{b}^{\alpha,\lambda}u(x_{i})+{ \mathcal {O}}\bigl(h^{2}\bigr) \\ =&\frac{1}{h^{\alpha}}\sum_{k=0}^{N-i+2}g_{k}^{(\alpha )}u(x_{i+k-1})- \frac{1}{h^{\alpha}}\phi({\lambda})u(x_{i})+{\mathcal {O}} \bigl(h^{2}\bigr), \end{aligned}$$

where \(\phi({\lambda})=(\gamma_{1}e^{h\lambda}+\gamma_{2}+\gamma _{3}e^{-h\lambda})(1-e^{-h\lambda})^{\alpha}\), and the weights \(g_{k}^{(\alpha)}\) are given as

$$ g_{k}^{(\alpha)}= \textstyle\begin{cases} \gamma_{1}w_{0}^{(\alpha)}e^{h\lambda}, &k=0,\\ \gamma_{1}w_{1}^{(\alpha)}+\gamma_{2}w_{0}^{(\alpha)}, &k=1,\\ (\gamma_{1}w_{k}^{(\alpha)}+\gamma_{2}w_{k-1}^{(\alpha)}+\gamma _{3}w_{k-2}^{(\alpha)} )e^{-(k-1)h\lambda},&k\geq2. \end{cases} $$
(2)

Here the weights \(w_{0}^{(\alpha)}=1\) and \(w_{k}^{(\alpha )}=(-1)^{k}\binom{\alpha}{k}\) can be evaluated recursively, i.e., \(w_{k}^{(\alpha)}= (1-\frac{1+\alpha}{k} )w_{k-1}^{(\alpha)}\) for all \(k\geq1\), see[7]. It is worth mentioning that the parameters \(\gamma_{i}\) (\(i=1,2,3\)) satisfy the linear system

$$ \textstyle\begin{cases} \gamma_{1}+\gamma_{2}+\gamma_{3}=1,\\ \gamma_{1}-\gamma_{3}=\alpha/2. \end{cases} $$
(3)

Note that there are infinite many solutions of linear system (3). However, the rank the coefficient matrix is 2 so that a solution can be uniquely determined when one of \(\gamma_{i}\) is provided. They can be collected by the following three sets:

$$S_{1}^{\alpha}(\gamma_{1}, \gamma_{2},\gamma_{3})= \biggl\{ \gamma_{1}\mbox{ is given},\gamma_{2}=\frac{2+\alpha}{2}-2\gamma_{1}, \gamma_{3}=\gamma_{1}-\frac {\alpha}{2} \biggr\} ; $$

or

$$S_{2}^{\alpha}(\gamma_{1}, \gamma_{2},\gamma_{3})= \biggl\{ \gamma_{1}= \frac {2+\alpha}{4}-\frac{\gamma_{2}}{2}, \gamma_{2}\mbox{ is given}, \gamma _{3}=\frac{2-\alpha}{4}-\frac{\gamma_{2}}{2} \biggr\} ; $$

or

$$S_{3}^{\alpha}(\gamma_{1}, \gamma_{2},\gamma_{3})= \biggl\{ \gamma_{1}= \frac {\alpha}{2}+\gamma_{3},\gamma_{2}=\frac{2-\alpha}{2}-2 \gamma_{3} ,\gamma_{3}\mbox{ is given} \biggr\} . $$

We remark that the above approach used to approximate the left and right Riemann-Liouville tempered fractional derivatives is simply a follow-up used by Li and Deng [17]. Our main contributions to this paper are to derive a Crank-Nicolson scheme for a class of variable-coefficient tempered-FDEs and to illustrate the stability and convergence of this scheme.

Let \(u^{m}_{i} \approx u(x_{i},t_{m})\), we can therefore consider the Crank-Nicolson technique to the tempered-FDEs (1) with the tempered-WSGD approximations to the tempered fractional derivatives and the second order central difference approximation to \(\frac{\partial u}{\partial x}\), see [17, 21]. Then, neglecting the truncation errors, we derive the following second order finite difference scheme:

$$\begin{aligned}& \frac{u_{i}^{m+1}-u_{i}^{m}}{\tau} \\& \quad = \frac{d_{i}}{2} \Biggl(\frac{\kappa_{1}}{h^{\alpha}}\sum _{k=0}^{i+1}g_{k}^{(\alpha)}u_{i-k+1}^{m}+ \frac{\kappa_{1}}{h^{\alpha }}\sum_{k=0}^{i+1}g_{k}^{(\alpha)}u_{i-k+1}^{m+1}+ \frac{\kappa _{2}}{h^{\alpha}}\sum_{k=0}^{N-i+2}g_{k}^{(\alpha)}u_{i+k-1}^{m} \\& \quad\quad{} +\frac{\kappa_{2}}{h^{\alpha}}\sum_{k=0}^{N-i+2}g_{k}^{(\alpha )}u_{i+k-1}^{m+1} \Biggr)-d_{i}\frac{(\kappa_{1}+\kappa_{2})}{h^{\alpha }}\phi{(\lambda)} \biggl( \frac{u_{i}^{m}+u_{i}^{m+1}}{2} \biggr) \\& \quad\quad{} +d_{i}\frac{\alpha\lambda^{\alpha-1}(\kappa_{2}-\kappa_{1})}{2} \biggl(\frac{u_{i+1}^{m+1}-u_{i-1}^{m+1}}{2h}+ \frac {u_{i+1}^{m}-u_{i-1}^{m}}{2h} \biggr)+f_{i}^{m+\frac{1}{2}}, \end{aligned}$$
(4)

for \(i=1, 2,\ldots, N\) and \(m=1, 2, \ldots, M-1\). We denote \(\varepsilon =\frac{\tau}{2h^{\alpha}}\geq0\), \(\eta=\frac{\alpha\lambda^{\alpha -1}\tau}{4h}\geq0\). In a matrix form, it is given as

$$ (I-A)u^{m+1}=(I+A)u^{m}+\tau f^{m}, $$
(5)

in which

$$ A=D \bigl(\varepsilon\kappa_{1}G+\varepsilon \kappa_{2}G^{T}+\eta(\kappa _{2}- \kappa_{1}) W \bigr), $$
(6)

where \(D=\operatorname {diag}(d_{1}, d_{2},\ldots,d_{N})\), \(u^{m}=[u_{1}^{m},u_{2}^{m},\ldots,u_{N}^{m}]^{T}\), \(f^{m+\frac{1}{2}}=[f_{1}^{m+\frac {1}{2}}, f_{2}^{m+\frac{1}{2}}, \ldots,f_{N}^{m+\frac{1}{2}}]^{T}\), the tridiagonal matrix \(W=\operatorname {tridiag}(-1, 0,1)\), I is the identity matrix, and \(G\equiv[g_{i,j}]\) is an \(N\times N\) Toeplitz matrix defined as

$$ g_{i,j}= \textstyle\begin{cases} 0, &j\geq i+2,\\ g_{0}^{(\alpha)}, &j=i+1,\\ g_{1}^{(\alpha)}-\phi(\lambda),&j=i,\\ g_{2}^{(\alpha)}, &j=i-1,\\ g_{i-j+1}^{(\alpha)}, &j\leq i-2. \end{cases} $$
(7)

3 Stability and convergence of the Crank-Nicolson finite difference scheme

To show the unconditional stability and convergence of the Crank-Nicolson finite difference scheme (4), the following results given in [17, 22–24] are required.

Lemma 1

Li and Deng [17]

Let \({\mathcal {S}}\) be the solution set of linear system (3). If \(1<\alpha<2\), \(\lambda\geq0\), \((\gamma_{1},\gamma _{2},\gamma_{3})\in{\mathcal {S}}\), and

  1. 1.

    \(\max \{\frac{2(\alpha^{2}+3\alpha-4)}{\alpha^{2}+3\alpha +2},\frac{\alpha^{2}+3\alpha}{\alpha^{2}+3\alpha+4} \}<\gamma_{1}< \frac {3(\alpha^{2}+3\alpha-2)}{2(\alpha^{2}+3\alpha+2)}\); or

  2. 2.

    \(\frac{(\alpha-4)(\alpha^{2}+3\alpha+2)+24}{2(\alpha^{2}+3\alpha +2)}< \gamma_{2}< \min \{\frac{(\alpha-2)(\alpha^{2}+3\alpha +4)+16}{2(\alpha^{2}+3\alpha+4)}, \frac{(\alpha-6)(\alpha^{2}+3\alpha +2)+48}{2(\alpha^{2}+3\alpha+2)} \}\); or

  3. 3.

    \(\max \{\frac{(2-\alpha)(\alpha^{2}+\alpha-8)}{\alpha ^{2}+3\alpha+2},\frac{(1-\alpha)(\alpha^{2}+2\alpha)}{2(\alpha^{2}+3\alpha +4)} \}< \gamma_{3}< \frac{(2-\alpha)(\alpha^{2}+2\alpha-3)}{2(\alpha ^{2}+3\alpha+2)}\),

we have

$$g_{1}^{(\alpha)}< 0,\quad \quad g_{2}^{(\alpha)}+g_{0}^{(\alpha)}>0,\quad \quad g_{k}^{(\alpha)}>0, \quad\forall k \geq3, $$

and

$$\sum_{k=0}^{\infty}g_{k}^{(\alpha)}= \bigl(\gamma_{1}e^{h\lambda }+\gamma_{2}+ \gamma_{3}e^{-h\lambda}\bigr) \bigl(1-e^{-h\lambda} \bigr)^{\alpha}. $$

Lemma 2

Quarteroni et al. [22]

If \(A\in\mathbb{C}^{n\times n}\), let \(H=\frac{A+A^{*}}{2}\) be the hermitian part of A, then for any eigenvalue λ of A, the real part \(\operatorname{Re}(\lambda(A))<0\) satisfies

$$\lambda_{\min}(H)\leq\operatorname{Re}\bigl(\lambda(A)\bigr) \leq \lambda_{\max}(H), $$

where \(\lambda_{\min}(H)\) and \(\lambda_{\max}(H)\) are the minimum and maximum of the eigenvalues of H, respectively.

Lemma 3

Quarteroni et al. [22]

A real matrix A of order N is negative definite if and only if its symmetric part \(H=\frac{A+A^{*}}{2}\) is negative definite; H is negative definite if and only if the eigenvalues of H are negative.

Definition 1

The numerical range of matrix A is defined as

$$\mathcal{W}(A)\equiv\bigl\{ \boldsymbol{v}^{*}A\boldsymbol{v}: \boldsymbol{v}\in\mathbb{C}^{n},\boldsymbol {v}^{*} \boldsymbol{v}=1\bigr\} . $$

Lemma 4

Horn and Johnson [23]

Let \(A, B\in\mathbb{C}^{n\times n}\), if B is positive definite, then \(\sigma(AB) \subset\mathcal{W}(A)\mathcal{W}(B)\), where \(\sigma(AB)\) is the spectrum of AB.

Lemma 5

Quarteroni and Valli [24]; Discrete Gronwall’s inequality

Assume that \(\{k_{n}\}\) and \(\{p_{n}\} \) are non-negative sequences, and the sequence \(\{\phi_{n}\}\) satisfies

$$\phi_{0}\leq c_{0}, \quad \quad\phi_{n}\leq c_{0}+\sum_{l=0}^{n-1}p_{l}+ \sum_{l=0}^{n-1}k_{l} \phi_{l},\quad n\geq1, $$

where \(c_{0}\geq0\). Then the sequence \(\{\phi_{n}\}\) satisfies

$$ \phi_{n}\leq \Biggl(c_{0}+\sum _{l=0}^{n-1}p_{l} \Biggr)\exp \Biggl(\sum _{l=0}^{n-1}k_{l} \Biggr), \quad n \geq1. $$

Next, we analyze the stability of finite difference scheme (5), we have the following theorem.

Theorem 1

For all \(\alpha\in(1,2)\), if the parameters \(\gamma_{1}\), \(\gamma_{2}\), and \(\gamma_{3}\) satisfy the hypothesis given in Lemma  1, then the difference scheme (5) is unconditionally stable.

Proof

Let \(\mathcal{M}:=\varepsilon\kappa_{1}G+\varepsilon\kappa _{2}G^{T}+\eta(\kappa_{2}-\kappa_{1}) W\), then \(A=D\mathcal{M}\), note that

$$\begin{aligned} \frac{\mathcal{M}+\mathcal{M}^{T}}{2} =&\varepsilon\frac{(\kappa _{1}+\kappa_{2})}{2}\bigl(G+G^{T} \bigr)+\eta\frac{(\kappa_{2}-\kappa _{1})}{2}\bigl(W+W^{T}\bigr) \\ =&\varepsilon\frac{(\kappa_{1}+\kappa_{2})}{2}\bigl(G+G^{T}\bigr). \end{aligned}$$

From [17], we note that the matrix G is negative definite. Since \(\kappa_{1}\geq0\), \(\kappa_{2}\geq0\) and \(\varepsilon\geq0\), then we have \(\frac{\mathcal{M}+\mathcal{M}^{T}}{2}\) is also negative definite. Thanks to Lemma 3, the matrix \(\mathcal{M}\) is negative definite. Denote by \(\mu(A)\) an eigenvalue of \(A=D\mathcal{M}\). Since D is non-negative, combining the negative definite properties of \(\mathcal{M}\) and Lemma 4, we obtain that

$$ \sigma(A)=\sigma(D\mathcal{M})\subseteq\mathcal{W}(D)\mathcal {W}( \mathcal{M})\subseteq\bigl\{ \delta\in\mathbb{C}|\operatorname{Re}(\delta)< 0\bigr\} . $$

Hence \(\operatorname{Re}(\mu(A))<0\), which implies that the inequality

$$\biggl\vert \frac{1+\mu(A)}{1-\mu(A)} \biggr\vert \leq1 $$

holds for any \(\alpha\in(1, 2)\). Therefore, the numerical scheme (5) is unconditionally stable.

In the sequel, we consider the convergence of the numerical scheme (4). Let

$$V_{h}=\bigl\{ v|v=(v_{0},v_{1},v_{2}, \ldots,v_{N},v_{N+1}), v_{0}=v_{N+1}=0 \bigr\} $$

be space grid functions defined on \(\{ x_{i}=ih\}_{i=0}^{N+1}\). For any \(u, v \in V_{h}\), we define

$$(u,v)=h\sum_{i=1}^{N}u_{i}v_{i} $$

and the corresponding discrete \(L^{2}\) norm

$$\Vert v \Vert =\sqrt{(v,v)}=\sqrt{h\sum _{i=1}^{N}v_{i}^{2}}. $$

 □

The following theorem describes the convergence of the Crank-Nicolson method when \(A=D\mathcal{M}\) is negative definite.

Theorem 2

Let \(U_{i}^{m}\) be the exact solution of tempered-FDEs (1) and \(u_{i}^{m}\) be the solution of discrete Eq. (4) at mesh point \((x_{i}, t_{m})\), respectively, where \(i=1, 2, \ldots, N\) and \(m=1, 2, \ldots, M\). For all \(\alpha\in(1,2)\), if \(A=D\mathcal{M}\) is negative definite, and the parameters \(\gamma_{1}\), \(\gamma_{2}\), and \(\gamma_{3}\) satisfy the hypothesis given in Lemma  1, we have

$$\bigl\Vert U^{m}-u^{m} \bigr\Vert \leq C \bigl(h^{2}+\tau^{2}\bigr), \quad m=1, 2,\ldots, M, $$

where C is a positive constant, and \(U^{m}=[U_{1}^{m}, U_{2}^{m},\ldots, U_{N}^{m}]^{T}\).

Proof

For \(i=1, 2, \ldots, N\) and \(m=0, 1, 2, \ldots, M-1\), the error satisfies the following equation:

$$\begin{aligned}& e_{i}^{m+1} - \frac{\tau d_{i}}{2} \bigl[ \kappa_{1} {_{a}}\mathfrak {D}_{x}^{\alpha,\lambda}e_{i}^{m+1}+ \kappa_{2} {_{x}}\mathfrak {D}_{b}^{\alpha,\lambda}e_{i}^{m+1}+ \alpha\lambda^{\alpha-1}(\kappa _{2}-\kappa_{1}) \,\partial_{x}{e_{i}^{m+1}} \bigr] \\& \quad = e_{i}^{m}+\frac{\tau d_{i}}{2} \bigl[ \kappa_{1} {_{a}}\mathfrak {D}_{x}^{\alpha,\lambda}e_{i}^{m}+ \kappa_{2} {_{x}}\mathfrak{D}_{b}^{\alpha ,\lambda}e_{i}^{m}+ \alpha\lambda^{\alpha-1}(\kappa_{2}-\kappa _{1}) \,\partial_{x}{e_{i}^{m}} \bigr] \\& \quad\quad {}+\tau{\mathcal {O}}\bigl(h^{2}+\tau^{2}\bigr), \end{aligned}$$
(8)

where \(e_{i}^{m}=U_{i}^{m}-u_{i}^{m}\), and \(e_{i}^{0}=0\), \(e_{0}^{m}=e_{N+1}^{m}=0\) for \(i=1,2,\ldots,N\) and \(m=1,\ldots,M-1\). Denote \(E^{m}=[e_{1}^{m},e_{2}^{m},\ldots,e_{N}^{m}]^{T}\), then the matrix form of Eq. (8) can be written as

$$(I-A)E^{m+1}=(I+A)E^{m}+\tau\rho^{m}, \quad\quad E^{0}=0,\quad m=0, 1,\ldots , M-1. $$

Through arrangement, we obtain

$$\begin{aligned} E^{m+1}-E^{m}-A\bigl(E^{m+1}+E^{m} \bigr)=\tau\rho^{m}, \quad \quad E^{0}=0,\quad m=0, 1,\ldots, M-1, \end{aligned}$$
(9)

where \(\rho^{m}=[\rho_{1}^{m},\rho_{2}^{m},\ldots,\rho_{N}^{m}]^{T}\) with \(\rho_{i}^{m}={\mathcal {O}}(h^{2}+\tau^{2})\).

Multiplying (9) by h and taking \((E^{m+1}+E^{m})^{T}\) on both sides, we have

$$ \begin{aligned}[b] & h\bigl(E^{m+1}+E^{m}\bigr)^{T} \bigl(E^{m+1}-E^{m}\bigr)-h\bigl(E^{m+1}+E^{m} \bigr)^{T}A\bigl(E^{m+1}+E^{m}\bigr) \\ &\quad =h \bigl(E^{m+1}+E^{m}\bigr)^{T}\tau \rho^{m}. \end{aligned} $$
(10)

Recall that the matrix A is negative definite, then

$$\bigl(E^{m+1}+E^{m}\bigr)^{T}A \bigl(E^{m+1}+E^{m}\bigr)< 0, $$

and from Eq. (10) we have

$$h\sum_{i=1}^{N} \bigl( \bigl(e_{i}^{m+1}\bigr)^{2}-\bigl(e_{i}^{m} \bigr)^{2} \bigr)\leq\tau h\sum_{i=1}^{N} \bigl(e_{i}^{m+1}+e_{i}^{m}\bigr) \rho_{i}^{m}. $$

Summing up for all \(0\leq m \leq k-1\) (\(k=1, 2,\ldots, M\)) leads to

$$\begin{aligned} h\sum_{i=1}^{N}\bigl(e_{i}^{k} \bigr)^{2} \leq&\tau h \sum_{i=1}^{N} \sum_{m=0}^{k-1}\bigl(e_{i}^{m+1}+e_{i}^{m} \bigr)\rho_{i}^{m} \\ =&\tau h \sum_{i=1}^{N}\sum _{m=1}^{k-1}\bigl(\rho_{i}^{m}+ \rho _{i}^{m-1}\bigr)e_{i}^{m}+\tau h \sum_{i=1}^{N}e_{i}^{k} \rho _{i}^{k-1} \\ \leq&\frac{\tau h}{2}\sum_{i=1}^{N}\sum _{m=1}^{k-1}\bigl(e_{i}^{m} \bigr)^{2}+\frac{\tau h}{2}\sum_{i=1}^{N} \sum_{m=1}^{k-1}\bigl(\rho_{i}^{m}+ \rho_{i}^{m-1}\bigr)^{2} \\ &{}+\frac{\tau h}{2}\sum _{i=1}^{N}\bigl( e_{i}^{k} \bigr)^{2}+\frac{\tau h}{2}\sum_{i=1}^{N} \bigl(\rho _{i}^{k-1}\bigr)^{2}. \end{aligned}$$

Since \(\rho_{i}^{m}={\mathcal {O}}(h^{2}+\tau^{2})\), it means that \(\rho _{i}^{m}\leq C(h^{2}+\tau^{2})\) for \(C>0\). It follows from Lemma 5 that

$$\begin{aligned} \bigl\Vert E^{k} \bigr\Vert ^{2} \leq& \bigl(C \bigl(h^{2}+\tau^{2}\bigr)\bigr)^{2}+\sum _{m=1}^{k} \bigl(\tau\cdot \bigl\Vert E^{m} \bigr\Vert ^{2} \bigr)\leq\bigl(C \bigl(h^{2}+\tau ^{2}\bigr)\bigr)^{2} \exp \Biggl( \sum_{m=1}^{k}\tau \Biggr) \\ \leq&\bigl(C\bigl(h^{2}+\tau^{2}\bigr)\bigr)^{2}e^{T}. \end{aligned}$$

Therefore, \(\Vert E^{k} \Vert = \Vert E^{m} \Vert = \Vert U^{m}-u^{m} \Vert \leq C(h^{2}+\tau^{2})\) (\(m=1, 2,\ldots, M\)), which is the desired result. □

4 Some examples

In this section, two numerical examples are given to show the effectiveness and convergence orders of the proposed schemes. In the test, we compute the maximum norm errors between the exact and the numerical solutions at the last time step by

$$ e(h,\tau)=\max_{1\leq i\leq N} \bigl\vert u(x_{i},t_{M})-u_{i}^{M} \bigr\vert , $$
(11)

where \(u(x_{i},t_{M})\) is the exact solution and \(u_{i}^{M}\) is the numerical solution with the mesh step sizes h and τ at the grid point \((x_{i},t_{M})\). The order in the following tables is calculated by

$$\mathrm{Order}=\log_{2} \bigl(e(2h,2\tau)/e(h,\tau) \bigr). $$

Example 1

Consider the following two-sided tempered fractional diffusion problem:

$$\begin{aligned}& {\frac{\partial u(x, t)}{\partial t}=x\bigl( {_{0}}\mathbf {D}_{x}^{{\alpha},\lambda}+ {_{x}}\mathbf{D}_{1}^{{\alpha},\lambda }\bigr)u(x,t)+f(x,t)}, \\ & u(0,t)=0,\quad \quad u(1,t)=0, \quad t\in[0,1], \\ & u(x,0)=e^{-\lambda x}x^{4}(1-x)^{4},\quad x\in[0,1]. \end{aligned}$$

The exact solution is given by \(u(x,t)=e^{-t-\lambda x}x^{4}(1-x)^{4}\). Then the source term is given as

$$ \begin{aligned} f(x,t) &\simeq -e^{-t} \Biggl[ e^{-\lambda x} \Biggl(x^{4}(1-x)^{4}+\sum _{m=0}^{4}\biggl((-1)^{m}\binom {4}{m} \frac{\Gamma(5+m)}{\Gamma(5+m-\alpha)}x^{5+m-\alpha}\biggr) \\ &\quad{} -2\lambda ^{\alpha}x^{5}(1-x)^{4} \Biggr) \Biggr] \\ &\quad {}-xe^{\lambda(x-2)-t}\sum_{j=0}^{50} \frac{(2\lambda)^{j}}{j!}\sum_{m=0}^{4} \biggl((-1)^{m}\binom{4}{m}\frac{\Gamma(5+m+j)}{\Gamma (5+m+j-\alpha)}(1-x)^{j+4+m-\alpha} \biggr). \end{aligned} $$

Example 2

This example is a modification of Example 1. We replace the diffusion coefficient function \(d{(x)}\) by \(x^{2}\), then the source term is given as

$$ \begin{aligned} f(x,t) \simeq{}&{-}e^{-t} \Biggl[ e^{-\lambda x} \Biggl(x^{4}(1-x)^{4}+\sum _{m=0}^{4}\biggl((-1)^{m}\binom {4}{m} \frac{\Gamma(5+m)}{\Gamma(5+m-\alpha)}x^{6+m-\alpha}\biggr) \\ &{}-2\lambda ^{\alpha}x^{6}(1-x)^{4} \Biggr) \Biggr] \\ &{}-x^{2}e^{\lambda(x-2)-t}\sum_{j=0}^{50} \frac{(2\lambda )^{j}}{j!}\sum_{m=0}^{4} \biggl((-1)^{m}\binom{4}{m}\frac{\Gamma (5+m+j)}{\Gamma(5+m+j-\alpha)}(1-x)^{j+4+m-\alpha} \biggr). \end{aligned} $$

Other data are the same as those in Example 1.

From Tables 1 and 2, we can observe the second order convergence rate in both spatial and temporal directions for different α in \(L_{\infty}\) norm, which is consistent with our theoretical analysis. It is remarked that we numerically test the eigenvalues of matrix \(D\mathcal{M}+\mathcal{M}^{T}D\) in Examples 1 and 2, respectively. We find that all eigenvalues of the matrix \(D\mathcal{M}+\mathcal{M}^{T}D\) in Example 1 are negative, which implies that the \(D\mathcal{M}\) is negative definite, hence our assumption in the convergence analysis is valid, and the numerical results are consistent with Theorem 2. However, when the assumption in Theorem 2 is not satisfied, see Example 2, we also get the desired second order convergence rate in both spatial and temporal directions.

Table 1 The maximum errors at time \(\pmb{t=1}\) and convergence orders in spatial and temporal directions with \(\pmb{h=\tau=\frac{1}{N+1}}\) for Example  1 with different α , and \(\pmb{\lambda=1.0}\) , the parameters \(\pmb{\gamma_{1}=0.7, 0.75, 0.80}\) , respectively, and \(\pmb{\gamma_{2}}\) and \(\pmb{\gamma _{3}}\) are selected in the set \(\pmb{S_{1}^{\alpha}(\gamma_{1},\gamma _{2},\gamma_{3})}\)
Full size table
Table 2 The maximum errors at time \(\pmb{t=1}\) and convergence orders in spatial and temporal directions with \(\pmb{h=\tau=\frac{1}{N+1}}\) for Example  2 with different α , and \(\pmb{\lambda=1.0}\) , the parameters \(\pmb{\gamma_{1}=0.7, 0.75, 0.80}\) , respectively, and \(\pmb{\gamma_{2}}\) and \(\pmb{\gamma _{3}}\) are selected in the set \(\pmb{S_{1}^{\alpha}(\gamma_{1},\gamma _{2},\gamma_{3})}\)
Full size table

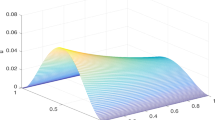
In Figures 1 and 2, we plot the curve figures of the approximating errors \(( \vert u(x_{i},t_{M})-u_{i}^{M} \vert )\) with different mesh sizes at the final time step \(t_{M}=1\) via a time-marching procedure, where \(\gamma_{1}=0.8\) and \(\lambda=1.0\) when \(\alpha=1.5\) for Example 1 and \(\alpha=1.8\) for Example 2, respectively. These figures show that the maximum norm error, defined in Eq. (11), becomes relatively smaller as the mesh size becomes smaller, which provides the validation of our results once again.

Figure 1
figure 1

The error curve figures with \(\pmb{h=\tau=\frac{1}{256}}\) (left) and \(\pmb{h=\tau=\frac{1}{512}}\) (right) at \(\pmb{t_{M}=1}\) when \(\pmb{\alpha=1.5}\) , \(\pmb{\gamma_{1}=0.8}\) and \(\pmb{\lambda=1.0}\) for Example  1 .

Full size image
Figure 2
figure 2

The error curve figures with \(\pmb{h=\tau=\frac {1}{256}}\) (left) and \(\pmb{h=\tau=\frac{1}{512}}\) (right) at \(\pmb{t_{M}=1}\) when \(\pmb{\alpha=1.8}\) , \(\pmb{\gamma_{1}=0.8}\) and \(\pmb{\lambda=1.0}\) for Example  2 .

Full size image

5 Conclusion

In this paper, the Crank-Nicolson method is proposed for solving a class of variable-coefficient tempered-FDEs (1). The method is proven to be unconditionally stable and convergent under a certain condition with rate \(\mathcal{O}(h^{2}+\tau^{2})\). Numerical examples show good agreement with the theoretical analysis.