1 Introduction

In recent decades, fractional partial differential equations have become a powerful tool to model the particle transport in anomalous diffusion in various fields. Effectively solving them naturally becomes an urgent topic of researchers. Luckily, some important achievements have been made for the fractional differential equations [1–10]. Recently, the tempered anomalous diffusion equations [11–13] have drawn the wide interests of the researchers. It is closer to reality in the sense of the finite life span or bounded physical space of the diffusion particles. The detailed introductions about the definitions and properties of the tempered fractional calculus can be seen in [14–17] and the references therein. As the generalization of fractional calculus, tempered fractional calculus does not simply have the properties of the fractional calculus, but can describe some of the other complex dynamics [18]. Tempered fractional derivatives and the corresponding tempered fractional differential equations have played a key role in physics [19], ground water hydrology [20], finance [21], poroelasticity [22], and so on.

In the continuous time random walk (CTRW) model, the corresponding time tempered fractional Fokker-Planck equation is derived [18, 23], where the jump length for Brownian particles is a constant. In practical application, however, the Brownian particles contain arbitrary distance and direction. Moreover, if the jump length probability \(\eta (x)\) follows the Lévy distribution [24, 25], i.e., \(\eta (x) \simeq \vert x \vert ^{ - \beta - 1}\) (\(0 < \beta \le 2\)), then the following time-space tempered fractional Fokker-Planck equation can well describe the probability density of particles [13, 18, 26]:

$$ \frac{\partial u(x,t)}{\partial t} = {}_{0}D_{t}^{1 - \alpha,\lambda} \biggl[ - \frac{\partial}{\partial x}F(x) + \frac{\partial^{\beta}}{ \partial \vert x \vert ^{\beta}} \biggr]u(x,t) - \lambda u(x,t), $$
(1.1)

where the tempering parameter \(\lambda \ge 0\), the function \(F(x)\) is the external force, \(u(x,t)\) representing the probability density, \({}_{0}D_{t}^{\alpha,\lambda} \) denotes the left Riemann-Liouville tempered fractional derivative of order \(\alpha \in (0,1)\), which is defined as [16]

$$ {}_{0}D_{t}^{\alpha,\lambda} u(t) = e^{ - \lambda t}{}_{0}D_{t}^{\alpha} \bigl(e^{\lambda t}u(t)\bigr) = \frac{e^{ - \lambda t}}{\Gamma (1 - \alpha )}\frac{d}{dt} \int_{0}^{t} (t - \tau )^{ - \alpha} e^{\lambda \tau} u(\tau )\,d\tau, $$
(1.2)

where \(\partial^{\beta} /\partial \vert x \vert ^{\beta} \) is the Riesz fractional derivative of order β defined by [27]

$$ \frac{\partial^{\beta} u(x,t)}{\partial \vert x \vert ^{\beta}} = - \frac{1}{2\cos (\pi \beta /2)\Gamma (2 - \beta )}\frac{d^{2}}{dx^{2}} \int_{ - \infty}^{\infty} \vert x - \xi \vert ^{1 - \beta} u(\xi,t)\,d\xi,\quad 1 < \beta \le 2, $$
(1.3)

and \(\Gamma ( \cdot )\) denotes the gamma function.

There are several ways to approximate the Riesz fractional derivative. At first, the Riesz fractional derivative was generally approached by the Grünwald-Letnikov derivative approximation with the first order of accuracy [28]. In order to improve the convergence order, various mathematical methods, such as Richardson extrapolation method, the method of lines, fractional central difference method, the matrix transform method and other high order algorithms, were developed and applied to numerically solve the Riesz fractional diffusion equation, one can see [27, 29–33] and the references therein. Here we use the second order fractional central difference method provided in [27, 34] to discrete the Riesz fractional derivative of equation (1.1). It is interesting to note that in the case of \(\lambda = 0\), the time-space tempered fractional Fokker-Planck equation (1.1) reduces to the time and space fractional Fokker-Planck equation with Riesz fractional derivative. And the numerical solutions of the fractional Fokker-Planck equations have recently been presented in a number of works. Many works have been done on the study of numerical methods for time fractional Fokker-Planck equations [35–38] and space fractional Fokker-Planck equations [39–41]. There are some efficient computational techniques for numerically solving the space and time fractional Fokker-Planck equations [42–44]. However, very few theoretical results were provided to validate the effectiveness of the presented numerical methods. Deng [45] developed the finite element method for numerical solutions of the time and space-symmetric fractional Fokker-Planck equation, the theoretical analysis of stability and convergence are rigorously established. They proved that the obtained numerical scheme has (\(2 - \alpha \)) order accuracy in time direction and numerically verified by extensive experiments. Deng et al. [46] proposed the finite difference/predictor-corrector approach for the time and space-symmetric fractional Fokker- Planck equation, their theoretical analysis and numerical experiment results show that the numerical scheme is stable and converges with order \(O(h + \tau^{\min \{ 1 + 2\alpha,2\}} )\).

So far, there have been only a limited number of works for the numerical solutions of the tempered fractional Fokker-Planck equations. Kullberg [47, 48] numerically solved the space tempered fractional Fokker-Planck equation with finite difference and spectral method. Gajda et al. [26, 49] established the numerical solution of the time tempered fractional Fokker-Planck equation via Monte Carlo methods. As far as we know, there are very few published papers for numerically solving the time-space tempered fractional Fokker-Planck equation. Therefore, the main objective of this paper is to design the high order numerical schemes for the time-space tempered fractional Fokker-Planck equation. The qth (\(q = 1,2,3,4,5\)) order operators, named the tempered and weighted and shifted Lubich difference (TWSLD) operators, are used to approximate the tempered fractional derivative, and the classical central difference and fractional centered difference are used in the spatial discretization. The detailed theoretical analysis and numerical experiments are given to confirm the validity of the numerical schemes.

The outline of this paper is as follows. In Section 2, based on some definitions and properties of the tempered fractional calculus, we derive the equivalent form of Eq. (1.1). In Section 3, we apply TWSLD operators and central difference operators to approximate the time derivative and spatial derivatives, respectively. In Section 4, we perform the detailed theoretical analysis for the stability and convergence of the presented schemes. Extensive numerical experiments are carried out in Section 5 to confirm the theoretical results of our schemes. In Section 6, the probability density distribution of diffusion particles is simulated. We conclude the paper in the last section.

2 The equivalent equation of Eq. (1.1)

In this section, using the definitions and properties of fractional calculus, we transform Eq. (1.1) into another equivalent form, which is more convenient for approximating by our methods.

Using the definition of Riemann-Liouville tempered fractional derivative, Eq. (1.1) can be rewritten as

$$ \frac{\partial (e^{\lambda t}u(x,t))}{\partial t} = {}_{0}D_{t}^{1 - \alpha} \biggl[ - \frac{\partial}{\partial x}F(x) + \frac{\partial^{\beta}}{ \partial \vert x \vert ^{\beta}} \biggr]\bigl(e^{\lambda t}u(x,t) \bigr). $$
(2.1)

Applying the operator \({}_{0}D_{t}^{\alpha - 1}\) (or \({}_{0}I_{t}^{1 - \alpha} \)) on both sides of Eq. (2.1) leads to

$$ {}_{0}D_{t}^{\alpha - 1} \biggl[ \frac{\partial (e^{\lambda t}u(x,t))}{\partial t} \biggr] = {}_{0}D_{t}^{\alpha - 1} \biggl\{ {}_{0}D_{t}^{1 - \alpha} \biggl[ - \frac{\partial}{\partial x}F(x) + \frac{\partial^{\beta}}{\partial \vert x \vert ^{\beta}} \biggr]\bigl(e^{\lambda t}u(x,t)\bigr) \biggr\} . $$
(2.2)

Recalling the composite properties of the Riemann-Liouville fractional calculus [50–53], the left-hand side and the right-hand side of Eq. (2.2) can be rewritten as

$$ {}_{0}D_{t}^{\alpha - 1} \biggl[ \frac{\partial (e^{\lambda t}u(x,t))}{\partial t} \biggr] = {}_{0}D_{t}^{\alpha} \bigl(e^{\lambda t}u(x,t) \bigr) - \frac{t^{ - \alpha}}{\Gamma (1 - \alpha )}u(x,0), $$
(2.3)

and

$$ \begin{aligned}[b] &{}_{0}D_{t}^{\alpha - 1} \biggl\{ {}_{0}D_{t}^{1 - \alpha} \biggl[ - \frac{\partial}{\partial x}F(x) + \frac{\partial^{\beta}}{ \partial \vert x \vert ^{\beta}} \biggr]\bigl(e^{\lambda t}u(x,t)\bigr) \biggr\} \\ &\quad = \biggl[ - \frac{\partial}{\partial x}F(x) + \frac{\partial^{\beta}}{ \partial \vert x \vert ^{\beta}} \biggr] \bigl(e^{\lambda t}u(x,t)\bigr) \\ &\qquad {}- {}_{0}D_{t}^{ - \alpha} \biggl\{ \biggl[ - \frac{\partial}{\partial x}F(x) + \frac{\partial^{\beta}}{\partial \vert x \vert ^{\beta}} \biggr]\bigl(e^{\lambda t}u(x,t) \bigr) \vert _{t = 0} \biggr\} \frac{t^{ - \alpha}}{\Gamma (1 - \alpha )}. \end{aligned} $$
(2.4)

If the function \(u(t)\) is continuously differentiable in the interval \([0,t]\), then

$$\begin{aligned} {}_{0}D_{t}^{ - \alpha} \bigl(e^{\lambda t}u(t) \bigr) \vert _{t = 0} &= \lim_{t \to 0^{ +}} \frac{1}{\Gamma (\alpha )} \int_{0}^{t} (t - \tau )^{\alpha - 1}e^{\lambda \tau} u(\tau ) \,d\tau \\ & = \lim_{t \to 0^{ +}} \biggl[ \frac{t^{\alpha} u(0)}{\Gamma (\alpha + 1)} + \frac{1}{\Gamma (\alpha + 1)} \int_{0}^{t} (t - \tau )^{\alpha} e^{\lambda \tau} \biggl( \lambda u(\tau ) + \frac{d(u(\tau ))}{d\tau} \biggr) \,d\tau \biggr] \\ & = 0. \end{aligned}$$
(2.5)

Since \(u(x,t) \in C_{x,t}^{2,1}([a,b] \times [0,T])\), we can obtain

$$ {}_{0}D_{t}^{ - \alpha} \biggl\{ \biggl[ - \frac{\partial}{\partial x}F(x) + \frac{\partial^{\beta}}{\partial \vert x \vert ^{\beta}} \biggr]\bigl(e^{\lambda t}u(x,t) \bigr) \vert _{t = 0} \biggr\} = 0. $$
(2.6)

From above Eqs. (2.2)-(2.6), we get

$$ {}_{0}D_{t}^{\alpha} \bigl(e^{\lambda t}u(x,t) \bigr) - \frac{t^{ - \alpha}}{\Gamma (1 - \alpha )}u(x,0) = \biggl[ - \frac{\partial}{\partial x}F(x) + \frac{\partial^{\beta}}{\partial \vert x \vert ^{\beta}} \biggr]\bigl(e^{\lambda t}u(x,t)\bigr), $$
(2.7)

multiplying both sides of Eq. (2.7) by \(e^{ - \lambda t}\) and using the definition defined in (1.2), we have

$$ {}_{0}D_{t}^{\alpha,\lambda} \bigl( u(x,t) \bigr) - \frac{t^{ - \alpha} e^{ - \lambda t}}{\Gamma (1 - \alpha )}u(x,0) = \biggl[ - \frac{\partial}{ \partial x}F(x) + \frac{\partial^{\beta}}{\partial \vert x \vert ^{\beta}} \biggr]u(x,t). $$
(2.8)

The relationship between Riemann-Liouville and the Caputo tempered fractional derivatives shows

$$ {}_{0}D_{t}^{\alpha,\lambda} u(x,t) - \frac{t^{ - \alpha} e^{ - \lambda t}}{\Gamma (1 - \alpha )}u(x,0) = {}_{0}^{C}D_{t}^{\alpha,\lambda} u(x,t) = {}_{0}D_{t}^{\alpha,\lambda} \bigl[ u(x,t) - e^{ - \lambda t}u(x,0) \bigr], $$
(2.9)

then the equivalent form of Eq. (1.1) can be rewritten as follows:

$$ {}_{0}D_{t}^{\alpha,\lambda} \bigl[ u(x,t) - e^{ - \lambda t}u(x,0) \bigr] = \biggl[ - \frac{\partial}{\partial x}F(x) + \frac{\partial^{\beta}}{ \partial \vert x \vert ^{\beta}} \biggr]u(x,t). $$
(2.10)

3 Numerical schemes of Eq. (2.10)

In this section, we consider Eq. (2.10) in a finite domain \([a,b]\) subject to the initial condition

$$ u(x,0) = \psi (x),\quad a \le x \le b, $$
(3.1)

and the homogeneous Dirichlet boundary conditions

$$ u(a,t) = 0,\qquad u(b,t) = 0,\quad 0 < t \le T. $$
(3.2)

Note that the non-zero boundary conditions can be homogenized mathematically.

3.1 TWSLD operators and the fractional centered difference operator

In this subsection, we derive the qth order (\(q \le 5\)) operators, named TWSLD operators, by the corresponding coefficients of the generating functions \(\Re {}^{q,\alpha} (\zeta )\) to approximate the Riemann-Liouville tempered fractional derivative of order α. The form of the generating functions is as follows:

$$ \Re {}^{q,\alpha} (\zeta ) = \Biggl( \sum_{i = 1}^{q} \frac{1}{i} \bigl( 1 - e^{ - \lambda \tau} \zeta \bigr)^{i} \Biggr)^{\alpha},\quad q = 1,2,3,4,5. $$
(3.3)

For \(\lambda = 0\), formula (3.3) reduces to the fractional Lubich methods. For \(\lambda = 0\), \(\alpha = 1\), the scheme reduces to the classical (\(q + 1\))-point backward difference formula [50]. We can also write formula (3.3) as the following form:

$$ \Re {}^{q,\alpha} (\zeta ) = \Biggl( \sum_{i = 1}^{q} \frac{1}{i} \bigl( 1 - e^{ - \lambda \tau} \zeta \bigr)^{i} \Biggr)^{\alpha} = \sum_{k = 0}^{\infty} d_{k}^{q,\alpha} \xi^{k}. $$
(3.4)

Then, for the Riemann-Liouville tempered fractional derivative, there is

$$ {}_{0}D_{t}^{\alpha,\lambda} u(t_{n}) = \tau^{ - \alpha} \sum_{k = 0}^{n} d_{k}^{q,\alpha} u(t_{n - k}) + O\bigl(\tau^{q} \bigr),\quad q = 1,2,3,4,5, $$
(3.5)

where τ is the step size, \(t_{n} = n\tau\), \(d_{k}^{q,\alpha} \) can also be rewritten as

$$ d_{k}^{q,\alpha} = e^{ - \lambda k\tau} l_{k}^{q,\alpha}, \quad q = 1,2,3,4,5, k = 0,1,2, \ldots,n. $$
(3.6)

For more about the detailed description of \(l_{k}^{q,\alpha} \), one can refer to [4].

Lemma 3.1

[54]

For \(q = 1\), the coefficients \(l_{k}^{q,\alpha}\) satisfy

$$ l_{0}^{1,\alpha} = 1,\qquad l_{k}^{1,\alpha} < 0\quad (k \ge 1),\qquad \sum_{k = 0}^{n - 1} l_{k}^{1,\alpha} > 0,\qquad \sum_{k = 0}^{\infty}l_{k}^{1,\alpha} = 0, $$
(3.7)

and

$$ \frac{1}{n^{\alpha} \Gamma (1 - \alpha )} < \sum_{k = 0}^{n - 1} l_{k}^{1,\alpha} = - \sum_{k = n}^{\infty} l_{k}^{1,\alpha} \le \frac{1}{n^{\alpha}}. $$
(3.8)

Lemma 3.2

[27]

Let \(f \in C^{5}(R)\) and all derivatives up to order five belong to \(L_{1}(R)\), and

$$\Delta_{h}^{\beta} f(x) = \sum_{j = - \infty}^{\infty} \frac{( - 1)^{j}\Gamma (\beta + 1)}{\Gamma ( \beta / 2 - j + 1 )\Gamma ( \beta / 2 + j + 1 )}f(x - jh) $$

be the fractional central difference. Then the Riesz fractional derivative for \(1 < \beta \le 2\) can be approximated as

$$ \frac{\partial^{\beta} f(x)}{\partial \vert x \vert ^{\beta}} = - \frac{\Delta_{h}^{\beta} f(x)}{h^{\beta}} + O\bigl(h^{2}\bigr). $$
(3.9)

If f̂ is defined by

$$\hat{f}(x) = \textstyle\begin{cases} f(x),& x \in [a,b] ,\\ 0, &x \notin [a,b] \end{cases} $$

such that f̂ satisfies the conditions of Lemma 3.2, then we have

$$\frac{\partial^{\beta} \hat{f}(x)}{\partial \vert x \vert ^{\beta}} = - h^{ - \beta} \sum_{j = - \infty}^{\infty} \frac{( - 1)^{j}\Gamma (\beta + 1)}{\Gamma ( \beta / 2 - j + 1 )\Gamma ( \beta / 2 + j + 1 )}\hat{f}(x - jh) + O\bigl(h^{2}\bigr). $$

Since \(\hat{f}(x) = 0\) for \(x \notin [a,b]\), then

$$ \frac{\partial^{\beta} f(x)}{\partial \vert x \vert ^{\beta}} = - h^{ - \beta} \sum_{j = - \frac{b - x}{h}}^{\frac{x - a}{h}} \frac{( - 1)^{j}\Gamma (\beta + 1)}{\Gamma ( \beta / 2 - j + 1 )\Gamma ( \beta / 2 + j + 1 )}f(x - jh) + O\bigl(h^{2}\bigr), $$
(3.10)

where \(h = (b - a)/M\), and M is the number of partitions of the interval \([a,b]\).

3.2 Derivation of numerical schemes

Let the mesh points \(x_{i} = a + ih\) (\(i = 0, \ldots,M\)) and \(t_{n} = n\tau\) (\(n = 0,1,2, \ldots,N\)), where \(\tau = T/N\) and \(h = (b - a)/M\) are the equidistant time step length and space step size, respectively.

Using the TWSLD operators (3.5) to approximate the Riemann-Liouville tempered fractional derivative \({}_{0}D_{t}^{\alpha,\lambda} u(x,t)\) and \({}_{0}D_{t}^{\alpha,\lambda} (e^{ - \lambda t}u(x,0))\), we arrive at

$$\begin{aligned} &{}_{0}D_{t}^{\alpha,\lambda} u(x,t) \vert _{(x_{i},t_{n})} = \tau^{ - \alpha} \sum_{k = 0}^{n} d_{k}^{q,\alpha} u(x_{i},t_{n - k}) + O\bigl( \tau^{q}\bigr),\quad q = 1,2,3,4,5, \end{aligned}$$
(3.11)
$$\begin{aligned} &{}_{0}D_{t}^{\alpha,\lambda} \bigl[ e^{ - \lambda t}u(x,0) \bigr]_{(x_{i},t_{n})} = \tau^{ - \alpha} \sum_{k = 0}^{n} d_{k}^{q,\alpha} e^{ - \lambda (n - k)\tau} u(x_{i},0) + O\bigl( \tau^{q}\bigr),\quad q = 1,2,3,4,5. \end{aligned}$$
(3.12)

To approximate Eq. (2.10), we apply the classical central difference formula and fractional centered difference formula (3.10) for the spatial derivatives, that is,

$$\begin{aligned} &\frac{\partial}{\partial x} \bigl( - F(x)u(x,t) \bigr) \vert _{(x_{i},t_{n})} = - \frac{F(x_{i + 1})u(x_{i + 1},t_{n}) - F(x_{i - 1})u(x_{i - 1},t_{n})}{2h} + O\bigl(h^{2}\bigr), \end{aligned}$$
(3.13)
$$\begin{aligned} &\frac{\partial^{\beta} u(x_{i},t_{n})}{\partial \vert x \vert ^{\beta}} = - h^{ - \beta} \sum_{j = - M + i}^{i} g_{j} u(x_{i - j},t_{n}) + O\bigl(h^{2} \bigr), \end{aligned}$$
(3.14)

where

$$ g_{j} = \frac{( - 1)^{j}\Gamma (\beta + 1)}{\Gamma ( \beta / 2 - j + 1 )\Gamma ( \beta / 2 + j + 1 )}. $$
(3.15)

Combining Eqs. (3.11)-(3.14) and (3.6), we can obtain the following equation:

$$ \begin{aligned}[b] &\tau^{ - \alpha} \Biggl[ \sum _{k = 0}^{n} e^{ - \lambda k\tau} l_{k}^{q,\alpha} u(x_{i},t_{n - k}) - e^{ - \lambda n\tau} \sum _{k = 0}^{n} l_{k}^{q,\alpha} u(x_{i},0) \Biggr] \\ &\quad = - \frac{F(x_{i + 1})u(x_{i + 1},t_{n}) - F(x_{i - 1})u(x_{i - 1},t_{n})}{2h} - \frac{1}{h^{\beta}} \sum _{j = - M + i}^{i} g_{j} u(x_{i - j},t_{n}) + r_{i}^{n}, \end{aligned} $$
(3.16)

with

$$ \bigl\vert r_{i}^{n} \bigr\vert \le C\bigl( \tau^{q} + h^{2}\bigr),\quad q = 1,2,3,4,5, $$
(3.17)

where C is a positive constant independent of τ and h.

Multiplying both sides of Eq. (3.16) by \(\tau^{\alpha} \) results in

$$ \begin{aligned}[b] &l_{0}^{q,\alpha} u(x_{i},t_{n}) + \sum_{k = 1}^{n - 1} e^{ - \lambda k\tau} l_{k}^{q,\alpha} u(x_{i},t_{n - k}) - e^{ - \lambda n\tau} \sum_{k = 0}^{n - 1} l_{k}^{q,\alpha} u(x_{i},0) \\ &\quad = - \tau^{\alpha} \frac{F(x_{i + 1})u(x_{i + 1},t_{n}) - F(x_{i - 1})u(x_{i - 1},t_{n})}{2h} - \frac{\tau^{\alpha}}{h^{\beta}} \sum _{j = - M + i}^{i} g_{j} u(x_{i - j},t_{n}) + R_{i}^{n}, \end{aligned} $$
(3.18)

with

$$ \bigl\vert R_{i}^{n} \bigr\vert = \bigl\vert \tau^{\alpha} r_{i}^{n} \bigr\vert \le C \tau^{\alpha} \bigl(\tau^{q} + h^{2}\bigr),\quad q = 1,2,3,4,5. $$
(3.19)

Denoting \(u_{i}^{n}\) as the numerical approximation of \(u(x_{i},t_{n})\) and omitting the local truncation errors \(R_{i}^{n}\), we obtain the numerical schemes of Eq. (2.10) as follows:

$$\begin{aligned} &l_{0}^{q,\alpha} u_{i}^{n} + \sum_{k = 1}^{n - 1} e^{ - \lambda k\tau} l_{k}^{q,\alpha} u_{i}^{n - k} - e^{ - \lambda n\tau} \sum_{k = 0}^{n - 1} l_{k}^{q,\alpha} u_{i}^{0}= - \tau^{\alpha} \frac{F_{i + 1}u_{i + 1}^{n} - F_{i - 1}u_{i - 1}^{n}}{2h} - \frac{\tau^{\alpha}}{h^{\beta}} \sum _{j = - M + i}^{i} g_{j} u_{i - j}^{n}, \\ &\quad i = 1,2, \ldots,M - 1, n \ge 1, \end{aligned}$$
(3.20)

or

$$\begin{aligned} &\frac{\tau^{\alpha}}{h^{\beta}} \sum_{j = - M + i}^{i} g_{j} u_{i - j}^{n} - \tau^{\alpha} \frac{F_{i - 1}}{2h}u_{i - 1}^{n} + l_{0}^{q,\alpha} u_{i}^{n} + \tau^{\alpha} \frac{F_{i + 1}}{2h}u_{i + 1}^{n} = e^{ - \lambda n\tau} \sum_{k = 0}^{n - 1} l_{k}^{q,\alpha} u_{i}^{0} - \sum _{k = 1}^{n - 1} e^{ - \lambda k\tau} l_{k}^{q,\alpha} u_{i}^{n - k}, \\ &\quad i = 1,2, \ldots,M - 1, n \ge 1. \end{aligned}$$
(3.21)

The discrete schemes of (3.1)-(3.2) are given by (3.22)-(3.23), respectively

$$\begin{aligned} &u_{i}^{0} = \psi (x_{i}),\quad 0 \le i \le M, \end{aligned}$$
(3.22)
$$\begin{aligned} &u_{0}^{n} = 0,\qquad u_{M}^{n} = 0, \quad n \ge 1. \end{aligned}$$
(3.23)

4 Stability and convergence analysis

In this section, we prove the stability and convergence of schemes (3.21) for \(q = 1\) by the discrete \(L_{\infty} \) norm. We first introduce several lemmas that will be used later.

Lemma 4.1

[27]

The coefficients \(g_{j}\) defined in Eq. (3.15) for \(j = 0, \pm 1, \pm 2, \ldots,\beta > - 1\), satisfy

$$\begin{aligned} &(1)\quad g_{0} \ge 0, \end{aligned}$$
(4.1)
$$\begin{aligned} &(2)\quad g_{ - j} = g_{j} \le 0\quad \textit{for all } \vert j \vert \ge 1, \end{aligned}$$
(4.2)
$$\begin{aligned} &(3)\quad \sum_{j = - \infty}^{\infty} g_{j} = 0\quad \textit{and}\quad \sum_{j = - M + i \atop j \ne 0}^{i} g_{j} \le g_{0}. \end{aligned}$$
(4.3)

Lemma 4.2

[55]

Let \(\{ u_{i}\}_{i = 0}^{M}\) be the grid functions defined on grid \(\bar{\Omega} = \{ x_{i}\}_{i = 0}^{M}\). For the difference operator equation

$$ \textstyle\begin{cases} \mathcal{L}_{h}u_{i}: = a_{i}u_{i} - \sum_{p \ne i} a_{p}u_{p} = \varphi_{i}, \quad x_{i} \in \Omega = \{ x_{i}\}_{i = 1}^{M - 1}, \\ u_{0} = 0, \qquad u_{M} = 0, \end{cases} $$
(4.4)

where \(a_{i} > 0\), and \(d_{i} = a_{i} - \sum_{p \ne i} a_{p} > 0\), \(i = 1,2, \ldots,M - 1\), there exists

$$ \max_{1 \le i \le M - 1} \vert u_{i} \vert \le \max _{1 \le i \le M - 1}\frac{ \vert \varphi_{i} \vert }{d_{i}}. $$
(4.5)

Theorem 4.1

Let \(F(x)\) be an increasing function in the interval \([a,b]\) and \(\lambda \ge 0\), then the numerical scheme (3.21) is unconditionally stable, i.e.,

$$ \bigl\Vert \varepsilon^{n} \bigr\Vert _{\infty} \le \bigl\Vert \varepsilon^{0} \bigr\Vert _{\infty},\quad n = 1,2, \ldots,N. $$
(4.6)

Proof

Let \(v_{i}^{n}\) (\(i = 0,1,2 ,\ldots,M,n = 0,1,2, \ldots,N\)) be the approximate solution of scheme (3.21). Denote \(\varepsilon^{n} = \{ \varepsilon_{i}^{n} = v_{i}^{n} - u_{i}^{n} \vert 0 \le i \le M ,n \ge 0 \}\), then from Eq. (3.21) we get

$$\begin{aligned} &\frac{\tau^{\alpha}}{h^{\beta}} \sum_{j = - M + i}^{i} g_{j} \varepsilon_{i - j}^{n} - \tau^{\alpha} \frac{F_{i - 1}}{2h}\varepsilon_{i - 1}^{n} + l_{0}^{1,\alpha} \varepsilon_{i}^{n} + \tau^{\alpha} \frac{F_{i + 1}}{2h} \varepsilon_{i + 1}^{n} = e^{ - \lambda n\tau} \sum _{k = 0}^{n - 1} l_{k}^{1,\alpha} \varepsilon_{i}^{0} - \sum_{k = 1}^{n - 1} e^{ - \lambda k\tau} l_{k}^{1,\alpha} \varepsilon_{i}^{n - k}, \\ &\quad i = 0,1,2, \ldots,M, n \ge 1, \end{aligned}$$
(4.7)

since \(\varepsilon_{0}^{n} = 0\), \(\varepsilon_{M}^{n} = 0\) and \(l_{0}^{1,\alpha} = 1\), we obtain

$$\begin{aligned} &\varepsilon_{i}^{n} + \frac{\tau^{\alpha} F_{i + 1}}{2h} \varepsilon_{i + 1}^{n} - \frac{\tau^{\alpha} F_{i - 1}}{2h} \varepsilon_{i - 1}^{n} + \frac{\tau^{\alpha}}{h^{\beta}} \sum _{j = - M + i + 1}^{i - 1} g_{j}\varepsilon_{i - j}^{n} = e^{ - \lambda n\tau} \sum_{k = 0}^{n - 1} l_{k}^{1,\alpha} \varepsilon_{i}^{0} - \sum _{k = 1}^{n - 1} e^{ - \lambda k\tau} l_{k}^{1,\alpha} \varepsilon_{i}^{n - k}, \\ &\quad i = 1,2, \ldots,M - 1, n \ge 1. \end{aligned}$$
(4.8)

According to Lemma 4.1, we have

$$0 = \sum_{j = - \infty}^{\infty} g_{j} = \sum _{j = - \infty}^{ - M + i} g_{j} + \sum _{j = - M + i + 1}^{i - 1} g_{j} + \sum _{j = i}^{\infty} g_{j},\quad i = 1,2, \ldots,M - 1, $$

and \(g_{ - j} = g_{j} \le 0\) for all \(\vert j \vert \ge 1\), then \(\sum_{j = - \infty}^{ - M + i} g_{j} \le 0\), \(\sum_{j = i}^{\infty} g_{j} \le 0\), we can further get

$$\sum_{j = - M + i + 1}^{i - 1} g_{j} \ge 0, \quad i = 1,2, \ldots,M - 1. $$

Since \(F(x)\) is an increasing function, we can easily obtain

$$ \biggl(1 + \frac{\tau^{\alpha}}{h^{\beta}} g_{0}\biggr) + \frac{\tau^{\alpha}}{ 2h}(F_{i + 1} - F_{i - 1}) + \frac{\tau^{\alpha}}{h^{\beta}} \sum_{j = - M + i + 1 \atop j \ne 0}^{i - 1} g_{j} \ge 1,\quad i = 1,2, \ldots,M - 1. $$
(4.9)

From Lemma 4.2, it yields

$$\begin{aligned} \max_{1 \le i \le M - 1} \bigl\vert \varepsilon_{i}^{n} \bigr\vert & \le \max_{1 \le i \le M - 1}\frac{ \vert e^{ - \lambda n\tau} \sum_{k = 0}^{n - 1} l_{k}^{1,\alpha} \varepsilon_{i}^{0} - \sum_{k = 1}^{n - 1} e^{ - \lambda k\tau} l_{k}^{1,\alpha} \varepsilon_{i}^{n - k} \vert }{1 + \frac{\tau^{\alpha}}{2h}(F_{i + 1} - F_{i - 1}) + \frac{\tau^{\alpha}}{h^{\beta}} \sum_{j = - M + i + 1}^{i - 1} g_{j}} \\ &\le \max_{1 \le i \le M - 1} \Biggl\vert e^{ - \lambda n\tau} \sum _{k = 0}^{n - 1} l_{k}^{1,\alpha} \varepsilon_{i}^{0} - \sum_{k = 1}^{n - 1} e^{ - \lambda k\tau} l_{k}^{1,\alpha} \varepsilon_{i}^{n - k} \Biggr\vert . \end{aligned}$$
(4.10)

Combining \(\sum_{k = 0}^{n - 1} l_{k}^{1,\alpha} > 0\), \(\sum_{k = 1}^{n - 1} l_{k}^{1,\alpha} < 0\), \(e^{ - \lambda n\tau} \in (0,1]\) and inequality (4.10), we obtain

$$\begin{aligned} \max_{1 \le i \le M - 1} \bigl\vert \varepsilon_{i}^{n} \bigr\vert &\le \max_{1 \le i \le M - 1} \Biggl\vert e^{ - \lambda n\tau} \sum_{k = 0}^{n - 1} l_{k}^{1,\alpha} \varepsilon_{i}^{0} \Biggr\vert + \max _{1 \le i \le M - 1} \Biggl\vert \sum_{k = 1}^{n - 1} e^{ - \lambda k\tau} l_{k}^{1,\alpha} \varepsilon_{i}^{n - k} \Biggr\vert \\ &\le \sum_{k = 0}^{n - 1} l_{k}^{1,\alpha} \Bigl( \max_{1 \le i \le M - 1} \bigl\vert \varepsilon_{i}^{0} \bigr\vert \Bigr) - \sum_{k = 1}^{n - 1} l_{k}^{1,\alpha} \Bigl( \max_{1 \le i \le M - 1} \bigl\vert \varepsilon_{i}^{n - k} \bigr\vert \Bigr), \end{aligned}$$
(4.11)

i.e.,

$$ \bigl\Vert \varepsilon^{n} \bigr\Vert _{\infty} \le \sum _{k = 0}^{n - 1} l_{k}^{1,\alpha} \bigl\Vert \varepsilon^{0} \bigr\Vert _{\infty} - \sum _{k = 1}^{n - 1} l_{k}^{1,\alpha} \bigl\Vert \varepsilon^{n - k} \bigr\Vert _{\infty}. $$
(4.12)

Next we prove the following estimate by mathematical induction:

$$ \bigl\Vert \varepsilon^{n} \bigr\Vert _{\infty} \le \bigl\Vert \varepsilon^{0} \bigr\Vert _{\infty}. $$
(4.13)

For \(n = 1\), from inequality (4.12), we can see (4.13) holds obviously. Assuming

$$ \bigl\Vert \varepsilon^{k} \bigr\Vert _{\infty} \le \bigl\Vert \varepsilon^{0} \bigr\Vert _{\infty},\quad k = 1,2, \ldots,n - 1, $$
(4.14)

and using inequality (4.12), we obtain

$$\begin{aligned} \bigl\Vert \varepsilon^{n} \bigr\Vert _{\infty} &\le \sum _{k = 0}^{n - 1} l_{k}^{1,\alpha} \bigl\Vert \varepsilon^{0} \bigr\Vert _{\infty} - \sum _{k = 1}^{n - 1} l_{k}^{1,\alpha} \bigl\Vert \varepsilon^{n - k} \bigr\Vert _{\infty} \\ &\le \sum_{k = 0}^{n - 1} l_{k}^{1,\alpha} \bigl\Vert \varepsilon^{0} \bigr\Vert _{\infty} - \sum _{k = 1}^{n - 1} l_{k}^{1,\alpha} \bigl\Vert \varepsilon^{0} \bigr\Vert _{\infty} = \bigl\Vert \varepsilon^{0} \bigr\Vert _{\infty}. \end{aligned}$$
(4.15)

Hence, \(\Vert \varepsilon^{n} \Vert _{\infty} \le \Vert \varepsilon^{0} \Vert _{\infty} \), i.e., scheme (3.21) is unconditionally stable. □

Lemma 4.3

[54]

Let \(R \ge 0\), \(a_{k} \ge 0\), \(k = 0,1, \ldots ,N\), and satisfy

$$ a_{n} \le - \sum_{k = 1}^{n - 1} l_{k}^{q,\alpha} a_{n - k} + R,\quad n \ge 1, $$
(4.16)

(a) when \(0 < \alpha < 1\),

$$ a_{n} \le \Biggl( \sum_{k = 0}^{n - 1} l_{k}^{q,\alpha} \Biggr)^{ - 1}R \le n^{\alpha} \Gamma (1 - \alpha ) R, $$
(4.17)

(b) when \(\alpha \to 1\),

$$ a_{n} \le nR. $$
(4.18)

Theorem 4.2

Let \(F(x)\) be an increasing function in the interval \([a,b]\) and \(\lambda \ge 0\), then the numerical scheme (3.21) is convergent, and the following error estimates hold:

$$ \bigl\Vert u(x_{i},t_{n}) - u_{i}^{n} \bigr\Vert _{\infty} \le C\Gamma (1 - \alpha )T^{\alpha} \bigl(\tau + h^{2}\bigr),\quad \textit{for } 0 < \alpha < 1, $$
(4.19)

and

$$ \bigl\Vert u(x_{i},t_{n}) - u_{i}^{n} \bigr\Vert _{\infty} \le CT\bigl(\tau + h^{2}\bigr),\quad \textit{for } \alpha \to 1, $$
(4.20)

where the constant \(C > 0\) is independent of τ and h.

Proof

Let \(u(x_{i},t_{n})\) and \(u_{i}^{n}\) be the exact solution and the numerical solution at \((x_{i},t_{n})\), respectively, and \(e^{n} = \{ e_{i}^{n} = u(x_{i},t_{n}) - u_{i}^{n} \vert 0 \le i \le M ,0 \le n \le N \}\). Notice that

$$\begin{aligned} &e_{i}^{0} = 0,\quad 1 \le i \le M - 1, \end{aligned}$$
(4.21)
$$\begin{aligned} &e_{0}^{n} = 0,\qquad e_{M}^{n} = 0,\quad 0 \le n \le N. \end{aligned}$$
(4.22)

Subtracting Eq. (3.18) from Eq. (3.21), we can get the following error equation:

$$\begin{aligned} &e_{i}^{n} + \frac{\tau^{\alpha} F_{i + 1}}{2h}e_{i + 1}^{n} - \frac{\tau^{\alpha} F_{i - 1}}{2h}e_{i - 1}^{n} + \frac{\tau^{\alpha}}{h^{\beta}} \sum _{j = - M + i + 1}^{i - 1} g_{j}e_{i - j}^{n} = - \sum_{k = 1}^{n - 1} e^{ - \lambda k\tau} l_{k}^{1,\alpha} e_{i}^{n - k} + R_{i}^{n}, \\ &\quad i = 1,2, \ldots,M - 1, n \ge 1, \end{aligned}$$
(4.23)

where \(R_{i}^{n}\) is defined by (3.19). From Lemma 4.2, we derive

$$ \begin{aligned}[b] \max_{1 \le i \le M - 1} \bigl\vert e_{i}^{n} \bigr\vert &\le \max_{1 \le i \le M - 1} \frac{ \vert - \sum_{k = 1}^{n - 1} e^{ - \lambda k\tau} l_{k}^{1,\alpha} e_{i}^{n - k} + R_{i}^{n} \vert }{1 + \frac{\tau^{\alpha}}{2h}(F_{i + 1} - F_{i - 1}) + \frac{\tau^{\alpha}}{h^{\beta}} \sum_{j = - M + i}^{i} g_{j}} \\ &\le \max_{1 \le i \le M - 1} \Biggl\vert - \sum _{k = 1}^{n - 1} e^{ - \lambda k\tau} l_{k}^{1,\alpha} e_{i}^{n - k} + R_{i}^{n} \Biggr\vert \\ &\le - \sum_{k = 1}^{n - 1} l_{k}^{1,\alpha} \Bigl( \max_{1 \le i \le M - 1} \bigl\vert e_{i}^{n - k} \bigr\vert \Bigr) + R_{\max}. \end{aligned} $$
(4.24)

Using the definition of discrete \(L_{\infty} \) norm leads to

$$ \bigl\Vert e^{n} \bigr\Vert _{\infty} \le - \sum _{k = 1}^{n - 1} l_{k}^{1,\alpha} \bigl\Vert e^{n - k} \bigr\Vert _{\infty} + R_{\max}, $$
(4.25)

where \(R_{\max} = \max_{1 \le i \le M - 1,n \ge 1} \vert R_{i}^{n} \vert \).

Hence, according to Lemma 4.3, we have

$$\begin{aligned} & \bigl\Vert u(x_{i},t_{n}) - u_{i}^{n} \bigr\Vert _{\infty} \le C\Gamma (1 - \alpha )T^{\alpha} \bigl(\tau + h^{2}\bigr),\quad 0 < \alpha < 1, \end{aligned}$$
(4.26)
$$\begin{aligned} & \bigl\Vert u(x_{i},t_{n}) - u_{i}^{n} \bigr\Vert _{\infty} \le CT\bigl(\tau + h^{2}\bigr),\quad \alpha \to 1. \end{aligned}$$
(4.27)

 □

5 Numerical examples

In this section, two examples are used to illustrate the effectiveness of the algorithms and to verify the above theoretical results. The first example is used to testify the efficiency of the TWSLD operators, the second example is calculated by the presented numerical schemes (3.21), and the validity of our developed algorithms is confirmed.

Example 5.1

In this example, we consider the following tempered fractional ordinary differential initial value problem:

$$ \textstyle\begin{cases} {}_{0}D_{t}^{\alpha,\lambda} [ u(t) - e^{ - \lambda t}u(0) ] = e^{ - \lambda t}\frac{\Gamma (4 + \alpha )}{\Gamma (4)}t^{3},\quad 0 < \alpha < 1, \\ u(0) = 0, \end{cases} $$
(5.1)

then the exact solution of this problem is \(u(t) = e^{ - \lambda t}t^{3 + \alpha} \). The numerical results are shown in Tables 1-4. The errors are measured by the \(L_{\infty} \) norm

$$\operatorname{Err}(\tau ) = \bigl\Vert u(t_{n}) - u^{n} \bigr\Vert _{\infty} = \max_{0 \le n \le N} \bigl\vert u(t_{n}) - u^{n} \bigr\vert , $$

and the convergent order is approximated by

$$\operatorname{Rate} = \log_{2}\frac{\operatorname{Err}(\tau )}{\operatorname{Err}(\tau / 2)}. $$
Table 1 Numerical errors and convergent orders with \(\pmb{\lambda = 2}\) , \(\pmb{T= 1}\) , when \(\pmb{q = 1}\)
Full size table
Table 2 Numerical errors and convergent orders with \(\pmb{\lambda = 2}\) , \(\pmb{T= 1}\) , when \(\pmb{q = 2}\)
Full size table
Table 3 Numerical errors and convergent orders with \(\pmb{\lambda = 2}\) , \(\pmb{T= 1}\) , when \(\pmb{q = 3}\)
Full size table
Table 4 Numerical errors and convergent orders with \(\pmb{\lambda = 2}\) , \(\pmb{T= 1}\) , when \(\pmb{q = 4}\)
Full size table

Example 5.2

Without loss of generality, we add a force term \(f(x,t)\) on the right-hand side of Eq. (2.10). We consider

$$ {}_{0}D_{t}^{\alpha,\lambda} \bigl[ u(x,t) - e^{ - \lambda t}u(x,0) \bigr] = \biggl[ - \frac{\partial}{\partial x}F(x) + \frac{\partial^{\beta}}{\partial \vert x \vert ^{\beta}} \biggr]u(x,t) + f(x,t), $$
(5.2)

where \(0 < \alpha < 1\), \(1 < \beta \le 2\), \(\lambda \ge 0\), \(0 < x < 1\), \(0 < t \le T\), with \(F(x) = x^{2}\) and the homogeneous initial boundary conditions

$$ \begin{aligned} &u(x,0) = 0,\quad 0 \le x \le 1, \\ &u(0,t) = 0,\qquad u(1,t) = 0,\quad 0 < t \le T, \end{aligned} $$
(5.3)

and the force term \(f(x,t)\) is

$$ \begin{aligned}[b] f(x,t) ={}& e^{ - \lambda t}\frac{\Gamma (4)}{\Gamma (4 - \alpha )}t^{3 - \alpha} x^{2}(1 - x)^{2} + e^{ - \lambda t}t^{3}2x^{3}(1 - x) (2 - 3x) \\ &{}+ \frac{e^{ - \lambda t}t^{3}}{2\cos (\frac{\pi \beta}{2})} \biggl[ \frac{\Gamma (5)}{\Gamma (5 - \beta )}\bigl(x^{4 - \beta} + (1 - x)^{4 - \beta} \bigr) \\ &{} - 2\frac{\Gamma (4)}{\Gamma (4 - \beta )}\bigl(x^{3 - \beta} + (1 - x)^{3 - \beta} \bigr) + \frac{\Gamma (3)}{\Gamma (3 - \beta )}\bigl(x^{2 - \beta} + (1 - x)^{2 - \beta} \bigr) \biggr]. \end{aligned} $$
(5.4)

The exact solution of this problem is

$$ u(x,t) = e^{ - \lambda t}t^{3}x^{2}(1 - x)^{2}. $$
(5.5)

Here, the error in the \(L_{\infty} \) norm is denoted by

$$\begin{aligned} \operatorname{Err}(\tau,h) = \bigl\Vert u(x_{i},t_{n}) - u_{i}^{n} \bigr\Vert _{\infty} = \max _{0 \le i \le M} \bigl\vert u(x_{i},t_{n}) - u_{i}^{n} \bigr\vert u(x_{i},t_{n}) - u_{i}^{n} \vert ,\quad n \ge 0. \end{aligned}$$

For theoretical convergent accuracy \(O(\tau^{q} + h^{p})\), the convergent order about step length h can be approximated by

$$\mbox{Rate} = \log_{2}\frac{\operatorname{Err}(\tau,h)}{\operatorname{Err}(2^{ - p / q}\tau,h / 2)}. $$

Problem (5.2)-(5.3) is calculated by the new numerical schemes (3.21), and the numerical results with different parameters α, β and λ are given in Tables 5-8. It is obvious that the numerical schemes with high order accuracy and the convergence orders are almost consistent with the theoretical results \(O(\tau^{q} + h^{2})\).

Table 5 Numerical errors and convergent orders with \(\pmb{\beta = 1.5}\) , \(\pmb{\lambda = 2}\) , \(\pmb{T = 1}\) , when \(\pmb{q = 1}\) , \(\pmb{\tau = h^{2}}\)
Full size table
Table 6 Numerical errors and convergent orders with \(\pmb{\beta = 1.5}\) , \(\pmb{\lambda = 2}\) , \(\pmb{T = 1}\) , when \(\pmb{q = 4}\) , \(\pmb{\tau = h^{1/2}}\)
Full size table
Table 7 Numerical errors and convergent orders with \(\pmb{\alpha =0.5}\) , \(\pmb{\lambda = 2}\) , \(\pmb{T = 1}\) , when \(\pmb{q = 1}\) , \(\pmb{\tau = h^{2}}\)
Full size table
Table 8 Numerical errors and convergent orders with \(\pmb{\alpha = 0.5}\) , \(\pmb{\beta = 1.5}\) , \(\pmb{T = 1}\) , when \(\pmb{q = 4}\) , \(\pmb{\tau = h^{1/2}}\)
Full size table

6 Numerical simulations

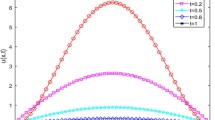
Using the numerical schemes (3.21), we simulate the probability density distribution \(u(x,t)\) of the diffusion particles on a finite domain \([0,4]\). We consider the Gaussian function which tends to the δ function when \(\sigma\rightarrow0\) [7]

$$u(x,0) = \frac{1}{\sigma \sqrt{2\pi}} \exp \biggl( - \frac{(x - 2)^{2}}{2\sigma^{2}} \biggr) $$

as the initial condition, and \(u(0,t) = u(4,t) = 0\) as the boundary conditions. In the calculation process, let the force term \(f(x,t) = 0\), \(h=1/40\), \(\tau=h^{2}\), \(\sigma=0.01\).

Let \(F(x) = x\), the numerical results under different parameters are shown in Figure 1. It can be seen that the values of α, β, λ, t have a different effect on the probability density of the particles, but all of these curves have a cusp. The experimental results are in agreement with the analytic results given in [56, 57], which indicates the effectiveness of our numerical schemes again.

Figure 1
figure 1

The probability density distribution of particles under different values of α , β , λ , t .

Full size image

7 Conclusions

It is well known that the time-space fractional Fokker-Planck equations play a key role in modelling relevant physical processes. The high order numerical algorithms for the differential equations naturally become an urgent topic. In this work, the high order schemes have been used to numerically solve the time-space tempered fractional Fokker-Planck equation with the space Riesz fractional derivative. We have proved theoretically that the numerical scheme is unconditionally stable and convergent with orders \(O(\tau^{q} + h^{2})\) (\(q = 1,2,3,4,5\)), which is higher than some recently studied schemes in terms of temporal direction. Extensive numerical experiments and simulations are carried out to verify the theoretical results.