1 Introduction

A famous predator-prey system with Beddington–DeAngelis type response in the following form

$$ \begin{aligned} &\frac{\mathrm{d}x(t)}{\mathrm{d}t}=x(t) \biggl(r-bx(t)- \frac{py(t)}{1+ux(t)+vy(t)} \biggr), \\ &\frac{\mathrm{d}y(t)}{\mathrm{d}t}=y(t) \biggl(-\gamma -\delta y(t)+ \frac{qx(t)}{1+ux(t)+vy(t)} \biggr), \end{aligned} $$
(1)

has been widely studied recently (see, e.g., [1,2,3,4,5]). In system (1), \(x(t)\) and \(y(t)\) represent the densities of prey and predators at time t, respectively, For biological significance of parameters r, γ, b, δ, p, q, u, v, we refer the reader to [6, 7].

In practice, due to competition or foraging, species dispersal among multiple patches (groups) is an inevitable phenomenon. Most existing results that are concerned with predator-prey models only considered the prey disperse among n (\(n>2\)) patches (see, e.g., [8, 9]). In reality, not only prey but predators can disperse among n patches. So considering the multiple dispersal situation is more practical. In [10, 11], continuous-time and discrete-time multi-patch predator-prey models with the dispersal of both predators and prey were considered, respectively. However, since time delay frequently occurs in almost every situation, it is essential to take time delay into account. And until now, few results concern multi-patch predator-prey model with time delay, especially the situation that both predators and prey disperse among multiple patch. And to our best knowledge, the method in [10, 11] cannot be used directly to cope with time delay.

Based on the above discussion, it is greatly meaningful to study the following Beddington–DeAngelis type predator-prey model with time-varying delay and multiple dispersal among l patches:

$$ \textstyle\begin{cases} \frac{\mathrm{d}x_{i}(t)}{\mathrm{d}t}= x_{i}(t) (r_{i}-b_{i}x _{i}(t)-e_{i}y_{i} (t-\tilde{\tau }_{1}(t) )-\frac{p_{i}y _{i}(t)}{1+u_{i}x_{i}(t)+ v_{i}y_{i}(t)} )\\ \hphantom{\frac{\mathrm{d}x_{i}(t)}{\mathrm{d}t}=}{}+\sum_{j=1}^{l}a _{ij} (x_{j}(t)-\alpha _{ij}x_{i}(t) ),\\ \frac{\mathrm{d}y _{i}(t)}{\mathrm{d}t}=y_{i}(t) (-\gamma _{i}-\delta _{i}y_{i}(t)+ \varepsilon _{i}x_{i} (t-\tilde{\tau }_{2}(t) )+ \frac{q _{i}x_{i}(t)}{1+u_{i}x_{i}(t)+v_{i}y_{i}(t)} ) \\ \hphantom{\frac{\mathrm{d}y _{i}(t)}{\mathrm{d}t}=}{}+\sum_{j=1} ^{l}b_{ij} (y_{j}(t)-\beta _{ij}y_{i}(t) ), \quad t\geq 0, i\in \mathbb{L}, \end{cases} $$
(2)

where \(\mathbb{L}=\{1,2,\ldots ,l\}\), \(r_{i}, b_{i}, e_{i}, \ldots \) denote the corresponding parameters in patch i and are all nonnegative constants, \(\tilde{\tau }_{1}\), \(\tilde{\tau }_{2}\) denote the time delays, \(a_{ij} (x_{j}(t)-\alpha _{ij}x_{i}(t) )\) and \(b_{ij} (y _{j}(t)-\beta _{ij}y_{i}(t) )\) stand for the dispersal of prey and predators from patch j to patch i respectively. Constants \(a_{ij}\), \(b_{ij}\) are the dispersal rate, and the meaning of \(\alpha _{ij}\), \(\beta _{ij}\) can be seen in [12]. It is worth noting that few results have been reported on the stability of system (2).

Moreover, it is important and interesting to investigate discrete-time predator-prey model, especially when the size of population is rarely small or the population has no overlapping generation. In this paper, we construct a nonstandard finite difference scheme and apply it to system (2). Then, by simple calculation, one can have the explicit expression as follows:

$$ \textstyle\begin{cases} x_{i}(n+1)=\frac{x_{i}(n)+h (r_{i}x_{i}(n)+\sum_{j=1}^{l}a_{ij}x _{j}(n) )}{1+h (b_{i}x_{i}(n)+e_{i}y_{i} (n-\tau _{1}(n) ) +\frac{p_{i}y_{i}(n)}{1+u_{i}x_{i}(n)+v_{i}y_{i}(n)}+\sum_{j=1}^{l}a _{ij}\alpha _{ij} )},\\ y_{i}(n+1)=\frac{y_{i}(n)+h (\varepsilon _{i}y _{i}(n)x_{i} (n-\tau _{2}(n) )+\frac{q_{i}x_{i}(n)y_{i}(n)}{1+u _{i}x_{i}(n)+v_{i}y_{i}(n)}+\sum_{j=1}^{l}b_{ij}y_{j}(n) )}{1+h (\gamma _{i}+\delta _{i}y_{i}(n)+\sum_{j=1}^{l}b_{ij}\beta _{ij} )}, \end{cases} $$
(3)

where \(i\in \mathbb{L}\), \(h>0\) is the time step size, and \(\tau _{1}(n)= [\frac{\tilde{\tau }_{1}(nh)}{h} ]\), \(\tau _{2}(n)= [\frac{ \tilde{\tau }_{2}(nh)}{h} ]\), where \([a]\) represents the integer part of \(a\in \mathbb{R}^{1}_{+}\), \(x_{i}(n)\) and \(y_{i}(n)\) are the numerical approximations of \(x_{i}\) and \(y_{i}\) at \(t_{n}=nh\), respectively. Clearly, the solutions of system (3) are positive unconditionally if the initial conditions are positive.

In this paper, a systematic method is provided to construct a global Lyapunov–Krasovskii function for system (3), that is the combination of Lyapunov–Krasovskii function of each patch and the graph-theoretical technique on multiple digraphs. Then a criterion is derived to ensure the stability of system (3), which is closely related to the topological structure of the dispersal networks and the bound of the time-varying delay. Finally, an example showing the effectiveness of the provided results is given.

2 Main results

Let \(\mathbb{N}=\{0,1,2,\ldots \}\), \(\mathbb{R}_{+}=[0,+\infty )\), and \(\mathbb{L}=\{1,2,\ldots ,l\}\). Write \(\mathbb{R}^{m}\) for an m-dimensional Euclidean space and denote by \(\mathbb{R}_{+}^{m}=\{(y _{1},y_{2},\ldots ,y_{m})^{\mathrm{T}}\in \mathbb{R}^{m}:y_{i}>0,i=1,2, \ldots ,m\}\). Define \(\mathbb{S}_{\delta }^{m}(x^{*})=\{x\in \mathbb{R}^{m}: |x-x^{*}|<\delta \}\). The nonnegative function \(\tau (n)\) denotes the time delay, satisfying \(\tau _{m}\leq \tau (n) \leq \tau _{M}\), \(n\in \mathbb{N}\), where \(\tau _{m}\) and \(\tau _{M}\) are positive integers.

A digraph \(\mathcal{G}\) can be represented by \(\mathcal{G}=( \mathcal{U},\mathcal{V})\), where \(\mathcal{U}=\mathbb{L}\) is a vertices set and \(\mathcal{V}\) is an arcs set. Arc \((i,j)\in \mathcal{V}\) stands for an arc leading from vertex i to vertex j and \((i,i)\notin \mathcal{V}\) for all \(i\in \mathcal{U}\). A digraph \(\mathcal{G}\) is weighted if each arc \((j,i)\) has a positive weight \(a_{ij}\) and \(a_{ij}>0\) if and only if there exists an arc \((i,j)\) in \(\mathcal{G}\). Denote by \(A=(a_{ij})_{l\times l}\) the weight matrix of \(\mathcal{G}\). We mean \((\mathcal{G},A)\) as a digraph \(\mathcal{G}\) with weight matrix A. Define the Laplacian matrix of \(\mathcal{G}\) to be \(L( \mathcal{G})=(\varphi _{ij})_{l\times l}\), where

$$ \varphi _{ij}= \textstyle\begin{cases} \sum_{r\neq i}a_{ir}, &i=j, \\ -a_{ij}, &i\neq j. \end{cases} $$

For other details on graph theory, the reader can be referred to [13].

Without loss of generality, assume system (3) has a unique positive equilibrium

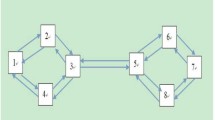
$$ X^{*}=\bigl(\bigl(X_{1}^{*} \bigr)^{\mathrm{T}},\bigl(X_{2}^{*} \bigr)^{\mathrm{T}},\ldots ,\bigl(X _{l}^{*} \bigr)^{\mathrm{T}}\bigr)^{\mathrm{T}}, $$

where \(X_{i}^{*}= (x_{i}^{*},y_{i}^{*} )^{\mathrm{T}}\). Furthermore, we introduce \(X_{i}^{(n)}= (x_{i}(n),y_{i}(n) ) ^{\mathrm{T}}\) and \(X_{n}= ((X_{1}^{(n)})^{\mathrm{T}}, (X_{2} ^{(n)})^{\mathrm{T}},\ldots ,(X_{l}^{(n)})^{\mathrm{T}} )^{ \mathrm{T}}\). Let \(\tilde{a}_{ij}=a_{ij}q_{i}(1+v_{i}y^{*})x_{j}^{*}\), \(\tilde{b}_{ij}=b_{ij}p_{i}(1+u_{i}x^{*})y_{j}^{*}\), \(\tilde{A}= (\tilde{a} _{ij} )_{l\times l}\), and \(\tilde{B}= (\tilde{b}_{ij} ) _{l\times l}\). Moreover, denote by \(c_{1}^{(i)}\) and \(c_{2}^{(i)}\) the cofactor of the ith diagonal element of the Laplacian matrix of \((\mathcal{G}_{1},\tilde{A})\) and \((\mathcal{G}_{2},\tilde{B})\), respectively. In this paper, we establish system (3) on diagraphs \((\mathcal{G}_{1},\tilde{A})\) and \((\mathcal{G}_{2},\tilde{B})\). In \((\mathcal{G}_{1},\tilde{A})\), the vertices represent prey and arcs denote the dispersal of prey. In \((\mathcal{G}_{2},\tilde{B})\), the vertices represent predators and arcs denote the dispersal of predators. In order to better illustrate our model, we present an illustrative diagram for the dispersal of both prey and predators as shown in Fig. 1.

Figure 1
figure 1

A structure for system (3) on four patches with two weighted digraphs: digraph \((\mathcal{G},\tilde{A})\) represents the dispersal of prey and digraph \((\mathcal{G},\tilde{B})\) represents the dispersal of predators

Full size image

From Fig. 1, we can see that there are two dispersal networks for our model, which, respectively, illustrate the dispersal of prey and predators. While in many previous results, see [8, 9] for example, the authors only considered the dispersal of prey. In this case, the illustrative diagram becomes the form of Fig. 2. While in reality, the dispersal of prey and predators among patches should be consistent. Hence, considering the dispersal of prey and predators simultaneously is more realistic. Another illustrative example is the epidemic model in a patchy environment [14], in which both susceptible individuals and infectious individuals disperse among patches.

Figure 2
figure 2

A structure for system (3) on four patches with the dispersal of prey denoted by digraph \((\mathcal{G},\tilde{A})\)

Full size image

Then a stability criterion for system (3) is given as follows.

Theorem 1

Suppose that digraphs \((\mathcal{G}_{1},\tilde{A})\) and \((\mathcal{G} _{2},\tilde{B})\) are strongly connected and there exists \(\theta >0\) such that \(c_{1}^{(i)}=\theta c_{2}^{(i)}\) for any \(i\in \mathbb{L}\). Suppose that there exist positive constants \(\sigma _{1}^{(i)}\) and \(\sigma _{2}^{(i)}\) satisfying the following inequality:

$$ \frac{ \varepsilon _{i}^{2}h}{2\sigma _{1}^{(i)}}< \theta < \frac{2\sigma _{2}^{(i)}}{ e_{i}^{2}h}, $$
(4)

and

$$ \begin{aligned} &\lambda _{1}^{(i)}h \biggl(\frac{p_{i}u_{i}y_{i}^{*}}{1+u_{i}x_{i}^{*}+v _{i}y_{i}^{*}}+\frac{\lambda _{1}^{(i)}}{2}-b_{i} \biggr)+ \sigma _{1} ^{(i)} \bigl(1+\tau _{M}^{(2)}- \tau _{m}^{(2)} \bigr)< 0, \\ &\lambda _{2}^{(i)}h \biggl(\frac{\lambda _{2}^{(i)}}{2}-\delta _{i} \biggr)+ \sigma _{2}^{(i)} \bigl(1+\tau _{M}^{(1)}-\tau _{m}^{(1)} \bigr)< 0, \quad i\in \mathbb{L}, \end{aligned} $$
(5)

where \(\lambda _{1}^{(i)}=q_{i}(1+v_{i}y^{*})\) and \(\lambda _{2}^{(i)}= \theta p_{i}(1+u_{i}x^{*})\). Then, for any ε and M satisfying \(0<\varepsilon <M\), there exist \(\tilde{h}(\varepsilon ,M)>0\) and \(\mathbb{S}_{M}^{2l}(X^{*})\in \mathbb{R}_{+}^{2l}\) such that, for any \(h\in (0,\tilde{h})\),

$$ \limsup_{n\rightarrow \infty } \bigl\vert X_{n}-X^{*} \bigr\vert < \varepsilon , \quad X_{0}\in \mathbb{S}_{M}^{2l} \bigl(X^{*}\bigr). $$

Proof

Define a Lyapunov function for system (3) as follows:

$$ V (X_{n} )=\sum_{i=1}^{l} \Biggl(c_{1}^{(i)}\sum_{r=1}^{3}V _{1,r}^{(i)} \bigl(x_{i}(n) \bigr)+ c_{2}^{(i)}\sum_{r=1}^{3}V_{2,r} ^{(i)} \bigl(y_{i}(n) \bigr) \Biggr), $$
(6)

where

$$\begin{aligned} &V_{1,1}^{(i)} \bigl(x_{i}(n) \bigr)=\lambda _{1}^{(i)} \bigl(x_{i}(n)-x _{i}^{*}\ln x_{i}(n) \bigr), \\ &V_{2,1}^{(i)} \bigl(y_{i}(n) \bigr)=\lambda _{2}^{(i)} \bigl(y_{i}(n)-y _{i}^{*}\ln y_{i}(n) \bigr), \\ &V_{1,2}^{(i)} \bigl(x_{i}(n) \bigr)=\sigma _{1}^{(i)} \sum_{r=n-\tau _{2}(n)}^{n-1} \bigl(x_{i}(r)-x_{i}^{*} \bigr)^{2}, \\ &V_{2,2}^{(i)} \bigl(y_{i}(n) \bigr)=\sigma _{2}^{(i)} \sum_{r=n-\tau _{1}(n)}^{n-1} \bigl(y_{i}(r)-y_{i}^{*} \bigr)^{2}, \\ &V_{1,3}^{(i)} \bigl(x_{i}(n) \bigr)=\sigma _{1}^{(i)} \sum_{q=n-\tau _{M}^{(2)}+1}^{n-\tau _{m}^{(2)}} \sum_{r=q}^{n-1} \bigl(x _{i}(r)-x_{i}^{*} \bigr)^{2}, \\ &V_{2,3}^{(i)} \bigl(y_{i}(n) \bigr)=\sigma _{2}^{(i)} \sum_{q=n-\tau _{M}^{(1)}+1}^{n-\tau _{m}^{(1)}} \sum_{r=q}^{n-1} \bigl(y _{i}(r)-y_{i}^{*} \bigr)^{2}. \end{aligned}$$

It is easy to show that \(V(X_{n})\in C^{1} (\mathbb{R}^{ml}; \mathbb{R}_{+} )\) and \(V (X^{*} )=0\).

Firstly, calculating \(\Delta V_{1,1}^{(i)} (x_{i}(n) )\) along (3), one can arrive at

$$\begin{aligned} &\Delta V_{1,1}^{(i)} \bigl(x_{i}(n) \bigr) \\ &\quad = V_{1,1}^{(i)} \bigl(x _{i}(n+1) \bigr)-V_{1,1}^{(i)} \bigl(x_{i}(n) \bigr) \\ &\quad = \lambda _{1}^{(i)} \biggl(x_{i}(n+1)-x_{i}(n)-x_{i}^{*} \ln \biggl(\frac{x _{i}(n+1)}{x_{i}(n)} \biggr) \biggr) \\ &\quad = \lambda _{1}^{(i)}h \bigl(x_{i}(n)-x_{i}^{*} \bigr) \Biggl(r_{i}-b _{i}x_{i}(n)-e_{i}y_{i} \bigl(n-\tau _{1}(n) \bigr) \\ &\qquad {}-\frac{p_{i}y_{i}(n)}{1+u _{i}x_{i}(n)+v_{i}y_{i}(n)} \\ &\qquad {}+\sum_{j=1}^{l}a_{ij} \biggl(\frac{x_{j}(n)}{x_{i}(n)}-\alpha _{ij} \biggr) \Biggr)+o(h) \\ &\quad = \lambda _{1}^{(i)}h \bigl(x_{i}(n)-x_{i}^{*} \bigr) \Biggl(-b_{i}\bigl(x _{i}(n)-x_{i}^{*} \bigr)-e_{i}\bigl(y_{i} \bigl(n-\tau _{1}(n) \bigr)-y_{i}^{*}\bigr) \\ &\qquad {}+ \sum_{j=1}^{l}a_{ij} \biggl(\frac{x_{j}(n)}{x_{i}(n)}-\frac{x_{j} ^{*}}{x_{i}^{*}} \biggr) \Biggr) - \lambda _{1}^{(i)}h \bigl(x_{i}(n)-x_{i}^{*} \bigr) \biggl(\frac{p _{i}y_{i}(n)}{1+ u_{i}x_{i}(n)+v_{i}y_{i}(n)} \\ &\qquad{} -\frac{p_{i}y_{i}^{*}}{1+u_{i}x_{i}^{*}+v_{i}y_{i}^{*}} \biggr)+o(h) \\ &\quad = -\lambda _{1}^{(i)}b_{i}h \bigl(x_{i}(n)-x_{i}^{*} \bigr)^{2}- \lambda _{1}^{(i)}e_{i}h \bigl(x_{i}(n)-x_{i}^{*} \bigr) \bigl(y_{i} \bigl(n- \tau _{1}(n) \bigr)-y_{i}^{*} \bigr) \\ &\qquad {}+\sum_{j=1}^{l}a_{ij} \lambda _{1}^{(i)}hx_{j}^{*} \biggl(\frac{x_{j}(n)}{x _{j}^{*}}-\frac{x_{i}(n)}{x_{i}^{*}}-\frac{x_{j}(n)x_{i}^{*}}{x_{i}(n)x _{j}^{*}}+1 \biggr) \\ &\qquad {}-\frac{\lambda _{1}^{(i)}p_{i}h(1+u_{i}x_{i}^{*}) (x_{i}(n)-x _{i}^{*} ) (y_{i}(n)-y_{i}^{*} )}{ (1+u_{i}x _{i}(n)+v_{i}y_{i}(n) ) (1+u_{i}x_{i}^{*}+v_{i}y_{i}^{*} )} \\ &\qquad {}+\frac{\lambda _{1}^{(i)}p_{i}hu_{i}y_{i}^{*} (x_{i}(n)-x_{i} ^{*} )^{2}}{ (1+ u_{i}x_{i}(n)+v_{i}y_{i}(n) ) (1+u _{i}x_{i}^{*}+v_{i}y_{i}^{*} )}+o(h) \\ &\quad \leq \lambda _{1}^{(i)}h \biggl(-b_{i}+ \frac{p_{i}u_{i}y_{i}^{*}}{ (1+ u_{i}x_{i}(n)+v_{i}y_{i}(n) ) (1+u_{i}x_{i}^{*}+v _{i}y_{i}^{*} )}+\frac{\lambda _{1}^{(i)}}{2} \biggr) \\ &\qquad {}\times \bigl(x_{i}(n)-x_{i}^{*} \bigr)^{2}+\frac{e_{i}^{2}h}{2}\bigl(y _{i} \bigl(n-\tau _{1}(n) \bigr)-y_{i}^{*} \bigr)^{2} \\ &\qquad {}-\frac{\lambda _{1}^{(i)}p_{i}h(1+u_{i}x_{i}^{*}) (x_{i}(n)-x _{i}^{*} ) (y_{i}(n)-y_{i}^{*} )}{ (1+ u_{i}x _{i}(n)+v_{i}y_{i}(n) ) (1+u_{i}x_{i}^{*}+v_{i}y_{i}^{*} )} \\ &\qquad {}+\sum_{j=1}^{l} \tilde{a}_{ij}F_{ij}\bigl(x_{i}(n),x_{j}(n) \bigr)+o(h), \end{aligned}$$
(7)

where \(F_{ij}(x_{i}(n),x_{j}(n))= h (\frac{x_{j}(n)}{x_{j}^{*}}-\frac{x _{i}(n)}{x_{i}^{*}}-\frac{x_{j}(n)x_{i}^{*}}{x_{i}(n)x_{j}^{*}}+1 )\). Similarly, \(\Delta V_{2,1}^{(i)} (y_{i}(n) )\) can be estimated as follows:

$$\begin{aligned} &\Delta V_{2,1}^{(i)} \bigl(y_{i}(n) \bigr) \\ &\quad =V_{2,1}^{(i)} \bigl(y _{i}(n+1) \bigr)-V_{2,1}^{(i)} \bigl(y_{i}(n) \bigr) \\ &\quad = \lambda _{2}^{(i)} \biggl(y_{i}(n+1)-y_{i}(n)-y_{i}^{*} \ln \biggl(\frac{y _{i}(n+1)}{y_{i}(n)} \biggr) \biggr) \\ &\quad = \lambda _{2}^{(i)}h \bigl(y_{i}(n)-y_{i}^{*} \bigr) \Biggl( \varepsilon _{i}x_{i} \bigl(n-\tau _{2}(n) \bigr)+\frac{q_{i}x_{i}(n)}{1+u _{i}x_{i}(n)+v_{i}y_{i}(n)} \\ &\qquad {}-\gamma _{i}-\delta _{i}y_{i}(n)+ \sum_{j=1}^{l}b_{ij} \biggl( \frac{y _{j}(n)}{y_{i}(n)}-\beta _{ij} \biggr) \Biggr)+o(h) \\ &\quad = \lambda _{2}^{(i)}h \bigl(y_{i}(n)-y_{i}^{*} \bigr) \Biggl( \varepsilon _{i} \bigl(x_{i} \bigl(n- \tau _{2}(n) \bigr)-x_{i}^{*} \bigr) -\delta _{i}\bigl(y_{i}(n)-y_{i}^{*} \bigr) \\ &\qquad {}+\sum_{j=1}^{l}b_{ij} \biggl(\frac{y_{j}(n)}{y_{i}(n)}-\frac{y_{j}^{*}}{y _{i}^{*}} \biggr) \Biggr)+\lambda _{2}^{(i)}h \bigl(y_{i}(n)-y_{i}^{*} \bigr) \\ &\qquad {}\times \biggl(\frac{q_{i}x_{i}(n)}{1+ u_{i}x_{i}(n)+v_{i}y_{i}(n)}-\frac{q _{i}x_{i}^{*}}{1+u_{i}x_{i}^{*}+v_{i}y_{i}^{*}} \biggr)+o(h) \\ &\quad = -\lambda _{2}^{(i)}\delta _{i}h \bigl(y_{i}(n)-y_{i}^{*} \bigr)^{2}+ \lambda _{2}^{(i)}\varepsilon _{i}h \bigl(y_{i}(n)-y_{i}^{*} \bigr) \bigl(x _{i} \bigl(n-\tau _{2}(n) \bigr)-x_{i}^{*}\bigr) \\ &\qquad {}+\sum_{j=1}^{l}b_{ij} \lambda _{2}^{(i)}hy_{j}^{*} \biggl(\frac{y_{j}(n)}{y _{j}^{*}}-\frac{y_{i}(n)}{y_{i}^{*}}-\frac{y_{j}(n)y_{i}^{*}}{y_{i}(n)y _{j}^{*}}+1 \biggr) \\ &\qquad {}+\frac{\lambda _{2}^{(i)}q_{i}h(1+v_{i}y_{i}^{*}) (x_{i}(n)-x _{i}^{*} ) (y_{i}(n)-y_{i}^{*} )}{ (1+u_{i}x _{i}(n)+v_{i}y_{i}(n) ) (1+u_{i}x_{i}^{*}+v_{i}y_{i}^{*} )} \\ &\qquad {}-\frac{\lambda _{2}^{(i)}q_{i}hv_{i}x_{i}^{*} (y_{i}(n)-y_{i} ^{*} )^{2}}{ (1+ u_{i}x_{i}(n)+v_{i}y_{i}(n) ) (1+u _{i}x_{i}^{*}+v_{i}y_{i}^{*} )}+o(h) \\ &\quad \leq \lambda _{2}^{(i)}h \biggl(-\delta _{i}+ \frac{\lambda _{2}^{(i)}}{2} \biggr) \bigl(y_{i}(n)-y_{i}^{*} \bigr) ^{2} +\frac{\varepsilon _{i}^{2}h}{2}\bigl(x_{i} \bigl(n- \tau _{2}(n) \bigr)-x _{i}^{*} \bigr)^{2} \\ &\quad {}+\frac{\lambda _{2}^{(i)}q_{i}h(1+v_{i}y_{i}^{*}) (x_{i}(n)-x _{i}^{*} ) (y_{i}(n)-y_{i}^{*} )}{ (1+ u_{i}x _{i}(n)+v_{i}y_{i}(n) ) (1+u_{i}x_{i}^{*}+v_{i}y_{i}^{*} )} \\ &\quad {}+\sum_{j=1}^{l} \tilde{b}_{ij}G_{ij}\bigl(y_{i}(n),y_{j}(n) \bigr)+o(h), \end{aligned}$$
(8)

where \(G_{ij}(y_{i}(n),y_{j}(n))=h\theta (\frac{y_{j}(n)}{y_{j} ^{*}}-\frac{y_{i}(n)}{y_{i}^{*}}-\frac{y_{j}(n)y_{i}^{*}}{y_{i}(n)y _{j}^{*}}+1 )\). Then we estimate \(\Delta V_{1,2}^{(i)} (x _{i}(n) )\), \(\Delta V_{1,3}^{(i)} (x_{i}(n) )\), \(\Delta V_{2,2}^{(i)} (y_{i}(n) )\), and \(\Delta V_{2,3} ^{(i)} (y_{i}(n) )\) as follows:

$$\begin{aligned} & \Delta V_{1,2}^{(i)} \bigl(x_{i}(n) \bigr) \\ &\quad = \sigma _{1}^{(i)}\sum _{r=n+1-\tau _{2}(n+1)}^{n} \bigl(x_{i}(r)-x _{i}^{*} \bigr)^{2}-\sigma _{1}^{(i)}\sum_{r=n-\tau _{2}(n)}^{n-1} \bigl(x_{i}(r)-x_{i}^{*} \bigr)^{2} \\ &\quad = \sigma _{1}^{(i)} \Biggl( \bigl(x_{i}(n)-x_{i}^{*} \bigr)^{2}- \bigl(x _{i}\bigl(n-\tau _{2}(n) \bigr)-x_{i}^{*} \bigr)^{2} \\ &\qquad {}+\sum_{r=n+1-\tau _{2}(n+1)}^{n-1} \bigl(x_{i}(r)-x_{i}^{*} \bigr) ^{2}-\sum_{r=n+1-\tau _{2}(n)}^{n-1} \bigl(x_{i}(r)-x_{i}^{*} \bigr) ^{2} \Biggr) \\ &\quad \leq \sigma _{1}^{(i)} \Biggl( \bigl(x_{i}(n)-x_{i}^{*} \bigr)^{2}- \bigl(x_{i}\bigl(n-\tau _{2}(n) \bigr)-x_{i}^{*} \bigr)^{2} \\ &\qquad {}+\sum_{r=n+1-\tau _{M}^{(2)}}^{n-1} \bigl(x_{i}(r)-x_{i}^{*} \bigr) ^{2}-\sum_{r=n+1-\tau _{m}^{(2)}}^{n-1} \bigl(x_{i}(r)-x_{i}^{*} \bigr) ^{2} \Biggr) \\ &\quad = \sigma _{1}^{(i)} \Biggl( \bigl(x_{i}(n)-x_{i}^{*} \bigr)^{2}- \bigl(x _{i}\bigl(n-\tau _{2}(n) \bigr)-x_{i}^{*} \bigr)^{2}+ \sum _{r=n+1-\tau _{M}^{(2)}} ^{n-\tau _{m}^{(2)}} \bigl(x_{i}(r)-x_{i}^{*} \bigr)^{2} \Biggr), \end{aligned}$$
(9)
$$\begin{aligned} &\Delta V_{1,3}^{(i)} \bigl(x_{i}(n) \bigr) \\ &\quad = \sigma _{1}^{(i)}\sum _{q=n-\tau _{M}^{(2)}+2}^{n-\tau _{m}^{(2)}+1} \sum_{r=q}^{n} \bigl(x_{i}(r)-x_{i}^{*} \bigr)^{2}- \sigma _{1}^{(i)} \sum _{q=n-\tau _{M}^{(2)}+1}^{n-\tau _{m}^{(2)}}\sum_{r=q}^{n-1} \bigl(x _{i}(r)-x_{i}^{*} \bigr)^{2} \\ &\quad = \sigma _{1}^{(i)} \Biggl( \bigl(x_{i}(n)-x_{i}^{*} \bigr)^{2}+ \sum_{r=n-\tau _{m}^{(2)}+1}^{n-1} \bigl(x_{i}^{(k)}(r)-x_{i}^{(k*)} \bigr) ^{2} \\ &\qquad {}-\sum_{r=n-\tau _{M}^{(2)}+1}^{n-1} \bigl(x_{i}(r)-x_{i}^{*} \bigr) ^{2}+ \bigl(\tau _{M}^{(2)}-\tau _{m}^{(2)}-1 \bigr) \bigl(x_{i}(n)-x _{i}^{*} \bigr)^{2} \Biggr) \\ &\quad = \sigma _{1}^{(i)} \Biggl( \bigl(\tau _{M}^{(2)}-\tau _{m}^{(2)} \bigr) \bigl(x_{i}(n)-x_{i}^{*} \bigr)^{2}-\sum_{r=n+1-\tau _{M}^{(2)}}^{n- \tau _{m}^{(2)}} \bigl(x_{i}(r)-x_{i}^{*} \bigr)^{2} \Biggr), \end{aligned}$$
(10)
$$\begin{aligned} &\Delta V_{2,2}^{(i)} \bigl(y_{i}(n) \bigr) \\ &\quad \leq \sigma _{2}^{(i)} \Biggl( \bigl(y_{i}(n)-y_{i}^{*} \bigr)^{2}- \bigl(y_{i}\bigl(n-\tau _{1}(n) \bigr)-y_{i}^{*} \bigr)^{2}+ \sum _{r=n+1-\tau _{M}^{(1)}}^{n-\tau _{m}^{(1)}} \bigl(y_{i}(r)-y_{i} ^{*} \bigr)^{2} \Biggr), \end{aligned}$$
(11)
$$\begin{aligned} &\Delta V_{2,3}^{(i)} \bigl(y_{i}(n) \bigr) \\ &\quad = \sigma _{2}^{(i)} \Biggl( \bigl(\tau _{M}^{(1)}-\tau _{m}^{(1)} \bigr) \bigl(y_{i}(n)-y_{i}^{*} \bigr)^{2}-\sum_{r=n+1-\tau _{M}^{(1)}}^{n- \tau _{m}^{(1)}} \bigl(y_{i}(r)-y_{i}^{*} \bigr)^{2} \Biggr). \end{aligned}$$
(12)

By (7), (8), (9), (10), (11), and (12), it follows that

$$\begin{aligned} &c_{1}^{(i)}\sum _{r=1}^{3}\Delta V_{1,r}^{(i)} \bigl(x_{i}(n) \bigr)+ c_{2}^{(i)}\sum _{r=1}^{3}\Delta V_{2,r}^{(i)} \bigl(y_{i}(n) \bigr) \\ &\quad \leq \lambda _{1}^{(i)}c_{1}^{(i)}h \biggl(-b_{i}+\frac{p_{i}u_{i}y _{i}^{*}}{ (1+u_{i}x_{i}^{*}+v_{i}y_{i}^{*} )}+\frac{ \lambda _{1}^{(i)}}{2}+ \frac{\sigma _{1}^{(i)} (1+\tau _{M}^{(2)}- \tau _{m}^{(2)} )}{\lambda _{1}^{(i)}h} \biggr) \\ &\qquad {}\times \bigl(x_{i}(n) -x_{i}^{*} \bigr)^{2}+\lambda _{2}^{(i)}c _{2}^{(i)}h \biggl(-\delta _{i}+ \frac{\lambda _{2}^{(i)}}{2}+\frac{\sigma _{2}^{(i)} (1+\tau _{M}^{(1)}-\tau _{m}^{(1)} )}{\lambda _{2} ^{(i)}h} \biggr) \\ &\qquad {}\times \bigl(y_{i}(n)-y_{i}^{*} \bigr)^{2}+ \biggl(\frac{c_{2}^{(i)} \varepsilon _{i}^{2}h}{2}-c_{1}^{(i)} \sigma _{1}^{(i)} \biggr) \bigl(x_{i} \bigl(n- \tau _{2}(n) \bigr)-x_{i}^{*} \bigr)^{2} \\ &\qquad {}+ \biggl(\frac{c_{1}^{(i)}e_{i}^{2}h}{2}-c_{2}^{(i)}\sigma _{2}^{(i)} \biggr) \bigl(y _{i} \bigl(n-\tau _{1}(n) \bigr)-y_{i}^{*} \bigr)^{2} \\ &\qquad {}+\sum_{j=1}^{l}c_{1}^{(i)} \tilde{a}_{ij}F_{ij}\bigl(x_{i}(n),x_{j}(n) \bigr)+ \sum_{j=1}^{l}c_{2}^{(i)} \tilde{b}_{ij}G_{ij}\bigl(y_{i}(n),y_{j}(n) \bigr)+o(h). \end{aligned}$$
(13)

Because \((\mathcal{G}_{1},\tilde{A})\) and \((\mathcal{G}_{2},\tilde{B})\) are both strongly connected, by Theorem 2.2 in [9], we have \(c_{1}^{(i)}>0\) and \(c_{2}^{(i)}>0\) for \(i\in \mathbb{L}\). Assume that there is \(i\in \mathbb{L}\) such that \(X_{i}^{(n)}\neq X_{i}^{*}\). For any ε and M satisfying \(0<\varepsilon <M\), we can derive from (13) that, for any \(X_{0}\in \mathbb{S}_{M}^{2l}\) and \(X_{0}\neq X^{*}\), there are \(\tilde{h}(\varepsilon ,M)>0\) and \(\mathbb{S}_{M}^{2l}(X^{*})\in \mathbb{R}_{+}^{2l}\) such that, for any \(h\in (0,\tilde{h})\), the following two cases hold.

(i) If \(X_{n}\in \mathbb{S}_{M}^{2l}\) and \(|X_{i}^{(n)}|> \varepsilon /2\), according to (4) and (5), we have that

$$ \begin{aligned}[b] & c_{1}^{(i)} \sum_{r=1}^{3}\Delta V_{1,r}^{(i)} \bigl(x_{i}(n) \bigr)+ c_{2}^{(i)}\sum_{r=1}^{3} \Delta V_{2,r}^{(i)} \bigl(y_{i}(n) \bigr) \\ &\quad < \sum_{j=1}^{l}c_{1}^{(i)} \tilde{a}_{ij}F_{ij}\bigl(x_{i}(n),x_{j}(n) \bigr)+ \sum_{j=1}^{l}c_{2}^{(i)} \tilde{b}_{ij}G_{ij}\bigl(y_{i}(n),y_{j}(n) \bigr). \end{aligned} $$
(14)

Combining (6), (14) with Theorem 2.2 in [9], we obtain that

$$\begin{aligned} \Delta V(X_{n})={} &\sum_{i=1}^{l} \Biggl(c_{1}^{(i)}\sum_{r=1}^{3} \Delta V_{1,r}^{(i)} \bigl(x_{i}(n) \bigr)+ c_{2}^{(i)}\sum_{r=1}^{3} \Delta V_{2,r}^{(i)} \bigl(y_{i}(n) \bigr) \Biggr) \\ \leq{} & \sum_{i=1}^{l}\sum _{j=1}^{l}c_{1}^{(i)} \tilde{a}_{ij}F_{ij}\bigl(x _{i}(n),x_{j}(n) \bigr)+\sum_{i=1}^{l}\sum _{j=1}^{l}c_{2}^{(i)} \tilde{b} _{ij}G_{ij}\bigl(y_{i}(n),y_{j}(n) \bigr) \\ \leq{} & \sum_{\mathcal{Q}_{1}\in \mathbb{Q}_{1}}W(\mathcal{Q}_{1}) \sum_{(\rho ,r)\in \mathcal{V}(\mathcal{C}_{\mathcal{Q}_{1}})}F_{r \rho } \bigl(x_{r}(n),x_{\rho }(n) \bigr) \\ &{} +\sum_{\mathcal{Q}_{2}\in \mathbb{Q}_{2}}W(\mathcal{Q}_{2}) \sum _{(\rho ,r)\in \mathcal{V}(\mathcal{C}_{\mathcal{Q}_{2}})}G_{r \rho } \bigl(y_{r}(n),y_{\rho }(n) \bigr), \end{aligned}$$

where \(n\in \mathbb{N}\), \(\mathbb{Q}_{1} \) and \(\mathbb{Q}_{2}\) are the sets of all spanning unicyclic graphs of \((\mathcal{G}_{1},A)\) and \((\mathcal{G}_{2},B)\), \(W(\mathcal{Q}_{1})\) and \(W(\mathcal{Q}_{2})\) stand for the weight of \(\mathcal{Q}_{1}\) and \(\mathcal{Q}_{2}\), \(\mathcal{C}_{\mathcal{Q}_{1}}\) and \(\mathcal{C}_{\mathcal{Q}_{2}}\) represent the directed cycle of \(\mathcal{Q}_{1}\) and \(\mathcal{Q} _{2}\), respectively.

Furthermore, for each directed cycle \(\mathcal{C}\) of \((\mathcal{G} _{1},\tilde{A})\) and \((\mathcal{G}_{2},\tilde{B})\), for all \(x_{i},x_{j},y_{i},y_{j}\in \mathbb{R}_{+}^{1}\), it holds that

$$\begin{aligned} \begin{aligned} \sum_{(j,i)\in \mathcal{V}(\mathcal{C})}F_{ij} \bigl(x_{i}(n),x_{j}(n) \bigr)={} &h \sum _{(j,i)\in \mathcal{V}(\mathcal{C})} \biggl(\frac{x_{j}(n)}{x_{j} ^{*}}-\frac{x_{i}(n)}{x_{i}^{*}}- \frac{x_{j}(n)x_{i}^{*}}{x_{i}(n)x _{j}^{*}}+1 \biggr) \\ \leq{} &h\sum_{(j,i)\in \mathcal{V}(\mathcal{C})} \biggl(-\frac{x_{i}(n)}{x _{i}^{*}}+ \mathrm{ln}\frac{x_{i}(n)}{x_{i}^{(*)}}+\frac{x_{j}(n)}{x _{j}^{(*)}}-\mathrm{ln} \frac{x_{j}(n)}{x_{j}^{(*)}} \biggr) \\ ={} &0. \end{aligned} \end{aligned}$$

By the same way, we can get \(\sum_{(j,i)\in \mathcal{V}(\mathcal{C})}G _{ij} (y_{i}(n),y_{j}(n) )\leq 0\).

Because \(W(\mathcal{Q}_{1})>0\) and \(W(\mathcal{Q}_{2})>0\), it is easy to see that \(\Delta V (X_{n} )<0\). That is to say \(|X_{n+1}|<|X_{n}|\).

(ii) If \(X_{n}\in \mathbb{S}_{M}^{2l}\) and for all \(k\in \mathbb{L}\), \(|X_{k}^{(n)}|<\varepsilon /2 \), by (3), we have \(|X_{n+1}|<\varepsilon \) holds.

Thus, the results of Theorem 1 could be obtained. □

Remark 1

Compared with previous references, some differences and novelties of our results should be mentioned here. In [3, 4], the stability of predator-prey systems with Beddington–DeAngelis functional response was studied, but the impact of dispersal among prey and predators was not considered. In [8, 9], predator-prey systems were investigated where only prey dispersal was considered. Because both prey and predators can disperse among multiple groups, in [10, 11], multiple disperse was taken into consideration by employing multi-digraph-based approach. However, time-varying delay should not be ignored since a predator can capture prey if and only if it reaches capturing age. In this paper, we study the stability of a predator-prey system with Beddington–DeAngelis functional response which contains both time-varying delay and multiple dispersal, which is more close to the realistic situation.

Remark 2

Recently, the graph-theoretic technique has been used to analyze a single patch population model and a coupled oscillators model; see [15, 16] and [17] for example. In [18,19,20,21,22,23,24,25,26], the stability of coupled systems on networks was analyzed effectively by the graph-theoretic technique. These works all considered a single coupling situation where the dispersal or coupling of only one component was studied. Hence the model in the above literature was built on a single digraph. Considering the practical meaning of multiple dispersal, the authors studied multi-patch model with multiple dispersal by multi-digraph theory [10, 11]. And in [27], Guo et al. extended this method to study the input-to-state stability for stochastic multi-group models with multi-dispersal. However, owning to time-varying delay, the analysis method proposed in [10, 11] is ineffective since the time-varying delay cannot be dealt with. To overcome this obstacle, we consider the Lyapunov–Krasovskii method, i.e., four more functions \(V_{1,2}^{(i)}\), \(V_{1,3}^{(i)}\), \(V_{2,2}^{(i)}\), and \(V_{2,3}^{(i)}\) are constructed to deal with time-varying delay.

Remark 3

In Theorem 1, two points should be stressed for the dispersal topologies of predators and prey: (I) The dispersal topologies should be strongly connected, which is helpful to cope with the dispersal among patches; (II) The dispersal topologies of predators and prey are proportional, i.e., \(c_{1}^{(i)}=\theta c_{2}^{(i)}\), which is helpful to deal with the cross term between predators and prey. In fact, for point (I), it could be well solved by layering the large-scale dispersal networks into several strongly connected parts; for more details, one can refer to [18]. For point (II), it is still difficult for multiple dispersal model if the dispersal topologies are not proportional.

Remark 4

In this paper, we require that the dispersal networks of prey and predators among patches are strongly connected. Biologically, this means that prey or a predator from patch i can always arrive at patch j. If the dispersal networks are not strongly connected, there exists at least one patch (set as patch \(i^{*}\)) such that prey or predators from other patches cannot reach patch \(i^{*}\), but the prey or predators in patch \(i^{*}\) can always leave patch \(i^{*}\) to other patches. Hence, the prey or predators in patch \(i^{*}\) may die out. Therefore, it is meaningful to require the strong connectedness of dispersal networks from biological viewpoint.

3 Numerical example

In this section, we consider a predator-prey model with dispersal among four patches and the parameters are selected as follows:

$$ \begin{aligned} &r_{i}= 4.2,\qquad b_{i}=2.0, \qquad e_{i}=0.1,\qquad \gamma _{i}=0.05,\qquad \delta _{i}=0.95,\qquad \varepsilon _{i}=0.475, \\ &u_{i}=1,\qquad v_{i}=1,\qquad p_{i}=0.4, \qquad q_{i}=0.1,\quad i=1,2,3,4. \end{aligned} $$

The dispersal coefficients for prey and predators are chosen as \(a_{12}=0.2549\), \(a_{13}=0.1755\), \(a_{21}=0.2879\), \(a_{23}=0.2085\), \(a_{31}=0.2085\), \(a_{34}=0.2879\), \(a_{43}=0.3749\), \(b_{12}=0.05353\), \(b_{13}=0.03686\), \(b_{21}=0.06046\), \(b_{23}=0.0438\), \(b_{31}=0.0438\), \(b_{34}=0.06046\), \(b_{43}=0.07873\). Except these, other dispersal coefficients \(a_{ij}=b_{ij}=0\). See the dispersal networks in Fig. 1.

Let \(h=0.001\), \(\sigma _{1}=\sigma _{1}=0.001\), \(\tau _{1}(n)=\tau _{2}(n)=[1.5+0.5 \sin (n)]\). To begin with, when \(\alpha _{ij}=1\), \(\beta _{ij}=1\), \(i,j=1,2,3,4\), we have

$$ \textstyle\begin{cases} r_{i}-b_{i}x_{i}^{*}-e_{i}y_{i}^{*}-\frac{p_{i}y_{i}^{*}}{1+u_{i}x _{i}^{*}+v_{i}y_{i}*}=0, \\ -\gamma _{i}-\delta _{i}y_{i}^{*}+ \varepsilon _{i}x_{i}^{*}+\frac{q_{i}x_{i}^{*}}{1+u_{i}x_{i}^{*}+v_{i}y _{i}^{*}}=0, \end{cases}\displaystyle i=1,2,3,4. $$

By simple calculation, we obtain that \(x_{i}^{*}=2\), \(y_{i}^{*}=1\), \(i=1,2,3,4\), which implies that the fixed point is \(X^{*}=(2,1,2,1, \ldots ,2,1)^{\mathrm{T}}_{8\times 1}\). By definitions \(\tilde{a}_{ij}=a _{ij}q_{i}(1+v_{i}y^{*})x_{j}^{*}\) and \(\tilde{b}_{ij}=b_{ij}p_{i}(1+u _{i}x^{*})y_{j}^{*}\), we have that \(\tilde{a}_{12}=0.1019\), \(\tilde{a}_{13}=0.0702\), \(\tilde{a}_{21}=0.115\), \(\tilde{a}_{23}=0.0834\), \(\tilde{a}_{31}=0.0834\), \(\tilde{a}_{34}=0.1151\), \(\tilde{a}_{43}=0.1499\), \(\tilde{b}_{12}=0.06424\), \(\tilde{b}_{13}=0.0442\), \(\tilde{b}_{21}=0.0725\), \(\tilde{b}_{23}=0.0525\), \(\tilde{b}_{31}=0.05256\), \(\tilde{b}_{34}=0.0725\), \(\tilde{b}_{43}=0.0944\). By calculation, we have \(\theta =c_{1}^{(i)}/c _{2}^{(i)}=4\), \(i=1,2,3,4\).

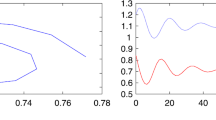
From the above dispersal coefficients, it is clear that digraphs \((\mathcal{G}_{1},A)\) and \((\mathcal{G}_{2},B)\) are strongly connected. All the conditions of Theorem 1 have been verified. Hence, we can conclude that the fixed point \(X^{*}\) remains stable in the positive cone \(\mathbb{R}_{+}^{8}\). The initial values are given as \((x_{1}(n),y _{1}(n),\ldots ,x_{4}(n),y_{4}(n))^{\mathrm{T}}=(0.8+0.1n,0.53+0.2n,1.7+0.2n,0.71+0.1n,2.1+0.1n,1.24+0.2n,2.4+0.1n,1.5+0.1n)^{ \mathrm{T}}\), where \(n=-2,-1,0\). Then the corresponding simulation results are shown in Fig. 3. Figure 3 illustrates that the fixed point \(X^{*}\) of system (3) is stable, which shows the effectiveness of our theoretical results.

Figure 3
figure 3

The solution of system (3) on four patches with time step size \(h=0.001\) and the dispersal networks as in Figure 1

Full size image

4 Conclusion

This paper studied the stability of a discrete-time multi-patch Beddington–DeAngelis type predator-prey model with time-varying delay, where the dispersal of both predators and prey was considered. By employing the Lyapunov–Krasovskii method and the graph-theoretical technique, a stability criterion was derived. Finally, an example with numerical simulation was given to demonstrate the effectiveness of the obtained results. Because noise disturbance in our real life is ubiquitous [28,29,30], in the future, we will try to take the effect of noise disturbance into our model.