Abstract
This paper regards function matrix projective synchronization of two different non-dissipatively coupled complex dynamical networks for different dimensions and different nodes. In this kind of complex dynamical networks the internal delays are different from the coupled delays. By using Lyapunov stability theory, using mathematical induction, two different hybrid feedback controllers are built to realize the function matrix projective synchronization. Compared with the existing results, the coupling matrices do not need to be symmetric or diffuse. By giving a numerical simulation we explain the validity and appropriateness of our conclusion.
Similar content being viewed by others
1 Introduction
Lots of large systems in the real world, for example, biological neural networks, social networks, food chains and food webs, can be depicted by complex networks. The complex dynamical networks are composed of coupled nodes, in which all the nodes form the edge-connected nonlinear dynamic system. In recent decades, the research of complex networks (CNs) has drawn wide attention from scholars of various fields [1,2,3,4,5,6]. Especially, synchronization as an important dynamic property of the coupled nonlinear systems has been extensively studied in [7,8,9,10,11].
In recent years, a novel synchronization, called function projective synchronization (FPS), was proposed and studied [12,13,14,15]. FPS is the coupled drive and the response systems could be synchronized to the scale function matrix. Therefore, FPS is a generalized synchronization of chaotic systems. Obviously, FPS includes complete synchronization, anti-synchronization and projective synchronization. If the scale function matrix is a unit matrix or a constant, we can obtain projective synchronization, complete synchronization or anti-synchronization. In the function matrix projective synchronization (FMPS) approach, the uncertainty of the scale function matrix can improve the security of communication [16, 17], therefore, FMS aroused wide interest of scholars.
For example, based on adaptive control, the function projective synchronization for a kind of chaotic system was considered in [18]. The function projective synchronization of complex networks by a hybrid feedback controller was proposed in [19]. Additionally, further consequences as regards the generalized matrix projective synchronization for general complex networks were studied in [20]. Even though synchronization of the complex networks for the same and different dynamic systems has been widely researched, the premise is that the dynamic dimensions of the nodes are the same. Actually, most systems are based on nonlinear dynamics, so the interactions between them may be completely different. On the other hand, during the information transmission process, because of the spatial and temporal characteristics of CNs, the time delays present in a single system and the coupled delays between the nodes may differ at different times.
Inspired by the discussion of the above issues, by constructing a Lyapunov function, applying mathematical induction, and using the matrix theory to study the complex networks for nonidentical nodes and different dimensions, we realize the function matrix projective synchronization by the hybrid feedback controller. It is worth noting that the coupling matrix is not required to obey symmetry or diffusion conditions. At last, a numerical simulation is given to explain the validity and appropriateness of our conclusion.
Notation: In this paper, \(|\cdot |\) respects the absolute value. \(I_{n}\) denotes the n-dimensional unit matrix. \(\Re ^{n}\) is n-dimensional Euclidean space, \(\Re ^{n\times n}\) respects the set of the \(n\times n\) real matrices. \(A > B\) (\(A\geq B \)) denotes the matrix \(A-B\) is positive definite (nonnegative). \(\operatorname{diag} (\cdots )\) means the block diagonal matrix. \(\lambda _{\mathrm{min}}(A)\) and \(\lambda _{\mathrm{max}}(A)\) are the minimum eigenvalue of A and the maximum eigenvalue of A, respectively. The symmetric terms in a symmetric matrix are respected by ∗. \(\|\cdot \|\) respects the Euclidean norm. If not clearly stated, all the matrices of this paper are assumed to have compatible dimensions.
2 Preliminaries
A typical complex dynamical networks consisting of N dynamical nodes with different intrinsic and coupled delays is described by
where \(x_{i}(t)=(x_{i1}(t),x_{i2}(t),\ldots ,x_{in_{i}}(t))^{T}\in \Re ^{n_{i}}\) stands for the state vector of the ith node, \(i=1,2,\ldots ,N\). \(f_{i}(\cdot ,\cdot )\in \Re ^{n_{i}}\) is the vector-valued function. \(\varepsilon >0\) denotes the coupling strength, \(\rho (t)\) and \(\tau (t)\) are the intrinsic time-varying delay and the coupled time-varying delay, respectively. \(Q_{ij}\in \Re ^{n_{i}\times n_{j}}\) stands for the inner coupling matrix, \(j=1,2,\ldots ,N\). \(C=(c_{ij})_{N\times N}\) represents the outer coupling matrix which satisfies \(c_{ij}\neq 0\), if there exists a connection from the ith to the jth node (\(i\neq j\)); otherwise \(c_{ij}=0\).
Considering (1) as the drive system, then the response system under the controller can be written as follows:
where \(y_{i}(t)=(y_{i1}(t),y_{i2}(t),\ldots ,y_{im_{i}}(t))^{T}\in \Re ^{m_{i}}\) stands for the state vector of the ith node, \(i=1,2,\ldots ,N\). \(g_{i}(\cdot )\in \Re ^{m_{i}}\) is a vector-valued function. \(\varepsilon >0\) represents the coupling strength. \(u_{i}(t)\) is the controller. \(G_{ij}\in \Re ^{m_{i}\times m_{j}}\) stands for the inner coupling matrix, \(j=1,2,\ldots ,N\). \(D=(d_{ij})_{N \times N}\) denotes the outer coupling matrix which satisfies \(d_{ij}\neq 0\), if there exists a connection from the jth node to the ith node (\(i\neq j\)); otherwise \(d_{ij}=0\).
Definition 2.1
The function matrix projective synchronization between the drive system (1) and the response system (2) is realized, if there is a matrix \(M_{i}(t)\in \Re ^{m_{i}\times n_{i}}\) which is a continuously differentiable scaling function such that
Remark 2.1
By using different special expressions for the scaling function matrix, the function matrix projective synchronization will be transformed into the complete synchronization, the anti-synchronization, the hybrid synchronization and the projective synchronization.
Definition 2.2
If for a continuously differentiable scaling function matrix \(M_{i}(t)\in \Re ^{m_{i}\times n_{i}}\), such that \(\|y_{i}(t)-M_{i}(t)x _{i}(t)\|\leq Me^{-\alpha t}\), then the exponentially FMPS between the drive system (1) and the response system (2) is called an implemented function matrix projective synchronization with the exponential rate α, where \(M, \alpha \in \Re ^{+}\).
Assumption 2.1
For different time-varying delays, \(\rho (t)\) and \(\tau (t)\) are differential expressions and satisfy \(0\leq \rho (t)\leq \rho \), \(0\leq \tau _{i}(t)\leq \tau _{i}\), \(\dot{\rho }(t)\leq \tilde{\rho }<1\) and \(\dot{\tau }(t)\leq \mu <1\), where ρ and \(\tau _{i}\) are two constants.
Assumption 2.2
For the function \(\sigma (\cdot ,\cdot )\in \Re ^{n}\) is called to satisfy the QUAD condition, that is, to say \(\sigma \in \operatorname{QUAD}(L,\Delta )\), if there are two diagonal matrices \(L \geq 0\) and \(\Delta \geq 0\) hold on
for \(\forall x, y, \tilde{x}, \tilde{y}\in \Re ^{n}\).
Lemma 2.1
For \(\forall x, y\in \Re ^{n}\) and a matrix \(R > 0\), we have \(2x^{T}y\leq x^{T}Rx+y^{T}R^{-1}y\).
3 FMPS of non-dissipatively coupled CNs via linear and nonlinear feedback control
In the following, we will give a linear and nonlinear feedback control methods to realize the FMPS.
The error state vector is
where \(M_{i}(t)\in \Re ^{m_{i}\times n_{i}}\) is the time-varying scaling matrix.
Then, from (1)–(3), the error system (EDS) would be deduced
Next, the hybrid controller is considered as
where
and \(\beta _{i}>0\) is the feedback gain. \(u_{i}^{o}(t)\) is the nonlinear controller, while \(u_{i}^{c}(t)\) is the linear feedback controller.
Thus, the SDE can be rewritten by
where \(\tilde{g}_{i}(e_{i}(t),e_{i}(t-\rho (t))) = g_{i}(y_{i}(t), y_{i}(t- \rho (t)))-g_{i}(M_{i}(t)x_{i}(t), M_{i}(t-\rho (t))x_{i}(t-\rho (t)))\), \(\tilde{G}_{ij}=d_{ij}G_{ij}\).
Theorem 3.1
Under Assumptions 2.1–2.2, for the considered synchronization scaling function matrix \(M_{i}(t)\in \Re ^{m_{i}\times n_{i}}\), if
then the drive system (1) and the response system (2) can realize FMPS by linear and nonlinear feedback control.
Proof
Build a Lyapunov functional as follows:
where
where \(P_{i} > 0\) and \(R_{i} > 0\) are the diagonal matrices which can be determined below.
The differential of \(V(e_{t})\) is obtained along the track of system (5), as follows:
It is worth noting \(\tilde{g}_{i}(\cdot ,\cdot )\) satisfies Assumption 2.2. Accordingly, there are matrices \(L_{i} > 0\) and \(\Delta _{i} > 0\), and we have
where \(L_{i}=\operatorname{diag}(l_{i1},l_{i2},\ldots ,l_{im_{i}})\), \(\Delta _{i}=\operatorname{diag}( \delta _{i1},\delta _{i2},\ldots ,\delta _{im_{i}})\), \(i=1,2,\ldots ,N\).
By Lemma 2.1, it is calculated that
Then, according to (8)–(11), it follows that
Let \(P_{i}=(1-\tilde{\rho })^{-1}e^{\alpha \rho }\Delta _{i}\), \(R_{i}=\frac{N\varepsilon }{2(1-\mu )}e^{\alpha \tau }I_{m_{i}}\), then
where \(\delta _{\mathrm{max}}=\max \{\delta _{ij}\}\), \(\ell _{\mathrm{max}}=\max \{l_{ij}\}\), \(i=1,2,\ldots ,N\), \(j=1,2,\ldots ,m_{i}\). □
4 FMPS of non-dissipatively coupled CNs via nonlinear and adaptive feedback control
Next, we put forward a nonlinear and adaptive feedback control methods to achieve FMPS. The hybrid controller is considered as
where
and \(k_{i}\) is positive constant, \(u_{i}^{o}(t)\) and \(u_{i}^{c}(t)\) are the nonlinear controller and the adaptive feedback controller, respectively.
By a similar analysis to above, one has
where \(\tilde{g}_{i}(e_{i}(t),e_{i}(t-\rho (t))) = g_{i}(y_{i}(t), y_{i}(t-\rho (t)))-g_{i}(M_{i}(t)x_{i}(t), M_{i}(t-\rho (t))x_{i}(t- \rho (t)))\), \(\tilde{G}_{ij}=d_{ij}G_{ij}\).
Theorem 4.1
Under the Assumptions 2.1–2.2, for the considered synchronization scaling function matrix \(M_{i}(t)\in \Re ^{m_{i}\times n_{i}}\), if there is a sufficiently large constant \(\beta ^{*} > 0\), satisfying
then the drive system (1) and the response system (2) can realize FMPS under nonlinear and adaptive feedback control.
Proof
Build a Lyapunov functional as follows:
where
where \(\beta ^{*} > 0 \) is a constant. \(P_{i}>0\) and \(R_{i}>0 \) are the diagonal matrices which can be determined as below.
The differential of \(V(e_{t})\) is obtained along the track of system (5), as follows:
Then, similar to the proof of Theorem 3.1, and letting \(P_{i}=(1- \tilde{\rho })^{-1}\Delta _{i}\), \(R_{i}=\frac{N\varepsilon }{2(1- \mu )}I_{m_{i}}\), we get the following result:
where \(\delta _{\mathrm{max}}=\max \{\delta _{ij}\}\), \(\ell _{\mathrm{max}}=\max \{l_{ij}\}\), \(i=1,2,\ldots ,N\) and \(j=1,2,\ldots ,m_{i}\).
In view of condition (16), one has \(\dot{V}(e_{t})\leq 0\). Let \(e(t)=(e^{T}_{1}(t),e^{T}_{2}(t),\ldots ,e^{T}_{N}(t))^{T}\), \(\tilde{\beta } = \beta ^{*} -(\frac{\varepsilon }{2}\lambda _{\mathrm{max}}( \sum^{N}_{j=1}\tilde{G}_{ij}\tilde{G}^{T}_{ij}) + (1-\tilde{\rho })^{-1} \delta _{\mathrm{max}} + \ell _{\mathrm{max}} + \frac{N\varepsilon }{2(1-\mu )})\), since \(V(e_{t})>0\), we have \(\int _{0}^{t}\tilde{\beta }\|e(s)\|^{2}\,ds \leq -\int _{0}^{t}\dot{V}(e_{s})\,ds \leq V(e_{0})-V(e_{t}) \leq V(e _{0})\). From (18), it is clear that \(V(e_{0})\) is bounded. Then, by Barbalat’s lemma, we have \(\lim_{t\rightarrow \infty }\|e(t)\|^{2}=0\), which means the FMPS is realized. □
5 Numerical example
A numerical simulation is provided to explain the validity and correctness of the theoretical results we have given.
Consider the drive network as follows:
where \(x_{i}(t)=(x_{in_{1}},x_{in_{2}})^{T}\), \(i=1,2\), \(n_{1}=3\), \(n_{2}=4\), \(\rho (t)=\frac{e^{t}}{(1+e^{t})}\), \(\tau (t)=1-0.2\cos (2t)\), \(f_{i}(x_{i}(t),x_{i}(t-\rho (t)))=f_{i}(x_{i}(t))+\frac{1}{2}\sin (x _{i}(t-\rho (t)))\). Here, we consider the nonlinear functions \(f_{i}(x_{i}(t))\) which are composed of the hyperchaotic Rossler system and the Lorenz system with nonidentical nodes:
The coupling matrices of system (20) are defined as
The response system with controller \(u_{i}(t)\) is described by
where
\(g_{i}(y_{i}(t),y_{i}(t-\rho (t)))=B_{i}y_{i}(t)+\frac{1}{2}(\cos ^{2}(y _{i}(t))-y_{i}(t-\rho (t)))\), and the parameters of system (21) are given by
Thus, we give the time-varying scaling matrices,
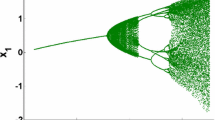
The other parameters are taken as \(\varepsilon =0.5\), \(k_{1}=k_{2}=5\), \(\beta _{1}(0)=\beta _{2}(0)=0.5\). The initial values of the state variables are random. Figures 1 and 2 demonstrate the state tracks of the drive system and the response system, respectively. From Fig. 3, we know the state tracks of the drive system and the response system can be realized as a function of matrix projective synchronization with the hybrid controller (23). In addition, Fig. 4 demonstrates the track of the adaptive feedback that obtains for \(\beta _{i}(t)\).
The state tracks of drive system (21)
The state tracks of response system (22)
6 Conclusion
This paper studies the problem of the function matrix projective synchronization for different coupled complex networks for the nonidentical nodes and the different dimensions. In order to obtain the FMPS in which the internal time delays are different from the coupled delays, the hybrid feedback controller is given, by utilizing Lyapunov stability theory and mathematical induction. The coupling matrices are not required to satisfy the symmetry and the diffusion conditions. Finally, through presenting a numerical simulation we display the validity and appropriateness of our given scheme.
References
Albert, R., Barabási, A.L.: Statistical mechanics of complex networks. Rev. Mod. Phys. 74, 47–97 (2002)
Pan, L., Cao, J., Hu, J.: Synchronization for complex networks with Markov switching via matrix measure approach. Appl. Math. Model. 39(18), 5636–5649 (2015)
Liu, X., Yu, W., Cao, J., Alsaadi, F.: Finite-time synchronisation control of complex networks via non-smooth analysis. IET Control Theory Appl. 9(8), 1245–1253 (2015)
Wang, Z., Cao, J., Guo, Z.: Dissipativity analysis and stabilization for discontinuous delayed complex-valued networks via matrix measure method. Adv. Differ. Equ. 2018, 340 (2018)
Cao, J., Guerrini, L., Cheng, Z.: Stability and Hopf bifurcation of controlled complex networks model with two delays. Appl. Math. Comput. 343, 21–29 (2019)
Boccaletti, S., Latora, V., Moreno, Y., Chavez, M., Hwang, D.U.: Complex networks: structure and dynamics. Phys. Rep. 424, 175–308 (2006)
Yang, H., Shu, L., Zhong, S., Wang, X.: Extended dissipative exponential synchronization of complex dynamical systems with coupling delay and sampled-data control. J. Franklin Inst. 353, 1829–1847 (2016)
Shi, Y., Cao, J., Chen, G.: Exponential stability of complex-valued memristor-based neural networks with time-varying delays. Appl. Math. Comput. 313, 222–234 (2017)
Wang, X., Liu, X., She, K., Zhong, S.: Pinning impulsive synchronization of complex dynamical networks with various time-varying delay sizes. Nonlinear Anal. Hybrid Syst. 26, 307–318 (2017)
Xiao, J., Zhong, S.: Extended dissipative conditions for memristive neural networks with multiple time delays. Appl. Math. Comput. 89, 145–163 (2018)
Yang, H., Shu, L., Zhong, S.: Pinning lag synchronization of complex dynamical networks with known state time-delay and unknown channel time-delay. Nonlinear Dyn. 89, 1793–1802 (2017)
Shi, Y., Zhu, P., Qin, K.: Projective synchronization of different chaotic neural networks with mixed time delays based on an integral sliding mode controller. Neurocomputing 123, 443–449 (2014)
Shi, L., Zhu, H., Zhong, S., Shi, K., Cheng, J.: Function projective synchronization of complex networks with asymmetric coupling via adaptive and pinning feedback control. ISA Trans. 65, 81–87 (2016)
Du, H., Zeng, Q., Wang, C., Ling, M.: Function projective synchronization in coupled chaotic systems. Nonlinear Anal., Real World Appl. 11, 705–712 (2010)
Al-mahbashi, G., Noorani, M., Bakar, S., Al-sawalha, M.: Robust projective lag synchronization in drive-response dynamical networks via adaptive control. Eur. Phys. J. Spec. Top. 225, 51–64 (2016)
Wu, X., Wang, H., Lu, H.: Hyperchaotic secure communication via generalized function projective synchronization. Nonlinear Anal., Real World Appl. 12, 1288–1299 (2011)
Chee, C., Xu, D.: Secure digital communication using controlled projective synchronisation of chaos. Chaos Solitons Fractals 23, 1063–1070 (2005)
Du, H., Zeng, Q., Wang, C.: Function projective synchronization of different chaotic systems with uncertain parameters. Phys. Lett. A 372, 5402–5410 (2008)
Du, H., Shi, P., Lü, N.: Function projective synchronization in complex dynamical networks with time delay via hybrid feedback control. Nonlinear Anal., Real World Appl. 14, 1182–1190 (2013)
Wu, Z., Xu, X., Chen, G., Fu, X.: Generalized matrix projective synchronization of general colored networks with different-dimensional node dynamics. J. Franklin Inst. 351, 4584–4595 (2014)
Funding
This work are supported by the scientific research starting project of SWPU (2017QHZ030), the National Natural Science Foundation of China (61703354, 71801060), the Youth Science and Technology Innovation Team of Southwest Petroleum University for Nonlinear Systems (2017CXTD02), Science and Technology Innovation Team of Education Department of Sichuan for Dynamical System and its Applications (No. 18TD0013).
Author information
Authors and Affiliations
Contributions
All authors contributed equally to the writing of this paper. All authors read and approved the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Shi, Y., Wang, X., Zeng, X. et al. Function matrix projective synchronization of non-dissipatively coupled heterogeneous systems with different-dimensional nodes. Adv Differ Equ 2019, 198 (2019). https://doi.org/10.1186/s13662-019-1984-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-019-1984-9