1 Introduction

During the past ten years, numerous papers were published to present some results on dynamics of complex-valued systems due to their wide applications in imaging processing, speech synthesis, data fusion, and dynamical programming [1–5]. Many advantages of complex-valued networks, such as powerful new capabilities and computing, have been shown in [6]. The first advantage is that complex-valued neural networks can significantly improve the generalization capabilities. For example, the authors proposed a simple structure of complex-valued neural networks, which can efficiently deal with several nonlinear data separation problems at a high symbol rate. In fact, a complex-valued neural network can learn and estimate the rotation and scaling in the two-dimensional space. Therefore there exist several storage models for complex-valued neural networks at the same time [7]. Though there are many good properties of complex-valued neural networks, it is difficult to design the activation functions. As we know, we usually choose a differential and the bounded function as an activation function in a traditional neural network. However, every analytic and bounded function in the complex plane is constant [8]. Therefore, as a weaker choice, plenty of continuous nonanalytic functions and discontinuous functions become important candidates in designing complex-valued neural networks.

In the past five years, many results on dynamics, including the existence and stability of equilibria and bifurcation analysis, of continuous complex-valued networks have been obtained [9–23]. However, all these mentioned results were obtained under the hypothesis of Lipschitz continuity. In fact, as shown by Hopfield [24, 25], the discontinuity is very common in mathematical models in many applied fields. In the following years, some dynamical behaviors, such as stability and periodic solutions, of discontinuous real-valued systems were extensively studied [26–34] via differential inclusion theory. In recent years, a small quantity of dynamical results, including multi-stability and μ-stability, have been obtained for piecewise continuous complex-valued neural networks (CVNNs) [35–38]. However, all these results did not consider the problem that the equilibria happen to fall on the boundaries of the discontinuous functions. Based on our knowledge, there is almost no result on dynamics of complex-valued networks with general discontinuous right-side functions. Since differential inclusion theory is an efficient way to deal with discontinuous problems, to discuss discontinuous complex-valued differential problems, we need to propose a framework of complex-valued differential inclusion theory correspondingly. This is the first motivation of this paper.

It is known that an important issue of dynamics of a neural network is dissipativity because of its wide applications in stability theory and control theory [39–45]. Compared with the definition of Lyapunov stability, the notion of dissipativity is more general because the dissipativity analysis is aimed at an attractive set. As we know, we only need to analyze the dynamics of attractive set since it contains an equilibrium point, periodic solution, or chaos attractor [46–52]. Dissipativity theory also provides a fundamental framework to study control problems of neural networks. The notion of stabilization is that controllers can be added to neural networks to guarantee the stability of equilibria even though the original neural network has no equilibrium point or unstable one. During the past decades, numerous results on dissipativity analysis of real-valued systems, such as switching systems, fuzzy neural networks, digital filters, and discontinuous neural networks, have been obtained [33, 47–52]. For example, the dissipativity of switching systems and fuzzy neural networks are obtained by Shi [51], respectively. Moreover, the authors of [51] extend the dissipativity results to digital filters systems. Recently, the dissipativity analysis of complex-valued networks of fractional order was studied in [53]. However, according to what we know, the issue of dissipativity analysis and stabilization of discontinuous delayed complex-valued networks are not yet considered.

To study the dynamic behavior of CVNNs, many methods were proposed, such as the complex-valued Lyapunov function method and the synthesis method [11, 16, 17, 54, 55]. In [54] and [55], the author studied the stability of CVNNs via synthesis method. However, this method usually is used to analyze discrete models. Later, the direct Lyapunov function method is used to study the stability of CVNNs [11, 16, 17]. However, all these methods are difficult to deal with discontinuous CVNNs since no proper theoretical tools can be used to deal with complex-valued Lyapunov functions. In recent years, the matrix measure method is widely used to study the stability of neural networks in [33, 56–58]. Since a matrix measure can be negative definite, which leads to less restrictive than matrix norm in handling matrix inequalities. Moreover, as we know, it is difficult to give a candidate function of discontinuous neural networks with multi-variable activation functions. The Lyapunov function is not necessary to construct by using a matrix measure strategy. For example, in [57], the authors studied the exponential stability of complex-valued networks with continuous function. In [58], the exponential stability of nonlinear continuous complex-valued differential equations is studied via the matrix measure method. However, as far as we know, there are no dynamical results on discontinuous CVNNs via the matrix measure method. Moreover, separating a CVNN into real ones and direct analysis are two different strategies to deal with complex-valued problems. For example, these two methods are used to study the stability of complex-valued delayed neural networks in [9] and [11], respectively. Thus, what is the difference of the obtained results if we study the same dynamical behavior of CVNNs by these two strategies? This is the second motivation of this paper.

Based on the matrix measure theory, we discuss the dissipativity and stabilization of discontinuous delayed CVNNs by using the mentioned different strategies. Compared with the existing results, the most great improvement is removing the hypothesis of Lipschitz continuity of the activation function. We list the main contributions of this paper:

  1. (1)

    We give an appropriate solution definition for a delayed complex-valued differential equation with discontinuous right-side by extending the real-valued functional differential inclusion theory.

  2. (2)

    We propose a sufficient condition to ensure the global dissipativity of discontinuous complex-valued networks by using a complex-valued matrix measure.

  3. (3)

    By separating the real and imaginary parts of discontinuous neural networks, we present a sufficient condition to realize global dissipativity by using the matrix measure method. This result is more general than the existing dissipativity results on real-valued neural networks.

  4. (4)

    We design state-dependent controllers with switching term to guarantee the exponential stability of the equilibria of the studied network model.

2 Neural network model and some preliminaries

The discontinuous delayed complex-valued network model is given as follows:

$$ \dot{w}(t)=-Dw(t)+Ah \bigl(w(t) \bigr)+Bh \bigl(w(t-\tau) \bigr)+J, $$
(2.1)

where \(w(t)=[w_{1}(t),w_{2}(t),\dots,w_{n}(t)]^{\mathrm{T}}\in \mathbb{C}^{n}\) denotes the state vector, \(D=\operatorname{diag}\{d_{1},d_{2},\dots,d_{n}\}\) is a self-inhibition matrix with \(d_{i}>0\), \(A\in\mathbb{C}^{n\times n}\) and \(B\in \mathbb{C}^{n\times n}\) show the connection weight matrices at times t and \(t-\tau\), respectively, \(h(w(t))=[h_{1}(w_{1}(t)),h_{2}(w_{2}(t)),\dots,h_{n}(w_{n}(t))]^{\mathrm {T}}\in \mathbb{C}^{n}\) denotes the complex-valued vector activation function, and \(J=[J_{1}, J_{2},\dots,J_{n}]^{\mathrm {T}}\in \mathbb{C}^{n}\) is an input vector.

To further study the dynamics, we make the following two hypotheses on the function \(h_{i}(w_{i})\).

\(A(1)\) For \(k=1,2,\dots,s\), \(h_{i}(w_{i})\) is continuous in finitely many open domains \(E^{i}_{k}\) and discontinuous at \(\partial E^{i}_{k}\); \(E^{i}_{k}\) satisfies \(\bigcup_{k=1}^{s}(E^{i}_{k}\cup\partial E^{i}_{k})=\mathbb{C}\) and \(E^{i}_{l}\cap E^{i}_{k}=\emptyset\) for \(1\leq l\neq k\leq s\). Moreover, the limit \(h_{ik}(w_{0})=\lim_{w\rightarrow w_{0},w\in E^{i}_{k}}h_{i}(w)\) exists for all \(w_{0}\in\partial E^{i}_{k}\).

\(A(2)\) There are two constants \(\alpha_{i}\geq0\) and \(\beta_{i}\geq0\) such that

$$ \sup_{\gamma_{i}\in K[h_{i}(w_{i})]} \Vert \gamma_{i} \Vert \leq \alpha_{i} \Vert w_{i} \Vert + \beta_{i}, $$
(2.2)

where \(K[h_{i}(w_{i})]=\{\sum_{k=1}^{s}\alpha_{k}h_{ik}(w_{i})| \alpha_{k}\geq0, \sum_{k=1}^{s}\alpha_{k}=1\}\) for \(w_{i} \in\partial E^{i}\) and \(K[h_{i}(w_{i}(t))]=h_{i}(w_{i})\) for \(w_{i}\in E^{i}\), where \(\partial E^{i}=\bigcup_{k=1}^{s}\partial E^{i}_{k}\) and \(E^{i}=\bigcup_{k=1}^{s}E^{i}_{k}\).

Remark 1

Frankly speaking, \(A(2)\) is an extension of the Lipschitz continuity condition, which is required in many papers [9, 15, 58]. In general, the constant \(\beta_{i}\neq0\) in \(A(2)\) because of the discontinuity of the functions \(h_{i}\). Here, we extend the neuron activation functions of system (2.1) to be discontinuous.

Since system (2.1) is a discontinuous network model, the classic theory of differential equations is out of work. Therefore one of the most important problems is giving an appropriate definition of a solution for a discontinuous system.

Consider the complex-valued differential equation

$$ \dot{w}(t)=h \bigl(t,w_{t}(\theta) \bigr) $$
(2.3)

with the historical state \(w_{t}(\theta)=w(t+\theta)\), where τ is a given positive number, \(h: \mathbb{R}\times C \mapsto \mathbb{C}^{n}\) is essentially locally bounded and measurable, where C is the space of continuous functions from \([-\tau,0]\) to \(\mathbb{C}^{n}\). Of course, \(h(t,w_{t}(\theta))\) may be discontinuous with respect to \(w_{t}(\theta)\).

Since \(h(t,w_{t}(\theta))\) is a discontinuous function, we explain the definition of a solution for discontinuous differential equation (2.3). To give a definition of a solution for system (2.3), we introduce the following set-valued mapping definition.

Definition 2.1

For any \(w\in E\subseteq\mathbb{C}^{n}\), if there exists a nonempty set \(H(w)\in\mathbb{C}^{n}\) corresponding to w, then \(w\mapsto H(w)\) is called a set-valued map. Furthermore, if for any \(v_{0}\in E\) and any open set N containing \(H(w_{0})\), there exists a neighborhood M of \(w_{0}\) such that \(H(M)\subset N\), where \(H(M)=\bigcup_{y\in M}H(y)\), then the set-valued map H with nonempty values is upper semicontinuous at \(w_{0}\).

Definition 2.2

For discontinuous system (2.3), we define

$$ H(t,w_{t})=\bigcap_{\delta>0}\bigcap _{\mu(\mathbb {N})=0}K \bigl[h \bigl(t,B(w_{t},\delta)\backslash \mathbb{N} \bigr) \bigr], $$

where \(K(\cdot)\) denotes the convex closure, \(B(w_{t},\delta)=\{w_{t}^{*}\in C|\|w_{t}^{*}-w_{t}\|\leq\delta\}\), and μ is the Lebesgue measure.

Definition 2.3

A complex-valued function \(w(t):I \mapsto \mathbb{C}^{n}\) is a solution of system (2.3) if it is absolutely continuous on \([t_{1},t_{2}]\subseteq I\) and satisfies \(\dot{w}(t)\in H(t,w_{t}(\theta))\) for almost all \(t\in I\).

In the following, by taking advantage of the above definitions of differential inclusion, we introduce the following definitions of a solution to a discontinuous complex-valued neural network of system (2.1). Before doing this, we first introduce the definition of absolute continuity and measurability of set-valued map.

Definition 2.4

A function \(w(t):[a,b] \mapsto\mathbb{C}\) is absolutely continuous if for any positive number \(\varepsilon>0\), there exists \(\delta>0\) such that \(\sum_{i=1}^{n}\|w(b_{i})-w(a_{i})\|<\varepsilon\) for any \((a_{i},b_{i})\subseteq[a,b]\) satisfying \(\sum_{i=1}^{n}(b_{i}-a_{i})<\delta\).

Definition 2.5

A complex set-valued map \(H:[a,b]\rightarrow\mathbb{C}^{n}\) is measurable if the nonnegative function \(t\mapsto\operatorname{ dist}(w,H(t))=\inf\{\|w-u\|,u\in H(t)\}\) is measurable for any \(w\in \mathbb{C}^{n}\).

Definition 2.6

A complex-valued function \(w(t)\) defined on \([-\tau,T)\) is a solution of system (2.1) on \([-\tau,T)\) if

  1. (i)

    \(w(t)\) is continuous on \([-\tau,T)\) and absolutely continuous on any compact subinterval of \([0,T)\), and

  2. (ii)

    for almost all \(t\in[0,T)\), \(w(t)\) satisfies

    $$ \dot{w}(t)\in-Dw(t)+AK \bigl[h \bigl(w(t) \bigr) \bigr]+BK \bigl[h \bigl(w(t-\tau) \bigr) \bigr]+J\triangleq H(t,w_{t}). $$
    (2.4)

It is easy to verify that the differential inclusion \(H(t,w_{t})\) is nonempty and compact convex. Moreover, \(H(t,w_{t})\) is upper semicontinuous and measurable in the sense of Definition 2.5. According to the measurable selection theorem in [59], there is a bounded measurable function \(\gamma=[\gamma_{1},\gamma_{2},\dots,\gamma_{n}]^{\mathrm {T}}\) satisfying

$$ \dot{w}=-Dw+A\gamma+B\gamma_{\tau}+J $$
(2.5)

for a.e. \(t\geq0\), where \(\gamma_{i}\in K[h_{i}(w_{i}]\) and \(\gamma_{\tau}=\gamma(t-\tau)\). By Definition 2.6, w is a solution of system (2.1), and γ is an output solution corresponding to w.

In the following, we mainly consider the global dissipativity of discontinuous complex-valued networks (2.1) via the matrix measure method. Before doing so, let us give the definition of global dissipativity and matrix measure.

Definition 2.7

The network model (2.1) is globally dissipative if for any initial valued \((t_{0},w_{0})\), we can find a compact set \(S\in\mathbb{C}^{n}\) and \(T(w_{0})\) such that the state solution \(w(t, t_{0},w_{0})\in S\) for \(t>t_{0}+T(w_{0})\). Furthermore, if \(w(t, t_{0},w_{0})\in S\) for all \(w_{0}\in S\) and \(t>T\), then the set S is a forward invariant.

Definition 2.8

([33, 58])

The matrix measure corresponding to a given matrix norm \(\|A\|_{\mathcal{P}}\) is defined as

$$ \mu_{\mathcal{P}}(A)=\lim_{\triangle t\rightarrow 0^{+}}\frac{ \Vert I+\triangle t A \Vert _{\mathcal{P}}-1}{\triangle t}, $$
(2.6)

where I is the identity matrix.

We now introduce an important lemma named generalized Halanay inequalities, which will be used later.

Lemma 2.9

([60])

For any nonnegative function \(W(t)\) defined on \((-\infty,+\infty)\), if there exist three continuous functions \(r(t)\geq0\), \(q(t)\geq0\), \(p(t)\leq0\) and a positive number σ such that

$$ D^{+}W(t)\leq r(t)+p(t)W(t)+q(t)\sup_{t-\tau\leq s\leq t}W(s), \quad t \geq t_{0}. $$

and

$$ q(t)+p(t)\leq-\sigma $$

for \(t\geq t_{0}\), then we have

$$ W(t)\leq\frac{r^{*}}{\sigma}+ \biggl(\sup_{-\infty\leq s\leq t_{0}} W(s)- \frac{r^{*}}{\sigma} \biggr)e^{-\mu^{*}(t-t_{0})}, $$

where \(r^{*}=\sup_{t_{0}\leq s\leq+\infty}r(t)\), \(\mu^{*}=\inf_{t\geq t_{0}}\{\mu(t)+p(t)+q(t)e^{\mu(t)\tau}\}\) and \(D^{+}W(t)= \overline{\lim_{\triangle t\rightarrow 0^{+}}}\frac{W(t+\triangle t)-W(t)}{\triangle t}\).

3 Global dissipativity analysis

Theorem 3.1

If the discontinuous functions of system (2.1) satisfy hypotheses \(A(1)\)–\(A(2)\), then for any initial values, there exists at least one solution \(w(t)\) defined on \([0,+\infty)\).

Proof

According to our discussion, the complex-valued map \(w(t)\mapsto H(t,w_{t})\) is upper semicontinuous, and \(H(t,w_{t})\) is nonempty compact convex. By analysis similar to that in [61, Thm. 1, p. 77] the local solution \(w(t)\) of (2.4) can be guaranteed.

From formula (2.2) we obtain that there exist two nonnegative constants ᾱ and β̄ such that

$$ \bigl\Vert K \bigl[h \bigl(w(t) \bigr) \bigr]\| \bigr\Vert \leq\bar{\alpha} \bigl\Vert w(t) \bigr\Vert +\bar{\beta}. $$
(3.1)

It follows that

$$\begin{aligned} \bigl\Vert H(t,w_{t}) \bigr\Vert ={}& \bigl\Vert -Dw(t)+AK \bigl[h \bigl(w(t) \bigr) \bigr]+BK \bigl[h \bigl(w(t-\tau) \bigr) \bigr]+J \bigr\Vert \\ \leq{}& \Vert D \Vert \bigl\Vert w(t) \bigr\Vert + \Vert A \Vert \bigl(\bar{\alpha} \bigl\Vert w(t) \bigr\Vert +\bar{\beta} \bigr)+ \Vert B \Vert \bigl(\bar {\alpha} \bigl\Vert w(t-\tau) \bigr\Vert +\bar{\beta} \bigr)+ \Vert J \Vert \\ ={}& \bigl( \Vert D \Vert +\bar{\alpha} \Vert A \Vert \bigr) \bigl\Vert w(t) \bigr\Vert +\bar{\alpha} \Vert B \Vert \bigl\Vert w(t-\tau) \bigr\Vert + \bigl(\bar {\beta} \bigl( \Vert A \Vert + \Vert B \Vert \bigr)+ \Vert J \Vert \bigr) \\ ={}&\bar{\bar{\alpha}} \bigl\Vert w(t) \bigr\Vert +\bar{\bar{\beta}} \bigl\Vert w(t-\tau) \bigr\Vert +\bar{\bar {\eta}}, \end{aligned}$$

where \(\bar{\bar{\alpha}}=\|D\|+\bar{\alpha}\|A\|\), \(\bar{\bar{\beta}}=\bar{\alpha}\|B\|\), and \(\bar{\bar{\eta}}=\bar{\beta}(\|A\|+\|B\|)+\|J\|\).

According to (2.4), for fixed t, we obtain

$$ w(t)\in w(0)+ \int_{0}^{t}H(s,w_{s})\,{\mathrm {d}}s. $$

It follows that

$$\begin{aligned} \bigl\Vert w(t) \bigr\Vert &\leq \sup_{s\in[-\tau,0]} \bigl\Vert w(s) \bigr\Vert + \int_{0}^{t} \bigl\Vert H(s,w_{s}) \bigr\Vert \,{\mathrm {d}}s \\ &\leq \Bigl(\sup_{s\in[-\tau,0]} \bigl\Vert w(s) \bigr\Vert +\bar{ \bar{\eta}}t \Bigr)+\bar{\bar{h}} \int _{0}^{t} \bigl( \bigl\Vert w(s) \bigr\Vert + \bigl\Vert w(s-\tau) \bigr\Vert \bigr)\,{\mathrm {d}}s, \end{aligned}$$

where \(\bar{\bar{h}}=\max\{\bar{\bar{\alpha}},\bar{\bar{\beta}}\}\). Since

$$ w(t-\tau)\in w(0)+ \int_{0}^{t-\tau}H(s,w_{s})\,{\mathrm {d}}s, $$

we obtain

$$ \bigl\Vert w(t-\tau) \bigr\Vert \leq \Bigl(\sup_{s\in[-\tau,0]} \bigl\Vert w(s) \bigr\Vert +\bar{\bar{\eta}}t \Bigr)+\bar{\bar{h}} \int _{0}^{t} \bigl( \bigl\Vert w(s) \bigr\Vert + \bigl\Vert w(s-\tau) \bigr\Vert \bigr)\,{\mathrm {d}}s. $$

From our analysis and the Gronwall inequality we have

$$\bigl\Vert w(t) \bigr\Vert \leq \bigl\Vert w(t) \bigr\Vert + \bigl\Vert w(t-\tau) \bigr\Vert \leq \Bigl(2\sup_{s\in[-\tau,0]} \bigl\Vert w(s) \bigr\Vert +2\bar{\bar{\eta}}t \Bigr)e^{2\bar{\bar{h}} t}. $$

According to the continuation theorem [61], \(w(t)\) is defined on \([0,+\infty)\) and satisfies

$$ \dot{w}(t)\in-Dw(t)+AK \bigl[h \bigl(w(s) \bigr) \bigr]+BK \bigl[h \bigl(w(t- \tau) \bigr) \bigr]+J. $$

In the following, we consider the global dissipativity of discontinuous CVNNs (2.1) via the matrix measure method. □

Theorem 3.2

If the discontinuous functions of system (2.1) satisfy hypotheses \(A(1)\)–\(A(2)\) and there exists \(\mu_{\mathcal{P}}(\cdot)\) satisfying

$$ \mu_{\mathcal{P}}(-D)+ \Vert A \Vert _{\mathcal{P}} \Vert \alpha \Vert _{\mathcal{P}} + \Vert B \Vert _{\mathcal{P}} \Vert \alpha \Vert _{\mathcal{P}} \leq-\sigma< 0, $$
(3.2)

where \(\alpha=\operatorname{ {diag}}(\alpha_{1},\alpha_{2},\ldots,\alpha_{n})\), then system (2.1) is globally dissipative. Moreover, for any sufficiently small number \(\varepsilon>0\),

$$ \mathcal{S}= \biggl\{ v\in\mathbb{C}^{n}: \Vert z \Vert _{\mathcal {P}}\leq\frac{r}{\sigma}+\varepsilon \biggr\} $$

is a globally positive attractive invariant set, where \(r=(\|A\|_{\mathcal{P}}+\|B\|_{\mathcal{P}})\|\beta\|_{\mathcal {P}}+\|J\|_{\mathcal{P}}\) and \(\beta=\operatorname{ {diag}}(\beta_{1},\beta_{2},\dots,\beta_{n})\).

Proof

We choose the positive radially unbounded function \(W(t)\) in Lemma 2.9 to be \(\|w\|_{\mathcal{P}}\). Calculating \(D^{+}W(t)\) along the trajectory of (2.5), we have

$$\begin{aligned} D^{+}W(t)={}&\overline{\lim_{\triangle t\rightarrow 0^{+}}}\frac{ \Vert w(t+\triangle t) \Vert _{\mathcal{P}}- \Vert w(t) \Vert _{\mathcal {P}}}{\triangle t} \\ ={}&\overline{\lim_{\triangle t\rightarrow 0^{+}}}\frac{ \Vert w+\triangle t\dot{w}+o(\triangle t) \Vert _{\mathcal{P}}- \Vert w \Vert _{\mathcal{P}}}{\triangle t} \\ ={}&\overline{\lim_{\triangle t\rightarrow 0^{+}}}\frac{ \Vert w+\triangle t[-Dw+A\gamma+B\gamma_{\tau}+J]+o(\triangle t) \Vert _{\mathcal{P}}- \Vert w \Vert _{\mathcal{P}}}{\triangle t} \\ \leq{}& \overline{\lim_{h\rightarrow 0^{+}}}\frac{ \Vert w+\triangle t(-D)w \Vert _{\mathcal{P}}- \Vert w \Vert _{\mathcal {P}}}{\triangle t}+ \Vert A\gamma \Vert _{\mathcal{P}}+ \Vert B\gamma_{\tau} \Vert _{\mathcal{P}}+ \Vert J \Vert _{\mathcal{P}} \\ \leq{}& \overline{\lim_{h\rightarrow 0^{+}}}\frac{ \Vert I+\triangle t(-D) \Vert _{\mathcal{P}}-1}{\triangle t} \Vert w \Vert _{\mathcal{P}}+ \Vert A\gamma \Vert _{\mathcal{P}}+ \Vert B \gamma_{\tau} \Vert _{\mathcal {P}}+ \Vert J \Vert _{\mathcal{P}} \\ \leq{}& \mu_{\mathcal{P}}(-D) \Vert w \Vert _{\mathcal{P}}+ \Vert A \Vert _{\mathcal{P}} \bigl( \Vert \alpha \Vert _{\mathcal{P}} \Vert w \Vert _{\mathcal{P}}+ \Vert \beta \Vert _{\mathcal{P}} \bigr) \\ &{} + \Vert B \Vert _{\mathcal{P}} \bigl( \Vert \alpha \Vert _{\mathcal{P}} \Vert w_{\tau} \Vert _{\mathcal {P}}+ \Vert \beta \Vert _{\mathcal{P}} \bigr)+ \Vert J \Vert _{\mathcal{P}} \\ \leq{}& \bigl(\mu_{\mathcal{P}}(-D)+ \Vert A \Vert _{\mathcal{P}} \Vert \alpha \Vert _{\mathcal{P}} \bigr) \Vert w \Vert _{\mathcal{P}}+ \Vert B \Vert _{\mathcal{P}} \Vert \alpha \Vert _{\mathcal{P}} \Vert w_{\tau} \Vert _{\mathcal{P}} \\ &{}+ \bigl( \Vert A \Vert _{\mathcal{P}}+ \Vert B \Vert _{\mathcal{P}} \bigr) \Vert \beta \Vert _{\mathcal {P}}+ \Vert J \Vert _{\mathcal{P}}. \end{aligned}$$

Let \(p=\mu_{\mathcal{P}}(-D)+\|A\|_{\mathcal {P}}\|\alpha\|_{\mathcal{P}}\), \(q=\|B\|_{\mathcal {P}}\|\alpha\|_{\mathcal{P}}\), and \(r=(\|A\|_{\mathcal {P}}+\|B\|_{\mathcal{P}})\|\beta\|_{\mathcal{P}}+\|J\|_{\mathcal {P}}\). Then by Lemma 2.9 and inequality (3.2) we obtain

$$ \Vert w \Vert _{\mathcal{P}}= W(t)\leq\frac{r}{\sigma}+ \biggl(\sup _{-\infty\leq s\leq 0}W(s)-\frac{r}{\sigma} \biggr)e^{-\mu^{*}t}, $$

where \(\mu^{*}\) is the solution of the equation \(\mu+p+q e^{\mu\tau}=0\). Thus, for any sufficiently small \(\varepsilon>0\), there exists \(T>0\) such that

$$ \Vert w \Vert _{\mathcal{P}}\leq\frac{r}{\sigma}+\varepsilon, \quad \forall t>T. $$
(3.3)

 □

Remark 2

In [58], the exponential stability on continuous complex-valued differential equations is studied by using the matrix measure method. However, there are almost no results on the dynamics of a discontinuous complex-valued network model via matrix measure method.

Suppose \(w^{*}\) is an equilibrium of system (2.1) with continuous function, that is, \(\beta_{i}=0\) in formula (2.2). We obtain the following corollary, which is an extensional result of [57] and [58].

Corollary 3.3

The continuous complex-valued system (2.1) is globally exponentially stable if there is \(\mu_{\mathcal{P}}(\cdot)\) such that

$$ \mu_{\mathcal{P}}(-D)+ \Vert A \Vert _{\mathcal{P}} \Vert \alpha \Vert _{\mathcal{P}} + \Vert B \Vert _{\mathcal{P}} \Vert \alpha \Vert _{\mathcal{P}} \leq-\sigma< 0, $$
(3.4)

where \(\alpha=\operatorname{ {diag}}(\alpha_{1},\alpha_{2},\dots,\alpha_{n})\).

In the following, we study the global dissipativity of system (2.1) by transforming it into the corresponding real-valued system. Let \(w=u+\mathbf{i}v\), \(A=A^{R}+\mathbf{i}A^{I}\), \(B=B^{R}+\mathbf{i}B^{I}\), \(h(w)=h^{R}(u,v)+\mathbf{i}h^{I}(u,v)\), \(\gamma(t)=\gamma^{R}+\mathbf{i}\gamma^{I}\), and \(J=J^{R}+\mathbf{i}J^{I}\). Then system (2.1) and system (2.5) can be transformed to

$$ \textstyle\begin{cases} \dot{u}=-Du+A^{R}h^{R}(u,v)-A^{I}h^{I}(u,v)+B^{R}h^{R}(u_{\tau},v_{\tau })-B^{I}h^{I}(u_{\tau},v_{\tau})+J^{R},\\ \dot{v}=-Dv+A^{I}h^{R}(u,v)+A^{R}h^{I}(u,v)+B^{I}h^{R}(u_{\tau},v_{\tau })+A^{R}h^{I}(u_{\tau},v_{\tau})+J^{I}, \end{cases} $$
(3.5)

and

$$ \textstyle\begin{cases} \dot{u}=-Du+A^{R}\gamma^{R}-A^{I}\gamma^{I}+B^{R}\gamma^{R}_{\tau}-B^{I}\gamma^{I}_{\tau}+J^{R},\\ \dot{v}=-Dv+A^{I}\gamma^{R}+A^{R}\gamma^{I}+B^{I}\gamma^{R}_{\tau}+B^{R}\gamma^{I}_{\tau}+J^{I}, \end{cases} $$
(3.6)

respectively, where the functions \(h^{R}(u,v)\) and \(h^{I}(u,v)\) are discontinuous in \(R^{2n}\).

From assumption A(1) we obtain that \(h_{i}^{R}(u,v)\) and \(h_{i}^{I}(u,v)\) are continuous at \(E_{k}\) and discontinuous at \(\partial E_{k}\); \(E_{k}\cap E_{l}=\emptyset\) for \(k\neq l\), and \(\bigcup_{k=1}^{s}(E_{k}\cup\partial E_{k})=\mathbb{R}^{2}\). Furthermore, the limits \(\lim_{(u,v)\rightarrow (u_{0},v_{0})}h_{i}^{R}(u,v)=h_{i}^{kR}(u_{0},v_{0})\) and \(\lim_{(u,v)\rightarrow (u_{0},v_{0})}h_{i}^{I}(u,v)=h_{i}^{kI}(u_{0},v_{0})\) exist, where \((u,v)\in E_{k}\) and \((u_{0},v_{0})\in \partial E_{k}\). According to A(2), there exist \(\alpha^{R}_{i},\beta^{R}_{i},\eta^{R}_{i}\), \(\alpha^{I}_{i},\beta^{I}_{i}\), and \(\eta^{I}_{i}\) such that

$$ \bigl\vert \gamma^{R}_{i} \bigr\vert \leq \alpha^{R}_{i} \vert u_{i} \vert + \beta^{R}_{i} \vert v_{i} \vert + \eta^{R}_{i},\qquad \bigl\vert \gamma^{I}_{i} \bigr\vert \leq \alpha^{I}_{i} \vert u_{i} \vert +\beta^{I}_{i} \vert v_{i} \vert + \eta^{I}_{i}. $$
(3.7)

Remark 3

By our analysis, assumption \(A(2)\) is more general than assumptions in many papers; see, for example, [9, 14]. In fact, a discontinuous activation function becomes a possible choice in mathematical model of describing complex-valued network problems because of Liouville’s theorem [8]. Differently from many papers, such as [11, 13, 15, 17, 19], since \(h^{R}_{i}\) and \(h^{I}_{i}\) are discontinuous activation functions, it is obvious that \(\partial h^{R}(u,v)/\partial u\), \(\partial h^{R}(u,v)/\partial v\), \(\partial h^{I}(u,v)/\partial u\) and \(\partial h^{I}(u,v)/\partial v\), may not exist.

Remark 4

It is obvious that \(g^{R}_{i}\) and \(g^{I}_{i}\) are bivariate functions and the definitions of differential inclusions in the previous literature are not valid; see [30–34, 60, 62]. Fortunately, the defined differential inclusions with bivariate functions under assumptions \(A(1)\)–\(A(2)\) is an extension of the case of single-variable functions.

Remark 5

According our analysis, we know that the bivariate functions \(h^{R}_{i}\) and \(h^{I}_{i}\) are nonmonotone in variables x and y, which are allowed to be unbounded. Therefore, the neuron activation functions \(h^{R}_{i}\) and \(h^{I}_{i}\) are more general than the functions in the existing results, such as [28, 30, 33, 34, 60, 62].

Theorem 3.4

If the discontinuous functions satisfy hypotheses \(A(1)\) and \(A(2)\) and there is a matrix measure \(\mu_{\mathcal{P}}(\cdot)\) satisfying

$$ \mu_{\mathcal{P}}(-D)+ \Vert \bar{A} \Vert _{\mathcal {P}} \max \bigl\{ \Vert \alpha \Vert _{\mathcal{P}}, \Vert \beta \Vert _{\mathcal{P}} \bigr\} + \Vert \bar{B} \Vert _{\mathcal{P}}\max \bigl\{ \Vert \alpha \Vert _{\mathcal {P}}, \Vert \beta \Vert _{\mathcal{P}} \bigr\} \leq-\sigma< 0, $$
(3.8)

where \(r=(\|\bar{A}\|_{\mathcal{P}}+\|\bar{B}\|_{\mathcal {P}})\|\eta\|_{\mathcal{P}}+\|\bar{J}\|_{\mathcal{P}}\), \(\|\bar{A}\|_{\mathcal{P}}=\|A^{R}\|_{\mathcal {P}}+\|A^{I}\|_{\mathcal{P}}\), \(\|\bar{B}\|_{\mathcal {P}}=\|B^{R}\|_{\mathcal{P}}+\|B^{I}\|_{\mathcal{P}}\), and \(\|\bar{J}\|_{\mathcal{P}}=\|J^{R}\|_{\mathcal {P}}+\|J^{I}\|_{\mathcal{P}}\), then the network model (2.1) is globally dissipative. Furthermore, for any sufficient small positive number ε,

$$ \mathcal{S}= \biggl\{ w\in\mathbb{C}^{n}: \bigl\Vert { \operatorname{Re}}(w) \bigr\Vert _{\mathcal {P}}+ \bigl\Vert { \operatorname{Im}}(w) \bigr\Vert _{\mathcal {P}}\leq\frac{r}{\sigma}+ \varepsilon \biggr\} $$

is a globally attractive positive invariant set.

Proof

We consider the auxiliary function \(W(t)=\|u\|_{\mathcal{P}}+\|u\|_{\mathcal{P}}\). Calculating \(D^{+}W(t)\) along the trajectory of system (3.6), we have

$$\begin{aligned} &D^{+}W(t)=\overline{\lim_{\triangle t\rightarrow 0^{+}}}\frac{ \Vert u(t+\triangle t) \Vert _{\mathcal{P}}- \Vert u(t) \Vert _{\mathcal {P}}}{\triangle t}+ \overline{\lim_{\triangle t\rightarrow 0^{+}}}\frac{ \Vert v(t+\triangle t) \Vert _{\mathcal{P}}- \Vert v(t) \Vert _{\mathcal {P}}}{\triangle t} \\ &\phantom{D^{+}W(t)}\leq \overline{\lim_{\triangle t\rightarrow 0^{+}}}\frac{ \Vert u+\triangle t(-D)u \Vert _{\mathcal{P}}- \Vert u \Vert _{\mathcal {P}}}{\triangle t}+ \bigl\Vert A^{R}\gamma^{R} \bigr\Vert _{\mathcal{P}}+ \bigl\Vert A^{I}\gamma ^{I} \bigr\Vert _{\mathcal{P}} \\ &\phantom{D^{+}W(t)\leq}{}+ \bigl\Vert B^{R}\gamma^{R}_{\tau}\bigr\Vert _{\mathcal {P}}+ \bigl\Vert B^{I}\gamma^{I}_{\tau}\bigr\Vert _{\mathcal{P}}+ \bigl\Vert J^{R} \bigr\Vert _{\mathcal {P}}+\overline{\lim_{\triangle t\rightarrow 0^{+}}}\frac{ \Vert v+\triangle t(-D)v \Vert _{\mathcal{P}}- \Vert v \Vert _{\mathcal {P}}}{\triangle t} \\ &\phantom{D^{+}W(t)\leq}{}+ \bigl\Vert A^{I}\gamma^{R} \bigr\Vert _{\mathcal{P}}+ \bigl\Vert A^{R}\gamma^{I} \bigr\Vert _{\mathcal {P}}+ \bigl\Vert B^{I}\gamma^{R}_{\tau}\bigr\Vert _{\mathcal {P}}+ \bigl\Vert B^{R}\gamma^{I}_{\tau}\bigr\Vert _{\mathcal{P}}+ \bigl\Vert J^{I} \bigr\Vert _{\mathcal {P}} \\ &\phantom{D^{+}W(t)}\leq \overline{\lim_{\triangle t\rightarrow 0^{+}}}\frac{ \Vert I+\triangle t(-D) \Vert _{\mathcal{P}}-1}{\triangle t} \Vert u \Vert _{\mathcal{P}}+ \bigl\Vert A^{R}\gamma^{R} \bigr\Vert _{\mathcal{P}}+ \bigl\Vert A^{I}\gamma^{I} \bigr\Vert _{\mathcal{P}}\\ &\phantom{D^{+}W(t)\leq}{}+ \bigl\Vert B^{R}\gamma^{R}_{\tau}\bigr\Vert _{\mathcal{P}}+ \bigl\Vert B^{I}\gamma ^{I}_{\tau}\bigr\Vert _{\mathcal{P}}+ \bigl\Vert J^{R} \bigr\Vert _{\mathcal{P}} \\ &\phantom{D^{+}W(t)\leq}{}+\overline{\lim_{\triangle t\rightarrow 0^{+}}}\frac{ \Vert I+\triangle t(-D) \Vert _{\mathcal{P}}-1}{\triangle t} \Vert v \Vert _{\mathcal{P}}+ \bigl\Vert A^{I}\gamma^{R} \bigr\Vert _{\mathcal{P}}+ \bigl\Vert A^{R}\gamma^{I} \bigr\Vert _{\mathcal{P}}+ \bigl\Vert B^{I}\gamma^{R}_{\tau}\bigr\Vert _{\mathcal{P}}\\ &\phantom{D^{+}W(t)\leq}{}+ \bigl\Vert B^{R}\gamma ^{I}_{\tau}\bigr\Vert _{\mathcal{P}}+ \bigl\Vert J^{I} \bigr\Vert _{\mathcal{P}} \end{aligned}$$
$$\begin{aligned} &\phantom{D^{+}W(t)}\leq \mu_{\mathcal{P}}(-D) \Vert u \Vert _{\mathcal{P}}+ \bigl\Vert A^{R} \bigr\Vert _{\mathcal{P}} \bigl( \bigl\Vert \alpha^{R} \bigr\Vert _{\mathcal{P}} \Vert u \Vert _{\mathcal{P}}+ \bigl\Vert \beta^{R} \bigr\Vert _{\mathcal {P}} \Vert v \Vert _{\mathcal{P}}+ \bigl\Vert \eta^{R} \bigr\Vert _{\mathcal{P}} \bigr) \\ &\phantom{D^{+}W(t)\leq}{}+ \bigl\Vert A^{I} \bigr\Vert _{\mathcal{P}} \bigl( \bigl\Vert \alpha^{I} \bigr\Vert _{\mathcal{P}} \Vert u \Vert _{\mathcal {P}}+ \bigl\Vert \beta^{I} \bigr\Vert _{\mathcal{P}} \Vert v \Vert _{\mathcal{P}}+ \bigl\Vert \eta^{I} \bigr\Vert _{\mathcal{P}} \bigr)\\ &\phantom{D^{+}W(t)\leq}{}+ \bigl\Vert B^{R} \bigr\Vert _{\mathcal{P}} \bigl( \bigl\Vert \alpha^{R} \bigr\Vert _{\mathcal {P}} \Vert u_{\tau} \Vert _{\mathcal{P}}+ \bigl\Vert \beta^{R} \bigr\Vert _{\mathcal{P}} \Vert v_{\tau} \Vert _{\mathcal{P}}+ \bigl\Vert \eta^{R} \bigr\Vert _{\mathcal{P}} \bigr) \\ &\phantom{D^{+}W(t)\leq}{}+ \bigl\Vert B^{I} \bigr\Vert _{\mathcal{P}} \bigl( \bigl\Vert \alpha^{I} \bigr\Vert _{\mathcal{P}} \Vert u_{\tau} \Vert _{\mathcal{P}}+ \bigl\Vert \beta^{I} \bigr\Vert _{\mathcal{P}} \Vert v_{\tau} \Vert _{\mathcal{P}}+ \bigl\Vert \eta^{I} \bigr\Vert _{\mathcal{P}} \bigr)+ \bigl\Vert J^{R} \bigr\Vert _{\mathcal{P}}+\mu_{\mathcal {P}}(-D) \Vert v \Vert _{\mathcal{P}} \\ &\phantom{D^{+}W(t)\leq}{}+ \bigl\Vert A^{I} \bigr\Vert _{\mathcal{P}} \bigl( \bigl\Vert \alpha^{R} \bigr\Vert _{\mathcal{P}} \Vert u \Vert _{\mathcal {P}}+ \bigl\Vert \beta^{R} \bigr\Vert _{\mathcal{P}} \Vert v \Vert _{\mathcal{P}}+ \bigl\Vert \eta^{R} \bigr\Vert _{\mathcal{P}} \bigr)\\ &\phantom{D^{+}W(t)\leq}{}+ \bigl\Vert A^{R} \bigr\Vert _{\mathcal{P}} \bigl( \bigl\Vert \alpha^{I} \bigr\Vert _{\mathcal {P}} \Vert u \Vert _{\mathcal{P}}+ \bigl\Vert \beta^{I} \bigr\Vert _{\mathcal{P}} \Vert v \Vert _{\mathcal {P}}+ \bigl\Vert \eta^{I} \bigr\Vert _{\mathcal{P}} \bigr) \\ &\phantom{D^{+}W(t)\leq}{}+ \bigl\Vert B^{I} \bigr\Vert _{\mathcal{P}} \bigl( \bigl\Vert \alpha^{R} \bigr\Vert _{\mathcal{P}} \Vert u_{\tau} \Vert _{\mathcal{P}}+ \bigl\Vert \beta^{R} \bigr\Vert _{\mathcal{P}} \Vert v_{\tau} \Vert _{\mathcal{P}}+ \bigl\Vert \eta^{R} \bigr\Vert _{\mathcal{P}} \bigr) \\ &\phantom{D^{+}W(t)\leq}{}+ \bigl\Vert B^{R} \bigr\Vert _{\mathcal{P}} \bigl( \bigl\Vert \alpha^{I} \bigr\Vert _{\mathcal{P}} \Vert u_{\tau} \Vert _{\mathcal{P}}+ \bigl\Vert \beta^{I} \bigr\Vert _{\mathcal{P}} \Vert v_{\tau} \Vert _{\mathcal{P}}+ \bigl\Vert \eta^{R} \bigr\Vert _{\mathcal{P}} \bigr)+ \bigl\Vert J^{I} \bigr\Vert _{\mathcal{P}} \\ &\phantom{D^{+}W(t)}\leq \mu_{\mathcal{P}}(-D) \bigl( \Vert u \Vert _{\mathcal{P}}+ \Vert v \Vert _{\mathcal{P}} \bigr)+ \bigl( \bigl\Vert A^{R} \bigr\Vert _{\mathcal{P}}+ \bigl\Vert A^{I} \bigr\Vert _{\mathcal{P}} \bigr) \bigl( \bigl\Vert \alpha^{R} \bigr\Vert _{\mathcal{P}}+ \bigl\Vert \alpha^{I} \bigr\Vert _{\mathcal{P}} \bigr) \bigl\Vert x(t) \bigr\Vert _{\mathcal{P}} \\ &\phantom{D^{+}W(t)\leq}{}+ \bigl( \bigl\Vert A^{R} \bigr\Vert _{\mathcal{P}}+ \bigl\Vert A^{I} \bigr\Vert _{\mathcal{P}} \bigr) \bigl( \bigl\Vert \beta^{R} \bigr\Vert _{\mathcal{P}}+ \bigl\Vert \beta^{I} \bigr\Vert _{\mathcal{P}} \bigr) \Vert v \Vert _{\mathcal{P}}+ \bigl( \bigl\Vert B^{R} \bigr\Vert _{\mathcal{P}}\\ &\phantom{D^{+}W(t)\leq}{}+ \bigl\Vert B^{I} \bigr\Vert _{\mathcal{P}} \bigr) \bigl( \bigl\Vert \alpha^{R} \bigr\Vert _{\mathcal{P}}+ \bigl\Vert \alpha^{I} \bigr\Vert _{\mathcal{P}} \bigr) \Vert u_{\tau} \Vert _{\mathcal {P}} \\ &\phantom{D^{+}W(t)\leq}{}+ \bigl( \bigl\Vert B^{R} \bigr\Vert _{\mathcal{P}}+ \bigl\Vert B^{I} \bigr\Vert _{\mathcal{P}} \bigr) \bigl( \bigl\Vert \beta^{R} \bigr\Vert _{\mathcal{P}}+ \bigl\Vert \beta^{I} \bigr\Vert _{\mathcal{P}} \bigr) \Vert v_{\tau} \Vert _{\mathcal{P}} \\ &\phantom{D^{+}W(t)\leq}{}+ \bigl( \bigl\Vert A^{R} \bigr\Vert _{\mathcal{P}}+ \bigl\Vert A^{I} \bigr\Vert _{\mathcal{P}}+ \bigl\Vert B^{R} \bigr\Vert _{\mathcal{P}}+ \bigl\Vert B^{I} \bigr\Vert _{\mathcal{P}} \bigr) \bigl( \bigl\Vert \eta^{R} \bigr\Vert _{\mathcal{P}}+ \bigl\Vert \eta^{I} \bigr\Vert _{\mathcal{P}} \bigr)+ \bigl\Vert J^{R} \bigr\Vert _{\mathcal{P}}+ \bigl\Vert J^{I} \bigr\Vert _{\mathcal {P}} \\ &\phantom{D^{+}W(t)}\leq \bigl\{ \mu_{\mathcal{P}}(-D)+ \Vert \bar{A} \Vert _{\mathcal{P}}\max \bigl\{ \Vert \alpha \Vert _{\mathcal{P}}, \Vert \beta \Vert _{\mathcal{P}} \bigr\} \bigr\} \bigl( \Vert u \Vert _{\mathcal{P}}+ \Vert v \Vert _{\mathcal{P}} \bigr) \\ &\phantom{D^{+}W(t)\leq}{}+ \Vert \bar{B} \Vert _{\mathcal{P}}\max \bigl\{ \Vert \alpha \Vert _{\mathcal {P}}, \Vert \beta \Vert _{\mathcal{P}} \bigr\} \max _{t-\tau\leq s\leq t} \bigl( \bigl\Vert u(s) \bigr\Vert _{\mathcal{P}}+ \bigl\Vert v(s) \bigr\Vert _{\mathcal {P}} \bigr)\\ &\phantom{D^{+}W(t)\leq}{}+ \bigl( \Vert \bar{A} \Vert _{\mathcal{P}}+ \Vert \bar{B} \Vert _{\mathcal {P}} \bigr) \Vert \eta \Vert _{\mathcal{P}}+ \Vert J \Vert _{\mathcal{P}}. \end{aligned}$$

Let \(p=\mu_{\mathcal{P}}(-D)+\|\bar{A}\|_{\mathcal {P}}\max\{\|\alpha\|_{\mathcal{P}},\|\beta\|_{\mathcal{P}}\}\), \(q=\|\bar{B}\|_{\mathcal{P}}\max\{\|\alpha\|_{\mathcal {P}},\|\beta\|_{\mathcal{P}}\}\), and \(r=(\|\bar{A}\|_{\mathcal {P}}+\|\bar{B}\|_{\mathcal{P}})\|\eta\|_{\mathcal {P}}+\|\bar{J}\|_{\mathcal{P}}\). By Lemma 2.9 and inequality (3.8) we obtain

$$ \Vert u \Vert _{\mathcal{P}}+ \Vert v \Vert _{\mathcal{P}}= W(t)\leq \frac{r}{\sigma}+ \biggl(\sup_{-\infty\leq s\leq 0}W(s)-\frac{r}{\sigma} \biggr)e^{-\mu^{*}t}, $$

where \(\mu^{*}\) is the solution of the equation \(\mu+p+q e^{\mu\tau}=0\). Therefore, for any sufficient small \(\varepsilon>0\), there exists \(T>0\) such that

$$ \bigl\Vert {\operatorname{Re}}(w) \bigr\Vert _{\mathcal{P}}+ \bigl\Vert { \operatorname{Im}}(w) \bigr\Vert _{\mathcal {P}}\leq\frac{r}{\sigma}+ \varepsilon, \quad \forall t>T. $$
(3.9)

 □

Remark 6

In [57], the authors present some sufficient conditions to ensure the stability of a continuous complex-valued network, where \(h(w)=h^{R}({\operatorname{Re}}(w))+\mathbf{i}h^{I}({\operatorname{Im}}(w))\). Here, we assume that the activation function has the form \(h(w)=h^{R}(\operatorname{ {Re}}(w),{\operatorname{Im}}(w))+\mathbf{i}h^{I}({\operatorname{Re}}(w),\operatorname{ {Im}}(w))\), which is more general than that in [57]. Furthermore, the function \(h(w)\) may be non-Lipschitz continuous or even discontinuous.

Remark 7

Compared with the existing results, we extend global dissipativity results to real-valued discontinuous networks with bivariate function. If all imaginary parts of system (2.1) equal zero, then the results of Theorem 3.4 degenerate into Theorem 2 in [33], which presents sufficient conditions for the global dissipativity of a discontinuous network with univariate function.

Suppose \(w^{*}=u^{*}+\mathbf{i}v^{*}\) is an equilibrium of (2.1) and \(\gamma^{*}=\gamma^{R*}+\mathbf{i}\gamma^{I*}\) is the output solution corresponding to \(w^{*}\). Furthermore, we suppose that the nonlinear function is continuous, that is, \(\eta_{i}^{R}=\eta_{i}^{I}=0\) in formula (3.7). We obtain the following corollary, which is an extensional result of [57].

Corollary 3.5

The continuous complex-valued network (2.1) is globally exponentially stable to \(w^{*}\) if

$$ \mu_{\mathcal{P}}(-D)+ \Vert \bar{A} \Vert _{\mathcal {P}}\max \bigl\{ \Vert \alpha \Vert _{\mathcal{P}}, \Vert \beta \Vert _{\mathcal{P}} \bigr\} + \Vert \bar{B} \Vert _{\mathcal{P}}\max \bigl\{ \Vert \alpha \Vert _{\mathcal {P}}, \Vert \beta \Vert _{\mathcal{P}} \bigr\} \leq- \sigma< 0. $$

4 Stabilization result

In this section, we design a set of state feedback controllers \(m_{i}\) to make the solution of system (2.1) stable. Suppose \(w^{*}\) is an equilibrium of (2.1) and \(\gamma^{*}\) is the output solution corresponding to \(w^{*}\). Then letting \(\tilde{w}=w-w^{*}\) and \(\tilde{\gamma}=\gamma-\gamma^{*}\), the control problem can be transformed into the following form:

$$ \dot{\tilde{w}}=-D\tilde{w}+A\tilde{\gamma}+B\tilde{ \gamma}_{\tau}+m, $$
(4.1)

where \(\tilde{\gamma}=\gamma-\gamma^{*}\), \(\gamma\in K[h(w^{*}+\tilde{w})]\), and \(m=[m_{1},m_{2},\dots,m_{n}]\) are feedback controllers.

Theorem 4.1

Assume that the discontinuous functions in (2.1) satisfy hypotheses \(A(1)\) and \(A(2)\). Then the complex-valued network model is exponentially stable under the state feedback controllers \(m_{i}=m_{i}^{R}+m_{i}^{I}\), where

$$ m_{i}^{R}=-\kappa\tilde{u}_{i}- \rho_{i}\operatorname{sgn}\tilde{u}_{i},\qquad m_{i}^{I}=-\kappa\tilde{v}_{i}-\rho_{i} \operatorname{sgn}\tilde{v}_{i}, $$
(4.2)

with

$$ \kappa>-\underline{d}+\bar{\xi}+\bar{\varsigma} \quad\textit{and}\quad \rho_{i}>\pi_{i}, $$
(4.3)

where \(\xi_{i}=\max\{\sum_{j=1}^{n}\|a_{ji}\|_{1}\|\alpha_{j}\|_{1}, \sum_{j=1}^{n}\|a_{ji}\|_{1}\|\beta_{j}\|_{1}\}\), \(\varsigma_{i}=\max\{\sum_{j=1}^{n}\|b_{ji}\|_{1}\|\alpha_{j}\|_{1}, \sum_{j=1}^{n}\|b\|_{1}\times \|\beta_{j}\|\}\), \(\bar{\xi}=\max_{1\leq i\leq n}\xi_{i}\), \(\bar{\varsigma}=\max_{1\leq i\leq n}\varsigma_{i}\), \(\pi_{i}=\max\{ \sum_{j=1}^{n}\|a_{ij}\|_{1}\|\alpha_{j}\|_{1}, \sum_{j=1}^{n}\|b_{ij}\|_{1})\|\eta_{j}\|_{1}\}\), and \(\underline{d}=\min_{1\leq i\leq n}\{d_{i}\}\).

Proof

By separating all the parameters of system and the control inputs into their corresponding real and imaginary parts, system (4.1) can be expressed as follows:

$$ \textstyle\begin{cases} \dot{\tilde{u}}=-(D+\mathcal {K})\tilde{u}+A^{R}\tilde{\gamma}^{R}-A^{I}\tilde{\gamma}^{I} +B^{R}\tilde{\gamma}_{\tau}-B^{I}\tilde{\gamma}^{I}_{\tau}-\rho\operatorname{ sgn}(\tilde{u}),\\ \dot{\tilde{v}}=-(D+\mathcal {K})\tilde{v}+A^{I}\tilde{\gamma}^{R}+A^{R}\tilde{\gamma}^{I} +B^{I}\gamma^{R}_{\tau}+B^{R}\tilde{\gamma}^{I}_{\tau}-\rho\operatorname{ sgn}(\tilde{v}), \end{cases} $$
(4.4)

where \(\mathcal{K}={\operatorname{diag}}\{\kappa,\kappa,\ldots,\kappa\}\), \(\rho={\operatorname{diag}}\{\rho_{1},\rho_{2},\ldots,\rho_{n}\}\), \(\operatorname{ sgn}(\tilde{u})=[\operatorname{ sgn}(\tilde{u}_{1}),\operatorname{ sgn}(\tilde{u}_{2}),\ldots, \operatorname{ sgn}(\tilde{u}_{n})]^{\mathrm{ T}}\), and \(\operatorname{ sgn}(\tilde{v})=[\operatorname{ sgn}(\tilde{v}_{1}),\operatorname{ sgn}(\tilde{v}_{2}),\ldots,\operatorname{ sgn}(\tilde{v}_{n})]^{\mathrm{ T}}\).

We choose a C-regular auxiliary function \(W_{i}=|\tilde{u}_{i}|+|\tilde{v}_{i}|\). Based on the definitions of generalized gradient, for any \(\upsilon_{i}\in\partial(|\tilde{u}_{i}|)\), we have \(\upsilon_{i}=\operatorname{sgn}(\tilde{u}_{i})\) if \(\tilde{u}_{i}\neq0\) and \(\upsilon_{i}\) can be arbitrarily chosen in \([-1,1]\) if \(\tilde{u}_{i}=0\). Especially, we choose \(\upsilon_{i}=\operatorname{ {sgn}}(\tilde{u}_{i})\), and it can be seen that \(\upsilon_{i}\tilde{u}_{i}=|\tilde{u}_{i}|\). By similar analysis we obtain \(\vartheta_{i}\tilde{v}_{i}=|\tilde{v}_{i}|\). Calculating \(\dot{W}_{i}\) along the trajectories of error system (4.4), we obtain

$$\begin{aligned} \dot{W}_{i}={}&\upsilon_{i}\dot{\tilde{u}}_{i}+ \vartheta_{i}\dot{\tilde {v}}_{i} \\ \leq{}& -(d_{i}+\kappa) \vert \tilde{u}_{i} \vert +\sum _{j=1}^{n} \bigl\vert a_{ij}^{R} \bigr\vert \bigl\vert \tilde{\gamma }^{R}_{j} \bigr\vert +\sum_{j=1}^{n} \bigl\vert a_{ij}^{I} \bigr\vert \bigl\vert \tilde{ \gamma}^{I}_{j} \bigr\vert +\sum _{j=1}^{n} \bigl\vert b_{ij}^{R} \bigr\vert \bigl\vert \tilde{\gamma}^{R}_{j,\tau} \bigr\vert \\ &{}+\sum_{j=1}^{n} \bigl\vert b_{ij}^{I} \bigr\vert \bigl\vert \tilde{ \gamma}^{I}_{j,\tau} \bigr\vert -\rho \bigl\vert \operatorname{ {sgn}}(\tilde{u}_{i}) \bigr\vert \\ &{}-(d_{i}+\kappa) \vert \tilde{v}_{i} \vert +\sum _{j=1}^{n} \bigl\vert a_{ij}^{I} \bigr\vert \bigl\vert \tilde{\gamma }^{R}_{j} \bigr\vert +\sum_{j=1}^{n} \bigl\vert a_{ij}^{R} \bigr\vert \bigl\vert \tilde{ \gamma}^{I}_{j} \bigr\vert +\sum _{j=1}^{n} \bigl\vert b_{ij}^{R} \bigr\vert \bigl\vert \tilde{\gamma}^{I}_{j,\tau} \bigr\vert \\ &{} +\sum_{j=1}^{n} \bigl\vert b_{ij}^{I} \bigr\vert \bigl\vert \tilde{ \gamma}^{R}_{j,\tau} \bigr\vert -\rho \bigl\vert \operatorname{ {sgn}}(\tilde{v}_{i}) \bigr\vert \\ \leq{}&{-}(d_{i}+\kappa) \vert \tilde{u}_{i} \vert +\sum _{j=1}^{n} \bigl\vert a_{ij}^{R} \bigr\vert \bigl(\alpha ^{R}_{j} \vert \tilde{u}_{j} \vert +\beta^{R}_{j} \bigl\vert \tilde{v}_{j}(t) \bigr\vert +\eta^{R}_{j} \bigr) +\sum_{j=1}^{n} \bigl\vert a_{ij}^{I} \bigr\vert \bigl(\alpha^{I}_{j} \vert \tilde{u}_{j} \vert +\beta ^{I}_{j} \vert \tilde{v}_{j} \vert +\eta^{I}_{j} \bigr) \\ &{}+\sum_{j=1}^{n} \bigl\vert b_{ij}^{R} \bigr\vert \bigl(\alpha^{R}_{j} \vert \tilde{u}_{j,\tau} \vert +\beta ^{R}_{j} \vert \tilde{v}_{j,\tau} \vert +\eta^{R}_{j} \bigr)+\sum_{j=1}^{n} \bigl\vert b_{ij}^{I} \bigr\vert \bigl(\alpha^{I}_{j} \vert \tilde {u}_{j,\tau} \vert +\beta^{I}_{j} \vert \tilde{v}_{j,\tau} \vert +\eta^{I}_{j} \bigr)-\rho _{i} \bigl\vert \operatorname{ {sgn}}( \tilde{u}_{i}) \bigr\vert \\ &{}-(d_{i}+\kappa) \vert \tilde{v}_{i} \vert +\sum _{j=1}^{n}|a_{ij}^{I} \bigl\vert \bigl(\alpha ^{R}_{j} \vert \tilde{u}_{j} \vert +\beta^{R}_{j} \vert \tilde{v}_{j} \vert +\eta^{R}_{j} \bigr) \bigr\vert +\sum_{j=1}^{n}\bigl|a_{ij}^{R}\bigr| \bigl(\alpha^{I}_{j} \vert \tilde{u}_{j} \vert +\beta^{I}_{j} \vert \tilde{v}_{j} \vert +\eta^{I}_{j} \bigr) \\ &{}+\sum_{j=1}^{n}\bigl|b_{ij}^{R}\bigr| \bigl(\alpha^{I}_{j} \vert \tilde{u}_{j,\tau} \vert +\beta ^{I}_{j} \vert \tilde{v}_{j,\tau} \vert +\eta^{I}_{j} \bigr)+\sum _{j=1}^{n}\bigl|b_{ij}^{I}\bigr| \bigl( \alpha^{R}_{j} \vert \tilde{u}_{j,\tau} \vert + \beta ^{R}_{j} \vert \tilde{v}_{j,\tau} \vert + \eta^{R}_{j} \bigr)-\rho_{i} \bigl\vert \operatorname{ {sgn}}(\tilde{v}_{i}) \bigr\vert \\ \leq{}&{-}(\underline{d}+\kappa) \bigl( \vert \tilde{u}_{i} \vert + \vert \tilde{v}_{i} \vert \bigr)+\xi _{i} \bigl( \vert \tilde{u}_{i} \vert + \vert \tilde{v}_{i} \vert \bigr)+ \varsigma_{j} \bigl( \vert \tilde{u}_{i,\tau } \vert + \vert \tilde{v}_{i,\tau} \vert \bigr)-(\rho_{i}-\pi_{i}) \\ \leq{}&-(\underline{d}+\kappa)W_{i}+\xi_{i}W_{i}+ \varsigma_{j}W_{i,\tau}. \end{aligned}$$

Letting \(W=\sum_{i=1}^{n}W_{i}\), we obtain

$$\begin{aligned} \dot{W}&\leq-(\underline{d}+\kappa)\sum_{i=1}^{n}W_{i}+ \bar{\xi}\sum_{i=1}^{n}W_{i}+\bar{ \varsigma}\sum_{i=1}^{n}W_{i,\tau} \\ &=-(\underline{d}+\kappa)W+\bar{\xi}W(t)+\bar{\varsigma}W_{\tau}. \end{aligned}$$

Then by Lemma 2.9 and inequality (4.3) we obtain

$$ \vert \tilde{u}_{i} \vert \leq W\leq\sup _{-\infty\leq s\leq 0}W(s)e^{-\mu^{*}t},\qquad \vert \tilde{v}_{i} \vert \leq W\leq\sup_{-\infty\leq s\leq0}W(s)e^{-\mu^{*}t}, $$

where \(\mu^{*}\) is the solution of the equation \(\mu-\underline{d}-\kappa+\bar{\xi}+\bar{\varsigma} e^{\mu\tau}=0\). Therefore, complex-valued network (2.1) is exponentially stable under the designed controllers (4.2). □

Remark 8

The inequality of \(\kappa>-\underline{d}+\bar{\xi}+\bar{\varsigma}\) in (4.3) is equivalent to formula (3.8) in Theorem 3.4 for \(\mathcal{P}=1\). Therefore, the result of Theorem 4.1 is a direct application of Theorem 3.4 in the control filed.

5 Numerical example

We give two examples to demonstrate the correction of the obtained results.

Example 1

Consider the one-dimensional neural network model (2.1) with \(D=2+2\sqrt{3}\), \(A=1+\mathbf{i}\sqrt{2}\), \(B=\sqrt{2}+\mathbf{i}\), \(J=1+\mathbf{i}\sqrt{5}\), and \(\tau=1\). We choose the following activation function:

$$ h(w)=\textstyle\begin{cases} w+1+\mathbf{i}, & \operatorname{ Re}(w)>0, \operatorname{ Im}(w)>0, \\ w-1, & \operatorname{ Re}(w)< 0, \operatorname{ Im}(w)< 0, \\ w+1, & \operatorname{ Re}(w)< 0, \operatorname{ Im}(w)>0, \\ w-1+\mathbf{i}, & \operatorname{ Re}(w)>0, \operatorname{ Im}(w)< 0, \end{cases} $$

and \(h(0)=0\), which is shown in Fig. 1. From assumption \(A(2)\) we obtain \(\alpha=1\), \(\beta=\sqrt{5}\), \(\|A\|_{1}=\sqrt{3}\), \(\|B\|_{1}=\sqrt{3}\), and \(\|J\|_{1}=\sqrt{6}\). According to Theorem 3.2, \(\mu_{1}(-D)+\|A\|_{1}\|\alpha\|_{1} +\|B\|_{1}\|\alpha\|_{1}=-2<0\) and \(r=3\sqrt{6}\), and it is easy to get that the invariant set is \(\mathcal {S}=\{w\in\mathbb{C}^{n}:\|w\|_{\mathcal {P}}\leq3.67+\varepsilon\}\).

Figure 1
figure 1

Time responses of the real part and imaginary part of \(h(w)\) in Example 1

Full size image

We separate \(h(w)\) into its real and imaginary parts:

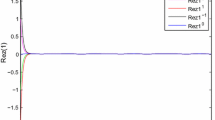
$$ h^{R}(u,v)=\textstyle\begin{cases} u+1,& v>0, \\ u-1, & v< 0, \end{cases}\displaystyle \quad\text{and}\quad h^{I}(u,v)=\textstyle\begin{cases} v+1, & u>0, \\ v, & u< 0. \end{cases} $$

We obtain that \(\alpha^{R}=1\), \(\beta^{R}=0\), \(\eta^{R}=2\), \(\alpha^{I}=0,\beta^{I}=1\), and \(\eta^{I}=1\) in (3.7). According to Theorem 3.4, it follows that \(\mu_{1}(-D)=-(2+2\sqrt{3})\), \(\|A^{R}\|_{1}=1\), \(\|A^{I}\|_{1}=\sqrt{2}\), \(\|B^{R}\|_{1}=\sqrt{2}\), \(\|B^{I}\|_{1}=1\), \(\|J^{R}\|_{1}=1\), and \(\|J^{I}\|_{1}=\sqrt{5}\). Choosing \(\sigma=2(\sqrt{3}-\sqrt{2})\) and \(r=7+6\sqrt{2}+\sqrt{5}\), it follows that the invariant set is \(\mathcal {S}=\{w\in\mathbb{C}^{n}:\|{\operatorname{Re}}(w)\|_{1}+\|{\operatorname{Im}}(w)\|_{1}\leq 27.8+\varepsilon\}\). The trajectories of real and imaginary parts of v are shown in Fig. 2, and the invariant sets of Theorem 3.2 and Theorem 3.4 are shown in Fig. 3.

Figure 2
figure 2

Time responses of the real part and imagine part of w in Example 1

Full size image
Figure 3
figure 3

The positive invariant sets in Theorem 3.2 and Theorem 3.4 of Example 1

Full size image

Remark 9

Obviously, from Fig. 3 we can see that the invariant set obtained from Theorem 3.2 is more accurate than that obtained in Theorem 3.4 because of the obvious inequality \(\|w\|_{\mathcal{P}}\leq\|u\|_{\mathcal {P}}+\|v\|_{\mathcal{P}}\). Therefore the conditions of Theorem 3.2 are less conservative than those in Theorem 3.4 and greatly reduce the complexity of computation.

Example 2

Here we consider the neural network model with two complex neurons:

$$ \dot{w}=-Dw+Ah(w)+Bh \bigl(w(t-\tau) \bigr), $$
(5.1)

where

D= [ 2 0 0 1 ] ,A= [ − 1 + 0.5 i 1 + 0.5 i − 0.5 − i − 1 + 0.5 i ] ,B= [ 2 + i 1 + 0.5 i − 0.5 − 2 i − 1 + 0.5 i ] ,

and \(h_{i}(\chi)=[(\operatorname{ Re}(\chi)-1)\operatorname{sgn}(\operatorname{ Re}(\chi))+\operatorname{ Im}(\chi)]+\mathbf{i}[(\operatorname{ Im}(\chi)-1)\operatorname{sgn}(\operatorname{ Im}(\chi))+\operatorname{ Re}(\chi)]\) for any \(\chi\in\mathbb{C}\), \(i=1,2\), \(\tau=1\). The trajectories for system (5.1) are shown in Fig. 4.

Figure 4
figure 4

Time responses for the real and imaginary parts of the state solution in Example 2 without control input

Full size image

We separate \(h(w)\) into its real part and parts:

$$ h_{i}^{R}(u_{i},v_{i})= (u_{i}-1)\operatorname{sgn}(u_{i})+v_{i},\qquad h_{i}^{I}(u_{i},v_{i})= (v_{i}-1)\operatorname{sgn}(v_{i})+u_{i}. $$

We obtain that \(\alpha_{i}^{R}=\beta_{i}^{R}=1\), \(\eta_{i}^{R}=2\), \(\alpha_{i}^{I}=\beta_{i}^{I}=1\), and \(\eta_{i}^{I}=2\) for \(i=1,2\). According to Theorem 4.1, it follows that \(\underline{d}=1\), \(\bar{\xi}=6\), \(\bar{\varsigma}=9\), and \(\bar{\pi}=15\). If we choose \(\kappa=15\) and \(\rho_{i}=16\), then the equilibrium of (5.1) is exponentially stable under the designed controllers. The trajectories of the designed controllers and the state variables under control input are shown in Figs. 5 and 6, respectively.

Figure 5
figure 5

Time responses of the real and imaginary parts of the designed controllers in Example 2

Full size image
Figure 6
figure 6

Time responses for the real and imaginary parts of the state solution in Example 2 under the designed controllers

Full size image

6 Conclusion

In this paper, we investigate the global dissipativity and stabilization problem of discontinuous complex-valued networks via the matrix measure method. Compared with the existing results on continuous complex-valued neural networks, we propose a sufficient condition for the global dissipativity of discontinuous complex-valued neural networks based on differential inclusion. Compared with the results on discontinuous neural networks, we extend global dissipativity results to discontinuous neural networks with bivariate activation functions. In future, we will study the synchronization control of complex networks composed by discontinuous complex-valued differential equations.