1 Introduction

Fractional calculus is a very hot area of research due to its ability to study many applications in physics and engineering, which cannot be studied by the ordinary calculus. There are many applications of this important type of calculus [1–4]. The approximate and numerical techniques must be used [5–9] because most fractional differential equations (FDEs) do not have exact solutions. Recently, several numerical methods to solve fractional differential equations have been proposed, such as variational iteration method [10], homotopy perturbation method [11], Adomian decomposition method [12], homotopy analysis method [13], finite difference method (FDM) [14, 15], and spectral methods [5, 6].

Many physical processes appear to exhibit fractional order behavior that may vary with time or space. This fact enables us to consider the order of the fractional integrals and derivatives to be a function of time or some other variables. The objective of this work is to identify the most appropriate definition of a variable-order operator for modeling dynamic systems and to assign the order of the derivative to give a physical meaning that will facilitate the understanding of its use in problems of vibration and control. However, until now, only few researchers have considered the numerical analysis of variable-order differential equations; see, for example, [16–20].

In this paper, we study the following variable order linear and nonlinear reaction–subdiffusion equation:

$$ \frac{\partial}{\partial t} y(x,t)=D_{t}^{1-\gamma(x,t)} \biggl[k_{\alpha}\frac{\partial^{2}}{\partial x^{2}} y(x,t)-\varepsilon y(x,t)\biggr]+g \bigl(x,t,y(x,t)\bigr),\quad 0< t\leq T, 0< x< L, $$
(1)

where we assume Dirichlet boundary conditions as follows:

$$ y(0,t)=\phi(t),\qquad y(L,t)=\psi(t),\quad 0< t\leq T, $$
(2)

with an initial condition

$$ y(x,0)=\omega(x),\quad 0\leq x \leq L. $$
(3)

On a finite domain \(a < x < b, 0 \leq t \leq T\), where f is the source term, which may be linear (\(g(x,t)\)) or nonlinear (\(g(x,t,y(x,t))\)), \(0<\gamma(x,t)<1\), ε is a positive constant and \(D_{t}^{1-\gamma(x,t)}\) is the variable order fractional derivative defined by the Riemann–Liouville operator of order \(1-\gamma\), which is defined for a function \(f(x,t)\) by (see [18, 20])

$$ D_{t}^{1-\gamma(x,t)}f(x,t)= \frac{1}{\varGamma(\gamma(x,t))} \biggl[ \frac{\partial}{\partial\xi} \int_{0}^{\xi}\frac{f(x,\eta )}{(\xi-\eta)^{1-\gamma(x,t)}}\,d\eta { \biggr]}_{\xi=t}. $$
(4)

And we use the weighted average FDM to solve this model.

2 Fractional reaction–subdiffusion equation

The standard mean-field model for the evolution of the concentrations \(a(x,t)\) and \(b(x,t)\) of A and B particles is given by the reaction–diffusion equations:

$$\begin{aligned} &\frac{\partial}{\partial t} a(x,t)= {D}\frac{\partial^{2}}{\partial x^{2}} a(x,t)- \varepsilon a(x,t)b(x,t), \end{aligned}$$
(5)
$$\begin{aligned} &\frac{\partial}{\partial t} b(x,t)=D\frac {\partial^{2}}{\partial x^{2}} b(x,t)-\varepsilon a(x,t)b(x,t), \end{aligned}$$
(6)

where D is the diffusion coefficient assumed in this paper to be equal for species and ε is the rate constant for the bimolecular reaction.

In order to generalize the reaction–diffusion problem to a reaction–subdiffusion problem, we must deal with the subdiffusive motion of the particles. Seki et al. [21] and Yuste et al. [22] replaced Eqs. (5) and (6) with the set of reaction–subdiffusion equations, in which both the motion and the reaction terms are affected by the subdiffusive character of the process:

$$\begin{aligned} &\frac{\partial}{\partial t} a(x,t)=D_{t}^{1-\alpha}{k_{\alpha} \frac{\partial^{2}}{\partial x^{2}} a(x,t)-\varepsilon a(x,t)b(x,t)}, \end{aligned}$$
(7)
$$\begin{aligned} &\frac{\partial}{\partial t} b(x,t)=D_{t}^{1-\alpha}{k_{\alpha} \frac{\partial^{2}}{\partial x^{2}} b(x,t)-\varepsilon a(x,t)b(x,t)}, \end{aligned}$$
(8)

where \(k_{\alpha}\) is the generalized diffusion coefficient and \(D_{t}^{1-\alpha}\) is the Riemann–Liouville fractional partial derivative of order \(1-\alpha\). The fractional reaction–subdiffusion equations (7) and (8) are decoupled, which is equivalent to solving the following fractional reaction–subdiffusion equation:

$$ \frac{\partial}{\partial t} y(x,t)=D_{t}^{1-\alpha} \biggl[k_{\alpha}\frac{\partial^{2}}{\partial x^{2}} y(x,t)-\varepsilon y(x,t) \biggr]+g(x,t),\quad 0< t\leq T, 0< x< L, $$
(9)

where \(0 < \alpha< 1\) and ε is a positive constant. We assume Dirichlet boundary conditions for this problem as follows:

$$ y(0,t)=\phi(t),\qquad y(L,t)=\psi(t),\quad 0< t\leq T, $$
(10)

with an initial condition

$$ y(x,0)=\omega(x),\quad 0\leq x \leq L. $$
(11)

In the last few years, many papers studied the proposed model (1)–(3) (see [21–27]).

3 Finite difference scheme for a variable order fractional reaction–subdiffusion equation

In this section, we will use the weighted average FDM to obtain a discretization finite difference formula of the variable order linear and nonlinear reaction–subdiffusion equation (1). For some positive constants M and N, we use Δt and Δx to denote the time-step length and space-step length, respectively. The coordinates of the mesh points are \(x_{j}=j\Delta x\) \((j=0,1,2,\dots,N)\), and \(t_{m}=m \Delta t\), \((m=0,1,2,\dots,M)\) and the values of the solution \(y(x, t)\) on these grid points are \(y(x_{j}, t_{m})\equiv y_{j}^{m}\simeq Y_{j}^{m}\), where \(\Delta x =\frac{L}{N}\), and \(\Delta t=\frac{T}{M}\).

In the first step, the ordinary differential operators are discretized as follows [28]:

$$ \frac{\partial y}{\partial t}\Bigm|_{x_{j},t_{m}}=\delta_{t}y_{j}^{m}+O (\Delta t )\equiv \frac{y_{j}^{m+1}-y_{j}^{m}}{\Delta t}+O (\Delta t ) $$
(12)

and

$$ \frac{\partial^{2} y}{\partial x^{2}}\Bigm|_{x_{j},t_{m}}=\delta_{xx}y_{j}^{m}+O \bigl((\Delta x)^{2} \bigr)\equiv\frac{y_{j-1}^{m}-2y_{j}^{m}+y_{j+1}^{m}}{{(\Delta x)}^{2}}+O \bigl((\Delta x)^{2} \bigr). $$
(13)

In the second step, the Riemann–Liouville operator is discretized as follows:

$$ D_{t}^{1-\alpha_{j}^{m}}y(x,t)\mid_{x_{j},t_{m}}=\delta _{t}^{1-\alpha _{j}^{m}}y_{j}^{m}+O\bigl((\Delta t)^{p}\bigr), $$
(14)

where p is the order of the approximation which depends on the choice of \(\rho_{k}^{(1-\alpha_{j}^{m})}\), and

$$ \delta_{t}^{1-\alpha_{j}^{m}}y_{j}^{m} \equiv \frac{1}{(\Delta t)^{1-\alpha_{j}^{m}}}\sum_{k=0}^{[\frac {t_{m}}{\Delta t}]} \rho_{k}^{(1-\alpha_{j}^{m})}y(x_{j},{t_{m}-kh})= \frac{1}{(\Delta t)^{1-\alpha_{j}^{m}}}\sum_{k=0}^{m} \rho_{k}^{(1-\alpha _{j}^{m})}y_{j}^{m-k}, $$
(15)

where \([\frac{t_{m}}{\Delta t}]\) means the integer part of \(\frac{t_{m}}{\Delta t}\). There are many choices of the weights \(\rho_{k}^{(\alpha_{j}^{m})}\) (see [4, 29]), so the above formula is not unique. Let us denote the generating function of the weights \(\rho_{k}^{(\beta)}\) by \(\rho(z,\beta)\), i.e.,

$$ \rho(z,\beta)=\sum_{k=0}^{\infty} \rho_{k}^{(\beta)}z^{k}. $$

If

$$ \rho(z,\beta)=(1-z)^{\beta}, $$
(16)

then (14) gives the backward difference formula of the first order, which is called the Grünwald–Letnikov formula. The coefficients \(\rho_{k}^{(\beta)}\) can be evaluated by the following formula:

$$ \rho_{k}^{(\beta)}= \biggl(1-\frac{\beta+1}{k} \biggr)\rho_{k-1}^{(\beta)},\qquad \rho_{0}^{(\beta)}=1. $$

For \(\alpha=1\), the operator \(D_{t}^{1-\alpha}\) becomes the identity operator so that the consistency of Eqs. (14) and (15) requires \(\rho_{0}^{(0)}=1\), and \(\rho_{k}^{(0)}=0\) for \(k\geq1\), which in turn means that \(\rho(z,0)=1\).

Now, we are going to obtain a finite difference scheme of the linear and nonlinear variable order reaction–subdiffusion equation (1). In our study we take \(k_{\alpha}=\varepsilon=1\).

To achieve this aim, we evaluate this equation at the points of the grid \((x_{j},t_{m})\) by

$$ \bigl[y_{t}(x,t)-D_{t}^{1-\alpha_{j}^{m}}y_{xx}(x,t)+D_{t}^{1-\alpha _{j}^{m}}y(x,t) \bigr]_{x_{j},t_{m}}=g(x_{j},t_{m}). $$

Then, we replace the first order time-derivative by the forward difference formula (12) and replace the second order space-derivative by the three-point centered formula (13) with respect to the weighed average formula (14) at the times \(t_{m}\) and \(t_{m+1}\) as

$$ \delta_{t}y_{j}^{m}-\bigl\{ \lambda \delta_{t}^{1-\alpha_{j}^{m}} \delta_{xx} y_{j}^{m}+(1-\lambda) \delta _{t}^{1-\alpha_{j}^{m}} \delta_{xx} y_{j}^{m+1}\bigr\} + \delta_{t}^{1-\alpha_{j}^{m}} y_{j}^{m}-g(x_{j},t_{m})=T_{j}^{m}, $$

with \(\lambda\in [0,1]\) being the weight factor and \(T_{j}^{m}\) is the resulting truncation error. The standard difference formula is given by

$$ \delta_{t}y_{j}^{m}- \bigl\{ \lambda \delta_{t}^{1-\alpha_{j}^{m}} \delta_{xx} y_{j}^{m}+(1-\lambda) \delta _{t}^{1-\alpha_{j}^{m}} \delta_{xx} y_{j}^{m+1}\bigr\} + \delta_{t}^{1-\alpha_{j}^{m}} y_{j}^{m}-g(x_{j},t_{m})=0. $$

Now, by substituting for the difference operators given by (12), (13) and (15), we can obtain the following scheme:

$$ -\phi Y_{j-1}^{m+1}+(1+2\phi )Y_{j}^{m+1}-\phi Y_{j+1}^{m+1}=R, $$
(17)

where

$$ \phi=(1-\lambda)\bar{S}, \qquad \bar{S}=\frac{(\Delta t)^{\alpha_{j}^{m}}}{(\Delta x)^{2}},\qquad S=(\Delta t)^{\alpha_{j}^{m}}, $$
(18)

and

$$\begin{aligned} R={}&Y_{j}^{m}+\bar{S} \sum_{r=0}^{m} \bigl[\lambda \rho_{r}^{(1-\alpha_{j}^{m})}+(1-\lambda)\rho_{r+1}^{(1-\alpha _{j}^{m})} { \bigr]} \bigl[Y_{j-1}^{m-r}-2Y_{j}^{m-r}+Y_{j+1}^{m-r} \bigr] \\ &{}- S\sum_{r=0}^{m} \rho_{r}^{(1-\alpha _{j}^{m})}Y_{j}^{m-r}+( \Delta t) g(x_{j},t_{m}), \quad j=1,2,\dots,N-1. \end{aligned}$$
(19)

The boundary conditions were treated using the backward difference formula. Equation (17) is the variable order weighted average finite difference scheme considered in this paper. Fortunately, Eq. (17) is a tridiagonal system. In the case of \(\lambda=1\) and \(\lambda=\frac{1}{2}\), we have the forward Euler fractional quadrature method and the Crank–Nicolson fractional quadrature methods, respectively, which have been studied, e.g., in [30], but at \(\lambda=0\) the scheme is called fully implicit.

Now, to study the solvability of the proposed FDM, let

$$\begin{aligned} &Y^{0}=\bigl[w(x_{1}), w(x_{2}), \dots, w(x_{N-1})\bigr]^{T} \quad\text{and} \\ & Y^{m}= \bigl[Y_{1}^{m}, Y_{2}^{m}, \dots, Y_{N-1}^{m}\bigr]^{T},\quad m=0,1,\dots, M, \end{aligned}$$

respectively. Therefore, the explicit difference approximation scheme (17) can be written in matrix from as

$$ AU^{m+1}=b^{m}, $$
(20)

where

$$A= \begin{bmatrix} (1+2\phi) & -\phi& & & \\ -\phi& (1+2\phi) &-\phi& & \\ & \ddots& \ddots& \ddots\\ & &-\phi& (1+2\phi)& -\phi\\ & & &-\phi& (1+2\phi)& -\phi \end{bmatrix} , $$

and \(b^{m}=R\).

Remark 1

It is worthy to report here that the number of arithmetic operations required to solve the system of equations (20) is approximately \(\frac{2}{3}(m+1)^{3} \), see [31].

Theorem 1

The difference equations (20) are uniquely solvable.

Proof

Because \(\phi> 0\), the coefficient matrix of the difference equations (20) is a strictly diagonally dominant matrix. Therefore, A is a nonsingular matrix, which proves the theorem. □

Lemma 1

The coefficients \(\rho_{k}^{1-\alpha}\), \((k=0,1,\dots)\), satisfy:

  1. (1)

    \(\rho_{0}^{1-\alpha}=1\); \(\rho_{1}^{1-\alpha}=\alpha-1\); \(\rho _{k}^{1-\alpha}<0\), \(k=2,3,\dots\);

  2. (2)

    \(\sum_{k=0}^{\infty}\rho_{k}^{1-\alpha}=1\); \(\forall n \in N^{+}\), \(-\sum_{k=1}^{n}\rho_{k}^{1-\alpha}<1\).

Proof

See [32]. □

4 Stability analysis

In this section, we use the John von Neumann method in the stability analysis of the weighted average scheme (17). In our study we neglected the source term (i.e., \(g(x,t)=0\)).

Proposition 1

Assuming that \(Y_{j}^{m}=\xi_{m}e^{{i}qj \Delta x}\),

$$\begin{aligned} &\biggl[ 1+4(1-\lambda)\bar{S} \sin^{2} \biggl(\frac{q\Delta x}{2}\biggr)\biggr]\xi_{m+1}+S\sum _{r=0}^{m}\rho_{r}^{(1-\alpha_{j}^{m})} \xi _{m-r}-\xi_{m} \\ &\quad+ 4\bar{S}\sin^{2} \biggl(\frac{q\Delta x}{2}\biggr)\sum _{r=0}^{m}\bigl[\lambda \rho_{r}^{(1-\alpha_{j}^{m})}+(1- \lambda)\rho_{r+1}^{(1-\alpha _{j}^{m})}\bigr]\xi _{m-r}=0. \end{aligned}$$
(21)

Proposition 2

Assuming in Proposition 1 that \(\xi_{m+1}=\eta\xi_{m}\), the scheme will be stable as long as

$$\begin{aligned} -1 &\leqslant\frac{1-4\bar{S}\sin^{2} (\frac {q\Delta x}{2})\sum_{r=0}^{m}[\lambda \rho_{r}^{(1-\alpha_{j}^{m})}+(1-\lambda)\rho_{r+1}^{(1-\alpha _{j}^{m})}]\eta^{-r}-S\sum_{r=0}^{m}\rho_{r}^{(1-\alpha _{j}^{m})}\eta ^{-r}}{1+4(1-\lambda)\bar{S}\sin^{2} (\frac{q\Delta x}{2})} \\ &\leqslant1. \end{aligned}$$
(22)

Proposition 3

Assuming in Proposition 2 that \(\psi=\bar{S}\sin^{2} (\frac{q\Delta x}{2})\) and that

$$ L_{m}=\frac{2-S\sum_{r=0}^{m}\rho_{r}^{(1-\alpha_{j}^{m})}(-1)^{-r}}{4\{(2\lambda -1)[1-\sum_{r=1}^{m} (-1)^{r-1}\rho_{r}^{(1-\alpha_{j}^{m})}]+(-1)^{m}(1-\lambda)\rho _{m+1}^{(1-\alpha_{j}^{m})}\}}, $$
(23)

the scheme will be stable when

$$ \psi\leq L_{m}. $$
(24)

Theorem 2

The variable order fractional weighted average finite difference scheme (derived in (17)) is stable under the following stability criterion:

$$ \frac{1}{\bar{S}}\geq\frac{4(2\lambda -1)2^{-\alpha _{j}^{m}}}{1-S2^{-\alpha_{j}^{m}}}. $$
(25)

Proof

Since \(L_{m}\) depends on m, it turns out that \(L_{m}\) tends towards its limit value

$$ L=\lim_{m\rightarrow\infty}L_{m}. $$
(26)

In this limit the stability condition is

$$ \psi\leq \frac{2-S\sum_{r=0}^{\infty}\rho_{r}^{(1-\alpha _{j}^{m})}(-1)^{-r}}{4\{(2\lambda-1)[1-\sum_{r=1}^{\infty} (-1)^{r-1}\rho_{r}^{(1-\alpha_{j}^{m})}]+\lim_{m\rightarrow\infty }(-1)^{m}(1-\lambda)\rho_{m+1}^{(1-\alpha_{j}^{m})}\}}, $$
(27)

but from Eq. (16) with \(z=-1\) one can see that \(\sum_{r=0}^{\infty} (-1)^{r}\rho_{r}^{(1-\alpha _{j}^{m})}=2^{1-\alpha _{j}^{m}}\), so that

$$ L=\frac{2-S2^{1-\alpha_{j}^{m}}}{4\{ (2\lambda-1)[2-2^{1-\alpha _{j}^{m}}]+\lim_{m\rightarrow\infty}(-1)^{m}(1-\lambda )w_{m+1}^{(1-\alpha _{j}^{m})}\}}, $$
(28)

and by replacing \(\sin^{2} (\frac{q\Delta x}{2})\) by its highest value, one gets \(\psi\rightarrow\bar{S}\) as \(\sin^{2} (\frac {q\Delta x}{2})\rightarrow1\) and \(\lim_{m\rightarrow\infty}(-1)^{m}(1-\lambda)\rho_{m+1}^{(1-\alpha _{j}^{m})}=0\), therefore we find a sufficient condition for the presented method to be stable and this completes the proof of the theorem. □

5 Numerical results

In this section we present a numerical example to illustrate the efficiency and the validation of the proposed numerical method when applied to solve numerically the variable order linear and nonlinear reaction–subdiffusion equation. In the second example our results are compared with those obtained in [33] under the same conditions listed in Table 1.

Table 1 Absolute error between the exact and numerical solutions of the variable order nonlinear reaction–subdiffusion equation (30) for different values of \(\alpha(x,t) \), Δt and Δx
Full size table

Example 5.1

Consider the following initial–boundary problem of the variable fractional reaction–subdiffusion equation:

$$ y_{t}(x,t)=D_{t}^{1-\alpha(x,t)} \bigl[y_{xx}(x,t)-y(x,t)\bigr]+f(x,t), $$
(29)

on a finite domain \(0 < x < 1\), with \(0 \leq t \leq T\), \(0<\alpha<1\) and the following source term:

$$g(x,t)=2 \biggl(\frac{t(\varGamma(2+\alpha(x,t)))+(\pi ^{2}+1)t^{\alpha (x,t)+1}}{\varGamma(2+\alpha(x,t))} \biggr)\sin(\pi x). $$

Under the boundary conditions \(y(0,t) = y(1, t) = 0\), and the initial condition \(y(x,0)=0\), the exact solution is \(y(x,t)=t^{2}\sin(\pi x)\).

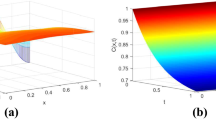
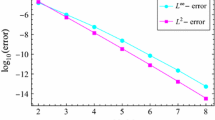
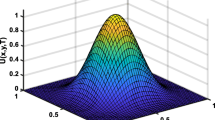
We will compare the numerical with the exact solution for some different values of \(\alpha (x,t)\), Δt, Δx, λ and the final time T (see Figures 1–5). Then in Table 2, we will show the dependency of the maximum absolute error on Δx and Δt.

Figure 1
figure 1

Numerical solution of the variable order fractional reaction–subdiffusion equation at \(\lambda= 0\) for \(\Delta x=\frac{1}{90}\), \(\Delta t=\frac{1}{100}\), final time \(T=0.02\), \(\alpha(x,t)=\frac{10 +(xt)^{4} -(xt)^{5}}{130}\) and the maximum absolute error is \(6.973845 \times10^{-5}\)

Full size image
Figure 2
figure 2

Absolute error between the exact and numerical solutions of the variable order fractional reaction–subdiffusion equation at \(\lambda= 0\) for \(\Delta x=\frac{1}{90}\), \(\Delta t=\frac{1}{100}\), final time \(T=0.02\), \(\alpha(x,t)=\frac{10 +(xt)^{4} -(xt)^{5}}{130}\), and the maximum absolute error is \(6.973845 \times10^{-5}\)

Full size image
Figure 3
figure 3

Numerical solution of the variable order fractional reaction–subdiffusion equation at \(\lambda= 0.5\) for \(\Delta x=\frac{1}{20}\), \(\Delta t=\frac{1}{200}\), final time \(T=0.1\), \(\alpha(x,t)=\frac {12-\sin^{3}(xt)}{12}\), and the maximum absolute error is \(3.456 \times10^{-3}\)

Full size image
Figure 4
figure 4

Unstable numerical solution of the variable order fractional reaction–subdiffusion equation at \(\lambda= 1\) for \(\Delta x=\frac{1}{40}\), \(\Delta t=\frac{1}{200}\), final time \(T=0.2\), \(\alpha(x,t)=\frac{12-\sin^{3}(xt)}{12}\), the stability condition does not hold

Full size image
Figure 5
figure 5

Unstable numerical solution of the variable order fractional reaction–subdiffusion equation at \(\lambda= 1\) for \(\Delta x=\frac{1}{25}\), \(\Delta t=\frac{1}{160}\), final time \(T=1\), \(\alpha(x,t)=\frac {16+(xt)^{5}}{17}\), the stability condition does not hold

Full size image
Table 2 Dependency of maximum absolute error on Δx, Δt with \(\lambda=0\), \(\alpha(x,t)=\frac{12-\sin^{3}(xt)}{12}\), where the final time is \(T=0.1\)
Full size table

According to Remark 1, the number of arithmetic operations required to solve the system in this case is approximately \(\frac{2}{3}(91+1)^{3} \simeq519{,}125\).

Example 5.2

Consider the following variable-order nonlinear reaction–subdiffusion equation

$$ y_{t}(x,t)=D_{t}^{1-\alpha(x,t)} \bigl[y_{xx}(x,t)-y(x,t)\bigr]+g\bigl(x,t,y(x,t)\bigr), $$
(30)

with the initial and boundary conditions:

$$\begin{aligned} &y(x,0)=0, \quad 0 \leq x \leq1, \\ &y(0,t) = t^{2},\qquad y(1, t) =e t^{2},\quad 0 \leq t \leq1, \end{aligned}$$

where

$$ g\bigl(x,t,y(x,t)\bigr)=y^{2}(x,t)+e^{x} t \bigl(2-e^{x} t^{3}\bigr). $$
(31)

The exact solution is

$$ u(x,t)=e^{x} t^{2}. $$
(32)

6 Conclusion and remarks

This paper presents a class of numerical methods for solving the variable order linear and nonlinear reaction–subdiffusion equation. The contribution in this paper is a generalization of the work done by Sweilam et al. [3]. This class of methods is very close to the weighted average FDM. Special attention is given to the stability of the fractional finite weighted average FDM. For this we have resorted to a kind of fractional John von Neumann stability analysis. From the theoretical study we can conclude that this procedure is suitable for the fractional finite weighted average FDM and leads to very good predictions for the stability bounds. The stability of the fractional finite weighted average FDM presented strongly depends on the value of the weighting parameter λ. Numerical solutions and exact solutions of the proposed problem are compared and the derived stability condition is checked numerically. From this comparison, we can conclude that the numerical solutions are in excellent agreement with the exact solutions. By comparing the results in this paper with the results in [33], we found that the same order of maximum error was obtained under the same values of \(\alpha(x,t)\), Δx and Δt.

All computations in this paper were performed using MATLAB software.