1 Introduction

Fractional calculus studies the several different possibilities of defining integral and derivative of arbitrary order, generalizing the classical integration operator \(Jf(t)=\int_{0}^{t} f(\tau){\,d\tau} \) and differentiation operator \(D f(t)=\frac{d}{dt}\,f(t)\). In this regard, the common definitions include the Grünwald–Letnikov fractional integral and derivative, the Riemann–Liouville fractional integral and derivative, and the Caputo fractional derivative [1–9].

It is found that fractional calculus can describe memory phenomena and hereditary properties of various materials and processes [2–7, 10]. In recent decades, fractional calculus has been applied to different fields of science and engineering, covering viscoelasticity theory, non-Newtonian flow, damping materials [4, 7, 11, 12], anomalous diffusion [13–16], control and optimization theory [17–19], financial modeling [20, 21], and so on.

For the scalar function \(f(t)\) on \(a< t<+\infty\), the Riemann–Liouville fractional integral of order β is defined as

$$\begin{aligned} {}_{a}J_{t}^{\beta}f(t)= \int_{a}^{t}\frac{(t-\tau)^{\beta-1}}{\Gamma(\beta)}f(\tau) \,d\tau, \end{aligned}$$
(1)

for \(\beta>0\), and \(f(t)\) for \(\beta=0\). The Riemann–Liouville and Caputo fractional derivatives of order α have the forms

$$\begin{aligned} {}_{a}^{R}D_{t}^{\alpha}f(t)= \frac{d^{n}}{dt^{n}} \bigl({}_{a}J_{t}^{n-\alpha}f(t) \bigr),\quad 0< n-1< \alpha\leq n, \end{aligned}$$
(2)

and

$$\begin{aligned} {}_{a} D_{t}^{\alpha}f(t)={}_{a}J_{t}^{n-\alpha}f^{(n)}(t), \quad 0< n-1< \alpha\leq n, \end{aligned}$$
(3)

respectively.

Fractional differential equations on scalar functions, including the existence, uniqueness and stability, and the analytic and numeric methods of solutions, were studied by many scholars [3–9, 13, 15, 17, 22–27]. In particular, new numerical schemes were designed [9, 23, 24, 28], and a Lie symmetry analysis was given and the conservation laws for fractional evolution equations were systematically investigated [29–32]. The solutions of many fractional differential equations involve a class of important special functions—Mittag–Leffler functions (AMS 2000 Mathematics Subject Classification 33E12). The Mittag–Leffler function with two parameters is defined by the series expansion [5, 33]

$$ E_{\lambda,\rho}(z)=\sum_{k=0}^{\infty}\frac {z^{k}}{\Gamma(\lambda k+\rho )},\quad \lambda>0,\rho>0,z\in C, $$
(4)

where \(\Gamma(\cdot)\) is Euler’s gamma function. The special case of \(\lambda=\rho=1\) degenerates to the exponential function, \(E_{1,1}(z)=e^{z}\). We note that the Mittag–Leffler functions were also used to define new fractional derivatives [34, 35].

The Laplace transform is an effective tool for the analysis of linear fractional differential equations. It is defined for a function \(f(t)\) as

$$\begin{aligned} \mathcal{L}\bigl[f(t)\bigr]=\tilde{f}(s)= \int_{0}^{+\infty} f(t) e^{-st}\,dt, \quad \operatorname{Re} (s)>c. \end{aligned}$$
(5)

The Laplace transforms of the fractional integral and the Caputo fractional derivative are

$$ \mathcal{L}\bigl[{}_{0}J_{t}^{\alpha}f(t)\bigr]= s^{-\alpha}\tilde{f}(s),\quad\alpha>0, $$
(6)

and

$$ \mathcal{L} \bigl[ {}_{0} D_{t}^{\alpha}f(t) \bigr]= s^{\alpha}\tilde{f}(s)-\sum_{k=0}^{n-1}s^{\alpha-1-k} f^{(k)}\bigl(0^{+}\bigr),\quad 0< n-1< \alpha\leq n. $$
(7)

Atanackovic and Stankovic [36] introduced the system of fractional differential equations into the analysis of lateral motion of an elastic column fixed at one end and loaded at the other. Daftardar-Gejji and Babakhani [37] and Deng et al. [38] studied the existence, uniqueness and stability for solution of system of linear fractional differential equations with constant coefficients. Other references include [39–41]. In the above literature, solutions of the fractional differential system were given for the case of a commensurate order system.

Incommensurate fractional order linear systems were considered in [42, 43]. Odibat [42] used the Laplace transform and the Mittag–Leffler function with two parameters, but the orders were limited to rational numbers. Daftardar-Gejji and Jafari [43] derived solutions using the Adomian decomposition method.

In this paper, we focus on the system of linear fractional differential equations of incommensurate orders and give analytic expressions for the solutions by using the Laplace transform and multi-variable Mittag–Leffler functions of matrix arguments. We verify the result with numeric solutions of an example.

In the sequel, we will use the Caputo fractional derivatives and denote \({}_{0} D_{t}^{\alpha}f(t) \) by \(D_{t}^{\alpha}f(t) \) for short.

2 A generalization of the Mittag–Leffler function

We introduce an n-variable Mittag–Leffler function with \(n+1\) parameters as

$$\begin{aligned} &\mathcal{E}_{(\alpha_{1},\alpha_{2},\dots,\alpha_{n}),\beta }(t_{1},t_{2},\dots ,t_{n}) \\ &\quad =\frac{1}{\Gamma(\beta)}+\sum_{k=1}^{\infty}\sum_{j_{1},j_{2},\dots,j_{k}=1}^{n} \frac{t_{j_{1}}t_{j_{2}}\dots t_{j_{k}}}{\Gamma(\alpha_{j_{1}}+\alpha_{j_{2}}+\cdots+\alpha_{j_{k}}+\beta)}, \end{aligned}$$
(8)

where \(\alpha_{i}\) for \(i=1,2,\dots,n\) and β are positive constants.

The explicit form of the first several terms on the right hand side is

$$\frac{1}{\Gamma(\beta)}+\sum_{j_{1}=1}^{n} \frac{t_{j_{1}}}{\Gamma (\alpha_{j_{1}}+\beta)}+\sum_{j_{1},j_{2}=1}^{n} \frac {t_{j_{1}}t_{j_{2}}}{\Gamma(\alpha_{j_{1}}+\alpha_{j_{2}}+\beta)} + \sum_{j_{1},j_{2},j_{3}=1}^{n} \frac{t_{j_{1}}t_{j_{2}} t_{j_{3}}}{\Gamma(\alpha _{j_{1}}+\alpha_{j_{2}}+\alpha_{j_{3}}+\beta)} + \cdots. $$

The special case of the single variable, i.e. \(n=1\), degenerates to the Mittag–Leffler function with two parameters as

$$\begin{aligned} \mathcal{E}_{(\alpha),\beta}(t) =&\frac{1}{\Gamma(\beta)}+ \frac {t}{\Gamma(\alpha+\beta)}+ \frac{t^{2}}{\Gamma(2 \alpha+\beta)} + \frac{t^{3}}{\Gamma(3 \alpha+\beta)} +\cdots \\ =&E_{\alpha,\beta}(t), \end{aligned}$$
(9)

where we express the parameter and the argument as α and t, instead of \(\alpha_{1}\) and \(t_{1}\).

The two-variable case, i.e. \(n=2\), is

$$\begin{aligned} \mathcal{E}_{(\alpha_{1},\alpha_{2}),\beta}(t_{1},t_{2}) =& \frac{1}{\Gamma (\beta )}+ \biggl( \frac{t_{1}}{\Gamma(\alpha_{1}+\beta)}+\frac {t_{2}}{\Gamma (\alpha_{2}+\beta)} \biggr) \\ &{}+ \biggl( \frac{t_{1}^{2}}{\Gamma(2 \alpha_{1}+\beta)}+ \frac{2t_{1}t_{2}}{\Gamma( \alpha_{1}+\alpha_{2}+\beta)}+ \frac{t_{2}^{2}}{\Gamma(2 \alpha_{2}+\beta)} \biggr) + \cdots. \end{aligned}$$
(10)

The series on the right hand side in Eq. (8) is absolutely convergent for \((t_{1},t_{2},\dots,t_{n}) \in\mathbf{R}^{n}\). In fact, we may suppose, without loss of generality, that \(\alpha_{1}=\min\{\alpha_{1},\alpha_{2},\dots,\alpha_{n}\}\). Then, for large enough k, we have

$$\alpha_{j_{1}}+\alpha_{j_{2}}+\cdots+\alpha_{j_{k}}+\beta \geq k\alpha _{1}+\beta>2. $$

So it follows that

$${\Gamma(\alpha_{j_{1}}+\alpha_{j_{2}}+\cdots+\alpha_{j_{k}}+ \beta)} \geq \Gamma (k\alpha_{1}+\beta). $$

We estimate the general term of the series in Eq. (8) as

$$\begin{aligned} & \Biggl\vert \sum_{j_{1},j_{2},\dots,j_{k}=1}^{n} \frac{t_{j_{1}}t_{j_{2}}\dots t_{j_{k}}}{\Gamma(\alpha_{j_{1}}+\alpha_{j_{2}}+\cdots+\alpha_{j_{k}}+\beta )} \Biggr\vert \\ &\quad \le \frac{1}{\Gamma(k\alpha_{1}+\beta)} \sum_{j_{1},j_{2},\dots,j_{k}=1}^{n} \vert t_{j_{1}}t_{j_{2}}\dots t_{j_{k}} \vert \\ &\quad =\frac{1}{\Gamma(k\alpha_{1}+\beta)} \bigl( \vert t_{1} \vert + \vert t_{2} \vert +\cdots+ \vert t_{n} \vert \bigr)^{k}. \end{aligned}$$
(11)

It is well known that the dominant series

$$\sum_{k=0}^{\infty}\frac{1}{\Gamma(k\alpha_{1}+\beta)} \bigl( \vert t_{1} \vert + \vert t_{2} \vert +\cdots+ \vert t_{n} \vert \bigr)^{k} $$

converges to the Mittag–Leffler function \(E_{\alpha_{1}, \beta }(|t_{1}|+|t_{2}|+\cdots+|t_{n}|)\).

If in the definition (8) the parameters satisfy \(\alpha _{1}=\alpha _{2}=\cdots=\alpha_{n}=\alpha\), then the n-variable Mittag–Leffler function in Eq. (8) also degenerates to the Mittag–Leffler function with two parameters as

$$\begin{aligned} \mathcal{E}_{(\alpha,\alpha,\dots,\alpha),\beta}(t_{1},t_{2},\dots ,t_{n}) =&\frac{1}{\Gamma(\beta)}+ \sum_{k=1}^{\infty}\frac{1}{\Gamma(\alpha k+\beta)} \sum_{j_{1},j_{2},\dots,j_{k}=1}^{n} {t_{j_{1}}t_{j_{2}}\dots t_{j_{k}}} \\ =&\frac{1}{\Gamma(\beta)}+\sum_{k=1}^{\infty}\frac{(t_{1}+t_{2}+\cdots+t_{n})^{k}}{\Gamma(\alpha k+\beta)} \\ =&E_{\alpha, \beta}(t_{1}+t_{2}+\cdots+t_{n}). \end{aligned}$$
(12)

In particular, if \(\alpha_{1}=\alpha_{2}=\cdots=\alpha_{n}=\beta=1\), the n-variable Mittag–Leffler function in Eq. (8) degenerates to the exponential function

$$ \mathcal{E}_{(1,1,\dots,1),1}(t_{1},t_{2}, \dots,t_{n})=E_{1, 1}(t_{1}+t_{2}+ \cdots+t_{n})=e^{t_{1}+t_{2}+\cdots+t_{n}}. $$
(13)

We remark that different versions of multi-variable Mittag–Leffler functions were presented, such as in [43–46]. But they are not exactly the same as the version in this paper.

3 Solution of system of fractional differential equations

We consider the following system of fractional differential equations:

$$ D_{t}^{\alpha_{i}} y_{i}(t) =\sum _{k=1}^{n} a_{ik} y_{k}(t) +f_{i}(t), \quad t>0, i=1,2,\dots,n, $$
(14)

where \(a_{ik} \) are constants, not all zero, \(f_{i}(t)\) are specified functions, \(D_{t}^{\alpha_{i}}\) are the Caputo fractional derivative operators with \(0<\alpha_{i}\leq1\), and \(y_{i}(t)\) are unknown functions with the specified initial values \(y_{i}(0)\).

We suppose that each \({f}_{i}(t)\) is locally integrable on the interval \(0< t<+\infty\) and the Laplace transforms exist. Equation (14) may be written in matrix equation as

$$\begin{aligned} \mathbf{D} { \mathbf{y}(t)}=\mathbf{A} \mathbf{y}(t)+\mathbf {f}(t), \quad t>0, \end{aligned}$$
(15)

where D is the diagonal matrix with the fractional derivative operators

$$\begin{aligned} \mathbf{D}=\operatorname{diag} \bigl( D_{t}^{\alpha_{1}},D_{t}^{\alpha_{2}}, \dots,D_{t}^{\alpha_{n}} \bigr), \end{aligned}$$
(16)

\(\mathbf{A}=(a_{ij})_{n\times n}\) is a non-zero coefficient matrix, \(\mathbf{f}(t)=(f_{1}(t),f_{2}(t),\dots,f_{n}(t))^{T}\), and \(\mathbf{y}=\mathbf{y}(t)=(y_{1}(t),y_{2}(t),\ldots,y_{n}(t))^{T}\).

Applying the Laplace transformation to Eq. (14) with respect to t we obtain

$$ s^{\alpha_{i}} \tilde{y}_{i}(s) -s^{\alpha_{i}-1} {y}_{i}(0) =\sum_{k=1}^{n} a_{ik} \tilde{y}_{k}(s) +\tilde{f}_{i}(s), \quad i=1,2,\dots,n, $$
(17)

where \(\operatorname{Re}(s)>c>0\), and c is constrained by the following derivation and can be taken as the value on the right hand side of inequality (21). In matrix form, Eq. (17) is

$$ \boldsymbol{\Lambda} \tilde{\mathbf{y}}(s) -s^{-1} \boldsymbol { \Lambda}\mathbf{y}(0)=\mathbf{A} \tilde{\mathbf{y}}(s) +\tilde {\mathbf{f}}(s), $$
(18)

where Λ denotes the diagonal matrix \(\boldsymbol {\Lambda}= \operatorname{diag}(s^{\alpha_{1}},s^{\alpha_{2}},\dots ,s^{\alpha_{n}})\). We rewrite Eq. (18) as

$$ ({\boldsymbol{\Lambda} -A}) \tilde{\mathbf{y}}(s) =s^{-1} \boldsymbol{ \Lambda} \mathbf{y}(0)+\tilde{\mathbf{f}}(s). $$
(19)

Left multiplication by the inverse matrix \(\boldsymbol{\Lambda }^{-1}=\operatorname{diag}(s^{-\alpha_{1}},s^{-\alpha_{2}},\dots ,s^{-\alpha _{n}})\) leads to

$$ \bigl(\mathbf{I}-\boldsymbol{\Lambda}^{-1} \mathbf{A}\bigr) \tilde{ \mathbf {y}}(s) =s^{-1} \mathbf{y}(0)+\boldsymbol{\Lambda}^{-1} {\tilde {\mathbf{f}}}(s), $$
(20)

where I is the unit matrix of order n.

We let

$$\begin{aligned} \operatorname{Re}(s)> \max_{1\leq i\leq n} \Biggl(2\sum _{k=1}^{n} \vert a_{ik} \vert \Biggr)^{1/\alpha_{i}}, \end{aligned}$$
(21)

then the matrix \(({\mathbf{I}-\Lambda^{-1} A})\) is invertible. This can be proved as follows.

In fact, by Eq. (21), we have

$$\begin{aligned} \vert s \vert ^{\alpha_{i}} > 2\sum_{k=1}^{n} \vert a_{ik} \vert ,\quad i=1,2,\dots,n, \end{aligned}$$
(22)

that is, the following holds:

$$\begin{aligned} \sum_{k=1}^{n} \bigl\vert s^{-\alpha_{i}} a_{ik} \bigr\vert < \frac{1}{2},\quad i=1,2, \dots,n. \end{aligned}$$
(23)

Thus the absolute values of the diagonal entries of the matrix \(({\mathbf{I}-\Lambda^{-1} A})\) are greater than \(1/2\), while the sum of the absolute values of the non-diagonal entries in the ith row is less than \(1/2\). By the Gershgorin circle theorem, the eigenvalues of the matrix \(({\mathbf{I}-\Lambda^{-1} A})\) are non-zero. Therefore, the matrix \(({\mathbf{I}-\Lambda^{-1} A})\) is invertible.

From Eq. (20), we solve for \(\tilde{\mathbf{y}}(s)\) as

$$ \tilde{\mathbf{y}}(s) =s^{-1} \bigl({\mathbf{I}-\Lambda^{-1} A}\bigr)^{-1} \mathbf{y}(0)+\bigl({\mathbf{I}-\Lambda^{-1} A} \bigr)^{-1}\boldsymbol{\Lambda }^{-1} \tilde{\mathbf{f}}(s). $$
(24)

Inverse Laplace transform yields

$$ \mathbf{y}(t) =\mathbf{G}(t) \mathbf{y}(0)+\mathbf{Q}(t)* \mathbf {f}(t), $$
(25)

where we introduce two matrix functions

$$\begin{aligned} &\mathbf{G}(t) = L^{-1} \bigl[s^{-1} \bigl({\mathbf{I}- \Lambda^{-1} A}\bigr)^{-1} \bigr] , \end{aligned}$$
(26)
$$\begin{aligned} &\mathbf{Q}(t)= L^{-1} \bigl[\bigl({\mathbf{I}-\Lambda^{-1} A}\bigr)^{-1}\boldsymbol{\Lambda }^{-1} \bigr], \end{aligned}$$
(27)

and the convolution is defined as

$$\begin{aligned} \mathbf{Q}(t)* \mathbf{f}(t)= \int_{0}^{t} \mathbf{Q}(t-\tau) \mathbf {f}(\tau) \,d\tau. \end{aligned}$$
(28)

First we consider the inverse Laplace transform of \(({\mathbf {I}-\Lambda^{-1} A})^{-1}\). We use the two decompositions of matrices as

$$\begin{aligned} \bigl({\mathbf{I} -\Lambda^{-1} A}\bigr)^{-1} =&\sum _{k=0}^{\infty}\bigl({\boldsymbol{ \Lambda}^{-1}A}\bigr)^{k} \end{aligned}$$
(29)

and

$$\begin{aligned} {\boldsymbol{\Lambda}^{-1}A}=\sum_{i=1}^{n} s^{-\alpha_{i} } \mathbf{A}_{i}, \end{aligned}$$
(30)

where \(\mathbf{A}_{i}\) denotes the matrix formed from A by rewriting each entry of A except that in the ith row into zeros. So the ith rows of the matrices A and \(\mathbf{A}_{i}\) are identical. Hence we have the following expression:

$$\begin{aligned} \bigl({\mathbf{I} -\Lambda^{-1} A}\bigr)^{-1} =&\sum _{k=0}^{\infty}\Biggl(\sum _{i=1}^{n} s^{-\alpha_{i} } \mathbf{A}_{i} \Biggr)^{k} \\ =&\mathbf{I}+\sum_{k=1}^{\infty}\sum _{j_{1},j_{2},\dots,j_{k}=1}^{n} s^{-(\alpha_{j_{1}}+\alpha_{j_{2}}+\cdots +\alpha _{j_{k}}) } \mathbf{A}_{j_{1}} \mathbf{A}_{j_{2}}\dots\mathbf{A}_{j_{k}}. \end{aligned}$$
(31)

Calculating the inverse Laplace transformation term by term we have

$$\begin{aligned} L^{-1} \bigl[ \bigl({\mathbf{I} -\Lambda^{-1} A} \bigr)^{-1} \bigr] =&\delta(t)\mathbf{I} \\ & {}+\sum_{k=1}^{\infty}\sum _{j_{1},j_{2},\dots,j_{k}=1}^{n} \frac{t^{\alpha_{j_{1}}+\alpha _{j_{2}}+\cdots +\alpha_{j_{k}}-1 }}{\Gamma(\alpha_{j_{1}}+\alpha_{j_{2}}+\cdots+\alpha_{j_{k}})} \mathbf{A}_{j_{1}} \mathbf{A}_{j_{2}}\dots\mathbf{A}_{j_{k}}, \end{aligned}$$
(32)

where \(\delta(t)\) is the Dirac delta function.

Further we have the following result for the matrix \(\mathbf{G}(t)\):

$$\begin{aligned} \mathbf{G}(t) =&L^{-1} \bigl[s^{-1} \bigl({\mathbf{I}- \Lambda^{-1} A}\bigr)^{-1} \bigr] \\ =&J_{t}^{1}L^{-1} \bigl[ \bigl({\mathbf{I} - \Lambda^{-1} A}\bigr)^{-1} \bigr] \\ =&\mathbf{I}+ \sum_{k=1}^{\infty}\sum _{j_{1},j_{2},\dots,j_{k}=1}^{n} \frac{t^{\alpha_{j_{1}}+\alpha _{j_{2}}+\cdots +\alpha_{j_{k}} }}{\Gamma(\alpha_{j_{1}}+\alpha_{j_{2}}+\cdots+\alpha_{j_{k}}+1)} \mathbf{A}_{j_{1}} \mathbf{A}_{j_{2}}\dots\mathbf{A}_{j_{k}}. \end{aligned}$$
(33)

We lift the generalized Mittag–Leffler function in Eq. (8) to a matrix function and use it to express the matrix \(\mathbf{G}(t)\) as

$$\begin{aligned} \mathbf{G}(t)=\mathcal{E} _{(\alpha_{1},\alpha_{2},\dots,\alpha _{n}),1}\bigl(t^{\alpha_{1}} \mathbf{A}_{1},t^{\alpha_{2}} \mathbf {A}_{2},\dots ,t^{\alpha_{n}} \mathbf{A}_{n}\bigr). \end{aligned}$$
(34)

To calculate the inverse Laplace transform in Eq. (27), we decompose the matrix \({\boldsymbol{\Lambda}^{-1}}\) as

$$\begin{aligned} {\boldsymbol{\Lambda}^{-1}}=\sum_{i=1}^{n} s^{-\alpha_{i} } \mathbf{I}_{i}, \end{aligned}$$
(35)

where \(\mathbf{I}_{j}\) are formed from the unit matrix I in a similar manner as \(\mathbf{A}_{j}\). We derive the expression for the matrix \(\mathbf{Q}(t)\) as

$$\begin{aligned} \mathbf{Q}(t) =& L^{-1} \bigl[\bigl({\mathbf{I}-\Lambda^{-1} A}\bigr)^{-1}\boldsymbol{\Lambda }^{-1} \bigr] \\ =& L^{-1} \Biggl[\sum_{i=1}^{n} s^{-\alpha_{i} }\bigl({\mathbf{I}-\Lambda^{-1} A}\bigr)^{-1} \mathbf{I}_{i} \Biggr] \\ =&\sum_{i=1}^{n} J_{t}^{\alpha_{i} }L^{-1} \bigl[\bigl({\mathbf{I}-\Lambda^{-1} A}\bigr)^{-1} \bigr] \mathbf{I}_{i} \\ =& \sum_{i=1}^{n} \Biggl[ \frac{t^{\alpha_{i}-1}}{\Gamma(\alpha_{i})} \mathbf{I}+ \sum_{k=1}^{\infty}\sum_{j_{1},j_{2},\dots,j_{k}=1}^{n} \frac{t^{\alpha _{j_{1}}+\alpha_{j_{2}}+\cdots+\alpha_{j_{k}}+\alpha_{i}-1 }}{\Gamma(\alpha _{j_{1}}+\alpha _{j_{2}}+\cdots+\alpha_{j_{k}}+\alpha_{i})} \mathbf{A}_{j_{1}} \mathbf{A}_{j_{2}} \dots\mathbf{A}_{j_{k}} \Biggr] \mathbf{I}_{i} . \end{aligned}$$
(36)

An equivalent expression is

$$\begin{aligned} \mathbf{Q}(t)= \sum_{i=1}^{n} \frac{t^{\alpha_{i}-1}}{\Gamma(\alpha_{i})} \mathbf{I}_{i}+ \sum_{k=1}^{\infty}\sum_{i=1}^{n} \sum _{j_{1},j_{2},\dots,j_{k}=1}^{n} \frac{t^{\alpha_{j_{1}}+\alpha_{j_{2}}+\cdots+\alpha_{j_{k}}+\alpha_{i}-1 }}{\Gamma (\alpha_{j_{1}}+\alpha_{j_{2}}+\cdots+\alpha_{j_{k}}+\alpha_{i})} \mathbf{A}_{j_{1}} \mathbf{A}_{j_{2}} \dots\mathbf{A}_{j_{k}} \mathbf{I}_{i}. \end{aligned}$$
(37)

In terms of the generalized Mittag–Leffler function of matrix arguments, \(\mathbf{Q}(t)\) has the form from Eq. (36)

$$\begin{aligned} \mathbf{Q}(t) =\sum_{i=1}^{n} t^{\alpha_{i}-1} \mathcal{E} _{(\alpha_{1},\alpha_{2},\dots,\alpha_{n}),\alpha _{i}}\bigl(t^{\alpha_{1}} \mathbf{A}_{1},t^{\alpha_{2}} \mathbf{A}_{2}, \dots,t^{\alpha_{n}} \mathbf {A}_{n}\bigr)\, \mathbf{I}_{i}. \end{aligned}$$
(38)

Thus the analytic solutions are obtained in Eqs. (25), (34) and (38) in terms of the generalized Mittag–Leffler function of matrix arguments. In practical computation, we can truncate the series expressions in Eqs. (33) and (37) and give analytic approximate solutions:

$$ \mathbf{y}^{[m]}(t) =\mathbf{G}^{[m]}(t) \mathbf{y}(0)+\mathbf {Q}^{[m]}(t)* \mathbf{f}(t), $$
(39)

where \(\mathbf{G}^{[m]}(t) \) and \(\mathbf{Q}^{[m]}(t)\) are the truncation with the first m terms in Eqs. (33) and (37) as

$$\begin{aligned} &\mathbf{G}^{[m]}(t) =\mathbf{I}+ \sum_{k=1}^{m-1} \sum_{j_{1},j_{2},\dots,j_{k}=1}^{n} \frac{t^{\alpha_{j_{1}}+\alpha _{j_{2}}+\cdots +\alpha_{j_{k}} }}{\Gamma(\alpha_{j_{1}}+\alpha_{j_{2}}+\cdots+\alpha_{j_{k}}+1)} \mathbf{A}_{j_{1}} \mathbf{A}_{j_{2}}\dots\mathbf{A}_{j_{k}}, \end{aligned}$$
(40)
$$\begin{aligned} & \begin{aligned}[b] \mathbf{Q}^{[m]}(t)={}& \sum_{i=1}^{n} \frac{t^{\alpha_{i}-1}}{\Gamma(\alpha_{i})} \mathbf{I}_{i} \\ &{}+ \sum_{k=1}^{m-1} \sum _{i=1}^{n} \sum_{j_{1},j_{2},\dots,j_{k}=1}^{n} \frac {t^{\alpha_{j_{1}}+\alpha_{j_{2}}+\cdots+\alpha_{j_{k}}+\alpha_{i}-1 }}{\Gamma(\alpha _{j_{1}}+\alpha_{j_{2}}+\cdots+\alpha_{j_{k}}+\alpha_{i})} \mathbf{A}_{j_{1}} \mathbf{A}_{j_{2}} \dots \mathbf{A}_{j_{k}} \mathbf{I}_{i}. \end{aligned} \end{aligned}$$
(41)

For the special case \(\alpha_{1}=\alpha_{2}=\cdots=\alpha_{n}=\alpha\), the two matrices \(\mathbf{G}(t)\) and \(\mathbf{Q}(t)\) are simplified to

$$\begin{aligned} \mathbf{G}(t) =& \mathcal{E} _{(\alpha,\alpha,\dots,\alpha),1} \bigl(t^{\alpha} \mathbf {A}_{1},t^{\alpha} \mathbf{A}_{2},\dots,t^{\alpha} \mathbf {A}_{n}\bigr) \\ =&{E} _{\alpha,1}\bigl(t^{\alpha} \mathbf{A}_{1}+t^{\alpha} \mathbf {A}_{2}+\cdots+t^{\alpha} \mathbf{A}_{n}\bigr) \\ =&{E} _{\alpha,1}\bigl(t^{\alpha} \mathbf{A}\bigr) \end{aligned}$$
(42)

and

$$\begin{aligned} \mathbf{Q}(t) =&\sum_{j=1}^{n} t^{\alpha-1} \mathcal{E} _{(\alpha,\alpha,\dots,\alpha),\alpha}\bigl(t^{\alpha} \mathbf {A}_{1},t^{\alpha} \mathbf{A}_{2}, \dots,t^{\alpha} \mathbf{A}_{n}\bigr) \mathbf{I}_{j} \\ =& t^{\alpha-1} \mathcal{E} _{(\alpha,\alpha,\dots,\alpha),\alpha}\bigl(t^{\alpha} \mathbf {A}_{1},t^{\alpha} \mathbf{A}_{2}, \dots,t^{\alpha} \mathbf {A}_{n}\bigr)\sum _{j=1}^{n} \mathbf{I}_{j} \\ =& t^{\alpha-1} {E} _{\alpha,\alpha}\bigl(t^{\alpha} \mathbf{A}_{1}+t^{\alpha} \mathbf {A}_{2}+ \cdots+t^{\alpha} \mathbf{A}_{n}\bigr) \\ =& t^{\alpha-1} {E} _{\alpha,\alpha}\bigl(t^{\alpha} \mathbf{A}\bigr). \end{aligned}$$
(43)

They are consistent with [39].

4 Comparison with numeric solutions

We take \(T>0\) and the number of nodes N, and we consider the numeric solutions on the interval \([0,T]\) with the step size \(h=T/N\). Denote the nodes as \(t_{i}=i h, i=0,1,\ldots,N\). Let \(x_{i}, y_{j,i}, f_{j,i}\) represent, respectively, the values of \(x(t), y_{j}(t),f_{j}(t)\) at \(t=t_{i}\).

In the L1 algorithm given by Oldham and Spanier [1], the fractional derivative at \(t=t_{i}\) is discretized as

$$\begin{aligned} D_{t}^{\alpha} x(t)|_{t_{i}} =& \int_{0}^{t_{i}}\frac{(t_{i}-\tau)^{-\alpha}}{\Gamma(1-\alpha)}x'(\tau )\,d\tau \\ =&\sum_{j=0}^{i-1} \int_{t_{j}}^{t_{j+1}}\frac{(t_{i}-\tau)^{-\alpha}}{\Gamma(1-\alpha )}x'( \tau )\,d\tau \\ \approx&\sum_{j=0}^{i-1} \frac{x_{j+1}-x_{j}}{h} \int_{t_{j}}^{t_{j+1}}\frac{(t_{i}-\tau)^{-\alpha }}{\Gamma(1-\alpha)} \,d\tau. \end{aligned}$$

Calculating the integration leads to

$$\begin{aligned} D_{t}^{\alpha} x(t)|_{t_{i}} \approx& \frac{1}{h^{\alpha}\Gamma(2-\alpha)}\sum_{j=0}^{i-1} (x_{j+1}-x_{j}) \bigl[(i-j)^{1-\alpha}-(i-j-1)^{1-\alpha} \bigr]. \end{aligned}$$
(44)

Regrouping the terms on the right hand side we have the approximation

$$\begin{aligned} D_{t}^{\alpha} x(t)|_{t_{i}} \approx& \frac{1}{h^{\alpha}\Gamma (2-\alpha)} \Biggl(x_{i}+\sum_{j=1}^{i} w_{j}(\alpha) x_{i-j} \Biggr), \end{aligned}$$
(45)

where

$$\begin{aligned} w_{j}(\alpha)= \textstyle\begin{cases} (j-1)^{1-\alpha} -2 j^{1-\alpha} +(j+1)^{1-\alpha},& 1\leq j\leq i-1,\\ (i-1) ^{1-\alpha} - i^{1-\alpha},& j=i. \end{cases}\displaystyle \end{aligned}$$
(46)

Now for the system of the fractional differential equations (15), we specify \(t=t_{i}\) for \(i=1,2,\dots,N\) as

$$ \mathbf{D} { \mathbf{y}(t)}|_{t_{i}} =\mathbf{A} \mathbf {y}_{i}+\mathbf{f}_{i}, $$
(47)

where \(\mathbf{y}_{i}=(y_{1,i},y_{2,i},\dots,y_{n,i})^{T}\), \(\mathbf{f}_{i}=(f_{1,i}, f_{2,i},\dots, f_{n,i})^{T}\) and

$$\mathbf{D} { \mathbf{y}(t)}|_{t_{i}}= \bigl( D_{t}^{\alpha_{1}}y_{1}(t),D_{t}^{\alpha_{2}}y_{2}(t), \dots,D_{t}^{\alpha _{n}}y_{n}(t) \bigr)^{T}|_{t=t_{i}} . $$

Substituting the discrete form of the fractional derivatives in Eq. (45), we obtain

$$ \boldsymbol{\Omega} \mathbf{y}_{i}+\mathbf{g} =\mathbf{A} \mathbf {y}_{i}+\mathbf{f}_{i}, $$
(48)

where

$$\begin{aligned} &\boldsymbol{\Omega}=\operatorname{diag} \biggl(\frac{1}{h^{\alpha _{1}} \Gamma(2-{\alpha_{1}})}, \frac{1}{h^{\alpha_{2}} \Gamma(2-{\alpha _{2}})},\dots,\frac{1}{h^{\alpha_{n}} \Gamma(2-{\alpha_{n}})} \biggr), \end{aligned}$$
(49)
$$\begin{aligned} &\begin{aligned}[b] \mathbf{g}&=\mathbf{g}( \mathbf{y}_{0},\mathbf{y}_{1}, \dots,\mathbf {y}_{i-1}) \\ &= \biggl( \frac{\sum_{j=1}^{i} w_{j}(\alpha_{1}) y_{1,i-j}}{h^{\alpha_{1}} \Gamma (2-{\alpha_{1}})}, \frac{\sum_{j=1}^{i} w_{j}(\alpha_{2}) y_{2,i-j}}{h^{\alpha_{2}} \Gamma (2-{\alpha _{2}})},\dots, \frac{\sum_{j=1}^{i} w_{j}(\alpha_{n}) y_{n,i-j}}{h^{\alpha_{n}} \Gamma (2-{\alpha_{n}})} \biggr)^{T}. \end{aligned} \end{aligned}$$
(50)

We rewrite Eq. (48) as

$$\begin{aligned} (\boldsymbol{\Omega}-\mathbf{A} ) \mathbf{y}_{i}=\mathbf {f}_{i}-\mathbf{g}. \end{aligned}$$
(51)

For small enough step size h, the matrix \(\boldsymbol{\Omega }-\mathbf{A}\) has large enough diagonal entries to ensure its invertibility due to the Gershgorin circle theorem. Thus we obtain the scheme for the numeric solutions as

$$\begin{aligned} \mathbf{y}_{i}= (\boldsymbol{\Omega}-\mathbf{A} )^{-1} \bigl(\mathbf{f}_{i} -\mathbf{g}( \mathbf{y}_{0}, \mathbf{y}_{1},\dots,\mathbf{y}_{i-1}) \bigr),\quad i=1,2, \dots,N. \end{aligned}$$
(52)

Finally, we test the analytic approximate solutions and the numeric solutions for the system of the fractional differential equations

$$ \textstyle\begin{cases} D_{t}^{0.7}y_{1}(t)=-2y_{1}-y_{2}-y_{3},\\ D_{t}^{0.5}y_{2}(t)=y_{1}-y_{2}+y_{3}+t,\\ D_{t}^{0.8}y_{3}(t)=-y_{2}-3y_{3}+1, \end{cases} $$
(53)

subject to the initial conditions

$$y_{1}(0)=2,\qquad y_{2}(0)=3,\qquad y_{3}(0)=5. $$

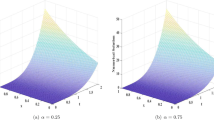
From Eqs. (39), (40) and (41), the analytic approximate solutions \(y^{[14]}_{1}(t)\), \(y^{[14]}_{2}(t)\) and \(y^{[14]}_{3}(t)\) are calculated using the approximations of the first 14 terms, \(\mathbf{G}^{[14]}(t) \) and \(\mathbf{Q}^{[14]}(t)\). The numeric solutions \(y_{1,i}\), \(y_{2,i}\) and \(y_{3,i}\) for \(i=1,2,\dots,40\) with the step size \(h=0.02\) are given by suing the scheme (52). We implement these algorithms by using MATHEMATICA 8. In Fig. 1, the solid line, dot-dash line and dash line represent the analytic approximate solutions \(y^{[14]}_{1}(t)\), \(y^{[14]}_{2}(t)\) and \(y^{[14]}_{3}(t)\), respectively, and the dot lines denote the numeric solutions \(y_{1,i}\), \(y_{2,i}\) and \(y_{3,i}\). The consistence of the two solutions verifies the effectiveness of our proposed analytic method.

Figure 1
figure 1

The analytic approximate solutions and numeric solutions

Full size image

5 Conclusions

The solutions of system of linear fractional differential equations of incommensurate orders are investigated in this paper. First, we introduce an n-variable Mittag–Leffler function with \(n+1\) parameters. Then we derive the analytic expressions for the solutions of the fractional system by using the Laplace transform and multi-variable Mittag–Leffler functions of matrix arguments. Finally, we verify the analytic result with numeric solutions by an example, where the numeric solutions are given by generalizing the L1 algorithm to the fractional system.

We generate the plots of analytic approximate solutions and numeric solutions with the help of MATHEMATICA 8. The obtained series solutions are convergent on the entire interval \(0< t<+\infty\) and are easy to program and are approximated by any symbolic computation software.