1 Introduction

Understanding fluid dynamics in the context of nano-blood flow through a sinusoidal wavy channel is highly significant in cardiovascular disease research. Cardiovascular infections (such as coronary heart disease [1], stroke, aneurysm, and stenosis) are regarded as the cause of the most significant number of deaths in the world [2]. Atherosclerosis, resulting in plaque accumulation and stenosis, obstructs blood flow, contributing to these diseases. Atherosclerosis is believed to play a pivotal role in aneurysmal disease. The different models of blood flow through normal, stenosed, or aneurysmal arteries have been investigated by numerous researchers [3–8]. Karim et al. [9] used a mathematical model to investigate blood flow through a stenosed tapered artery, finding increased wall shear stress and decreased blood velocity with both stenosis and tapering angle. Gandhi et al. [10] employed a novel EMHD Casson nanofluid model to analyse blood flow through a stenosed and aneurysmal artery, investigating the combined effects of nanoparticle size and magnetic field on heat transfer and momentum diffusion. Shahzadi et al. [11] demonstrate a novel fractional fluid model with ternary nanoparticles (Cu, Ag, CuO) to analyse blood flow in an oblique stenosed aneurysmal artery, finding ternary nanoparticles more effective at reducing hemodynamic factors like wall shear stress than hybrid or copper nanoparticles. In recent decades, pulsatile blood flow has garnered significant attention from researchers owing to its pivotal role in understanding cardiovascular dynamics and associated pathologies. Periodic variations in blood flow velocity and pressure within the cardiovascular system characterise the pulsatile flow. This variation is driven by the rhythmic contraction and relaxation of the heart during the cardiac cycle. Understanding pulsatile flow dynamics is essential for elucidating various physiological processes, such as regulating blood pressure, distributing nutrients and oxygen to tissues, and developing arterial diseases like atherosclerosis and hypertension. Consequently, numerous investigations have delved into the study of pulsatile blood flow, aiming to unravel its intricate mechanisms and clinical implications [12–16].

The study of the flow through a channel with permeable walls possesses a theoretical appeal and models biological and engineering systems. The primary activity of the entire cardiovascular system is to supply blood to tissues under a sufficient pressure gradient to exchange materials through the arterial wall. Incorporating a porous medium into the study of fluid flow enriches its physical realism, particularly in modelling blood vessels and pulmonary systems where fatty deposits and artery blockages are present. Numerous researchers have theoretically examined the dynamics of blood flow across permeable walls [17–22]. Sinha and Misra [23] delved into the impact of slip velocity on blood flow through a permeable-walled artery, using a perturbation technique to unravel the complex interplay between blood flow dynamics and wall permeability. Makinde and Osalusi [24] discussed the interaction of electromagnetic forces, fluid viscosity, and permeable boundaries by analysing the steady flow of a conducting fluid through a channel with slip conditions at the walls. Mishra et al. [25] studied the impact of arterial wall permeability and flow dynamics in composite stenosis. Ijaz and Nadeem [26] delved into the potential of copper nanoparticles as drug carriers to mitigate the hemodynamic effects of composite stenosed arteries with permeable walls.

The presence of slip at the arterial wall significantly impacts blood flow dynamics. Considering the slip velocity effect at the boundary, the problems can be modelled close to real-life applications such as blood flow in the arteries. It can be defined as a velocity gradient between two different mediums: a solid boundary and adjacent fluid flow on it [27]. This relative movement between fluid layers and the artery surface reduces the overall flow rate, necessitating its inclusion in accurate blood flow analysis. Previous research has explored the role of slip velocity in stenosed arteries, demonstrating the presence of slip conditions on the vessel wall [28–31]. Biswas and Chakraborty [32] investigated pulsatile blood flow in catheterised arteries with varying stenosis geometry, observing decreased wall shear stress and effective viscosity alongside increased axial velocity under velocity slip conditions. Eldesoky [33] examined unsteady, incompressible, pulsatile blood flow in a porous medium, which is influenced by slip, body acceleration, and magnetic-field impacts, highlighting slip’s significant impact on spurt, skin shear, and hysteresis. Lukendra et al. [34] explored pulsatile blood flow past a permeable porous artery with inclined and tapered mild stenosis, noting that increased slip velocity correlated with higher axial blood flow and volumetric flow rate.

The investigation of electrically conducting fluid flow through a permeable wall in a channel holds both theoretical attraction and practical significance for various biological and engineering scenarios. The influence of magnetic fields on fluid dynamics, particularly in blood flow, is a subject of considerable interest. When an electrically conducting fluid, such as the nano-blood investigated in these studies [35, 36], interacts with a magnetic field, it induces the generation of electric and magnetic fields, creating a Lorentz force. This force acts as a body force that can impede fluid movement. The nano-blood exhibits significantly higher conductivity compared to normal blood flo, due to the presence of nanoparticles designed to enhance thermal and electrical conductivity. Consequently, the nano-blood is more prone to interactions with magnetic fields, leading to more substantial Lorentz force effects than those typically observed in conventional blood flow. These insights are particularly relevant in biomedical applications such as targeted drug delivery or magnetic resonance imaging, where external magnetic fields are commonly employed to manipulate and control nano-blood behaviour. Numerous authors [37–42] have delved into blood flow in arteries under the influence of magnetic fields for different scenarios. Kolin [43] initially proposed utilizing electromagnetic fields in medical investigations. Subsequently, Korchevskii and Marochnik [44] delved into the exploration of applying a magnetic field to regulate blood movement within the human system. Furthermore, Gold [45] provided a comprehensive analytical solution for the magnetohydrodynamic equations. This analysis considered a no-slip wall condition and the imposition of a transverse uniform magnetic field. Ponalagusamy and Selvi [46] presented a mathematical model for a two-phase blood flow model in a stenosed artery, incorporating the combined effects of heat transfer, magnetic field, and a peripheral plasma layer. Amos et al. [47] investigate the combined impact of slip velocity, blood flow pulsatility, body acceleration, and an inclined, permeable, stenosed artery on Newtonian unsteady blood flow in the presence of a magnetic field. In the field of cancer treatment, hyperthermia has emerged as a promising approach for tumors resistant to chemotherapy. Michele et al. [48] present a novel mathematical model for magnetic nanoparticle hyperthermia, incorporating nanoparticle infusion and heating dynamics to optimize treatment design. Their work proposes a quantitative framework to predict temperature profiles based on factors like infusion duration, nanoparticle concentration, and external magnetic field.

Nanofluid is one of the innovative ideas to improve the heat transfer process of fluids. It can be defined as a fluid that consists of metallic nanometer-sized particles dispersed in the low thermal conductivity base fluid. In recent years, nanoparticles, or nanofluids, have been used strategically in numerous heat transfer applications with outstanding success. Their exceptional adsorption capabilities render them invaluable for clinical applications for transporting drugs, proteins, and other substances to specific cellular targets. Previous research endeavours have meticulously investigated the influence of nanoparticles across diverse contexts, laying a solid foundation for further exploration [49–57]. This new kind of nanotechnology was first introduced by Choi and Eastman [58]. Buongiorno [59] showed that Brownian motion and thermophoresis effects are significant in the dynamics of nanofluids. Akbar [60] investigated the impact of nanoparticles on incompressible viscous fluid by considering an asymmetric channel. Sharma et al. [61] analysed the impact of heat transfer and body acceleration on unsteady magnetohydrodynamics (MHD) blood flow through a curved artery, considering the presence of stenosis and aneurysm and incorporating hybrid nanoparticles. Ellahi et al. [62] explored mixed convection nanofluid flow over a wedge, considering particle shape effects. Their findings highlight that increased volume friction and smaller particle sizes enhance heat transfer rates.

The literature survey shows that previous studies mainly concentrated on analysing momentum and heat transfer within Newtonian incompressible one-dimensional models. It also entailed the assumption of a constant pressure gradient along the length of the artery. However, Chow and Abumandour et al. [63, 64] identified a significant variation in pressure gradient relative to the restricted channel length, impacting other associated parameters. In light of the constraints observed in the current literature, the present analysis aims to discuss the effects of slip on the behaviour of unsteady pulsatile flow in a two-dimensional sinusoidal wavy channel. Additionally, this analysis considers the variations in pressure gradient, including the impact of magnetic field, nanoparticle volume fraction, slip parameter, radiation, and heat source parameters. The perturbation technique solves the governing equations of nano-blood flow in a horizontal wavy channel. The analytical solutions of stream function, velocity, wall shear stress, pressure gradient, and temperature are illustrated graphically, considering various values of the pertinent physical parameters. In this research, Sect. 1 represents the introduction, Sect. 2 presents the mathematical formulation, Sect. 3 shows the solution method, Sect. 4 shows the validation of results, and Sect. 5 presents the discussion and results. Last, Sect. 6 concludes the summary.

2 Mathematical formulation

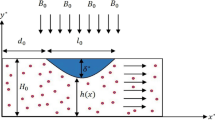
The research investigates a Newtonian nanofluid unsteady, incompressible flow through a symmetric, two-dimensional porous sinusoidal-wall channel, as depicted in Fig. 1 [14]. This study aims to analyse the behaviour of nano-blood flow with the effects of a magnetic field, slip boundary, and heat transfer. Specifically, a uniform magnetic field \(B_{0}\) is applied to the pulsatile nano-blood flow in the transverse direction. Also, the temperature of the bottom wall is denoted by \(T_{0}\), while \(T_{w}\) indicates the temperature of the top wall. The boundary of the wavy channel is expressed by:

$$ \eta ^{*} = d^{*} +a \sin \biggl( \frac{2\pi}{\lambda} x^{*} \biggr), $$
(1)

where \(x^{*}\) is the longitudinal axis of the channel, a is the height of the wall constriction, \(d^{*}\) is the half-width of the channel, λ is the length of the wall constriction. The governing equations for conservative momentum and energy in the general form are as follows [65–67]:

Figure 1
figure 1

A schematic diagram for the flow geometry

Full size image

A. Continuity Equation

$$ \frac{\partial u^{*}}{\partial x^{*}} + \frac{\partial v^{*}}{\partial y^{*}} =0, $$
(2)

B. Momentum Equation

$$\begin{aligned} \begin{aligned} & \frac{\partial u^{*}}{\partial t^{*}} + u^{*} \frac{\partial u^{*}}{\partial x^{*}} + v^{*} \frac{\partial u^{*}}{\partial y^{*}} \\ &\quad =- \frac{1}{\rho _{nf}} \frac{\partial p^{*}}{\partial x^{*}} +\ \upsilon _{nf} \biggl( \frac{\partial ^{2} u^{*}}{\partial x^{* 2}} + \frac{\partial ^{2} u^{*}}{\partial y^{* 2}} \biggr) - \biggl( \frac{\sigma B_{O}^{2}}{\rho _{nf}} \biggr) u^{*} - \biggl( \frac{\upsilon _{nf}}{k} \biggr) u^{*}, \end{aligned} \end{aligned}$$
(3)
$$\begin{aligned} &\frac{\partial v^{*}}{\partial t^{*}} + u^{*} \frac{\partial v^{*}}{\partial x^{*}} + v^{*} \frac{\partial v^{*}}{\partial y^{*}} =- \frac{1}{\rho _{nf}} \frac{\partial p^{*}}{\partial y^{*}} +\ \upsilon _{nf} \biggl( \frac{\partial ^{2} v^{*}}{\partial x^{* 2}} + \frac{\partial ^{2} v^{*}}{\partial y^{* 2}} \biggr), \end{aligned}$$
(4)

C. Energy Equation

$$ \frac{\partial T^{*}}{\partial t^{*}} + u^{*} \frac{\partial T^{*}}{\partial x^{*}} + v^{*} \frac{\partial T^{*}}{\partial y^{*}} = \frac{k_{nf}}{ ( \rho C_{p} )_{nf}} \biggl( \frac{\partial ^{2} T^{*}}{\partial y^{* 2}} \biggr) - \frac{1}{ ( \rho C_{p} )_{nf}} \frac{\partial q_{r}}{\partial y^{*}} + \frac{Q_{0}}{ ( \rho C_{p} )_{nf}} \bigl( T^{*} - T_{0} \bigr) . $$
(5)

Rosseland approximation for radiative heat flux, \(q_{r}\) is defined as [68]:

$$ q_{r} =- \biggl( \frac{4 \sigma ^{*}}{3 k^{*}} \frac{\partial T^{*4}}{ \partial \mathrm{y}^{*}} \biggr). $$
(6)

The Rosseland mean absorption coefficient is denoted as \(k^{*}\), and the Stefan–Boltzmann constant is denoted as \(\sigma ^{*}\). It is assumed that the temperature variation within the flow is slight enough to permit the expansion of \(T^{*4} \) in a Taylor’s series. The expansion of \(T^{*4} \) around \(T_{0}\) and the neglect of higher-order terms result in the following expression [69]:

$$ T^{*4} \cong 4 T_{0}^{3} T^{*} -3 T_{0}^{4}. $$
(7)

Upon substituting Eqs. (6)–(7) into Eq. (5), the following expression is obtained:

$$ \begin{aligned} \frac{\partial T^{*}}{\partial t^{*}} + u^{*} \frac{\partial T^{*}}{ \partial x^{*}} + v^{*} \frac{\partial T^{*}}{\partial y^{*}} ={}& \frac{k_{nf}}{ ( \rho C_{p} )_{nf}} \biggl( \frac{\partial ^{2} T^{*}}{\partial y^{*2}} \biggr)\\ &{} + \frac{16 \sigma ^{*} T_{0}^{3}}{3 k^{*} ( \rho C_{p} )_{nf}} \biggl( \frac{\partial ^{2} T^{*}}{\partial \mathrm{y}^{*2}} \biggr) + \frac{Q_{0}}{ ( \rho C_{p} )_{nf}} \bigl( T^{*} - T_{0} \bigr). \end{aligned} $$
(8)

In blood flow analysis, the fulfilment of slip conditions becomes pivotal, particularly when considering the presence of permeability at the artery wall. This requirement is essential for the blood to adhere to the arterial boundary. While the blood still adheres to the Navier-Stokes equation, the no-slip condition is replaced with the slip condition, which accounts for relative movement between the fluid and the wall. This condition states that the tangential velocity of the blood at the wall is not zero, but proportional to the normal derivative of the velocity perpendicular to the surface. The proportionality constant is represented by \(A_{p}\), a coefficient close to the mean free path of the blood’s molecules [70]. Although the Navier–Stokes equation appears simple, its analytical solution under slip conditions is significantly more complex compared to the no-slip scenario. With slip conditions incorporated, the boundary conditions on the artery wall become [71–73]:

$$\begin{aligned} & \left . \textstyle\begin{array}{l} u^{*} =\mp A_{p} \frac{\partial u^{*}}{\partial y^{*}} \\ v^{*} =0 \end{array}\displaystyle \right \} \quad \text{at }y^{*} =\pm \eta ^{*}, \end{aligned}$$
(9a)
$$\begin{aligned} & T^{*} = T_{w} \quad \text{at } y^{*} = \eta ^{*}, \end{aligned}$$
(9b)
$$\begin{aligned} & T^{*} = T_{0} \quad \text{at } y^{*} =- \eta ^{*}. \end{aligned}$$
(9c)

The thermophysical properties of the nanofluid, as presented by Zahir et al. [74], are as follows:

$$ \left . \textstyle\begin{array}{l} \rho _{nf} = ( 1-\varphi ) \rho _{f} +\varphi \rho _{n}, \\ \mu _{nf} = \frac{\mu _{f}}{(1-\varphi )^{2.5}}, \\ \upsilon _{nf} = \frac{\mu _{nf}}{\rho _{nf}}, \\ ( \rho C_{p} )_{nf} = ( 1-\varphi ) ( \rho C_{p} )_{f} +\varphi ( \rho C_{p} )_{n}, \\ \frac{k_{nf}}{k_{f}} = \frac{ ( 2 k_{f} + k_{n} ) -2\varphi ( k_{f} - k_{n} )}{ ( 2 k_{f} + k_{n} ) +\varphi ( k_{f} - k_{n} )}. \end{array}\displaystyle \right \} $$
(10)

Furthermore, the function \(\psi ^{*}\) is chosen in the following manner:

$$ \left . \textstyle\begin{array}{l} u^{*} = \frac{\partial \psi ^{*}}{\partial y^{*}}, \\ v^{*} =- \frac{\partial \psi ^{*}}{\partial x^{*}}. \end{array}\displaystyle \right \} $$
(11)

After substituting \(\psi ^{*}\) into Eqs. (3)–(9c) and eliminating the pressure from Eqs. (3)–(4), these equations can be expressed as follows:

$$\begin{aligned} & \frac{\partial}{\partial t^{*}} \bigl( \nabla ^{2} \psi ^{*} \bigr) + \frac{\partial \psi ^{*}}{\partial y^{*}} \nabla ^{2} \frac{\partial \psi ^{*}}{\partial x^{*}} - \frac{\partial \psi ^{*}}{\partial x^{*}} \nabla ^{2} \frac{\partial \psi ^{*}}{\partial y^{*}} = \upsilon _{nf} \nabla ^{4} \psi ^{*} - \biggl( \frac{\sigma B_{O}^{2}}{\rho _{nf}} + \frac{\upsilon _{nf}}{k} \biggr) \frac{\partial ^{2} \psi ^{*}}{\partial y^{*2}}, \end{aligned}$$
(12)
$$\begin{aligned} \begin{aligned} & \frac{\partial T^{*}}{\partial t^{*}} + \frac{\partial \psi ^{*}}{\partial y^{*}} \frac{\partial T^{*}}{\partial x^{*}} - \frac{\partial \psi ^{*}}{ \partial x^{*}} \frac{\partial T^{*}}{\partial y^{*}} \\ &\quad = \frac{k_{nf}}{ ( \rho C_{p} )_{nf}} \biggl( \frac{\partial ^{2} T^{*}}{\partial y^{*2}} \biggr) + \frac{16 \sigma ^{*} T_{0}^{3}}{3 k^{*} ( \rho C_{p} )_{nf}} \biggl( \frac{\partial ^{2} T^{*}}{\partial \mathrm{y}^{*2}} \biggr) + \frac{Q_{0}}{ ( \rho C_{p} )_{nf}} \bigl( T^{*} - T_{0} \bigr), \end{aligned} \end{aligned}$$
(13)

where

$$ \nabla ^{2} = \frac{\partial ^{2}}{\partial x^{*2}} + \frac{\partial ^{2}}{ \partial y^{*2}}, $$
(14)

The relevant boundary conditions are as follows:

$$\begin{aligned} & \left . \textstyle\begin{array}{l} \frac{\partial \psi ^{*}}{\partial y^{*}} =\mp A_{p} \frac{\partial ^{2} \psi ^{*}}{\partial y^{*2}}\\ \frac{\partial \psi ^{*}}{\partial x^{*}} =0 \end{array}\displaystyle \right \} \quad \text{at } y^{*} =\pm \eta ^{*}, \end{aligned}$$
(15a)
$$\begin{aligned} & \psi ^{*} =0 \quad \text{at } y^{*} =0, \end{aligned}$$
(15b)
$$\begin{aligned} & \psi ^{*} =Q \quad ( \text{constant} ) \quad \text{at } y^{*} = \eta ^{*}, \end{aligned}$$
(15c)
$$\begin{aligned} & T^{*} = T_{w} \quad \text{at } y^{*} = \eta ^{*}, \end{aligned}$$
(15d)
$$\begin{aligned} & T^{*} = T_{0} \quad \text{at } y^{*} =- \eta ^{*}. \end{aligned}$$
(15e)

Introducing the following non-dimensional variables as follows:

$$ \left . \textstyle\begin{array}{l} \textstyle\begin{array}{l} x= \frac{x^{*}}{\lambda},\qquad y= \frac{y^{*}}{d},\qquad \eta = \frac{\eta ^{*}}{d}, \\ \zeta = \frac{y}{\eta},\qquad t= \frac{\upsilon _{f} t^{*}}{\lambda d},\qquad \psi = \frac{\psi ^{*}}{\upsilon _{f}}, \end{array}\displaystyle \\ P= \frac{\lambda d P^{*}}{\rho _{f} \upsilon _{f}^{2}},\qquad \theta = \frac{T^{*} - T_{0}}{T_{w} - T_{0}}. \end{array}\displaystyle \right \} $$
(16)

Using the dimensionless variables stated above, Eqs. (12)–(15e) are obtained as follows:

$$\begin{aligned} \begin{aligned} &\nabla ^{4} \psi - \biggl( H a^{2} (1-\varphi )^{2.5} + \frac{1}{Da} \biggr) \frac{\partial ^{2} \psi}{\partial y^{2}} \\ &\quad =\delta (1-\varphi )^{2.5} \biggl( 1-\varphi + \biggl( \frac{\varphi \rho _{n}}{\rho _{f}} \biggr) \biggr) \biggl( \frac{\partial}{\partial t} \bigl( \nabla ^{2} \psi \bigr) + \frac{\partial \psi}{\partial y} \nabla ^{2} \frac{\partial \psi}{\partial x} - \frac{\partial \psi}{\partial x} \nabla ^{2} \frac{\partial \psi}{ \partial y} \biggr), \end{aligned} \end{aligned}$$
(17)
$$\begin{aligned} \begin{aligned} & \biggl( \frac{ ( ( \frac{k_{nf}}{k_{f}} ) + ( \frac{4}{3} ) Rd )}{\Pr} \frac{\partial ^{2} \theta}{\partial y^{2}} + Q_{t} \theta \biggr) \\ &\quad = \delta \biggl( 1-\varphi + \biggl( \frac{\varphi ( \rho C_{p} )_{n}}{ ( \rho C_{p} )_{f}} \biggr) \biggr) \biggl( \frac{\partial \theta}{\partial t} + \frac{\partial \psi}{ \partial y} \frac{\partial \theta}{\partial x} - \frac{\partial \psi}{ \partial x} \frac{\partial \theta}{\partial y} \biggr), \end{aligned} \end{aligned}$$
(18)

where amplitude ratio ε, wall slope parameter δ, Knudsen number kn, Darcy number Da, Hartmann number Ha, radiation parameter Rd, Prandtl number Pr, and heat source parameter \(Q_{t}\) are defined respectively by:

$$ \left . \textstyle\begin{array}{l} \varepsilon = \frac{a}{d},\qquad \delta = \frac{d}{\lambda},\qquad kn= \frac{A_{p}}{d}, \\ Da= \frac{k}{d^{2}},\qquad Ha= B_{0} d \sqrt{\frac{\sigma}{\mu _{f}},} \\ Rd= \frac{4 \sigma ^{*} T_{0}^{3}}{k_{f} k^{*}},\qquad \Pr= \frac{ ( \mu C_{p} )_{f}}{k_{f}}, \\ Q_{t} = \frac{Q_{0} d^{2}}{ ( \rho C_{p} )_{f} \nu _{f}},\qquad \nabla ^{2} = \delta ^{2} \frac{\partial ^{2}}{\partial x^{*2}} + \frac{\partial ^{2}}{\partial y^{*2}}. \end{array}\displaystyle \right \} $$
(19)

The new boundary conditions corresponding to this transformation are as follows:

$$\begin{aligned} & \left . \textstyle\begin{array}{l} \frac{\partial \psi}{\partial y} =\mp kn \frac{\partial ^{2} \psi}{\partial y^{2}}\\ \frac{\partial \psi}{\partial x} =0 \end{array}\displaystyle \right \} \quad \text{at } y=\pm \eta , \end{aligned}$$
(20a)
$$\begin{aligned} & \psi =0 \quad \text{at } y=0, \end{aligned}$$
(20b)
$$\begin{aligned} & \psi =Q \quad ( \text{constant} ) \quad \text{at } y= \eta , \end{aligned}$$
(20c)
$$\begin{aligned} & \theta =1 \quad \text{at } y= \eta , \end{aligned}$$
(20d)
$$\begin{aligned} & \theta =0 \quad \text{at } y=- \eta . \end{aligned}$$
(20e)

3 Solution method

After applying the dimensionless technique, it is possible to assume that the stream function ψ, temperature θ, and pressure P have expansions in terms of the small parameter δ, representing the slope of the channel, as indicated in [14]. These expansions can be expressed as follows:

$$\begin{aligned} & \psi = \psi _{0} +\delta \psi _{1} + \delta ^{2} \psi _{2} +\cdots, \end{aligned}$$
(21a)
$$\begin{aligned} & \theta = \theta _{0} +\delta \theta _{1} + \delta ^{2} \theta _{2} +\cdots, \end{aligned}$$
(21b)
$$\begin{aligned} & P= P_{0} +\delta P_{1} + \delta ^{2} P_{2} + \cdots, \end{aligned}$$
(21c)

By substituting Eq. (21a)-(21c) into Eqs. (17)–(20e) and collecting terms of the same powers of δ, including zero and first order terms, yields the subsequent perturbed equations:

Zero order:

$$\begin{aligned} & \frac{\partial ^{4} \psi _{0}}{\partial y^{4}} - m^{2} \frac{\partial ^{2} \psi _{0}}{\partial y^{2}} = 0, \end{aligned}$$
(22)
$$\begin{aligned} & \frac{\partial ^{2} \theta _{0}}{\partial y^{2}} + m_{1}^{2} \theta _{0} =0, \end{aligned}$$
(23)
$$\begin{aligned} & \left . \textstyle\begin{array}{l} \frac{\partial \psi _{0}}{\partial y} =\mp kn \frac{\partial ^{2} \psi _{0}}{\partial y^{2}}\\ \frac{\partial \psi _{0}}{\partial x} =0 \end{array}\displaystyle \right \} \quad \text{at } y=\pm \eta , \end{aligned}$$
(24a)
$$\begin{aligned} & \psi _{0} =Q \quad ( \text{constant} )\quad \text{at } y=\eta , \end{aligned}$$
(24b)
$$\begin{aligned} & \psi _{0} =0 \quad \text{at } y=0, \end{aligned}$$
(24c)
$$\begin{aligned} & \theta _{0} =1 \quad \text{at } y=\eta , \end{aligned}$$
(24d)
$$\begin{aligned} & \theta _{0} =0 \quad \text{at } y=-\eta . \end{aligned}$$
(24e)

First order:

$$\begin{aligned} & \frac{\partial ^{4} \psi _{1}}{\partial y^{4}} - m^{2} \frac{\partial ^{2} \psi _{1}}{\partial y^{2}} = B_{1} \biggl( \frac{\partial ^{3} \psi _{0}}{ \partial t \partial y^{2}} + \frac{\partial \psi _{0}}{\partial y} \frac{\partial ^{3} \psi _{0}}{\partial x \partial y^{2}} - \frac{\partial \psi _{0}}{\partial x} \frac{\partial ^{3} \psi _{0}}{\partial y^{3}} \biggr), \end{aligned}$$
(25)
$$\begin{aligned} & \frac{\partial ^{2} \theta _{1}}{\partial y^{2}} + m_{1}^{2} \theta _{1} = B_{2} \biggl( \frac{\partial \theta _{0}}{\partial t} + \frac{\partial \psi _{0}}{\partial y} \frac{\partial \theta _{0}}{\partial x} - \frac{\partial \psi _{0}}{\partial x} \frac{\partial \theta _{0}}{\partial y} \biggr), \end{aligned}$$
(26)
$$\begin{aligned} & \left . \textstyle\begin{array}{l} \frac{\partial \psi _{1}}{\partial y} =\mp kn \frac{\partial ^{2} \psi _{1}}{\partial y^{2}}\\ \frac{\partial \psi _{1}}{\partial x} =0 \end{array}\displaystyle \right \} \quad \text{at } y=\pm \eta , \end{aligned}$$
(27a)
$$\begin{aligned} & \psi _{1} =0 \quad \text{at } y=\eta , \vadjust{\goodbreak} \end{aligned}$$
(27b)
$$\begin{aligned} & \psi _{1} =0 \quad \text{at } y=0, \end{aligned}$$
(27c)
$$\begin{aligned} & \theta _{1} =0 \quad \text{at } y=\eta , \end{aligned}$$
(27d)
$$\begin{aligned} & \theta _{1} =0 \quad \text{at } y=-\eta . \end{aligned}$$
(27e)

Furthermore, it is assumed:

$$\begin{aligned} & \psi _{0} = \psi _{00} ( x,y ) e^{i\omega t}, \end{aligned}$$
(28a)
$$\begin{aligned} & \theta _{0} = \theta _{00} ( x,y ) e^{i\omega t}, \end{aligned}$$
(28b)
$$\begin{aligned} & P_{0} = P_{00} ( x,y ) e^{i\omega t}, \end{aligned}$$
(28c)
$$\begin{aligned} & \psi _{1} = \psi _{10} ( x,y ) + \psi _{11} ( x,y ) e^{i\omega t} + \psi _{12} ( x,y ) e^{2i\omega t}, \end{aligned}$$
(28d)
$$\begin{aligned} & \theta _{1} = \theta _{10} ( x,y ) + \theta _{11} ( x,y ) e^{i\omega t} + \theta _{12} ( x,y ) e^{2i\omega t}, \end{aligned}$$
(28e)
$$\begin{aligned} & P_{1} = P_{10} ( x,y ) + P_{11} ( x,y ) e^{i\omega t} + P_{12} ( x,y ) e^{2i\omega t}. \end{aligned}$$
(28f)

By substituting Eq. (28a)–(28f) into Eqs. (22)–(27e), equating similar harmonic terms, and solving the resulting partial differential equations under the corresponding boundary conditions, the following results are obtained:

$$\begin{aligned}& \begin{aligned} \psi ={}&Q C_{1} m \biggl( \frac{\sinh ( my )}{m} -y \bigl( \cosh ( m \eta ) +kn m \sinh ( m\eta ) \bigr) \biggr) e^{i\omega t} \\ &{}+\delta \biggl\{ C_{2} \biggl[ \frac{C_{1} C_{3}}{2} \biggl( y- \frac{\eta \sinh ( my )}{\sinh ( m\eta )} \biggr) - \frac{\eta \cosh ( m\eta ) \sinh ( my )}{2 m^{3} \sinh ( m\eta )} + \frac{y \cosh ( my )}{2 m^{3}} \biggr] e^{i\omega t} \\ &{}+ C_{4} \biggl[ C_{5} \biggl( \frac{2 \sinh ( my )}{m^{5}} - \frac{5 y \cosh ( my )}{4 m^{4}} + \frac{y^{2} \sinh ( my )}{4 m^{3}} \biggr) \\ &{}+ C_{6} \biggl( \frac{ y \cosh ( my )}{2 m^{3}} - \frac{ \sinh ( my )}{m^{4}} \biggr) + C_{7} \biggl( \frac{\sinh ( my )}{ m^{2}} - \frac{y \sinh ( m\eta )}{\eta m^{2}} \biggr) \\ &{}+ C_{8} y \biggr] e^{2i\omega t} \biggr\} , \end{aligned} \end{aligned}$$
(29)
$$\begin{aligned}& \begin{aligned} \theta ={}& \biggl[ \frac{\cos ( m_{1} y )}{2 \cos ( m_{1} \eta )} + \frac{\sin ( m_{1} y )}{2 \sin ( m_{1} \eta )} \biggr] \\ &{}+\delta \biggl\{ C_{9} \biggl[ C_{10} \cos ( m_{1} y ) + C_{11} \sin ( m_{1} y ) + C_{12} \frac{\sin ( m_{1} y ) \sinh ( my )}{m( m^{2} +4 m_{1}^{2} )}\\ &{} + C_{13} \frac{\cos ( m_{1} y ) \cosh ( my )}{m( m^{2} +4 m_{1}^{2} )} + C_{14} \frac{\cos ( m_{1} y ) \sinh ( my )}{m( m^{2} +4 m_{1}^{2} )} + C_{15} \frac{\sin ( m_{1} y ) \cosh ( my )}{m( m^{2} +4 m_{1}^{2} )}\\ &{} + C_{16} \frac{y \sin ( m_{1} y )}{4 m_{1}^{2}} + C_{17} \frac{y \cos ( m_{1} y )}{4 m_{1}^{2}} + C_{18} \frac{y^{2} \sin ( m_{1} y )}{ 4 m_{1}} + C_{19} \frac{y^{2} \cos ( m_{1} y )}{4 m_{1}} \biggr] e^{i\omega t} \biggr\} , \end{aligned} \end{aligned}$$
(30)

The axial velocity can be determined by substituting Eq. (29) into Eq. (11):

$$ \begin{aligned} u={}&Q C_{1} m e^{i\omega t} \bigl( \cosh ( my ) - \cosh ( m\eta ) -kn m \sinh ( m\eta ) \bigr)\\ &{} +\delta \biggl\{ C_{2} \biggl[ \frac{C_{1} C_{3}}{2} \biggl( 1- \frac{\eta m \cosh ( my )}{\sinh ( m\eta )} \biggr) - \biggl( \frac{\eta \cosh ( m\eta )}{2 m^{2} \sinh ( m\eta )} - \frac{1}{2 m^{3}} \biggr) \cosh ( my ) \\ &{}+ \frac{y \sinh ( my )}{ 2 m^{2}} \biggr] e^{i\omega t} + C_{4} \biggl[ C_{5} \biggl( \frac{3\cosh ( my )}{4 m^{4}} - \frac{3 y \sinh ( my )}{4 m^{3}} + \frac{y^{2} \cosh ( my )}{4 m^{2}} \biggr) \\ &{}+ C_{6} \biggl( \frac{ y \sinh ( my )}{2 m^{2}} - \frac{\cosh ( my )}{2 m^{3}} \biggr) + C_{7} \biggl( \frac{\cosh ( my )}{ m} - \frac{ \sinh ( m\eta )}{\eta m^{2}} \biggr) + C_{8} \biggr] e^{2i\omega t} \biggr\} , \end{aligned} $$
(31)

The non-dimensional shear stress exerted on the wall is expressed as:

$$ \tau _{w} = \biggl[ \frac{\partial ^{2} \psi}{\partial y^{2}} \biggr]_{y=\eta}, $$
(32)

By employing Eq. (29) in Eq. (32), the wall shear stress can be expressed as:

$$ \begin{aligned} \tau _{w} ={}&Q C_{1} m^{2} e^{i\omega t} \sinh ( m\eta ) \\ &{}+\delta \biggl\{ C_{2} \biggl[ \frac{\sinh ( m\eta )}{m^{2}} - \frac{C_{1} C_{3} \eta m^{2}}{2} \biggr] e^{i\omega t} + C_{4} \biggl[ C_{5} \biggl( \frac{\eta ^{2} \sinh ( m\eta )}{4m} - \frac{ \eta \cosh ( m\eta )}{4 m^{2}} \biggr) \\ &{}+ \frac{ C_{6} \eta \cosh ( m\eta )}{2m} + C_{7} \sinh ( m\eta ) \biggr] e^{2i\omega t} \biggr\} , \end{aligned} $$
(33)

The non-dimensional axial pressure gradient can be derived from Eq. (2) as follows:

$$ \begin{aligned} P&= \frac{\partial p/ \partial x}{\rho _{f} v_{f}^{2} / d^{3}} \\ &= \biggl( \frac{1}{(1-\varphi )^{2.5}} \biggr) \biggl( \nabla ^{2} \frac{\partial \psi}{\partial y} - m^{2} \frac{\partial \psi}{\partial y} -\delta B_{1} \biggl( \frac{\partial ^{2} \psi}{\partial t \partial y} + \frac{\partial \psi}{\partial y} \frac{\partial ^{2} \psi}{\partial x \partial y} - \frac{\partial \psi}{\partial x} \frac{\partial ^{2} \psi}{\partial y^{2}} \biggr) \biggr), \end{aligned} $$
(34)

By substituting Eqs. (21a)–(21c) and (28a)–(28f) into Eq. (34), equating similar terms and simplifying, it results in:

$$ \begin{aligned} P={}& \frac{Q C_{1} m^{3} e^{i\omega t}}{(1-\varphi )^{2.5}} \bigl( \cosh ( m\eta ) +kn m \sinh ( m\eta ) \bigr) \\ &{}+ \frac{\delta}{(1-\varphi )^{2.5}} \biggl\{ C_{2} \biggl[ \frac{\cosh ( m\eta )}{m} +kn \sinh ( m\eta ) - \frac{C_{1} C_{3} m^{2}}{2} \biggr] e^{i\omega t}\\ &{} + C_{4} \biggl[ \frac{-C_{5} ( \cosh ( m\eta ) +kn m \sinh ( m\eta ) )}{m^{2}} - \biggl( \frac{\eta}{m} + \frac{kn}{m} + \frac{\eta kn \cosh ( m\eta )}{\sinh ( m\eta )} \biggr) \\ &{} + \frac{ C_{7} \sinh ( m\eta )}{\eta} - C_{8} m^{2} \biggr] e^{2i\omega t} \biggr\} . \end{aligned} $$
(35)

The coefficients \(C_{1}\), \(C_{2}\), \(C_{3}\)... etc. are provided in the appendix.

4 Validation of results

For validation, the present results for the pulsatile flow of the base fluid (i.e., with \(\varphi =0\)) are compared with those obtained by Abumandour et al. [64]. In the case of steady flow, Fig. 2 shows a good agreement of the present results with [64], the variation of pressure gradient with axial distance, with the relevant parameter values \(\epsilon =0.1,\ 0.25,\ 0.5\). with \(Ha = kn=\varphi = \frac{1}{Da} = Rd = \Pr = Q_{t} =0\).

Figure 2
figure 2

Pressure gradient for various values of the amplitude ratio \(( \varepsilon )\)

Full size image

5 Results and discussion

In this section, numerical simulations were conducted to investigate the impact of biophysical parameters, including the amplitude ratio parameter, Hartmann number, Knudsen number, Darcy number, nanoparticle concentration, radiation parameter, and Prandtl number, on profiles of pressure gradient, velocity, wall shear stress, and temperature, as governed by Eqs. (29)–(35). The graphical representation of these profiles can be observed in Figs. 3–23. Table 1 provides the default values for the biophysical parameters utilized in the simulation.

Figure 3
figure 3

Pressure gradient for various values of the amplitude ratio \(( \varepsilon )\)

Full size image
Table 1 Default values for critical parameters employed in simulations
Full size table

Moreover, Table 2 presents the thermophysical numerical parameters for both blood and gold nanoparticles [75, 76].

Table 2 Numerical values of base fluid and nanoparticles
Full size table

The simulations in Figs. 3–8 provide insights into the pressure gradient variations along the axial distance of the wavy channel. Figure 3 illustrates the interaction between the amplitude ratio parameter and the pressure gradient, highlighting its impact on stenosis and dilatation regions. In regions with stenosis, an increased amplitude ratio parameter intensifies the pressure gradient, while in dilatations, it diminishes the pressure gradient along the axial distance. This observation is further supported by the boundary layer thickness considerations, where the pressure gradient variation across dilatations is less pronounced than across stenotic regions, as aneurysms lead to a thicker boundary layer. Consequently, lower shear stresses near the vessel wall contribute to a lower pressure gradient across dilatations, contrasting with the steeper gradient across stenosis induced by thinner boundary layers and higher shear stresses, and this observation agrees qualitatively well with [64]. Figure 4 depicts the variation of the pressure gradient along the length of the stenosis for different Hartmann number values. The pressure gradient increases with increasing Hartmann number, as demonstrated by [6]. Conversely, Fig. 5 indicates that boundary layer thickness increases with increasing Knudsen number, leading to a reduced pressure gradient. Figure 6 illustrates the periodic variation of the pressure gradient over time. In regions with stenosis, a rise in the amplitude ratio parameter leads to an increase in the peak value of each oscillation. On the contrary, in the segments with a dilatation, an opposite trend is apparent, with elevated amplitude ratio parameters causing a decline in the peak values of each oscillation. Figure 7 illustrates that the pressure gradient varies periodically with time and the peak value of each oscillation increases with the rise of the Hartmann number. Figure 8 highlights the contrasting effect of the Knudsen number, where the peak value of each oscillation decreases with an increase in the Knudsen number.

Figure 4
figure 4

Pressure gradient for various values of Hartmann number \(( Ha )\)

Full size image
Figure 5
figure 5

Pressure gradient for various values of Knudsen number \(( kn )\)

Full size image
Figure 6
figure 6

Pressure gradient for various values of the amplitude ratio \(( \varepsilon )\) over time

Full size image
Figure 7
figure 7

Pressure gradient for various values of Hartmann number \(( Ha )\) over time

Full size image
Figure 8
figure 8

Pressure gradient for various values of Knudsen number \(( kn )\) over time

Full size image

The velocity profiles, depicted in Figs. 9–14, offer insightful observations. Figure 9 shows the velocity profile for the wavy channel geometry. As expected, velocity is maximum at the centre of the channel for x = 0.75 and minimum at x = 0.25, representing the stenosis and dilatation segments, respectively. Figure 10 illustrates a substantial increase in velocity as the wavy channel constricts (stenosis), accompanied by a reduction in velocity as the channel widens (dilatation). This behaviour reflects the influence of channel geometry on fluid flow dynamics, where constriction accelerates flow, while widening leads to velocity reduction. Figure 11 illustrates the relationship between the Hartmann number and velocity. With an increase in the Hartmann number, the centreline velocity decreases, leading to a rise in near-wall velocity due to mass flow rate conservation. Consequently, applying an external magnetic field leads to a flattened velocity profile near the centreline, resulting in a reduced rate of velocity change. This phenomenon is attributed to the induction of the Lorentz force, which decelerates the fluid motion, as discussed in [47]. In Fig. 12, depicting the influence of the Hartmann number on velocity for fluid flow with two scenarios, pure blood (\(\varphi =0\)) and nano-blood (\(\varphi =0.15\)), the observed behaviour can be attributed to distinct physical mechanisms. In the case of nano-blood, the lower decreasing rate of velocity compared to pure blood suggests that nanoparticles contribute to a more stabilized flow. Practically, the observed lower rate of velocity decrease in the nanofluid scenario implies a potential advantage. It suggests that utilizing nanofluids in medical procedures might result in a more controlled and stable blood flow environment, presenting a valuable consideration for optimising procedures and ensuring patient safety [77]. Figure 13 presents a contrasting trend concerning the impact of porosity on velocity. It demonstrates that with an increase in the Darcy number, there is a corresponding growth in centreline velocity, coupled with a decline in near-wall velocity. Figure 14 delves into the connection between the Knudsen number and velocity behaviour, rooted in the conservation of mass flow rate. The centreline velocity decreases as the Knudsen number increases, signifying specific flow conditions. This reduction in centreline velocity is compensated by an increase in near-wall velocity, ensuring that the overall mass flow rate remains constant.

Figure 9
figure 9

Velocity profile for various values of the cross sections \(( x )\)

Full size image
Figure 10
figure 10

Velocity profile for various values of the amplitude ratio \(( \varepsilon )\)

Full size image
Figure 11
figure 11

Velocity profile for various values of Hartmann number \(( Ha )\)

Full size image
Figure 12
figure 12

Velocity profile for various values of Hartmann number \(( Ha )\) and the nanoparticle concentration (φ)

Full size image
Figure 13
figure 13

Velocity profile for various values of Darcy number \(( Da )\)

Full size image
Figure 14
figure 14

Velocity profile for various values of Knudsen number \(( kn )\)

Full size image

The distribution of wall shear stress along the longitudinal direction provides significant insights, as demonstrated in Figs. 15–19, with different rheological parameters. As depicted in Fig. 15, the narrowed segments lead to higher velocity gradients, resulting in elevated shear stresses near these regions. Conversely, in the widened segments, reduced velocity gradients lead to lower shear stresses near these areas. These observations are consistent with the findings in [6]. Figure 16 provides significant insights, demonstrating that as the Hartmann number increases, the slope of the velocity profile near the wall also rises. This increased slope leads to a corresponding wall shear stress elevation, which aligns with [14]. Figure 17 illustrates the impact of the Hartmann number on wall shear stress for fluid flow in two scenarios (\(\varphi =0\)) for pure blood and (\(\varphi =0.15\)) for nano-blood. Notably, lower wall shear stress was observed in the case of nano-blood compared to pure blood. Figure 18 demonstrates a decrease in the shear stress at the wall with an increasing Darcy number. This reduction can be attributed to the diminishing slope of the velocity profile near the wall. Similarly, Fig. 19 shows the relationship between the Knudsen number and wall shear stress. As the Knudsen number increases, the slope of the velocity profile near the wall decreases, leading to a corresponding decrease in wall shear stress.

Figure 15
figure 15

Wall shear stress profile for various values of the amplitude ratio \(( \varepsilon )\)

Full size image
Figure 16
figure 16

Wall shear stress profile for various values of Hartmann number \(( Ha ) \)

Full size image
Figure 17
figure 17

Wall shear stress profile for various values of Hartmann number \(( Ha )\) and the nanoparticle concentration (φ)

Full size image
Figure 18
figure 18

Wall shear stress profile for various values of Darcy number \(( Da )\)

Full size image
Figure 19
figure 19

Wall shear stress profile for various values of Knudsen number \(( kn )\)

Full size image

Regarding the temperature profiles, as depicted in Fig. 20, as the volume fraction of nanoparticles increases, there is a substantial enlargement of the surface area exposed to blood flow, facilitating enhanced heat transfer within the fluid, and this result closely agrees with [8]. A higher Prandtl number signifies a lower thermal diffusivity relative to momentum diffusivity, resulting in less efficient heat conduction than momentum transfer, which leads to a lower temperature profile with an increasing Prandtl number, as illustrated in Fig. 21. Figure 22 demonstrates that temperature increases as the radiation parameter grows, this finding is consistent with the discourse highlighted in [32]. The temperature profile for different values of \(Q_{t}\) (heat source) is plotted in Fig. 23, revealing an enhancement in temperature significance with increasing \(Q_{t}\). As the heat source rises, the heat input from nanoparticles intensifies, contributing to a notable rise in temperature, and this result closely aligns with [78]. This enhanced temperature is primarily due to the effective thermal properties of nanoparticles, which facilitate heat conduction or absorption. In the context of blood flow applications involving nanoparticles, this phenomenon carries practical significance. For example, in hyperthermia treatments, controlled heating targets specific areas for therapeutic purposes [79].

Figure 20
figure 20

Temperature profile for various values of the nanoparticle concentration (φ)

Full size image
Figure 21
figure 21

Temperature profile for various values of Prandtl number (Pr)

Full size image
Figure 22
figure 22

Temperature profile for various values of the radiation parameter (Rd)

Full size image
Figure 23
figure 23

Temperature profile for various values of the heat source/sink (\(Q_{t} \))

Full size image

6 Conclusions

The present study investigates the unsteady flow characteristics of nano-blood within a two-dimensional porous wavy channel. The model incorporates the effects of a magnetic field and slip boundary conditions on the flow behaviour. The governing equations, nonlinear partial differential equations, are solved using a perturbation technique. The influence of various parameters on the flow is analysed, and the obtained results are validated against existing literature, demonstrating good agreement with [6, 14, 64]. The main findings from the graphical representations can be summarised as follows:

  • The pressure gradient exhibits an inverse relationship with stenosis size and a positive correlation with dilatation size.

  • A magnetic field increases the pressure gradient, while a higher slip parameter leads to a decrease.

  • Velocity positively correlated with stenosis size and an inverse relationship with dilatation size.

  • A magnetic field decreases the centerline velocity, whereas permeability and slip parameters increase it.

  • Pure blood exhibits higher velocities than nano-blood under a magnetic field.

  • Wall shear stress peaked within the stenosis region before dropping sharply. Conversely, the dilatation segment displayed the opposite trend.

  • The wall shear stress profile increases with an increase in the magnetic field. It is also apparent that the wall shear stress decreases as the permeability and slip parameters increase.

  • The temperature profile increases with increasing magnetic field, nanoparticle volume fraction, heat source, and radiation parameter but decreases with the permeability parameter and Prandtl number rising.

Limitations and future perspectives: The investigation of nano-blood flow holds significance in therapeutic approaches for various ailments. However, limitations arise concerning the magnetic-field’s strength, necessitating further consideration for a more physically precise magnetic model, as advocated by the recent analytical model [80]. Additionally, while the current study focuses on fixed nanoparticle concentrations, future research endeavours could explore the impact of varying nanoparticle concentrations on key flow characteristics, thereby enhancing comprehension of nano-blood flow dynamics. Furthermore, prospective investigations could entail detailed comparisons between the analytical solutions proposed herein and outcomes derived from diverse numerical schemes applied to analogous scenarios. Such comparative analyses would yield valuable insights into the accuracy and efficacy of different numerical methodologies in simulating pulsatile nanofluid flow within wavy geometries. Addressing these limitations and broadening the research scope will significantly advance understanding nano-blood flow phenomena in pertinent biological contexts.