Multi-effect analysis of nanofluid flow in stenosed arteries with variable pressure gradient: analytical study

Abstract

This study advances the understanding of nanofluid behaviour within stenosed arteries, highlighting the importance of considering multifaceted effects in the modelling process. It investigates the combined impact of pressure gradient variation, heat transfer, chemical reactions, and magnetic field effects on nano-blood flow in stenosed arteries. Unlike previous studies that made the assumption that the pulsatile pressure gradient remains constant during channel narrowing, this novel investigation introduces a variable pressure gradient. This, in turn, significantly impacts several associated parameters. The mathematical model describing nano-blood flow in a horizontally stenosed artery is solved using perturbation techniques. Analytical solutions for key variables, including velocity, temperature, concentration, wall shear stress, flow rate, and pressure gradient, are visually presented for various physical parameter values.

Article highlights

• Velocity decreases with a higher magnetic field but increases with greater permeability, stenosis height, and nanoparticle volume fraction.

• Temperature rises with increasing magnetic field, radiation parameter, and nanoparticle volume fraction. However, it decreases as the permeability parameter increases.

• The pressure gradient increases as the height of constriction rises along the channel's length.

1 Introduction

Studying blood flow through arteries under stenosed conditions is crucial due to its direct link to vascular diseases and cardiovascular dysfunction. Stenosis caused by intravascular plaques disrupts flow patterns and contributes to complications like tissue ingrowth, thrombosis, and weakened arteries. In normal physiological conditions, blood transport relies on a heart-driven pressure gradient. Mathematical modelling of blood flow through constricted channels is essential in clinical contexts, offering insights into circulatory disorders. Numerous theoretical and numerical studies have been conducted recently [1,2,3,4,5,6,7] to investigate blood flow through arteries with a single stenosis, leading to a deeper understanding of flow characteristics under various assumptions and considering diverse arterial geometries. To comprehend the impact of stenosis on arterial blood flow, multiple investigations were conducted by Hung and Tsai [8], Pedley [9], and Tu et al. [10], many of which operate under the assumption that blood behaves as a Newtonian fluid. Misra and Ghosh [11] and Ellahi et al. [12] explored blood flow in stenosed arteries, considering wall shear stress and wall resistance, while Ratchagar and Subasri [13] developed a mathematical model elucidating blood flow through arteries with composite stenosis.

The application of Magnetohydrodynamics (MHD) in physiological flow is of growing interest. MHD can be used to control blood flow by applying an appropriate magnetic field. Blood is an electrically conducting fluid, and the Lorentz force acts on the constituent particles of blood, opposing the motion of blood and reducing its velocity. Therefore, it is essential to study blood flow in the presence of a magnetic field. Many investigators have conducted research in this area [14,15,16,17,18]. The concept of electromagnetic fields in medical research was initially introduced by Kolin [19]. Subsequently, Korchevskii et al. [20] explored the potential of utilizing magnetic fields to control blood circulation within the human system. Haik et al. [21] demonstrated a 30% reduction in blood flow rate under a 10 T magnetic field, while Yadav et al. [22] observed a comparable decrease in blood flow rate under a significantly lower magnetic field of 0.002 T. The combined effect of these fields generates a Lorentz force, termed as such, which opposes liquid movement [23, 24]. In arterial studies to detect stenosis, non-invasive MRI techniques are employed, utilizing a powerful magnetic field [25]. This MRI device influences the velocity field within the specific body region it targets. Pulsatile blood flow through a porous medium affected by periodic body acceleration was investigated by Rathod and Tanveer [26]. The study incorporated a magnetic field and treated blood as an incompressible, electrically conducting fluid with couple stress properties. Sankar and Lee [27] devised a computational model to assess magnetic field effects on pulsatile blood flow through narrow arteries with mild stenosis, employing the Casson fluid model. Their investigation revealed that velocity and flow rate decrease with increasing Hartmann number. Moreover, skin friction and longitudinal impedance increase with the amplitude parameter of the artery radius. Mirza et al. [28] presented a mathematical model analysing the effect of a magnetic field on transient laminar electromagneto-hydrodynamic two-phase blood flow using a continuum approach. By solving the model analytically, they separately demonstrated that the magnetic field has effects on blood and particle velocities. They concluded that as the magnetic field's influence increases, both blood and particle velocities decrease in electromagneto-hydrodynamic two-phase blood flow. In a recent investigation conducted by Tanveer et al. [29], the study focused on entropy generation induced by a peristaltic process on a curved surface, taking into account the influence of magnetohydrodynamics (MHD), variable viscosity, and convective conditions. Their findings indicate that velocity and temperature profiles experience enhancement with higher values of the Biot number and magnetic parameter. Furthermore, Tanveer et al. [30] examined entropy generation and Joule heating effects in the context of MHD peristaltic flow over an asymmetric channel with mixed convective conditions.

In recent times, nanofluid dynamics has emerged as a pivotal field within fluid mechanics. Nanofluids, characterized by the presence of nanoparticles at the nanometer scale, have a wide range of scientific and technological applications across various fields. They play a crucial role in medical science and therapy, including in vivo therapy, drug delivery, and the coating of medical devices for improved biocompatibility and cancer treatment. Their unique properties, such as enhanced thermal conductivities and convective heat transfer, make them valuable in heat transfer technologies, including microelectronics cooling and thermal management systems [31,32,33,34,35,36,37,38]. The study of nanofluid-blood flow is critical for treating arterial stenosis, considering changes in viscosity and the potential for innovative applications that can advance biomedical science and save lives. Choi [39] introduced the term “nanofluid” and demonstrated increased thermal conductivity in base fluids infused with nanometer-sized particles. Sandeep et al. [40] examined the impact of radiation on the pulsatile convective flow of an ethylene glycol-based nanofluid along a vertical plate. Radiation effects on the magnetohydrodynamic stagnation point flow of a nanofluid towards a stretching surface with convective boundary conditions were investigated by Akbar et al. [41]. Gireesha et al. [42] addressed the magnetohydrodynamic flow and heat transfer of a dusty fluid over a stretching surface, while Mohankrishna et al. [43] studied radiation effects on the unsteady magnetohydrodynamic natural convection flow of a nanofluid past an infinite vertical plate with a heat source. Subsequently, numerous researchers investigated diverse nano-blood flow models across varying aspects and conditions [44,45,46,47,48,49,50,51,52,53,54,55,56].

The literature review revealed that no efforts have been made to investigate the simultaneous impact of pressure gradient variation on nanofluid flow along the length of the stenosed artery. In previous research, the prevailing assumption was that the pressure gradient can be simplified into steady and unsteady components, both remaining constant with the stenosed artery’s length. Contrary to this, Chow and Abumandour et al. [57, 58] discovered a substantial variation in the pressure gradient's relationship with the restricted channel length, exerting an influence on other associated parameters. This study addresses this gap by investigating nanofluid flow in a stenosed artery, accounting for pressure gradient variation, as well as radiation, chemical reaction, and magnetic field effects. The governing equations of nanofluid flow in a horizontal stenosed artery are solved using the perturbation method. The analytical solutions of velocity, temperature, concentration, wall shear stress, flow rate, and pressure gradient are presented graphically, considering different values of the relevant physical parameters.

2 Mathematical formulation

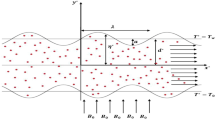
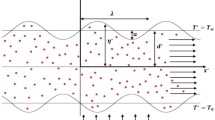
The statement describes blood as an unsteady, incompressible nanofluid flow through a porous stenosed arterial segment with heat and chemical reaction. The artery is assumed to be a three-dimensional vessel with a small radius. It can be approximated as a two-dimensional channel, and the pressure gradient is in the horizontal direction (See Fig. 1) [16, 59]. The uniform magnetic field is applied perpendicularly to the direction of the nanofluid flow. The following equations govern the flow field [16]:

Fig. 1

A schematic diagram of the problem

Momentum equation

$$ \frac{{\partial u^{*} }}{{\partial t^{*} }} = - \frac{1}{{\rho_{nf} }}\frac{{\partial p^{*} }}{{\partial x^{*} }} + \upsilon_{nf} \left( {\frac{{\partial^{2} u^{*} }}{{\partial y^{*2} }}} \right) - \left( {\frac{{\upsilon_{nf} }}{k}} \right)u^{*} - \left( {\frac{{\sigma B_{O}^{2} }}{{\rho_{nf} }}} \right)u^{*} , $$

(1)

Energy equation

$$ \frac{{\partial T^{*} }}{{\partial t^{*} }} = \frac{{k_{nf} }}{{\left( {\rho C_{p} } \right)_{nf} }}\left( {\frac{{\partial^{2} T^{*} }}{{\partial y^{{{*}2}} }}} \right) + \frac{{\mu_{nf} }}{{\left( {\rho C_{p} } \right)_{nf} }}\left( {\frac{{\partial u^{*} }}{{\partial y^{*} }}} \right)^{2} - \frac{{\sigma B_{0}^{2} }}{{\left( {\rho C_{p} } \right)_{nf} }}u^{*2} - \frac{1}{{\left( {\rho C_{p} } \right)_{nf} }}\frac{{\partial q_{r} }}{{\partial y^{*} }}, $$

(2)

Concentration equation

$$ \frac{{\partial C^{*} }}{{\partial t^{*} }} = D_{m} \left( {\frac{{\partial^{2} C^{*} }}{{\partial y^{*2} }}} \right) + \frac{{D_{T} K_{bT} }}{{T_{m} }}\left( {\frac{{\partial^{2} T^{*} }}{{\partial y^{*2} }}} \right). $$

(3)

Rosseland approximation for radiative heat flux, ${q}_{r}$ is defined as [60]:

$$ q_{r} = - \left( {\frac{{4\sigma^{*} }}{{3k^{*} }}\frac{{\partial T^{*4} }}{{\partial y^{*} }}} \right). $$

(4)

where ${k}^{*}$ is the Rosseland mean absorption coefficient, ${\sigma }^{*}$ is the Stefan–Boltzmann constant. We presume that the temperature variation within the flow is sufficiently small such that ${T}^{*4}$ may be expanded in a Taylor’s series. Expanding ${T}^{*4}$ about ${T}_{\infty }$ and neglecting higher-order terms we obtain [61]:

$$ T^{*4} \cong 4T_{\infty }^{3} T^{*} - 3T_{\infty }^{4} . $$

(5)

Substituting Eqs. (4) and (5) into Eq. (2), we get:

$$ \frac{{\partial T^{*} }}{{\partial t^{*} }} = \frac{{k_{nf} }}{{\left( {\rho C_{p} } \right)_{nf} }}\left( {\frac{{\partial^{2} T^{*} }}{{\partial y^{*2} }}} \right) + \frac{{\mu_{nf} }}{{\left( {\rho C_{p} } \right)_{nf} }}\left( {\frac{{\partial u^{*} }}{{\partial y^{*} }}} \right)^{2} - \frac{{\sigma B_{0}^{2} }}{{\left( {\rho C_{p} } \right)_{nf} }}u^{*2} + \frac{{16\sigma^{*} T_{\infty }^{3} }}{{3k^{*} \left( {\rho C_{p} } \right)_{nf} }}\left( {\frac{{\partial^{2} T^{*} }}{{\partial y^{*2} }}} \right). $$

(6)

Since the nanofluid-blood flow is driven by the pumping action of the heart, which produces a pulsatile pressure gradient, it can be approximated as a function of ${x}^{*}$ and ${t}^{*}$ [3, 62]. So, it can be taken as:

$$\frac{\partial {p}^{*}}{\partial {x}^{*}}\left({x}^{*},{t}^{*}\right)={P}^{*}\left({x}^{*}\right){ P}^{*}\left({t}^{*}\right).$$

(7)

which,

$$ \left. {\begin{array}{*{20}l} {P^{*} \left( {x^{*} } \right) = \frac{{\partial p^{*} }}{{\partial x^{*} }}\left( {x^{*} } \right),} \hfill \\ {P^{*} \left( {t^{*} } \right) = 1 + A\sin \omega t^{*} .} \hfill \\ \end{array} } \right\} $$

(8)

$A$ is the amplitude of the nanofluid flow and $\omega$ is the angular frequency of the flow.

The geometry of the stenosis is given as follows:

$$ h^{*} \left( {x^{*} } \right) = \left\{ {\begin{array}{*{20}l} {H_{0} \left[ {1 - \frac{{\delta ^{*} }}{2}\left\{ {1 + \cos \frac{{2\pi }}{{l_{0}^{*} }}\left( {x^{*} - d_{0}^{*} - \frac{{l_{0}^{*} }}{2}} \right)} \right\}} \right],\quad d_{0}^{*} \le x^{*} \le d_{0}^{*} + l_{0}^{*} } \hfill \\ {H_{0} ,\qquad \qquad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad\; Otherwise} \hfill \\ \end{array} } \right. $$

(9)

The maximum projection of the stenosis ${\delta }^{*}$ is located at a distance,${x}^{*}={d}_{0}^{*}+\frac{{l}_{0}^{*}}{2}$, from the inlet of the artery. The stenosis length is ${l}_{0}^{*}$, and its location is${d}_{0}^{*}$. The variable height of the channel at the stenosed portion is${h}^{*}\left({x}^{*}\right)$.

The boundary conditions for the wall of the porous channel under the no-slip condition are as follows:

$$ \frac{{\partial u^{*} \left( {y^{*} ,t^{*} } \right)}}{{\partial y^{*} }} = 0,\;\frac{{\partial T^{*} \left( {y^{*} ,t^{*} } \right)}}{{\partial y^{*} }} = 0,\;\frac{{\partial C^{*} \left( {y^{*} ,t^{*} } \right)}}{{\partial y^{*} }} = 0,\quad at\;y^{*} = 0. $$

(10.a)

$$ u^{*} \left( {y^{*} ,t^{*} } \right) = 0,\;T^{*} \left( {y^{*} ,t^{*} } \right) = T_{w} ,\;C^{*} \left( {y^{*} ,t^{*} } \right) = C_{w} ,\quad at\;y^{*} = h^{*} \left( {x^{*} } \right). $$

(10.b)

The nanofluid thermophysical properties according to Zahir et al. [63]:

$$ \left. {\begin{array}{*{20}l} {\begin{array}{*{20}l} {\begin{array}{*{20}l} {\begin{array}{*{20}l} {\rho _{{nf}} = \left( {1 - \varphi } \right)\rho _{f} + \varphi \rho _{n} ,} \hfill \\ {\mu _{{nf}} = \frac{{\mu _{f} }}{{(1 - \varphi )^{{2.5}} }},} \hfill \\ \end{array} } \hfill \\ {\upsilon _{{nf}} = \frac{{\mu _{{nf}} }}{{\rho _{{nf}} }},} \hfill \\ \end{array} } \hfill \\ {\left( {\rho C_{p} } \right)_{{nf}} = \left( {1 - \varphi } \right)\left( {\rho C_{p} } \right)_{f} + \varphi \left( {\rho C_{p} } \right)_{n} ,} \hfill \\ \end{array} } \hfill \\ {\frac{{k_{{nf}} }}{{k_{f} }} = \frac{{\left( {2k_{f} + k_{n} } \right) - 2\varphi \left( {k_{f} - k_{n} } \right)}}{{\left( {2k_{f} + k_{n} } \right) + \varphi \left( {k_{f} - k_{n} } \right)}}.} \hfill \\ \end{array} } \right\} $$

(11)

We introduce the dimensionless parameters as follows:

$$ \left. {\begin{array}{*{20}l} {u = \frac{{u^{*} H_{0} }}{{\upsilon _{f} }},\;x = \frac{{x^{*} }}{{l_{0} }},\;y = \frac{{y^{*} }}{{H_{0} }},\;t = t^{*} \omega ,} \hfill \\ {P = \frac{{p^{*} H_{0}^{2} }}{{\rho _{f} \upsilon _{f}^{2} }},\;d_{0} = \frac{{d_{0}^{*} }}{{H_{0} }},\;l_{0} = \frac{{l_{0}^{*} }}{{H_{0} }},\;\delta = \frac{{\delta ^{*} }}{{H_{0} }},} \hfill \\ {\theta = \frac{{T^{*} - T_{\infty } }}{{T_{w} - T_{\infty } }},\;\emptyset = \frac{{C^{*} - C_{\infty } }}{{C_{w} - C_{\infty } }}.} \hfill \\ \end{array} } \right\} $$

(12)

Using the dimensionless variables stated above in Eqs. (1), (3), (6), (9), and (10) we obtain:

$$ \frac{{\partial^{2} u }}{{\partial y^{2} }} - \left( {Ha^{2} (1 - \varphi )^{2.5} + \frac{1}{Da}} \right)u = (1 - \varphi )^{2.5} \left( {1 - \varphi + \left( {\frac{{\varphi \rho_{n} }}{{\rho_{f} }} } \right)} \right)\alpha^{2} \frac{\partial u}{{\partial t}} + P\left( x \right)P\left( t \right), $$

(13)

$$ \frac{{\left( {\left( {\frac{{k_{nf} }}{{k_{f} }}} \right) + \left( \frac{4}{3} \right)Rd} \right)}}{\Pr }\frac{{\partial^{2} \theta }}{{\partial y^{2} }} = \left( {1 - \varphi + \left( {\frac{{\varphi \left( {\rho C_{p} } \right)_{n} }}{{\left( {\rho C_{p} } \right)_{f} }} } \right)} \right)\alpha^{2} \frac{\partial \theta }{{\partial t}} + \frac{{Ec\left( {Ha^{2} u^{2} + \frac{1}{{(1 - \varphi )^{2.5} }} \left( {\frac{\partial u}{{\partial y}}} \right)^{2} } \right)}}{{(1 - \varphi )^{5} \left( {1 - \varphi + \left( {\frac{{\varphi \rho_{n} }}{{\rho_{f} }} } \right)} \right)^{2} }}, $$

(14)

$$ \frac{{\partial^{2} \emptyset }}{{\partial y^{2} }} = Sc \alpha^{2} \frac{\partial \emptyset }{{\partial t}} - Sc Sr\frac{{\partial^{2} \theta }}{{\partial y^{2} }}. $$

(15)

where, the Womersley parameter $\alpha$, the Darcy number $Da$, the Hartmann number$Ha$, the radiation parameter $Rd$, the Prandtl number $Pr$, the Eckert number $Ec$, the Schmidt number $Sc$, the Soret number $Sr$ are defined respectively by:

$$ \left. {\begin{array}{*{20}l} {\begin{array}{*{20}l} {\alpha = H_{0} \sqrt {\frac{\omega }{{\upsilon _{f} }}} ,\;Da = \frac{k}{{H_{0}^{2} }},\;Ha = B_{0} H_{0} \sqrt {\frac{\sigma }{{\mu _{f} }}} } \hfill \\ {Rd = \frac{{4\sigma ^{*} T_{\infty }^{3} }}{{k_{f} k^{*} }},\;\Pr = \frac{{\left( {\mu C_{p} } \right)_{f} }}{{k_{f} }},\;Ec = \frac{{\upsilon _{f}^{2} }}{{H_{0}^{2} Cp_{f} \left( {T_{w} - T_{\infty } } \right)}},} \hfill \\ \end{array} } \hfill \\ {Sc = \frac{{\upsilon _{f} }}{{D_{m} }},\;Sr = \frac{{D_{T} K_{{bT}} \left( {T_{w} - T_{\infty } } \right)}}{{T_{m} \upsilon _{f} \left( {C_{w} - C_{\infty } } \right)}}.} \hfill \\ \end{array} } \right\} $$

(16)

In dimensionless form, the geometry of the stenosis is given by:

$$ h\left( x \right) = \left\{ {\begin{array}{*{20}l} {\left[ {1 - \frac{\delta }{2}\left\{ {1 + \cos \frac{{2\pi }}{{l_{0} }}\left( {x - d - \frac{{l_{o} }}{2}} \right)} \right\}} \right],\quad d \le x \le d + l_{o} } \hfill \\ {1,\quad \quad \quad \quad \qquad \quad \quad \quad \quad \quad \quad \quad \quad \quad \,Otherwise} \hfill \\ \end{array} } \right. $$

(17)

and the dimensionless transverse coordinate is:

$$ \zeta = \frac{y}{h\left( x \right)}. $$

The corresponding new boundary conditions are:

$$ \frac{{\partial u\left( {y,t} \right)}}{\partial y} = 0,\;\frac{{\partial \theta \left( {y,t} \right)}}{\partial y} = 0,\;\frac{{\partial \emptyset \left( {y,t} \right)}}{\partial y} = 0,\quad {\text{at}}\;y = 0. $$

(18.a)

$$ u\left( {y,t} \right) = 0{,}\;\theta \left( {y,t} \right) = 1,\;\emptyset \left( {y,t} \right) = 1,\quad {\text{at}}\;y = h\left( x \right). $$

(18.b)

3 Method of solution

After using dimensionless technique, the velocity$u$, temperature $\theta$,and concentration $\varnothing$ can be assumed to have expansions in terms of the parameter ${\alpha }^{2}$ [62], which are of the form:

$$ u\left( {y,t} \right) = u_{0} \left( {y,t} \right) + \alpha^{2} u_{1} \left( {y,t} \right) + \cdots , $$

(19)

$$ \theta \left( {y,t} \right) = \theta_{0} \left( {y,t} \right) + \alpha^{2} \theta_{1} \left( {y,t} \right) + \cdots , $$

(20)

$$ \emptyset \left( {y,t} \right) = \emptyset_{0} \left( {y,t} \right) + \alpha^{2} \emptyset_{1} \left( {y,t} \right) + \cdots . $$

(21)

where ( $\alpha$ < 1.0) is the Womersley frequency parameter.

The following equations are the result of substituting Eqs. (19–21) into Eqs. (13–15), and (18), then comparing the coefficients of both sides we obtain the following equations subject to the corresponding boundary conditions:

(i) Zero order:

$$ \frac{{\partial^{2} u_{0} }}{{\partial y^{2} }} - B_{2}^{2} u_{0} = P\left( x \right)P\left( t \right), $$

(22)

$$ B_{5} \frac{{\partial^{2} \theta_{0} }}{{\partial y^{2} }} = - B_{6} \left( { Ha^{2} u_{0}^{2} + \frac{1}{{(1 - \varphi )^{2.5} }} \left( {\frac{{\partial u_{0} }}{\partial y}} \right)^{2} } \right), $$

(23)

$$ \frac{{\partial^{2} \emptyset_{0} }}{{\partial y^{2} }} = - Sc Sr\frac{{\partial^{2} \theta_{0} }}{{\partial y^{2} }}, $$

(24)

$$ \frac{{\partial u_{0} \left( {y,t} \right)}}{\partial y} = 0,\;\frac{{\partial \theta_{0} \left( {y,t} \right)}}{\partial y} = 0,\;\frac{{\partial \emptyset_{0} \left( {y,t} \right)}}{\partial y} = 0,\quad {\text{at}}\;y = 0. $$

(25.a)

$$ u_{0} \left( {y,t} \right) = 0,\;\theta_{0} \left( {y,t} \right) = 1,\;\emptyset_{0} \left( {y,t} \right) = 1,\quad {\text{at}}\;y = h\left( x \right). $$

(25.b)

(ii) First order:

$$ \frac{{\partial^{2} u_{1} }}{{\partial y^{2} }} - B_{2}^{2} u_{1} = B_{1} \frac{{\partial u_{0} }}{\partial t}, $$

(26)

$$ B_{5} \frac{{\partial^{2} \theta_{1} }}{{\partial y^{2} }} = B_{4} \frac{{\partial \theta_{0} }}{\partial t} + B_{6} \left( { Ha^{2} u_{0} u_{1} + \frac{1}{{(1 - \varphi )^{2.5} }} \left( {\frac{{\partial u_{0} }}{\partial y}} \right)\left( {\frac{{\partial u_{1} }}{\partial y}} \right)} \right), $$

(27)

$$ \frac{{\partial^{2} \emptyset_{1} }}{{\partial y^{2} }} = Sc\frac{{\partial \emptyset_{0} }}{\partial t} - Sc Sr\frac{{\partial^{2} \theta_{1} }}{{\partial y^{2} }}, $$

(28)

$$ \frac{{\partial u_{1} \left( {y,t} \right)}}{\partial y} = 0,\;\frac{{\partial \theta_{1} \left( {y,t} \right)}}{\partial y} = 0,\;\frac{{\partial \emptyset_{1} \left( {y,t} \right)}}{\partial y} = 0,\quad {\text{at}}\;y = 0. $$

(29.a)

$$ u_{1} \left( {y,t} \right) = 0,\;\theta_{1} \left( {y,t} \right) = 0,\;\emptyset_{1} \left( {y,t} \right) = 0,\quad {\text{at}}\;y = h\left( x \right). $$

(29.b)

By solving Eqs. (22–28) with the corresponding boundary conditions in Eqs. (25) and (29), we obtain:

$$ u_{0} \left( {y,t} \right) = P\left( x \right)P\left( t \right)\left[ {C_{1} e^{{m_{1} y}} + C_{2} e^{{m_{2} y}} + C_{3} } \right], $$

(30)

$$ u_{1} \left( {y,t} \right) = P\left( x \right)\left[ {(C_{4} + C_{5} y)e^{{m_{1} y}} + (C_{6} + C_{7} y)e^{{m_{2} y}} + C_{8} } \right], $$

(31)

$$ \theta_{0} \left( {y,t} \right) = C_{9} e^{{2m_{1} y}} + C_{10} e^{{2m_{2} y}} + C_{11} e^{{m_{1} y}} + C_{12} e^{{m_{2} y}} + C_{13} y^{2} + C_{14} y + C_{15} , $$

(32)

$$ \begin{aligned} \theta_{1} \left( {y,t} \right) = & C_{16} e^{{2m_{1} y}} + C_{17} e^{{2m_{2} y}} + C_{18} e^{{m_{1} y}} + C_{19} e^{{m_{2} y}} + C_{20} y e^{{2m_{1} y}} + C_{21} y e^{{2m_{2} y}} \\ + C_{22} y e^{{m_{1} y}} + C_{23} y e^{{m_{2} y}} + C_{24} y^{4} + C_{25} y^{3} + + C_{26} y^{2} + C_{27} y + C_{28} , \\ \end{aligned} $$

(33)

$$ \emptyset_{0} \left( {y,t} \right) = C_{29} e^{{2m_{1} y}} + C_{30} e^{{2m_{2} y}} + C_{31} e^{{m_{1} y}} + C_{32} e^{{m_{2} y}} + C_{33} y^{2} + C_{34} y + C_{35} , $$

(34)

$$ \begin{aligned} \emptyset_{1} \left( {y,t} \right) = &C_{36} e^{{2m_{1} y}} + C_{37} e^{{2m_{2} y}} + C_{38} e^{{m_{1} y}} + C_{39} e^{{m_{2} y}} + C_{40} y e^{{2m_{1} y}} + C_{41} y e^{{2m_{2} y}} \\& +C_{42} y e^{{m_{1} y}} + C_{43} y e^{{m_{2} y}} + C_{44} y^{4} + C_{45} y^{3} + C_{46} y^{2} + C_{47} y + C_{48} . \\ \end{aligned} $$

(35)

where ${C}_{1},{C}_{2},{C}_{3},$ · · · etc. given in the appendix.

Substituting Eqs. (30–35) into Eqs. (19–21), we obtain an expression for velocity$u$, temperature $\theta$,and concentration $\varnothing$ as:

$$ u\left( {y,t} \right) = P\left( x \right)P\left( t \right)\left[ {\left( {C_{1} e^{{m_{1} y}} + C_{2} e^{{m_{2} y}} + C_{3} } \right) + \frac{{\alpha^{2} }}{P\left( t \right)}\left( {(C_{4} y + C_{5} } \right)e^{{m_{1} y}} + (C_{6} y + C7)e^{{m_{2} y}} + C_{8} )} \right], $$

(36)

$$ \begin{aligned} \theta \left( {y,t} \right) = & C_{9} e^{{2m_{1} y}} + C_{10} e^{{2m_{2} y}} + C_{11} e^{{m_{1} y}} + C_{12} e^{{m_{2} y}} + C_{13} y^{2} + C_{14} y + C_{15} \\ + \alpha^{2} \left[ {C_{16} e^{{2m_{1} y}} + C_{17} e^{{2m_{2} y}} + C_{18} e^{{m_{1} y}} + C_{19} e^{{m_{2} y}} + C_{20} y e^{{2m_{1} y}} + C_{21} y e^{{2m_{2} y}} } \right. \\ \left. { + C_{22} y e^{{m_{1} y}} + C_{23} y e^{{m_{2} y}} + C_{24} y^{4} + C_{25} y^{3} + C_{26} y^{2} + C_{27} y + C_{28} } \right], \\ \end{aligned} $$

(37)

$$ \begin{aligned} \emptyset \left( {y,t} \right) = & C_{29} e^{{2m_{1} y}} + C_{30} e^{{2m_{2} y}} + C_{31} e^{{m_{1} y}} + C_{32} e^{{m_{2} y}} + C_{33} y^{2} + C_{34} y + C_{35} \\ + \alpha^{2} \left[ {C_{36} e^{{2m_{1} y}} + C_{37} e^{{2m_{2} y}} + C_{38} e^{{m_{1} y}} + C_{39} e^{{m_{2} y}} + C_{40} y e^{{2m_{1} y}} + C_{41} y e^{{2m_{2} y}} } \right. \\ \left. { + C_{42} y e^{{m_{1} y}} + C_{43} y e^{{m_{2} y}} + C_{44} y^{4} + C_{45} y^{3} + C_{46} y^{2} + C_{47} y + C_{48} } \right]. \\ \end{aligned} $$

(38)

After having determine $u$, we can obtain the volumetric flow rate $Q$, defined by:

$$ Q = \mathop \smallint \limits_{0}^{h\left( x \right)} u\left( {y,t} \right) dy. $$

(39)

Which on integration yields after substituting from Eq. (36) into Eq. (39) results in:

$$ \begin{aligned} Q = & P\left( x \right)P\left( t \right)\left[ {\left( {\frac{{C_{1} }}{{m_{1} }}(e^{{m_{1} h\left( x \right)}} - 1) + \frac{{C_{2} }}{{m_{2} }}(e^{{m_{2} h\left( x \right)}} - 1) + C_{3} h\left( x \right)} \right)} \right. \\ + \frac{{\alpha^{2} }}{p\left( t \right)}\left( {\frac{{C_{4} }}{{m_{1}^{2} }}(e^{{m_{1} h\left( x \right)}} \left( {m_{1} h\left( x \right) - 1} \right) + 1) + \frac{{C_{5} }}{{m_{1} }}(e^{{m_{1} h\left( x \right)}} - 1)} \right. \\ \left. {\left. { + \frac{{C_{6} }}{{m_{2}^{2} }}(e^{{m_{2} h\left( x \right)}} \left( {m_{2} h\left( x \right) - 1} \right) + 1) + \frac{{C_{7} }}{{m_{2} }}(e^{{m_{2} h\left( x \right)}} - 1) + C_{8} h\left( x \right)} \right)} \right]. \\ \end{aligned} $$

(40)

The pressure gradient $P\left(x\right)$ can be obtained from Eq. (40):

$$ \begin{aligned} p\left( x \right) \;= & \;\frac{Q}{P\left( t \right)}\left[ {\left( {\frac{{C_{1} }}{{m_{1} }}(e^{{m_{1} h\left( x \right)}} - 1) + \frac{{C_{2} }}{{m_{2} }}(e^{{m_{2} h\left( x \right)}} - 1) + C_{3} h\left( x \right)} \right)} \right. \\ &+ \frac{{\alpha^{2} }}{p\left( t \right)}\left( {\frac{{C_{4} }}{{m_{1}^{2} }}(e^{{m_{1} h\left( x \right)}} \left( {m_{1} h\left( x \right) - 1} \right) + 1) + \frac{{C_{5} }}{{m_{1} }}(e^{{m_{1} h\left( x \right)}} - 1)} \right. \\& \left. {\left. { + \frac{{C_{6} }}{{m_{2}^{2} }}(e^{{m_{2} h\left( x \right)}} \left( {m_{2} h\left( x \right) - 1} \right) + 1) + \frac{{C_{7} }}{{m_{2} }}(e^{{m_{2} h\left( x \right)}} - 1) + C_{8} h\left( x \right)} \right)} \right]^{ - 1} . \\ \end{aligned} $$

(41)

The non-dimensional wall shear stress ${\tau }_{w}$ is a physiologically important quantity given by:

$$ \tau_{w} = \left[ {\frac{\partial u}{{\partial y}}} \right]_{y = h\left( x \right)} , $$

(42)

Use of Eq. (36) into Eq. (42), the wall shear stress can be written as:

$$ \begin{aligned} \tau_{w}\; = & \;P\left( x \right)P\left( t \right)\left[ {\left( {C_{1} m_{1} e^{{m_{1} h\left( x \right)}} + C_{2} m_{2} e^{{m_{2} h\left( x \right)}} } \right) + \frac{{\alpha^{2} }}{p\left( t \right)}(C_{4} e^{{m_{1} y}} } \right. \\ &\left. { + m_{1} \left( {C_{4} h\left( x \right) + C_{5} } \right)e^{{m_{1} y}} + C_{6} e^{{m_{2} y}} + m_{2} \left( {C_{6} h\left( x \right) + C_{7} } \right)e^{{m_{1} y}} } \right]. \\ \end{aligned} $$

(43)

4 Results and discussion

In this section, we performed numerical simulations of Eqs. (36–43) to study the effect of the biophysical parameters such as Hartmann number, Darcy number, stenosis growth parameter, radiation parameter, nanoparticle concentration, Eckert number, Prindle number, Schmidt number, and Soret number on velocity, wall shear stress, temperature, concentration, pressure gradient, and flow rate profiles which are presented graphically in Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26. Table 1 contains the default values for the biophysical parameters used in the simulation.

Fig. 2

Axial velocity profile $u(y,t)$ with dimensionless transverse coordinate at the throat of the stenosis for different values of the Hartmann number $\left(Ha\right)$

Fig. 3

Axial velocity profile $u(y,t)$ with dimensionless transverse coordinate at the throat of the stenosis for different values of the Darcy number $\left(Da\right)$

Fig. 4

Axial velocity profile $u(y,t)$ with dimensionless transverse coordinate at the throat of the stenosis for different values of the nanoparticle concentration $(\varphi )$

Fig. 5

Axial velocity profile $u(y,t)$ with dimensionless transverse coordinate at the throat of the stenosis for different values of the Stenosis height $\left(\delta \right)$

Fig. 6

Distribution of wall shear stress $\left({\tau }_{w}\right)$ for various Hartmann number $\left(Ha\right)$

Fig. 7

Distribution of wall shear stress $\left({\tau }_{w}\right)$ for various Darcy number $\left(Da\right)$

Fig. 8

Distribution of wall shear stress $\left({\tau }_{w}\right)$ for various nanoparticle concentration $\left(\varphi \right)$

Fig. 9

Distribution of wall shear stress $\left({\tau }_{w}\right)$ for various Stenosis height $\left(\delta \right)$

Fig. 10

Temperature profile $\theta (y,t)$ with dimensionless transverse coordinate at the throat of the stenosis for different values of the Hartmann number $(Ha)$

Fig. 11

Temperature profile $\theta (y,t)$ with dimensionless transverse coordinate at the throat of the stenosis for different values of the Darcy number $\left(Da\right)$

Fig. 12

Temperature profile $\theta (y,t)$ with dimensionless transverse coordinate at the throat of the stenosis for different values of the nanoparticle concentration $(\varphi )$

Fig. 13

Temperature profile $\theta (y,t)$ with dimensionless transverse coordinate at the throat of the stenosis for different values of the Stenosis height $\left(\delta \right)$

Fig. 14

Temperature profile $\theta (y,t)$ with dimensionless transverse coordinate at the throat of the stenosis for different values of the Eckert number $(Ec)$

Fig. 15

Temperature profile $\theta (y,t)$ with dimensionless transverse coordinate at the throat of the stenosis for different values of the Prandtl number $(Pr)$

Fig. 16

Temperature profile $\theta (y,t)$ with dimensionless transverse coordinate at the throat of the stenosis for different values of the Radiation parameter $(Rd)$

Fig. 17

Concentration profile $\varnothing (y,t)$ with dimensionless transverse coordinate at the throat of the stenosis for different values of the Hartmann number $(Ha)$

Fig. 18

Concentration profile $\varnothing (y,t)$ with dimensionless transverse coordinate at the throat of the stenosis for different values of the Darcy number $(Da)$

Fig. 19

Concentration profile $\varnothing (y,t)$ with dimensionless transverse coordinate at the throat of the stenosis for different values of the nanoparticle concentration $(\varphi )$

Fig. 20

Concentration profile $\varnothing (y,t)$ with dimensionless transverse coordinate at the throat of the stenosis for different values of the Stenosis height $(\delta )$

Fig. 21

Concentration profile $\varnothing (y,t)$ with dimensionless transverse coordinate at the throat of the stenosis for different values of the Schmidt number $(Sc)$

Fig. 22

Concentration profile $\varnothing (y,t)$ with dimensionless transverse coordinate at the throat of the stenosis for different values of the Soret number $(Sr)$

Fig. 23

Distribution of Pressure gradient $\left(\partial p/\partial x\right)$ for various Stenosis height $(\delta )$

Fig. 24

Variation of volumetric flow rate $(Q)$ with time for various Stenosis height $(\delta )$

Table 1 Default values of key parameters used in simulations

In addition, the thermophysical numerical parameters of blood and gold nanoparticles [51, 64] are listed in Table 2.

Table2 Numerical values of base fluid and solid material nanoparticles

The velocity profiles are presented in Figs. 2, 3, 4, 5. Figure 2 demonstrates that as the Hartmann number increases, the centreline velocity decreases, leading to an increase in near-wall velocity due to conservation of mass flow rate. This behaviour results in a flattening of the velocity profile near the centreline, accompanied by a decrease in the rate of velocity change. These findings have potential implications for surgical patients as mentioned in [65]. They suggest a decrease in blood velocity during surgery. Conversely, Fig. 3 exhibits a contrasting trend related to porosity's effect on velocity. It reveals that as the Darcy number increases, the centreline velocity increases while causing a decrease in near-wall velocity. Similar to the previous case, this increase in Darcy number leads to a flatter velocity profile near the centreline with a diminishing rate of velocity change. Figure 4 delves into the influence of nanoparticle concentration on axial velocity. A notable upsurge in velocity is observed as the nanoparticle volume fraction escalates, and this can be explained by the effect of increasing nanoparticles concentration leads to a decrease in the available area for the blood to flow through the channel. Furthermore, Fig. 5 highlights a significant increase in velocity as the height of the stenosis at the throat of the channel increases. This indicates a direct correlation between flow velocity and the narrowing of the channel based on the continuity equation [53].

Conducting a comprehensive analysis of wall shear stress distribution along the axial distance, as illustrated in Figs. 6, 7, 8, 9, under various rheological parameters. It is a well-established fact that elevated wall shear stresses can induce damage to the vessel wall, resulting in intimal thickening. Conversely, low wall shear stresses facilitate mass transport, leading to the deposition of substances such as cholesterol, which leads to an increase in stenosis height. Figure 2 provides valuable insights, revealing that the slope of the velocity profile near the wall increases with higher Hartmann numbers. Consequently, this increase in slope translates into a corresponding rise in wall shear stress, as exemplified in Fig. 6. In sharp contrast, Fig. 7 showcases a noteworthy phenomenon. Here, a decline in wall shear stress can be observed with increasing Darcy numbers. This decrease is attributable to the diminishing slope of the velocity profile near the wall, as vividly demonstrated in Fig. 3. Furthermore, Fig. 8 sheds light on the relationship between wall shear stress and nanoparticle concentration. The data unequivocally indicate that as nanoparticle concentration increases, wall shear stress follows suit, strengthening this correlation. Figure 9 unveils yet another intriguing finding. It demonstrates that as the height of the stenosis increases, wall shear stress experiences a corresponding upsurge. This phenomenon aligns with an evident escalation in the velocity gradient near the stenotic region in Fig. 5, providing crucial insights into the interplay between stenosis height and wall shear stress.

Regarding the temperature profiles, the effect of the Hartmann number on the temperature profile is shown in Fig. 10, which shows an increase with increasing Hartmann number at the centreline. As the Hartmann number rises, the magnetic field strength becomes stronger, which in turn impedes the fluid motion as shown in Fig. 2. Reduced fluid motion leads to a lower heat transfer rate, causing the temperature to rise at the centreline. The inverse relationship between the Darcy number and temperature profile is linked to fluid permeability. In Fig. 11, as the Darcy number increases, it signifies greater fluid permeability through porous media. This increased permeability allows for enhanced heat dissipation, resulting in a lower temperature profile. As shown in Fig. 12, the increase in temperature distribution with the presence of nanoparticles can be attributed to their thermal properties. Nanoparticles exhibit efficient thermal conduction or absorption, and as the nanoparticle concentration increases, there is a notable increase in the surface area exposed to the blood flow, leading to enhanced heat transfer within the fluid. Consequently, this results in a broader temperature distribution. Figure 13 further illustrates the effect of stenosis height on the temperature profile. The positive correlation between stenosis height and temperature profile is due to the narrowing of the flow passage, which gives less time for heat transfer through the blood flow. As the stenosis height increases, the flow becomes more constrained, leading to increased flow resistance and subsequently higher temperatures along the channel. The temperature increase with an increasing Eckert number is indicative of the enhanced contribution from kinetic energy, as shown in Fig. 14. A higher Eckert number implies a greater proportion of kinetic energy in the flow, which, in turn, elevates the temperature through increased internal energy. Conversely, the decrease in temperature with an increasing Prandtl number is associated with fluid properties. A higher Prandtl number signifies a lower thermal diffusivity relative to momentum diffusivity. This results in less efficient heat conduction compared to momentum transfer, leading to a lower temperature profile, as illustrated in Fig. 15. Figure 16 shows that the temperature increases with an increasing radiation parameter, which indicates the significance of radiative heating. A higher radiation parameter signifies an intensified radiation effect within the flow, which directly contributes to elevated temperatures by adding thermal energy to the system [16].

For the concentration profiles, the influence of the Hartmann number on the concentration profile is shown in Fig. 17. The decreasing concentration profile with increasing Hartmann number is attributed to the amplified magnetic field strength, which leads to enhanced electromagnetic forces acting on the nanoparticles. This results in more efficient removal of solute from the bloodstream. Clinically, this insight can be valuable in understanding the mechanisms behind diseases like anaemia, where altered blood chemistry plays a pivotal role. It may also guide therapeutic strategies by suggesting ways to modulate magnetic fields for targeted drug delivery in blood-related disorders [66]. Figure 18 demonstrates a similar decreasing trend. The decreasing concentration profile as the Darcy number increases is linked to heightened resistance within the porous medium, reducing solute transport. This phenomenon has clinical implications for disorders related to blood clotting and thrombosis. In contrast, Fig. 19 shows that the increase in the concentration profile with rising nanoparticle concentration can be attributed to enhanced solute-NP interactions, altering the transport properties. This finding not only contributes to our understanding of blood flow dynamics but also has implications for therapeutic interventions. Manipulating nanoparticle concentration could potentially improve drug delivery to specific targets within the bloodstream, offering new avenues for disease treatment and management [67]. Figure 20 illustrates that the decrease in the concentration profile with increasing stenosis height suggests reduced diffusion and transport of solute due to the restricted area. This insight can be applied to conditions involving vascular stenosis, shedding light on the chemical reactions underlying blood flow in narrowed vessels. Clinical applications extend to disorders related to blood flow obstructions, such as atherosclerosis and thrombosis. It is observed that as mentioned by [55] the downward trend in concentration with rising Schmidt numbers in Fig. 21 can be linked to increased molecular diffusion, which disperses solute more effectively. This understanding is crucial in elucidating blood chemical reactions and their implications for diseases like diabetes, where altered blood chemistry is a hallmark. The increase in concentration with rising the Soret number in Fig. 22 can be attributed to thermal gradients driving solute transport. This phenomenon enhances our understanding of the chemical reactions taking place in pulsatile blood flow. Clinically, it may have implications for managing blood-related disorders where temperature gradients play a role, potentially offering new avenues for therapeutic interventions [68].

The effect of stenosis height on the pressure gradient can be seen in Fig. 23, where the pressure gradient increases with the height of the stenosis as it increases the flow resistance along the length of the stenosed arterial segment and this observation agrees qualitatively well with [58]. This rise in resistance is a consequence of the narrowing of the artery's cross-sectional area due to the stenosis. According to fundamental principles of fluid dynamics, an increase in flow resistance necessitates a higher pressure gradient to sustain the flow rate. In practical terms, this means that as stenosis height increases, the heart must generate greater force to maintain adequate blood flow through the narrowed region, which subsequently results in an elevated pressure gradient. These observations hold significance in the assessment of hemodynamic consequences associated with arterial stenosis, offering valuable insights into conditions such as atherosclerosis.

Finally, Fig. 24 illustrates the volumetric flow rate's periodic oscillations over time, reflecting the pulsatile nature of blood flow driven by the heart's rhythmic contractions. Notably, an increase in stenosis height leads to a marked decline in the volumetric flow rate. This reduction stems from stenosis-induced narrowing of the artery's cross-sectional area, leading to heightened flow resistance, as demonstrated in Fig. 23. Consequently, the heart's ability to pump the same amount of blood diminishes. Beyond these mathematical trends, the clinical repercussions of heightened stenosis and increased flow resistance are profound. Elevated resistance restricts blood flow to the specific vascular bed supplied by the affected artery, potentially causing tissue ischemia. Furthermore, slowed blood circulation in the presence of stenosis triggers platelet adhesion to the vessel wall, fostering platelet aggregation and thrombus formation [62]. This thrombus may detach or fibrillate, leading to abrupt physiological changes. Most critically, clotting within a stenosed coronary artery can impair myocardial contractility, reduce ventricular function, and, in severe cases, precipitate sudden cardiac death, often attributed to ventricular fibrillation. These findings emphasize the intricate connection between stenosis, blood flow dynamics, and the predictive value of flow rate measurement in assessing narrowing issues' pivotal role in cardiovascular health and pathology.

5 Conclusion

The innovative use of a variable steady pressure gradient represents a notable departure from prior studies. Conventional research primarily concentrated on fixed steady pressure gradients for studying pulsatile blood flow in stenotic arteries and associated phenomena. This research represents a substantial step forward in comprehending nanofluid behaviour in constricted arteries, emphasizing the importance of multifactorial considerations in modelling. The investigation explores the confluence of diverse factors, including pressure gradients, heat transfer, chemical reactions, and magnetic fields, influencing the flow of nanoscale blood particles within stenosed arteries. We have obtained exact solutions and thoroughly examined the effects of crucial parameters. The results and observations align well with findings reported in references [16, 53, 55, 58]. The following is a summary of the main conclusions from the graphical representations:

• The velocity profile decreases with rising in the magnetic field at the centreline, while it increases with increasing the permeability parameter. Additionally, velocity rises with greater stenosis height and nanoparticle volume fraction.

• The artery wall shear stress in the stenosis segment decreases with higher permeability parameter but increases with stenosis height, magnetic field, and nanoparticle volume fraction.

• The temperature profile increases with rising magnetic field, nanoparticle volume fraction, stenosis height, Eckert number, and radiation parameter, while decreasing with increasing the permeability parameter and Prandtl number.

• The concentration profile decreases with increasing magnetic field, the permeability parameter, stenosis height, and Schmidt number, but increases with rising nanoparticle volume fraction and Soret number.

• The pressure gradient rises as the constriction height increases along the channel's length.

• The volumetric flow rate decreases with time as the stenosis height increases.

Appendix

$$ B_{1} = (1 - \varphi )^{2.5} \left( {1 - \varphi + \left( {\frac{{\varphi \rho_{n} }}{{\rho_{f} }} } \right)} \right), B_{2} = \sqrt {\left( {Ha^{2} (1 - \varphi )^{2.5} + \frac{1}{Da}} \right)} , $$

$$ B_{3} = (1 - \varphi )^{2.5} \left( {1 - \varphi + \left( {\frac{{\varphi \rho_{n} }}{{\rho_{f} }} } \right)} \right)\frac{dP\left( t \right)}{{dt}}, B_{4} = \left( {1 - \varphi + \left( {\frac{{\varphi \left( {\rho C_{p} } \right)_{n} }}{{\left( {\rho C_{p} } \right)_{f} }} } \right)} \right), $$

$$ B_{5} = \frac{{\left( {\left( {k_{nf} /k_{f} } \right) + \left( {4/3} \right)Rd} \right)}}{\Pr }, B_{6} = \frac{Ec}{{(1 - \varphi )^{5} \left( {1 - \varphi + \left( {\frac{{\varphi \rho_{n} }}{{\rho_{f} }} } \right)} \right)^{2} }}, $$

$m_{1} = \sqrt {\left( {Ha^{2} (1 - \varphi )^{2.5} + \frac{1}{Da}} \right)} , m_{2} = - \sqrt {\left( {Ha^{2} (1 - \varphi )^{2.5} + \frac{1}{Da}} \right)} ,$

$$ C_{1} = \frac{{m_{2} }}{{B_{2}^{2} \left( {m_{2} e^{{m_{1} h\left( x \right)}} - m_{1} e^{{m_{2} h\left( x \right)}} } \right)}},\; C_{2} = - \frac{{m_{1} }}{{B_{2}^{2} \left( {m_{2} e^{{m_{1} h\left( x \right)}} - m_{1} e^{{m_{2} h\left( x \right)}} } \right)}}, \;C_{3} = - \frac{1}{{\left( {Ha^{2} (1 - \varphi )^{2.5} + \frac{1}{Da}} \right)}}, $$

$$ C_{5} = \frac{{B_{3} C_{1} }}{{2m_{1} }}, \;C_{7} = \frac{{B_{3} C_{2} }}{{2m_{2} }}, \;C_{8} = - \frac{{B_{3} C_{3} }}{{B_{2}^{2} }}, $$

$$ C_{4} = - \frac{{m_{2} \left( {C_{5} h\left( x \right)e^{{m_{1} h\left( x \right)}} + C_{7} h\left( x \right)e^{{m_{2} h\left( x \right)}} + C_{8} - \frac{{\left( {C_{5} + C_{7} } \right)e^{{m_{2} h\left( x \right)}} }}{{m_{2} }}} \right)}}{{\left( {m_{2} e^{{m_{1} h\left( x \right)}} - m_{1} e^{{m_{2} h\left( x \right)}} } \right)}}, $$

$$ C_{6} = \frac{{m_{1} \left( {C_{5} h\left( x \right)e^{{m_{1} h\left( x \right)}} + C_{7} h\left( x \right)e^{{m_{2} h\left( x \right)}} + C_{8} - \frac{{\left( {C_{5} + C_{7} } \right)e^{{m_{1} h\left( x \right)}} }}{{m_{1} }}} \right)}}{{\left( {m_{2} e^{{m_{1} h\left( x \right)}} - m_{1} e^{{m_{2} h\left( x \right)}} } \right)}}, $$

$$ \begin{gathered} C_{9} = - \frac{{B_{6} C_{1}^{2} P\left( x \right)^{2} P\left( t \right)^{2} }}{{4B_{5} m_{1}^{2} }}\left( {Ha^{2} + \frac{1}{{(1 - \varphi )^{2.5} }}} \right), \hfill \\ C_{10} = - \frac{{B_{6} C_{2}^{2} P\left( x \right)^{2} P\left( t \right)^{2} }}{{4B_{5} m_{2}^{2} }}\left( {Ha^{2} + \frac{1}{{(1 - \varphi )^{2.5} }}} \right), \hfill \\ \end{gathered} $$

$$ \begin{gathered} C_{11} = - \frac{{2 B_{6} C_{1} C_{3} P\left( x \right)^{2} P\left( t \right)^{2} Ha^{2} }}{{B_{5} m_{1}^{2} }}, \hfill \\ C_{12} = - \frac{{2 B_{6} C_{2} C_{3} P\left( x \right)^{2} P\left( t \right)^{2} Ha^{2} }}{{B_{5} m_{2}^{2} }}, \hfill \\ \end{gathered} $$

$$ C_{13} = - \frac{{B_{6} P\left( x \right)^{2} P\left( t \right)^{2} \left( {2 C_{1} C_{2} \left( {Ha^{2} + \frac{1}{{(1 - \varphi )^{2.5} }}} \right) + C_{3}^{2} Ha^{2} } \right) }}{{2 B_{5} }}, $$

$$ C_{14} = - \left( {\frac{{C_{9} }}{{2 m_{1} }} + \frac{{C_{10} }}{{2 m_{2} }} + \frac{{C_{11} }}{{m_{1} }} + \frac{{C_{12} }}{{ m_{2} }}} \right), $$

$$ \begin{aligned} C_{15} = & 1 - \left( {\frac{{C_{9} }}{{4 m_{1}^{2} }}e^{{2 m_{1} h\left( x \right)}} + \frac{{C_{10} }}{{4 m_{2}^{2} }}e^{{2 m_{2} h\left( x \right)}} + \frac{{C_{11} }}{{m_{1}^{2} }}e^{{ m_{1} h\left( x \right)}} + \frac{{C_{12} }}{{ m_{2}^{2} }}e^{{ m_{2} h\left( x \right)}} } \right. \\ \left. { + C_{13} h\left( x \right)^{2} + C_{14} h\left( x \right)} \right), \\ \end{aligned} $$

$$ C_{{16}} = - \frac{{2B_{6} P\left( x \right)^{2} P\left( t \right)}}{{4m_{1}^{2} B_{5} }}\left( {\frac{{B_{4} C_{1}^{2} \frac{{dP\left( t \right)}}{{dt}}\left( {Ha^{2} + \frac{1}{{(1 - \varphi )^{{2.5}} }}} \right)}}{{4m_{1}^{2} B_{5} }} + Ha^{2} C_{1} \left( {C_{4} - \frac{{C_{5} }}{{m_{1} }}} \right) + \frac{{C_{1} C_{4} m_{1}^{2} }}{{(1 - \varphi )^{{2.5}} }}} \right), $$

$$ C_{{17}} = - \frac{{2B_{6} P\left( x \right)^{2} P\left( t \right)}}{{4m_{2}^{2} B_{5} }}\left( {\frac{{B_{4} C_{2}^{2} \frac{{dP\left( t \right)}}{{dt}}\left( {Ha^{2} + \frac{1}{{(1 - \varphi )^{{2.5}} }}} \right)}}{{4m_{2}^{2} B_{5} }} + Ha^{2} C_{2} \left( {C_{6} - \frac{{C_{7} }}{{m_{1} }}} \right) + \frac{{C_{2} C_{6} m_{2}^{2} }}{{(1 - \varphi )^{{2.5}} }}} \right), $$

$$ \begin{aligned} C_{18} = & - \frac{{2 B_{6} P\left( x \right)^{2} P\left( t \right)}}{{m_{1}^{2} B_{5} }}\left( {\frac{{2 B_{4} Ha^{2} \frac{dP\left( t \right)}{{dt}} C_{1} C_{3} }}{{ m_{1}^{2} B_{5} }}} \right. \\ \left. { + Ha^{2} \left( {C_{1} C_{8} + C_{3} C_{4} - \frac{{2C_{3} C_{5} }}{{m_{1} }}} \right)} \right), \\ \end{aligned} $$

$$ \begin{aligned} C_{19} = & - \frac{{2 B_{6} P\left( x \right)^{2} P\left( t \right)}}{{m_{2}^{2} B_{5} }}\left( {\frac{{2 B_{4} Ha^{2} \frac{dP\left( t \right)}{{dt}} C_{2} C_{3} }}{{ m_{2}^{2} B_{5} }}} \right. \\ \left. { + Ha^{2} \left( {C_{2} C_{8} + C_{3} C_{6} - \frac{{2C_{3} C_{7} }}{{m_{2} }}} \right)} \right), \\ \end{aligned} $$

$$ \begin{gathered} C_{20} = - \frac{{2 B_{6} P\left( x \right)^{2} P\left( t \right) C_{1} C_{5} }}{{4 m_{1}^{2} B_{5} }}\left( {Ha^{2} + \frac{{ m_{1}^{2} }}{{(1 - \varphi )^{2.5} }} } \right), \hfill \\ C_{21} = - \frac{{2 B_{6} P\left( x \right)^{2} P\left( t \right) C_{2} C_{7} }}{{4 m_{2}^{2} B_{5} }}\left( {Ha^{2} + \frac{{ m_{2}^{2} }}{{(1 - \varphi )^{2.5} }} } \right), \hfill \\ \end{gathered} $$

$$ \begin{gathered} C_{22} = - \frac{{2 B_{6} P\left( x \right)^{2} P\left( t \right) C_{3} C_{5} Ha^{2} }}{{ m_{1}^{2} B_{5} }}, \hfill \\ C_{23} = - \frac{{2 B_{6} P\left( x \right)^{2} P\left( t \right) C_{3} C_{7} Ha^{2} }}{{ m_{2}^{2} B_{5} }}, \hfill \\ \end{gathered} $$

$$ C_{24} = - \frac{{ B_{4} B_{6} P\left( x \right)^{2} P\left( t \right) \frac{dP\left( t \right)}{{dt}}}}{{12 B_{5}^{2} }}\left( {2 C_{1} C_{2} \left( {Ha^{2} + \frac{1}{{(1 - \varphi )^{2.5} }}} \right) + Ha^{2} C_{3}^{2} } \right), $$

$$ \begin{aligned} C_{25} = & - \frac{{ B_{6} P\left( x \right)^{2} P\left( t \right) }}{{6 B_{5} }}\left( {\frac{{ B_{4} \frac{dP\left( t \right)}{{dt}}}}{{B_{5} }}\left( {} \right.\left( {\left( {\frac{{C_{1}^{2} }}{{m_{1} }} + \frac{{C_{2}^{2} }}{{m_{2} }}} \right)\left( {Ha^{2} + \frac{1}{{(1 - \varphi )^{2.5} }}} \right) + 4 C_{3} Ha^{2} \left( {\frac{{C_{1} }}{{m_{1} }} + \frac{{C_{2} }}{{m_{2} }}} \right)} \right)} \right. \\ \left. { + 2\left( {Ha^{2} + \frac{{m_{1} m_{2} }}{{(1 - \varphi )^{2.5} }}} \right)\left( {C_{1} C_{7} + C_{2} C_{5} } \right)} \right) \\ - 2 B_{6} P\left( x \right)^{2} P\left( t \right)\left( {Ha^{2} \left( {C_{2} C_{4} + C_{1} C_{6} + C_{3} C_{8} } \right) + \left( {\frac{{C_{1} C_{7} m_{1} + C_{2} C_{5} m_{1} + m_{1} m_{2} \left( {C_{1} C_{6} + C_{2} C_{4} } \right)}}{{(1 - \varphi )^{2.5} }}} \right)} \right) \\ - 2 B_{6} P\left( x \right)^{2} P\left( t \right)\left( {Ha^{2} \left( {C_{2} C_{4} + C_{1} C_{6} + C_{3} C_{8} } \right) + \left( {\frac{{C_{1} C_{7} m_{1} + C_{2} C_{5} m_{1} + m_{1} m_{2} \left( {C_{1} C_{6} + C_{2} C_{4} } \right)}}{{(1 - \varphi )^{2.5} }}} \right)} \right) \\ \end{aligned} $$

$$ \begin{aligned} C_{26} = & B_{4} \left( {1 + \frac{{ B_{6} P\left( x \right)^{2} P\left( t \right) \frac{dP\left( t \right)}{{dt}}}}{{ B_{5}^{2} }}\left( {\left( {\frac{{C_{1}^{2} e^{{2m_{1} h\left( x \right)}} }}{{2m_{1}^{2} }} + \frac{{C_{2}^{2} e^{{2m_{2} h\left( x \right)}} }}{{2m_{2}^{2} }}} \right)\left( {Ha^{2} + \frac{1}{{(1 - \varphi )^{2.5} }}} \right)} \right.} \right. \\ + 4 C_{3} Ha^{2} \left( {\frac{{C_{1} e^{{m_{1} h\left( x \right)}} }}{{m_{1}^{2} }} + \frac{{C_{2} e^{{m_{2} h\left( x \right)}} }}{{m_{2}^{2} }}} \right) \\ + 2 h\left( x \right)^{2} \left( {2 C_{1} C_{2} \left( {Ha^{2} + \frac{1}{{(1 - \varphi )^{2.5} }}} \right) + Ha^{2} C_{3}^{2} } \right) \\ \left. {\left. { + h\left( x \right)\left( {\left( {\frac{{C_{1}^{2} }}{{m_{1} }} + \frac{{C_{2}^{2} }}{{m_{2} }}} \right)\left( {Ha^{2} + \frac{1}{{(1 - \varphi )^{2.5} }}} \right) + 4 C_{3} Ha^{2} \left( {\frac{{C_{1} }}{{m_{1} }} + \frac{{C_{2} }}{{m_{2} }}} \right)} \right)} \right)} \right) \\ - 2 B_{6} P\left( x \right)^{2} P\left( t \right)\left( {Ha^{2} \left( {C_{2} C_{4} + C_{1} C_{6} + C_{3} C_{8} } \right) + \left( {\frac{{C_{1} C_{7} m_{1} + C_{2} C_{5} m_{1} + m_{1} m_{2} \left( {C_{1} C_{6} + C_{2} C_{4} } \right)}}{{(1 - \varphi )^{2.5} }}} \right)} \right), \\ \end{aligned} $$

$$ C_{27} = - \left( {2m_{1} C_{16} + 2m_{2} C_{17} + m_{1} C_{18} + m_{2} C_{19} + C_{20} + C_{21} + C_{22} + C_{23} } \right) $$

$$ \begin{aligned} C_{28} = & - \left( {C_{16} e^{{2m_{1} h\left( x \right)}} + C_{17} e^{{2m_{2} h\left( x \right)}} + C_{18} e^{{m_{1} h\left( x \right)}} + C_{19} e^{{m_{2} h\left( x \right)}} } \right. \\ + C_{20} h\left( x \right)e^{{2m_{1} h\left( x \right)}} + C_{21} h\left( x \right)e^{{2m_{2} h\left( x \right)}} + C_{22} h\left( x \right)e^{{m_{1} h\left( x \right)}} \\ \left. { + C_{23} h\left( x \right)e^{{m_{2} h\left( x \right)}} + C_{24} h\left( x \right)^{4} + C_{25} h\left( x \right)^{3} + C_{26} h\left( x \right)^{2} + C_{27} h\left( x \right)} \right), \\ \end{aligned} $$

$$ C_{29} = \frac{{Sr Sc B_{6} C_{1}^{2} P\left( x \right)^{2} P\left( t \right)^{2} }}{{4B_{5} m_{1}^{2} }}\left( {Ha^{2} + \frac{1}{{(1 - \varphi )^{2.5} }}} \right), $$

$$ C_{30} = \frac{{Sr Sc B_{6} C_{2}^{2} P\left( x \right)^{2} P\left( t \right)^{2} }}{{4B_{5} m_{2}^{2} }}\left( {Ha^{2} + \frac{1}{{(1 - \varphi )^{2.5} }}} \right), $$

$$ C_{31} = - \frac{{2 B_{6} C_{1} C_{3} P\left( x \right)^{2} P\left( t \right)^{2} Ha^{2} }}{{B_{5} m_{1}^{2} }}, $$

$$ C_{32} = - \frac{{2 Sr Sc B_{6} C_{2} C_{3} P\left( x \right)^{2} P\left( t \right)^{2} Ha^{2} }}{{B_{5} m_{2}^{2} }}, $$

$$ C_{33} = \frac{{Sr Sc B_{6} P\left( x \right)^{2} P\left( t \right)^{2} \left( {2 C_{1} C_{2} \left( {Ha^{2} + \frac{1}{{(1 - \varphi )^{2.5} }}} \right) + C_{3} Ha^{2} } \right) }}{{2 B_{5} }}, $$

$$ C_{34} = - \left( {\frac{{C_{29} }}{{2 m_{1} }} + \frac{{C_{30} }}{{2 m_{2} }} + \frac{{C_{31} }}{{m_{1} }} + \frac{{C_{32} }}{{ m_{2} }}} \right), $$

$$ C_{35} = 1 - \left( {\frac{{C_{29} }}{{4 m_{1}^{2} }}e^{{2 m_{1} h\left( x \right)}} + \frac{{C_{30} }}{{4 m_{2}^{2} }}e^{{2 m_{2} h\left( x \right)}} + \frac{{C_{31} }}{{m_{1}^{2} }}e^{{ m_{1} h\left( x \right)}} + \frac{{C_{32} }}{{ m_{2}^{2} }}e^{{ m_{2} h\left( x \right)}} + C_{33} h\left( x \right)^{2} + C_{34} h\left( x \right)} \right), $$

$$ C_{{36}} = \frac{{SrScB_{6} P\left( x \right)^{2} P\left( t \right)}}{{2B_{5} m_{1}^{2} }}\left( {\frac{{C_{1}^{2} \frac{{dP\left( t \right)}}{{dt}}\left( {Ha^{2} + \frac{1}{{(1 - \varphi )^{{2.5}} }}} \right)\left( {Sc + \frac{{B_{4} }}{{B_{5} }}} \right)}}{{4m_{1}^{2} }} + C_{1} Ha^{2} \left( {C_{4} - \frac{{C_{5} }}{{m_{1} }}} \right) + \frac{{C_{1} C_{4} m_{1}^{2} }}{{(1 - \varphi )^{{2.5}} }}} \right), $$

$$ C_{{37}} = \frac{{SrScB_{6} P\left( x \right)^{2} P\left( t \right)}}{{2B_{5} m_{2}^{2} }}\left( {\frac{{C_{2}^{2} \frac{{dP\left( t \right)}}{{dt}}\left( {Ha^{2} + \frac{1}{{(1 - \varphi )^{{2.5}} }}} \right)\left( {Sc + \frac{{B_{4} }}{{B_{5} }}} \right)}}{{4m_{2}^{2} }} + C_{2} Ha^{2} \left( {C_{6} - \frac{{C_{7} }}{{m_{2} }}} \right) + \frac{{C_{2} C_{6} m_{2}^{2} }}{{(1 - \varphi )^{{2.5}} }}} \right), $$

$$ C_{38} = \frac{{2Sr Sc B_{6} Ha^{2} P\left( x \right)^{2} P\left( t \right)}}{{B_{5} m_{1}^{2} }}\left( {\frac{{2C_{1} C_{3} \frac{dP\left( t \right)}{{dt}} \left( {Sc + \frac{{B_{4} }}{{B_{5} }}} \right)}}{{4B_{5} m_{1}^{2} }} - \frac{{2C_{3} C_{5} }}{{m_{1} }} + C_{1} C_{8} + C_{3} C_{4} } \right), $$

$$ C_{39} = \frac{{2Sr Sc B_{6} Ha^{2} P\left( x \right)^{2} P\left( t \right)}}{{B_{5} m_{2}^{2} }}\left( {\frac{{2C_{2} C_{3} \frac{dP\left( t \right)}{{dt}} \left( {Sc + \frac{{B_{4} }}{{B_{5} }}} \right)}}{{4 B_{5} m_{2}^{2} }} - \frac{{2C_{3} C_{7} }}{{m_{2} }} + C_{2} C_{8} + C_{3} C_{6} } \right), $$

$$ C_{40} = \frac{{Sr Sc B_{6} P\left( x \right)^{2} P\left( t \right)C_{1} C_{5} \left( {Ha^{2} + \frac{{m_{1}^{2} }}{{(1 - \varphi )^{2.5} }}} \right)}}{{2B_{5} m_{1}^{2} }}, $$

$$ C_{41} = \frac{{Sr Sc B_{6} P\left( x \right)^{2} P\left( t \right)C_{2} C_{7} \left( {Ha^{2} + \frac{{m_{2}^{2} }}{{(1 - \varphi )^{2.5} }}} \right)}}{{2B_{5} m_{2}^{2} }}, $$

$$ C_{42} = \frac{{2Sr Sc B_{6} P\left( x \right)^{2} P\left( t \right)C_{3} C_{5} Ha^{2} }}{{B_{5} m_{1}^{2} }}, $$

$$ C_{43} = \frac{{2Sr Sc B_{6} P\left( x \right)^{2} P\left( t \right)C_{3} C_{7} Ha^{2} }}{{B_{5} m_{1}^{2} }}, $$

$$ C_{44} = \frac{{Sr Sc B_{6} P\left( x \right)^{2} P\left( t \right)\frac{dP\left( t \right)}{{dt}}\left( {Ha^{2} \left( { C_{3}^{2} + 2C_{1} C_{2} } \right) + \frac{{2C_{1} C_{2} }}{{(1 - \varphi )^{2.5} }}} \right)\left( {B_{4} + Sc} \right)}}{{12B_{5} }}, $$

$$ C_{{45}} = \frac{{B_{6} SrScP\left( x \right)^{2} P\left( t \right)}}{6}\left( {\frac{{\frac{{dP\left( t \right)}}{{dt}}\left( {B_{4} + Sc} \right)}}{{B_{5} }}\left( {\left( {\frac{{C_{1}^{2} }}{{m_{1} }} + \frac{{C_{2}^{2} }}{{m_{2} }}} \right)\left( {Ha^{2} + \frac{1}{{(1 - \varphi )^{{2.5}} }}} \right)} \right.\left. {\left( { + 4C_{3} Ha^{2} \left( {\frac{{C_{1} }}{{m_{1} }} + \frac{{C_{2} }}{{m_{2} }}} \right)} \right)} \right) + 2\left( {Ha^{2} + \frac{{m_{1} m_{2} }}{{(1 - \varphi )^{{2.5}} }}} \right)\left( {C_{1} C_{7} + C_{2} C_{5} } \right)} \right), $$

$$ \begin{aligned} C_{46} = & - \frac{{ SrScB_{6} \left( {B_{4} + Sc} \right) P\left( x \right)^{2} P\left( t \right) \frac{dP\left( t \right)}{{dt}}}}{{B_{5} }}\left( {\left( {\frac{{C_{1}^{2} e^{{2m_{1} h\left( x \right)}} }}{{2m_{1}^{2} }} + \frac{{C_{2}^{2} e^{{2m_{2} h\left( x \right)}} }}{{2m_{2}^{2} }}} \right)\left( {Ha^{2} + \frac{1}{{(1 - \varphi )^{2.5} }}} \right)} \right. \\ + 4 C_{3} Ha^{2} \left( {\frac{{C_{1} e^{{m_{1} h\left( x \right)}} }}{{m_{1}^{2} }} + \frac{{C_{2} e^{{m_{2} h\left( x \right)}} }}{{m_{2}^{2} }}} \right) + h\left( x \right)^{2} \left( {2 C_{1} C_{2} \left( {Ha^{2} + \frac{1}{{(1 - \varphi )^{2.5} }}} \right) + Ha^{2} C_{3}^{2} } \right) \\ \left. { - h\left( x \right)\left( {\left( {\frac{{C_{1}^{2} }}{{m_{1} }} + \frac{{C_{2}^{2} }}{{m_{2} }}} \right)\left( {Ha^{2} + \frac{1}{{(1 - \varphi )^{2.5} }}} \right) + 4 C_{3} Ha^{2} \left( {\frac{{C_{1} }}{{m_{1} }} + \frac{{C_{2} }}{{m_{2} }}} \right)} \right)} \right) \\ + \frac{{Sc\left( {1 - SrB_{4} } \right)}}{2} + 2Sr Sc B_{6} P\left( x \right)^{2} P\left( t \right)\left( {Ha^{2} \left( {C_{2} C_{4} + C_{1} C_{6} + C_{3} C_{8} } \right)} \right. \\ \left. { + \left( {\frac{{C_{1} C_{7} m_{1} + C_{2} C_{5} m_{1} + m_{1} m_{2} \left( {C_{1} C_{6} + C_{2} C_{4} } \right)}}{{(1 - \varphi )^{2.5} }}} \right)} \right), \\ \end{aligned} $$

$$ C_{47} = - \left( {2m_{1} C_{36} + 2m_{2} C_{37} + m_{1} C_{38} + m_{2} C_{39} + C_{44} + C_{41} + C_{42} + C_{43} } \right), $$

$$ \begin{aligned} C_{48} = & - \left( {C_{36} e^{{2m_{1} h\left( x \right)}} + C_{37} e^{{2m_{2} h\left( x \right)}} + C_{38} e^{{m_{1} h\left( x \right)}} + C_{39} e^{{m_{2} h\left( x \right)}} } \right. \\ + C_{40} h\left( x \right)e^{{2m_{1} h\left( x \right)}} + C_{41} h\left( x \right)e^{{2m_{2} h\left( x \right)}} + C_{42} h\left( x \right)e^{{m_{1} h\left( x \right)}} \\ \left. { + C_{43} h\left( x \right)e^{{m_{2} h\left( x \right)}} + C_{44} h\left( x \right)^{4} + C_{45} h\left( x \right)^{3} + C_{46} h\left( x \right)^{2} + C_{47} h\left( x \right)} \right). \\ \end{aligned} $$