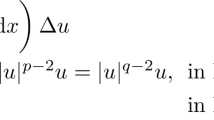Multiple positive solutions for a class of Kirchhoff type equations in $\mathbb{R}^{N}$

Abstract

In this paper, we study the following nonlinear Kirchhoff type equation:

$$\begin{aligned} - \biggl(a+b \int_{\mathbb{R}^{N}} \vert \nabla u \vert ^{2}\,dx \biggr) \triangle u+Vu=f(u)+h(x),\quad x\in\mathbb{R}^{N}, \end{aligned}$$

where a, b, V are positive constants, $N=2$ or 3. Under appropriate assumptions on f and h, we get that the equation has two positive solutions by using variational methods.

1 Introduction and main results

We consider the following nonlinear Kirchhoff type equation:

$$\begin{aligned} - \biggl(a+b \int_{\mathbb{R}^{N}} \vert \nabla u \vert ^{2}\,dx \biggr) \triangle u+Vu=f(u)+h(x),\quad x\in\mathbb{R}^{N}, \end{aligned}$$

(1.1)

where a, b, V are positive constants, $N=2$ or 3.

In recent years, the existence or multiplicity of solutions for the following Kirchhoff type equation

$$\begin{aligned} - \biggl(a+b \int_{\mathbb{R}^{N}} \vert \nabla u \vert ^{2}\,dx \biggr) \triangle u+V(x)u=f(x,u),\quad x\in\mathbb{R}^{N}, \end{aligned}$$

where a, b are positive constants, $N=1,2,3$, has been widely investigated by many authors, for example [1–6], etc. But in those papers, the nonlinearity f satisfies 3-superlinear growth at infinity, which assures the boundedness of any Palais-Smale sequence or Cerami sequence.

Very recently, Guo [7], Li and Ye [8], Liu and Guo [9], Tang and Chen [10] studied respectively the following equation:

$$\begin{aligned} - \biggl(a+b \int_{\mathbb{R}^{3}} \vert \nabla u \vert ^{2}\,dx \biggr) \triangle u+V(x)u=f(u),\quad x\in\mathbb{R}^{3}, \end{aligned}$$

where $a,b$ are positive constants, f only needs to satisfy superlinear growth at infinity. By using the Pohozaev equality, it is easy to obtain a bounded Palais-Smale sequence. Thus they obtained the existence of positive solution.

Inspired by [7–10], we study equation (1.1); in here, very weak conditions are assumed on f. Exactly, $f\in C(\mathbb {R}^{+},\mathbb{R})$ satisfies

$(f_{1})$ :

when $N=2$, there exists $p\in(2,+\infty)$ such that $\lim_{t\rightarrow+\infty}\frac{f(t)}{t^{p-1}}=0$; when $N=3$, $\lim_{t\rightarrow+\infty}\frac{f(t)}{t^{5}}=0$;

$(f_{2})$ :

$\lim_{t\rightarrow0^{+}}\frac{f(t)}{t}=m\in(-\infty,V)$;

$(f_{3})$ :

$\lim_{t\rightarrow+\infty}\frac{f(t)}{t}=+\infty$.

On h, we make the following hypotheses:

$(h_{1})$ :

$h\in L^{2}(\mathbb{R}^{N})\cap C^{1}(\mathbb{R}^{N})$ is nonnegative and $h\not\equiv0$;

$(h_{2})$ :

when $N=2$, $0\leq(\nabla h(x),x)\in L^{2}(\mathbb{R}^{2})$; when $N=3$, $(\nabla h(x),x)\in L^{2}(\mathbb{R}^{3})$;

$(h_{3})$ :

h is radially symmetric.

By using Ekeland’s variational principle [11] and Struwe’s monotonicity trick [12], we get the following.

Theorem 1.1

Suppose that $(f_{1})$-$(f_{3})$ and $(h_{1})$-$(h_{3})$ hold. Then there exists $m_{0}>0$ such that, when $(\int_{\mathbb{R}^{N}}h^{2}\,dx )^{\frac{1}{2}}< m_{0}$, equation (1.1) has two positive solutions.

When $f(t)<0$, by $(f_{2})$ and $(f_{3})$, there exists $l>0$ such that $f(t)+lt\geq0$ for all $t\geq0$. Thus equation (1.1) is equivalent to the following equation:

$$\begin{aligned} - \biggl(a+b \int_{\mathbb{R}^{N}} \vert \nabla u \vert ^{2}\,dx \biggr) \triangle u+Wu=k(u)+h(x),\quad x\in\mathbb{R}^{N}, \end{aligned}$$

(1.2)

where $W=V+l>0$ and $k(t)=f(t)+lt\in C(\mathbb{R}^{+},\mathbb{R}^{+})$ satisfies

$(k_{1})$ :

when $N=2$, there exists $p\in(2,+\infty)$ such that $\lim_{t\rightarrow+\infty}\frac{k(t)}{t^{p-1}}=0$; when $N=3$, $\lim_{t\rightarrow+\infty}\frac{k(t)}{t^{5}}=0$;

$(k_{2})$ :

$\lim_{t\rightarrow0^{+}}\frac{k(t)}{t}=m+l:=d\in[0,W)$;

$(k_{3})$ :

$\lim_{t\rightarrow+\infty}\frac{k(t)}{t}=+\infty$.

Hence in order to prove Theorem 1.1, we only need to prove the following.

Theorem 1.2

Suppose that $(k_{1})$-$(k_{3})$ and $(h_{1})$-$(h_{3})$ hold. Then there exists $m_{0}>0$ such that when $(\int_{\mathbb{R}^{N}}h^{2}\,dx )^{\frac {1}{2}}< m_{0}$, equation (1.2) has two positive solutions.

Remark 1.3

Under hypotheses on k, we are not able to obtain directly the boundedness of the Palais-Smale sequences. Inspired by Jeanjean’s idea in [13] and [14], we will use an indirect approach, i.e., Struwe’s monotonicity trick developed by Jeanjean. It is worth pointing out that comparing with $N=3$, when $N=2$, it is more complex to prove the boundedness of the Palais-Smale sequences, which will be seen in Lemma 3.8.

2 Preliminaries

From now on, we will use the following notations.

• $E:=\{u\in H^{1}(\mathbb{R}^{N}):u(x)=u( \vert x \vert )\}$ is the usual Sobolev space endowed with the norm

  $$\begin{aligned} \Vert u \Vert = \biggl( \int_{\mathbb{R}^{N}} \vert \nabla u \vert ^{2}+u^{2}\,dx \biggr)^{\frac{1}{2}}. \end{aligned}$$

• $D^{1,2}(\mathbb{R}^{N})$ is completion of $C_{0}^{\infty}(\mathbb {R}^{N})$ with respect to the norm

  $$\begin{aligned} \Vert u \Vert _{D^{1,2}(\mathbb{R}^{N})}= \biggl( \int_{\mathbb {R}^{N}} \vert \nabla u \vert ^{2}\,dx \biggr)^{\frac{1}{2}}. \end{aligned}$$

• For any $1\leq p<\infty$, $L^{p}(\mathbb{R}^{N})$ denotes the Lebesgue space and its norm is denoted by

  $$\begin{aligned} \vert u \vert _{p}= \biggl( \int_{\mathbb{R}^{N}} \vert u \vert ^{p}\,dx \biggr)^{\frac{1}{p}}. \end{aligned}$$

• $\langle\cdot,\cdot\rangle$ denotes the action of dual, $(\cdot,\cdot)$ denotes the inner product in $\mathbb{R}^{N}$.

• C, $C_{i}$ denote various positive constants.

Since we are looking for positive solution, we may assume that $k(t)=0$ for all $t<0$. Under the assumptions on k and h, it is obvious that the functional $I:E\rightarrow\mathbb{R}$ defined by

$$\begin{aligned} I(u)=\frac{a}{2} \int_{\mathbb{R}^{N}} \vert \nabla u \vert ^{2}\,dx+ \frac{b}{4} \biggl( \int_{\mathbb{R}^{N}} \vert \nabla u \vert ^{2}\,dx \biggr)^{2}+\frac{W}{2} \int_{\mathbb{R}^{N}}u^{2}\,dx- \int_{\mathbb {R}^{N}}K(u)\,dx- \int_{\mathbb{R}^{N}}hu\,dx \end{aligned}$$

is of class $C^{1}$, where $K(t)=\int_{0}^{t}k(s)\,ds$ and

$$\begin{aligned} \bigl\langle I'(u),v\bigr\rangle =& \biggl(a+b \int_{\mathbb{R}^{N}} \vert \nabla u \vert ^{2}\,dx \biggr) \int_{\mathbb{R}^{N}}(\nabla u,\nabla v)\,dx+W \int _{\mathbb{R}^{N}}uv\,dx- \int_{\mathbb{R}^{N}}k(u)v\,dx \\ &{}- \int_{\mathbb{R}^{N}}hv\,dx, \end{aligned}$$

for all $u, v\in E$. As is well known, the weak solution of equation (1.2) is the critical point of I in E.

3 Proof of the main results

Next lemma can be viewed as a generalization of Struwe’s monotonicity trick [12] and is the main tool for obtaining a bounded Palais-Smale sequence.

Lemma 3.1

(see [13] or [14])

Let X be a Banach space equipped with a norm $\Vert \cdot \Vert _{X}$, and let $J\subset\mathbb{R}^{+}$ be an interval. We consider a family $\{\Phi_{\mu}\}_{\mu\in J}$ of $C^{1}$-functionals on X of the form

$$\Phi_{\mu}(u)=A(u)-\mu B(u),\quad\forall\mu\in J, $$

where $B(u)\geq0$ for all $u\in X$ and such that either $A(u)\rightarrow +\infty$ or $B(u)\rightarrow+\infty$ as $\Vert u \Vert _{X}\rightarrow+\infty$. We assume that there are two points $v_{1}$, $v_{2}$ in X such that

$$c_{\mu}=\inf_{\gamma\in\Gamma}\max_{t\in[0,1]} \Phi_{\mu}\bigl(\gamma(t)\bigr)>\max\bigl\{ \Phi_{\mu}(v_{1}), \Phi_{\mu}(v_{2})\bigr\} , $$

where

$$\Gamma=\bigl\{ \gamma\in C\bigl([0,1],X\bigr):\gamma(0)=v_{1}, \gamma(1)=v_{2}\bigr\} . $$

Then, for almost every $\mu\in J$, there is a bounded $(PS)_{c_{\mu}}$ sequence for $\Phi_{\mu}$, that is, there exists a sequence $\{u_{n}\}\subset X$ such that

• (1) $\{u_{n}\}$ is bounded in X,

• (2) $\Phi_{\mu}(u_{n})\rightarrow c_{\mu}$,

• (3) $\Phi'_{\mu}(u_{n})\rightarrow0$ in $X^{*}$, where $X^{*}$ is the dual of X.

Remark 3.2

In [13], it is also proved that, under the assumptions of Lemma 3.1, the map $\mu\mapsto c_{\mu}$ is left-continuous.

In the paper, we set $X:=E$, $\Vert \cdot \Vert _{X}:= \Vert \cdot \Vert$ and $J:=[\frac{1}{2},1]$. Let us define $I_{\mu}:E\rightarrow\mathbb{R}$ by $I_{\mu}(u)=A(u)-\mu B(u)$, where

$$\begin{aligned}& A(u)=\frac{a}{2} \int_{\mathbb{R}^{N}} \vert \nabla u \vert ^{2}\,dx+ \frac{b}{4} \biggl( \int_{\mathbb{R}^{N}} \vert \nabla u \vert ^{2}\,dx \biggr)^{2}+\frac{W}{2} \int_{\mathbb{R}^{N}}u^{2}\,dx- \int_{\mathbb{R}^{N}}hu\,dx, \\& B(u)= \int_{\mathbb{R}^{N}}K(u)\,dx. \end{aligned}$$

Then $I_{1}(u)=I(u)$. By $(k_{1})$-$(k_{3})$ and $(h_{1})$, it is obvious that $I_{\mu}\in C^{1}(E,\mathbb{R})$, $B(u)\geq0$ for all $u\in E$ and $A(u)\geq\frac{\min\{a,W\}}{2} \Vert u \Vert ^{2}-C \vert h \vert _{2} \Vert u \Vert \rightarrow+\infty$ as $\Vert u \Vert \rightarrow+\infty$.

Lemma 3.3

Assume that $(k_{1})$-$(k_{3})$ and $(h_{1})$ hold. Then there exist $\rho >0$, $\alpha>0$ and $m_{0}>0$ such that $I_{\mu}(u)\vert_{\Vert u\Vert=\rho}\geq\alpha$ for all h satisfying $\vert h\vert_{2}< m_{0}$ and for all $\mu\in J$.

Proof

First, we consider $N=2$. It follows from $(k_{1})$ and $(k_{2})$ that, for all $t\in\mathbb{R}$, we have

$$\begin{aligned} \bigl\vert K(t) \bigr\vert \leq\frac{W+d}{4} \vert t \vert ^{2}+C \vert t \vert ^{p}. \end{aligned}$$

(3.1)

By (3.1), the Hölder inequality and the Sobolev inequality, for all $\mu\in J$ and $u\in E$, one has

$$\begin{aligned} I_{\mu}(u) \geq&\frac{a}{2} \int_{\mathbb{R}^{2}} \vert \nabla u \vert ^{2}\,dx+ \frac{W}{2} \int_{\mathbb{R}^{2}}u^{2}\,dx- \int_{\mathbb {R}^{2}}K(u)\,dx- \int_{\mathbb{R}^{2}}hu\,dx \\ \geq&\frac{a}{2} \int_{\mathbb{R}^{2}} \vert \nabla u \vert ^{2}\,dx+ \frac{W}{2} \int_{\mathbb{R}^{2}}u^{2}\,dx-\frac{W+d}{4} \int_{\mathbb {R}^{2}}u^{2}\,dx-C \int_{\mathbb{R}^{2}} \vert u \vert ^{p}\,dx- \vert h \vert _{2} \vert u \vert _{2} \\ \geq&\frac{\min\{2a,W-d\}}{4} \Vert u \Vert ^{2}-C_{1} \Vert u \Vert ^{p}-C_{2} \vert h \vert _{2} \Vert u \Vert \\ =& \Vert u \Vert \biggl(\frac{\min\{2a,W-d\}}{4} \Vert u \Vert -C_{1} \Vert u \Vert ^{p-1}-C_{2} \vert h \vert _{2} \biggr). \end{aligned}$$

Let $g_{1}(t)=\frac{\min\{2a,W-d\}}{4}t-C_{1}t^{p-1}$ for $t\geq0$. Since $p>2$, we know that there exists a constant $\rho>0$ such that $\max_{t\geq 0}g_{1}(t)=g_{1}(\rho)>0$. Choose $m_{0}=\frac{1}{2C_{2}}g_{1}(\rho)$, then there exists $\alpha>0$ such that $I_{\mu}(u)\vert_{\Vert u\Vert=\rho}\geq\alpha$ for all h satisfying $\vert h\vert_{2}< m_{0}$.

Next when $N=3$, it follows from $(k_{1})$ and $(k_{2})$ that, for all $t\in\mathbb{R}$, we have

$$\begin{aligned} \bigl\vert K(t) \bigr\vert \leq\frac{W+d}{4} \vert t \vert ^{2}+C \vert t \vert ^{6}. \end{aligned}$$

(3.2)

By (3.2), the Hölder inequality and the Sobolev inequality, for all $\mu\in J$ and $u\in E$, one has

$$\begin{aligned} I_{\mu}(u) \geq&\frac{a}{2} \int_{\mathbb{R}^{3}} \vert \nabla u \vert ^{2}\,dx+ \frac{W}{2} \int_{\mathbb{R}^{3}}u^{2}\,dx- \int_{\mathbb {R}^{3}}K(u)\,dx- \int_{\mathbb{R}^{3}}hu\,dx \\ \geq&\frac{a}{2} \int_{\mathbb{R}^{3}} \vert \nabla u \vert ^{2}\,dx+ \frac{W}{2} \int_{\mathbb{R}^{3}}u^{2}\,dx-\frac{W+d}{4} \int_{\mathbb {R}^{3}}u^{2}\,dx-C \int_{\mathbb{R}^{3}} \vert u \vert ^{6}\,dx- \vert h \vert _{2} \vert u \vert _{2} \\ \geq&\frac{\min\{2a,W-d\}}{4} \Vert u \Vert ^{2}-C_{3} \Vert u \Vert ^{6}-C_{4} \vert h \vert _{2} \Vert u \Vert \\ =& \Vert u \Vert \biggl(\frac{\min\{2a,W-d\}}{4} \Vert u \Vert -C_{3} \Vert u \Vert ^{5}-C_{4} \vert h \vert _{2} \biggr). \end{aligned}$$

Let $g_{2}(t)=\frac{\min\{2a,W-d\}}{4}t-C_{3}t^{5}$ for $t\geq0$, we know that there exists a constant $\rho>0$ such that $\max_{t\geq0}g_{2}(t)=g_{2}(\rho)>0$. Choose $m_{0}=\frac {1}{2C_{4}}g_{2}(\rho)$, then there exists $\alpha>0$ such that $I_{\mu}(u)\vert_{\Vert u\Vert =\rho}\geq\alpha$ for all h satisfying $\vert h\vert_{2}< m_{0}$. □

Lemma 3.4

Assume that $(k_{1})$-$(k_{3})$ and $(h_{1})$ hold. Then $-\infty< c:=\inf\{ I(u): \Vert u \Vert \leq\rho\}<0$, where ρ is given by Lemma 3.3.

Proof

Since $h\in L^{2}(\mathbb{R}^{N})$ and $h\not\equiv0$, then for $\varepsilon=\frac{ \vert h \vert _{2}}{2}$, there exists $\phi \in C^{\infty}_{0}(\mathbb{R}^{N})$ such that $\vert h-\phi \vert _{2}<\varepsilon$. Thus

$$\begin{aligned} \int_{\mathbb{R}^{N}}\bigl(h^{2}-h\phi\bigr)\,dx\leq \int_{\mathbb {R}^{N}} \bigl\vert h^{2}-h\phi \bigr\vert \,dx \leq \vert h-\phi \vert _{2} \vert h \vert _{2}< \varepsilon \vert h \vert _{2}, \end{aligned}$$

and then

$$\begin{aligned} \int_{\mathbb{R}^{N}}h\phi \,dx\geq \vert h \vert _{2}^{2}- \varepsilon \vert h \vert _{2}=\frac{ \vert h \vert _{2}^{2}}{2}>0. \end{aligned}$$

Hence

$$\begin{aligned} I(t\phi)\leq\frac{at^{2}}{2} \int_{\mathbb{R}^{N}} \vert \nabla\phi \vert ^{2}\,dx+ \frac{bt^{4}}{4} \biggl( \int_{\mathbb{R}^{N}} \vert \nabla\phi \vert ^{2}\,dx \biggr)^{2}+\frac{Wt^{2}}{2} \int_{\mathbb {R}^{N}}\phi^{2}\,dx-t \int_{\mathbb{R}^{N}}h\phi \,dx< 0 \end{aligned}$$

for $t>0$ small enough. Then we get $c=\inf\{I(u): \Vert u \Vert \leq\rho\}<0$. $c>-\infty$ is obvious. □

In order to prove the compactness, we define $g(t)=k(t)-dt$, $\forall t\in\mathbb{R}$. Then, by $(k_{1})$ and $(k_{2})$, we get that

$$\begin{aligned} \lim_{t\rightarrow0^{+}}\frac{g(t)}{t}=0, \end{aligned}$$

(3.3)

and when $N=2$,

$$\begin{aligned} \lim_{t\rightarrow+\infty}\frac{g(t)}{t^{p-1}}=0, \end{aligned}$$

(3.4)

when $N=3$,

$$\begin{aligned} \lim_{t\rightarrow+\infty}\frac{g(t)}{t^{5}}=0. \end{aligned}$$

(3.5)

Lemma 3.5

Suppose that $(k_{1})$-$(k_{3})$, $(h_{1})$ and $(h_{3})$ hold. Assume that $\{ u_{n}\}\subset E$ is a bounded Palais-Smale sequence of $I_{\mu}$ for each $\mu\in J$. Then $\{u_{n}\}$ has a convergent subsequence in E.

Proof

Since $\{u_{n}\}$ is bounded in E and $E\hookrightarrow L^{s}(\mathbb{R}^{3})$, $\forall s\in(2,6)$, $E\hookrightarrow L^{s}(\mathbb {R}^{2})$, $\forall s\in(2,+\infty)$ are compact (see [15]), up to a subsequence, we can assume that there exists $u\in E$ such that $u_{n}\rightharpoonup u$ in E, $u_{n}\rightarrow u$ in $L^{s}(\mathbb{R}^{3})$, $\forall s\in(2,6)$, $u_{n}\rightarrow u$ in $L^{s}(\mathbb{R}^{2})$, $\forall s\in(2,+\infty)$, $u_{n}(x)\rightarrow u(x)$ a.e. in $\mathbb{R}^{N}$.

By (3.3) and (3.4), for any $\varepsilon>0$, we have

$$\begin{aligned} \bigl\vert g(t) \bigr\vert \leq\varepsilon \vert t \vert +C_{\varepsilon} \vert t \vert ^{p-1},\quad \forall t\geq0. \end{aligned}$$

(3.6)

Then, by (3.6) and the Hölder inequality, one has

$$\begin{aligned}& \biggl\vert \int_{\mathbb{R}^{2}}g(u_{n}) (u_{n}-u)\,dx \biggr\vert \\& \quad\leq\varepsilon \int_{\mathbb{R}^{2}} \vert u_{n} \vert \vert u_{n}-u \vert \,dx+C_{\varepsilon}\int_{\mathbb{R}^{2}} \vert u_{n} \vert ^{p-1} \vert u_{n}-u \vert \,dx \\& \quad\leq\varepsilon \vert u_{n} \vert _{2} \vert u_{n}-u \vert _{2}+C_{\varepsilon}\biggl( \int_{\mathbb{R}^{2}} \vert u_{n} \vert ^{p}\,dx \biggr)^{\frac{p-1}{p}} \vert u_{n}-u \vert _{p} \\& \quad\leq C\varepsilon+o_{n}(1). \end{aligned}$$

Similarly, we can obtain that

$$\begin{aligned} \biggl\vert \int_{\mathbb{R}^{2}}g(u) (u_{n}-u)\,dx \biggr\vert =o_{n}(1). \end{aligned}$$

By (3.3) and (3.5), for any $\varepsilon>0$, we have

$$\begin{aligned} \bigl\vert g(t) \bigr\vert \leq\varepsilon\bigl( \vert t \vert + \vert t \vert ^{5}\bigr)+C_{\varepsilon} \vert t \vert ^{3},\quad \forall t\geq0. \end{aligned}$$

(3.7)

Hence, by (3.7) and the Hölder inequality, one has

$$\begin{aligned}& \biggl\vert \int_{\mathbb{R}^{3}}g(u_{n}) (u_{n}-u)\,dx \biggr\vert \\& \quad\leq\varepsilon \int_{\mathbb{R}^{3}} \vert u_{n} \vert \vert u_{n}-u \vert \,dx+\varepsilon \int_{\mathbb{R}^{3}} \vert u_{n} \vert ^{5} \vert u_{n}-u \vert \,dx+C_{\varepsilon}\int _{\mathbb{R}^{3}} \vert u_{n} \vert ^{3} \vert u_{n}-u \vert \,dx \\& \quad\leq\varepsilon \vert u_{n} \vert _{2} \vert u_{n}-u \vert _{2}+\varepsilon \biggl( \int_{\mathbb{R}^{3}} \vert u_{n} \vert ^{6}\,dx \biggr)^{\frac{5}{6}} \vert u_{n}-u \vert _{6} +C_{\varepsilon}\biggl( \int_{\mathbb{R}^{3}} \vert u_{n} \vert ^{\frac {9}{2}}\,dx \biggr)^{\frac{2}{3}} \vert u_{n}-u \vert _{3} \\& \quad\leq C\varepsilon+o_{n}(1). \end{aligned}$$

Similarly, we can obtain that

$$\begin{aligned} \biggl\vert \int_{\mathbb{R}^{3}}g(u) (u_{n}-u)\,dx \biggr\vert =o_{n}(1). \end{aligned}$$

Hence when $N=2$ or 3, one has

$$\begin{aligned} \biggl\vert \int_{\mathbb{R}^{N}} \bigl(g(u_{n})-g(u) \bigr) (u_{n}-u)\,dx \biggr\vert =o_{n}(1). \end{aligned}$$

It is clear that

$$\bigl\langle I'_{\mu}(u_{n})-I'_{\mu}(u),u_{n}-u \bigr\rangle =o_{n}(1) $$

and

$$b \biggl( \int_{\mathbb{R}^{N}}\bigl( \vert \nabla u \vert ^{2}- \vert \nabla u_{n} \vert ^{2}\bigr)\,dx \biggr) \int_{\mathbb{R}^{N}}\bigl(\nabla u,\nabla(u_{n}-u) \bigr)\,dx=o_{n}(1). $$

Note that

$$\begin{aligned} \bigl\langle I_{\mu}'(u_{n})-I'_{\mu}(u),u_{n}-u \bigr\rangle =& \biggl(a+b \int_{\mathbb {R}^{N}} \vert \nabla u_{n} \vert ^{2}\,dx \biggr) \int_{\mathbb {R}^{N}} \bigl\vert \nabla(u_{n}-u) \bigr\vert ^{2}\,dx \\ &{}+(W-\mu d) \int_{\mathbb{R}^{N}} \vert u_{n}-u \vert ^{2}\,dx \\ &{}-b \biggl( \int_{\mathbb{R}^{N}}\bigl( \vert \nabla u \vert ^{2}- \vert \nabla u_{n} \vert ^{2}\bigr)\,dx \biggr) \int_{\mathbb{R}^{N}}\bigl(\nabla u,\nabla(u_{n}-u)\bigr)\,dx \\ &{}-\mu \int_{\mathbb{R}^{N}} \bigl(g(u_{n})-g(u) \bigr) (u_{n}-u)\,dx \\ \geq& \min\{a,W-\mu d\} \Vert u_{n}-u \Vert ^{2} \\ &{}-b \biggl( \int_{\mathbb{R}^{N}}\bigl( \vert \nabla u \vert ^{2}- \vert \nabla u_{n} \vert ^{2}\bigr)\,dx \biggr) \int_{\mathbb{R}^{N}}\bigl(\nabla u,\nabla(u_{n}-u)\bigr)\,dx \\ &{}-\mu \int_{\mathbb{R}^{N}} \bigl(g(u_{n})-g(u) \bigr) (u_{n}-u)\,dx. \end{aligned}$$

Therefore we get that $\Vert u_{n}-u \Vert \rightarrow0$ as $n\rightarrow\infty$. □

Proof of the first solution of Theorem 1.2

By Lemma 3.4 and Ekeland’s variational principle [11], there exists a sequence $\{u_{n}\}\subset E$ such that $\Vert u_{n} \Vert \leq\rho$, $I(u_{n})\rightarrow c$ and $I'(u_{n})\rightarrow 0$ as $n\rightarrow\infty$. From Lemma 3.5 with $\mu=1$, there exists $u_{0}\in E$ such that $u_{n}\rightarrow u_{0}$ in E and then $I'(u_{0})=0$ and $I(u_{0})=c<0$. Put $u_{0}^{-}:=\max\{-u_{0},0\}$, one has

$$ \begin{aligned}[b] 0&=\bigl\langle I'(u_{0}),u_{0}^{-} \bigr\rangle \\ &=-a \int_{\mathbb{R}^{N}} \bigl\vert \nabla u_{0}^{-} \bigr\vert ^{2}\,dx-b \int _{\mathbb{R}^{N}} \vert \nabla u_{0} \vert ^{2}\,dx \int_{\mathbb {R}^{N}} \bigl\vert \nabla u_{0}^{-} \bigr\vert ^{2}\,dx-W \int_{\mathbb{R}^{N}} \bigl\vert u_{0}^{-} \bigr\vert ^{2}\,dx \\ &\quad{}- \int_{\mathbb{R}^{N}}hu_{0}^{-}dx, \end{aligned} $$

(3.8)

which implies that $u_{0}^{-}=0$ and then $u_{0}\geq0$. By the strong maximum principle, we get $u_{0}>0$. □

For ρ and α in Lemma 3.3, we have following result.

Lemma 3.6

Assume that $(k_{1})$-$(k_{3})$ and $(h_{1})$ hold. Then

$(*)$ :

$\exists v_{2}\in E$ with $\Vert v_{2} \Vert >\rho$ such that $I_{\mu}(v_{2})<0$, $\forall\mu\in J$.

$(**)$ :

$c_{\mu}=\inf_{\gamma\in\Gamma}\max_{t\in[0,1]}I_{\mu}(\gamma (t))>\max\{I_{\mu}(0),I_{\mu}(v_{2})\}$, $\forall\mu\in J$, where

$$\begin{aligned} \Gamma=\bigl\{ \gamma\in C\bigl([0,1],E\bigr):\gamma(0)=0,\gamma(1)=v_{2} \bigr\} . \end{aligned}$$

Proof

It follows from $(k_{3})$ that, for any $L>0$, there exists $C_{L}>0$ such that, for all $t\geq0$, one has

$$ K(t)\geq Lt^{2}-C_{L}. $$

(3.9)

Fix $0\leq w\in C_{0}^{\infty}(\mathbb{R}^{N})$ with $\operatorname {supp}w\subset B_{1}:=\{x\in\mathbb{R}^{N}: \vert x \vert <1\}$ and $w\not\equiv0$. Define $w_{t}(x)=tw(\frac{x}{t^{2}})$ for $t>0$, then

$$\begin{aligned} \operatorname{supp}w_{t}=\bigl\{ t^{2}y: y\in\operatorname{supp}w\bigr\} . \end{aligned}$$

By direct computation, we have

$$\begin{aligned}& \int_{\mathbb{R}^{N}} \vert \nabla w_{t} \vert ^{2}\,dx=t^{2N-2} \int _{\mathbb{R}^{N}} \vert \nabla w \vert ^{2}\,dx, \\& \int_{\mathbb{R}^{N}}w_{t}^{2}\,dx=t^{2N+2} \int_{\mathbb{R}^{N}}w^{2}\,dx \end{aligned}$$

and, by (3.9),

$$\begin{aligned} \int_{\mathbb{R}^{N}}K(w_{t})\,dx =& \int_{\operatorname{supp}w_{t}}K(w_{t})\,dx \\ \geq& L \int_{\operatorname{supp}w_{t}}w_{t}^{2}\,dx-C_{L} \int_{\operatorname{supp}w_{t}}\,dx \\ \geq& Lt^{2N+2} \int_{\operatorname{supp}w}w^{2}\,dx-C_{L} \int_{\{t^{2}y:y\in B_{1}\} }\,dx \\ =&Lt^{2N+2} \int_{\mathbb{R}^{N}}w^{2}\,dx-C_{L}Ct^{2N}. \end{aligned}$$

Therefore

$$\begin{aligned}& I_{\mu}(w_{t}) \\& \quad =\frac{a}{2} \int_{\mathbb{R}^{N}} \vert \nabla w_{t} \vert ^{2}\,dx+\frac{b}{4} \biggl( \int_{\mathbb{R}^{N}} \vert \nabla w_{t} \vert ^{2}\,dx \biggr)^{2}+\frac{W}{2} \int_{\mathbb{R}^{N}}w_{t}^{2}\,dx\\& \qquad {}-\mu \int _{R^{N}}K(w_{t})\,dx- \int_{\mathbb{R}^{N}}hw_{t}\,dx \\& \quad \leq\frac{at^{2N-2}}{2} \int_{\mathbb{R}^{N}} \vert \nabla w \vert ^{2}\,dx+ \frac{bt^{4N-4}}{4} \biggl( \int_{\mathbb{R}^{N}} \vert \nabla w \vert ^{2}\,dx \biggr)^{2}+\frac{Wt^{2N+2}}{2} \int_{\mathbb {R}^{N}}w^{2}\,dx \\& \qquad {}-\frac{Lt^{2N+2}}{2} \int_{\mathbb{R}^{N}}w^{2}\,dx+ C_{L}Ct^{2N} \end{aligned}$$

for all $\mu\in J$. When $N=2$, we choose $L=2W$. When $N=3$, we choose $L=2W+b\frac{ (\int_{\mathbb{R}^{N}} \vert \nabla w \vert ^{2}\,dx )^{2}}{\int_{\mathbb{R}^{N}}w^{2}\,dx}$. Then $I_{\mu}(w_{t})\rightarrow -\infty$ as $t\rightarrow+\infty$. Hence there exists $t'>0$ such that $v_{2}:=w_{t'}$ with $\Vert v_{2} \Vert >\rho$ and $I_{\mu}(v_{2})<0$, $\forall\mu\in J$. This completes the proof of $(*)$.

By Lemma 3.3 and the definition of $c_{\mu}$, for all $\mu\in J$, we have

$$0< \alpha\leq c_{1}\leq c_{\mu}\leq c_{\frac{1}{2}}\leq\max _{t\in [0,1]}I_{\frac{1}{2}}(tv_{2})< +\infty. $$

Therefore, by $I_{\mu}(0)=0$ and $I_{\mu}(v_{2})<0$, we obtain the proof of $(**)$. □

So far we have verified all the conditions of Lemma 3.1. Then there exists $\{\mu_{j}\}\subset J$ such that

• (i) $\mu_{j}\rightarrow1^{-}$ as $j\rightarrow\infty$, $\{u_{n}^{j}\}$ is bounded in E;

• (ii) $I_{\mu_{j}}(u_{n}^{j})\rightarrow c_{\mu_{j}}$ as $n\rightarrow \infty$;

• (iii) $I'_{\mu_{j}}(u_{n}^{j})\rightarrow0$ as $n\rightarrow\infty$.

Using (i)-(iii) and Lemma 3.5, there exists $u_{j}\in E$ such that $u_{n}^{j}\rightarrow u_{j}$ in E as $n\rightarrow\infty$ and then $I_{\mu_{j}}(u_{j})=c_{\mu_{j}}$ and $I'_{\mu_{j}}(u_{j})=0$. Hence, from $I_{\mu_{j}}(u_{j})=c_{\mu_{j}}$ and $\langle I'_{\mu _{j}}(u_{j}),u_{j}\rangle=0$, we get respectively

$$\begin{aligned}& \begin{aligned}[b] &\frac{a}{2} \int_{\mathbb{R}^{N}} \vert \nabla u_{j} \vert ^{2}\,dx+\frac{b}{4} \biggl( \int_{\mathbb{R}^{N}} \vert \nabla u_{j} \vert ^{2}\,dx \biggr)^{2}+\frac{W}{2} \int_{\mathbb{R}^{N}}u_{j}^{2}\,dx \\ &\quad-\mu_{j} \int _{\mathbb{R}^{N}}K(u_{j})\,dx- \int_{\mathbb{R}^{N}}hu_{j}\,dx=c_{\mu_{j}}, \end{aligned} \end{aligned}$$

(3.10)

$$\begin{aligned}& \begin{aligned}[b] & a \int_{\mathbb{R}^{N}} \vert \nabla u_{j} \vert ^{2}\,dx+b \biggl( \int _{\mathbb{R}^{N}} \vert \nabla u_{j} \vert ^{2}\,dx \biggr)^{2}+W \int _{\mathbb{R}^{N}}u_{j}^{2}\,dx \\ &\quad-\mu_{j} \int_{\mathbb{R}^{N}}k(u_{j})u_{j}\,dx- \int_{\mathbb {R}^{N}}hu_{j}\,dx=0. \end{aligned} \end{aligned}$$

(3.11)

Next, for obtaining $\{u_{j}\}$ is bounded in E, we need the following lemma (Pohozaev type identity). The proof is similar to Lemma 2.6 in [16], and we omit its proof in here.

Lemma 3.7

Suppose that $(h_{1})$ and $(h_{2})$ hold. If $I'_{\mu}(u)=0$, we have

$$ \begin{aligned} &\frac{a(N-2)}{2} \int_{\mathbb{R}^{N}} \vert \nabla u \vert ^{2}\,dx+ \frac{b(N-2)}{2} \biggl( \int_{\mathbb{R}^{N}} \vert \nabla u \vert ^{2}\,dx \biggr)^{2}+\frac{NW}{2} \int_{\mathbb{R}^{N}}u^{2}\,dx \\ &\quad{}-N\mu \int_{\mathbb{R}^{N}}K(u)\,dx-N \int_{\mathbb{R}^{N}}hu\,dx- \int _{\mathbb{R}^{N}}\bigl(\nabla h(x),x\bigr)u\,dx=0. \end{aligned} $$

Since $I'_{\mu_{j}}(u_{j})=0$, by Lemma 3.7, we get that

$$ \begin{aligned}[b] &\frac{a(N-2)}{2} \int_{\mathbb{R}^{N}} \vert \nabla u_{j} \vert ^{2}\,dx+\frac{b(N-2)}{2} \biggl( \int_{\mathbb{R}^{N}} \vert \nabla u_{j} \vert ^{2}\,dx \biggr)^{2}+\frac{NW}{2} \int_{\mathbb{R}^{N}}u_{j}^{2}\,dx \\ &\quad{}-N\mu_{j} \int_{\mathbb{R}^{N}}K(u_{j})\,dx-N \int_{\mathbb {R}^{N}}hu_{j}\,dx- \int_{\mathbb{R}^{N}}\bigl(\nabla h(x),x\bigr)u_{j}\,dx=0. \end{aligned} $$

(3.12)

Lemma 3.8

Assume that $(k_{1})$-$(k_{3})$ and $(h_{1})$-$(h_{3})$ hold. Then $\{u_{j}\}$ is bounded in E.

Proof

It follows from (3.10) and (3.12) that

$$ a \int_{\mathbb{R}^{N}} \vert \nabla u_{j} \vert ^{2}\,dx+\frac {b(4-N)}{4} \biggl( \int_{\mathbb{R}^{N}} \vert \nabla u_{j} \vert ^{2}\,dx \biggr)^{2}+ \int_{\mathbb{R}^{N}}\bigl(\nabla h(x),x\bigr)u_{j}\,dx=Nc_{\mu_{j}}. $$

(3.13)

Be similar to (3.8), by $I'_{\mu_{j}}(u_{j})=0$, we obtain $u_{j}\geq0$.

Firstly, we consider $N=2$. From (3.13) and $c_{\mu_{j}}\leq c_{\frac{1}{2}}$, we get

$$ \begin{aligned}[b] a \int_{\mathbb{R}^{2}} \vert \nabla u_{j} \vert ^{2}\,dx &\leq a \int_{\mathbb{R}^{2}} \vert \nabla u_{j} \vert ^{2}\,dx+\frac {b}{2} \biggl( \int_{\mathbb{R}^{2}} \vert \nabla u_{j} \vert ^{2}\,dx \biggr)^{2} \\ &\quad{}-2c_{\mu_{j}}+2c_{\mu_{j}} \\ &=- \int_{\mathbb{R}^{2}}\bigl(\nabla h(x),x\bigr)u_{j}\,dx+2c_{\mu_{j}}. \end{aligned} $$

(3.14)

Since $(\nabla h(x),x)\geq0$, by (3.14) and $u_{j}\geq0$, one has $\{\int_{\mathbb{R}^{2}} \vert \nabla u_{j} \vert ^{2}\,dx\}$ is bounded. Next we prove $\{\int_{\mathbb{R}^{2}}u_{j}^{2}\,dx\}$ is bounded. Inspired by [14], we suppose by contradiction that $\lambda _{j}:= \vert u_{j} \vert _{2}\rightarrow+\infty$. Define $w_{j}:=u_{j}(\lambda_{j}x)$, then

$$ \int_{\mathbb{R}^{2}} \vert \nabla w_{j} \vert ^{2}\,dx= \int_{\mathbb {R}^{2}} \vert \nabla u_{j} \vert ^{2}\,dx\leq C $$

and

$$ \int_{\mathbb{R}^{2}} \vert w_{j} \vert ^{2}\,dx= \frac{1}{\lambda _{j}^{2}} \int_{\mathbb{R}^{2}} \vert u_{j} \vert ^{2}\,dx=1. $$

(3.15)

Hence $\{w_{j}\}$ is bounded in E. Up to a subsequence, we may assume that $w_{j}\rightharpoonup w$ in E, $w_{j}\rightarrow w$ in $L^{s}(\mathbb {R}^{2})$, $\forall s\in(2,+\infty)$, $w_{j}\rightarrow w$ in $L_{\mathrm{loc}}^{s}(\mathbb{R}^{2})$, $\forall s\in[1,+\infty)$, $w_{j}(x)\rightarrow w(x)$ a.e. in $\mathbb{R}^{2}$. By $I'_{\mu_{j}}(u_{j})=0$, one has

$$ - \biggl(a+b \int_{\mathbb{R}^{2}} \vert \nabla w_{j} \vert ^{2}\,dx \biggr)\frac{1}{\lambda_{j}^{2}}\triangle w_{j}+(W-d \mu_{j})w_{j}=\mu_{j}g(w_{j})+h( \lambda_{j}x). $$

(3.16)

For any $v\in C_{0}^{\infty}(\mathbb{R}^{2})$, one has

$$ \biggl\vert \int_{\mathbb{R}^{2}}h(\lambda_{j}x)v\,dx \biggr\vert \leq \vert v \vert _{2} \biggl( \int_{\mathbb{R}^{2}} \bigl\vert h(\lambda _{j}x) \bigr\vert ^{2}\,dx \biggr)^{\frac{1}{2}} =\frac{1}{\lambda_{j}} \vert v \vert _{2} \vert h \vert _{2}\rightarrow0 $$

(3.17)

and by the Lebesgue dominated convergence theorem, we have

$$ \biggl\vert \int_{\mathbb{R}^{2}}g(w_{j})v\,dx- \int_{\mathbb{R}^{2}}g(w)v\,dx \biggr\vert \leq C \int_{\operatorname{supp}v} \bigl\vert g(w_{j})-g(w) \bigr\vert \,dx \rightarrow0. $$

(3.18)

Hence by (3.16)-(3.18), we have $(W-d)w=g(w)$ in $\mathbb{R}^{2}$, from which we get that $w=0$. Indeed, since 0 is an isolated solution of $(W-d)z=g(z)$, $w=0$. Therefore by (3.6), (3.15) and (3.16), one has

$$ \begin{aligned} W-d&=(W-d) \int_{\mathbb{R}^{2}} \vert w_{j} \vert ^{2}\,dx \\ &\leq \biggl(a+b \int_{\mathbb{R}^{2}} \vert \nabla w_{j} \vert ^{2}\,dx \biggr)\frac{1}{\lambda_{j}^{2}} \int_{\mathbb{R}^{2}} \vert \nabla w_{j} \vert ^{2}\,dx+(W-d\mu_{j}) \int_{\mathbb{R}^{2}} \vert w_{j} \vert ^{2}\,dx \\ &=\mu_{j} \int_{\mathbb{R}^{2}}g(w_{j})w_{j}\,dx+ \int_{\mathbb{R}^{2}}h(\lambda _{j}x)w_{j}\,dx \\ &\leq\varepsilon \int_{\mathbb{R}^{2}} \vert w_{j} \vert ^{2}\,dx+C_{\varepsilon}\int_{\mathbb{R}^{2}} \vert w_{j} \vert ^{p}\,dx+ \frac{1}{\lambda_{j}} \vert h \vert _{2} \vert w_{j} \vert _{2} \\ &\leq C\varepsilon+o_{n}(1), \end{aligned} $$

which implies a contradiction. Hence $\{\int_{\mathbb{R}^{2}} \vert u_{j} \vert ^{2}\,dx\}$ is bounded and then $\{u_{j}\}$ is bounded in E.

Secondly, for $N=3$, we have a simple proof. From (3.13), $(h_{2})$ and $c_{\mu_{j}}\leq c_{\frac{1}{2}}$, we get

$$ \begin{aligned}[b] a \int_{\mathbb{R}^{3}} \vert \nabla u_{j} \vert ^{2}\,dx &\leq a \int_{\mathbb{R}^{3}} \vert \nabla u_{j} \vert ^{2}\,dx+\frac {b}{4} \biggl( \int_{\mathbb{R}^{3}} \vert \nabla u_{j} \vert ^{2}\,dx \biggr)^{2}-3c_{\mu_{j}}+3c_{\mu_{j}} \\ &=- \int_{\mathbb{R}^{3}}\bigl(\nabla h(x),x\bigr)u_{j}\,dx+3c_{\mu_{j}} \\ &\leq \bigl\vert \bigl(\nabla h(x),x\bigr) \bigr\vert _{2} \vert u_{j} \vert _{2}+3c_{\frac{1}{2}} \\ &\leq C \vert u_{j} \vert _{2}+3c_{\frac{1}{2}}. \end{aligned} $$

(3.19)

We prove directly $\{\int_{\mathbb{R}^{3}}u_{j}^{2}\,dx\}$ is bounded. Similar to (3.19), we obtain

$$ \begin{aligned}[b] \frac{b}{4} \biggl( \int_{\mathbb{R}^{3}} \vert \nabla u_{j} \vert ^{2}\,dx \biggr)^{2} &\leq a \int_{\mathbb{R}^{3}} \vert \nabla u_{j} \vert ^{2}\,dx+\frac {b}{4} \biggl( \int_{\mathbb{R}^{3}} \vert \nabla u_{j} \vert ^{2}\,dx \biggr)^{2}-3c_{\mu_{j}}+3c_{\mu_{j}} \\ &\leq C \vert u_{j} \vert _{2}+3c_{\frac{1}{2}}. \end{aligned} $$

(3.20)

By the Hölder inequality, we have

$$\begin{aligned} \biggl( \int_{\mathbb{R}^{3}} \vert \nabla u_{j} \vert ^{2}\,dx \biggr)^{3}\leq C \biggl( \int_{\mathbb{R}^{3}}u_{j}^{2}\,dx \biggr)^{\frac{3}{4}}+C. \end{aligned}$$

(3.21)

By (3.3) and (3.5), for all $t\in\mathbb{R}$, one has

$$ \bigl\vert g(t)t \bigr\vert \leq\frac{W-d}{2} \vert t \vert ^{2}+C \vert t \vert ^{6}. $$

(3.22)

From (3.11), (3.21), (3.22), $\mu_{j}\leq 1$ and $D^{1,2}(\mathbb{R}^{3})\hookrightarrow L^{6}(\mathbb{R}^{3})$, it follows that

$$\begin{aligned} (W-d) \int_{\mathbb{R}^{3}}u_{j}^{2}\,dx \leq& a \int_{\mathbb{R}^{3}} \vert \nabla u_{j} \vert ^{2}\,dx+b \biggl( \int_{\mathbb{R}^{3}} \vert \nabla u_{j} \vert ^{2}\,dx \biggr)^{2}+(W-\mu_{j}d) \int_{\mathbb{R}^{3}}u_{j}^{2}\,dx \\ =&\mu_{j} \int_{\mathbb{R}^{3}}g(u_{j})u_{j}\,dx+ \int_{\mathbb{R}^{3}}hu_{j}\,dx \\ \leq&\frac{W-d}{2} \int_{\mathbb{R}^{3}}u_{j}^{2}\,dx+C \int_{\mathbb {R}^{3}}u_{j}^{6}\,dx+ \vert h \vert _{2} \biggl( \int_{\mathbb {R}^{3}}u_{j}^{2}\,dx \biggr)^{\frac{1}{2}} \\ \leq&\frac{W-d}{2} \int_{\mathbb{R}^{3}}u_{j}^{2}\,dx+C \biggl( \int_{\mathbb {R}^{3}} \vert \nabla u_{j} \vert ^{2}\,dx \biggr)^{3}+ \vert h \vert _{2} \biggl( \int_{\mathbb{R}^{3}}u_{j}^{2}\,dx \biggr)^{\frac{1}{2}} \\ \leq&\frac{W-d}{2} \int_{\mathbb{R}^{3}}u_{j}^{2}\,dx+C \biggl( \int_{\mathbb {R}^{3}}u_{j}^{2}\,dx \biggr)^{\frac{3}{4}} +C+ \vert h \vert _{2} \biggl( \int_{\mathbb{R}^{3}}u_{j}^{2}\,dx \biggr)^{\frac{1}{2}}, \end{aligned}$$

which implies that $\{\int_{\mathbb{R}^{3}}u_{j}^{2}\,dx\}$ is bounded. Combining with (3.19), we get that $\{u_{j}\}$ is bounded in E. □

Proof of the second solution of Theorem 1.2

By $I_{\mu_{j}}(u_{j})=c_{\mu_{j}}$, $I'_{\mu_{j}}(u_{j})=0$, $\mu_{j}\rightarrow 1^{-}$ and Remark 3.2, we get $I(u_{j})\rightarrow c_{1}$ and $I'(u_{j})\rightarrow0$ as $n\rightarrow +\infty$. By Lemmas 3.5 and 3.8, there exists $v_{0}\in E$ such that $u_{j}\rightarrow v_{0}$ in E as $n\rightarrow+\infty$ and then $I(v_{0})=c_{1}>0$, $I'(v_{0})=0$. Be similar to (3.8), we get $v_{0}\geq0$. By the strong maximum principle, one has $v_{0}>0$. □

4 Conclusions

The goal of this paper is to study the multiplicity of positive solutions for the following nonlinear Kirchhoff type equation:

$$\begin{aligned} - \biggl(a+b \int_{\mathbb{R}^{N}} \vert \nabla u \vert ^{2}\,dx \biggr) \triangle u+Vu=f(u)+h(x),\quad x\in\mathbb{R}^{N}, \end{aligned}$$

where a, b, V are positive constants, $N=2$ or 3. Under very weak conditions on f, we get that the equation has two positive solutions by using variational methods.