1 Introduction

An integral equation is a mathematical expression that includes a required function under an integration sign. Such equations often describe an elementary or a complex physical process wherein the characteristics at a given point depend on values in the whole domain and cannot be defined only on the bases of the values near the given point.

A differential equation is said to be an integro-differential equation (IDE) if it contains the integrals of the unknown function. Most frequently, integral equations as well as IDEs are found in such problems of heat and mass transfer as diffusion, potential theory, and radiation heat transfer. Integral equations have a lot of applications such as actuarial science (ruin theory), computational electromagnetics, inverse problems, for example, Marchenko equation (inverse scattering transform), options pricing under jump-diffusion, radiative transfer, and viscoelasticity (see, for example, [12, 13, 17, 37, 39, 47] and the references cited in therein).

In biological applications, the population dynamics and genetics are modeled by a system of IDEs (see Kheybari et al. [19]). Next, initial value problems for a nonlinear system of IDEs are used to model the competition between tumor cells and the immune system (see Nicola et al. [9]).

Besides, in engineering, two systems of specific inhomogeneous IDEs are studied to examine the noise term phenomenon (see Wazwaz [46]). In addition, the scattered electromagnetic fields from resistive strips and RLC circuits are governed by IDEs (see Hatamzadeh et al. [16]).

An IDE is said to have a delay when the rate of variation in the equation state depends on past states. In this case such an IDE is called delay integro-differential equation (DIDE).

Numerous sectors of science and technology, including biology, medicine, engineering, information systems, control theory, and finance mathematics, have utilized the stability and boundedness qualities of solutions for IDEs with and without delays.

The Lyapunov’s direct method, which includes an energy-like function, has proven to be an effective tool in the qualitative study of ordinary differential equations (ODEs). Many researchers have used this technique to solve delay differential equations (DDEs) and IDEs over the last five decades. In contrast to Lyapunov functionals, which are frequently employed in the study of DDEs and IDEs (see, for instance, Burton [11, 40]).

The basic theory of stochastic differential equations (SDEs) has been systematically established in [8, 14, 30, 32, 34]. There are many interesting results in the literature on the stability and boundedness of solutions for stochastic delay differential equations (SDDEs), see, for example, [18, 20, 21, 28, 29, 36] and others.

To the best of our information, we observe that only a few excellent and interesting works on the stochastic stability and boundedness of solutions for second-, third-, and fourth-order SDDEs have been developed in [1–6, 22–24, 26, 27, 38, 45] (see also the references of these sources).

There are a number of results on the qualitative characteristics of first-, second-, and third-order IDEs with and without delays, but none on the qualitative characteristics of solutions for a particular class of second-order SDIDE.

The qualitative properties of DIDEs for the second- and third-order have been considered by numerous authors such as Adeyanju et al. [7], Bohner and Tunç [10], Graef and Tunç [15], Mohammed [31], Napoles [33], Pinelas and Tunç [35], Tunç and Ayhan [41, 42], Tunç [44], and Zhao and Meng [48] (see also the references therein). To the best of our knowledge, this is the first attempt on the subject in the second-order SDIDE literature.

As a result, the goal of this paper is to investigate the stability, continuity, and boundedness of solutions for a type of second-order SDIDE as follows:

$$ \begin{aligned} &\ddot{x}(t)+P\bigl(t,x(t),\dot{x}(t) \bigr)\dot{x}(t)+Q\bigl(x\bigl(t-\tau (t)\bigr),\dot{x}\bigl(t- \tau (t)\bigr) \bigr)+R(x\bigl(t-\tau (t)\bigr) \\ &\quad {}+g\bigl(t,x(t)\bigr)\dot{\omega}(t) = \int _{0}^{t}\mathcal{C}(t,s)f\bigl(s,\dot{x}(s) \bigr)\,ds , \end{aligned} $$
(1.1)

where \(\tau (t)\) is a variable delay with \(0\leq \tau (t)\leq \gamma \), γ is a positive constant that will be determined later, \(\dot{\tau}(t)\leq \beta \), \(\beta \in (0,1)\).

The functions Q and R are continuous differentiable functions such that \(Q\in C(\mathbb{R}^{2}, \mathbb{R})\) and \(R \in C(\mathbb{R}, \mathbb{R})\) for all \(R(x)\neq 0\), \(R(0)=0\) and \(Q(0,0)=0\). The functions \(P\in C(\mathbb{R}^{+}\times \mathbb{R}^{2}, \mathbb{R})\), \(f\in C(\mathbb{R}^{+}\times \mathbb{R}, \mathbb{R})\), \(f(t,0)=0\), and \(\mathcal{C}\in C(\mathbb{R}^{+}\times \mathbb{R}^{+}, \mathbb{R})\) is such that \(\mathcal{C}(t,s)\) is a continuous function for \(0\leq s\leq t<\infty \), \(g(t,x(t))\) is a continuous function, and \(\omega (t)\in \mathbb{R}^{m}\) is a standard Wiener process.

Equation (1.1) can be expressed in the following system form:

$$ \begin{aligned} &\dot{x}=y, \\ & \dot{y}=-P(t,x,y)y-Q(x,y)-R(x)-g(t,x)\dot{\omega}(t)+ \int _{0}^{t} \mathcal{C}(t,s)f\bigl(s,y(s) \bigr)\,ds \\ &\hphantom{\dot{y}={}}{}+\Delta (t), \end{aligned} $$
(1.2)

where

$$ \Delta (t)= \int ^{t}_{t-\tau (t)} \bigl\{ Q_{x} \bigl(x(s),y(s)\bigr)+R'\bigl(x(s)\bigr) \bigr\} y(s)\,ds . $$

In addition, it is supposed that the derivatives \(Q_{x}(x,y)=\frac{\partial Q}{\partial x}(x,y)\) and \(R'(x)=\frac{dR}{dx}(x)\) exist and are continuous.

Let us consider the n-dimensional SDDE (see [25, 43]):

$$ dx(t) = F(t,x_{t})\,dt + G(t,x_{t})\,dB (t), \qquad x_{t}(\theta )=x(t+\theta )\quad{}-r \leq \theta \leq 0,\ t \geq t_{0}, $$
(1.3)

with the initial condition \(x_{0}\in \mathcal{C}([-r,0];\mathbb{R}^{n})\). Suppose that \(F :\mathbb{R}^{+}\times \mathbb{R}^{2n}\rightarrow \mathbb{R}^{n}\) and \(G:\mathbb{R}^{+}\times \mathbb{R}^{2n}\rightarrow \mathbb{R}^{n \times m}\) are measurable functions such that \(F(t,0)=0\) and \(G(t,0)=0\).

To formulate the stability and boundedness criteria, we suppose that \(C^{1,2}(\mathbb{R}^{+} \times \mathbb{R}^{n};\mathbb{R}^{+})\) denotes the family of all nonnegative Lyapunov functionals \(W(t,x_{t})\) defined on \(\mathbb{R}^{+} \times \mathbb{R}^{n}\), which are twice continuously differentiable in x and one in t. By Itô’s formula, we have

$$ dW(t,x_{t})=\mathcal{L}W_{t}(t,x_{t})+W_{x}(t,x_{t})G(t,x_{t})\,dB (t), $$

where

$$ \mathcal{L}W(t,x_{t}) = W_{t}(t,x_{t})+ W_{x}(t,x_{t})F(t,x_{t}) + \frac{1}{2}\operatorname{trace} \bigl[G^{T}(t,x_{t})W_{xx}(t,x_{t}) G(t,x_{t}) \bigr] $$
(1.4)

with \(W_{t}=\frac{\partial W}{\partial t}\), \(W_{x}=(\frac{\partial W}{\partial x_{1}},\ldots , \frac{\partial W}{\partial x_{n}})\) and

$$ W_{xx}=\biggl(\frac{\partial ^{2} W}{\partial x_{i}\partial x_{j}}\biggr)_{n \times n}= \begin{pmatrix} \frac{\partial ^{2} W}{\partial x_{1}\partial x_{1}} & \cdots & \frac{\partial ^{2} W}{\partial x_{1}\partial x_{n}} \\ \vdots & & \vdots \\ \frac{\partial ^{2} W}{\partial x_{n}\partial x_{1}} & \cdots & \frac{\partial ^{2} W}{\partial x_{n}\partial x_{n}} \end{pmatrix}_{n\times n}. $$

2 Stochastic qualitative results

We introduce the following hypotheses before proving our main results.

Assume that there are positive constants \(f_{0}\), \(g_{0}\), \(p_{0}\), \(c_{0}\), \(\alpha _{0}\), α, \(K^{\ast}\), c, d, and N that satisfy the following conditions:

  1. (i)

    \(|f(t,y)|\leq f_{0}|y|\) for all \(t\in \mathbb{R}^{+}\) and \(y\in \mathbb{R}\);

  2. (ii)

    \(P(t,x,y)\geq p_{0}>0\) and \(g(t,x)\leq g_{0} x\) for all \(t \in \mathbb{R^{+}}\) and \(x,y \in \mathbb{R}\);

  3. (iii)

    \(Q(0,0)=0\), \(c\leq \frac{Q(x,y)}{x}\leq c_{0}\) for \(x\neq 0\) and \(|\frac{\partial Q}{\partial x}(x,y)|\leq d\) for all \(x,y \in \mathbb{R}\);

  4. (iv)

    \(\alpha \leq \frac{R(x)}{x}\leq \alpha _{0}\) for \(x\neq 0\) and \(|R'(x)|\leq K^{\ast}\) for all \(x \in \mathbb{R}\);

  5. (v)

    \(\max \{f_{0}^{2}\int _{t}^{\infty}|\mathcal{C}(u,s)|\,du , \int _{0}^{t}| \mathcal{C}(t,s)|\,ds \}< N\);

  6. (vi)

    There are \(\gamma >0\) and \(\beta \in (0,1)\) such that \(0\leq \tau (t)\leq \gamma \) and \(\dot{\tau}(t)\leq \beta \).

The following theorem is the first result of this paper.

Theorem 2.1

Let conditions (i)–(vi) hold. Then all the solutions of system (1.2) are continuous and bounded provided that

$$ \gamma < \min \biggl\{ \frac{2c+2\alpha -p_{0}-g_{0}^{2}-N}{2(d+K^{\ast})}, \frac{(2p_{0}-3N)(1-\beta )}{2(d+K^{\ast})(3-\beta )} \biggr\} $$

with

$$ \begin{aligned} 2p_{0}>3N, \qquad 2c+2\alpha -p_{0}-N>g_{0}^{2}. \end{aligned} $$

Proof

The proof of this theorem rests on the differentiable scalar Lyapunov functional \(V(t):=V(t, x_{t}, y_{t})\) defined as follows:

$$ \begin{aligned} V(t)={}&\frac{1}{2}y^{2}+xy+ \int ^{x}_{0} Q(\eta ,y)\,d\eta + \int ^{x}_{0} R(\eta )\,d\eta +\lambda \int ^{0}_{-\tau (t)}\,d\theta \int ^{t}_{t+ \theta} y^{2}(\phi )\,d\phi \\ &{}+ \int ^{t}_{0}\,ds \int ^{\infty}_{t} \bigl\vert \mathcal{C}(u,s) \bigr\vert f^{2}\bigl(s,y(s)\bigr)\,du , \end{aligned} $$
(2.1)

where λ is a positive constant that will be determined later.

In view of assumptions (iii) and (iv), we obtain

$$ \begin{aligned} V(t)\geq {}&\frac{1}{2}y^{2}+xy+ \frac{1}{2}c x^{2}+\frac{1}{2}\alpha x^{2}+ \lambda \int ^{0}_{-\tau (t)}\,d\theta \int ^{t}_{t+\theta} y^{2}(\phi )\,d\phi \\ &{}+ \int ^{t}_{0}\,ds \int ^{\infty}_{t} \bigl\vert \mathcal{C}(u,s) \bigr\vert f^{2}\bigl(s,y(s)\bigr)\,du . \end{aligned} $$

It follows that

$$ \begin{aligned} V(t)&\geq \biggl(x+\frac{1}{2}y \biggr)^{2}+\frac{1}{2}(c+\alpha -2)x^{2}+ \frac{1}{4}y^{2}+\lambda \int ^{0}_{-\tau (t)}\,d\theta \int ^{t}_{t+ \theta} y^{2}(\phi )\,d\phi \\ &\quad{}+ \int ^{t}_{0}\,ds \int ^{\infty}_{t} \bigl\vert \mathcal{C}(u,s) \bigr\vert f^{2}\bigl(s,y(s)\bigr)\,du \\ & \geq \frac{1}{2}(c+\alpha -2)x^{2}+\frac{1}{4}y^{2}+ \lambda \int ^{0}_{- \tau (t)}\,d\theta \int ^{t}_{t+\theta} y^{2}(\phi )\,d\phi \\ &\quad{}+ \int ^{t}_{0}\,ds \int ^{\infty}_{t} \bigl\vert \mathcal{C}(u,s) \bigr\vert f^{2}\bigl(s,y(s)\bigr)\,du . \end{aligned} $$

Then we obtain

$$ V(t)\geq \frac{1}{2}(c+\alpha -2)x^{2}+ \frac{1}{4}y^{2}. $$

Hence, it is clear that there exists a sufficiently small positive constant \(\delta _{1}\) such that

$$ V(t)\geq \delta _{1}\bigl(x^{2}+y^{2} \bigr) \quad \text{for all } x,y, $$
(2.2)

where

$$ \delta _{1}=\frac{1}{2}\min \biggl\{ c+\alpha -2, \frac{1}{2}\biggr\} >0. $$

As a result, the Lyapunov functional \(V(t)\) is positive definite at all \((x,y)\) points and zero only at \(x=y=0\).

Itô’s formula (1.4) gives the derivative of the Lyapunov functional \(V(t)\) in (2.1) along any solution \((x(t),y(t))\) of system (1.2) as follows:

$$ \begin{aligned} \mathcal{L}V(t)={}&(x+y) \biggl\{ -P(t,x,y)y-Q(x,y)-R(x)+ \int _{0}^{t} \mathcal{C}(t,s)f\bigl(s,y(s) \bigr)\,ds +\Delta (t) \biggr\} \\ &{} +y^{2}+Q(x,y)y+R(x)y+\lambda \tau (t)y^{2}-\lambda \bigl(1-\dot{\tau}(t)\bigr) \int ^{t}_{t-\tau (t)}y^{2}(s)\,ds \\ &{} +f^{2}(t,y) \int ^{\infty}_{t} \bigl\vert \mathcal{C}(u,s) \bigr\vert \,du - \int ^{t}_{0} \bigl\vert \mathcal{C}(t,s) \bigr\vert f^{2}\bigl(s,y(s)\bigr)\,ds +\frac{1}{2}g^{2}(t,x). \end{aligned} $$

It follows that

$$ \begin{aligned} \mathcal{L}V(t)={}&{-}P(t,x,y)y^{2}+y \int _{0}^{t}\mathcal{C}(t,s)f\bigl(s,y(s) \bigr)\,ds +y \Delta (t)+x\Delta (t)+y^{2} \\ &{} -P(t,x,y)xy-xQ(x,y)-R(x)x+x \int _{0}^{t}\mathcal{C}(t,s)f\bigl(s,y(s) \bigr)\,ds \\ &{}+\lambda \tau (t)y^{2}-\lambda \bigl(1-\dot{\tau}(t)\bigr) \int ^{t}_{t-\tau (t)}y^{2}(s)\,ds +f^{2}(t,y) \int ^{\infty}_{t} \bigl\vert \mathcal{C}(u,s) \bigr\vert \,du \\ &{}- \int ^{t}_{0} \bigl\vert \mathcal{C}(t,s) \bigr\vert f^{2}\bigl(s,y(s)\bigr)\,ds +\frac{1}{2}g^{2}(t,x). \end{aligned} $$
(2.3)

By assumption (i), we get the following inequality:

$$ \begin{aligned} f^{2}(t,y) \int ^{\infty}_{t} \bigl\vert \mathcal{C}(u,s) \bigr\vert \,du \leq f_{0}^{2}y^{2} \int ^{\infty}_{t} \bigl\vert \mathcal{C}(u,s) \bigr\vert \,du . \end{aligned} $$
(2.4)

From the inequality \(2|mn|\leq m^{2}+n^{2}\), we get the following relations:

$$ \begin{aligned} y \int _{0}^{t}\mathcal{C}(t,s)f\bigl(s,y(s) \bigr)\,ds &\leq \vert y \vert \int _{0}^{t} \bigl\vert \mathcal{C}(t,s) \bigr\vert \bigl\vert f\bigl(s,y(s)\bigr) \bigr\vert \,ds \\ & \leq \frac{1}{2} \int _{0}^{t} \bigl\vert \mathcal{C}(t,s) \bigr\vert \bigl(y^{2}(t)+f^{2}\bigl(s,y(s)\bigr) \bigr)\,ds \\ & =\frac{1}{2} \int _{0}^{t} \bigl\vert \mathcal{C}(t,s) \bigr\vert y^{2}(t)\,ds +\frac{1}{2} \int _{0}^{t} \bigl\vert \mathcal{C}(t,s) \bigr\vert f^{2}\bigl(s,y(s)\bigr)\,ds \\ & =\frac{1}{2}y^{2} \int _{0}^{t} \bigl\vert \mathcal{C}(t,s) \bigr\vert \,ds +\frac{1}{2} \int _{0}^{t} \bigl\vert \mathcal{C}(t,s) \bigr\vert f^{2}\bigl(s,y(s)\bigr)\,ds . \end{aligned} $$
(2.5)

In the same way, we obtain

$$ \begin{aligned} x \int _{0}^{t}\mathcal{C}(t,s)f\bigl(s,y(s) \bigr)\,ds \leq \frac{1}{2}x^{2} \int _{0}^{t} \bigl\vert \mathcal{C}(t,s) \bigr\vert \,ds +\frac{1}{2} \int _{0}^{t} \bigl\vert \mathcal{C}(t,s) \bigr\vert f^{2}\bigl(s,y(s)\bigr)\,ds . \end{aligned} $$
(2.6)

The following estimations can be confirmed using assumptions (ii)–(iv) and the inequality \(2|mn|\leq m^{2}+n^{2}\):

$$ \begin{aligned} &\frac{1}{2}g^{2}(t,x) \leq \frac{1}{2}g_{0}^{2} x^{2}, \\ & {-}P(t,x,y)y^{2}\leq -p_{0} y^{2}, \\ & {-}P(t,x,y)xy\leq -p_{0} xy\leq \frac{1}{2}p_{0} \bigl(x^{2}+y^{2}\bigr)\quad \text{since } p_{0}>0, \\ & {-}xQ(x,y)\leq -c x^{2}, \\ & {-}R(x)x\leq -\alpha x^{2}. \end{aligned} $$
(2.7)

Hence, in view of assumptions (iii), (iv) and by using the inequality \(2|mn|\leq m^{2}+n^{2}\), we can conclude that

$$ \begin{aligned} x\Delta (t)&=x \int ^{t}_{t-\tau (t)} \bigl\{ Q_{x} \bigl(x(s),y(s)\bigr)y(s)+R'\bigl(x(s)\bigr)y(s) \bigr\} \,ds \\ & \leq \vert x \vert \int ^{t}_{t-\tau (t)} \bigl\vert Q_{x} \bigl(x(s),y(s)\bigr) \bigr\vert \bigl\vert y(s) \bigr\vert \,ds + \vert x \vert \int ^{t}_{t- \tau (t)} \bigl\vert R' \bigl(x(s)\bigr) \bigr\vert \bigl\vert y(s) \bigr\vert \,ds \\ & \leq \frac{1}{2}d \int ^{t}_{t-\tau (t)}\bigl(x^{2}(t)+y^{2}(s) \bigr)\,ds + \frac{1}{2}K^{\ast} \int ^{t}_{t-\tau (t)}\bigl(x^{2}(t)+y^{2}(s) \bigr)\,ds \\ & =\frac{1}{2}x^{2}(t) \bigl(d+K^{\ast}\bigr) \tau (t)+\frac{1}{2}\bigl(d+K^{\ast}\bigr) \int ^{t}_{t-\tau (t)}y^{2}(s)\,ds . \end{aligned} $$

Similar to the preceding, we have

$$ \begin{aligned} y\Delta (t)&\leq \frac{1}{2}d \int ^{t}_{t-\tau (t)}\bigl(y^{2}(t)+y^{2}(s) \bigr)\,ds + \frac{1}{2}K^{\ast} \int ^{t}_{t-\tau (t)}\bigl(y^{2}(t)+y^{2}(s) \bigr)\,ds \\ & =\frac{1}{2}y^{2}(t) \bigl(d+K^{\ast}\bigr) \tau (t)+\frac{1}{2}\bigl(d+K^{\ast}\bigr) \int ^{t}_{t-\tau (t)}y^{2}(s)\,ds . \end{aligned} $$

By adding the above two inequalities and since \(0\leq \tau (t)\leq \gamma \), we get the following:

$$ \begin{aligned} (x+y)\Delta (t)\leq \frac{1}{2}\gamma \bigl(d+K^{\ast}\bigr) \bigl(x^{2}(t)+y^{2}(t) \bigr)+\bigl(d+K^{\ast}\bigr) \int ^{t}_{t-\tau (t)}y^{2}(s)\,ds . \end{aligned} $$
(2.8)

Furthermore, from condition (vi), it follows that

$$ \begin{aligned} \lambda \tau (t)y^{2}- \lambda \bigl(1-\dot{\tau}(t)\bigr) \int ^{t}_{t-\tau (t)}y^{2}(s)\,ds \leq \lambda \gamma y^{2}(t)-\lambda (1-\beta ) \int ^{t}_{t-\tau (t)}y^{2}(s)\,ds . \end{aligned} $$
(2.9)

By considering the preceding inequalities (2.4)–(2.8) in the derivative (2.3), we can arrive at

$$\begin{aligned} \mathcal{L}V(t)={}&{-}p_{0} y^{2}-c x^{2}-\alpha x^{2}+f_{0}^{2}y^{2} \int ^{\infty}_{t} \bigl\vert \mathcal{C}(u,s) \bigr\vert \,du +\frac{1}{2}y^{2} \int _{0}^{t} \bigl\vert \mathcal{C}(t,s) \bigr\vert \,ds \\ &{}+ \frac{1}{2}x^{2} \int _{0}^{t} \bigl\vert \mathcal{C}(t,s) \bigr\vert \,ds +\frac{1}{2}p_{0}\bigl(x^{2}+y^{2} \bigr)+ \frac{1}{2}g_{0}^{2} x^{2} \\ &{}+\frac{1}{2}\gamma \bigl(d+K^{\ast}\bigr) \bigl(x^{2}+y^{2}\bigr)+\bigl(d+K^{\ast}\bigr) \int ^{t}_{t- \tau (t)}y^{2}(s)\,ds \\ &{}+\lambda \gamma y^{2}-\lambda (1-\beta ) \int ^{t}_{t-\tau (t)}y^{2}(s)\,ds . \end{aligned}$$

With some rearrangement of terms, we can get

$$ \begin{aligned} \mathcal{L}V(t)\leq {}&{-} \biggl\{ c+\alpha - \frac{1}{2}p_{0}-\frac{1}{2} \gamma \bigl(d+K^{\ast}\bigr)-\frac{1}{2}g_{0}^{2} \biggr\} x^{2} \\ &{}- \biggl\{ p_{0}-\frac{1}{2}\gamma \bigl(d+K^{\ast} \bigr)-\lambda \gamma \biggr\} y^{2}+ \frac{1}{2}x^{2} \int _{0}^{t} \bigl\vert \mathcal{C}(t,s) \bigr\vert \,ds \\ &{} + \bigl\{ d+K^{\ast}-\lambda (1-\beta ) \bigr\} \int ^{t}_{t-\tau (t)}y^{2}(s)\,ds \\ &{} + \biggl\{ f_{0}^{2} \int ^{\infty}_{t} \bigl\vert \mathcal{C}(u,s) \bigr\vert \,du + \frac{1}{2} \int _{0}^{t} \bigl\vert \mathcal{C}(t,s) \bigr\vert \,ds \biggr\} y^{2}. \end{aligned} $$

Then, from condition (v), we obtain

$$ \begin{aligned} \mathcal{L}V(t)\leq{} &{-} \biggl\{ c+\alpha - \frac{1}{2}p_{0}-\frac{1}{2}\bigl(d+K^{ \ast} \bigr)\gamma -\frac{1}{2}g_{0}^{2}- \frac{1}{2}N \biggr\} x^{2} \\ &{}- \biggl\{ p_{0}-\frac{1}{2}\bigl(d+K^{\ast} \bigr)\gamma -\lambda \gamma - \frac{3}{2}N \biggr\} y^{2} \\ &{} + \bigl\{ d+K^{\ast}-\lambda (1-\beta ) \bigr\} \int ^{t}_{t-\tau (t)}y^{2}(s)\,ds . \end{aligned} $$

If we now choose

$$ \lambda =\frac{d+K^{\ast}}{1-\beta}, $$

then we can observe

$$ \begin{aligned} \mathcal{L}V(t)\leq{} &{-}\frac{1}{2} \bigl\{ 2c+2\alpha -p_{0}-\bigl(d+K^{\ast}\bigr) \gamma -g_{0}^{2}-N \bigr\} x^{2} \\ &{}-\frac{1}{2} \biggl\{ 2p_{0}-\bigl(d+K^{\ast} \bigr)\gamma - \frac{2(d+K^{\ast})}{1-\beta}\gamma -3N \biggr\} y^{2}. \end{aligned} $$

If we take

$$ \gamma < \min \biggl\{ \frac{2c+2\alpha -p_{0}-g_{0}^{2}-N}{2(d+K^{\ast})}, \frac{(2p_{0}-3N)(1-\beta )}{2(d+K^{\ast})(3-\beta )} \biggr\} , $$

then there exists a positive constant \(\delta _{2}\) such that

$$ \mathcal{L}V(t)\leq -\delta _{2} \bigl(x^{2}+y^{2}\bigr), \quad \delta _{2}\in \mathbb{R}. $$
(2.10)

This implies that \(\mathcal{L}V(t)\leq 0\). Because of all functions appearing in (1.1), it is obvious that there exists at least one solution of (1.1) defined on \([t_{0}, t_{0}+\rho )\) for some \(\rho >0\).

It is necessary to show that the solution can be extended onto the entire interval \([t_{0}, \infty )\). We suppose on the contrary that there is a first time \(T<\infty \) such that the solution exists on \([t_{0}, T)\) and

$$ \lim_{t\rightarrow T^{-}}\bigl( \vert x \vert + \vert y \vert \bigr)=\infty . $$

Suppose that \((x(t), y(t))\) is a solution of system (1.2) with the initial condition \((x_{0}, y_{0})\). Since the Lyapunov functional \(V(t)\) is a positive definite and decreasing functional on the trajectories of system (1.2), also we have

$$ \mathcal{L}V(t)\leq 0. $$

Then we can say that \(V(t)\) is bounded on \([t_{0}, T)\). Now, integrating the above inequality from \(t_{0}\) to T, we have

$$ V\bigl(T, x(T), y(T)\bigr)\leq V\bigl(t_{0}, x(t_{0}), y(t_{0})\bigr)=V_{0}. $$

Hence, it follows from (2.2) that

$$ x^{2}(T)+y^{2}(T)\leq \frac{V_{0}}{\delta _{1}}. $$

This inequality implies that \(|x(t)|\) and \(|y(t)|\) are bounded on \(t\rightarrow T^{-}\). Thus, we conclude that \(T<\infty \) is not possible, we must have \(T=\infty \).

This completes the proof of Theorem 2.1. □

Theorem 2.2

If assumptions (i)–(vi) of Sect. 2hold, then the null solution of system (1.2) is uniformly stochastically asymptotically stable.

Proof

From (2.1), using assumptions (iii) and (iv) and the inequality \(2|mn|\leq m^{2}+n^{2}\), we have

$$ \begin{aligned} V(t)\leq \delta _{3} \bigl(x^{2}+y^{2}\bigr)+\lambda \int ^{0}_{-\tau (t)}\,d\theta \int ^{t}_{t+\theta} y^{2}(\phi )\,d\phi + \int ^{t}_{0}\,ds \int ^{ \infty}_{t} \bigl\vert \mathcal{C}(u,s) \bigr\vert f^{2}\bigl(s,y(s)\bigr)\,du , \end{aligned} $$

where

$$ \delta _{3}=:\frac{1}{2}\max \{1, 1+c_{0}+ \alpha _{0}\}. $$

Then, from conditions (i) and (v), we obtain

$$ V(t)\leq \delta _{3}\bigl(x^{2}+y^{2} \bigr)+\kappa \Vert y \Vert ^{2}. $$
(2.11)

Therefore, by combining the two inequalities (2.2) and (2.11), we get

$$ \delta _{1}\bigl(x^{2}+y^{2} \bigr)\leq V(t)\leq \delta _{3}\bigl(x^{2}+y^{2} \bigr)+ \kappa \Vert y \Vert ^{2}. $$
(2.12)

It follows from (2.10) and (2.12) that the Lyapunov functional \(V(t)\) satisfies the following inequalities:

$$\begin{aligned}& \zeta _{1}\bigl( \vert x \vert \bigr)\leq V(t,x) \leq \zeta _{2}\bigl( \vert x \vert \bigr),\\& \mathcal{L}V(t,x)\leq -\zeta _{3} \bigl( \vert x \vert \bigr) \quad \text{for all } (t,x) \in \mathbb{R}^{+}\times \mathbb{R}^{n}. \end{aligned}$$

Thus, by taking note of how the discussion above developed, the stability theorems 1 and 2 in [8, 30, 45] were established.

This completes the proof of Theorem 2.2. □

3 Example

In this section, we consider an example of how to illustrate the results for second-order SDIDE.

$$ \begin{aligned} &\ddot{x}(t)+ \bigl(11+t+x^{2}+ \dot{x}^{2} \bigr)\dot{x}(t)+10x\bigl(t-\tau (t)\bigr)+ \frac{x(t-\tau (t))}{1+x^{2}(t-\tau (t))} \\ &\quad {} +2x\bigl(t-\tau (t)\bigr)+xe^{-\dot{x}^{2}}+\frac{4t}{t^{2}+1}x(t) \dot{ \omega}(t)=2 \int _{0}^{t}e^{2(s-t)}\dot{x}(s)\,ds . \end{aligned} $$
(3.1)

Then we can express (3.1) as the equivalent system:

$$ \begin{aligned} &\dot{x}=y, \\ &\dot{y}=- \bigl(11+t+x^{2}+y^{2} \bigr)y- \biggl(10x+ \frac{x}{1+x^{2}} \biggr)+ \bigl(2x+xe^{-y^{2}} \bigr) \\ &\hphantom{\dot{y}={}}{}+ \int ^{t}_{t-\tau (t)} \biggl\{ 12+ \frac{1-x^{2}(s)}{ (1+x^{2}(s) )^{2}} \biggr\} y(s)\,ds \\ &\hphantom{\dot{y}={}}{}-\frac{4t}{1+t^{2}}x \dot{\omega}(t)+2 \int _{0}^{t}e^{2(s-t)}y(s)\,ds . \end{aligned} $$
(3.2)

When we compare systems (3.2) and (1.2), we see the following relationships:

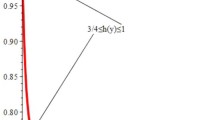
$$\begin{aligned}& P(t,x,y)=11+t+x^{2}+y^{2}\geq 11\quad \text{for all } t \in \mathbb{R^{+}} \text{ as } x,y\in \mathbb{R}, \\& R(x)=10x+\frac{x}{1+x^{2}},\qquad R(0)=0,\qquad 10\leq \frac{R(x)}{x}=10+ \frac{1}{1+x^{2}}\leq 11,\\& R'(x)=10+\frac{1-x^{2}}{(1+x^{2})^{2}} \quad \text{such that } \bigl\vert R'(x) \bigr\vert \leq 11. \end{aligned}$$

The functions \(\frac{R(x)}{x}\) and \(R'(x)\) with their bounds are shown in Fig. 1.

$$\begin{aligned}& Q(x,y)=2x+xe^{-y^{2}}, \quad \text{then} \quad Q(0,0)=0,\qquad 2\leq \frac{Q(x,y)}{x}=2+e^{-y^{2}}\leq 3\quad \text{and} \\& \frac{\partial Q(x,y)}{\partial x}=2+e^{-y^{2}}\leq 3\quad \text{for all } x\neq 0 \text{ as } x,y\in \mathbb{R}, \\& g(t,x)=\frac{4t}{1+t^{2}}x,\qquad g^{2}(t,x)= \frac{16t^{2}}{(1+t^{2})^{2}}x^{2} \leq 4x^{2}=g_{0}^{2}x^{2}, \\& f(t,y)=2y, \qquad \bigl\vert f(t,y) \bigr\vert \leq 2 \vert y \vert , \\& \int _{0}^{t}\mathcal{C}(t,s)\,ds = \int _{0}^{t}e^{2(s-t)}\,ds = \frac{1}{2}- \frac{1}{2}e^{-2t}, \\& \tau (t)=\frac{1}{16}\sin t+\frac{1}{64}\leq \frac{5}{64}=\gamma \cong 0.07825, \\& \dot{\tau}(t)=\frac{1}{16}\cos t\leq \frac{1}{16}=\beta \cong 0.0625\quad \text{for all } t\geq 0. \end{aligned}$$
Figure 1
figure 1

Behaviors of the functions \(\frac{R(x)}{x}\) and \(R'(x)\) for \(x\in [-40, 40]\)

Full size image

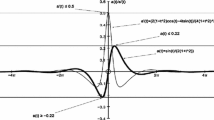
In Fig. 2, the behaviours of the functions \(\frac{Q(x,y)}{x}\), (\(x\neq0\)), were plotted in \([-20, 20]\) by MATLAB software.

Figure 2
figure 2

The behavior of the functions \(\frac{Q(x,y)}{x}\) for \(x\in [-20, 20]\)

Full size image

The shape and path of \(\tau (t)\) and \(\dot{\tau}(t)\) are shown in Fig. 3.

Figure 3
figure 3

The paths of the functions \(\tau (t)\) and \(\dot{\tau}(t)\) for \(t\in [-20, 20]\)

Full size image

Then we obtain

$$\begin{aligned}& P_{0}=11,\qquad c=2,\qquad d=3,\qquad K^{\ast}=11, \qquad g_{0}=2, \\& f_{0}=2,\qquad \alpha =10,\qquad \alpha _{0}=11,\quad \text{and}\quad c_{0}=3. \end{aligned}$$

Therefore, we get

$$\begin{aligned}& f_{0}^{2} \int _{t}^{\infty} \bigl\vert \mathcal{C}(u,s) \bigr\vert \,du =4 \int _{t}^{\infty} \bigl\vert e^{2(s-u)} \bigr\vert \,du =2 \bigl\vert e^{2(s-t)} \bigr\vert \leq 2, \\& \begin{aligned} \max \biggl\{ f_{0}^{2} \int _{t}^{\infty} \bigl\vert \mathcal{C}(u,s) \bigr\vert \,du , \int _{0}^{t} \bigl\vert \mathcal{C}(t,s) \bigr\vert \,ds \biggr\} &=\max \biggl\{ 2, \frac{1}{2}- \frac{1}{2}e^{-2t} \biggr\} =2< N=3. \end{aligned} \end{aligned}$$

We can estimate the following from the information above:

$$\begin{aligned}& 2p_{0}=22>9=3N,\\& 2c+2\alpha -p_{0}-N=10>4=g_{0}^{2}. \end{aligned}$$

Finally, if

$$ \gamma =\frac{5}{64}< \min \{0.214, 0.1482\}\cong 0.1482, $$

then the null solution of (3.1) is uniformly stochastically asymptotically stable.

Thus, all the conditions of Theorems 2.1 and 2.2 are fulfilled. Therefore, their results hold.

In Fig. 4, the nonlinear SDIDE (3.1) of second order was solved by MATLAB software.

Figure 4
figure 4

Trajectory of the solution to (3.1) for time t with \(x(t)\)

Full size image

In Fig. 5, the nonlinear SDIDE (3.1) of second order without stochastic term was solved by MATLAB software.

Figure 5
figure 5

Trajectory of the solution for (3.1) without stochastic term

Full size image

In Fig. 6, the nonlinear SDIDE (3.1) of second order with stochastic term that equals 30 was solved by MATLAB software.

Figure 6
figure 6

Trajectory of the solution of (3.1) with stochastic term equals 30

Full size image

As a result, we may say that all the solutions of equation (3.1) are stable, continuous, and bounded.

4 Conclusions

In this paper, a class of second-order SDIDE has been considered. Three new results have been given on the qualitative properties of solutions for the investigated equation. The proofs of the results are based on the construction of a new Lyapunov functional. To the best of our knowledge, the considered SDIDE has not been investigated in the literature to date. This work has contributed to the qualitative properties of ordinary, delay, stochastic, and integro differential equations of the second order.