1 Introduction

The rapid development of modern communication technology provides more advanced communication technology for the construction of the Internet of things [1, 2]. As multimedia communication technology becomes more mature, data information transfer is faster, anti-interference ability is stronger, and data is more secure. The process of wireless communication is to transform the required information, including text, voice, video, etc., into digital signal [3, 4] under the packaging and conversion of baseband. Then, the digital signal is converted into waveform in the RF modulation center, transmitted in the antenna after power amplifier and filter, and logistics distribution is carried out in the base station [5, 6]. After reaching the destination antenna, the filter extracts the original wave again, and then the wave is demodulated and decoded into the original information form. In the process of wireless communication, the influence of noise in the channels needs to be considered. Filter, as a frequency selection and interference elimination device, can be said to be the channel of any information transmission, which is the key link of the mobile communication industry chain [7,8,9].

Compared with the traditional filter, the adaptive filter has stronger adaptability and better filtering performance. Adaptive filters have a strong effect on signal processing, such as adaptive beamforming [10], acoustic echo cancelation [11, 12] and channel equalization [13]. As the core of adaptive filters, adaptive filter algorithms are the key to the development of filters. Among them, mean square error (MSE) has been the typical criterion of adaptive filtering algorithms. Owing to its simple structure and rapid convergence, the LMS algorithm has been applied in many fields [14,15,16]. Nevertheless, the performance of the LMS algorithm is not optimal, one problem is that the algorithm is vulnerable to the input signal, the other problem is the contradiction between step size and steady-state error. Subsequently, the NLMS algorithm was proposed to solve these problems by normalizing the power of the input signal [17]. However, when signals are disturbed by abnormal values such as impulse noise, the performance of the LMS-type algorithm will be seriously degraded. Therefore, some robustness criteria have been proposed and successfully applied to adaptive filtering algorithms to deal with adaptive signal under impulsive noise, such as adaptive wireless channel tracking [18] and blind source decomposition [19]. Some typical robustness criteria include maximum correntropy criterion (MCC) [20, 21], minimum error entropy (MEE) [22, 23] and generalized MCC [24]. They are insensitive to large outliers, which can effectively deal with impulse noise interference.

However, the current adaptive filtering algorithms only can be used for one-dimensional signals processing. It is worth noting that combined with geometric algebra, these algorithms can be extended to higher dimensions, so that the correlation of each dimension can be considered in the process of analyzing problems, and the performance of algorithms can be effectively improved.

Geometric algebra (GA) gives an effective computing framework for multi-dimensional signal processing [25, 26]. GA has a wide range of applications, such as image processing [27, 28], multi-dimensional signal processing [29, 30] and computer vision [31, 32]. Combined with this framework, Lopes et al. [33] devised the GA-LMS algorithm and analyzed the feasibility of the algorithm. After that, Al-Nuaimi et al. [34] further exploited the potential of the algorithm, which is applied for point cloud registration. However, the LMS algorithm extended to the GA space still has some limitations, such as its poor performance in non-Gaussian environment. Wang et al. [35] deduced and proposed the GA-MCC algorithm, analyzing its performance in \(\alpha\)-stable noise. The results show that GA-MCC has good robustness, but there is still room for improvement in its convergence rate. Due to the superiority of MEE criterion over MCC criterion, the GA-MEE and GA-MSEMEE algorithms are proposed in this paper to improve the effectiveness of existing GA adaptive filtering algorithms and expand the scope of application.

Our contributions are as follows. Firstly, according to the GA theory, the multi-dimensional problem is transformed into mathematical description, represented by multivectors. Secondly, the algorithms based on the MEE and MSEMEE are deduced in GA space. The original MEE and MSEMEE algorithms can be used for higher dimensional signal processing with the help of GA theory; finally, some experiments validate the effectiveness and robustness of the GA-MEE and GA-MSEMEE algorithms.

The rest of this paper is arranged as follows. Section 2 classifies and systematically reviews the existing studies on adaptive filtering algorithms. Section 3 briefly reviews the basic theory of geometric algebra and the traditional MEE and MSEMEE adaptive filtering algorithms, and gives the derivation process of the GA-MEE and GA-MSEMEE algorithms. The Experimental analysis of the two novel algorithms in \(\alpha\)-stable noise environment is provided in Sect. 4. Section 5 concludes this paper.

2 Related works

As an important branch of information processing, adaptive filtering algorithms have obtained great research results in real and complex domains, especially in signal processing in non-Gaussian environment. Previously, Professor J.C. and his team proposed to use the error signal of Renyi entropy instead of the MSE. Minimum error entropy is capable of getting better error distribution according to [36]. Although MEE criterion can obtain high accuracy, it does not take the mean factor into account, while the characteristics of MSE are just opposite to that of MEE. In this regard, B. Chen et al. [36] proposed a joint criterion building up a connection between MSE and MEE by adding the weight. In addition, recent studies have shown that MEE criterion is superior to MCC criterion and can be used for adaptive filtering [23] and Kalman filtering [22]. Therefore, G. Wang et al. [37] improved the MEE criterion and proposed the recursive MEE algorithm. In the complex domain, Horowitz et al. [16] proposed and verified the performance advantages of complex LMS algorithm. Qiu et al. [38] recently proposed Fractional-order complex correntropy algorithm for signal processing in \(\alpha\)-stable environment. These mature real and complex adaptive filtering algorithms are widely used in various fields [10,11,12, 39]. However, the real adaptive filtering algorithms cannot consider the internal relationship of the signals of each dimension, and the complex filtering algorithms need to convert multi-dimensional signals into complex signals for processing, respectively. Similarly, it cannot well describe the correlation between multi-dimensional signals, which will cause some performance loss and application limitations.

Quaternion, as an extension of real and complex domains, was first proposed by Hamilton and applied to the field of attitude control. Took et al. [40] successfully expressed multi-dimensional signals in meteorology in the form of quaternion, and proposed the quaternion least mean square (QLMS) and the augmented quaternion least mean square (AQLMS) algorithms. The research of the QLMS and AQLMS algorithms provides a theoretical basis for the development of quaternion adaptive filtering algorithms. The quaternion distributed filtering, the widely linear quaternion recursive total least squares, the widely linear power QLMS and the reduced-complexity widely linear QLMS algorithms are proposed one after another [41,42,43,44]. However, these algorithms are more suitable for Gaussian signals in linear systems. In order to make the quaternion adaptive filtering algorithms better used in signal processing in nonlinear channels and improve the universality of the algorithms, Paul et al. [45] further proposed quaternion kernel adaptive filtering algorithm via gradient definition and Hilbert space. The introduction of quaternion tool paves the way for the research of adaptive filtering algorithms for 3D and 4D signals. However, the quaternion-based adaptive filtering algorithms cannot be used in higher dimensional signal processing, and the quaternion-based methods will produce a lot of data redundancy and huge complexity.

Since geometric algebra can provide an ideal mathematical framework for the expression and modeling of multi-dimensional signals, some scholars have applied GA to adaptive filtering [46], feature extraction [26] and image processing [47]. GA-based adaptive filtering algorithms have attracted more and more scholars’ attention. Lopes and Al-Nuaimi et al. [33, 34] deduced the updating rules of the GA-LMS algorithm by using geometric algebra and applied them to 6DOF point cloud registration. Since the GA-LMS algorithm cannot achieve a good trade-off between the convergence rate and the steady-state error, Wang et al. [48, 49] proposed GA-based least-mean Kurtosis (GA-LMK) and GA-based normalized least mean square (GA-NLMS) adaptive filtering algorithms successively to make up for the deficiency of the GA-LMS algorithm. And then, in order to reduce the computational complexity of the GA-LMK algorithm, He et al. [50] continued to deduce and propose the GA-based least-mean fourth (GA-LMF) and least-mean mixed-norm (GA-LMMN) adaptive filtering algorithms. In order to further improve the performance of GA-based adaptive filtering algorithms in non-Gaussian environment, Wang et al. [35] theoretically deduced geometric algebraic correlation (GAC) and proposed an adaptive filtering algorithm (GA-MCC) based on the maximum GAC criterion.

Most of these existing GA-based adaptive filtering algorithms are mainly to improve the performance of the filters in Gaussian environment. For non-Gaussian noise, especially the noise interference similar to that in wireless communication channels, the performance of this kind of algorithms will be greatly reduced. How to optimize the existing GA-based adaptive filtering algorithms and improve their performance in non-Gaussian environment is a problem worth studying. Compared with MCC criterion, the MEE criterion and the joint criterion (MSEMEE) have more advantages in non-Gaussian environment. Hence, this paper extends these two criteria to the GA space and proposes novel GA-based robust algorithms. The \(\alpha\)-stable distribution fits very well with the actual data, and is consistent with multichannel interference in wireless networks and backscatter echoes in radar systems. Therefore, the use of \(\alpha\)-stable distribution to simulate non-Gaussian noise has more general significance.

3 Methods

3.1 Basic theory

Geometric Algebra contains all geometric operators and permits specification of constructions in a coordinate-free manner [47]. Compared with several particular cases of vector and matrix algebras, complex numbers and quaternions, using geometric algebra can deal with higher dimensional signals.

Assuming that an orthogonal basis of \(\mathbb {R}_{n}\) is \(\left\{ e_{1}, e_{2}, \cdots , e_{n}\right\}\), the basis of \(\mathbb {G}_{n}\) can be generated by multiplying the n basis elements (plus the scalar 1) via geometric product. The geometric product of two basis elements is non-commutative, its property is defined as:

$$e_{i} e_{j}= e_{i j}=-e_{j i}=-e_{j} e_{i}, i, j=1, \ldots , n,\quad \forall i \ne j$$
(1)
$$e_{i} e_{i j}= e_{i} e_{i} e_{j}=e_{j},\quad i, j=1, \ldots , n, i \ne j$$
(2)

Given \(n= p + q\), the expression of the operation rule of orthonormal basis is:

$$\begin{aligned} e_{i}^{2}=\left\{ \begin{array}{cc} 1, &{} 1 \le i \le p \\ -1, &{} p+1 \le i \le n \end{array}\right. \end{aligned}$$
(3)

Thus, the basis of \(G_n\) is:

$$\begin{aligned} \left\{ 1, e_{i}, e_{i} e_{j}, \cdots , e_{1} e_{2} \cdots e_{n}\right\} \end{aligned}$$
(4)

The core product in GA space is geometric product. The expression of the geometric product of vector a and b is:

$$\begin{aligned} a b \triangleq a \cdot b+a \wedge b \end{aligned}$$
(5)

in which \(a \cdot b\) represents the inner product, which is commutative, \(a \wedge b\) denotes the outer product, which is not commutative. According to their properties, the following expression can be obtained:

$$\begin{aligned} \left\{ \begin{array}{l} a \cdot b=\frac{1}{2}(a b+b a) \\ a \wedge b=\frac{1}{2}(a b-b a) \end{array}\right. \end{aligned}$$
(6)

Suppose A is a general multivector in \(\mathbb {G}_{n}\), the basic element of \(\mathbb {G}_{n}\) can be defined as:

$$\begin{aligned} A=\langle A\rangle _{0}+\langle A\rangle _{1}+\langle A\rangle _{2}+\cdots =\sum _{s}\langle A\rangle _{s} \end{aligned}$$
(7)

which is made up of its s-vector part \(\langle \cdot \rangle _{s}\).

Actually, any multivector can be decomposed according to [51]:

$$\begin{aligned} B=\sum _{s=0}^{2^{n}-1} e_{s}\left( e^{s} * B\right) =\sum _{s=0}^{2^{n}-1} e_{s}\left\langle e^{s} B\right\rangle =\sum _{s=0}^{2^{n}-1} e_{s} B_{s} \end{aligned}$$
(8)

In the operation of geometric algebra, the main properties used are as follows:

  1. (1)

    Scalar product: \(A^{*} B=\langle A B\rangle _{0}\)

  2. (2)

    Cyclic reordering: \(\langle A B \cdots C\rangle =\langle B \cdots C A\rangle\)

  3. (3)

    Clifford reverse: \(\tilde{A} \triangleq \sum _{s=0}^{n}(-1)^{s(s-1) / 2}\langle A\rangle _{s}\)

  4. (4)

    Magnitude: \(|A| \triangleq \sqrt{A^{*} \tilde{A}}=\sqrt{\sum _{s}\left| \langle A\rangle _{s}\right| ^{2}}\)

3.2 The related adaptive filtering algorithms

3.2.1 The MEE algorithm

Professor J.C. and his research team proposed to replace MSE with the error signal of Renyi entropy in the training of supervised adaptive systems; this method uses a nonparametric estimator-Parzen window to estimate the probability density of a random variable directly from the sample points.

The Renyi entropy of the error sample is defined as:

$$\begin{aligned} \begin{array}{l} H_{a}(e)=\frac{1}{1-\alpha } \log \int f_{e}^{\alpha }(e) d e \\ f_{e}^{\alpha }(e)=\mathbb {E}\left[ f_{e}^{\alpha -1}(e)\right] \approx V_{\alpha }\left( e_{k}\right) \\ V_{\alpha }\left( e_{k}\right) =\left[ \frac{1}{L} \sum _{i=k-L}^{k-1} k_{\sigma }\left( e_{k}-e_{i}\right) \right] ^{\alpha -1} \end{array} \end{aligned}$$
(9)

where \(\alpha\) is the order of entropy, and \(\alpha >0\), \(V_{\alpha }\left( e_{k}\right)\) is information potential. when \(\alpha \rightarrow 1\), Renyi entropy is equivalent to Shannon entropy. In addition, to keep the orientation consistent with the LMS algorithm (minimization), select \(\alpha <1\). In this case, the minimum error entropy can be converted into minimizing the information potential.

Hence, for the traditional minimum error entropy (MEE) algorithm, its core expressions are:

$$\begin{aligned} \begin{array}{l} J(n)=V_{\alpha }\left( e_{n}\right) \\ w(n+1)=w(n)-\mu \left\{ \begin{array}{l} (1-\alpha )\left[ \frac{1}{L} \sum _{i=n-L}^{n-1} k_{\sigma }(e(n)-e(i))\right] ^{\alpha -2} \\ {\left[ \frac{1}{L} \sum _{i=n-L}^{n-1} k_{\sigma }^{\prime }(e(n)-e(i))(x(n)-x(i))\right] } \end{array}\right\} \end{array} \end{aligned}$$
(10)

3.2.2 The MSEMEE algorithm

The mean square error standard has good sensitivity. The minimum error entropy has a good error distribution, especially in the case of high-order statistics. Therefore, based on these two methods, a new performance index is proposed, which combines the advantages of each method to realize the synchronization effectiveness of sensitivity and error distribution.

The core expressions of the LMS algorithm are:

$$\begin{aligned} \begin{array}{l} J(n)=\mathbb {E}\left\{ e^{2}(n)\right\} \\ w(n+1)=w(n)+2 \mu e(n) x(n) \end{array} \end{aligned}$$
(11)

While the MSEMEE algorithm is the mixed of square power of LMS and information potential of MEE. Then the MSEMEE cost function is:

$$\begin{aligned} J(n)=\mathbb {E}\left\{ \eta e^{2}(n)+(1-\eta ) V_{\alpha }(e)\right\} \end{aligned}$$
(12)

in which \(\eta\) is the mixing parameter and \(\eta \in [0,1]\).

Then the corresponding gradient algorithm is:

$$\begin{aligned}&w(n+1)=w(n)+\mu \\ &\qquad \left\{ \begin{array}{c} 2 \eta e(n) x(n)-(1-\eta )(1-\alpha )\left[ \frac{1}{L} \sum _{i=n-L}^{n-1} k_{\sigma }(e(n)-e(i))\right] ^{\alpha -2} \\ \qquad \left[ \frac{1}{L} \sum _{i=n-L}^{n-1} k_{\sigma }^{\prime }(e(n)-e(i))(x(n)-x(i))\right] \end{array}\right\} \end{aligned}$$
(13)

3.3 Problem formulation of adaptive filtering

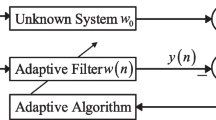
Regarding the linear filtering model, its formulation involves the input signal of length L \(u(n)=\left[ U_{n},U_{n-1},\cdots ,U_{n-L+1}\right] ^{T}\), the system vector to be estimated \(w_{o}=\left[ W_{o 1},W_{o 2},\cdots ,W_{o L}\right] ^{T}\), the weight vector \(w(n)=\left[ W_{1}(n),W_{2}(n),\cdots ,W_{L}(n)\right] ^{T}\) and the desired signal d(n):

$$\begin{aligned} d(n)=u(n)^{H} w_{o}+v_{n}=\sum _{i=1}^{L} \tilde{U}_{n-i+1} W_{o i}+v_{n} \end{aligned}$$
(14)

In this research, we give some assumptions as follows:

  1. (A1)

    The multivector valued components of the input signal u(n) are zero-mean white Gaussian processes with variance \(\sigma _{\mathrm {s}}^{2}\).

  2. (A2)

    The multivector valued components of the additive noise are described by \(\alpha\)-stable processes. \(\alpha\)-stable distribution is a family of four parameter distributions, which can be represented by S (\(\alpha , \beta , \gamma , \sigma\)), in which \(\alpha\) denotes the characteristic index, which describes the tail of the distribution; \(\beta\) denotes the skewness, \(\gamma\) denotes the dispersion coefficient, \(\sigma\) denotes the distribution position.

  3. (A3)

    The noise \(v_{n}\), the initial weight vector \(w_{o}\), the input signal u(n) and the weight error vector \(\Delta w_{n}\) are uncorrelated.

3.4 The proposed GA-MEE algorithm

In this part, we deduce the GA-MEE algorithm with the help of GA theory [35]. In traditional algorithms, the cost function of MEE is expressed by information potential. When \(\alpha \in (0,1)\), the minimum error entropy is equal to minimize the cost function. The GA-MEE cost function can be obtained by rewriting formula (9) in the GA form.

$$\begin{aligned} J\left( w_{i-1}\right) =V_{\alpha }\left( e_{i}\right) =\left[ \frac{1}{L} \sum _{l=i-L}^{i-1} k_{\sigma }(E(i)-E(l))\right] ^{\alpha -1} \end{aligned}$$
(15)

in which \(E(i)=D(i)-\hat{D}(i), \hat{D}(i)=u_{i}^{H} w_{i-1}\), L denotes the length of the sliding window, \(k_{\sigma }(x)\) denotes the Gaussian kernel defined as \(k_{\sigma }(x)=\exp \left( -\frac{x^{2}}{\sigma ^{2}}\right)\), where \(\sigma\) is the kernel size.

Our algorithms keep the same direction as the LMS algorithm, which is opposite to that of the steepest-descent rule [48], yielding the adaptive rule based on GA:

$$\begin{aligned} w_{i}=w_{i-1}-\mu B\left[ \partial _{w} J\left( w_{i-1}\right) \right] \end{aligned}$$
(16)

where B denotes a multivectors matrix. Choosing different B, we will get various types of adaptive filtering algorithm [48]. let B be the identity matrix here.

The derivative term \(\partial _{w} J\left( w_{i-1}\right)\) in (10) can be calculated as:

$$\begin{aligned} \partial _{w} J\left( w_{i-1}\right)&=\partial _{w} \left[ \frac{1}{L} \sum _{l=i-L}^{i-1} \exp \left( -\frac{|E(i)-E(l)|^{2}}{\sigma ^{2}}\right) \right] ^{\alpha -1} \\ &=\left\{ \begin{array}{c} \frac{1-\alpha }{L^{\alpha } \sigma ^{2}}\left[ \sum _{l=i-L}^{i-1} \exp \left( -\frac{|E(i)-E(l)|^{2}}{\sigma ^{2}}\right) \right] ^{\alpha -2} \\ {\left[ \sum _{l=i-L}^{i-1} \exp \left( -\frac{|E(i)-E(l)|^{2}}{\sigma ^{2}}\right) \partial _{w}|E(i)-E(l)|^{2}\right] } \end{array}\right\} \end{aligned}$$
(17)

where \(|E(i)-E(l)|^{2}\) is given by

$$\begin{aligned} |E(i)-E(l)|^{2}&=(E(i)-E(l)) *(E(i)-E(l) \tilde{)}\\ &=E(i)*\tilde{E}(i)-E(i)*\tilde{E}(l)-E(l)*\tilde{E}(i)+E(l)*\tilde{E}(l).\\ &=|E(i)|^{2}+|E(l)|^{2}-2\langle E(i) \tilde{E}(l)\rangle \end{aligned}$$
(18)

According to formula (8), the differential operator \(\partial _{w}\) can be expressed in another form. Thus, we obtain the new expression of \(\partial _{w}\):

$$\begin{aligned} \partial _{w}=\sum _{k=1}^{2^{n}} \gamma _{k}\left\langle \tilde{\gamma }_{k} \partial _{w}\right\rangle =\sum _{k=1}^{2^{n}} \gamma _{k} \partial _{w, k} \end{aligned}$$
(19)

in which \(\partial _{w,k}\) is the common derivative from standard calculus and only relates to blade \(k, \left\{ \gamma _{k}\right\}\) is the basis of \(\mathbb {G}_{n}\).

Similarly, given \(\hat{D}(i)=u_{i}^{H} w_{i-1}\), then \(\hat{D}(i)\) can be expanded as follows according to (8):

$$\begin{aligned} \hat{D}(i)=u_{i}^{H} w_{i-1}=\sum _{A=1}^{2^{n}} \gamma _{A}\left\langle \tilde{\gamma }_{A}\left( u_{i}^{H} w_{i-1}\right) \right\rangle \end{aligned}$$
(20)

Since \(u_{i}\) and \(w_{i-1}\) are arrays with M multivector entries, they can be decomposed as follows by employing (8),

$$\begin{aligned} u_{i}^{H}=\sum _{A=1}^{2^{n}}\left\langle u_{i}^{T} \gamma _{A}\right\rangle \tilde{\gamma }_{A}=\sum _{A=1}^{2^{n}} u_{i, A}^{T} \tilde{\gamma }_{A} \end{aligned}$$
(21)

and

$$\begin{aligned} w_{i-1}=\sum _{A=1}^{2^{n}} \gamma _{A}\left\langle \tilde{\gamma }_{A} w_{i-1}\right\rangle =\sum _{A=1}^{2^{n}} \gamma _{A} w_{i-1, A} \end{aligned}$$
(22)

Plugging (21) and (22) back into (20),

$$\begin{aligned} \hat{D}(i)=u_{i}^{*} w_{i-1}&=\sum _{A=1}^{2^{n}} \gamma _{A}\left\langle \tilde{\gamma }_{A}\left( u_{i}^{*} w_{i-1}\right) \right\rangle \\ &=\sum _{A=1}^{2^{n}} \gamma _{A}\left\langle \tilde{\gamma }_{A}\left( \sum _{B=1}^{2^{n}} u_{B}^{T} \tilde{\gamma }_{B} \sum _{C=1}^{2^{n}} \gamma _{C} w_{C}\right) \right\rangle \\ &=\sum _{A=1}^{2^{n}} \gamma _{A} \sum _{B, C=1}^{2^{n}}\left\langle \tilde{\gamma }_{A}\left( u_{B}^{T} \tilde{\gamma }_{B} \gamma _{C} w_{C}\right) \right\rangle \\ &=\sum _{A=1}^{2^{n}} \gamma _{A} \sum _{B, C=1}^{2^{n}}\left\langle \tilde{\gamma }_{A} \tilde{\gamma }_{B} \gamma _{C}\right\rangle \left( u_{B}^{T} w_{C}\right) \\ &=\sum _{A=1}^{2^{n}} \gamma _{A} \hat{D}_{A} \end{aligned}$$
(23)

in which

$$\begin{aligned} \hat{D}_{A}=\sum _{B, C=1}^{2^{n}}\left\langle \tilde{\gamma }_{A} \tilde{\gamma }_{B} \gamma _{C}\right\rangle \left( u_{B}^{T} w_{C}\right) , A=1, \cdots , 2^{n} \end{aligned}$$
(24)

Thus, the derivative term \(\partial _{w}|E(i)-E(l)|^{2}\) in (17) can be calculated as:

$$\begin{aligned} \partial _{w}|E(i)-E(l)|^{2}=\partial _{w}|E(i)|^{2}+\partial _{w}|E(l)|^{2}-2 \partial _{w}\langle E(i) \tilde{E}(l)\rangle \end{aligned}$$
(25)

According to (19), each term of equation (25) can be expanded:

$$\begin{aligned} \begin{array}{l} \partial _{w}|E(i)|^{2}=\left( \sum _{D=1}^{2^{n}} \gamma _{D} \partial _{w, D}\right) \left( \sum _{A=1}^{2^{n}} e_{i, A}^{2}\right) =\sum _{A, D=1}^{2^{n}} \gamma _{D} \partial _{w, D} e_{i, A}^{2} \\ \partial _{w}|E(l)|^{2}=\left( \sum _{D=1}^{2^{n}} \gamma _{D} \partial _{w, D}\right) \left( \sum _{A=1}^{2^{n}} e_{l, A}^{2}\right) =\sum _{A, D=1}^{2^{n}} \gamma _{D} \partial _{w, D} e_{l, A}^{2} \\ \partial _{w}\langle E(i) \tilde{E}(l)\rangle =\left( \sum _{D=1}^{2^{n}} \gamma _{D} \partial _{w, D}\right) \left( \sum _{A=1}^{2^{n}} \gamma _{A} e_{i, A} * \sum _{A=1}^{2^{n}} e_{l, A} \tilde{\gamma }_{A}\right) \\ \qquad =\sum _{A, D=1}^{2^{n}} \gamma _{D} \partial _{w, D} e_{i, A} e_{l, A} \end{array} \end{aligned}$$
(26)

in which

$$\begin{aligned} \begin{array}{l} \partial _{w, D} e_{i, A}^{2}=2 e_{i, A}\left( \partial _{w, D}\left( d_{i, A}-\hat{d}_{i, A}\right) \right) =-2 e_{i, A}\left( \partial _{w, D} \hat{d}_{i, A}\right) \\ \partial _{w, D} e_{l, A}^{2}=2 e_{l, A}\left( \partial _{w, D}\left( d_{l, A}-\hat{d}_{l, A}\right) \right) =-2 e_{l, A}\left( \partial _{w, D} \hat{d}_{l, A}\right) \\ \partial _{w, D} e_{i, A} e_{l, A}=e_{i, A}\left( \partial _{w, D} e_{l, A}\right) +\left( \partial _{w, D} e_{i, A}\right) e_{l, A}\\ \qquad =-e_{i, A}\left( \partial _{w, D} \hat{d}_{l, A}\right) -\left( \partial _{w, D} \hat{d}_{i, A}\right) e_{l, A} \end{array} \end{aligned}$$
(27)

According to (24), the parts \(\hat{d}_{i, A}\) and \(\hat{d}_{l, A}\) in formula (27) can be expressed as:

$$\begin{aligned} \begin{array}{l} \hat{d}_{i, A}=\sum _{B, C=1}^{2^{n}}\left\langle \tilde{\gamma }_{A} \tilde{\gamma }_{B} \gamma _{C}\right\rangle \left( u_{i B}^{T} w_{C}\right) , A=1, \cdots , 2^{n} \\ \hat{d}_{l, A}=\sum _{B, C=1}^{2^{n}}\left\langle \tilde{\gamma }_{A} \tilde{\gamma }_{B} \gamma _{C}\right\rangle \left( u_{l B}^{T} w_{C}\right) , A=1, \cdots , 2^{n} \end{array} \end{aligned}$$
(28)

From (27), \(\partial _{w, D} \hat{d}_{i, A}\) and \(\partial _{w, D} \hat{d}_{l, A}\) need to be calculated, according to (28), \(\partial _{w, D} \hat{d}_{i, A}\) can be unfolded as:

$$\begin{aligned} \partial _{w, D} \hat{d}_{i, A}&=\partial _{w, D}\left[ \sum _{B, C=1}^{2^{n}}\left\langle \tilde{\gamma }_{A} \tilde{\gamma }_{B} \gamma _{C}\right\rangle \left( u_{i B}^{T} w_{C}\right) \right] \\ &=\sum _{B, C=1}^{2^{n}}\left\langle \tilde{\gamma }_{A} \tilde{\gamma }_{B} \gamma _{C}\right\rangle \partial _{w, D}\left( u_{i B}^{T} w_{C}\right) \\ &=\sum _{B, C=1}^{2^{n}}\left\langle \tilde{\gamma }_{A} \tilde{\gamma }_{B} \gamma _{C}\right\rangle \delta _{C D} u_{i B}^{T} \end{aligned}$$
(29)

in the same way,

$$\begin{aligned} \partial _{w, D} \hat{d}_{l, A}=\sum _{B, C=1}^{2^{n}}\left\langle \tilde{\gamma }_{A} \tilde{\gamma }_{B} \gamma _{C}\right\rangle \delta _{C D} u_{l B}^{T} \end{aligned}$$
(30)

Plugging (27), (29) and (30) into (26) yields

$$\begin{aligned} \partial _{w}|E(i)|^{2}&=-2 e_{i, A}\left( \partial _{w, D} \hat{d}_{i, A}\right) \\ &=-2 \sum _{A, D=1}^{2^{n}} \gamma _{D} e_{i, A} \sum _{B, C=1}^{2^{n}}\left\langle \tilde{\gamma }_{A} \tilde{\gamma }_{B} \gamma _{C}\right\rangle \delta _{C D} u_{i B}^{T} \\ &=-2 \sum _{A, D=1}^{2^{n}} e_{i, A} \sum _{B, C=1}^{2^{n}} \gamma _{D}\left\langle \tilde{\gamma }_{A} \tilde{\gamma }_{B} \gamma _{D}\right) u_{i B}^{T} \\ &=-2 \sum _{A, D=1}^{2^{n}} e_{i, A} \gamma _{D}\left\langle \tilde{\gamma }_{A} u_{i}^{H} \gamma _{D}\right\rangle \\ &=-2 \sum _{A=1}^{2^{n}} e_{i, A} \gamma _{D}\left\langle \tilde{\gamma }_{D} u_{i} \gamma _{A}\right\rangle \\ &=-2 \sum _{A=1}^{2^{n}} e_{i, A} u_{i} \gamma _{A} \\ &=-2 u_{i} E(i) \end{aligned}$$
(31)

in the same way,

$$\begin{aligned} \partial _{w}|E(l)|^{2}&=-2 u_{l} E(l) \end{aligned}$$
(32)

and

$$\begin{aligned} \partial _{w}\langle E(i) \tilde{E}(l)\rangle&=-\sum _{A, D=1}^{2^{n}} \gamma _{D}\left\{ \begin{array}{c} e_{i, A} \sum _{B, C=1}^{2^{n}}\left\langle \tilde{\gamma }_{A} \tilde{\gamma }_{B} \gamma _{C}\right\rangle \delta _{C D} u_{l B}^{T}+ \\ \left( \sum _{B, C=1}^{2^{n}}\left\langle \tilde{\gamma }_{A} \tilde{\gamma }_{B} \gamma _{C}\right\rangle \delta _{C D} u_{i B}^{T}\right) e_{l, A} \end{array}\right\} \\ &=-\sum _{A=1}^{2^{n}} e_{i, A} \gamma _{D}\left\langle \tilde{\gamma }_{D} u_{l} \gamma _{A}\right\rangle -\sum _{A=1}^{2^{n}} \gamma _{D}\left\langle \tilde{\gamma }_{D} u_{i} \gamma _{A}\right\rangle e_{l, A} \\ &=-u_{l} E(i)-u_{i} E(l) \end{aligned}$$
(33)

Plugging (31), (32) and (33) into (25) yields the following expression:

$$\begin{aligned} \partial _{w}|E(i)-E(l)|^{2}&=-2 u_{i} E(i)-2 u_{l} E(l)-2\left( -u_{l} E(i)-u_{i} E(l)\right) \\ &=-2 u_{i} E(i)-2 u_{l} E(l)+2 u_{l} E(i)+2 u_{i} E(l) \\ &=-2\left( u_{i}-u_{l}\right) (E(i)-E(l)) \end{aligned}$$
(34)

Finally, plugging (34) into (17), the gradient expression can be written as:

$$\begin{aligned} \partial _{w} J\left( w_{i-1}\right)&=\partial _{w} \left[ \frac{1}{L} \sum _{l=i-L}^{i-1} \exp \left( -\frac{|E(i)-E(l)|^{2}}{\sigma ^{2}}\right) \right] ^{\alpha -1} \\ &=\left\{ \begin{array}{l} \frac{2(\alpha -1)}{L^{\alpha } \sigma ^{2}}\left[ \sum _{l=i-L}^{i-1} \exp \left( -\frac{|E(i)-E(l)|^{2}}{\sigma ^{2}}\right) \right] ^{\alpha -2} \\ {\left[ \sum _{l=i-L}^{i-1} \exp \left( -\frac{|E(i)-E(l)|^{2}}{\sigma ^{2}}\right) \left( u_{i}-u_{l}\right) (E(i)-E(l))\right] } \end{array}\right\} \end{aligned}$$
(35)

Then, plugging (35) into (16), we can obtain the GA-MEE updating rule:

$$\begin{aligned} w_{i}=w_{i-1}+\mu \left\{ \begin{array}{c} \frac{2(1-\alpha )}{L^{\alpha } \sigma ^{2}}\left[ \sum _{l=i-L}^{i-1} \exp \left( -\frac{|E(i)-E(l)|^{2}}{\sigma ^{2}}\right) \right] ^{\alpha -2} \\ {\left[ \sum _{l=i-L}^{i-1} \exp \left( -\frac{|E(i)-E(l)|^{2}}{\sigma ^{2}}\right) \left( u_{i}-u_{l}\right) (E(i)-E(l))\right] } \end{array}\right\} \end{aligned}$$
(36)

in which \(\upmu\) denotes the step size.

3.5 The proposed GA-MSEMEE algorithm

In the same way, according to GA theory, we can obtain the GA-MSEMEE cost function as follows by rewriting formula (12) in the GA form.

$$\begin{aligned} J\left( w_{i-1}\right) =\mathbb {E}\left\{ \eta |E(i)|^{2}+(1-\eta ) V_{\alpha }\left( e_{i}\right) \right\} \end{aligned}$$
(37)

where \(\eta\) is the mixing parameter and \(\eta \in [0,1]\).

When we replace the mathematical expectation of the preceding and subsequent terms of equation (37) with instantaneous value and sample average, respectively, \(\partial _{w} J\left( w_{i-1}\right)\) can be expressed as:

$$\begin{aligned} \partial _{w} J\left( w_{i-1}\right)&=\partial _{w}\left( \mathbb {E}\left\{ \eta |E(i)|^{2}+(1-\eta ) V_{\alpha }\left( e_{i}\right) \right\} \right) \\ &=\partial _{w}\left( \eta |E(i)|^{2}+(1-\eta ) \partial _{w} V_{\alpha }\left( e_{i}\right) \right) \\ &=\eta {\partial }_{w}|E(i)|^{2}+(1-\eta ) \partial _{w} V_{\alpha }\left( e_{i}\right) \end{aligned}$$
(38)

The former term of formula (38) is equivalent to GA-LMS algorithm, and the latter term of formula (38) is to seek deviation guide to information potential. In order to keep the whole direction consistent (minimized), select \(\alpha \in (0,1)\). According to (32), \(\partial _{w}|E(i)|^{2}\) is:

$$\begin{aligned} \partial _{w}|E(i)|^{2}=-2 u_{i} E(i) \end{aligned}$$
(39)

According to (15) and (35), \(\partial _{w} V_{\alpha }\left( e_{i}\right)\) is:

$$\begin{aligned} \partial _{w} V_{\alpha }\left( e_{i}\right) =\left\{ \begin{array}{c} \frac{2(\alpha -1)}{L^{\alpha } \sigma ^{2}}\left[ \sum _{l=i-L}^{i-1} \exp \left( -\frac{|E(i)-E(l)|^{2}}{\sigma ^{2}}\right) \right] ^{\alpha -2} \\ {\left[ \sum _{l=i-L}^{i-1} \exp \left( -\frac{|E(i)-E(l)|^{2}}{\sigma ^{2}}\right) \left( u_{i}-u_{l}\right) (E(i)-E(l))\right] } \end{array}\right\} \end{aligned}$$
(40)

Plugging (39) and (40) into (38), we can obtain the GA-MSEMEE updating rule:

$$\begin{aligned} w_{i}=w_{i-1}+\mu \left\{ \begin{array}{c} 2 \eta u_{i} E(i)+\frac{2(1-\eta )(1-\alpha )}{L^{\alpha } \sigma ^{2}}\left[ \sum _{l=i-L}^{i-1} \exp \left( -\frac{|E(i)-E(l)|^{2}}{\sigma ^{2}}\right) \right] ^{\alpha -2} \\ {\left[ \sum _{l=i-L}^{i-1} \exp \left( -\frac{|E(i)-E(l)|^{2}}{\sigma ^{2}}\right) \left( u_{i}-u_{l}\right) (E(i)-E(l))\right] } \end{array}\right\} \end{aligned}$$
(41)

in which \(\mu\) denotes the step size, \(\eta\) denotes the mixing parameter and \(\eta \in [0,1]\).

4 Results and discussion

This section carries out some experiments, analyzing the performance of the two novel algorithms in \(\alpha\)-stable noise environment. First of all, in order to know how to select appropriate adjustable parameters for the GA-MEE and GA-MSEMEE algorithms, the experimental part analyzes the influence of these parameters (the kernel width \(\sigma\), the order of entropy \(\alpha\) and weight coefficient \(\eta\)) on the mean-square deviation (MSD) learning curves in detail. Secondly, the GA-MEE and GA-MSEMEE algorithms are compared with other GA-based algorithms to verify their superiority. Finally, the algorithms are applied to multi-dimensional signal denoising in \(\alpha\)-stable noise environment.

All MSD learning curves and the experimental data are averaged 50 independent runs. In this paper, initial weight vector \(\omega _{0}\) denotes a \(5 \times 1\) multivector, and the length of the sliding window is \(L = 8\). The input signal and noise are shown in A1 and A2, \(\alpha\)-stable distribution is given by S (1.5, 0, 1, 0) in the experiment. In addition, we use the generalized signal-to-noise ratio (\(\text {GSNR}=10 \log \left( \sigma _{s}^{2} / \gamma _{v}\right)\)) to describe the relationship between the input signal and noise, \(\sigma _{s}^{2}\) is the variance of input signal multivector, \(\gamma _{v}\) is the dispersion coefficient of noise.

4.1 The performance of GA-MEE and GA-MSEMEE algorithms under different parameters

Herein, we discuss the effect of the parameters \(\sigma , \eta\) and \(\alpha\) on the performance of the two novel algorithms for 4-dimension signals. The performance of the two novel algorithms is estimated by the MSD, \(\text {MSD}=\mathbb {E}\left\{ \left\| w_{0}-w(n)\right\| _{2}^{2}\right\}\). According to equation (36) and (41), the GA-MEE algorithm mainly involves the parameters \(\sigma\) and \(\alpha\), and the GA-MSEMEE algorithm mainly involves the parameters \(\sigma , \eta\) and \(\alpha\). In the following experiments, we select \(\mu _{\text {GA-MEE}}=\mu _{\text {GA-MSEMEE}}=0.5\) and \(\text {GSNR}=0\) dB for the GA-MEE and GA-MSEMEE algorithms.

4.1.1 GA-MEE algorithm

This section selects different parameters \(\sigma\) and \(\alpha\), then calculates the MSD of the GA-MEE algorithm under different parameters. Table 1 displays the steady-state MSDs under different parameters (\(\sigma\) and \(\alpha\)) of the GA-MEE algorithm.

Table 1 The steady-state MSD of the GA-MEE algorithm
Full size table

To further instinctively analyze the effect of kernel width and order of entropy on the GA-MEE algorithm, the steady-state MSD taken as a function of kernel width and order of entropy is plotted in Fig. 1 for various values of the kernel width \(\sigma\) and the order of entropy \(\alpha\).

The tendency of steady-state values in respect of kernel width and order of entropy is clearly highlighted in Fig. 1. It can be obtained from Table 1 and the 3-dimensional diagram that the steady-state MSD is smaller with both larger values of \(\sigma\) and \(\alpha\).

Figure 2 demonstrates the instantaneous MSDs of the GA-MEE under various parameters. The GA-MEE1, GA-MEE2, GA-MEE3, GA-MEE4, and GA-MEE5 denote [\(\alpha =0.3, \sigma =50\)], [\(\alpha =0.5, \sigma =60\)], [\(\alpha =0.6, \sigma =70\)], [\(\alpha =0.7, \sigma =90\)] and [\(\alpha =0.8, \sigma =100\)], respectively. Since increasing two parameters at the same time leads to the decrease in steady-state value and slow convergence rate, it is difficult to determine the role of a single parameter in the performance of the GA-MEE. Therefore, it is necessary to use the method of controlling variables.

Fig. 1
figure 1

The steady-state MSD is taken as a function of kernel width and order of entropy

Full size image
Fig. 2
figure 2

The instantaneous MSDs of the GA-MEE under various parameters

Full size image
Fig. 3
figure 3

The instantaneous MSDs of the GA-MEE under different \(\sigma\)

Full size image
Fig. 4
figure 4

The instantaneous MSDs of the GA-MEE under different \(\alpha\)

Full size image
Fig. 5
figure 5

The steady-state MSD is taken as a function of kernel width and weight coefficient

Full size image

Different parameter \(\sigma\): The value of parameter \(\alpha\) is setting as 0.6, and the values of parameter \(\sigma\) are setting as 50, 60, 70, 90, 100, respectively. Figure 3 shows the instantaneous MSDs of the GA-MEE under various \(\sigma\). It can be seen from Fig. 3, as kernel width increases, the steady-state MSD decreases and convergence rate increases. But when the parameter \(\sigma\) exceeds a certain value, the convergence rate decreases gradually. So, the selection of \(\sigma\) should balance the steady-state MSD and convergence rate. In this group of experiments, its convergence rate is the best when \(\sigma =70\).

Different parameter \(\alpha\): The value of parameter \(\sigma\) is setting as 70, and the values of parameter \(\alpha\) are setting as 0.3, 0.5, 0.6, 0.7, 0.8, respectively. Figure 4 demonstrates the instantaneous MSDs of the GA-MEE under various \(\alpha\). the steady-state MSD increases with the increase in the order of entropy \(\alpha\), and the convergence rate decreases obviously. So, the selection of \(\alpha\) should balance the steady-state MSD and convergence rate.

4.1.2 GA-MSEMEE algorithm

From the experimental part of the GA-MEE algorithm, it is concluded that the greater the parameter \(\alpha\), the slower the convergence rate. In order to study the influence of parameters on the GA-MSEMEE algorithm, this section selects different parameters \(\sigma\) and \(\eta\), to analyze the performance of the GA-MSEMEE when \(\alpha =0.8\). Table 2 displays the steady-state MSDs under different parameters (\(\sigma\) and \(\eta\)) of the GA-MSEMEE algorithm.

To further instinctively analyze the effect of kernel width and weight coefficient on the GA-MSEMEE algorithm, the steady-state MSD taken as a function of kernel width and weight coefficient is plotted in Fig. 5 for various values of kernel width \(\sigma\) and weight coefficient \(\eta\).

Table 2 The steady-state MSD of the GA-MSEMEE algorithm
Full size table

Figure 5 clearly shows the tendency of steady-state MSD in relation to kernel width and weight coefficient. It is shown as Table 2 and 3-dimensional diagram that the steady-state value is smaller as \(\sigma\) becomes larger. However, from the numerical point of view, the influence of the weight coefficient \(\eta\) on MSD is not obvious.

Figure 6 shows the MSD learning curves of the GA-MSEMEE under various parameters, in which GA-MSEMEE1, GA-MSEMEE2, GA-MSEMEE3, GA-MSEMEE4, and GA-MSEMEE5 denote [\(\eta =9 \times 10^{-6}, \sigma =50\)], [\(\eta =8.5 \times 10^{-6}, \sigma =60\)], [\(\eta =8 \times 10^{-6}, \sigma =70\)], [\(\eta =7.5 \times 10^{-6}, \sigma =90\)] and [\(\eta =7 \times 10^{-6}, \sigma =100\)], respectively. Since it is difficult to determine the role of a single parameter in the performance of the GA-MSEMEE, it is necessary to use the method of controlling variables.

Different parameter \(\sigma\): The value of parameter \(\eta\) is setting as \(8.5 \times 10^{-6}\), and the values of parameter \(\sigma\) are setting as 50, 60, 70, 90, 100, respectively. Figure 7 shows the instantaneous MSDs of the GA-MSEMEE under various \(\sigma\). It is concluded from Fig. 7 that as the kernel width becomes more larger, the steady-state MSD and convergence rate decrease gradually. Comprehensively considering the above two indicators, GA-MSEMEE has better performance when \(\sigma =70\) in this group of experiments.

Fig. 6
figure 6

The instantaneous MSDs of the GA-MSEMEE under various parameters

Full size image
Fig. 7
figure 7

The instantaneous MSDs of the GA-MSEMEE under different \(\sigma\)

Full size image
Fig. 8
figure 8

The instantaneous MSDs of the GA-MSEMEE under different \(\eta\)

Full size image
Fig. 9
figure 9

The instantaneous MSDs of different algorithms. a GSNR = 0 dB; b GSNR = −1 dB

Full size image

Different parameter \(\eta\): The value of parameter \(\sigma\) is setting as 70. Since the values of parameters \(\eta\) are similar in Table 2, it is difficult to see the impact of these parameters on the MSDs of the GA-MSEMEE. Thus, we set the parameters \(\eta\) at large intervals, which are: \(7 \times 10^{-6}, 7 \times 10^{-5}, 7 \times 10^{-4}, 8 \times 10^{-4}\) and \(9 \times 10^{-4}\). Figure 8 shows the instantaneous MSDs of the GA-MSEMEE under different \(\eta\). As \(\eta\) increases by ten times, the convergence rate becomes faster, the steady-state MSD gradually increases, and the robustness of the algorithm becomes worse. Therefore, the selection of weight coefficient should comprehensively compare the performance of three aspects. In this group of experiments, GA-MSEMEE has the best performance when \(\eta =7 \times 10^{-5}\).

4.2 Comparison of different GA-based algorithms

In this part, we contrast the MSD learning curves of the two novel algorithms to that of GA-LMS [33], GA-NLMS [49], GA-MCC [35] algorithms under different GSNR. Their parameters are set as follows: \(\mu _{\text {G A-LMS}}=8 \times 10^{-4}, \mu _{\text {G A-NLMS}}=0.8, \mu _{\text {GA-MCC}}=0.5(\sigma =40), \mu _{\text {GA-MEE}}=0.5(\alpha =0.1, \sigma =90), \mu _{\text {GA-MSEMEE}}=0.5(\alpha =0.1, \sigma =300, \eta =0.0006)\), trying to make the convergence rate of each algorithm consistent. Figure 9 demonstrates the instantaneous MSDs of different algorithms.

As can be seen from Fig. 9, compared with GA-MCC, the GA-MEE has better steady-state MSD and convergence rate, but its convergence rate slows down significantly with the decrease in GSNR. Compared with GA-based LMS-type algorithms, the GA-MEE has better steady-state MSD and robustness, but GA-MEE needs more iterations to converge. The improved GA-MSEMEE algorithm solves this problem to a certain extent. The GA-MSEMEE always maintains superior convergence rate, good steady-state MSD and robustness under different GSNR.

4.3 Application and multi-dimensional signal analysis

In this part, the two novel algorithms are applied to signal denoising. In order to test their superiority in \(\alpha\)-stable noise environment, we performed the following experiments.

Fig. 10
figure 10

The denoising results of 4-dimensional signal with different algorithms. a GA-LMS; b GA-NLMS; c GA-MCC; d GA-MEE; e GA-MSEMEE

Full size image
Fig. 11
figure 11

The average 4-dimensional signal recovery errors of different algorithms

Full size image
Fig. 12
figure 12

The denoising results of 8-dimensional signal with different algorithms. a GA-MEE; b GA-MSEMEE

Full size image

Figure 10 demonstrates the denoising results of 4-dimension signal with GA-LMS, GA-NLMS, GA-MCC, GA-MEE and GA-MSEMEE when GSNR = 0 dB. Their parameters are set as follows: \(\mu _{\text {GA-LMS}}=7 \times 10^{-7}, \mu _{\text {GA-NLMS}}=7 \times 10^{-4}, \mu _{\text {GA-MCC}}=0.5(\sigma =200), \mu _{\text {GA-MEE}}=0.5(\alpha =0.8, \sigma =300), \mu _{\text {GA-MSEMEE}}=0.5(\alpha =0.1, \sigma =300, \eta =2 \times 10^{-6})\). As shown in Fig. 10, the GA-LMS, GA-NLMS and GA-MCC algorithms all need an adaptive process at the beginning of denoising, which the proposed algorithms do not need. Figure 11 shows the average 4-dimensional signal recovery errors of different algorithms with different GSNR. The recovery error of 4-dimensional signal is described by \(\left\| u^{\prime }-u\right\| _{2}^{2}\), which represents the norm square of the difference between the denoised signal and the clean signal.

What is more, it is worth noting that the two novel algorithms can be applied to higher dimensional signal processing. Figure 12 demonstrates the denoising results of 8-dimensional signal with GA-MEE and GA-MSEMEE when GSNR = 0 dB.

4.4 Computational Complexity

The running time of different algorithms for 4-dimensional and 8-dimensional signal denoising is shown in Table 3. The experiments are carried out via MATLAB with Intel (R) Core (TM) i7-6500U 2.50GHz CPU and 4 GB memory.

Table 3 The running time (second) of different algorithms
Full size table

Table 3 shows that the proposed algorithms in this paper have higher computational complexity. The reason for the higher computational complexity of GA-MEE algorithm is that it involves the calculation of minimum error entropy, which includes exponential operation of different error signals. The computational complexity of GA-MSEMEE is the highest, mainly because GA-MSEMEE algorithm is acquired by fusing MSE and MEE through a weight coefficient.

5 Conclusions

Two novel GA-based algorithms GA-MEE and GA-MSEMEE are proposed, which are deduced from the MEE criterion and the joint criterion, respectively, combined with GA theory. The GA-MEE and GA-MSEMEE algorithms show strong robustness and high precision for high-order signal processing in \(\alpha\)-stable noise environment. However, although the GA-MEE shows more robustness than other algorithms, its convergence rate and sensitivity are low. The GA-MSEMEE can effectively compensate for the lack of the GA-MEE. The experiments demonstrate that the GA-MSEMEE achieves a good balance between robustness and convergence rate.

Due to the high accuracy and sensitivity of the GA-MSEMEE, the algorithm can also be applied to more aspects, such as signal prediction, which can be further studied. Moreover, how to reduce the computational complexity is also a major direction of further research.