1 Introduction

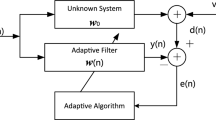
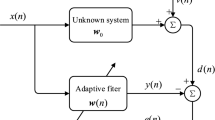
In many cases where adaptive algorithms are used for channel estimation, fixed step sizes are often designed to facilitate engineering applications. Under this case, a compromise is often required between fast adaptation to overcome input variations and slow adaptation to cope with system noise in order to obtain the best performance [1]. For this problem, a large strand of research has made improvements on the basis of the traditional fixed step-size least mean square (LMS) adaptive algorithm, so that the algorithm can change the step size with the change of the mean square error, thus solving the problem faced previously and achieving better results [2, 3]. However, the above methods are applied in the environment of Gaussian noise, but in practical engineering applications the system is often disturbed by a large amount of non-Gaussian noise. The literature has shown that the most coastal areas around the world are flooded with impulsive interference in the hydroacoustic channel due to the presence of a large number of drum shrimp family organisms (which emit strong pulses by opening and closing the knuckles of their large cheeks) [4]. The traditional LMS algorithm only takes into account the second-order statistics of data, and so it works well under Gaussian noise interference but performs generally when it encounters non-Gaussian noise such as impulse noise [5]. To overcome this problem, researchers have proposed the least mean p-power (LMP) algorithm by using lower-order statistics of the data to replace the second-order statistics [6, 7]. LMP algorithm is a nonlinear filtering algorithm that uses generalized correntropy as the cost function. Compared with traditional adaptive filtering algorithms, LMP algorithm has better robustness in dealing with impulsive interference, sparse channels or abrupt channel changes. Therefore, this paper improves the LMP algorithm when estimating the underwater acoustic channel under impulse interference. The system block diagram of the general adaptive filtering algorithm to implement channel estimation is shown in Fig. 1.

Fig. 1
figure 1

Adaptive filter system block

Full size image

2 Proposed algorithm

The step size of the traditional LMP algorithm is a fixed value, which cannot meet the requirements of faster convergence speed and lower steady-state error at the same time. Therefore, it is necessary to speed up convergence speed in the initial stage of adaptation and reduce system error after reaching a steady state. Variable step size is an effective method to solve the algorithm’s convergence speed and steady-state error, but the traditional variable step-size algorithm only considers the current update error and ignores the influence of errors at other moments. In an actual simulation, it is found that although the convergence effect is better than those of other algorithms, it does not meet expectations. Therefore, based on the traditional variable step-size LMP (VSS-LMP) algorithm, this paper considers the influence of the error of the previous several times on the current state and constructs the error function about the previous k times as the step-size update basis of the adaptive algorithm. The block diagram of proposed algorithm appears in Fig. 2.

Fig. 2
figure 2

System block of proposed algorithm

Full size image

One effective way to improve the convergence speed is to design a formula with variable step size. The error can be used to update the step size. Thus, a larger step size can be given by the variable step-size function when the error between the desired signal and the output signal is large, which can accelerate the convergence process. In the presence of impulsive noise disturbance that produces results far from the actual situation, the connection between the previous and the generated step size is hard to establish because of the large error signal.

As such, some scholars construct a deformation Gaussian function to resolve the effect of convergence due to the sudden change of error [8]. The formula is:

$$\mu \left( {e\left( {n + 1} \right)} \right) = \theta \mu \left[ {e\left( n \right)} \right] + \left( {1 - \theta } \right)\alpha \left| {e\left( {n + 1} \right)} \right|^{2} e^{{ - \beta \left| {e\left( {n + 1} \right)} \right|^{2} }}$$
(1)

This is a step-update function, thus achieving anti-pulse interference. However, when studying the algorithm, it is found that the effect is not ideal in the case of large impulsive noise. To further improve its conversion effect, we enhance the algorithm and propose an Improved Variable Step-Size Least Mean p-Power (IVSS-LMP) algorithm, by introducing the equation:

$$f_{e} \left( n \right) = k_{{{\text{ap}}}} \times \sqrt {\sum\limits_{i = n - k + 1}^{n} {\left| {e\left( i \right)} \right|}^{2} }$$
(2)

where \(k_{{{\text{ap}}}} > 0\). We use this formula to correct the step size, which makes the algorithm give a better convergence effect. Since the error of the previous k terms is introduced, the value of the parameter k cannot be large in order to ensure a real-time update. Hence, choosing a suitable value of the parameter k is crucial for this algorithm.

The weighted moving average method is often used in mathematics to predict future values. Considering the correlation between steps, we also use the weighted moving average method to build the performance stable. The formula is

$$\mu \left( {f_{e} \left( {n + 1} \right)} \right) = \theta \mu \left[ {f_{e} \left( n \right)} \right] + \left( {1 - \theta } \right)af_{e} \left( {n + 1} \right)e^{{ - \beta f_{e} \left( {n + 1} \right)}}$$
(3)

This weighs the steady-state misalignment and convergence speed. The pseudo-code process of proposed algorithm is shown in Table 1.

Table 1 The proposed algorithm
Full size table

3 Convergence analysis

To prove the stability of the algorithm, it is necessary to analyze the convergence score of the algorithm by first defining the initial conditions, \(f_{e} \left( 0 \right) = 0\) and \(\mu \left( 0 \right) = 0\). We modify Eqs. (2) and (3) to:

$$\begin{aligned} \mu \left( {f_{e} \left( {n + 1} \right)} \right) & = \theta \mu \left[ {f_{e} \left( n \right)} \right] + \left( {1 - \theta } \right)\alpha f_{e} \left( {n + 1} \right)e^{{ - \beta f_{e} \left( {n + 1} \right)}} \\ & = \sum\limits_{i = 1}^{n} {\theta^{n - i} \left( {1 - \theta } \right)af_{e} \left( i \right)\exp \left( { - \beta f_{e} \left( i \right)} \right) + } \theta^{n} \mu \left( {f_{e} \left( 0 \right)} \right) \\ & = \left( {1 - \theta } \right)\alpha \sum\limits_{i}^{n} {\theta^{n - i} f_{e} \left( i \right)\exp \left( { - \beta f_{e} \left( i \right)} \right)} \\ \end{aligned}$$
(4)

Here,

$$f_{e} \left( n \right) = 0,\;\;n < 0$$
(5)
$$f_{e} \left( i \right)\exp \left( { - \beta f_{e} \left( i \right)} \right) = \frac{{\beta f_{e} \left( i \right)\exp \left( { - \beta f_{e} \left( i \right)} \right)}}{\beta }$$
(6)

We constructing the function g(y):

$$g\left( y \right) = ye^{ - y}$$
(7)

By calculating the derivative of this function, we can see that the function has a maximum value \(e^{ - 1}\) at \(y = 1\). Therefore, Eq. (6) can be written as:

$$f_{e} \left( i \right)\exp \left( { - \beta f_{e} \left( i \right)} \right) = \frac{{\beta f_{e} \left( i \right)\exp \left( { - \beta f_{e} \left( i \right)} \right)}}{\beta } \le \frac{{e^{ - 1} }}{\beta }$$
(8)

Bringing Eq. (8) into (4), we get:

$$\begin{aligned} \mu \left( {f_{e} \left( {n + 1} \right)} \right) & = \left( {1 - \theta } \right)\alpha \sum\limits_{i = 1}^{n} {\theta^{n - i} f_{e} \left( i \right)\exp \left( { - \beta f_{e} \left( i \right)} \right)} \\ & \le \left( {1 - \theta } \right)\alpha \sum\limits_{i = 1}^{n} {\theta^{n - i} \frac{{e^{ - 1} }}{\beta } = \frac{{\alpha \left( {1 - \theta } \right)e^{ - 1} }}{\beta }} \cdot \frac{{1 - \theta^{n} }}{1 - \theta } \\ \end{aligned}$$
(9)

When \(0 < \theta < 1\), we get the following inequality:

$$\mu \left( {f_{e} \left( {n + 1} \right)} \right) \le \frac{{\alpha e^{ - 1} }}{\beta }$$
(10)

The formula for updating the weights of the IVSS-LMP algorithm is:

$$w\left( {n + 1} \right) = w\left( n \right) + \mu \left[ {f_{e} \left( n \right)} \right]\left| {e\left( n \right)} \right|^{p - 2} e\left( n \right)x\left( n \right)$$
(11)

Here, \(\mu [f_{e} (n)]\left| {e\left( n \right)} \right|^{{\left( {p - 1} \right)}}\) can be considered as the total step length of the LMS algorithm, The algorithm converges only when the step size in the LMS algorithm satisfies \(0 < \mu < \frac{2}{{3{\text{tr}}\left( R \right)}}\) [9]. Therefore, the IVSS-LMP algorithm step size should satisfy:

$$0 \le \mu \left[ {f_{e} \left( n \right)} \right]\left| {e\left( n \right)} \right|^{p - 2} \le \frac{2}{{3{\text{tr}}\left( R \right)}}$$
(12)

Here, \({\text{tr}}\left( \cdot \right)\) denotes the trace of the matrix, \(R = E\left[ {x^{T} \left( n \right)x\left( n \right)} \right]\) is the auto-correlation matrix of the input signal, and \(0 < p < \alpha\) (α is the parameter of impulsive noise). Thus, \(\left| {e\left( n \right)} \right|^{p - 2} \le 1\).

Bringing Eq. (9) into (12) yields the inequality:

$$\frac{\alpha }{\beta } \le \frac{2e}{{3{\text{tr}}\left( R \right)}}$$
(13)

Therefore, the proposed LMP algorithm converges when the parameters satisfy the above formula.

4 Simulation analysis

This study applies the proposed IVSS-LMP algorithm to channel estimation under α-stable distributed impulsive noise interference, where the input signal x(n) obeys a Gaussian distribution with mean 0 and variance 1. The weight vector w0 of the unknown system also obeys a Gaussian distribution with mean 0. The filter order is M = 128, and the number of sampling points performed is 20,000 points each time. In order to reflect the performance of the algorithm in the case of abrupt changes in the system, the system is abruptly changed at 10,000 iterations (using the method of changing the weight vector to the opposite of the original). The final simulation results are then averaged over 20 Monte Carlo simulations to obtain a more easily comparable simulation [10].

To better measure the performance of the algorithm in channel estimation, this paper applies Normalized Mean Square Deviation (NMSD) of the weights to reflect the effect of the algorithm. The estimated channel parameters are compared with the original simulated channel parameters by normalizing the difference, so as to reflect the effectiveness of the algorithm more intuitively and accurately. A smaller NMSD value indicates that the convergence of the algorithm is better. The expression is:

$${\text{NMSD}} = 10\log_{10} \left[ {\frac{{\left\| {w_{0} - w\left( n \right)} \right\|^{2} }}{{\left\| {w_{0} } \right\|^{2} }}} \right]$$
(14)

In the simulation experiments, α-stable distribution is used as the impulsive noise model. The steady-state distribution noise is a class of random noise with linear spikes and trailing effect. It does not have a uniform probability density function, but rather a unified characteristic function [11], which can be expressed as:

$$\varphi \left( t \right) = \exp \left\{ {jat - \gamma \left| t \right|^{\alpha } \left[ {1 + j\beta {\text{sgn}} \left( t \right)\omega \left( {t,\alpha } \right)} \right]} \right\}$$
(15)

Here, \({\text{sgn}} \left( \cdot \right)\) is the sign function:

$$\omega \left( {t,\alpha } \right) = \left\{ {\begin{array}{*{20}c} {\tan \left( {\alpha \pi } \right)/2,} & {\alpha \ne 1} \\ {\left( {2/\pi } \right)\log \left| t \right|} & {\alpha = 1} \\ \end{array} } \right.$$
(16)

Since impulsive noise does not have second-order statistics such as variance and correlation functions, the traditional signal-to-noise ratio function is ineffective under the α-stable distributed noise. Hence, the following equation can be used to measure the signal-to-noise ratio of impulsive noise to the useful signal [12]:

$${\text{SNR}} = 10\log \left( {\sigma_{s}^{2} /\gamma } \right)$$
(17)

Here, σs2 is the variance of the input signal, and γ is the dispersion coefficient of the α-stable distribution.

4.1 Comparison with unimproved algorithm

By comparing the error functions before and after the improvement, we can visually analyze the difference between the improved algorithm and the one before the improvement. The following involves parameter θ taking the value of 0.98, parameter kap taking the value of 1, parameter α taking the value of 0.0007, parameter β taking the value of 0.004, and parameter k taking the value of 3. In order to compare the effect of two error functions more intuitively, the error function is treated logarithmically, as shown in Fig. 3.

Fig. 3
figure 3

Comparison of different error functions

Full size image

In this figure the variance of the error function of VSS-LMP is 543.4234, and the variance of the error function of IVSS-LMP is 191.2481. From the figure we also find in the face of impulsive noise that the error function constructed by IVSS-LMP has smaller fluctuations than the direct use of error; i.e., better robustness against impulsive noise. Using this property, the algorithm can achieve a lower normalized mean square error at convergence.

From a comparison with the algorithm before the improvement, the following is the result of the simulation with the same parameters except for the newly added variables. Here, 123 represents the three parameter cases respectively, as shown in Table 2.

Table 2 the parameters of different cases
Full size table

The simulation of VSS-LMP and the improved IVSS-LMP are compared according to the parameters in the table. The comparison results appear in Fig. 4.

Fig. 4
figure 4

Comparison of the algorithms under random parameters

Full size image

A comparison of the performance under random parameters shows that the errors at convergence of the IVSS-LMP algorithm are lower than those of the VSS-LMP algorithm before the improvement. The remaining parameters are guaranteed to be unchanged except for the newly added parameters.

4.2 Parameter analysis

To investigate the effect of parameter k on the performance of the algorithm, parameter kap is taken as 1, smoothing factor θ is taken as 0.97, parameter α is taken as 0.001, parameter β is taken as 0.0038, and algorithm parametric number p is taken as 1.15, The above parameters are selected by trial-and-error method under the condition of step stability to obtain the best value [13]. Parameter k is taken as 2, 3, 4, and 5 respectively, in order to compare the effect of parameter k on the algorithm more intuitively. The algorithm before improvement is also added as a reference. The simulation pulsive noise parameters are N = [1.5, 0, 0.04, 0], and the noise signal is shown in Fig. 5.

Fig. 5
figure 5

Reference impulsive noise

Full size image

Under the simulation pulse noise, the algorithm performance curve is shown in Fig. 6.

Fig. 6
figure 6

Comparison under different parameter k

Full size image

Analysis of the graph shows that the NMSD values when the algorithm converges are − 26.82 dB, − 23.33 dB, − 22.08 dB, and − 20.14 dB when the values of k are taken as 1, 2, 3, 4, and 5, respectively. Compared to VSS-LMP (i.e., when no forward multiple error correction is made, with an increasing value of k, the convergence rate gradually decreases. However, after convergence in order to achieve a lower NMSD, for the variable hydroacoustic channel environment, a low error is particularly important, and from the simulation it can be seen that the algorithm with forward error correction has a significant improvement in the convergence effect. The difference in the steady state achieved for values of k greater than 3 is not significant. Moreover, the performance of the improved algorithm decreases compared to the original algorithm for values of parameter k greater than or equal to 5. Combining the time required to reach steady state with the value of NMSD, the simulation is relatively better at parameter k = 3.

To research the effect of parameter θ on the performance of the algorithm, the value of parameter k is taken as 3, the value of θ is taken as 0.86, 0.87, 0.88, 0.89, 0.96, 0.97, 0.98, and 0.99, and other parameters remain constant. The performance of the algorithm is shown in Fig. 7.

Fig. 7
figure 7

Comparison under different parameter θ

Full size image

By analyzing the graph, we see that as the value of θ becomes larger, the time required to reach steady state increases while still being able to reach a lower steady state. The simulation figure shows that θ of the algorithm can affect system convergence. With all other parameters being the same, the convergence is better when θ is close to 1. In the case of changing only θ, the better the convergence effect is, the more times it takes to reach steady-state convergence. At θ = 0.98, the fluctuation of NMSD after reaching steady state is smaller, and so the value of parameter θ is taken as 0.98.

To study the effect of parameter α on the performance of the algorithm, the value of parameter θ is taken as 0.98, the value of parameter α is taken as 0.0004, 0.0005, 0.0006, 0.0007, 0.0008, and 0.0009, and other parameters remain constant. The performance of the algorithm appears as the Fig. 8.

Fig. 8
figure 8

Comparison under different parameter α

Full size image

Analyzing this figure, the value of parameter α affects convergence speed as well as the convergence effect when the steady state is reached. As the value of α increases from 0.0004 to 0.0009, the number of algorithm convergence steps are respectively 5467, 4399, 3940, 3520, 3043, and 2621, and the convergence speed keeps getting faster. After convergence of the algorithm, NMSD values are − 27.43 dB, − 26.11 dB, − 25.45 dB, − 24.71 dB, − 24.08 dB, and − 23.18 dB, respectively. From the data, we see that the gain is very high at the beginning when the value of α decreases; i.e., sacrificing less convergence speed in exchange for better convergence. However, as α decreases further, the gains start to decline, even sacrificing more than double the previous number of steps while gaining the same convergence effect. Therefore, considering the two factors, parameter α is taken as 0.0006.

To study the effect of parameter β on the performance of the algorithm, the value of parameter α is taken as 0.0007 and the value of parameter β is taken as 0.001, 0.003, 0.004, 0.005, 0.007, and 0.01. The simulation results appear as the Fig. 9.

Fig. 9
figure 9

Comparison under different parameter β

Full size image

Analyzing this figure, the steady-state fluctuation is larger when β is small. As β increases, the convergence speed decreases, but the steady-state error turns higher. The magnitude of fluctuation after reaching the steady state is integrated, and parameter β at 0.004 in this algorithm is better.

To analyze the effect of parameter kap on the algorithm, the parameter β value is 0.004 and the parameter kap values are set to 0.8, 0.9, 1.0, 1.1, 1.2, and 1.3. The simulation yields in Fig. 10.

Fig. 10
figure 10

Comparison under different parameter kap

Full size image

The figure shows that as the kap value increases, the convergence speed becomes faster, the convergence error increases, and better gains can be obtained by increasing the kap value when the kap value is low (getting faster at the expense of the same NMSD). We also find when the parameter kap value is greater than 1 that the ratio of convergence speed to the number of iterations changes rapidly. In the case of kap values of 1.1 and 1.2, the convergence effect is similar, but in the case of kap value of 1.1, there is less fluctuation after convergence. Taking this into account, the value of kap in this algorithm is 1.1.

4.3 Comparison of simulated channel algorithms

We now introduce the improved sigmoid function-based [14] into the LMP algorithm to form the sigmoid variable step-size least mean p-power (SVS-LMP) algorithm. We then add the improved inverse hyperbolic tangent function [15] into the LMP algorithm to form the inverse hyperbolic tangent variable step-size LMP (IHTVS-LMP) algorithm. Lastly, we present a normal distribution curve [16] to construct a normal distribution curve step-size LMP (NDCS-LMP) algorithm. Here, each algorithmic parameter is adjusted to the appropriate value, as shown in Table 3.

Table 3 the parameters of different algorithm under simulated channel
Full size table

The simulation is shown in Fig. 11.

Fig. 11
figure 11

Comparison of different algorithms under simulated channel

Full size image

Comparing the simulation plots of different algorithms in the literature with a signal-to-noise ratio of 24 dB, the LMS algorithm suffers from poor convergence performance when faced with impulse interference. Therefore, we adopt the LMP algorithm to improve the convergence performance under impulse interference. Through comparison of the convergence performance, we show that the proposed algorithm achieves better convergence performance with the same number of iterations, and has lower steady-state error than the existing algorithms. Moreover, the proposed algorithm exhibits significant improvement in scenarios where the channel undergoes abrupt changes.

4.4 Comparison of actual channel algorithms

To further investigate the performance of each algorithm, this section applies IVSS-LMP to an actual channel for comparison. Under impulsive noise, the measured hydroacoustic channel impulse response is identified as a weight vector in this section, and the estimation performance of each algorithm is simulated. The actual measured channel impact response at a given moment in Norwegian waters [17] is shown in Fig. 12.

Fig. 12
figure 12

The actual channel impact response

Full size image

The impulse response of the actual hydroacoustic channel is sampled at 1 kHz, and the length of the channel is 256 ms. Thus, this section selects it as the unknown system response to be identified. The number of sampling points is 2 × 104, and at 1 × 104 sampling moments, the system undergoes a sudden change; i.e., the channel impulse response is inverted, where the parameters of the comparison signal are shown in Table 4.

Table 4 the parameters of different algorithm under actual channel
Full size table

The convergence curves of each algorithm are shown in Figs. 13 and 14.

Fig. 13
figure 13

Comparison of LMS and LMP under actual channel

Full size image
Fig. 14
figure 14

Comparison of different algorithms under actual channel

Full size image

The data in Fig. 13 shows that the LMS algorithm fails to converge in the presence of impulse interference in a realistic underwater acoustic channel. By contrast, the experimental data we find in Fig. 14 demonstrates that the proposed algorithm can obtain better convergence in channel estimation of real hydroacoustic channels under impulsive interference with the same number of iterations when comparing the algorithm before improvement and the LMP algorithm using other criteria.

5 Conclusion

Under the background of α-stable impulsive noise, this paper considers the influence of the error of the current moment and several previous moments on the convergence effect of the algorithm. The study then optimizes the algorithm on the basis of the improved Gaussian function, constructs a variable-step function by using the moving average method, and proposes an improved variable-step LMP adaptive filtering algorithm with robustness to impulse noise. Simulation experiments show that the IVSS-LMP algorithm has faster convergence and better system tracking capability than the fixed-step LMP algorithm and existing variable-step algorithms. The proposed IVSS-LMP algorithm also achieves faster convergence while guaranteeing low steady-state error through actual hydroacoustic channel identification experiments.