1 Introduction

One of the most interesting and useful pursuits in radars today is the study of electronic scanned arrays. Electronic scanned arrays have long been of great research interest in numerous applications such as radar, sonar, navigation and wireless communications [1,2,3,4,5,6,7,8,9,10,11]. A considerable amount of effort has been expended in the investigation of methods for electronic scanning of antenna systems. During World War II, the United States and Britain were actively engaged in research on array antennas [12,13,14]. It was not until the 1950s that the first fully electronic scanning was realized [15,16,17]. In the interim, several mechanical scanners were invented and used [18]. The significant advances in the 1950s and early 1960s have made the electronic scanning using array antennas feasible with the development of ferrite phase shifters in 1954-1955. Consequently, the development of Lincoln Laboratory’s phased array (PA) radar began around 1958 [19]. Historically, electronically steerable phased arrays (ESA) are designed in two ways, the passive ESA and the active ESA [20]. The former utilizes a single transmitter and receiver, the latter utilizes multiple Transmit/Receive modules, typically one per element, to provide amplitude and phase control. Although scanning antenna arrays had been developed for various electronic communications applications, radar system was the first application in which PA was broadly used for the first time [20,21,22].

Conventional PA radars using fixed carrier frequencies are widely recognized for their capability to electronically steer a beam with high directivity [23, 24]. The effective beam of a PA radar can be electronically steered in the desired direction using phase-shifters across the array elements [25, 26]. The resulting beampattern is angle-dependent but range-independent [27]. Therefore, PA radars cannot be deployed in applications involving range-dependent sources. On the other hand, the cost and complexity are other major concerns in PA radars because phase-shifters deployed at each antenna element represent a considerable portion of the overall system cost [23,24,25,26,27]. In addition, since the element-spacing in a PA system is usually fixed at half-a-wavelength corresponding to the carrier frequency, it is necessary to expand the aperture size by employing more sensors to achieve a more directed beam [20,21,22,23,24,25,26,27]. However, this will further increase the complexity, and cost. Antenna spacing could be increased above half-a-wavelength, however, this will come at the expense of multiple large side-lobes or grating-lobes in the real space when scanning the main beam [28]. Therefore, the array size dictates the number of elements in a PA beamformer [29]. Although substantial advances have taken place in PA technology since the early 1970’s, affordability is still a major concern, and the design factors such as aperture sizing, pattern synthesis, and beam-switching speeds have changed little [27].

To overcome these disadvantages, and emphasizing aspects of simplicity, reliability, and versatility required by modern systems, it is necessary to find more innovative array beam steering techniques [27]. Consequently, more attention is paid to new concepts for electronic scanning of antenna systems. New concepts for electronic beam scanning proposed in this connection include waveform diversity techniques i.e., to vary the excitation across the array in either the time or frequency domain. These new configurations regarded as time-modulated arrays [30,31,32,33] and frequency scanning arrays [34, 35] can provide beam steering ability without using the expensive phase-shifters. In time-modulated arrays, high speed RF switches are used instead of expensive phase shifters to electronically steer and shape the radiation pattern [36]. The RF switches periodically turned on and off the excitations of the individual array elements according to pre-fixed time sequences [37]. In frequency scanned arrays, beam steering is achieved by the variation of frequency as a function of time, and the same signal is simultaneously applied to all the spatial channels. However, the resulted beampatterns of these techniques are still range-independent, which limit their applicability in applications involving range-dependent sources, e.g., range-dependent interference suppression, and localization of multiple targets with the same direction but distinct ranges, etc.

Recently, a new concept, namely, frequency diverse array (FDA) radar has emerged as a popular beam steering technique that generates a range-angle dependent beampattern [38]. The essential difference between a PA radar and an FDA radar is the carrier frequency of each array element. In contrast to PA radars using fixed carrier frequencies, FDA radars employ a small frequency increment across each array element to achieve beam steering in both the angle and range domains [39, 40]. The concept of FDA radar was first proposed by Antonik et. al in [41], where a progressive incremental frequency shift is applied to the array signals. This progressive frequency shift generates a natural time-dependent progressive phase difference across the array elements, which enables the FDA beampattern to scan in range and angle domains as a function of time [42]. Consequently, the expensive phase-shifters are dispensed in FDA radars to steer their beam in a particular direction. The FDA radar [43] has attracted noticeable attention because the range-angle dependent beampattern is attractive to various real-time array signal processing applications including radar, sonar, wireless communications and acoustics [44,45,46].

FDA radar is different from orthogonal frequency division multiplexing (OFDM) radar [47,48,49] and multiple-input multiple-output (MIMO) radar [50,51,52]. OFDM radar uses orthogonal subcarriers, but non-orthogonal carriers are employed in FDA radar. MIMO radars either emit unique and independent waveforms using multiple antennas to achieve waveform diversity (i.e., collocated MIMO) or employs orthogonal signals from widely separated antennas (i.e., widely spaced MIMO) over multiple independent paths to provide spatial diversity, whereas FDA radar transmits overlapping signals with closely spaced frequencies to provide additional functionalities, such as range-dependent beamforming, increased range resolution and degree-of-freedoms (DOFs), effective mitigation of range-angle dependent interference sources and clutter. Likewise, FDA radar is also different from conventional frequency scanning radar [53, 54]. Conventional frequency scanning radar using frequency offsets as a function of time has the same frequency at each element in a given time, but FDA frequency offsets are characterized by the element index. The time-modulated array antenna [55, 56] proposed by H. E. Shanks in 1962 is a new technique for electronic scanning, which weights each element using on/off switching operation. It is noteworthy that the synthetic antenna and impulse radar (RIAS) pioneered by French researchers in early 1970’s [57,58,59], and sparse-array synthetic antenna and impulse radar (SIAR) [60, 61] developed by Chinese researchers in 1980’s are typical kinds of MIMO radar even before the concept of MIMO radar was put forward. They exploit both spatial and spectral diversity to achieve more degrees of freedom, higher angular resolution and target detection probability. MIMO radar is mainly adopted from the idea of SIAR. RIAS and SIAR simultaneously transmits a unique pulse – orthogonally phased, frequency modulated and coded and receive echoes via multiple receive antennas [62]. The concept of RIAS and SIAR also paved a way for the development of the FDA radar.

Conventional PA radar is well developed in the literature for electronically steering the beam direction with high directivity. However, the range-dependent sources cannot be unambiguously estimated from its inherent range-independent beampattern. Although space-frequency or space-time adaptive processing (STAP) based techniques can estimate the range of sources, they usually have a high computational cost and complexity [63,64,65,66]. FDA radar looks particularly promising technique for the electronic beam steering. Reference [44] overviews the basic FDA system architecture in radar and navigation applications, and its potential applications in range-dependent energy control and technical challenges in system implementation are discussed in [45]. Since then, there have been a number of recent advances in FDA beampattern synthesis techniques. With the increasing importance of range-angle dependent beampattern, and recent advances in FDAs, a review incorporating more recent findings has become necessary. This paper aims to briefly analyze the range-angle dependent beampattern of the FDA radar from its origin to the current state-of-the-art FDA beampatterns. While the range-angle dependent beampatterns achieved in FDAs are encouraging, the realism of the simulations is limited. More attention has been paid to achieve range-dependent beampatterns, which neglects the practical constraint of wave propagation. Therefore, we have dedicated a section to discuss the wave propagation in FDAs. In addition, we also discuss the potential applications of FDAs in wireless communications.

The outline of this paper is organized as follows. In Sect. 2, we present the PA signal model and beampattern synthesis. In Sect. 3, we describe the preliminaries of the FDA, including signal model and the time-invariant FDA beampattern synthesis. In Sect. 4, we explain the neglected propagation process of the transmitted signals in FDAs. Recent trends in FDAs are discussed in Sect. 5, and the areas that are suitable for continuing research are provided in Sect. 6. Finally, Sect. 7 concludes this study.

2 Phased arrays

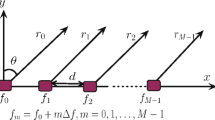
Consider the simple case of an M-element uniform linear array (ULA) of isotropic radiating antenna elements with half-a-wavelength inter-element spacing as shown in Fig. 1. The far-field array radiation pattern, or array factor (AF) in this case, in terms of standard spherical coordinates, can be expressed by superposition of the M radiating currents as [20,21,22,23]

$$\begin{aligned} \begin{aligned} AF^{PA}(\theta )=\sum _{m=0}^{M-1}w_m \exp \left\{ jm(\kappa d\sin \theta )\right\} , \end{aligned} \end{aligned}$$
(1)

where \(w_m\) is the complex weight related to the m-th element, \(\kappa = 2\pi /\lambda\) is referred to as the wavenumber with \(\lambda\) denotes the wavelength of the signal, d is the spacing between adjacent antenna elements, and \(\theta\) is the direction of the target.

Fig. 1
figure 1

Uniform linear phased array with M elements

Full size image

In what follows, the operations of transposition, complex conjugation, and Hermitian transposition are denoted by superscripts T, \(*\), and H, respectively. Lowercase and uppercase boldface characters denote the vectors and matrices, respectively.

In vector form, Eq. (1) can be rewritten as

$$\begin{aligned} AF^{PA}(\theta )=\varvec{w}^{H} \varvec{a}(\theta ), \end{aligned}$$
(2)

where \(\varvec{w}\) and \(\varvec{a}(\theta )\), respectively, denote the weight vector and the array steering vector, which are given as [19]

$$\begin{aligned} \varvec{w}=[w_0, w_1,\ldots ,w_{M-1}]^T, \end{aligned}$$
(3)

and

$$\begin{aligned} \begin{aligned} \varvec{a}(\theta )=[&1, \exp (j\kappa d\sin \theta ), \exp (j2\kappa d\sin \theta ),\ldots ,\\&\exp (j(M-1)\kappa d\sin \theta )]^T. \end{aligned} \end{aligned}$$
(4)

The beam can be steered by controlling the phase shift in the weight associated with individual element. With uniform weights, i.e., \(w_{m}=1\), the array factor can be expressed in closed-form as [27]

$$\begin{aligned} AF^{PA}(\theta )\vert _{w_m=1}=\frac{\sin ((M/2)\kappa d\sin \theta )}{\sin ((1/2)\kappa d\sin \theta )}. \end{aligned}$$
(5)

The beampattern for the PA antenna is given as [27]

$$\begin{aligned} B^{PA}(\theta )=\vert AF^{PA}(\theta )\vert ^2 = \vert \varvec{w}^{H}\varvec{a}(\theta )\vert ^2 . \end{aligned}$$
(6)

For the linear PA antenna to steer its main beam to angle \(\theta _d\), \(w_m\) must be equal to \(\exp (-jm\kappa d\sin \theta _d)\), so that \(B^{PA}(\theta )\) gives a maximum magnitude at that value [20,21,22,23,24].

$$\begin{aligned} \begin{aligned} B^{PA}(\theta )&=\vert \sum _{m=0}^{M-1}\exp \lbrace jm(\kappa d(\sin \theta -\sin \theta _d))\rbrace \vert ^2 ,\\&=\bigg |\frac{\sin ((M/2)\kappa d(\sin \theta - \sin \theta _d))}{\sin ((1/2)\kappa d(\sin \theta - \sin \theta _d))}\bigg |^2. \end{aligned} \end{aligned}$$
(7)

In Fig. 2, we plot the normalized beampattern of a 20-elements PA. Figure  2a, b shows the PA beampattern in range-angle dimension, and angle-dimension with the main lobe steered to \(30^{\circ }\), respectively. It is observed that the PA has an angle-dependent but range-independent beampattern.

Fig. 2
figure 2

Normalized beampattern of a 20-element phased array with scan angle at \(30^{\circ }\). a Range-angle dimension. b Angle dimension

Full size image

To further illustrate the characteristics of the PA beampattern, several array patterns with different number of elements M and inter-element spacing d as a function of wavelength \(\lambda\) have been plotted in Fig. 3. Note that phase-shift has not been applied, and the main lobe is in the broadside direction. From Fig. 3a, it is observed that as the number of elements increases, the array directivity increases. Extending the inter-element spacing toward \(\lambda\) leads to narrow main lobe but suffers high grating lobe effect as shown in Fig. 3b. The maximum grating lobe amplitude equal to the main lobe magnitude at an element spacing \(\lambda\). Clearly, increasing the inter-element spacing results in a narrower main lobe but it comes at the expense of multiple large side-lobes or grating-lobes, whereas more antenna elements not only further decrease the main lobe width but also increase the main-to-sidelobe ratio.

Fig. 3
figure 3

Normalized phased array beampatterns with \(\theta _d = 0^{\circ }\). a Beampattern when \(M=5\), \(M=10\), and \(M=15\), and \(d = \frac{\lambda }{2}\). b Beampattern for a 10-elements phased array when \(d = \lambda\), \(d = \frac{\lambda }{2}\), and \(d = \frac{\lambda }{4}\)

Full size image

3 Frequency diverse arrays

In this section, we briefly investigate the FDA beampattern characteristics. The first subsection formulates the signal model of FDA radars. The next subsection discusses the nonlinear frequency offsets for range-angle decoupling of the FDA beampattern. The final subsection presents the time-modulated frequency offsets to achieve the time-invariant range-angle dependent FDA beampattern.

3.1 FDA signal model

Assume a ULA composed of M omni-directional elements with half a wavelength inter-element spacing as shown in Fig. 4. The signal transmitted by the m-th element is [43,44,45]

$$\begin{aligned} s_m(t)= w_m \exp \lbrace -j2\pi f_mt\rbrace ,\quad 0\le m \le M-1, t\in [0,T], \end{aligned}$$
(8)

where T denotes the transmitted pulse duration, and \(f_m\) is the radiation frequency of the m-th element given by [38,39,40,41,42,43,44,45]

$$\begin{aligned} f_m= f_0+m\Delta f. \end{aligned}$$
(9)

Here, \(f_0\) is the carrier frequency radiated by the first element, and \(m\Delta f\) is the frequency offset of the m-th element. The overall signal arriving at an arbitrary point \(P(r,\theta )\) (r and \(\theta\) are the range and the azimuth angle with respect to the first array element) in the space can be expressed as [44]

$$\begin{aligned} \begin{aligned} S(t,r,\theta )=\sum _{m=0}^{M-1}s_m(t-\frac{r_m}{c})=\sum _{m=0}^{M-1}w_m\exp \left\{ -j2\pi f_m (t-\frac{r_m}{c})\right\} , \end{aligned} \end{aligned}$$
(10)

where \(r_m\cong r-md\sin \theta\) is the target slant range with respect to the m-th element [45], and c is the wave speed. Substituting \(r_m\cong r-md\sin \theta\) and (9) into (10), we have [26, 45]

$$\begin{aligned} \begin{aligned} S(t,r,\theta )=&\sum _{m=0}^{M-1}w_m \exp \Big \{-j2\pi (f_0+m\Delta f)\Big [t-\frac{r-md\sin \theta }{c}\Big ]\Big \}\\ =&\exp \Big \{ -j2\pi f_0(t-\frac{r}{c})\Big \} \sum _{m=0}^{M-1}w_m \exp \Big \{ -j2\pi \Big [ m\Delta f \\&(t-\frac{r}{c})+{m}^2\Delta f(\frac{d\sin \theta }{c})+f_0(\frac{md\sin \theta }{c})\Big ]\Big \}. \end{aligned} \end{aligned}$$
(11)

According to the fundamental condition of the FDA radar, the quadratic phase term \({m}^2 \Delta f \frac{d\sin \theta }{c}\) satisfies the condition \({m}^2 \vert \Delta f \vert \frac{d\sin \theta }{c}<\frac{\pi }{4}\) because the maximum frequency offset is far less than the carrier frequency i.e., max\(\lbrace \Delta f\rbrace \ll f_0\) [26, 45]. Hence, it can be ignored in the further analysis. In (11), the terms inside the summation sign are determined by the array geometry and frequency offsets of the FDA, therefore, the array factor can be expressed as [38,39,40,41,42,43,44,45]

$$\begin{aligned} \begin{aligned} AF^{FDA}(t,r,\theta )=\sum _{m=0}^{M-1}w_m \exp \left\{ -j2\pi \left[ m\Delta f (t-\frac{r}{c}) + f_0(\frac{md\sin \theta }{c})\right] \right\} . \end{aligned} \end{aligned}$$
(12)
Fig. 4
figure 4

Uniform linear frequency diverse array

Full size image

Consider the case that \(w_0=w_1=...w_{m-1}=1\), the FDA transmit beampattern is given by

$$\begin{aligned} \begin{aligned} B^{FDA}(t,r,\theta )=\bigg | \sum _{m=0}^{M-1} \exp\left\{ -j2\pi \left[ m\Delta f (t-\frac{r}{c}) + f_0(\frac{md\sin \theta }{c})\right] \right\} \bigg |^2 . \end{aligned} \end{aligned}$$
(13)

The beampattern can also be expressed as [44, 45]

$$\begin{aligned} B^{FDA}(t,r,\theta )=\bigg | \frac{\sin [M\pi ( \Delta f t+f_0d\sin \theta /c-\Delta fr/c)]}{\sin [\pi ( \Delta f t+f_0d\sin \theta /c-\Delta fr/c)]} \bigg |^2. \end{aligned}$$
(14)

Note that when \(\Delta f=0\), the beampattern becomes [45]

$$\begin{aligned} B^{PA}(\theta )=\bigg | \frac{\sin [M\pi ( f_0d\sin \theta /c)]}{\sin [\pi (f_0d\sin \theta /c)]} \bigg |^2, \end{aligned}$$
(15)

which is only angle-dependent just like conventional PA radar.

For steering a target positioned at \(P(r_{d}, \theta _{d})\), the weights \(w_m\) for the transmitted beampattern can be computed as [26]

$$\begin{aligned} w_m=\exp \left\{ -j2\pi \left[ \frac{m\Delta fr_d}{c} - f_0\frac{md\sin \theta _d}{c}\right] \right\} . \end{aligned}$$
(16)

The corresponding array factor becomes

$$\begin{aligned} \begin{aligned} AF^{FDA}(t,r_d,\theta _d)=\sum _{m=0}^{M-1} \exp&\left\{ -j2\pi \left[ m\Delta f (t-(\frac{r-r_d}{c})) \right. \right. \\&\left. \left. + f_0(\frac{md(\sin \theta -\sin \theta _d)}{c})\right] \right\} , \end{aligned} \end{aligned}$$
(17)

and its magnitude squared, known as transmit beampattern, is given as

$$\begin{aligned} B^{FDA}(t,r_d,\theta _d)=\vert AF^{FDA}(t,r_d,\theta _d)\vert ^2. \end{aligned}$$
(18)

Assume the following parameters: \(M=10\), \(f_0=10\) GHz, \(\Delta f=3\) kHz, and \(d=\frac{\lambda _0}{2}\). In Fig. 5, we plot the normalized transmit beampatterns of the PA, the standard FDA, and the symmetrical FDA. Note that \(\Delta f=0\) is employed for the PA. From Fig. 5a, it can be observed that the PA has an angle-dependent but range-independent beampattern. In contrast, from Fig. 5b we can see that the standard FDA with a progressive frequency increment yields a periodic range and angle coupled S-shaped beampattern. The symmetrical FDA has range–angle decoupled beampattern as shown in Fig. 5c.

Fig. 5
figure 5

Comparison of transmit beampatterns. a Phased array. b Standard FDA. c Symmetrical FDA

Full size image

In the transmit beampattern derived in Eq. (14), the maximum field can be obtained when the phase term satisfies the condition [44, 45]

$$\begin{aligned} \Delta ft+\frac{f_0d\sin \theta }{c}-\frac{\Delta fr}{c}=i, \quad i=0,\pm 1,\pm 2,..... \end{aligned}$$
(19)

It can be observed from Eq. (19) that the maximum field depends not only on the angle but also on the range and time. Moreover, when only one parameter is fixed, there are multiple solutions for the unfixed parameters. On the other hand, when two parameters are fixed, the pattern periodicity depends on the unfixed variable.

For instance, if Eq. (19) is solved for time t, we have [44, 45]

$$\begin{aligned} t = \frac{i}{\Delta f}-\frac{f_0d\sin \theta }{c\Delta f}+\frac{r}{c}, \end{aligned}$$
(20)

This implies the periodic nature of the FDA beampattern in time. When the range r and angle \(\theta\) are fixed, the fundamental period is \(\frac{1}{\Delta f}\).

Similarly, the periodicity in range dimension is derived by solving Eq. (19) for range r as [44]

$$\begin{aligned} r = ct-\frac{ci}{\Delta f}-\frac{f_0d\sin \theta }{\Delta f}, \end{aligned}$$
(21)

whose fundamental period is \(\frac{c}{\Delta f}\) for a fixed \(\theta\) and t.

In the same manner, if Eq. (19) is solved for \(\theta\), we can obtain [45]

$$\begin{aligned} \sin \theta = \frac{ci-\Delta f(ct-r)}{f_0d}, \end{aligned}$$
(22)

Obviously, \(\sin \theta\) depends on both the time and range variables. The periodicity in time, range, and angle is also shown graphically in Fig. 6 for a 17-element FDA with 10 kHz inter-element frequency offset.

Fig. 6
figure 6

FDA beampattern periodicity. a Time periodicity. b Range periodicity. c Angle periodicity

Full size image

It is clear from (20)–(22) that the FDA beampattern is time-dependent, and its maxima drifts in space with the time, which facilitates the auto-scanning feature of FDA radars. That is to say, the entire space can be scanned without using the expensive phase-shifters. This unique auto-scanning feature of FDAs can also be useful in wireless communication systems such as at the base station and communication devices [29].

The standard FDA using progressive incremental frequency offsets generates a periodic range and angle coupled S-shaped beampattern. The range dependency of FDA beampatterns is investigated in [67,68,69,70,71], whereas its ability in increasing DOFs is studied in [38, 72]. The auto-scanning property of the FDA radar is analyzed in [42, 69]. Higgins and Blunt [73] explored the range–angle coupled beamforming in FDAs, and Secmen et al. [68] described the time and angle periodicity of FDA beampatterns. In [74], Eker et al. introduced a practical FDA system using linear frequency modulated continuous waveform, wherein both the transmit and receiver architectures together with the waveform processing is being analyzed in detail. The application of the FDA for forward-looking-radar ground moving target indication, and in bistatic radar is studied in [75] and [76, 77], respectively. In [78,79,80], the application of FDA is extended to synthetic aperture radar for improved performance, and the frequency diversity applied to the phased-MIMO radar for range-dependent beamforming is proposed in [81]. The multipath characteristics of FDAs over a ground plane are studied in [82]. In [83], the localization performance of FDA is analyzed. Additional investigations on the two-dimensional imaging of targets and suppressing the range-dependent clutters in FDAs are, respectively, given in [84, 85] and [86, 87].

Since the range-angle coupled beampattern introduces ambiguity into target indication, the range and angle of a target cannot be unambiguously estimated using FDAs [84, 85]. There has been a long line of research in FDAs, where a series of efforts have been made to decouple its beampattern in range and angle dimensions. Among the various methods, utilizing nonlinearly increasing frequency offsets in a ULA and utilizing linearly increasing frequency offsets in nonuniform linear array are the two most representative methods to decouple the FDA beampattern in range and angle dimensions [44, 45].

Numerous other techniques were also proposed to get improved localization performance. To name a few, a double-pulse FDA radar was proposed in [88] for the range-angle localization of targets. A pulse with zero frequency increment degenerates the system into a PA radar detecting the targets in the angle dimension, and then localize them in the range dimension using a nonzero frequency increment pulse. In [89], a stepped frequency pulse FDA (SFP-FDA) radar is proposed, which can be regarded as an upgraded version of the double-pulse FDA in [88]. The first pulse of SFP-FDA radar is same as conventional FDA with a bit of frequency increment. There is an additional small frequency increment from pulse to pulse. Another doubled pulsed MIMO-FDA has been proposed in [90], where the FDA transmit array is partitioned into subarrays and then transmits a unique waveform from each subarray with zero and nonzero frequency increment pulse, respectively. A vertical FDA, which applies frequency diversity in the vertical of a planar array, is explored in [91] to circumvent the range ambiguity problem in STAP radar. An FDA MIMO adaptive beamforming and localization scheme for range-dependent targets and interferences is proposed in [92], where the ranges and angles of targets can be solely estimated with MUSIC-based algorithm. Similarly, two FDA-MIMO hybrid radar transmitter design schemes, namely, FDA–MIMO radar, and transmit subarray FDA–MIMO radar are proposed in [93] for range-dependent target localization, where the targets are localized using the beamspace-based multiple signal classification algorithm. Although these methods have improved the localization performance, the range-angle decoupling is not achieved completely.

Considering the array configuration design, several researchers exploit the nonuniform array in FDA radars for improved localization performance. For example, a nonuniform FDA radar is proposed in [94] for range-angle imaging of targets. Likewise, a new FDA framework is proposed in [95], where the logarithmically spaced array elements were distributed symmetrically to produce a well-shaped “dot” main beam, facilitating the application in target indication. An FDA scheme utilizing nonuniform element spacing and nonlinear frequency offset is proposed in [96] to provide a range-angle decoupled beampattern with narrower main lobe and no periodicity. Moreover, a nonuniformly distributed FDA is proposed in [97], where both the frequency offsets and element positions are optimally determined via particle swarm optimization algorithm. However, it is difficult to alter the carrier frequency or frequency offsets in real time, and the relocation requirement for the accurate physical placement of transmitter and receiver at each scanning is impractical [26]. Therefore, this approach is not feasible in practice.

Another viable solution to decouple the FDA beampattern is through frequency offset design [26, 44]. By employing nonlinear and random frequency offsets, the FDA beampattern can be efficiently decoupled into the range and angle dimensions. Therefore, the nonlinear frequency offsets are intensively researched and extensively applied in FDA’s mainly for a range and angle decoupled beampattern.

3.2 FDA with nonuniform frequency offset

Frequency offset design has attracted great interests in the range-angle decoupling of FDA beampatterns. Until recently, several attractive functions have been proposed to design the nonlinear frequency offsets such as square increasing and cubic increasing frequency offsets [98], Hamming window-based nonuniform frequency offsets [99], Costas sequence modulated frequency offsets [100], piecewise trigonometric frequency offsets [101], and nonuniform logarithmic frequency offsets [102].

A multi-carrier nonlinear frequency modulation FDA scheme based on logistic map is presented in [103], which is capable to reduce the main lobe width and the sidelobe peaks simultaneously. Both single-dot and multi-dot shaped range-angle dependent beampatterns are obtained in [104] by using multi-carrier frequency offsets and convex optimization. In [105], a MIMO-log-FDA radar is proposed, where the range bins concept along with logarithmic offset in each subarray of MIMO-FDA is used to produce single maxima for multiple targets present in different range bins. A uniformly spaced linear FDA with logarithmically increasing frequency offset (log-FDA), and nonuniform but symmetric frequency offsets calculated using well known mu-law formula are, respectively, proposed in [106] and [107] to achieve a beampattern with a single maximum at the target location. Moreover, an adaptive frequency offset selection scheme for FDA radar is proposed in [108], where the frequency offset is determined at each step with an iterative algorithm. Likewise, an FDA framework with Taylor windowed frequency offsets is proposed in [109] where the adjustable tapering windows determine the optimized parameters of the window function. The relationship among ambiguity, frequency pattern and target relative location is derived in [110] to identify the unambiguous frequency patterns for two-target localization. The unambiguous target localization is achieved in [111] by combining the subarray-based FDA and full-band FDA, as the transmitter and the receiver, respectively. In [112], a gridless compressed sensing-based range-angle estimation algorithm is proposed for FDA-MIMO radar via Atomic Norm Minimization and Accelerated Proximal Gradient. By optimizing frequency offsets with a genetic algorithm, a single-dot and multi-dot shape transmit beampatterns is synthesized in [113].

For illustration purpose, few typical nonlinear frequency offset functions are briefly reviewed here, and their comparative beampatterns are also analyzed.

Since the inter-element frequency offset is not uniform, therefore the frequency input at m-th element is

$$\begin{aligned} f_m= f_0+\Delta f_m,\quad 0\le m \le M-1 \end{aligned}$$
(23)

where \(\Delta f_m\) is the frequency offset of the m-th element.

The Hamming window based frequency offsets can be expressed as [99]

$$\begin{aligned} \Delta f_m= \delta \left\{ 0.54-0.46\cos \left( \frac{2\pi m}{M}\right) \right\} . \end{aligned}$$
(24)

This is the general Hamming window equation where \(\delta\) is an adjustable parameter.

The logarithmically increasing frequency offsets are computed as [106]

$$\begin{aligned} \Delta f_m= \log \left( m+1\right) \delta . \end{aligned}$$
(25)

The piecewise frequency offsets based on a simple trigonometric are given as [101]

$$\begin{aligned} \Delta f_m= h(m)\delta , \end{aligned}$$
(26)

where

$$\begin{aligned} h(m)={\left\{ \begin{array}{ll} \cos (2M m+\phi _1), \quad -M_s\le m \le 0\\ \cos (M m+\phi _2), \qquad 1\le m \le M_s. \end{array}\right. } \end{aligned}$$
(27)

Here, \(\phi _{1}=0\), and \(\phi _{2}=\frac{\pi }{2}\). Since a symmetrical array configuration is utilized here, therefore \(M=2M_s+1\).

The square increasing and cubic increasing frequency offsets are derived as [98]

$$\begin{aligned} \Delta f_m={\left\{ \begin{array}{ll} m^{2}\Delta f, \\ m^{3}\Delta f. \end{array}\right. } \end{aligned}$$
(28)

Graphical representations of the aforementioned frequency offset functions are shown in Fig. 7.

Fig. 7
figure 7

Frequency offsets comparison. a Hamming window based frequency offsets. b Logarithmically increasing frequency offsets. c Piecewise trigonometric frequency offsets. d Square increasing frequency offsets. e Cubic increasing frequency offsets

Full size image

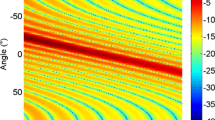
In Fig. 8, we compare the FDA transmit beampatterns generated using the Hamming window based frequency offsets, logarithmically increasing frequency offsets, and piecewise frequency offsets based on a simple trigonometric. In this experiment, the simulation parameters are as follows: M=17, \(f_0=10\) GHz, \(\delta =2\) kHz, \(d=\frac{\lambda _0}{2}\), and target location, \((r_d, \theta _d)=\) (500 km, \(30^{\circ }\)). The results indicate that all the three FDAs achieve a focused range-angle decoupled beampattern with a single maximum pointing at the target location.

Fig. 8
figure 8

Beampattern synthesis results. a Hamming FDA. b Log-FDA. c Piecewise FDA

Full size image

These nonlinear frequency offsets can decouple the FDA beampattern into range and angle dimensions. However, the actual beampatterns of aforementioned FDAs are time-variant. They are range-angle dependent only for a fixed time, neglecting the influence of time. Nevertheless, the performance degradation is inevitable because the time-periodicity still exists.

3.3 FDA with time-modulated frequency offsets

In order to overcome the time-periodicity in FDA beampatterns, a number of improved methods have been proposed [114,115,116,117,118,119,120,121]. Among those are the time-dependent frequency offsets (TDFO) proposed by Khan and Qureshi [114] and a pulsed-FDA with constraints on both pulse duration and frequency shift proposed by Xu et.al. [115]. Instead of using fixed frequency offsets, the TDFO-FDA considers time-modulated frequency offsets to generate a range-angle dependent as well as time-independent beampattern. The pulsed-FDA is proposed to form a quasi-static range-angle-dependent beampattern by properly choosing the pulse duration and the frequency shift. However, the beampatterns achieved in [114, 115] are time-independent only for a particular range-angle pair but they remain time-dependent for other ranges and angles. To address this issue, a time-modulated optimized frequency offset FDA (TMOFO-FDA) has been proposed in [116], which exploits the combination of time-modulated and nonlinear distributed frequency offset across the array elements to obtain a time-invariant range-angle-decoupled beampattern. By now, various improved methods based on the unified configuration of nonlinear and time-modulated frequency offsets have been proposed in [117,118,119,120,121] to design time-invariant spatial focusing beampatterns.

In general, the time-varying frequency offsets are given as

$$\begin{aligned} \Delta f_m(t) = \frac{\Delta f(m)}{t-\frac{r_d}{c}}, \quad t\in [0,T], \end{aligned}$$
(29)

where \(\Delta f(m)\) is a nonlinear function with respect to the element index m.

As an example, we review here the TDFO-FDA [114], time-modulated logarithmically increasing frequency offset FDA (TMLFO-FDA) [116], and the time-modulated double-parameter FDA (TMDP-FDA) [120].

The TDFO applied to the \(m-th\) element is [114]

$$\begin{aligned} \Delta f_m^{TDFO}(t) = m\Delta f (t) = m\frac{1-\frac{f_0\sin \theta _d}{c}}{t-\frac{r_d}{c}}, \end{aligned}$$
(30)

and the array factor at the target point is expressed as

$$\begin{aligned} \begin{aligned} AF^{TDFO}(t,r_d,\theta _d) = \sum _{m=0}^{M-1} \exp &\left\{ j2\pi m \left[ \frac{(t-\frac{r}{c})}{(t-\frac{r_d}{c})}(1- \right.\right.\\&\left. \left. \frac{f_0d\sin \theta _d}{c}) + \frac{f_0d\sin \theta }{c}\right] \right\} . \end{aligned} \end{aligned}$$
(31)

The TMLFO applied to the \(m-th\) element is given as [116]

$$\begin{aligned} \Delta f_m^{TMLFO}(t) = \frac{g(m)-\frac{f_0\sin \theta _d}{c}}{t-\frac{r_d}{c}}, \end{aligned}$$
(32)

where g(m) is a logarithmic function defined as

$$\begin{aligned} g(m) = \ln {(m+1)}^k, \end{aligned}$$
(33)

where k is a control parameter for the frequency offset. The array factor at the target point is then expressed as

$$\begin{aligned} AF^{TMLFO}(t,r_d,\theta _d) =\sum _{m=0}^{M-1} \exp&\left\{ j2\pi \left[ \ln {(m+1)}^k(\frac{t-\frac{r}{c}}{t-\frac{r_d}{c}}-1)\right. \right. \\&\left. \left. +(m\frac{f_0d}{c}) (\sin \theta -\sin \theta _d\frac{t-\frac{r}{c}}{t-\frac{r_d}{c}})\right] \right\} . \end{aligned}$$
(34)

The time-modulated logistic map based frequency offsets and chirpiness constant considered in the TMDP-FDA are defined as [120]

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta f_{m, n}^{TMDP}(t) = \Delta f \frac{p_{m, n}}{t-\frac{r_d}{c}}, \\ u_{m,n}^{TMDP} = \Delta u \frac{2q_{m, n}}{(t-\frac{r_d}{c})^2}, \end{array}\right. } \end{aligned}$$
(35)

where \(0\le n \le N-1\); Here \(\Delta f\) and \(\Delta u\) are the control coefficients for the frequency offsets and chirpiness constant, respectively. It must be remembered that TMDP-FDA utilizes multi-carrier architecture, and frequency diverse chirp signal. The parameters \(p_{m, n}\) and \(q_{m, n}\) are generated by logistic map as [120]

$$\begin{aligned} {\left\{ \begin{array}{ll} p_{m, n} = 4p_{m, n-1}(1-p_{m, n-1}), \quad 0< p_{m, 0}< 1\\ q_{m,n} = 4q_{m, n-1}(1-q_{m, n-1}, \qquad 0< q_{m, 0} < 1 \end{array}\right. } \end{aligned}$$
(36)

and the corresponding array factor at the target point is given as

$$\begin{aligned} AF^{TMDP}(t,r_d,\theta _d) =\sum _{m=0}^{M-1} \sum _{n=0}^{N-1}\exp& \left\{ -j2\pi \left[ \frac{f_0 md(\sin \theta -\sin \theta _d)}{c}\right. \right. \\&\qquad \left. \left. +\Delta f \frac{p_{m, n}(r-r_d)}{r_d}+\Delta u \frac{q_{m, n}(r^2-r_d^2)}{r_d^2}\right] \right\} . \end{aligned}$$
(37)

In this example, we assume a 10-elements ULA operating at a reference carrier frequency of \(f_0=10\) GHz. The inter-element spacing is equal to half-a-wavelength. The pulse duration is \(T = 1\) ms, and the target is located at \((r_d, \theta _d)=\) (500 km, \(0^{\circ }\)). Since the multi-carrier technique is adopted in the TMDP-FDA, the number of carriers considered is \(N = 10\). Fig. 9 provides comparisons of beampattern generated by TDFO-FDA, TMLFO-FDA and the TMDP-FDA. It is shown in Fig. 9a that the time-independent beampattern of TDFO-FDA is periodic in range, and coupled in the range and angle dimensions. The periodicity, and range-angle coupling is eliminated in the time-invariant beampattern of TMLFO-FDA as depicted in Fig. 9b. Although the TMLFO-FDA generates a single maximum beampattern, its spatial focusing performance is degraded due to the high spatial peak sidelobe levels (P-SLL) and a broader spatial half-power beamwidth (HPBW). Furthermore, as Fig. 9c shows, the TMDP-FDA generate a well-shaped “dot” main beam and outperforms the other two schemes with a more focused beampattern due to multi-carrier architecture.

Fig. 9
figure 9

Beampattern synthesis results. a TDFO-FDA. b TMLFO-FDA. c TMDP-FDA

Full size image

To further demonstrate the resolution and side-lobe suppression performance, the corresponding range, and angle dimension beampatterns are plotted in Fig. 10. From Fig. 10a, it can be found that all the three FDAs have equal response in angle dimension except that the TDFO-FDA beampattern exhibit periodicity. However, from Fig. 10b, it is observed that the TMDP-FDA outperforms the TDFO-FDA and TMLFO-FDA with narrow HPBW in range dimension. The TDFO-beampattern exhibit periodicity in range dimension, and the performance of TMLFO-FDA is not satisfactory due to the high P-SLL and the broad spatial HPBW. Instead of a single carrier signal, each array element of the multi-carrier TMDP-FDA transmit a weighted summation of signals with a small frequency offset. Therefore, the effect of multi-carrier architecture on the performance of the TMDP-FDA is also demonstrated in Fig. 10c. It is observed that as the number of carrier frequencies increases, the P-SLL suppression and the HPBW gets improved.

Fig. 10
figure 10

Comparison of beampatterns in a angle dimension. b range dimension. c TMDP-FDA with varying numbers of carrier frequencies

Full size image

Although much attention has been paid to the uniform linear array configurations in existing FDAs due to its simple structure and well-developed techniques, other array configurations are also very appealing for non-communication applications such as radar, localization and positioning [122]. Numerous related works exploring FDAs with different array configurations for improved performance can be found in [123,124,125,126,127,128,129]. For instance, a multitarget localization algorithm for the sparse-FDA radar is proposed in [123], which incorporates both coprime arrays and coprime frequency offsets. Likewise, the compressive sensing technique is applied to FDA in [124] for range-angle estimation with a new type of array antenna, named random frequency diverse array. In [125], a joint optimization design scheme for FDA-MIMO radar is proposed, where virtual coprime planar array with ‘unfolded’ coprime frequency offsets framework is utilized to achieve three-dimensional (3D) localization without ambiguity. Similarly, a new waveform synthesis model of time modulation and range compensation FDA-MIMO is proposed in [126] to achieve a joint range-angle estimation based on the optimized time-invariant and dot-shaped beampattern. The beampattern analysis in terms 3D beam steering and auto scanning capabilities of the uniform circular FDA (UC-FDA) and the planar FDA were discussed in [127, 128] and [129], respectively. A flat-top range-angle dependent beampattern synthesis method has been proposed in [130] for FDA based on second-order cone programming. Similarly, a subarray-based FDA framework is devised in [131] to achieve a range-angle decoupled beampattern. A circular FDA utilizing tangent hyperbolic function for frequency offsets selection scheme is proposed in [132], where three different configurations of an FDA can be generated by adjusting a single function parameter of the tangent hyperbolic function.

The aforementioned FDA techniques can obtain a time-invariant range-angle decoupled beampattern, however, some recent studies indicate that FDA beampatterns are always time-variant in free space [133]. The existing FDA techniques designed for the range-angle dependent beampattern synthesis have not considered the propagation process of the transmitted signals, and may suffer performance degradation caused by the wave-propagation [133]. Consequently, it is necessary to revisit the FDA signal model and considering the wave propagation phenomenon into account, the new signal model is devised with time-variant focusing capability.

4 Wave propagation effect in FDAs

4.1 Correction of the time parameters

The original array factor of the FDA is a function of time t, which indicates that the EM waves propagate at the speed of light. More importantly, the term “\(t-\frac{r}{c}\)” in (12) indicates that the range r and time t are correlated, and their relationship cannot be ignored [133, 134]. As highlighted in [134], the propagation process of the transmitted signals is neglected in the early FDA literature, and the time-invariant beampatterns for FDAs were obtained by assuming the time variable t to be a fixed value (e.g., \(t = 0\)) or defining the variable t in the range from 0 to T [135]. This assumption that the signals propagated to the target location without time consumption is not valid in practice [133, 134].

Recall the array factor of TMLFO-FDA given by Eq. (34) as follows

$$\begin{aligned} AF^{TMLFO}(t,r,\theta ) =\sum _{m=0}^{M-1} \exp&\left\{ j2\pi \left[ \ln {(m+1)}^k(\frac{t-\frac{r}{c}}{t-\frac{r_d}{c}}-1)\right. \right. \\&\left. \left. +(m\frac{f_0d}{c}) (\sin \theta -\sin \theta _d\frac{t-\frac{r}{c}}{t-\frac{r_d}{c}})\right] \right\} . \end{aligned}$$
(38)

In (38), when \((r, \theta )=(r_d, \theta _d)\), we have

$$\begin{aligned} AF^{TMLFO}(t,r_d,\theta _d))=\sum _{m=0}^{M-1} \exp \lbrace -j2\pi (0)\rbrace =M \end{aligned}$$
(39)

In (38)–(39), the maximum of the range-angle-dependent beampattern stayed at the target location is independent of time as long as the range and angle are satisfied with \(r=r_d\) and \(\theta =\theta _d\). Furthermore, the beampattern is calculated during \(t\in [0, T]\). However, considering the propagation process of the transmitted signals, it is impractical that the EM waves propagate to a certain point \(P(r, \theta )\) without consuming time, i.e., at \(t = 0\). Similarly, it is also unconvincing to achieve the desired beampattern within the pulse duration that is at \(t = T\), because the desired range is usually taken as \(r_d\gg T.c\) [135].

Similarly, in the FDA schemes proposed in [114,115,116,117,118,119,120,121], the time-modulated frequency offsets were directly substituted in (12), and the variation of \(\Delta f_m(t)\) is supposed to propagate to any position without time consumption [134,135,136,137,138]. Hence, the beampatterns at the target point remain static all the time for \(r = r_d\) and \(\theta = \theta _d\). It is worth noticing that the range factor is introduced by the time factor in FDAs, however, the direct substitution of \(\Delta f_m(t)\) also indicates that the range influence is ignored. In other words, the range r is bounded up with time t, i.e., where there is t, there is r, and where there is r, there is t.

Hence, the array factor of these FDAs should be corrected by incorporating \(t-\frac{r}{c}\) as a single quantity variable of function f for the signals propagating in free space. Therefore, Eq. (29) can be revised as [134,135,136]

$$\begin{aligned} \Delta f_m(t) = \frac{\Delta f(m)}{t-\frac{r_m}{c}-\frac{r_d}{c}}. \end{aligned}$$
(40)

The corrected array factor of TMLFO-FDA [116] is then derived as

$$\begin{aligned} AF^{TMLFO}(t,r,\theta ) =\sum _{m=0}^{M-1} \exp&\left\{ j2\pi \left[ \ln {(m+1)}^k(\frac{t-\frac{r}{c}}{t-\frac{r}{c}-\frac{r_d}{c}}-1)\right. \right. \\&\left. \left. +(m\frac{f_0d}{c}) (\sin \theta -\sin \theta _d\frac{t-\frac{r}{c}}{t-\frac{r}{c}-\frac{r_d}{c}})\right] \right\} . \end{aligned}$$
(41)

It can be observed from (41), that the maximum of the correct beampattern of TMLFO-FDA no longer stays at the target point \((r_d, \theta _d)\). The original and correct beampattern of the TMLFO-FDA is compared in Fig. 11. From the beampatterns projected on the range-time dimension shown in Fig.  11a, b, it is observed that the original beampattern of TMLFO-FDA at the target point is time-invariant, however, when the propagation process of the transmitted signals is taken into account, the focus line disappears. The correct TMLFO-FDA beampattern is unable to focus the transmit energy at the desired target, when the practical signal propagation process is taken into account. The comparison of original and corresponding corrected models of some prominent FDAs is shown in Table 1.

Fig. 11
figure 11

Transmit beampattern of TMLFO-FDA in range-time dimensions with \((r_d, \theta _d) = (500 km, 0^{\circ })\). a Original time-invariant beampattern. b Corresponding correct beampattern

Full size image
Table 1 Comparison of original and corrected FDA array factors
Full size table

The unnoticed misconceptions about the time-range relationship, and frequency-phase relationship in FDAs are briefly analyzed in [134]. Additionally, the difference between the time-index within the pulse duration T, and the actual time t is also explained in [136]. It is shown that the variable t represents the actual time of the signal traveling in the space, whereas T is the time index within the pulse duration. More importantly, it is shown that the range parameter is related to the wave propagation i.e., time variable t, while phase of the wave signal is related to the pulse duration T, but not vice versa [136]. Based on the frequency-phase relationship, and the time-range relationship, these studies reestablish the correct signal models. It is proved that the beampattern of FDA is always time-variant as long as the electromagnetic waves travel at the velocity of light. It is worthy of note that existing FDA techniques mainly designed for time-invariant beampattern synthesis will essentially lead to a range-invariant beampattern as in conventional antenna arrays [137]. In other words, the design of time-invariant range-dependent beampattern is impractical. Consequently, these FDA schemes cease to focus the transmit energy at the desired target location when the wave propagation property is considered [138].

4.2 Scope of the time variable

Practically, \(c\Delta t\) movement in range is obvious for an elapsed time \(\Delta t\). For instance, the minimum time required for EM waves propagating with the speed of light to reach the target located at range \(r_d\) is \(t = \frac{r_d}{c}\). For a signal with pulse duration T, the target can be illuminated for T seconds and beyond that time, there is no signal. So, the scope of the time related to wave propagation for a desired target located at \(P(r_d, \theta _d)\) can be revised as \(t\in [\frac{r_d}{c}, \frac{r_d}{c}+T]\). The corrected array factor can then be expressed as [133]

$$\begin{aligned} AF(t,r_d,\theta _d)= \left\{ \begin{array}{l} \sum _{m=0}^{M-1} w_m \exp \lbrace j \psi _m\rbrace , \quad t\in [\frac{r_d}{c}, \frac{r_d}{c}+T] \\ 0, \qquad \qquad \qquad \qquad \qquad otherwise, \end{array} \right. \end{aligned}$$
(42)

where \(\psi _m=-2\pi [\Delta f_m(t-\frac{r}{c})+\frac{f_0md\sin \theta }{c}]\).

In summary, most signal models in time-invariant theories are actually inappropriate because the time-range relationship is ignored. The neglected propagation process of the transmitted signals causes essential misconception and results in erroneous conclusions. The term “\(t-\frac{r}{c}\)” indicates that maximum of the FDA beampattern cannot be independently controlled in time and range dimension, and the focusing point always moves with the velocity of light. Nevertheless, the performance degradation in time-invariant FDAs is inevitable when the wave propagation is considered, leading to the movement of focusing point with time. However, it is important to note that constant range for the focus point of FDAs appears to be unattainable but achieving a dot-shaped beampattern with FDAs in an instant of time is not in contradiction with the physical phenomenon of EM wave propagation [134, 138].

5 Recent trends in FDAs

5.1 Time-variant focusing FDA beampattern synthesis

Considering the propagation process of transmitted signals in FDAs, several researchers strive to focus the transmit energy on the desired target in an instant of time. For example, a short-range symmetrical FDA radar is proposed in [135] by incorporating an arc-tangent function modulated frequency scheme. Likewise, a transmit beampattern synthesis method based on arc-tangent function is proposed in [139] for waveform diverse array radar to focus the signal energy on the desired target for a period of time. A multi-carrier symmetrical FDA radar with frequency diverse chirp signal is proposed in [140] for short-range applications. They achieve a time-variant focused range-angle dependent beampattern by compensating the propagation delays of transmitting signals. In [141], a focused angle-range beamforming synthesis method with time-varying characteristics is proposed, where the frequency offsets, amplitude weighting and phase weighting are optimized by bat metaheuristic algorithm to achieve single-dot and multi-dot shape transmit beamforming. A logarithm-based optimized static nonlinear frequency offset for FDA is proposed in [142] to alleviate its intrinsic time-variant problem, which depends on a frequency offset control function and the duration of a short-time interval rather than introducing the time variable. More recently, investigations on exploring different array configurations for improved performance have been made in [143,144,145,146]. A dual function range-angle dependent sidelobe control using FDA-MIMO is proposed in [143] for joint radar-communications. The proposed system considers the time-variance of an FDA beampatterm. A high-speed user-centric beampattern synthesis method for FDA is devised in [144], where the time-variant beampattern peak accompany the quickly-moving user without altering the frequency offsets. A UC-FDA radar is proposed in [145] to realize time-variant spatial focusing in short-range at the target location. The UC-FDA radar is capable to provide \(360^{\circ }\) of coverage in the azimuth plane, which cannot be achieved by the linear array-based FDA radar. Similarly, a hemi-spherical FDA is exploited in [146] to demonstrate the unique advantage of conformal FDA in terms of 3D localization ability. It alleviates the inherent time-variant problem, and generate a quasi-time-invariant 3D focusing beampattern. The FDA schemes presented in [145, 146] incorporates pulse-dependent frequency offsets to achieve time-variant spatial focusing beampattern.

The array factor for the short-range FDA radar proposed in [135] is given as

$$\begin{aligned} AF(t,r_d,\theta _d) = \sum _{m=-M}^{M} \exp \left\{ -j2\pi \psi _m \left[ t-\frac{r_m}{c} + \Delta \tau _m\right] \right\} , \end{aligned}$$
(43)

where \(\psi _m (t) =\Delta f_m \frac{2}{\pi } (t-\frac{T}{2}) \arctan [\frac{\alpha }{T}(t-\frac{T}{2})] - \Delta f_m \frac{T}{\alpha \pi } \ln [\frac{\alpha ^2}{T^2} (t-\frac{T}{2})^2 +1]\), and \(\Delta \tau _m = \frac{r_m^\prime - r_d}{c}\) is the corresponding transmit delay, where \(r_m^\prime = r_d -md\sin \theta _d\).

The pulse-dependent nonlinear frequency offset proposed in [145] is defined as

$$\begin{aligned} \Delta f_{m,n} (t)= \frac{\alpha g(m,n)-f_0\frac{a}{c} \sin \theta _d \cos (\varphi _d-\varphi _m)}{t-\frac{r_d}{c}+\frac{a}{c}\sin \theta _d \cos (\varphi _d-\varphi _m)}, \end{aligned}$$
(44)

where \(\varphi\) denotes the elevation angle, and g(m, n) is a nonlinear function generated by a logistic map with a control parameter \(\alpha\). Since the transmitted signals can propagate to the target location \(P(r_d, \theta _d, \varphi _d)\) within the time interval \(t\in [\frac{r_d}{c}, \frac{r_d}{c}+T]\), therefore, assuming the value of t within this range, the final form of pulse-dependent frequency offsets becomes

$$\begin{aligned} \Delta f_{m,n}(m,n)= \frac{\alpha g(m,n)-f_0\frac{a}{c} \sin \theta _d \cos (\varphi _d-\varphi _m)}{\beta T+\frac{a}{c}\sin \theta _d \cos (\varphi _d-\varphi _m)}, \end{aligned}$$
(45)

where the introduced coefficient \(\beta\) satisfies the condition \(0\le \beta \le 1\).

Similarly, the optimized static nonlinear frequency offset (OSNFO) for general conformal FDA in [146] is given by

$$\begin{aligned} \Delta f_{m,n}^{OSNFO}= \frac{g_{OSNFO}(m)}{T/2}, \end{aligned}$$
(46)

where \(g_{OSNFO}(m)\) is a nonlinear function to be optimized by the conventional evolutionary methodology.

In Fig. 12, we have demonstrated the significance of the wave propagation effect in FDAs. Figure 12a shows the original time-invariant beampattern generated by the compensated TMOFO (C-TMOFO) FDA [119], where a focused beampattern with a single maximum at the target position is achieved. Figure 12b shows its corresponding corrected beampattern projected on the time-range dimension when wave propagation is considered. Obviously, the focused point disappears, and the beampattern is unable to be steered to the target position. The beampattern of the short-range FDA radar based on arc-tangent function [135] is shown in Fig. 12c. It is observed that the transmit energy is focused when the pulse signals reach the desired spatial region \(r_d = 6\) m at \(t = 25\) ns only. The analysis of time-invariant FDAs, and their corrected models with simulated examples are briefly discussed in [134,135,136,137,138,139,140, 145].

Fig. 12
figure 12

Significance of the wave propagation effect. a C-TMOFO FDA original time-invariant beampattern. b C-TMOFO FDA corrected time-variant beampattern. c Original time-variant beampattern of the short-range FDA radar based on arc-tangent function

Full size image

5.2 Applications

While most current research activities mainly focus on radar applications, such as localization, FDA is also very appealing for communication applications. The security issue in wireless communication systems is of great concern due to its broadcasting nature of transmission [29]. In this scenario, the communications between the transmitter and the legitimate destination receiver are more likely to be intercepted easily by eavesdroppers. Therefore, an active research topic has been focused on how to prevent eavesdroppers access to the desired information in wireless communication systems.

Directional modulation (DM) is recognized as one of the most promising techniques in the point-to-point physical layer secure communications [147]. DM projects digitally modulated signals into a pre-defined secure communication spatial direction, while simultaneously distorting the constellation of these signals in all other directions [148]. This can significantly decrease the risk of these signals being eavesdropped. As such, DM techniques using PA antenna have been widely applied in wireless communications, which only achieves one-dimension security, i.e., angle-dependent directional modulation [149]. Therefore, the PA based DM techniques are less successful when an eavesdropper and the legitimate user are located in the same direction.

On the other hand, frequency diversity has been shown to be a highly effective technique in wireless communications, which provides a number of advantages, including increased system capacity and SNR, security and robustness. Motivated by the range-angle dependent beampattern of FDAs, researches have been carried out on FDA based DM techniques to enhance physical layer security of wireless communications [150, 151]. Both the PA and FDA based DM techniques can be typically applied to secure communication in the line-of-propagation channels such as millimeter wave, satellite communications, unmanned aerial vehicles, and smart transportation. Compared with the PA-based DM techniques, the FDA based DM technique can achieve the physical layer security in both range and angle dimensions. Since the FDA apparent scan angle is different than its nominal scan angle, precise beam steering depends on both the range and the angle. Consequently, the actual beam steering direction in FDAs cannot be effectively predicted as conventional phased arrays. Equation (22) demonstrates how the scan angle changed with frequency increment and generated an apparent scan angle.The FDA based DM techniques have provable performance guarantee when the legitimate user and eavesdropper locate in the same direction but different ranges [152].

Until recently, several attractive FDA based DM techniques have been proposed to ensure secure communication with low probability of interception and low probability of detection. To name a few, a decoupled range-angle dependent DM scheme using FDA with symmetrically and nonlinearly increasing frequency offsets is proposed in [150] for secure wireless communications. In [151], frequency offsets optimized with genetic algorithm are used to achieve the physical layer security in both angle and range dimensions. Two time-invariant range-angle dependent DM schemes based on time-modulated frequency offsets FDA were proposed in [152] to achieve time-invariant spatial fine focusing point-to-point physical layer secure communications. In the DM transmission schemes, artificial noise plays a pivotal role. In artificial noise-aided secure transmission, the transmitter also sends artificial noise as an interference signal of eavesdropper, which only interferes the eavesdropper without affecting the legitimate user. The DM with artificial noise based on random FDA, referred to as the RFDA-DM-AN scheme, is presented in [153] to enhance physical layer security of wireless communications. Similarly, DM with an artificial-noise-aided approach, and FDA beamforming-based approach are, respectively, proposed for the security of proximal legitimate user and eavesdropper in [154] and [155]. In contrast to the single-user FDA-DM schemes, multi-beam DM synthesis based on FDA is investigated in [156,157,158,159].

As such, DM utilizing FDA is shown to be more robust than using PA antenna, and becomes a preferred choice to achieve enhanced physical layer secure communications. Therefore, FDA based DM has been an intensive research topic, owing to their superior performance to the PA based DM techniques [160,161,162,163,164]. Similar to FDA, a new transmit diversity technique, namely, hybrid code, is presented in [165], where the operation of the PA radar and the functionality of the coherent MIMO radar are unified for use in electronically steered phased array radars. The hybrid code demonstrates low range sidelobes and better angular selectivity. Instead of scanning, the hybrid code obtains the transmit beampatterns for any/all chosen angular directions by signal processing means. The hybrid code is a promising concept that can play an important role in future radar, and communication applications.

6 Future work

This work has looked at broad concepts that provide a basis for continuing research in FDAs. In particular, areas that are suitable for continuing research includes:

  1. 1

    Optimization of array geometry: Further research may explore optimal geometry for FDA radars. Various array configurations merit further consideration, including parabolic geometries and multi-ring UCA.

  2. 2

    Optimization of frequency offsets: More investigations should be carried out to optimally design computationally efficient FDA frequency offsets.

  3. 3

    Waveform optimization: Most of the investigations to date have focused on FDAs with narrowband signal sources, further efforts are required to its application in wideband and ultra-wideband systems.

  4. 4

    Optimal signal processing: FDAs should be researched in more complex electromagnetic environment such as mainlobe and sidelobe clutters, jamming, and intense interference environment.

  5. 5

    Advanced applications: Much of the recent work in FDAs has been focused on localization related applications such as navigation and radar. Although some studies discuss their application in various other fields including communication, more research is required to explore its advantages in other fields.

  6. 6

    Wave Propagation: To mitigate the performance degradation caused by wave propagation, and ensure the applicability of FDA radars in practical applications, improved time-variant focusing techniques with longer dwell time is an emerging research direction in FDAs.

  7. 7

    Multi-target localization: Although various FDAs with time-variant consideration is proposed for a single target scenario, extension to multi-target detection may also be included in future studies.

  8. 8

    Hardware Implementation: A future effort may also focus on implementation of time-variant FDAs with hardware implementation.

7 Conclusion

This paper provides an overview of the FDA radar, and briefly discuss its performance and implementation issues with an emphasis on recent research. The FDA radar is a newly emerging concept, which has a range-angle dependent beampattern. Unlike PA radars, which work with fixed carrier frequencies, the FDA radar employ a small frequency increment across the array elements to achieve DOFs in both the angle and range dimensions. We have briefly analyzed the characteristics of the FDA beampattern from its origin to the current state-of-the-art. Many different approaches to FDA radar for improved performance have been discussed briefly. The conventional FDA radar using progressive incremental frequency offsets yields a range-angle coupled beampattern. To decouple the FDA beampattern in range-angle dimensions, nonlinear arrays or nonlinear frequency offsets were utilized. However, the resulting beampatterns exhibit time-periodicity. To deal with these time-periodic beampatterns, time-modulated frequency offsets were reported, which achieve range-angle decoupled, and time-invariant beampatterns at the target position. However, some recent studies indicate that the propagation process of transmitted signals was ignored in the FDA literature. The FDA beampattern is always time-variant in free space. Therefore, the focused beampattern for FDAs using time-invariant techniques cannot be realized practically. Although some researchers were successful in focusing the transmit energy over the desired target location, the dwell-time is very short. Future work will likely address the time-variant focusing problem with longer dwell time, and extension to multi-target scenarios is also a subject for future work. FDAs were also shown to have provable performance in wireless communication applications such as physical layer secure point-to-point communication. However, unlike the PA which is a mature technology, FDA has yet to achieve super resolution capabilities, and many practical problems still need to be investigated.