1 Introduction

Beampattern is widely used to assess the performance of phased arrays [1]. However, a limitation of phased array is that the beam steering is fixed at one angle for all the ranges [2]. Recently, a flexible array called frequency diverse array (FDA) has been proposed [3-5]. Different from phased array, a small frequency increment, as compared to the carrier frequency, is applied across the array elements [6]. This small frequency increment results in a range angle-dependent beampattern [7,8]. Several investigations have been carried on FDA radars. The time and angle periodicity of FDA beampattern was analyzed in [9]. A linear FDA was proposed in [10] for forward-looking radar ground moving target indication. The multipath characteristics of FDA radar over a ground plane were investigated and compared with phased array in [11]. FDA radar full-wave simulation and implementation with linear frequency-modulated continuous waveform were presented in [12,13]. In [14], we have investigated the FDA Cramér-Rao lower bounds for estimating direction, range, and velocity. More recent work about the applications of FDA in MIMO radars can be found in [15-19].

Perfect frequency increments are often assumed in existing literatures [20]. However, in an actual array system, there will have imperfect errors including element position errors, mutual coupling, phase errors, and frequency increment errors [21-24]. Some results have been reported about the impacts of element position error, mutual coupling and phase error on beampattern, and direction-of-arrival (DOA) estimation performances. Since FDA beampattern has similar properties with conventional phased array for the impacts of element position errors, mutual coupling, and phase errors, this paper considers only the impacts of frequency increment errors on FDA beampattern. Since FDA beampattern is dependent on the angle and range, it has a potential for target localization, which is different from traditional time-of-arrival (TOA) and angle-of-arrival (AOA)-based localization [25-28]. The contributions can be summarized as follows. (i) More tighter bounds of FDA beampattern deviation are derived. (ii) Statistical analysis of FDA beampattern in terms of expectation value, variance, and probability density function (PDF) are provided.

The rest of this paper is organized as follows. Section 2 formulates the data models of FDA radar without and with frequency increment errors, respectively. Section 3 analyzes the impacts of deterministic frequency increment errors on FDA beampattern. Thereafter, the impacts of random frequency increment errors are investigated in Section 4. Finally, simulation results are provided in Section 5, and conclusions are drawn in Section 6.

2 FDA beampattern without frequency increment errors

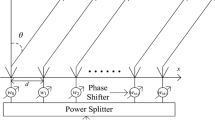
Suppose an N-element uniform linear FDA with inter-element spacing denoted as d. The radiated frequency from the nth element is as follows:

$$ f_{n}=f_{0}+n\Delta f, n=0, 1, 2, \ldots, N-1 $$
((1))

where f 0 and Δ f are the carrier frequency and frequency increment, respectively. Taking the first element as the reference for the array, under far-field condition, one might express the direct wave component of the electric field emitted from the FDA at the observation point (θ,r) as [17]:

$$ \begin{aligned} A(\theta,r,t) = \sum\limits_{n = 0}^{N - 1} {{a_{n}}{\varsigma_{n}}\left(\theta \left| {{w_{n}}} \right.\right)} \frac{{{e^{j{w_{n}}\left(t - \frac{{r + {d_{n}}\sin \theta }}{{{c_{0}}}}\right)}}}}{r} \end{aligned} $$
((2))

where N is the number of FDA elements, a n represents the complex excitation coefficient for the nth element, ς n (θ|w n ) stands for the far-field vector radiation pattern for the nth element at range r and angular frequency w n =2π f n , c 0 is the light speed, d n is the element position of the nth element reference relative to the first element, and t is the time parameter. In accordance with the far-field assumption, \({{e^{j{w_{n}}\left (t - \frac {{r + {d_{n}}\sin \theta }}{{{c_{0}}}}\right)}}}/r\) corresponds to the delayed carrier with free space loss.

To interpret the effect of frequency diversity within the scope of an array factor, we should factor the vector element pattern out of Equation 2. This can indeed be done under certain conditions. Assuming all elements in the FDA are identical, we can eliminate the frequency dependence in the element factor. Since r≫d n , we have:

$$ {\varsigma_{n}}({\theta }{|{{w_{n}}}}) \approx \varsigma(\theta {|{{w_{0}}}}). $$
((3))

where w 0 is the carrier angular frequency. So Equation 2 can be rewritten as:

$$ A(\theta,r,t) = \varsigma(\theta \left| {{w_{0}}} \right.)\sum\limits_{n = 0}^{N - 1} {{a_{n}}} \frac{{{e^{j{w_{n}}\left(t - \left(\frac{{r + {d_{n}}\sin \theta }}{{{c_{0}}}}\right)\right)}}}}{r}. $$
((4))

Further simplification becomes possible by considering particular FDA arrangements that are simple to handle and yet able to provide valuable insight. A uniform linear FDA utilizing discrete, linear frequency increments is such a practical configuration, and it is examined in this section as a special case. By definition, the elements are excited with uniform amplitude, but they are allowed to have a phase progression across the array. These specifications translate to the following expressions for d n and a n :

$$ {d_{n}} = nd ~~\text{and}~~ {a_{n}} = {e^{- jn \phi_{a}}} $$
((5))

where ϕ a stands for the phase progression. Submitting Equations 1 and 5 into Equation 4 yields:

$$ {\footnotesize{\begin{aligned} A(\theta,r,t) &= \varsigma\left(\theta \left| {{w_{0}}} \right.\right)\sum\limits_{n = 0}^{N - 1} {{e^{- jn\phi_{a} }}} \frac{{{e^{j2\pi \left({f_{0}} + n\Delta f\right)\left(t - \left(\frac{{r + nd\sin \theta }}{{{c_{0}}}}\right)\right)}}}}{r}\\ &= \frac{{\varsigma\left(\theta \left| {{w_{0}}} \right.\right)}}{r}{e^{j{\varphi_{0}}}}\sum\limits_{n = 0}^{N - 1} {{e^{- jn\phi_{a} }}{e^{j2\pi n\Delta f\left(t - \left(\frac{{r + nd\sin \theta }}{{{c_{0}}}}\right)\right) - j2\pi {f_{0}}\frac{{nd\sin \theta }}{{{c_{0}}}}}}} \end{aligned}}} $$
((6))

where \(\varphi _{0}=2\pi {f_{0}}t - 2\pi {f_{0}}\frac {r}{{{c_{0}}}}\). For notation convenience, we define \(\bar \varsigma = \varsigma \left (\theta \left | {{w_{0}}} \right.\right){e^{j2\pi {f_{0}}t - j2\pi {f_{0}}\frac {r}{{{c_{0}}}}}}\), Equation 6 can then be rewritten as:

$$ \begin{aligned} A(\theta,r,t) = \frac{{\bar \varsigma}}{r}\sum\limits_{n = 0}^{N - 1} {{e^{- jn\phi_{a} }}{e^{j2\pi n\left(t\Delta f - \frac{{r + nd\sin \theta }}{{{c_{0}}}}\Delta f - {f_{0}}\frac{{d\sin \theta }}{{{c_{0}}}}\right)}}} \end{aligned} $$
((7))

Since n dsinθ≪r, Equation 7 can be reformulated as:

$$ \begin{array}{l} A(\theta,r,t) \approx \frac{{\bar \varsigma }}{r}\sum\limits_{n = 0}^{N - 1} {{e^{- jn\phi_{a} }}{e^{j2\pi n\left(t\Delta f - \frac{r}{{{c_{0}}}}\Delta f - {f_{0}}\frac{{d\sin \theta }}{{{c_{0}}}}\right)}}} \\ \qquad\qquad= \frac{{\bar \varsigma }}{r}{\mathbf{w}^{H}}\mathbf{v}(\theta, r, t) \end{array} $$
((8))

where

$$\textbf{w} = {\left[\,\, 1 {{e^{j\phi_{a} }}} \,\,{\ldots}\,\,{{e^{j(N-1)\phi_{a} }}} \,\,\right]^{T}}$$
((9))

and

$$ \begin{aligned} \textbf{v}(\theta, r, t) = \left[ {\begin{array}{*{20}{c}} 1&{{e^{j2\pi \left(t\Delta f - \frac{r}{{{c_{0}}}}\Delta f - {f_{0}}\frac{{d\sin \theta }}{{{c_{0}}}}\right)}}} \end{array}} \right.{\ldots}\\&\left.{}{\begin{array}{*{1}{c}} {{e^{j2\pi (N - 1)\left(t\Delta f - \frac{r}{{{c_{0}}}}\Delta f - {f_{0}}\frac{{d\sin \theta }}{{{c_{0}}}}\right)}}} \end{array}} \right]^{T}. \end{aligned} $$
((10))

with [·]T and [·]H being the transpose operator and hermitian transpose operator, respectively. For simplicity, \(\bar {\varsigma }=1\) is assumed in the following discussions. Figure 1 shows the ideal linear uniform FDA beampattern with t=1/Δ f.

Figure 1
figure 1

Ideal two-dimension FDA beampattern with N=16, Δ f=30 K H z,t=1/(3×104), ϕ a =0, and w=1 N×1.

Full size image

2.1 FDA beampattern with frequency increment errors

Suppose the frequency increment errors being \({\rho } = [\begin {array}{*{20}{c}} 0&{{\rho _{1}}}&{\ldots }&{{\rho _{N - 1}}}\end {array}]\), Equation 8 can be rewritten as:

$$ A(\theta,r) = \frac{{{\textbf{w}^{H}}\tilde{\mathbf{v}}(\theta,r,t)}}{r} $$
((11))

where

$${} {\footnotesize{\begin{aligned} \tilde{\mathbf{v}}(\theta,r,t) &=\left[1\quad e^{j2\pi \left(t\left(\Delta f + {\rho_{1}}\right) - \frac{r}{{{c_{0}}}}\left(\Delta f + {\rho_{1}}\right) - {f_{0}}\frac{{d\sin \theta }}{{{c_{0}}}}\right)} {\ldots}\right.\\&\left.{\kern1.95pc}e^{j2\pi (N - 1)\left(t\left(\Delta f + {\rho_{N - 1}}\right) - \frac{r}{{{c_{0}}}}\left(\Delta f + {\rho_{N - 1}}\right) - {f_{0}}\frac{{d\sin \theta }}{{{c_{0}}}}\right)} \right]^{T}\\ &=\left[1\quad e^{j2\pi \left(t\Delta f - \frac{r}{{{c_{0}}}}\Delta f - {f_{0}}\frac{{d\sin \theta}}{c_{0}}\right)}{e^{j2\pi \left(t{\rho_{1}} - \frac{r}{{{c_{0}}}}{\rho_{1}}\right)}} {\ldots}\right.\\&\left.{\kern1.9pc}e^{j2\pi (N - 1)\left(t\Delta f - \frac{r}{{{c_{0}}}}\Delta f - {f_{0}}\frac{{d\sin \theta }}{{{c_{0}}}}\right)}e^{j2\pi \left(N - 1)(t{\rho_{N - 1}} - \frac{r}{{{c_{0}}}}{\rho_{N - 1}}\right)} \right]^{T}. \end{aligned}}} $$
((12))

Then Equation 11 can be reformulated as:

$$ \begin{aligned} \tilde A(\theta,r) &= \frac{{{\textbf{w}^{H}}\tilde{\mathbf{v}}(\theta,r,t)}}{r}\\ &= \frac{{{\textbf{w}^{H}}(\textbf{v}(\theta,r,t) \odot \Delta \textbf{v}(r,t))}}{r}\\ &= \frac{{{\textbf{w}^{H}}diag(\Delta \textbf{v}(r,t))\textbf{v}(\theta,r,t)}}{r}\\ &= \frac{{{\textbf{w}^{H}}\textbf{C}(r,t)\textbf{v}(\theta,r,t)}}{r} \end{aligned} $$
((13))

where

$${}\Delta \textbf{v}(r,t) = \left[1\quad{{e^{j2\pi \left(t\rho - \frac{r}{{{c_{0}}}}\rho \right)}}}\quad{\ldots}\quad{{e^{j2\pi (N - 1)\left(t\rho - \frac{r}{{{c_{0}}}}\rho \right)}}}\right]^{T} $$

and

$$\textbf{C} = \text{diag }\left(\Delta \textbf{v}(r,t)\right) $$

and ⊙ denotes Hadamard product. Note that diag(Δ v(r,t)) denotes a diagonal matrix with Δ v(r,t) being its diagonal elements. For small frequency increment errors, Taylor series expansion about C is performed as follows:

$$ {\mathbf{C}(r,t)} = \textbf{I} + {\textbf{C}_ + (r,t)}. $$
((14))

According to Equation 13, it can be known that:

$$ \begin{aligned}{\mathbf{C}}_{+}\left(r,t\right)& =\mathrm{diag}\left(j2\pi \left(-\frac{\left(\mathbf{N}\odot \rho \right)r}{c_0}+t\left(\mathbf{N}\odot \rho \right)\right)\right.\\ &\quad\odot \left.\left({e}^{j2\pi \left(-\frac{\left(\mathbf{N}\odot \rho \right)r}{c_0}+t\left(\mathbf{N}\odot \rho \right)\right)}\right)\right)+O\left(\rho \right)\\ &{}\approx \mathrm{diag}\left(j2\pi \left(-\frac{\left(\mathbf{N}\odot \rho \right)r}{c_0}+t\left(\mathbf{N}\odot \rho \right)\right)\right.\left.\odot \left({e}^{j2\pi \left(-\frac{\left(\mathbf{N}\odot \rho \right)r}{c_0}+t\left(\mathbf{N}\odot \rho \right)\right)}\right)\right).\end{aligned} $$
((15))

where N=[0,1,2,…,N−1] denotes element number of FDA radar, and O(ρ) represents for the high order terms about ρ, which can be ignored for Equation 15. Using Equation 15, we can rewrite the beampattern (13) as:

$$ \begin{aligned} \tilde A(\theta,r,t) &= \frac{{{\textbf{w}^{H}}\textbf{C}(r,t)\textbf{v}(\theta,r,t)}}{r}\\ &= \frac{{{\textbf{w}^{H}}\textbf{v}(\theta,r,t) + {\textbf{w}^{H}}{\textbf{C}_ + }(r,t)\textbf{v}(\theta,r,t)}}{r}\\ &= A(\theta,r,t) + \frac{{{\textbf{w}^{H}}{\textbf{C}_ + }(r,t)\textbf{v}(\theta,r,t)}}{r}\\ &= A(\theta,r,t) + \Delta A(r,t) \end{aligned} $$
((16))

where \(\Delta A(r,t)=\frac {{{\textbf {w}^{H}}{\textbf {C}_ + }(r,t)\textbf {v}(\theta,r,t)}}{r}\) denotes the FDA beampattern deviation. Figure 2 shows the FDA beampattern with frequency increment errors. The array parameters are the same as that for Figure 1. Due to the frequency increment errors, the FDA beampattern sidelobes are different from Figure 1. Stronger sidelobe peaks will make the FDA energy scattering and consequently degrade the array performance.

Figure 2
figure 2

Two-dimension FDA beampattern with frequency increment error ρ n and ρ n ∼N(0,ρ 2) with ρ=500.

Full size image

3 Impacts of deterministic frequency increment errors

Firstly, we consider uniform frequency increment errors, i.e., ρ=[0 ρ 1 … ρ N−1]=[0 ρ … ρ]. In this case, Equation 13 can be rewritten as:

$${} {\small{\begin{aligned} \tilde A(\theta,r) &\,=\, \frac{{{\textbf{w}^{H}}\text{diag }\left(\Delta \textbf{v}(r,t)\right)\textbf{v}(\theta,r,t)}}{r}\\ &\,=\, \sum\limits_{n = 1}^{N} {\frac{{{e^{j2\pi (n - 1)\left(t\left(\Delta f + \rho \right) - \frac{r}{{{c_{0}}}}\left(\Delta f + \rho \right) - {f_{0}}\frac{{d\sin \theta }}{{{c_{0}}}}\right)}}}}{r}} \\ &\,=\, \frac{{k}}{r}\frac{{\sin \left(\frac{\pi N}{2}\left(t\left(\Delta f + \rho \right) - \frac{r}{{{c_{0}}}}(\Delta f + \rho) - {f_{0}}\frac{{d\sin \theta }}{{{c_{0}}}}\right)\right)}}{{\sin \left(\pi\frac{{t\left(\Delta f + \rho \right) - \frac{r}{{{c_{0}}}}\left(\Delta f + \rho\right) - {f_{0}}\frac{{d\sin \theta }}{{{c_{0}}}}}}{2}\right)}}\\ &\,=\, \frac{{k}}{r}\frac{{\sin \left(\frac{\pi N}{2} \left(\Delta f\left(t \!+ \frac{\rho }{{\Delta f}}t\right) - \frac{{\Delta f}}{{{c_{0}}}}\left(r \,+\, \frac{\rho }{{\Delta f}}r\right) - {f_{0}}\frac{{d\sin \theta }}{{{c_{0}}}}\right)\!\right)}}{{\sin \left(\pi\frac{{\Delta f\left(t + \frac{\rho }{{\Delta f}}t\right) - \frac{{\Delta f}}{{{c_{0}}}}\left(r + \frac{\rho }{{\Delta f}}r\right) - {f_{0}}\frac{{d\sin \theta }}{{{c_{0}}}}}}{2}\right)}} \end{aligned}}} $$
((17))

where \(k = {e^{j\pi N\left (t(\Delta f + \rho) - \frac {r}{{{c_{0}}}}(\Delta f + \rho) - {f_{0}}\frac {{d\sin \theta }}{{{c_{0}}}}\right)}}\) and w=1 N×1. Equation 17 arrives the maximum value when:

$${} {\small{\begin{aligned} \Delta f\left(t + \frac{\rho }{{\Delta f}}t\right) - \frac{{\Delta f}}{{{c_{0}}}}\left(r + \frac{\rho }{{\Delta f}}r\right) - \left({f_{0}}\frac{{d\sin \theta }}{{{c_{0}}}}\right)=2m&\\ m=0,1,2,\ldots.& \end{aligned}}} $$
((18))

If no frequency increment error exists, the FDA mainlobe will pass the location \(\left (0^{\circ },~\frac {{c_{0} }}{{{\Delta f}}}\right) \) at \(t=~\frac {{1}}{{{\Delta f}}}\). However, when there are frequency increment errors, the location \(\left (0^{\circ },~\frac {{c_{0} }}{{{\Delta f}}}\right) \) may be not at the beampattern maximum point. According to Equation 18, the corresponding range error is as follows:

$$ \Delta r= \frac{\rho}{{\Delta f}}r. $$
((19))

Since the phase error caused by time error can be equivalently regarded as range error and angle error, Equation 18 can be reformulated as:

$${} {\small{\begin{aligned} &\Delta f\left(t + \frac{\rho }{{\Delta f}}t\right) - \frac{{\Delta f}}{{{c_{0}}}}\left(r + \frac{\rho }{{\Delta f}}r\right) - \left({f_{0}}\frac{{d\sin \theta }}{{{c_{0}}}}\right)\\ &= \Delta ft + \frac{\rho }{{\Delta f}}t - \frac{{\Delta f}}{{{c_{0}}}}\left(r + \frac{\rho }{{\Delta f}}r\right) - \left({f_{0}}\frac{{d\sin \theta }}{{{c_{0}}}}\right)\\ &= \Delta ft - \frac{{\Delta f}}{{{c_{0}}}}\left(r + \frac{\rho }{{\Delta f}}r - \frac{{\rho {c_{0}}}}{{2\Delta {f^{2}}}}t\right) - {f_{0}}\frac{d}{{{c_{0}}}}\left(\sin \theta - \frac{{\rho {c_{0}}}}{{2\Delta f{f_{0}}d}}t\right)\\ &= 2m,{\mathrm{~~~~~~m} = 0,1,2,}\ldots \end{aligned}}} $$
((20))

Therefore, the corresponding range error is as follows:

$$ \begin{aligned} \Delta r= \frac{\rho }{{\Delta f}}r-\frac{{\rho {c_{0}}}}{{2\Delta {f^{2}}}}t \end{aligned} $$
((21))

and the angle error is as follows:

$$ \begin{aligned} \Delta \theta=\text{arcsin}\left(\frac{{\rho {c_{0}}}}{{2\Delta f{f_{0}}d}}t\right). \end{aligned} $$
((22))

If the range error and angle error are required to be smaller than 50 m and 0.5∘, respectively, the frequency increment error should be smaller than 150 Hz.

Figure 3a,b shows the FDA beampattern with uniform frequency increment errors ρ, frequency increment Δ f=30 KHz, and t=1/Δ f. It can be noticed that the phase error for θ=0.5∘ is ρ/Δ f=5×10−3. Note that since the range attenuation exists, the range error has a small deviation from the calculation of Equation 21.

Figure 3
figure 3

FDA beampattern profiles with frequency increment errors.(a) In angle dimension. (b) In range dimension.

Full size image

4 Impacts of stochastic frequency increment errors

In this section, we investigate the statistical properties of FDA beampattern with random frequency increment errors.

4.1 Error boundary of FDA beampattern

Suppose the frequency increment errors are random. In this case, it is not possible to derive a deterministic beampattern expression like Equation 17. Here, we are interested in the maximum beampattern deviation, namely:

$$ \underset{t,r,\theta}{\max} \left| {\Delta A(t,r,\theta)} \right|. $$
((23))

According to Equation 16 and using the Cauchy-Schwarz inequality, we have:

$$ \begin{aligned} \underset{t,r,\theta}{\max} \left| {\Delta A(\theta,r,t)} \right| &\le \frac{1}{r}{\left\| {{w_{\max }}{\textbf{C}_ + }} \right\|_{2}}{\left\| {\textbf{v}(\theta,r)} \right\|_{2}}\\ &= \frac{1}{r}{\left\| {{w_{\max }}{\textbf{C}_ + }} \right\|_{2}}\sqrt N\\ & \le \frac{1}{r}|{w_{\max }}|{\left\| {{\textbf{C}_ + }} \right\|_{2}}\sqrt N \\ &= \Delta {A_{\max }} \end{aligned} $$
((24))

where |·| and ∥·∥2 denote the absolute value and Euclidean norm, respectively, and w max denotes the maximum element of w. Note that compared with [29], |w max|≤|w|2, the bound expressed in Equation 24 is much tighter. According to Equation 16, C + can be rewritten as:

$$ {\small{\begin{aligned} {\left\| {{\textbf{C}_ + }} \right\|_{2}} &= \left\| {\text{diag}\left(\left(j2\pi \left(-\frac{{(\textbf{N} \odot {\rho })r}}{{{c_{0}}}} + t(\textbf{N} \odot {\rho })\right)\right)\right.} \right.\\ &~~~~~~~~~~~~~~~~~~~~~~~~{\left.{\left. \odot \left({e^{j2\pi (-\frac{{(\textbf{N} \odot {\rho })r}}{{{c_{0}}}} + t(\textbf{N} \odot {\rho }))}}\right)\right)} \right\|_{2}}\\ &= {\left\| {\text{diag}\left(j2\pi \left(-\frac{r}{{{c_{0}}}} + t\right)(\textbf{N} \odot {\rho })\right)} \right\|_{2}}\\ &= 2\pi \left|-\frac{r}{{{c_{0}}}} + t\right|\cdot{\left\| {\text{diag}(\textbf{N} \odot {\rho })} \right\|_{2}}. \end{aligned}}} $$
((25))

The maximum deviation, in a linear scale, is the same over the whole beampattern. When only C + (and thus C) is known, or when the influence of unknown factors on C +, e.g., aging or temperature, comes into play, it makes sense to consider as random matrix, with some statistical model for the entries of C +. We then have to calculate:

$$ \begin{aligned} \max ~~~~{\left\| {{\textbf{C}_ + }} \right\|_{2}} \end{aligned} $$
((26))

for the random matrix C + to find an upper bound.

$$ \begin{aligned} \max {\left\| {{\textbf{C}_ + }} \right\|_{2}} &= \max 2\pi \left(-\frac{r}{{{c_{0}}}} + t\right){\left\| {\text{diag}(\textbf{N} \odot \mathbf{\rho })} \right\|_{2}}\\ & = \max 2\pi \left(-\frac{r}{{{c_{0}}}} + t\right){\left\| {\textbf{N} \odot \mathbf{\rho }} \right\|_{2}}\\ &= 2\pi \left|-\frac{r}{{{c_{0}}}} + t\right|\cdot{\left\| \textbf{N} \right\|_{2}}\left| {{\rho_{\max }}} \right|. \end{aligned} $$
((27))

When applying this result to an array with uniform weighting w max=1, Equation 24 leads to:

$$ \Delta {A_{\max }} = \frac{{2\pi }}{r}\left|-\frac{r}{{{c_{0}}}} + t\right|\cdot{\left\| \textbf{N} \right\|_{2}}\left| {{\rho_{\max }}} \right|\sqrt N. $$
((28))

For a constant time t=1/Δ f, the time error caused by frequency increment error will become amplitude error of FDA beampattern, as shown follows:

$$ \Delta {A_{\max }} = \frac{{2\pi }}{r}\left|-\frac{r}{{{c_{0}}}} + \frac{1}{{{\Delta f}}}\right|\cdot{\left\| \textbf{N} \right\|_{2}}\left| {{\rho_{\max }}} \right|\sqrt N. $$
((29))

It can be noticed from Equation 29 that the errors caused by time and by range counterbalance the total beampattern error. Therefore, we delete 1/Δ f. Then, Equation 29 can be reformulated as:

$$ \begin{aligned} \Delta {A_{\max }} &\le \frac{{2\pi }}{r}\left|-\frac{r}{{{c_{0}}}} \right|{\left\| \textbf{N} \right\|_{2}}\left| {{\rho_{\max }}} \right| \sqrt N\\ &= \frac{{2\pi }}{{{c_{0}}}} {\left\| \textbf{N} \right\|_{2}}\left| {{\rho_{\max }}} \right| \sqrt N. \end{aligned} $$
((30))

Equation 30 gives FDA beampattern error bound which indicates its worst case. Since it is caused by the frequency increment errors, the maximum device errors which produce the FDA frequency increment are regulated by the bound. This gives guideline about device selections and predicts the possible FDA beampattern derivation bound.

4.2 Statistical properties of FDA beampattern

In most cases, we know the statistical properties of frequency increment errors and would like to derive the respective properties of impacted beampattern. In this subsection, we will give the formulas of expectation value, variance, and PDF about FDA beampattern based on different PDFs of the frequency increment errors.

4.2.1 4.2.1 Expected value

Using Equations 8 and 13, it is straightforward to show that:

$$ \begin{aligned} E\left\{ {\Delta A(\theta,r,t)} \right\} &= E\left\{ {{\textbf{w}^{H}}\textbf{C}(r,t)\textbf{v}(\theta,r,t)} \right\} - {\textbf{w}^{H}}\textbf{v}(\theta,r,t)\\ &= {\textbf{w}^{H}}E\left\{ {\textbf{C}(r,t)} \right\}\textbf{v}(\theta,r,t) - {\textbf{w}^{H}}\textbf{v}(\theta,r,t) \end{aligned} $$
((31))

where E{·} denotes the expected value.

Assume that the frequency increment error ρ n of the nth element satisfies the Gaussian statistical model ρ n ∼N(0,σ 2) and the PDF is as follows:

$$ {f_{n}}(\rho) = \frac{1}{{\sqrt {2\pi} \sigma }}{e^{- \frac{{{\rho^{2}}}}{{2{\sigma^{2}}}}}}. $$
((32))

Therefore, the expected value of the nth element in diag(C) can be calculated as [30]:

$$ \begin{aligned} E\left\{ {{\textbf{C}_{nn}}(r,t)} \right\} &= E\left\{ {{e^{j2\pi (n - 1)\left(t\rho - \frac{{\rho r}}{{{c_{0}}}}\right)}}} \right\}\\ &= \frac{1}{{\sqrt {2\pi} \sigma }}\int\limits_{- \infty }^{+ \infty} {{e^{j2\pi (n - 1)\left(t\rho - \frac{{\rho r}}{{{c_{0}}}}\right)}}} {e^{- \frac{{{\rho^{2}}}}{{2{\sigma^{2}}}}}}d\rho \\ &= {e^{- 2{\pi^{2}}{{(n - 1)}^{2}}{{\left(t - \frac{r}{{{c_{0}}}}\right)}^{2}}{\sigma^{2}}}}. \end{aligned} $$
((33))

where C nn denotes the nth element of diag(C). When applying Equation 33 onto 31, we can get the expected value of FDA beampattern deviation with Gaussian distribution frequency increment errors as follows:

$$ \begin{aligned} E\left\{ {\Delta A(\theta,r,t)} \right\} &= {\textbf{w}^{H}}E\left\{ {\textbf{C}(r,t)} \right\}\textbf{v}(\theta,r,t) - {\textbf{w}^{H}}\textbf{v}(\theta,r,t)\\ &= {\textbf{w}^{H}}\left(\text{diag}\left({\bf{b_{g}}}\right) - \textbf{I}\right)\textbf{v}(\theta,r,t) \end{aligned} $$
((34))

where

$$ \begin{aligned} {\bf{b_{g}}} = \left[ {1,{e^{- 2{\pi^{2}}{{\left(t - \frac{r}{{{c_{0}}}}\right)}^{2}}{\sigma^{2}}}},\ldots,{e^{- 2{\pi^{2}}{{(N - 1)}^{2}}{{\left(t - \frac{r}{{{c_{0}}}}\right)}^{2}}{\sigma^{2}}}}} \right]. \end{aligned} $$
((35))

and I denotes N×N unit matrix. In this case, the expected value of the FDA beampattern deviation is dependent on the variance of frequency increment errors and is not 0 for the Gaussian distribution model.

For another case, we assume that ρ n is uniform distribution, i.e., ρ n ∼u(−ρ max,ρ max) with minimum and maximum values −ρ max and ρ max. We can get the expected value of nth element in diag(C) as follows:

$$ \begin{aligned} E\left\{ {{\textbf{C}_{nn}}(r,t)} \right\} = E\left\{ {{e^{j2\pi (n - 1)\left(t\rho - \frac{{\rho r}}{{{c_{0}}}}\right)}}} \right\}\\ = \int\limits_{- {\rho_{\text{max}}}}^{{\rho_{\text{max}}}} {{e^{j2\pi (n - 1)\left(t - \frac{r}{{{c_{0}}}}\right)\rho }}} \frac{1}{{2{\rho_{\text{max}}}}}d\rho \\ = \frac{{\sin (2\pi (n - 1)\left(t - \frac{r}{{{c_{0}}}}\right){\rho_{\text{max}}})}}{{2\pi (n - 1)\left(t - \frac{r}{{{c_{0}}}}\right){\rho_{\text{max}}}}}. \end{aligned} $$
((36))

By using Equation 36 onto 31, the expected value of FDA beampattern deviation with uniform distribution frequency increment error can be reformulated as:

$$ \begin{aligned} E\left\{ {\Delta A(\theta,r,t)} \right\} &= {\textbf{w}^{H}}E\left\{ {\textbf{C}(r,t)} \right\}\textbf{v}(\theta,r,t) - {\textbf{w}^{H}}\textbf{v}(\theta,r,t)\\ &= {\textbf{w}^{H}}\left(\text{diag}\left({\bf{b_{u}}}\right) - \textbf{I}\right)\textbf{v}(\theta,r,t) \end{aligned} $$
((37))

where

$$ \begin{aligned} {\textbf{b}_{\textbf{u}}} &= \left[ {1,\frac{{\sin \left(2\pi \left(t - \frac{r}{{{c_{0}}}}\right){\rho_{\text{max}}}\right)}}{{2\pi \left(t - \frac{r}{{{c_{0}}}}\right){\rho_{\text{max}}}}},\ldots,}\right.\\&{\kern2.25pc}\left.{\frac{{\sin \left(2\pi(N - 1)\left(t - \frac{r}{{{c_{0}}}}\right){\rho_{\text{max}}}\right)}}{{2\pi (N - 1)\left(t - \frac{r}{{{c_{0}}}}\right){\rho_{\text{max}}}}}} \right]. \end{aligned} $$
((38))

Similarly, the expected value of the FDA beampattern deviation is dependent on the maximum value of frequency increment error and not 0 for the uniform distribution model. From Equations 34 and 37, the expected values of FDA beampattern have range offset and angle offset, which is caused by time dependent error on the two distributions.

4.2.2 4.2.2 Variance

The beampattern deviation variance var{Δ A(θ,r,t)} equals to the beampattern variance:

$$ \begin{aligned} {\text{var}} \left\{ {\Delta A(\theta,r,t)} \right\} &= {\text{var}} \left\{ {A(\theta,r,t)} \right\}\\ &= \text{var} \left\{ {{\textbf{w}^{H}}\textbf{C}(r,t)\textbf{v}(\theta,r,t)} \right\}. \end{aligned} $$
((39))

As we deal with vectors and matrices, we utilize the covariance matrix cov{·}, and var{·}=cov{·} for any scalar. We thus have:

$$ \begin{aligned} {\text{var}} \left\{ {\Delta A(\theta,r,t)} \right\} = {\text{cov}} \left\{ {{\textbf{w}^{H}}\textbf{C}(r,t)\textbf{v}(\theta,r,t)} \right\} \end{aligned} $$
((40))

Using the Kronecker product ⊗, the vectorization transformation vec(·) and the identity:

$$ \begin{aligned} \text{vec}\left\{ {{\bf{ABC}}} \right\} = {\textbf{C}^{T}} \otimes \textbf{A}\text{vec}\left\{ \textbf{B} \right\}. \end{aligned} $$
((41))

Since

$$ {\textbf{w}^{H}}\textbf{C}(r,t)\textbf{v}(\theta,r,t) = {\textbf{v}^{T}}(\theta,r,t) \otimes {\textbf{w}^{H}} \text{vec}\left\{ {\textbf{C}(r,t)} \right\} $$
((42))

we use c=vec{C(r,t)} and the vector t(θ,r,t)=v T(θ,r,t)⊗w H, which utilizing:

$$ {\text{cov}} \left\{ {{\bf{AX}}} \right\} = \textbf{A}{\text{cov}} \left\{ \textbf{X} \right\}{\textbf{A}^{H}} $$
((43))

to yield:

$${} \begin{aligned} {\text{var}} \left\{ {\Delta A(\theta,r,t)} \right\} = \textbf{t}(\theta,r,t){\text{cov}} \left\{ {\textbf{c}(r,t)} \right\}{\textbf{t}^{H}}(\theta,r,t). \end{aligned} $$
((44))

Since C is a diagonal matrix and its entries are independent random variables, cov(c) is a diagonal matrix and has non-zero value with the nNth entry. We then have:

$$ \begin{aligned} {\text{var}} \left\{ {\Delta A(\theta,r,t)} \right\} = \sum\limits_{k} {{\textbf{t}_{k}}(\theta,r,t)} \textbf{t}_{k}^{H}(\theta,r,t){\text{cov}} {\left\{ {\textbf{c}(r,t)} \right\}_{kk}} \end{aligned} $$
((45))

where k=(n−1)N+1 denotes the kth entry of vector. So calculating the \({\text {var}} \left \{ {\Delta A(\theta,r)} \right \}\) can be equivalently obtained by calculating \({\text {cov}} {\left \{ {\textbf {c}(r)} \right \}_{\textit {kk}}}\). This again is a very general result that we can evaluate and review for different statistical models for \({\text {cov}} {\left \{ {\textbf {c}(r)} \right \}_{\textit {kk}}}\).

$${} {\small{\begin{aligned} {\text{cov}} {\left\{ {\textbf{c}(r,t)} \right\}_{kk}} &= \int\limits_{- \infty }^{+ \infty} {{{\left[\vphantom{\frac{s}{s}} {\textbf{c}{{(r,t)}_{kk}} - E(\textbf{c}{{(r,t)}_{kk}})} \vphantom{\frac{s}{s}}\right]}^{2}}} f(\rho)d\rho \\ &= \int\limits_{- \infty }^{+ \infty} {{{\left[ \vphantom{\frac{s}{s}}{\textbf{C}{{(r,t)}_{nn}} - E(\textbf{C}{{(r,t)}_{nn}})} \vphantom{\frac{s}{s}}\right]}^{2}}} f(\rho)d\rho \end{aligned}}} $$
((46))

Assume that all the random frequency increment errors have the same distribution. For the first case, frequency increment error ρ n of the nth element satisfies the Gaussian statistical model ρ n ∼N(0,σ 2). According to the Equations 13 and 36, 46 can be rewritten as:

$${} {\small{\begin{aligned} &{\text{cov}} {\left\{ {\textbf{c}(r,t)} \right\}_{kk}} = \int\limits_{- \infty }^{+ \infty} {\left[\vphantom{\frac{s}{s}} {\textbf{C}{{(r,t)}_{nn}} - E(\textbf{C}{{(\theta,r,t)}_{nn}})} \right]}\\&{\kern5pc}\times {\left[\vphantom{\frac{s}{s}} {\textbf{C}{{(r,t)}_{nn}} - E(\textbf{C}{{(r,t)}_{nn}})} \right]^{*}}f(\rho)d\rho \\ &= \int\limits_{- \infty }^{+ \infty} {\left[ {\textbf{C}{{(r,t)}_{nn}}\textbf{C}(r,t)_{nn}^{*}} \right.} - E(\textbf{C}{(r,t)_{nn}})\textbf{C}(r,t)_{nn}^{*}\\&\quad- \textbf{C}{(r,t)_{nn}}E(\textbf{C}(r,t)_{nn}^{*})\left. { + E(\textbf{C}{{(r,t)}_{nn}})E(\textbf{C}(r,t))_{nn}^{*}} \right]f(\rho)d\rho \\ & = \int\limits_{- \infty }^{+ \infty} {\textbf{C}{{(r,t)}_{nn}}\textbf{C}(r,t)_{nn}^{*}f(\rho)d\rho} \\&\quad- \int\limits_{- \infty }^{+ \infty} E{{(\textbf{C}(r,t))}_{nn}}\textbf{C}((r,t)_{nn}^{*}) f(\rho)d\rho\\ &~~~~- \int\limits_{- \infty }^{+ \infty} {\textbf{C}{{(r,t)}_{nn}}E(\textbf{C}(r,t))_{nn}^{*}f(\rho)d\rho} &\quad+ \int\limits_{- \infty }^{+ \infty} {E{{(\textbf{C}(r,t))}_{nn}}E(\textbf{C}(r,t))_{nn}^{*}f(\rho)} d\rho \\ &= \int\limits_{- \infty }^{+ \infty} {\textbf{C}{{(r,t)}_{nn}}\textbf{C}(r,t)_{nn}^{*}f(\rho)d\rho} - E(\textbf{C}(r,t))_{nn}^{2} \end{aligned}}} $$
((47))

where [·]∗ denotes the conjugate operator. Here, the \(E\left (\textbf {C}(r,t)_{\textit {nn}}\right)={e^{- 2{\pi ^{2}}{{(n - 1)}^{2}}{{\left (t - \frac {r}{{{c_{0}}}}\right)}^{2}}{\sigma ^{2}}}}=E\left (\textbf {C}(r,t)_{\textit {nn}}^{*}\right)\) is utilized. Applying Equation 32, the first term of Equation 47 can be rewritten as:

$$ {\small{\begin{aligned} &\int\limits_{- \infty }^{+ \infty} {\textbf{C}{{(r,t)}_{nn}}\textbf{C}(r,t)_{nn}^{*}f(\rho)d\rho }= \frac{1}{{\sqrt {2\pi} \sigma }}\\&\int\limits_{- \infty }^{+ \infty} {{e^{j2\pi (n - 1)\left(t\rho - \frac{{\rho r}}{{{c_{0}}}}\right)}}{e^{- j2\pi (n - 1)\left(t\rho - \frac{{\rho r}}{{{c_{0}}}}\right)}}{e^{- \frac{{{\rho^{2}}}}{{2{\sigma^{2}}}}}}d\rho} = 1 \end{aligned}}} $$
((48))

Applying it to Equation 47 yields:

$$ \begin{aligned} {\text{cov}} {\left\{ {\textbf{c}(r,t)} \right\}_{kk}} &= 1 - E(\textbf{C}(r,t))_{nn}^{2}\\ &= 1 - {e^{- 4{\pi^{2}}{{(n - 1)}^{2}}{{\left(t - \frac{r}{{{c_{0}}}}\right)}^{2}}{\sigma^{2}}}} \end{aligned} $$
((49))

where k is the kth element of c(r,t), which is used to distinguish from n. Consequently, we can get the FDA beampattern deviation variance:

$$ {\small{\begin{aligned} {\text{var}} \left\{ {\Delta A(\theta,r,t)} \right\} &=\sum\limits_{k} {{\textbf{t}_{k}}(\theta,r,t)\textbf{t}_{k}^{H}(\theta,r,t)}\\ &\quad{\times\left({1 - {e^{- 4{\pi^{2}}{{(n - 1)}^{2}}{{\left(t - \frac{r}{{{c_{0}}}}\right)}^{2}}{\sigma^{2}}}}} \right)}. \end{aligned}}} $$
((50))

Similarly, we can get the FDA beampattern variance with the random frequency increment errors, which are uniformly distributed as aforementioned:

$${} {\small{\begin{aligned} {\text{var}} \left\{ {\Delta A(\theta,r,t)} \right\} &=\sum\limits_{k} {{\textbf{t}_{k}}(\theta,r,t)\textbf{t}_{k}^{H}(\theta,r,t)}\\&\quad{\times\left(\!{1 - \left(\frac{{\sin (2\pi (n - 1)\left(t - \frac{r}{{{c_{0}}}}\right){\rho_{\text{max}}})}}{{2\pi (n - 1)\left(t - \frac{r}{{{c_{0}}}}\right){\rho_{\text{max}}}}}\!\right)^{\!\!2}} \right)}. \end{aligned}}} $$
((51))

Compared with Equations 50 and 51, we can see that the FDA beampattern variances at both kinds of random frequency increment error distributions are dependent on the statistics properties. Given the same frequency increment errors, the variances will decrease when the number of elements is increased.

4.2.3 4.2.3 PDF

We have shown how to calculate the expectation value and the variance of the beampattern deviation and the beampattern itself. A remained question is: What form will their respective PDF have? In this subsection, we will derive the PDF of beampattern based on the PDF of the frequency increment errors.

For the first case, we investigate the PDF of beampattern when the frequency increment errors obey the Gaussian distribution as aforementioned. According to Equation 13, we derive the PDF of C. It is known that:

$$ \begin{aligned} {C_{nn}} &= {e^{- j2\pi (n - 1)\left(t - \frac{r}{{{c_{0}}}}\right)\rho }}\\ &= \cos \left(2\pi (n - 1)\left(t - \frac{r}{{{c_{0}}}}\right)\rho \right) \\&\quad- j\sin \left(2\pi (n - 1)\left(t - \frac{r}{{{c_{0}}}}\right)\rho \right)\\ &= \text{real}(C_{nn}) - j\left(\text{imag}(C_{nn})\right) \end{aligned} $$
((52))

where \(\text {real}(C_{\textit {nn}})=\cos \left (2\pi (n - 1)\left (t - \frac {r}{{{c_{0}}}}\right)\rho \right)\) and \(\text {imag}(C_{\textit {nn}})=\sin \left (2\pi (n - 1)\left (t - \frac {r}{{{c_{0}}}}\right)\rho \right)\) denote the real part and imaginary part of C nn , respectively. Consequently, we have:

$$ \begin{aligned} \rho &= \frac{{\arcsin (\text{imag}({C_{nn}}))}}{{2\pi (n - 1)\left(t - \frac{r}{{{c_{0}}}}\right)}}\\ &= \frac{{\arcsin ({g_{n}})}}{{2\pi (n - 1)\left(t - \frac{r}{{{c_{0}}}}\right)}}\\ &= h({g_{n}}) \end{aligned} $$
((53))

where g n =imag(C nn ) denotes the imaginary part of C nn . As we known that if a variable x has PDF f x (x), the PDF of y=h g(x) is as follows:

$$ \begin{aligned} {f_{y}}(y) = {f_{x}}[h(y)]\left| {h'(y)} \right| \end{aligned} $$
((54))

where x=h(y) is the inverse function of h g(x), f y (·) denotes the PDF responding to y, and [·]′ denotes the derivation operation. We have:

$$ \begin{aligned} {f_{{g_{n}}}}({g_{n}}) &= {f_{\rho} }[h({g_{n}})]\left| {h'({g_{n}})} \right|\\ &= \frac{1}{{\sqrt {2\pi} \sigma }}{e^{- \frac{{{h^{2}}({g_{n}})}}{{2{\sigma^{2}}}}}}\left| {h'({g_{n}})} \right|, - 1 < {g_{n}} < 1 \end{aligned} $$
((55))

where

$$h'({g_{n}}) = \frac{1}{{2\pi (n - 1)\sqrt {1 - {g_{n}^{2}}} \left(t - \frac{r}{{{c_{0}}}}\right)}} $$

denotes the derivation of h(g n ). Utilizing g n , Equation 13 can be rewritten as:

$${} {\small{\begin{aligned} \tilde A(\theta,r,t) &= \frac{{{\textbf{w}^{H}}\textbf{C}(\theta,r,t)\textbf{v}(\theta,r,t)}}{r}\\ &= \sum\limits_{n = 2}^{N} {\left(\sqrt {1 - {{g_{n}^{2}}}} + j{g_{n}}\right)} \frac{{{\textbf{v}_{n}}(\theta,r,t)}}{r}+\frac{{\textbf{v}_{1}}(\theta,r,t)}{r}\\ &= \sum\limits_{n = 2}^{N} {\left(\sqrt {1 - {{g_{n}^{2}}}} + j{g_{n}}\right)} {v_{n}}+v_{1} \end{aligned}}} $$
((56))

where v n denotes the nth element of v. Defining \(v_{n}=\frac {{{\textbf {v}_{n}}(\theta,r,t)}}{r}\) for notation convenience, we can find

$${} {\small{\begin{aligned} \sqrt {1 - {{g_{2}^{2}}}} + j{g_{2}} = \left(\tilde A(\theta,r,t) \,-\, \sum\limits_{n = 3}^{N} {\left(\sqrt {1 - {{g_{n}^{2}}}} + j{g_{n}}\right)} {v_{n}}\,-\,v_{1}\right)\!\!/{v_{2}}. \end{aligned}}} $$
((57))

Let

$${}\begin{array}{l} {a_{2}} = \text{imag}\left(\tilde A(\theta,r) - \sum\limits_{n = 3}^{N} {\left(\sqrt {1 - {g_{n}^{2}}} + j{g_{n}}\right)} {v_{n}} - {v_{1}}\right)\\ ~~= \text{imag}(\tilde A(\theta,r)) - \text{imag}\left(\sum\limits_{n = 3}^{N} {\left(\sqrt {1 - {g_{n}^{2}}} + j{g_{n}}\right)} {v_{n}} - {v_{1}}\right) \end{array} $$

and v 2=cosϕ+jsinϕ, where ϕ is the phase of v 2, utilizing Equation 57, we can get:

$$ \begin{aligned} {g_{2}}\cos \varphi + \sqrt {1 - {g_{2}}^{2}} \sin \varphi = {a_{2}}. \end{aligned} $$
((58))

Solving Equation 58, it yields:

$$ \begin{aligned} {g_{2}} &= {a_{2}}\cos \varphi + \sin \varphi \sqrt {1 - {a_{2}}^{2}} \\ &= \xi_{2}({{\tilde A}_{i}}) \end{aligned} $$
((59))

where \({{\tilde A}_{i}}=\text {imag}\left (\tilde A(\theta,r)\right)\) denotes the imaginary part of \(\tilde A\). And we define:

$$ \begin{aligned} {g_{3}} = &{g_{3}} = {\xi_{3}}({g_{3}})\\ &\ldots\\ {g_{N}} = &{g_{N}} = {\xi_{N}}({g_{N}}). \end{aligned} $$
((60))

The joint PDF of the variables above is as follows:

$$ \begin{aligned} &{\kern15pt}{f_{\tilde A_{i}{g_{3}}\ldots{g_{N}}}}(\tilde A_{i}{g_{3}}\ldots{g_{N}})\\&= {f_{{g_{1}}{g_{3}}\ldots{g_{N}}}}\left[{\xi_{2}}\left(\tilde A_{i}(\theta,r,t)\right),{\xi_{3}}({g_{3}}),\ldots,{\xi_{N}}({g_{N}})\right]\left| {{J}} \right| \end{aligned} $$
((61))

According to Equations 59 and 60, we can get that:

$$ \begin{aligned} J &= \left| {\begin{array}{cccc} {\frac{{\partial {\xi_{2}}}}{{\partial \tilde A_{i}}}}&{\frac{{\partial {\xi_{2}}}}{{\partial {g_{3}}}}}&{\ldots}&{\frac{{\partial {\xi_{2}}}}{{\partial {g_{N}}}}}\\ {\frac{{\partial {\xi_{3}}}}{{\partial \tilde A_{i}}}}&{\frac{{\partial {\xi_{3}}}}{{\partial {g_{3}}}}}&{\ldots}&{\frac{{\partial {\xi_{3}}}}{{\partial {g_{N}}}}}\\ {\ldots}&{\ldots}&{\ldots}&{\ldots}\\ {\frac{{\partial {\xi_{N}}}}{{\partial \tilde A_{i}}}}&{\frac{{\partial {\xi_{N}}}}{{\partial {g_{3}}}}}&{\ldots}&{\frac{{\partial {\xi_{N}}}}{{\partial {g_{N}}}}} \end{array}} \right|= \left| {\begin{array}{cccc} {\frac{{\partial {\xi_{2}}}}{{\partial \tilde A_{i}}}}&{\frac{{\partial {\xi_{2}}}}{{\partial {g_{3}}}}}&{\ldots}&{\frac{{\partial {\xi_{2}}}}{{\partial {g_{N}}}}}\\ 0&1&{\ldots}&0\\ {\ldots}&{\ldots}&{\ldots}&{\ldots}\\ 0&0&{\ldots}&1 \end{array}} \right| \\&= \text{cos}\phi-\frac{\text{sin}\phi}{\sqrt{1-{a_{2}^{2}}}} \end{aligned} $$
((62))

where \(\frac {{\partial {\xi _{1}}}}{{\partial \tilde A_{i}}} = \text {cos}\phi -\frac {\text {sin}\phi }{\sqrt {1-{a_{2}^{2}}}} \). Since the each element of C is responding to only one frequency increment error which is random and independent, g n is the independent with other g m with m=1,2,…,N−1 and m≠n. Therefore, Equation 61 can be rewritten as:

$$ \begin{aligned} &{\kern1.2pc} {f_{{g_{2}}{g_{3}}\ldots{g_{N}}}}\left[{\xi_{2}}(\tilde A_{i}(\theta,r,t)),{\xi_{3}}({g_{3}}),\ldots,{\xi_{N}}({g_{N}})\right]\\&= {f_{{g_{2}}}}\left[{\xi_{2}}(\tilde A_{i}(\theta,r,t))\right]{f_{{g_{3}}}}\left[{g_{3}}\right]\ldots{f_{{g_{N}}}}\left[{g_{N}}\right] \end{aligned} $$
((63))

Moreover, we can get the PDF of FDA beampattern as:

$${} {\small{\begin{aligned} {f_{\tilde A_{i}}}(\tilde A_{i}) &= \int\limits_{- 1}^{1} {\ldots\int\limits_{- 1}^{1} {{f_{{g_{2}}{g_{3}}\ldots{g_{N}}}}\left[{\xi_{2}}(\tilde A_{i}(\theta,r,t)),{\xi_{3}}({g_{3}}),\ldots,{\xi_{N}}({g_{N}})\right]}} \\&\quad\times\left(\text{cos}\phi-\frac{\text{sin}\phi}{\sqrt{1-{a_{2}^{2}}}}\right){d_{{g_{3}}}}\ldots{d_{{g_{N}}}}. \end{aligned}}} $$
((64))

Utilizing the same approach, we can get the PDF of real part of FDA beampattern. Since the relationship between real part and imaginary part is complex, so we cannot give the PDF of the whole FDA beampattern.

Similarly, we can derive the FDA beampattern variance with the random frequency increment errors, which are uniformly distributed as aforementioned. The PDF of g n is as follows:

$$ \begin{aligned} {f_{{g_{n}}}}({g_{n}}) &= {f_{\rho} }[h({g_{n}})]\left| {h'({g_{n}})} \right|\\ &= \frac{1}{{2{\rho_{\max }}}}\frac{1}{{2\pi (n - 1)\left(t - \frac{r}{{{c_{0}}}}\right)\sqrt {1 - {g_{n}^{2}}} }}, \\&\quad- 1 < {g_{n}} < 1 \end{aligned} $$
((65))

and the PDF of FDA beampattern imaginary part is as follows:

$${} {\small{\begin{aligned} {f_{\tilde A_{i}}}(\tilde A_{i})& = \int\limits_{- 1}^{1} {\ldots\int\limits_{- 1}^{1} {{f_{{g_{2}}{g_{3}}\ldots{g_{N}}}}\left[{\xi_{2}}(\tilde A_{i}(\theta,r,t)),{\xi_{3}}({g_{3}}),\ldots,{\xi_{N}}({g_{N}})\right]}} \\&\quad\times\left(\text{cos}\phi-\frac{\text{sin}\phi}{\sqrt{1-{a_{2}^{2}}}}\right){d_{{g_{3}}}}\ldots{d_{{g_{N}}}}. \end{aligned}}} $$
((66))

5 Simulation results

5.1 Example 1: FDA beampattern bound

Consider a 16-element uniform linear FDA with half of wavelength λ spacing between neighbor elements. The center frequency f 0 is 10 GHz, and the increment frequency Δ f is 30 KHz. The target is located at the range 10 km, angle 0∘, and the time is on 1/Δ f. Figure 4a,b shows the comparisons of ideal FDA beampattern B ideal, FDA beampattern upper and lower bound B bound, and FDA beampattern with random frequency increment errors B Random. In the FDA beampattern with random frequency increment errors, the frequency increment errors are Gaussian distribution, i.e., ρ n ∼N(0,902) and the random FDA beampatterns are based on 50 independent Monte Carlo simulation runs. It can be shown that the present bounds hold for all the simulated beampattern realizations for both Figure 4a,b. Simulations results show that the bounds are tighter in range dimension than that in the angle dimension which is caused by range counterbalance of the total error in beampattern.

Figure 4
figure 4

Profiles for the ideal, the bounds, and the errors FDA beampattern.(a) In angle dimension. (b) In range dimension.

Full size image

Furthermore, we give two figures about expectation and variance about FDA beampattern errors caused by frequency increment errors, shown as in Figures 5 and 6, respectively. Figure 5 compares the expectation value of theoretical result and empirical result. The theoretical result is based on the method of Section 4.2.1. The empirical result is based on the 10,000 independent Monte Carlo simulation runs. The comparisons show that when the FDA beampattern errors have smaller value, two results are close to each other. The variances of theoretical result and empirical result are shown in Figure 6. Similar with Figure 5, the theoretical result is based on the method of Section 4.2.2. The empirical result is based on the 1,000 independent Monte Carlo simulation runs. Different from the expectation, the empirical result fluctuates around the theoretical result along with increase of σ.

Figure 5
figure 5

The comparison of Gaussian random FDA beampattern error expectation value.

Full size image
Figure 6
figure 6

The comparison of Gaussian random FDA beampattern error variance value.

Full size image

5.2 Example 2: FDA beampattern PDF

Consider a uniform linear FDA with four elements. In this example, FDA beampattern amplitude error does not divide into the factor r 0, and its value is very large compared with that of Figures 5 and 6. Other array parameters are the same to that of example 1. Figure 7 shows PDFs of theoretical and empirical results, and Figure 8 shows the PDFs of imaginary part of random FDA beampattern with different σs. It can be known that lower σ enjoys the smaller beampattern errors, and PDF curves are centrosymmetric with the center about A i =0. One might use this figure and Equation 64 to specify tolerance requirements of frequency increment errors to fulfill a given beampttern requrement with certain probability. For instance, if probability of the beampttern errors at the domain (−0.5 to 0.5) is not smaller than 0.95, the standard deviations of ρ for every elements of FDA array will be required to be no larger than 60.

Figure 7
figure 7

The PDF of Gaussian random FDA beampattern error.

Full size image
Figure 8
figure 8

The PDF of imaginary part of random FDA beampattern.

Full size image

6 Conclusions

In this paper, we have investigated the impacts of frequency increment errors on FDA beampattern based on deterministic errors and random errors. For uniform and linear deterministic frequency increment errors, the specific beampattern error formulations are provided, which gives guideline for device selection. For the stochastic frequency increment errors, we have derived a very tight worst-case boundary of the FDA beampattern. Simulation results show that all the random beampatterns are held for the derived bounds, and the worst-case boundary is helpful to the FDA system design. At last, we derived the statistical properties of the expectation, variance, and PDF. They can be used to analyze the probability of FDA beampattern fluctuations for the given distribution frequency increment errors.