Abstract
In topology optimization the goal is to find the ideal material distribution in a domain subject to external forces. The structure is optimal if it has the highest possible stiffness. A volume constraint ensures filigree structures, which are regulated via a Ginzburg–Landau term. During 3D printing overhangs lead to instabilities. As a remedy an additive manufacturing constraint is added to the cost functional. First order optimality conditions are derived using a formal Lagrangian approach. With an Allen-Cahn interface propagation the optimization problem is solved iteratively. At a low computational cost the additive manufacturing constraint brings about support structures, which can be fine tuned according to demands and increase stability during the printing process.
Similar content being viewed by others
1 Introduction
Additive manufacturing or 3D printing is understood as the process of building up a structure layer by layer. Traditional manufacturing methods, such as injection molding [36], place constraints on the achievable shapes, whereas with 3D printing the complexity of the possible forms is much less limited. Traditional methods allow for a cheaper and faster production in high volume orders. However, as order volumes decrease and need for customizability increases, additive manufacturing becomes more attractive. It allows for production of parts just in time as they are needed. This reduces the logistical burden tremendously. Some even call 3D printing the next industrial revolution, [10].
According to [6] the industry sector of additive manufacturing has shown remarkable growth in previous years and is predicted to continue growing at a rate of 15% in the coming years. The additive manufacturing industry, spanning from machine sales to the service sector, is anticipated to reach $21.5 billion by 2025. The greatest market potential is seen in the sectors of consumer electronics, automotive, medical & dental, aerospace, industrial and architecture.
Additive manufacturing comes with its own constraints and problems. The production of a single unit takes longer and the surface structure has a rougher finish. This paper focuses on eliminating instabilities during the printing process which are caused by overhangs. These are problematic, because printing layer by layer can cause sagging of material. Avoiding these instabilities is mandatory for a reliable and reproducible printing process, which is necessary for a safe application of additive manufacturing on an industrial level.
Commonly, external support structures are added to alleviate that problem. On the downside, this method uses more material and takes longer to print. Removing support structures after the printing process is both time and labor intensive.
Topology optimization is concerned with the automatic optimal design of structures for a given physical setting, see [9]. From a mathematical point of view, topology optimization belongs to the area of optimal control of partial differential equations, [39]. Physical settings could for example include fluid dynamics, heat conduction or, as in the present setting, mechanics. Realizing the resulting designs can be challenging with traditional manufacturing methods, but is possible via additive manfucturing. For a broad overview of trends in topology optimization for additive manufacturing see [32].
Topology optimization is conducted by solving the arising partial differential equations and iteratively updating the design to improve a given objective function. Three common approaches are the SIMP method [8], the level set method [42] and the phase field method.
The phase field method was first introduced for free boundary problems [24] and phase transformations [31]. It has been widely used in solidification [16, 44], but also for example to model dendritic growth [28] or crack propagation [34]. It has been applied to topology optimization in [12, 18, 21, 38, 41, 43] and [13].
The problem of overhangs has been approached in different ways. As long as overhangs do not extend past an allowable self-supporting angle, they are printable. This is used in the work of [25] by incorporating projection operations to limit overhang angles. Another approach is to determine wether enough supporting material is present under a certain point. This method was developed in [30] and requires regular meshes. The problem of instabilities is here alleviated by incorporating an additive manufacturing constraint (AMC) in the modeling stage. Rigidness of the structure during the building process is taken into consideration.
When executing the topology optimization, the AMC is accounted for via a penalty term. While being printed, the resulting structure shall be stable without relying on manually added supports. This approach is introduced in the work of [2] and results are presented in [1]. In contrast to the phasefield approach used in the present paper, the authors use a level-set method, where the topology is perturbed by solving a Hamilton-Jacobi equation with a velocity term derived from the shape gradient.
As a novel approach the AMC is incorporated into the phase field method for topology optimization. Optimality conditions are derived. The approach is validated numerically by showing that the AMC increases stability during the manufacturing process.
This paper is structured in the following way: After explaining linear elasticity, the theoretical foundation of topology optimization is laid out in Sect. 2.3. The AMC is introduced in Sect. 2.4 and incorporated into the optimal control problem. First order optimality conditions are derived via a formal Lagrangian approach in Sect. 3. The discretization is explained in Sect. 4. To examine the influence of the AMC, numerical experiments are done with and without it in Sect. 5.
2 Problem setting
The aim of this chapter is to define the optimal control problem. After modeling the mechanics, topology optimization is explained and the AMC is formalized. First of all some notations are introduced.
2.1 Notation
Let \(\Omega \subset \mathbb{R}^{d}\), \(d=2,3\) be a bounded, regular domain and with a piecewise Lipschitz boundary Γ. Assume there exists a Dirichlet boundary \(\Gamma _{D}\subset \partial \Omega \) with surface area \(\vert \Gamma _{D} \vert > 0\). The space of square integrable functions \(L^{2}(\Omega )\) is used to define the Sobolev spaces
For more details see [39]. The Frobenius inner product for the matrices \(\mathcal{M}\), \(\mathcal{N}\) is defined by the pairwise sum of element-products
With the fourth order tensor C, the product \(C\mathcal{M}\) is defined via
2.2 Linear elasticity problem
Using the displacement \(u: \Omega \rightarrow \mathbb{R}^{d}\), the linearized strain tensor
is defined.
The distribution of material in Ω is described by a phase field \(\varphi \in L^{\infty } (\Omega )\) with
almost everywhere in Ω. Here, \(\varphi = 0\) describes void and \(\varphi = 1\) represents areas containing material. In a physically accurate setting each point in space either does or does not contain material, i.e. \(\varphi \in \{ 0,1 \} \), leading to a sharp transition. However, in the realm of optimization a smooth transition between material and void is desired in order to calculate derivatives. This is achieved by explicitly allowing impure phases, i.e. states with \(0 < \varphi < 1\). The transition is seen as the interface between material and void.
Consider the symmetric fourth order stiffness tensor \(C (\varphi )\) with continuously differentiable entries. It is assumed that the derivative of the stiffness tensor \(C' (\varphi )\) is globally Lipschitz continuous. A transition function with cubic behavior for \(\varphi \in [0,1 ]\) is employed. This is not essential in the phase field approach, but empirically leads to a faster convergence. For \(\zeta >0\) the transition function is defined via
where \(s_{r}\) is a monotone \(C^{1,1}\)-function such that s is in \(C^{1,1}\).
The elasticity tensor for the whole domain is defined in the following way
where
for a quadratic matrix \(\mathcal{E}\). The constants \(\lambda _{\mathrm{mat}}\geq 0 \) and \(\mu _{\mathrm{mat}} > 0\) are called Lamé parameters. The constant \(\epsilon >0\) is a small parameter, which will be related later to the interface width when defining the Ginzburg–Landau term in Equation (8).
A load f is acting on a part of the boundary labeled \(\Gamma _{f}\) and a volume force g is present where material φ is located. The above definition warrants \(0 \neq C_{\mathrm{void}} \ll C_{\mathrm{mat}}\), which ensures low stiffness in void, but avoids degeneracy.
With the outer normal vector n, the strong form of the mechanical system is defined via
The weak formulation is written as
Definition 1
(Weak solution of the mechanical system)
The function \(u^{m}\in H^{1}_{D} ( \Omega , \mathbb{R}^{d} )\) is a weak solution of the mechanical system \(( MS )\), if it fulfills the weak formulation (5).
The superscript m is used throughout this paper in connection with the mechanical system. A unique \(u^{m}\) exists, as proven for the phase field method in [11]. A more general and thorough discussion on existence theory for elasticity problems can be found in [20].
2.3 Topology optimization
This section is based on [14]. The aim of topology optimization is to distribute a limited amount of material in an optimal sense. Without limiting the material usage, the solution of the optimal control problem defined in Sect. 2.5 would be trivial: \(\varphi \equiv 1\) on Ω, i.e. covering the whole domain with material.
An additional constraint makes the problem more interesting. Let m be the mass parameter with \(0 < m < 1\). The amount of material is restricted via a volume constraint
where \(| \Omega |\) denotes the Lebesque measure of the domain Ω. The admissible set is defined as
The objective is to find a material distribution \(\varphi \in \mathcal{G}^{m}\) and a corresponding solution of the elasticity problem \(u:\Omega \rightarrow \mathbb{R}^{d}\) such that the mean compliance
is minimized. If \(C(\varphi )\) would be allowed to become zero for \(\varphi = 0\), boundary forces could be avoided trivially by not placing material where these forces act. On the other hand, soft surrogate material close to \(\Gamma _{f}\) leads to large displacements, increasing the compliance. This ensures that optimal solutions always have material placed where boundary forces act. However, this minimization problem is not well-posed as explained in [3]. The regularity of the solution is not ensured. In computational examples this can lead to a checkerboard solution. Checkerboarding is the frequent occurrence of jumps between material and void, which is not desirable, see [37]. The algorithm might produce so-called porous solutions, which can be thought of as sponge-like microstructures. In many industrial cases this type of material is hard to realize and therefore undesirable. The ill-posedness can be alleviated by adding a perimeter regularization which was proven in [7]. The paper [38] explains that the perimeter can be approximated by the Ginzburg–Landau term
for \(\epsilon > 0\) and \(\varphi \in H^{1} ( \Omega ,\mathbb{R} )\cap L^{\infty } (\Omega )\). For convergence properties as the interface parameter ϵ approaches zero see [40]. The first term penalizes transitions between material and void through the gradient of the material distribution. The second term contains a potential \(\psi \in C^{1,1} (\mathbb{R}, \mathbb{R} )\) with \(\psi \geq 0\). A commonly used potential is the double well potential
The aim of the potential is to penalize impure phases, which are states where the phase field φ is not equal to 0 or 1.
Lemma 1
There exist positive constants  , Λ̄ and \(\Lambda '\) such that for all symmetrical \(\mathcal{M}, \mathcal{N}\in \mathbb{R}^{d\times d}\setminus \{ 0 \} \) and all \(\varphi \in \mathbb{R}\) the following relationships hold:
, Λ̄ and \(\Lambda '\) such that for all symmetrical \(\mathcal{M}, \mathcal{N}\in \mathbb{R}^{d\times d}\setminus \{ 0 \} \) and all \(\varphi \in \mathbb{R}\) the following relationships hold:

Proof
Follows from construction of \(C(\varphi )\). □
Assumption A1
The data lays in \(L^{2}\)
2.4 Additive manufacturing constraint
In additive manufacturing a structure is created in a layer-by-layer approach. Following [2] the intermediate states are taken into consideration to ensure stability during manufacturing. This can be thought of as slicing the final topology into horizontal layers and leads to the definition of the intermediate shape up to height \(h>0\)
With a layer thickness \(l>0\), the layer from height \(h-l\) to height h is defined via
The Dirichlet boundary for the AMC problems differs from the Dirichlet boundary of the mechanical problem. In the mechanical problem it describes areas where the structure is supported when forces are applied. In the constraint problems the process of additive manufacturing is simulated. Homogeneous Dirichlet boundary conditions are assumed for all parts of the geometry touching the building plate \(\Gamma _{0}\). Notice that \(\Gamma _{0}\) does not change for different intermediate shapes. During the manufacturing process no surface forces are applied to the structure. Each intermediate shape \(\Omega _{h}\) is only subjected to gravity g. It is assumed that gravity is the primary opponent to successful 3D printing, which is the case for example for fused deposition modeling. Other issues, like thermal problems in powder bed fusion [29], are not considered here.
As opposed to [2], where gravity acts on the whole intermediate structure, it is here restricted to the newest, upmost layer. Otherwise the compliances of the lower layers of the structure would be taken into account multiple times, whereas the top layer is only considered once. This would lead to designs with a heavy bias towards stability during the beginning of the printing process. Support structures would mainly arise in the lower parts of the design. Restricting gravity to the upmost layer can also be motivated physically: Since the lower layers of the structure are already cooled down and hardened, they will not be displaced much under the influence of gravity. Only applying gravity to the newly printed layer can be thought of as implicity considering the phase change of molten to hardened plastic filament. For a given height \(h>0\) the AMC system is defined as
Note that one cannot just define the system on the layer \(L_{h}\), since the Dirichlet boundary is not part of that domain. The weak formulation is written as
Definition 2
(Weak solution of the AMC system)
The function \(u_{h}^{c}\in H^{1}_{0} ( \Omega _{h},\mathbb{R}^{d} )\) is a weak solution of the AMC system \(( \operatorname{AMCS} )\), if it fulfills the weak formulation (11) on the corresponding space \(\Omega _{h}\).
The mechanical system \(( \operatorname{MS} )\) describes the load case where a force is acting on the structure. On the other hand the AMC system \(( \operatorname{AMCS} )\) models the printing process, where only gravity is considered. To help distinguish between both systems the superscript c is used in conjunction with the constraint problems.
In order to judge the stiffness during the manufacturing process, the compliance of the layer \(L_{h}\) is defined
For large overhang angles gravity will cause large displacements and therefore increase the compliance. Since compliance is the inverse of stiffness, low compliance values are desirable, because they coincide with high stiffness during the printing process. A penalty function is defined with \(H>0\) via
The idea is to slice the domain Ω into N layers and define successively growing domains \(\Omega _{h}\) with \(\Omega _{h_{i}} \subseteq \Omega _{h_{j}}\) for \({h_{i}}\leq {h_{j}}\).
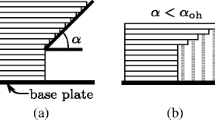
A test geometry is created to show the effect of the weighting term \(\frac{1}{h}\). In Fig. 1(a) the material is represented by the red areas. Two vertical beams are connected via eight horizontal beams, which have large overhangs. The bottom beam touches the building plate and is therefore not critical. Each of the other horizontal beams would lead to problems during additive manfucturing. However, Fig. 1(b) shows that without weighting, the AMC penalty term \(P^{d}\) increases for higher layers. This is caused by a linearly growing amount of material beneath the current layer, which is also subject to displacement. The algorithm would focus on decreasing overhangs towards the top of the domain. With weighting the AMC penalty term is more evenly distributed independent of layer height. As desired, the algorithm would decrease overhangs everywhere in the domain.
Up to this point, the height h has been a continuous parameter. To avoid double subscripts it is now used as an index of the domain. For example, \(u_{h}^{c}\) is the displacement of the structure up to the h-th layer. The layer \(L_{h}\) corresponds to \(\Omega _{h}\setminus \Omega _{h-1}\). The following notation is used:
The outer integral of \(P (u^{c},\varphi )\) is approximated via a Riemann sum. For the discretized penalty function the constant factor \(\frac{H}{N}\) is dropped, yielding
Not only the final structure shall bend as little as possible, but also all intermediate structures. Towards calculating the penalty function an additional N elasticity problems have to be solved.
2.5 Optimal control problem
With \(\beta , \gamma > 0\) all ingredients have been gathered to write down the optimization problem
3 Formal derivation of optimality conditions
The aim of this chapter is to derive optimality conditions. A rigorous mathematical analysis was conducted in [11], where the AMC could be incorporated. Here, only the formal Lagrange approach is covered, see [39].
With the weak formulation of the mechanical system (5) and the weak forms of the AMC systems (11) the Lagrange functional can be defined via
The Gâteaux derivatives of the Lagrange function with respect to the states \(u^{m}\), \(u_{h}^{c}\), \(h=1,\ldots ,N\) in the directions \(q^{m}\), \(q_{h}\), \(h=1,\ldots ,N\) respectively are calculated. This results in the adjoint equations
for \(h=1,\ldots ,N\). Note that these adjoint equations match the state equations (5), (11) for \(h=1,\ldots ,N\) respectively. With \(|\Gamma _{D}|>0\), \(|\Gamma _{0}|>0\) one can deduce
The derivative of the Lagrange function with respect to φ in direction ω is
Since \(\mathcal{G}^{m}\) is convex, any optimal control satisfies the corresponding variational inequality, see [39, Thm. 1.2.]. The results are summarized in the following theorem.
Theorem 1
Let \(\bar {\varphi }\in \mathcal{G}^{m}\) be a local solution of the optimality problem \(( P^{\epsilon } )\). The following first order necessary optimality conditions hold
State Equations
Variational Inequality
4 Discretization
Observations and theoretical derivations of linear elasticity take place in the three-dimensional space. However, two-dimensional models are computationally less demanding and will therefore be studied here. An Allen-Cahn interface propagation is explained, which allows stationary problems to be solved iteratively. The Primal-Dual Active-Set Method is presented to solve the optimal control problem.
The goal is to construct a thin, 3D-printable structure. The plane stress model is feasible since it assumes that the z-dimension is very small in comparison to the other dimensions. The Lamé parameters have to be adjusted, as explained in [22].
The goal is to iteratively solve the stationary problem. The idea of a phase field interface propagations stems from the work of [19] and [4]. After an initial material distribution \(\varphi _{0}\) is set, pseudo timestepping is used to evolve the solution. The negative derivative of the reduced cost functional is chosen as the direction of interface movement, thus
where τ is the length of a pseudo time-step. Thus
Towards better stability the equation is discretized in time using a semi-implicit approach
Note that the time-step τ is just a numerical construct and does not represent a physically relevant time, hence the word pseudo.
When formulating the optimality system the box constraint \(0\leq \varphi \leq 1\) was taken into account via the space \(\mathcal{G}^{m}\). In accordance with [39] Karush–Kuhn–Tucker multipliers \(\mu _{+}, \mu _{-} \in L^{p} (\Omega )\) with \(1< p\ll 2\) are introduced such that
The box constraint for the phase field is made up of the two inequalities \(-\varphi ( x ) \leq 0\) and \(\varphi ( x )-1\leq 0 \). For example the second inequality is called active in \(x \in \Omega \) if \(\varphi ( x ) -1 = 0\) and inactive if \(\varphi ( x ) -1 < 0\). Adding the equations of (18) to the Lagrange function yields
which leads to the unconstrained optimality problem
where
In an optimum the following holds:
If \(0<\varphi <1\), then \(\mu _{-} = \mu _{+} = 0\). Otherwise,
The regularity of \(\mu _{-}\), \(\mu _{+}\) follows from standard arguments by making use of the regularity of \(\frac{\partial \mathcal{L}}{\partial \varphi }\), see [26]. This incorporation of the box constraint via Karush–Kuhn–Tucker-multipliers leads to the Primal-Dual Active-Set Method, see [14]. In each step the active sets are updated using the result from the previous iteration. If there are no further changes in these sets, the algorithm has converged and terminates. The pseudocode is displayed in Algorithm 1.
Intuitively one can think of material flowing to the areas where it has the largest impact on decreasing the Lagrange functional. Notice that φ is not constrained per se and thus might end up being significantly smaller than 0 or larger than 1 in parts of the domain. The idea behind this algorithm is to enforce the box constraints. Start with a \(\varphi ^{0}\) that does fulfill all constraints and \(\mu _{+}^{0}, \mu _{-}^{0} \equiv 0\), leading to \(\mathcal{A}_{+}^{1}\) and \(\mathcal{A}_{-}^{1}\) being empty and thus \(\mu _{+}^{1}, \mu _{-}^{1} \equiv 0\). Eventually \(\varphi ^{k}\) will exceed 1 or fall below 0 in parts of the domain. Then the corresponding active set \(\mathcal{A}_{+}^{k+1}\) or \(\mathcal{A}_{-}^{k+1}\) will be nonempty and in turn φ set to 1 or 0, respectively. This ensures that the box constraints are met.
The potential ψ introduced in Sect. 2.3 has a local maximum in \(\varphi = 0.5\). As an initialization \(\varphi ^{0}\equiv 0.5\) is used throughout our numerical experiments. In [14] it is explained why numerical oscillations can occurr if the active set parameter c is chosen too small with respect to the mesh resolution. In our numerical experiments we did not observe oscillations when setting \(c=\frac{2}{h_{\min }^{2}}\), with \(h_{\min }\) being the minimum mesh size. The elasticity equations and the gradient equation are solved via the Finite Element Method. According to the work of [27] the Primal-Dual Active-Set-Method can be interpreted as a semismooth Newton method. This yields local superlinear convergence.
5 Numerical examples
The goal of this section is to show the effect of the AMC on the optimal topologies. Standard topology optimization examples of an MBB beam and a cantilever were chosen. The code is implemented using P1 finite elements in FEniCS, see [33] and [5]. The main computational challenge arises from a high number of layers leading to many intermediate elasticity problems that need to be solved in each iteration. If done in serial, this is quite time consuming. Here, multiprocessing is used to solve the different elasticity problems concurrently on different processors. This leads to a considerable speedup.
Here, only linearly elastic, homogeneous, isotropic materials are considered. For a formal definition see [17]. Without explicitly mentioning them, SI-units are used throughout. Young’s modulus E is set to \(3.5\times 10^{6}\) and the Poisson ratio ν is assumed to be 0.3. According to [35], this corresponds to the widely used 3D printing filament PLA. Computations are done for a surface force \(f = ( 0 , -1 )^{T}\) and the maximum number of iteration steps is set to 100. The results of the topology optimization depend on the following three parameters: the Ginzburg–Landau parameter ϵ, the Ginzburg–Landau term prefactor γ and AMC prefactor β.
5.1 Parameter study for ϵ and γ
The findings of this section do not take the AMC into account. This is achieved by setting \(\beta =0\). The parameters ϵ, γ can be varied to influence the topologies resulting from the optimization. The parameter γ is the prefactor of the Ginzburg–Landau term and thus controls the influence of the perimeter regularization, which can be interpreted as a surface tension. Larger values of γ cause the material to lump together to simple, non-filigree structures. A sensibly small γ allows for the creation of more filigree structures while still avoiding checkerboarding. The parameter ϵ regulates the influence of the two summands within the Ginzburg–Landau term. When ϵ is increased, the gradient term receives a higher weight. Penalizing the derivative causes less jumps to occur. However, impure phases with \(0<\varphi <1\) are more likely to appear. Often, ϵ is referred to as the interface thickness parameter. If it is set too large, filigree structures cannot emerge. When ϵ is decreased, a transition from material to void is penalized less. A smaller interface thickness brings about more filigree structures. If ϵ is very small, the potential term dominates. Fine, pure-phased, porous structures arise. It helps to decrease the mesh size, which allows for thinner beams to be displayed. These effects of the parameters ϵ and γ are summarized in Fig. 2.
Finding a suitable pairing can be very time consuming. In order to alleviate this problem, the parameters ϵ and γ are chosen adaptively as suggested in [23]. The following turned out to be a good choice:
with \(c_{\mathrm{GL}}\) set to 0.1.
5.2 Cantilever beam
The setting of a cantilever beam is shown in Fig. 3. The structure is fixed at the left hand side and a downward force is applied in the middle of the right hand side. The domain is discretized using \(26{,}667\) degrees of freedom. The material usage is fixed at 40%. Ten layers corresponding to ten intermediate building steps are considered for the AMC. Computations take around 14 minutes.
In order to test the influence of AMC, calculations are done for different factors β. The results can be seen in Fig. 4. Blue areas represent void and red areas correspond to material. The white parts are the interface, where \(0<\varphi <1\).
Figure 4(a) depicts the structure without influence of the AMC, i.e. \(\beta =0\). The material is concentrated in major beams. Not a lot of support structures are present to hold the major beams in place. Generally, the severity of an overhang can be measured by its angle to the normal axis. As a rule of thumb, an angle of over 45∘ is critical. Here diagonal structures can be seen that have an angle to the vertical axis of well above 45∘, making it difficult to print the structure.
The penalty term is introduced by successively increasing the factor β. A change in topology can be seen when β reaches 0.01, see Fig. 4(b). Supporting structures arise, which hold up the major beams while they are being printed. This leads to less deformations during additive manufacturing. The small beams are mostly vertically oriented and thus can be manufactured easily.
As the AMC parameter β is increased, more and more support structures arise, which can be observed in Figs. 4(e) and 4(f). More material is placed near the bottom of the domain. Beams are oriented more vertically than before and intersect each other. Smaller beams deform less, which makes the structure more stable.
Notice that opposed to the geometric approach in [25], overhangs are tackled indirectly and thus are not fully avoided.
The resulting values for the compliance, Ginzburg–Landau term and AMC penalty term can be found in Table 1. As one would expect the compliance increases as the influence of the AMC gets larger. However, for the largest β value it only increases by around 10%, whereas the AMC penalty term is decreased by 80%, making the printing process more stable.
5.3 MBB beam
The setting of an MBB beam can be seen in Fig. 5. The structure is fixed in both directions at the bottom left hand side, but allowed to move in the horizontal direction at the bottom right hand side. A vertical force is applied in the middle of the top of the domain. Making use of the symmetry axis in the middle of the MBB beam, only half of the domain is discretized. The \(400 \times 133\) crossed P1 finite elements lead to a total of \(106{,}934\) degrees of freedom. Different from the cantilever example, the number of layers is increased from 10 to 100, making multiprocessing even more valueable. In [2] the computation for the same number of layers using \(300 \times 100\) Q1 elements, corresponding to \(30{,}401\) degrees of freedom, is reported to take 237 hours. With more than three times the degrees of freedom, computations here take less than 3 hours. When \(30{,}401\) degrees of freedom are used, this time reduces to 24 minutes.
The amount of material is set to 20%. As before, β is increased to see the influence of the AMC. The results can be seen in Fig. 6. Without the AMC large overhangs arise. Especially the long horizontal beam at the top of the structure is difficult to print. It is not supported from below, likely causing molten material to sag during the manufacturing processing. As β is increased, a lot of smaller supporting structures are created. In Fig. 6(f) the area below the long horizontal beam is evenly filled with supports. One also notices that the thick 45∘ beam near the force boundary is becoming thinner and more vertical as β is increased. More support structures and vertically aligned beams make it easier to manufacture the design. In Table 2 the results are gathered. As β is increased, the compliance is increased by less than 10%, but the AMC penalty term decreases by almost 90%. While the structure with \(\beta =64\) deforms slightly more during its original use case, it is considerablly more stable during the printing process.
6 Conclusion
Instabilities during additive manufacturing motivated research on this topic. The AMC was incorporated into the optimal control problem. Optimality conditions arose from a formal Lagrangian approach. The numerical approach was discussed. Experiments showed that the AMC decreases overhangs and brings about support structures.
To the author’s best knowledge this is the first time the AMC is applied to the phase field method for topology optimization. First order optimality conditions were derived. An Allen-Cahn interface propagation iteratively solved the stationary optimality problem. After a pseudo time discretization the Primal Dual Active Set Algorithm was executed. It was discussed how the topology can be influenced by setting the parameters ϵ and γ. After applying the AMC noticeable changes occured. More support structures emerged, leading to smaller intermediate compliances and in turn to a higher stiffness during the manufacturing process. The influence of the penalty term is adjustable, which allows the structures to be fine-tuned according to demands. Less labor intensive post processing is necessary, giving this approach an advantage over manually added support structures. However, opposed to the geometric approach, large overhang angles are tackled indirectly and thus are not fully avoided. It would be beneficial to print different structures to find out how this influences the manufacturing process. Further research on this topic could include the incorporation of a micro field to represent lattice structures. This helps create printable light-weight constructions. Here, a phase flow approach was used. An implementation of the projected gradient method, see [15], could speed up the convergence. Additionally, one could implement an adaptive mesh, which is fine in the interface region and coarser otherwise. This would reduce computational costs and make three dimensional calculations less demanding. An integration of stress constraints is desirable for industrial applications. On a larger scope there are many more problems in additive manufacturing which can be tackled with optimization methods.
Availability of data and materials
Not applicable.
Abbreviations
- AMC:
-
additive manufacturing constraint
References
Allaire G, Dapogny C, Estevez R, Alexis F, Michailidis G. Structural optimization under overhang constraints imposed by additive manufacturing technologies. J Comput Phys. 2017;351:295–328.
Allaire G, Dapogny C, Faure A, Michailidis G. Shape optimization of a layer by layer mechanical constraint for additive manufacturing. C R Math. 2017;355(6):699–717.
Allaire G, Jouve F, Toader A-M. Structural optimization using sensitivity analysis and a level-set method. J Comput Phys. 2004;194(1):363–93.
Allen S, Cahn J. A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening. Acta Metall. 1979;27(6):1085–95.
Alnaes MS, Blechta J, Hake J, Johansson A, Kehlet B, Logg A, Richardson C, Ring J, Rognes ME, Wells GN. 2019. Fenics project – automated solution of differential equations by the finite element method. version 2019.1.0. http://fenicsproject.org.
AM-motion. A strategic approach to increasing europe’s value proposition for additive manufacturing technologies and capabilities. Grant Agreement No. 723560. 2018.
Ambrosio L, Buttazzo G. An optimal design problem with perimeter penalization. Calc Var. 1993;1(1):55–69.
Bendsøe MP, Kikuchi N. Generating optimal topologies in structural design using a homogenization method. Comput Methods Appl Mech Eng. 1988;71(2):197–224.
Bendsøe MP, Sigmund O. Topology optimization – theory, methods, and applications. Berlin Heidelberg: Springer; 2004.
Berman B. 3-d printing: the new industrial revolution. Bus Horiz. 2012;55(2):155–62.
Blank L, Garcke H, Farshbaf-Shaker MH, Styles V. Relating phase field and sharp interface approaches to structural topology optimization. ESAIM Control Optim Calc Var. 2014;20(4):1025–58.
Blank L, Garcke H, Sarbu L, Srisupattarawanit T, Styles V, Voigt A. Phase-field approaches to structural topology optimization. In: Constrained optimization and optimal control for partial differential equations. Berlin: Springer; 2012. p. 245–56.
Blank L, Garcke H, Sarbu L, Srisupattarawanit T, Styles V, Voigt A. Phase-field approaches to structural topology optimization. In: Constrained optimization and optimal control for partial differential equations. Berlin: Springer; 2012. p. 245–56.
Blank L, Garcke H, Sarbu L, Styles V. Primal-dual active set methods for Allen–Cahn variational inequalities with nonlocal constraints. Numer Methods Partial Differ Equ. 2013;29(3):999–1030.
Blank L, Rupprecht C. An extension of the projected gradient method to a Banach space setting with application in structural topology optimization. SIAM J Control Optim. 2017;55(3):1481–99.
Boettinger WJ, Warren JA, Beckermann C, Karma A. Phase-field simulation of solidification. Annu Rev Mater Res. 2002;32(1):163–94.
Braess D. Finite elements: theory, fast solvers, and applications in solid mechanics. Cambridge: Cambridge University Press; 2007.
Burger M, Stainko R. Phase-field relaxation of topology optimization with local stress constraints. SIAM J Control Optim. 2006;45(4):1447–66.
Cahn J, Hilliard J. Free energy of a nonuniform system. I. interfacial free energy. J Chem Phys. 1958;28(2):258–67.
Ciarlet PG. Mathematical elasticity: volume I: three-dimensional elasticity. Amsterdam: North-Holland; 1988.
Dedè L, Borden MJ, Hughes TJ. Isogeometric analysis for topology optimization with a phase field model. Arch Comput Methods Eng. 2012;19(3):427–65.
Dym CL, Shames IH. Solid mechanics: a variational approach. Berlin: Springer; 2013.
Eigel M, Neumann J, Schneider R, Wolf S. Risk averse stochastic structural topology optimization. Comput Methods Appl Mech Eng. 2018;334:470–82.
Fix G. Phase field models for free boundary problems. In: Fasano A, Primicerio M, editors. Free boundary problems: theory and applications, volume II. London: Pitman; 1983. p. 580–90.
Gaynor A, Guest J. Topology optimization considering overhang constraints: eliminating sacrificial support material in additive manufacturing through design. Struct Multidiscip Optim. 2016;54(5):1157–72.
Gilbarg D, Trudinger NS. Elliptic partial differential equations of second order. vol. 224. Berlin: Springer; 2015.
Hintermüller M, Ito K, Kunisch K. The primal-dual active set strategy as a semismooth Newton method. SIAM J Optim. 2002;13(3):865–88.
Karma A, Rappel W-J. Quantitative phase-field modeling of dendritic growth in two and three dimensions. Phys Rev E. 1998;57(4):4323.
King W, Anderson AT, Ferencz RM, Hodge NE, Kamath C, Khairallah SA. Overview of modelling and simulation of metal powder bed fusion process at Lawrence livermore national laboratory. Mater Sci Technol. 2015;31(8):957–68.
Langelaar M. Topology optimization of 3d self-supporting structures for additive manufacturing. Addit Manuf. 2018;12:60–70.
Langer J. Models of pattern formation in first-order phase transitions. In: Directions in condensed matter physics: memorial volume in honor of Shang-Keng Ma. Singapore: World Scientific; 1986. p. 165–86.
Liu J, Gaynor A, Chen S. Current and future trends in topology optimization for additive manufacturing. Struct Multidiscip Optim. 2018;57(6):2457–83.
Logg A, Mardal K-A, Wells G. Automated solution of differential equations by the finite element method: the FEniCS book. Berlin: Springer; 2012.
Miehe C, Hofacker M, Welschinger F. A phase field model for rate-independent crack propagation: robust algorithmic implementation based on operator splits. Comput Methods Appl Mech Eng. 2010;199(45–48):2765–78.
Rodríguez-Panes A, Claver J, Camacho AM. The influence of manufacturing parameters on the mechanical behaviour of PLA and ABS pieces manufactured by FDM: a comparative analysis. Materials. 2018;11(8):1333.
Rosato DV, Rosato MG. Injection molding handbook. Berlin: Springer; 2012.
Shukla A, Misra A, Kumar S. Checkerboard problem in finite element based topology optimization. Int J Adv Eng Technol. 2013;6(4):1769–74.
Takezawa A, Nishiwaki S, Kitamura M. Shape and topology optimization based on the phase field method and sensitivity analysis. J Comput Phys. 2010;229(7):2697–718.
Tröltzsch F. Optimal control of partial differential equations, theory methods and applications. vol. 112. Providence: Am. Math. Soc.; 2010.
Van Gennip Y, Bertozzi A et al.. Gamma-convergence of graph Ginzburg–Landau functionals. Adv Differ Equ. 2012;17(11/12):1115–80.
Wallin M, Ristinmaa M, Askfelt H. Optimal topologies derived from a phase-field method. Struct Multidiscip Optim. 2012;45(2):171–83.
Wang MY, Wang X, Guo D. A level set method for structural topology optimization. Comput Methods Appl Mech Eng. 2003;192(1–2):227–46.
Wang MY, Zhou S. Phase field: a variational method for structural topology optimization. Comput Model Eng Sci. 2004;6(6):547–66.
Wang S-L, Sekerka R, Wheeler A, Murray B, Coriell S, Braun R, McFadden G. Thermodynamically-consistent phase-field models for solidification. Phys D: Nonlinear Phenom. 1993;69(1–2):189–200.
Acknowledgements
We thank the anonymous reviewer for many helpful ideas and suggestions, which significantly helped to improve the manuscript.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
MER developed the model, implemented the numerics and ran simulations under the supervision of DH and TP. RL helped with the analysis. All authors discussed the results and planned the manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ebeling-Rump, M., Hömberg, D., Lasarzik, R. et al. Topology optimization subject to additive manufacturing constraints. J.Math.Industry 11, 19 (2021). https://doi.org/10.1186/s13362-021-00115-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13362-021-00115-6