Abstract
We review applications of the Fokker–Planck equation for the description of systems with event trains in computational and cognitive neuroscience. The most prominent example is the spike trains generated by integrate-and-fire neurons when driven by correlated (colored) fluctuations, by adaptation currents and/or by other neurons in a recurrent network. We discuss how for a general Gaussian colored noise and an adaptation current can be incorporated into a multidimensional Fokker–Planck equation by Markovian embedding for systems with a fire-and-reset condition and how in particular the spike-train power spectrum can be determined by this equation. We then review how this framework can be used to determine the self-consistent correlation statistics in a recurrent network in which the colored fluctuations arise from the spike trains of statistically similar neurons. We then turn to the popular drift-diffusion models for binary decisions in cognitive neuroscience and demonstrate that very similar Fokker–Planck equations (with two instead of only one threshold) can be used to study the statistics of sequences of decisions. Specifically, we present a novel two-dimensional model that includes an evidence variable and an expectancy variable that can reproduce salient features of key experiments in sequential decision making.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Fokker–Planck equation has a long history in statistical physics and is an essential element in the theory of stochastic processes [1,2,3]. Over the last decades, it has also found application in computational and cognitive neuroscience, fields in which different kinds of temporal functions that drive the nonlinear dynamics of the system (a neuron, a neural network, or a decision process) can be described by Gaussian noise. A popular example is the integrate-and-fire (IF) neuron model driven by white Gaussian noise [4,5,6,7,8,9], in which the driving uncorrelated fluctuations could represent intrinsic channel noise, external synaptic background noise, or even complex time-dependent stimuli. Another example is a whole network of such neurons [10,11,12,13,14,15], in which a single neuron is subject to a barrage of spikes coming from many other (presynaptic) cells—a kind of input that can be approximated as Gaussian but not necessarily uncorrelated (i.e., white) noise [16,17,18,19,20,21]. The third problem would be a competition between networks driven by binary stimuli to a ‘decision’ which can phenomenologically be modeled by a noisy evidence variable that can reach one of the two decision thresholds (see, e.g., [22,23,24]).
Characteristic for the problems sketched above is the emergence of thresholds and uncommon boundary conditions for the associated Fokker–Planck equations. Mechanisms for memory are implemented via Markovian embedding of colored (non-white, i.e., temporally correlated) noise, of adaptation variables and via the aforementioned threshold-and-reset conditions. In this paper, we review our own recent attempts to extend the application of the Fokker–Planck equation in computational and cognitive neuroscience in terms of the three problems outlined above: the firing statistics of IF neurons driven by external colored noise, the self-consistent fluctuation statistics in recurrent networks of IF neurons, and the statistics of stochastic decision models for sequential decisions. Furthermore, we present new results on a modified decision model with an expectancy variable that can reproduce the essential features of a set of experimental data on decision making and its history dependence.
2 Fokker–Planck equation for neural spike-train statistics
While elaborated conductance-based models can describe the action-potential generation in fine details, for many applications in computational neuroscience simplified phenomenological models of the integrate-and-fire type are used [25]. These models can also be treated analytically in simple limit cases and, thus, provide insights about the kinds of spike statistics one can expect in different situations [6, 7, 9].
Generally, an IF model is given by the dynamics of its voltage variable:
The first line is not the complete dynamics—a fire-and-reset rule (second line) renders the model highly nonlinear even if the function f(v) would be constant or vanish. The reset rule works as follows: whenever v(t) reaches a threshold \(v_{{\mathrm{th}}}\), a spike is generated at time \(t_i\) (the index i indicates the count of spikes) and the voltage is reset to \(v_r\), possibly after a dead time, the absolute refractory period \(\tau _{\mathrm{ref}}\). The essential output of the model is, thus, not the voltage variable but the spike train:
where the \(t_i\) are the aforementioned instances of threshold crossings (and subsequent resets). The input consists of a constant \(\mu \) and a time-dependent input current I(t) (here multiplied by the membrane resistance) that is often approximated by a Gaussian noise process with a certain input power spectrum (see Fig. 1), but could also contain other variables, e.g., an adaptation variable a(t) that constitutes a feedback of the model’s spike train x(t) (see below). The neural dynamics is characterized by a subthreshold function f(v) that can be quadratic (\(f(v)=v^2\), quadratic IF model), linear (\(f(v)=-v\), leaky IF model) or identically vanish (\(f(v)=0\), perfect IF model). As a model that can be related to conductance based models [26] and to experimental data [27], the exponential IF model with \(f(v)=-v+\varDelta \exp ((v-v_{{\mathrm{th}}})/\varDelta )\) (where \(v_{{\mathrm{th}}}\) and \(\varDelta \) are threshold parameters) has gained popularity over recent years [28]; it is in between the LIF model (obtained with \(\varDelta \rightarrow 0\)) and QIF model (obtained with \(\varDelta \rightarrow \infty \)).
2.1 Neurons driven by white noise
A classical example of a stochastic neuron model is the white-noise-driven IF neuron, given by the stochastic differential equation:
where \(\xi (t)\) is Gaussian white noise with a delta correlation function (\(\left\langle \xi (t)\xi (t') \right\rangle =\delta (t-t')\)); the impact of the noise on the voltage dynamics is determined by the noise intensity D.
This model is analytically tractable to a large extent: the probability density and the stationary firing rate can be found in terms of integral expressions (involving the nonlinear function f(v), the base current \(\mu \) and the strength of the noise D) [6, 29,30,31]; the ISI density [32], or at least its Laplace transform [29, 33], is known for particularly simple choices of f(v) (perfect and leaky IF models); and also the linear [11, 12, 34,35,36] and weakly nonlinear response [34, 37, 38] with respect to an additional signal can be calculated. These solutions have been also used in stochastic mean-field theories of recurrent neural networks [12, 34] in which it is assumed that the spiking in the network is temporally uncorrelated (equivalent to a Poisson process).
The dynamics of this one-dimensional white-noise-driven IF neurons is particularly simple because it generates a renewal spike train: due to the reset of the voltage after firing, there is no memory of previous interspike intervals carried by the voltage, and the driving noise itself is uncorrelated and cannot contribute to statistical dependencies among interspike intervals (this does not change in model variants with a time-dependent threshold starting at the same value after each spike [39, 40]). So, knowing the interspike interval distribution gives us access to all statistics of interest for this model class. The latter can be numerically determined in an efficient way by Richardson’s threshold integration method [41, 42].
We note two more variants of white noise that go beyond the form in Eq. (4). First, if the main source of noise are the spikes from other neurons, one may also consider white Poissonian shot noise (instead of white Gaussian noise) as a source of driving fluctuations. Richardson and Swarbrick [43] have solved the problem for a driving Poisson process with exponential weight distribution and put forward expressions for the firing rate, the rate modulation in linear response, and the power spectrum of the spike train. They demonstrated that, for instance, the stationary firing rate with white shot noise can deviate substantially from the predictions of the model with Gaussian white noise [43]. In the context of neural network simulations, however, the Gaussian approximation seems to be often less severe than the approximation of uncorrelated fluctuations (see e.g. [18]).
Furthermore, more realistic than the current noise we use in this paper is certainly to model fluctuations as a conductance noise, which enters the dynamics as a multiplicative noise, i.e., a noise that is multiplied by a function of the voltage. This entails also the problem of the interpretation of the stochastic differential equation (see, e.g., [2]), which is not unique for systems with multiplicative white noise. In particular, it has been shown that effects of the shot-noise character and of the multiplicativity of the noise can be equally important in shaping the asymmetry of the subthreshold voltage distribution [44, 45] (see also [46]).
Both complicating aspects of biophysical noise, the shot-noise character and the multiplicative-noise character, are certainly also present with colored noise but have so far received less attention in the literature, presumably because of the considerably more difficult mathematical description. It is, to the best of our knowledge, an unsolved problem, for instance, how to model a driving shot noise with prescribed (non-white) power spectrum.
2.2 Neurons driven by colored noise
Stochastic dynamics of a neuron (middle), that is driven by external noise (left upper corner) with a given power spectrum (left lower corner). The neuron is subject to intrinsic noise and spike-frequency adaptation both mediated by ion channels (middle). The neuron generates a spike train x(t) (right upper corner) the statistics of which can be characterized by the spike-train power spectrum (right lower corner). If the neuron’s input noise is caused by the superposition of spike trains from other (similar) neurons within a recurrent network, the input power spectrum and the spike-train spectrum would be related (self-consistence problem, addressed in Sect. 2.4)
A simple example for an IF neuron driven by colored Gaussian noise is
where \(\xi (t)\) is Gaussian white noise and the second equation generated a low-pass-filtered noise, the Ornstein–Uhlenbeck process with an exponential correlation function. Following the Wiener–Khinchin theorem, the power spectrum is the Fourier-transformed correlation function, in this case, a Lorentzian function. As a more general input process, a colored noise with a wide range of power spectra is given by the multidimensional Markovian embedding:
Here, \(\mathbf {\xi }(t)\) is a vector of independent Gaussian white noise of which the components obey \(\langle \mathbf {\xi }_i(t)\mathbf {\xi }_j(t+\tau ) \rangle =\delta (\tau )\delta _{ij}\). The first component of the noise vector \(\mathbf {\xi }_1(t)\) times the scalar \(\beta \) directly enters \(\eta (t)\). \(\underline{{{\underline{\varvec{{A}}}}}}\) and \(\underline{{{\underline{\varvec{{B}}}}}}\) are matrices. The power spectrum of this process with d-dimensional vectors \(\mathbf {a}\) and \(\mathbf {\xi }\) can be written as a rational function (see [47, 48] for details):
where \(\tilde{\eta }^*\) is the complex conjugate of \(\tilde{\eta }\). In the high-frequency limit, the second term vanishes because the order of the denominator being 2d is higher than the order of the numerator being \(2(d-1)\). Thus, the high-frequency limit of the power spectrum is given by \(\beta ^2\). The low-frequency limit is given by \(S_{\eta \eta } (0)=\beta ^2+X_0\). Note that for a sufficiently high-dimensional process, coefficients of the Markovian embedding can be found such that the spectrum of \(\eta \) is in a good approximation to a given input power spectrum. The coefficients \(X_k\) and \(Y_\ell \) can be calculated from the matrices \(\underline{{{\underline{\varvec{{A}}}}}}\) and \(\underline{{{\underline{\varvec{{B}}}}}}\) as:
Here, \(\mathbb {1}\) is the identity matrix and \(\mathbf {1}\) denotes a d-dimensional vector that is in every entry equal to one. Note that different matrices \(\underline{{{\underline{\varvec{{A}}}}}}\) and \(\underline{{{\underline{\varvec{{B}}}}}}\) exist that yield the same coefficients \(X_k\) and \(Y_\ell \). Furthermore, the range of values for \(X_k\) and \(Y_\ell \) is restricted by Eq. (8) such that \(S_{\eta \eta }\) is always positive and does not diverge.
The determination of a proper process \(\eta \) with a power spectrum that approximates a given one may be a difficult task, especially if we have to use a high-dimensional process. At first, we determine the coefficients \(\mathbf {\beta }\), \(X_k\) and \(Y_\ell \) of the rational function in Eq. (7), for instance, by a least square fitting procedure. The resulting function has to be larger than zero and is not allowed to have poles. Second, we determine the solution of the inverse problem of Eq. (8) to obtain the coefficients of the Ornstein–Uhlenbeck process. For \(d=1\), where the matrices \(\underline{{{\underline{\varvec{{A}}}}}}\) and \(\underline{{{\underline{\varvec{{B}}}}}}\) reduce to scalars A and B, solutions for these scalars can be found:
Also for \(d=2\) an analytical solution can be found as presented in the Appendix B of [47] in Eq. (B3). With the further increase of the dimensionality, it is more difficult to find a solution of the inverse problem of Eq. (8).
The statistics of the spike-train generated by a neuron driven by the general colored-noise input given by Eq. (1) with \(\text {RI}=\eta \) and Eq. (6) can be derived from the solution of the corresponding Fokker–Planck equation. This gives us the temporal evolution of the probability density \(P(v,\mathbf {a},t)\):
The subthreshold dynamics of v and \(\mathbf {a}\) are incorporated by the operator \({{\,\mathrm{\hat{\mathcal {L}}}\,}}\) that reads:
As a consequence of the white noise term that directly enters the v dynamics, P obeys absorbing boundary conditions at the threshold (see [49] for details) and natural boundary conditions elsewhere:
The total efflux of probability at the threshold is the probability for a neuron to fire an action potential which is the firing rate:
Here, we integrate over all dimensions of \(\mathbf {a}\) represented by the manifold \(M_{\mathbf {a}}\). The operator \({{\,\mathrm{\hat{\mathcal {R}}}\,}}\) in the Fokker–Planck equation takes into account the reset of probability that crossed the threshold. For simplicity, we consider only a vanishing refractory period \(\tau _{\text {ref}}=0\) (see [47] for detailed calculation with \(\tau _{\text {ref}}>0\)) for which the operator reads:
The stationary probability density \(P_0\) and firing rate \(r_0\) are given by the solution of the stationary Fokker–Planck equation and the normalization condition for \(P_0\):
As shown in [47], the Fourier-transformed probability density \(\tilde{Q}(v,\mathbf {a},\omega )\) is given by the solution of the partial differential equation:
and can be used to calculate the spike-train power spectrum as:
In Fig. 2, the solution of the theory for one example is compared to the spike-train power spectrum determined by direct simulation of a two-dimensional leaky integrate-and-fire neuron.
Stationary solution in panel a and spike-train power spectrum from simulation and theory as well as the power spectrum of the input noise in panel b. The model dynamics are given by \(\tau _m \dot{v}=-v+\mu +a+\beta \xi (t)\) and \(\dot{a}=Aa+B\xi (t)\) and the fire-and-reset rule. Used parameters are \(\tau _m=20\,\hbox {ms}\), \(v_{{\mathrm{th}}}=20\,\hbox {mV}\), \(v_r=0\,\hbox {mV}\), \(\mu =15\,\hbox {mV}\), \(\beta =4\,\hbox {mV}\sqrt{\text {s}}\), \(A=-25\,\hbox {s}^{-1}\) and \(B=-68.4\,\hbox {mV}/\sqrt{\text {s}}\)
2.3 Adapting neurons
The formalism introduced in [47] is not only useful to determine the spike-train power spectra of integrate-and-fire neurons driven by colored noise, but can also be generalized to deal with other stochastic multi-dimensional integrate-and-fire models. One important example for a neural feature modeled by an additional dimension is adaptation that generates a negative feedback to the membrane voltage (see for instance [28, 50]). This kind of multidimensional IF model is capable to generate spike trains with negatively correlated inter-spike intervals or complex spiking patterns [51,52,53,54], both features that have been observed experimentally (for reviews, see [55, 56]). We consider the following model:
\(\xi _1\) and \(\xi _2\) are independent Gaussian white noise. The term Av in the second line incorporates subthreshold adaptation (see, e.g., [54, 57]). If the neuron fires an action potential, the adaptation variable is increased by \(\delta _a\) (spike-triggered adaptation). The spike-train statistics of the model can be determined analogously to colored-noise driven neuron models by Eqs. (15)–(17), if the operators \({{\,\mathrm{\hat{\mathcal {L}}}\,}}\) and \({{\,\mathrm{\hat{\mathcal {R}}}\,}}\) are generalized. The operator for the subthreshold dynamics of the model reads
The reset operator \({{\,\mathrm{\hat{\mathcal {R}}}\,}}\) has to include the spike-triggered adaptation by a shift of the efflux of probability along the a-axis before the reinsertion. It is given by:
If the corresponding Fokker–Planck equation is numerically solved, its results agree well with stochastic simulations of the Langevin model (not shown here but see [47]).
2.4 Neurons subject to network noise
Mean-field theory of large and sparsely connected networks of spiking neurons. Top: Sketch of the considered network. Excitatory (blue) and inhibitory (red) neurons are randomly connected to each other. Each neuron obeys the same dynamics and has the same number of excitatory and inhibitory input synapses (here for visualization only \(C_E=4\) and \(C_I=1\), the theory assumes at least hundred). Bottom: The mean-field approach. Neural input in the network is the sum of the presynaptic neurons’ spike trains. For a sparsely connected network, the input spike trains are almost independent of each other. For a sufficient number of presynaptic connections, the sum of the input spike trains can be modeled as a stochastic process with Gaussian statistics, although the network is fully deterministic. The power spectra of the input spike trains determine the power spectrum of the quasistochastic input \(\eta \) [see Eq. (22)]. In turn, the spike-train power spectrum of a representative neuron and the power spectrum of its input are self-consistent. The approximation of the input \(\eta \) by a multidimensional Markovian embedding given by Eq. (6) with the assumption that its power spectrum must be self-consistent with the spike-train power spectrum of a representative neuron yields the mean-field theory that considers the temporal correlations of spike-trains
In networks of deterministic integrate-and-fire neurons, neural input is given by the sum of the spike trains generated by the presynaptic neurons. A simple paradigmatic case is the Brunel network [12]:
Spikes of excitatory neurons increase the membrane voltage of the postsynaptic neuron by J and spikes of inhibitory neurons decrease it by gJ; both sorts of spikes arrive after a delay D. Here, each neuron has the same numbers \(C_E\) and \(C_I\) of excitatory and inhibitory presynaptic neurons, respectively, and the numbers \(C_E,C_I\) are both large (about \(10^3\)) but much smaller than the total number of neurons (\(10^4{-}10^5\)), i.e., we deal with a sparse network. This simple model has distinct states characterized by different levels of synchrony among the cells and irregularity of individual firing that can be characterized by a stochastic mean-field analysis (see, e.g., [11, 12, 58,59,60]). We focus here on the important asynchronous irregular state that is often observed in the awake behaving animal in different brain areas [61]. Standard mean-field theories and theories using a linear-response ansatz [14, 62] employ the diffusion approximation and, thus, neglect that nontrivial temporal correlation of the input spike trains are maintained in the sum [63] and have to be considered by colored noise [16,17,18, 20]. Each neuron in the recurrent network is not only a driven element but also a driver implying a number of self-consistency conditions for the neural statistics (See Fig. 3). First of all, the mean output of the neuron will determine the mean input to the typical neuron. Most importantly, in a homogeneous network of statistically equivalent neurons, the correlation of the neuron’s spike train will be proportional to the correlation of its input, yielding a condition of self-consistency for the power spectrum of the input noise \(S_{\eta \eta }(\omega )\) and the resulting spike-train power spectrum \(S(\omega )\) (see also [18]):
This self-consistency condition can be used to determine the power spectrum of network noise by an iterative scheme of single-neuron simulations [18], which can be even generalized to the case of heterogeneous networks [64].
The introduced formalism in Eqs. (15)–(17) can be regarded as the open-loop version of the problem: the computation of the spike-train power spectrum of an integrate-and-fire neuron driven by colored Gaussian noise with a given power spectrum. If we consider the noise coming from the nonlinear neural interactions within the network, we do not know the input noise anymore but we know that it is related to the spike-train power spectra, i.e., to output of the model. If we approximate neural input by the multidimensional process in Eq. (6), the framework can be used to develop a mean-field theory that takes the temporal correlation of spike trains into account by the self-consistency of input and spike-train power spectrum in Eq. (22):
The coefficients \(\mu \), \(\beta \), \(\underline{{{\underline{\varvec{{A}}}}}}\) and \(\underline{{{\underline{\varvec{{B}}}}}}\) are initially unknown but they are the self-consistent solution of the closed-loop problem. Of course, for any numerical solution of the problem, we have to restrict ourselves to a finite-dimensional Ornstein–Uhlenbeck process for the colored noise. However, the shape of the power spectrum for such a process cannot attain an arbitrary shape and thus, it may (and generally will) not fit the self-consistent power spectrum. Thus, we can require only approximate self-consistency that can be achieved with a given finite dimension of the process.
For any dimensionality, even with a zero-dimensional process, it is useful to assume self-consistency of the first order statistics, i.e., the firing rate r that is represented by the high-frequency limit of the power spectrum. The diffusion approximation of neural input as white Gaussian noise used by Brunel [12] corresponds to a zero-dimensional process in our framework. In this case, the mean input \(\text {RI}_{\mathrm{ext}}\) and noise intensity \(\beta \) only depend on the firing rate using:
The condition of a self-consistent firing rate was used in [12] to determine the firing rate but also formed the basis for the stability analysis of the asynchronous irregular state.
Increasing the dimensionality to \(d=1\) or 2 (where d is the dimensionality of the process \(\mathbf {a}\)) allows us to approximate the self-consistency better. It is reasonable to assume self-consistency at zero frequency yielding the condition:
The remaining degrees of freedom in the input power spectrum should be used to make the spike-train power spectrum approximately self-consistent to the input power spectrum. A reasonable ansatz is to assume self-consistency at predetermined frequencies \(\omega _i\):
The number of frequencies at which self-consistencies is given by the \(2d+1\) degrees of freedom of the input power spectrum that are the number of coefficients on the right-hand side of Eq. (7). In addition to the self-consistency of firing rates (spectrum for \(\omega \rightarrow \infty \)) and at \(\omega =0\), \(2d-1\) frequencies have to be predetermined. In a numerical example, we have assumed self-consistency at the firing rate (\(\omega _1=2\pi r_0\)) for \(d=1\) and in addition at double and half the firing rate (\(\omega _1=\pi r_0\), \(\omega _2=2\pi r_0\), \(\omega _3=4\pi r_0\)) for \(d=2\). The solution for one example network is presented in Fig. 4a and has been determined iteratively (see also [47]): starting with an initial input power spectrum, we calculated the stationary firing rate and the spike-train power spectrum at all values of \(\omega _i\). The input power spectrum for the next iteration is determined such that it goes through the calculated point times the factor in Eq. (26). Ten iterations are typically enough to yield input and spike-train power spectra that are very close to each other, i.e., to match approximately the self-consistency condition at the selected frequencies.
An alternative approximation of self-consistency is the minimization of mean squared difference between input power spectrum and the spike-train power spectrum times the factor in Eq. (22), additionally to self-consistency of the firing rates and at zero frequency [Eqs. (24) and (25)]:
Here, the integral is numerically carried out up to a cutoff frequency \(\varOmega _c\) of several multiples of the firing rate (the exact value does not affect the resulting spectra significantly as long as it is large enough). The solution for the example network is presented in Fig. 4b and has also been determined iteratively. The input power spectrum for the next iteration has been determined by a least square fitting of the spike-train power spectrum times the factor in Eq. (22). Both approximations yield similar results and improve with increasing dimensionality.
Approximate solutions of the mean-field theory for different dimensionalities of the Markovian embedding. Spike-train power spectra are plotted as solid lines, input power spectra divided by the factor \(\phi =\tau _m^2 J^2(C_E+g^2C_I)\) as dashed lines. Note that self-consistency in Eq. (22) means \(S_{\eta \eta }=\phi S\). In panel a, self-consistency is achieved at predetermined frequencies. For \(d=0\), the flat input spectrum shown as dashed lightgreen line is determined such that Eq. (24) is fulfilled. Input and spike-train power spectrum (solid green line) are self-consistent at the high-frequency limit that represents the firing rate. For \(d=1\), the input is determined such that its spectrum (dashed lightblue line) and spike-train power spectrum (solid blue line) are self-consistent also at zero frequency [Eq. (25)] and at one further frequency for which we chose the firing rate (dotted vertical blue line). For \(d=2\), self-consistency can be assumed at three more frequencies [see Eq. (26)] for which we chose half, single and double the firing rate (dotted vertical red lines). Increasing dimensionality improved the approximation of the spike-train power spectrum in the network simulation, shown as solid black line. In panel b, input and spike-train power spectra are approximately self-consistent by minimizing the integrated difference in Eq. (27)
3 Fokker–Planck equation for decision processes
Primates and humans but also, for instance, rodents make decisions based on visual and other cues. If they have to choose between two alternatives, we talk about binary decision making. In some experimental settings isolated decisions are enforced, and self-explanatory statistics like the error rate or the decision time is measured. These statistics can be surprisingly well modeled by stochastic drift-diffusion (DD) models in which a variable representing the accumulated evidence performs a biased diffusion (the bias being associated with the binary stimulus) and a decision is made if this variable reaches one of the two absorbing boundaries.
However, many real life tasks consist of sequences of decisions to be made. Think of a rat running in a maze and opting for a certain path at every parting of the ways—it will make a sequence of decisions that is obviously influenced by fatigue, learning, the growth or decrease of external background noise, and many other effects. Experiments attempting to approach this problem have studied the history-dependence of decision rates and times. As shown in many studies [65,66,67,68], the performance of making binary decision depends on the stimulus history even if the sequence is fully randomized.
Here, we review models that consider an experiment in which a subject performs a sequence of binary decisions. We start with the renewal model that we recently developed and studied in Ref. [69], a model to which Richardson’s threshold-integration method for nonlinear integrate-and-fire neurons [41, 42] can be readily applied to determine the stationary statistics. We then extend the model by an additional variable that, very similar to the adaptation variable for neural spike trains, can act as a source of memory in the system. We demonstrate that such a model can reproduce essential aspects of the dependence on stimulus history in decision experiments.
3.1 Drift-diffusion model for a sequence of decisions
The classical drift-diffusion model (DDM) of binary decision-making works as follows. The accumulated evidence is represented by a stochastic process y(t) that starts at \(y(0)=y_0=0\) and evolves according to the stochastic differential equation:
where \(\mu \) is a bias term, representing the sign and strength of the signal and taken without loss of generality to be positive for the specific example considered; \(\xi (t)\) is Gaussian white noise that enters via the prefactor with an intensity of \(\sigma ^2 \tau _y\); we have also added a time scale \(\tau _y\) that could be easily absorbed into the other two parameters. A decision is reached if one of two thresholds, \(y_\pm =\pm 1\), is reached. For \(\mu >0\), reaching \(y_+=1\) would correspond to a correct detection; hitting the uphill threshold \(y_-=-1\) (which could happen due to the effect of noise) would correspond to a erroneous decision. One can formulate and solve a Fokker–Planck equation with two absorbing boundaries for the corresponding first-passage-time problem to determine the error rate (the probability to hit the wrong threshold) and the distribution of decision times [22, 23, 70]. This very simple description of a complicated signal-affected competition between different neural populations works surprisingly well in comparison to experimental data (see, e.g., [24, 71]). Obvious generalizations of the problem concern an asymmetry of the threshold distances (\(|y_+-y_0|\ne |y_- -y_0|\)), time-dependent thresholds, multi-dimensional generalizations, etc.
Here, we briefly review two generalizations in the Fokker–Planck framework that we have recently put forward [69]: one concerning the model and one concerning the kind of statistics considered. For once, instead of a biased random walk, we can also consider more generally the diffusion in a nonlinear potential landscape. This is motivated by studies of neural population dynamics in which a decision is made if one of the two interacting neural populations is activated: simplified to the level of a drift-diffusion model, Roxin and Ledberg [72] arrive at a model in which the dynamics depend in a nonlinear manner on the actual value of the accumulated evidence. This nonlinear drift can always be understood as the (negative) derivative of an effective potential \(U_\pm (y)\) (the potential is shaped by the signal). Adding also a time scale to the left-hand side, we consider the dynamics
Second, we may consider not only an isolated decision but also an entire sequence of decisions. We imagine, similar to the reset mechanism in the stochastic integrate-and-fire neuron, that the cognitive system (possibly after a break) is reset after a decision is made, a new signal is presented, evidence about this signal is accumulated, again a decision is made, the system is once more reset, and so on. In this kind of experiment, we observe a sequence of (correct or incorrect) decisions that all take different times (the interdecision intervals). In general, this may also depend on the signal. There are two aspects in the decision problem that change when we go from a \(+\) signal to a − signal: (i) the potential shape changes from \(U_+(y)\) to \(U_-(y)\); and (ii) the threshold of correct detection changes from \(y_+\) to \(y_-\). If the decision process is symmetric with respect to the signal, we may assume that \(U_+(y) = U_-(-y)\) and \(y_\pm =-y_\mp \) (for an initial point at zero, \(y_0=0\)). In this symmetric case, we can describe all subsequent decisions by the same type of equation for an evidence variable that accumulates evidence for the correct (threshold \(x_c=y_+\)) or incorrect decision (threshold \(x_i=y_-\)), captured by the Langevin dynamics in a potential \(U(x)=U_+(x)\):
Assuming a fixed break of \(\varDelta \), we can formulate the reset condition as follows:
The time instances of correct and incorrect decisions form two distinct point processes \(d_c(t)\) and \(d_i(t)\), which we endow by an amplitude (\(-1\) for incorrect decisions and \(+1\) for correct decisions); the sum of these two trains is called the decision train D(t):
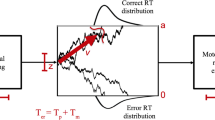
The model and the different point processes associated with the decisions are illustrated in Fig. 5.

Adopted and modified from Ref. [69]
A renewal model for a sequence of binary decisions. The evidence variable x(t) undergoes a Brownian motion in a nonlinear potential U(x) (shown on the right) and a correct (incorrect) decision is made if the x(t) reaches the right boundary \(x_c\) (left boundary \(x_i\)). After a decision is made, there is a short break \(\varDelta \) after which the evidence variable is reset to the initial point \(x_0=0\) and the next decision is made. The sequence of correct decisions is associated with a train of positive-amplitude spikes, \(d_c(t)\) (green); incorrect decisions are marked by negative spikes (red) in the train \(d_i(t)\), and the information on all decisions is covered in the sum of both trains, the so-called decision train, D(t) (bottom). Note that (somewhat surprisingly) a signal in this model is absent, because we assume that (i) there is no memory about previous decisions; (ii) the original decision process is perfectly symmetric in the sense that evidence accumulation is the same for left and right stimuli.
3.1.1 Fokker–Planck equation for the renewal decision process
Conventional statistics like the response time as well as neuroscience-inspired statistics like the power spectrum of the decision train can be determined from solutions of the Fokker–Planck equation that is associated with Eq. (30) and the reset condition, which we formulate as a continuity equation (in analogy to Richardson’s treatment of stochastic integrate-and-fire models [41, 42]):
This set of equations has to be solved with absorbing boundary conditions:
There are different statistics of interest: the stationary density of the evidence variable x, the rates of correct and of incorrect decisions, the distribution of times between decisions, the distribution of times between correct decisions, the power spectra of the different decision trains, etc. All these statistics can be determined by solving the Fokker–Planck equation with different source functions \(\nu (x,t)\) (for some statistics we need the Fourier transformed Fokker–Planck equation as in the case of the neuron models reviewed above). For a thorough discussion of all the different cases, we refer the interested reader to [69]; here, we restrict ourselves to two simple example statistics, the stationary distribution and the power spectrum of the decision train D(t).
If we want to know how often a correct decision is made and how likely a certain value of the evidence variable x will occur, we have to solve Eq. (33) in the steady state case (\(\partial _t P(x,t)=0\)) and with a likewise stationary flux function \(\nu _0(x)=(r_{c,0}+r_{i,0})\delta (x)-r_{c,0}\delta (x-x_c)-r_{i,0}\delta (x-x_i)\) that reflects the influx of reset trajectories into the reset point at \(x_0=0\) (first term) and the outflux of probability at the boundaries (last two terms). The stationary rates for correct (\(r_{c,0}\)) and incorrect decisions (\(r_{i,0}\)) are determined from the normalization of the probability density over the domain (taking into account also the amount of probability that sits in the refractory state) and from the continuity of the density over the domain. Specifically, we can reduce the computational problem of solving the partial differential equation of second order to solving two coupled equations of first order [69]
that can be solved by the threshold integration method. The aforementioned continuity and normalization conditions read
The determination of the power spectra of the decision trains is more involved. We first use a Fourier-transformed version of the Fokker–Planck equation and split again into two first-order ordinary differential equations for the current and for the probability density:
All decision times are independent of each other and so are the intervals between subsequent correct decisions. If we want to determine the power spectrum of the train of correct decisions, we can thus apply the renewal formula [73]
where \(\tilde{\varrho }_{c}(\omega )\) is the (one-sided) Fourier transform of the PDF of the interdecision intervals. It is useful to discuss how we would have to solve the Fokker–Planck equation in the time domain in order to determine \(\varrho _{c}(t)\). First of all, because there is the refractory period \(\varDelta \) we will start the density at \(t=\varDelta \) at the reset point \(x_0=0\). Second, whenever probability leaves the interval through \(x_i\) (corresponding to realizations with incorrect decisions), this probability current is redirected to \(x_0\) (the corresponding probability is reset to \(x_0\)). Third, we measure the time-dependent probability current through the threshold \(x_c\) and may identify it with \(\varrho _{c}(t)\). The conditions we have formulated lead to the following source-and-sink function in the Fourier domain
where \(-(\sigma ^2/\tau _x)\left. \partial _x\tilde{P}(x,\omega )\right| _{x_i}\) is the Fourier-transformed current through \(x_i\) (its sign is negative because the current through the left boundary is negative). This system of equations, together with the absorbing boundary conditions and the continuity at the reset point
can be numerically efficiently solved for the density \(\tilde{\varrho }_c(\omega )\). An analogous procedure can be carried out to determine \(\tilde{\varrho }_c(\omega )\) (the one-sided Fourier transform of the PDF of intervals between subsequent incorrect decisions). From the latter, we can get via Eq. (39) the power spectrum of the train of incorrect decisions \(d_i(t)\). The spectrum for the full decision train \(D(t)=d_c(t)+d_i(t)\) can be shown to obey [69]
One remarkable feature of this result is, that no matter how complicated the single spectra \(s_c(\omega )\) and \(s_i(\omega )\) may look like, if the probability of either decisions is equal (\(r_{c,0}=r_{i,0}\)), the power spectrum of the decision train will be always flat like for a white noise. This has been verified numerically in Ref. [69].
3.1.2 Stationary distribution and spectra of the decision trains for an example renewal decision process
We look at one example with a cubic potential (see Fig. 6, left panel, black line), motivated by the derivation of such a nonlinear binary-decision model from a model of competing neural networks put forward by Roxin and Ledberg [72]. The potential is asymmetric such that the correct decision, i.e., an absorption at \(x_c\), is favored. The steady-state profile (left panel, blue line) displays features that are also known from the integrate-and-fire dynamics [31, 74]: At the absorbing boundaries, the density vanishes; in the middle at the reset point, its derivative suffers a jump due to the influx of probability. The flux of probability can be imagined like a fountain with the water running off through the boundaries being pumped again into the system at the reset point. Because in addition to this source of probability, the potential possesses also a local minimum close to \(x_0\), the density exhibits a pronounced maximum close to this point.

Adopted and modified from Ref. [69]
Statistics for a sequence of binary decisions. a For a polynomial potential landscape \(U(x)=-x^4/2+x^2/2-x/5\) (black line) and a noise amplitude of \(\sigma =0.1\), and a time scale \(\tau _x=0.1\), the stationary distribution is shown (blue). b Power spectra of the trains of correct decisions (green), incorrect decisions (red), and of the entire decision train (black).
The power spectra (see Fig. 6, right) show different shapes for the trains of correct (green) and incorrect (red) decisions. For the incorrect decisions, the spectrum is lower (reflecting the low probability of a incorrect decision, i.e., a low rate \(r_{0,i}\), which determines the high-frequency limit of the spectrum) and is rather flat. Because incorrect decisions are rather rare with the chosen parameters and for this potential shape, the train of incorrect decisions obeys approximately a rare-event statistics of a Poisson process, which is a sequence of completely independent spikes that would have a white-noise (perfectly flat) power spectrum.
Correct decisions are more frequent and display a certain regularity due to the refractory period \(\varDelta \) and the passage from the barrier to the threshold point—consequently, the corresponding power spectrum reveals peaks at the rate of correct decisions and multiples. The power spectrum of the complete decision train inherits features of the latter spectrum: it shows peaks at the decision rate and its higher harmonics. The plot compares numerical simulations of the system to the solution of the Fokker–Planck equation as outlined in the previous subsection; in all cases, the results of both approaches agree very well.
The above illustrates that the concept of a spike train, which is of such great relevance in neuroscience, can also be used in the modified form of decision trains for an important problem in cognitive neuroscience. Spectra like the ones simulated above could be measured in experiments and then models could be fitted not only by means of the response time densities, error rates, etc. but also by power spectra of the decision trains. Of course, this approach would be particularly interesting when the intervals between decisions are not independent. Our results from Ref. [69] give only new statistics (the decision trains) for the simple renewal model. A more complicated model is discussed in the following, a model that can reproduce features of memory seen in certain experiments.
3.2 Drift-diffusion model with sequential effects: capturing the experimentally observed sequence-dependence of decisions
To model the binary decision-making process for two types of stimuli (\(+\) and −) and account for sequential effects, we consider the following two-dimensional DDM (see Fig. 7):
The variable y represents the accumulated evidence for either decision. The increase and decrease of y correspond to the perception of evidence for \(+\) and − stimuli, respectively. The leak term in the dynamics of y ensures that evidence that was perceived a long time ago is forgotten. The stimulus enters the model by a mean evidence \(\mu \) and its sign reflects the current stimulus. We assume symmetry between the two types of stimuli such that the statistics of \(+\) decisions for a given \(+\) stimulus are equal to the statistics of − decisions for a given − stimulus. Fluctuations that occur from noisy perception and stimulus or from intrinsic noise in neural networks are incorporated by the Gaussian white noise term that obeys \(\langle \xi (t)\xi (t+\tau )\rangle =\delta (\tau )\). Memory of the stimulus history is stored in the variable b. The leak term in the dynamics of b ensures that the memory decays exponentially in time. Decisions are made when sufficient evidence is accumulated for a decision, i.e., y exceeds one of the thresholds \(y_{-}\) or \(y_{+}\) with \(y_-=-y_+\). For simplicity, we measure y in units of \(y_+\) such that \(y_+=1\) and \(y_-=-1\). A − decision yields an instantaneous decrease of b by the amount of \(-\delta _b\), a \(+\) decision an increase by the amount of \(\delta _b\). After the non-decision time \(\varDelta \), y is reset to zero and again evolves according to Eq. (44) in the subsequent trial, in which the stimulus is chosen randomly to \(+\) or − with probability 0.5 for each independent of the stimulus history. Note that the non-decision time does not represent the response–stimulus intervals but times within a trial in which no evidence is accumulated, for instance, time to recognize the start of a new trial and time to push a response button. Here, we assume that during the RSIs y and b are constant. As a consequence, in our model we only consider times within experimental trials such that t does not represent the physical time, but stringing together the times within the subsequent trials. In summary, decisions are made following the decision-and-reset rule:
The intervals T between the time at which the stimulus is faded in and the time at which the button is pressed are the response times. The variable b incorporates sequential effects in the model such that the repetitions of the stimulus yield shorter response times than alternations. As experimentally observed, for instance by [65,66,67], the four previous stimuli influence the response times. Here, we note the stimulus history by four indices, for example, the response time \(T_{\mathrm{ARAR}}\) belongs to the stimulus history \(+--++\) and \(-++--\).
Drift-diffusion model with adaptation: a when the accumulated evidence y exceeds one of the thresholds \(y_-\) or \(y_+\), a decision is made. After the non-decision time \(\varDelta \) has elapsed, y is reset to zero and the stimulus for the next trial is chosen randomly. The current stimulus is indicated by the upper blue and lower orange areas for \(+\) and − stimuli, respectively. The shown sequence is \(+--++\). After reset, y evolves again according to Eq. (44). b Information about past decisions enters the dynamics by the variable b that is increased or decreases by the increment \(\delta _b\) when a \(+\) or a − decision is made, respectively. Within a trial, the variable decays exponentially
For the following calculations, it is convenient to consider correct and incorrect decisions instead of \(+\) and − decisions. Thus, we introduce the accumulated evidence for a correct decision x and the variable a that stores memory of past decisions that obey the subthreshold dynamics:
Note that Eq. (46) directly follows from Eq. (44) if \(\tau _a=\tau _b\), \(\tau _x=\tau _y\) and
Due to the assumed symmetry between \(+\) and − decisions mentioned above, only the history of repetitions and alternations and not the actual stimulus history is relevant. Corresponding to the thresholds, \(y_+\) and \(y_-\), correct or incorrect decisions are made when x exceeds \(x_c\) or \(x_i\), respectively. If a \(+\) stimulus is presented, \(x_c=y_+\) and \(x_i=y_-\), otherwise \(x_c=y_-\) and \(x_i=y_+\). After a decision is made, x is undefined during the non-decision time \(\varDelta \) and reset to zero afterwards. If the stimulus in the subsequent trial decision is a repetition, a is increased or decreased by the amount \(\delta _a=\delta _b\) or \(-\delta _a\) if a correct or incorrect decision was made, respectively. In case of the stimulus alternation, the sign of the entire variable a has to be flipped due to the definition of x in Eq. (47) and the modified decision-and-reset rules are given by:
In the following, we determine the response statistics for a given alternation-repetition history based on the Fokker–Planck equation that corresponds to Eqs. (46) and (48).
Example experiment for sequential effects in binary decision making: the subject is placed in front of a monitor that presents one of two stimuli, here a \(+\) or a − symbol. As soon as the subject perceived the stimulus, it makes a decision by pressing the corresponding button. After a decision has been made, no stimulus is presented for the response–stimulus interval (RSI). After the time has elapsed, the next stimulus is presented that is randomly chosen and independent of the stimulus history. The responses to both types of stimuli are symmetric in the sense that the response statistics are equal for \(+\) responses on \(+\) stimuli and − response to − stimuli. Thus, sequential effects on the response times only depend on the history of alternations and repetitions of stimuli and not on the actual stimulus
3.2.1 Fokker–Planck equation and boundary condition
Corresponding to the subthreshold dynamics in Eq. (46), the Fokker–Planck equation that describes the evolution of an ensemble is given by:
The white noise term in Eq. (46) causes absorbing boundary conditions at the thresholds. We assume natural boundary conditions for a:
The total efflux of probability at the correct or incorrect thresholds gives us the probability density for the next correct or incorrect decision, respectively:
Note that only the sum of \(g_c\) and \(g_i\) is normalized. The time integral over \(g_c\) or \(g_i\) gives us the probability that the decision is correct or incorrect, respectively.
3.2.2 Reset operations and stationary solution
To determine the stationary statistics of the model, we have to take into account the decision-and-reset rule in Eq. (48). Probability that crosses either threshold has to be reinserted at \(x=0\) after the non-decision time \(\varDelta \) has elapsed. The location at which the probability has to be reinserted is depending on which threshold has been crossed and if the subsequent stimulus is a repetition or an alternation. For a repeated stimulus, the reset of probability that crosses \(x_c\) can be incorporated in the Fokker–Planck equation by the operator \({{\,\mathrm{\hat{\mathcal {R}}}\,}}_{\mathrm{R},c}\) that measures the efflux of probability at the correct threshold, performs shifts in a and reinserts probability at x. It acts on the probability density as:
The second argument of P on the right-hand side is the result of the increase of a after the decision was made and the exponential decay during the non-decisions time. A trajectory that crosses the threshold at \(a'\) has to be reinserted at \(a=e^{-\frac{\varDelta }{\tau _a}}(a'+\delta _a)\), hence, probability that is reinserted at a has crossed the threshold at the inverse expression \(a'=ae^{\frac{\varDelta }{\tau _a}}-\delta _a\) which is the argument of the probability density on the right hand side. The efflux of probability is measured by the negative derivative at the correct threshold and the reinsertion is performed by the \(\delta \) function. The other reset operations, namely for a correct decision and an alternating stimulus and an incorrect decision with repeating or alternating stimuli are given by:
In the stationary case, probability that is reinserted from both thresholds and the probability for a repetition or an alternation are 0.5 in both cases. Thus, the stationary probability density \(P_0(x,a)\) is determined by the solution of the partial differential equation:
A decision process is either in the subthreshold regime or in the non-decision state for the time \(\varDelta \) after a decision was made. The fraction of decision-making processes in the non-decision state is given by \(\varDelta \) times the stationary efflux of probability at both thresholds yielding the normalization condition:
The stationary solution is uniquely determined by Eqs. (54) and (55) and can be found numerically using finite difference methods as described in Appendix A.1.
3.2.3 Initial distributions for a sequence of stimuli
The initial distribution for one trial considers the distribution in a at which the previous decision was made and the probability that the decision was correct. Let us consider the probability density \(P_X(x,a,t)\) of a trial with the stimulus history X, for which the probability densities for correct and incorrect decisions to be made at a are given by the time integral over the efflux of probability at the respective threshold:
Probability that has crossed \(x_c\) or \(x_i\) is increased or decreased by \(\delta _a\) and a decays exponentially during the non-decision time before it is inserted in the subthreshold dynamics for the next trial. It is convenient to calculate the efflux, the shift and the decay by the reset operations introduced in Eqs. (52) and (53). We may obtain the initial distribution of the subsequent trial with alternating stimulus by:
where \(P_{\infty ,\text {X}}(x,a)\) is the time integral over \(P_X(x,a,t)\) and the factor \(\alpha \) ensures the normalization of the initial distribution \(P_\text {XA}(x,a,0)\):
To calculate the initial distribution for a repeating stimulus \(P_{XR}(x,a,0)\), the reset operations \(({{\,\mathrm{\hat{\mathcal {R}}}\,}}_{\mathrm{A},c}+{{\,\mathrm{\hat{\mathcal {R}}}\,}}_{\mathrm{A},i})\) in Eqs. (57) and (58) have to be replaced by \(({{\,\mathrm{\hat{\mathcal {R}}}\,}}_{\mathrm{R},c}+{{\,\mathrm{\hat{\mathcal {R}}}\,}}_{\mathrm{R},i})\). Note, that the we have inserted the probability at \(t=0\) in contrast to the previous section where we inserted the probability after the non-decision time has elapsed.
To determine \(P_{\infty ,\text {X}}(x,a)\), an expression can be derived from the time integration of the Fokker–Planck equation in Eq. (49) yielding:
The partial differential equation in the second line can be solved numerically as shown in the Appendix and yields us \(P_{\infty ,\text {X}}(x,a)\) if we know the initial distribution on the left hand side.
At the beginning of each sequence, we assume the stationary probability density such that the initial distribution for the first repetition or alternation is given by:
The probability densities integrated in time are given by the solutions of Eq. (59), from which the initial distributions of the subsequent trials can be calculated using Eq. (57). Subsequently, the iterative use of Eqs. (57) and (59) using the respective operators \(({{\,\mathrm{\hat{\mathcal {R}}}\,}}_{\mathrm{A},c}+{{\,\mathrm{\hat{\mathcal {R}}}\,}}_{\mathrm{A},i})\) for an alternating stimulus and \(({{\,\mathrm{\hat{\mathcal {R}}}\,}}_{\mathrm{R},c}+{{\,\mathrm{\hat{\mathcal {R}}}\,}}_{\mathrm{R},i})\) for a repeating stimulus enables us to determine the initial condition and the time integrated probability density of a trial with any given stimulus history.
3.2.4 Error rate and mean response time
The error rate of a trial is the fraction of incorrect decisions and can be calculated for a stimulus history X by the efflux of probability at the incorrect threshold integrated over time divided by the efflux at both thresholds integrated over time:
The total efflux of probability that crosses the correct threshold gives us the probability density for a correct decision at t which is the response time density. Its mean value \(\langle T_\text {X} \rangle \) is the most important measure for the sequential effects and given by:
To determine the term in the large brackets, a partial differential equation can be derived from the Fokker–Planck equation in Eq. (49), if we consider its temporal mean value and apply the operator \({{\,\mathrm{\hat{\mathcal {L}}}\,}}\) on it. The left-hand side then reads:
With the right-hand side, we obtain the partial differential equation:
This partial differential equation of fourth order may appear more difficult to solve at first glance; however, using the finite-size method introduced in the Appendix, a solution can easily be found. Subsequently, the mean-response time can be calculated by Eq. (62).
Fit results of the two-dimensional DDM to experimental data. Data set 1 on the left-hand side is extracted from [66] and data set 2 on the right-hand side from [67]. Mean response times (top) and error rates (bottom) are encoded at the y axes, the respective sequence of repetitions (R) and alternations (A) of the stimuli on the x axis. Experimental data are shown as gray crosses and the fit results as black dots. To test the theory, mean response times and error rates are also determined by direct simulations of the models with the fit parameters shown as white diamonds. Fit parameters for data set 1 are \(\tau _x=0.37\,\hbox {s}\), \(\tau _a=0.90\,\hbox {s}\), \(\mu =3.0\), \(\sigma =\)1.04, \(\delta _a=0.66\), \(\varDelta =0.22\,\hbox {s}\) and \(\tau _x=0.60\,\hbox {s}\), \(\tau _a=0.86\,\hbox {s}\), \(\mu =2.5\), \(\sigma =1.03\), \(\delta _a=0.64\), \(\varDelta =0.16\,\hbox {s}\) for data set 2
3.2.5 Fit to experimental data
To show that the model is capable to describe sequential effects of the decision making processes, we have fitted the mean response times and error rates of a decision made after a sequence of five stimuli to the experimental data that are presented in Fig. 9 as gray crosses. Data set 1 and data set 2 are shown on the left and right hand sides and are extracted from Refs. [66, 67], respectively. In both studies two-alternative forced choice tasks as sketched in Fig. 8 were performed by volunteers. In the experiment corresponding to data set 1 two stimuli, a white lowercase ‘o’ and a white uppercase ‘O’ were presented on a black background. If an ‘o’ stimulus or an ‘O’ stimulus appear, participants should press buttons with their index or middle fingers, respectively. The stimuli are presented in a random order but with equal frequency in each series with a response–stimulus interval of 800 ms. The response times were measured for six volunteers from which each performed 13 series of 120 trials. In data set 2, the subjects should press a button with their index finger if an uppercase letter except of ‘X’ appears, and a button with their middle finger if a single digit ‘5’ appears on the computer screen. Stimuli that do not belong to these two categories were not shown. A response–stimulus interval was not fixed. The stimuli were presented for 250 ms with a subsequent break of 1-s interstimulus interval. The response times were measured for 65 participants who performed three series of 150 trials. In the series, the percentage of stimuli that belonged to the first category was 17, 50, and 83%. For both data sets, the model parameters have been determined by least square fitting as described below. To reduce the number of fitting parameters, we set \(\tau _x=1\) s and consider the mean response times of given sequences divided by the average of the mean response times over all considered sequences. We also consider the error rates by the cost function:
where \(T_{\mathrm{exp},X}\) are the median of the response times and \(E_{\mathrm{exp},X}\) are the error rates of the experimental data for a given sequence X and the sum over X goes over all 16 considered sequences (RRRR, ARRR, RARR, ..., RAAA, AAAA). The \(\langle T_X \rangle \) and \(E_X\) are calculated as presented above for each parameter set. Note that \(\langle T_X \rangle \) depends on the choice of \(\tau _x\) but due to the scaling, the cost function does not depend on it, nor does \(E_X\). In the fitting procedure, we determine the parameters that minimize the cost function:
Subsequently, we calculate the mean response times with \(\tau _x=1\) s and the solution of the minimization \(\tau _a'\). In a last step, the temporal parameters of the model have to be scaled by the factor:
ensuring that the average of the mean response times from the model over the sequences is equal to the average of the median response times from the experiment.
The mean response times that result from the fitting procedure are presented in Fig. 9 as black dots for both data sets. In order to validate the theory for the calculation of the mean response times, results from direct simulations of the model with the fitted parameters are presented as white diamonds and are very close to the theory.
The model is capable to fit the essential sequential effects that are the longest response times and highest error rate for the sequence RRRA, shortest time and lowest error rate for RRRR and some local maxima and minima. One may argue that we compare the mean values calculated with the introduced theory to the medians of the experimental data. Thus, we have checked the median response times from the direct simulations that are similar to the mean values and maxima and minima are at the same locations. Compared to the mean values, the median values have a negative bias. The distributions of the simulated response times for data set 1 and 2 are characterized by a similar skewness (2.0 for set 1 and 2.1 for set 2) but differ in their coefficients of variation (0.28 and 0.46). These values are in line with experimental findings, e.g., in [75].
4 Conclusions
We have reviewed applications of the Fokker–Planck equation for systems that generate event trains. The events are spikes (action potentials) in the case of neural integrate-and-fire (IF) models or (correct or incorrect) decisions in the case of generalized drift-diffusion (DD) models. Concepts like the decision train are straightforward generalizations of the neural spike train, generalizations that may prove useful in the future study of behaviorally realistic sequences of decisions. One purpose of this paper is that we would like to highlight the opportunities and benefits of the transfer of (fairly recent) methods from computational neuroscience to stochastic problems in cognitive neuroscience.
While the application to the one-dimensional versions of the IF model is a standard approach in computational neuroscience for decades [4, 5, 25], the extension to the multidimensional case to incorporate colored noise [20, 26, 76, 77] and adaptation [78] has been limited largely to the simple two-dimensional setup. Here, we demonstrated that the approach developed in Ref. [47] permits to model more general (and biophysically relevant) noise spectra and even provides a closed system of equations for the difficult problem of the self-consistent network noise: this theory describes how the static disorder of random connections between deterministic neurons leads to a quasi-random stochastic network noise. Although the governing equations look rather cumbersome, it is possible to approximately solve them in some cases. We showed explicitly that results are robust and that different numerical approaches yield similar results for the self-consistent spike-train power spectrum. However, the application of the formalism is limited, since the determination of a solution is computationally expensive and only applicable if the input spectrum can be achieved by a two-dimensional Markovian embedding. For a detailed discussion, see [47].
We note for the studied IF models, it is also possible to include colored fluctuations as conductance noise instead of current noise (see [79] as an example for a recent analytical approach to this problem). It may, however, be misleading to take into account the multiplicative character of the noise but still to neglect its shot-noise character [44, 80]. Especially, if we want to take into account arbitrarily correlated spike train input with non-small and possibly random amplitudes that acts on a conductance dynamics of an IF neuron, we still lack a general framework that would be comparable to the multidimensional Fokker–Planck equation discussed in this paper.
The standard statistics of decision models in cognitive neuroscience often do not take into account that in many real-life situations decisions are not made in isolation but in a sequence—think again of the rat running in a maze or of tourists in a big city finding their way to the museum. Here we introduced the decision train, showed how the Fokker–Planck equation for the drift-diffusion model has to be solved to determine the correlation statistics of these event trains for the simplest renewal version of the drift-diffusion model. Moreover, we introduced a novel two-dimensional stochastic model of sequential decision making and explained how experimentally measured stimulus-history-dependent statistics can be extracted from numerical solutions of the Fokker–Planck equation under different initial conditions. Remarkably. this simple model can reproduce salient features of the experimental data.
On a final note, we would like to point out that the framework we have reviewed can be also applied to study the response to time-dependent signals. For simple IF models, this is standard in computational neuroscience to investigate the flow of information in single neurons (e.g., in [6, 38, 81,82,83]) and populations (cf. [84,85,86,87]). There are still many open problems when it comes to the information transmission in neurons under the influence of colored noise (intrinsic channel noise or network fluctuations) and adaptation (see, however, [88]). For the cognitive models, the response statistics would allow to probe and calibrate drift-diffusion models in new ways if experimental conditions over a sequence of binary decisions would be changed in a controlled time-dependent manner. This could lead to fruitful experiment–theory interactions on a novel quantitative level in this field of research.
References
H. Risken, The Fokker–Planck Equation (Springer, Berlin, 1984)
C.W. Gardiner, Handbook of Stochastic Methods (Springer, Berlin, 1985)
N.G. van Kampen, Stochastic Processes in Physics and Chemistry (North-Holland, Amsterdam, 1992)
L.M. Ricciardi, Diffusion Processes and Related Topics on Biology (Springer, Berlin, 1977)
H.C. Tuckwell, Stochastic Processes in the Neuroscience (SIAM, Philadelphia, 1989)
N. Fourcaud, N. Brunel, Dynamics of the firing probability of noisy integrate-and-fire neurons. Neural Comput. 14, 2057 (2002)
A.N. Burkitt, A review of the integrate-and-fire neuron model: I. Homogeneous synaptic input. Biol. Cyber. 95, 1 (2006)
R.D. Vilela, B. Lindner, Are the input parameters of white-noise-driven integrate & fire neurons uniquely determined by rate and CV? J. Theor. Biol. 257, 90 (2009)
S. Ostojic, Interspike interval distributions of spiking neurons driven by fluctuating inputs. J. Neurophysiol. 106, 361 (2011)
A. Treves, Mean-field analysis of neuronal spike dynamics. Netw. Comput. Neural Syst. 4, 259 (1993)
L. Abbott, C. van Vreeswijk, Asynchronous states in networks of pulse-coupled oscillators. Phys. Rev. E 48, 1483 (1993)
N. Brunel, Dynamics of sparsely connected networks of excitatory and inhibitory spiking neurons. J. Comput. Neurosci. 8, 183 (2000)
S. Ostojic, Two types of asynchronous activity in networks of excitatory and inhibitory spiking neurons. Nat. Neurosci. 17, 594 (2014)
D. Grytskyy, T. Tetzlaff, M. Diesmann, M. Helias, A unified view on weakly correlated recurrent networks. Front. Comput. Neurosci. 7, 131 (2013)
H. Bos, M. Diesmann, M. Helias, Identifying anatomical origins of coexisting oscillations in the cortical microcircuit. PLoS Comput. Biol. 12, e1005132 (2016)
A. Lerchner, G. Sterner, J. Hertz, M. Ahmadi, Mean field theory for a balanced hypercolumn model of orientation selectivity in primary visual cortex. Netw. Comput. Neural Syst. 17, 131 (2006)
H. Câteau, A.D. Reyes, Relation between single neuron and population spiking statistics and effects on network activity. Phys. Rev. Lett. 96, 058101 (2006)
B. Dummer, S. Wieland, B. Lindner, Self-consistent determination of the spike-train power spectrum in a neural network with sparse connectivity. Front. Comp. Neurosci. 8, 104 (2014)
S. Wieland, D. Bernardi, T. Schwalger, B. Lindner, Slow fluctuations in recurrent networks of spiking neurons. Phys. Rev. E 92, 040901(R) (2015)
T. Schwalger, F. Droste, B. Lindner, Statistical structure of neural spiking under non-Poissonian or other non-white stimulation. J. Comput. Neurosci. 39, 29 (2015)
A. Van Meegen, B. Lindner, Self-consistent correlations of randomly coupled rotators in the asynchronous state. Phys. Rev. Lett. 121, 258302 (2018)
R. Ratcliff, A theory of memory retrieval. Psychol. Rev. 85(2), 59 (1978)
R. Ratcliff, A diffusion model account of response time and accuracy in a brightness discrimination task: fitting real data and failing to fit fake but plausible data. Psychon. Bull. Rev. 9(2), 278 (2002)
P. Cisek, G.A. Puskas, S. El-Murr, Decisions in changing conditions: the urgency-gating model. J. Neurosci. 29(37), 11560–11571 (2009)
W. Gerstner, W.M. Kistler, R. Naud, L. Paninski, Neuronal Dynamics from Single Neurons to Networks and Models of Cognition (Cambridge University Press, Cambridge, 2014)
N. Brunel, S. Sergi, Firing frequency of leaky integrate-and-fire neurons with synaptic current dynamics. J. Theor. Biol. 195, 87 (1998)
L. Badel, S. Lefort, R. Brette, C.C.H. Petersen, W. Gerstner, M.J.E. Richardson, Dynamic I–V curves are reliable predictors of naturalistic pyramidal-neuron voltage traces. J. Neurophysiol. 99, 656 (2008)
R. Brette, W. Gerstner, Adaptive exponential integrate-and-fire model as an effective description of neuronal activity. J. Neurophysiol. 94, 3637 (2005)
A.V. Holden, Models of the Stochastic Activity of Neurons (Springer, Berlin, 1976)
H.C. Tuckwell, Introduction to Theoretical Neurobiology (Cambridge University Press, Cambridge, 1988)
B. Lindner, Coherence and Stochastic Resonance in Nonlinear Dynamical Systems (Logos, Berlin, 2002)
G.L. Gerstein, B. Mandelbrot, Random walk models for the spike activity of a single neuron. Biophys. J. 4, 41 (1964)
D.A. Darling, A.J.F. Siegert, The 1st passage problem for a continuous Markov process. Ann. Math. Stat. 24, 624 (1953)
D.J. Amit, N. Brunel, Dynamics of a recurrent network of spiking neurons before and following learning. Netw. Comput. Neural Syst. 8, 373 (1997)
N. Brunel, F.S. Chance, N. Fourcaud, L.F. Abbott, Effects of synaptic noise and filtering on the frequency response of spiking neurons. Phys. Rev. Lett. 86, 2186 (2001)
B. Lindner, L. Schimansky-Geier, Transmission of noise coded versus additive signals through a neuronal ensemble. Phys. Rev. Lett. 86, 2934 (2001)
S. Voronenko, B. Lindner, Nonlinear response of noisy neurons. New J. Phys. 19, 033038 (2017)
S. Voronenko, B. Lindner, Improved lower bound for the mutual information between signal and neural spike count. Biol. Cybern. 112, 523 (2018)
H.C. Tuckwell, Recurrent inhibition and after hyperpolarization: effects on neuronal discharge. Biol. Cybern. 30, 115 (1978)
B. Lindner, A. Longtin, Effect of an exponentially decaying threshold on the firing statistics of a stochastic integrate-and-fire neuron. J. Theor. Biol. 232, 505 (2005)
M.J.E. Richardson, Firing-rate response of linear and nonlinear integrate-and-fire neurons to modulated current-based and conductance-based synaptic drive. Phys. Rev. E. 76, 021919 (2007)
M.J.E. Richardson, Spike-train spectra and network response functions for non-linear integrate-and-fire neurons. Biol. Cybern. 99, 381 (2008)
M.J.E. Richardson, R. Swarbrick, Firing-rate response of a neuron receiving excitatory and inhibitory synaptic shot noise. Phys. Rev. Lett. 105, 178102 (2010)
M.J.E. Richardson, W. Gerstner, Synaptic shot noise and conductance fluctuations affect the membrane voltage with equal significance. Neural Comput. 17, 923 (2005)
M.J.E. Richardson, W. Gerstner, Statistics of subthreshold neuronal voltage fluctuations due to conductance-based synaptic shot noise. Chaos 16, 026106 (2006)
B. Lindner, A. Longtin, Comment on “Characterization of subthreshold voltage fluctuations in neuronal membranes” by M. Rudolph and A. Destexhe. Neural Comput. 18, 1896 (2006)
S. Vellmer, B. Lindner, Theory of spike-train power spectra for multidimensional integrate-and-fire models. Phys. Rev. Res. 1, 023024 (2019)
S. Vellmer, Applications of the Fokker–Planck equation in computational and cognitive neuroscience, PhD thesis, Humboldt University Berlin, Germany (2020)
D.R. Cox, H.D. Miller, The Theory of Stochastic Processes (Methuen & Co, London, 1965)
E.M. Izhikevich, Simple model of spiking neurons. IEEE Trans. Neural Netw. 14, 1569 (2003)
Y.H. Liu, X.J. Wang, Spike-frequency adaptation of a generalized leaky integrate-and-fire model neuron. J. Comput. Neurosci. 10, 25 (2001)
M.J. Chacron, A. Longtin, L. Maler, Negative interspike interval correlations increase the neuronal capacity for encoding time-dependent stimuli. J. Neurosci. 21, 5328 (2001)
T. Schwalger, B. Lindner, Patterns of interval correlations in neural oscillators with adaptation. Front. Comput. Neurosci. 7, 164 (2013)
L. Shiau, T. Schwalger, B. Lindner, Interspike interval correlation in a stochastic exponential integrate-and-fire model with subthreshold and spike-triggered adaptation. J. Comput. Neurosci. 38, 589 (2015)
F. Farkhooi, M.F. Strube-Bloss, M.P. Nawrot, Serial correlation in neural spike trains: experimental evidence, stochastic modeling, and single neuron variability. Phys. Rev. E 79, 021905 (2009)
O. Avila-Akerberg, M.J. Chacron, Nonrenewal spike train statistics: causes and consequences on neural coding. Exp. Brain Res. 210, 353 (2011)
S.A. Prescott, T.J. Sejnowski, Spike-rate coding and spike-time coding are affected oppositely by different adaptation mechanisms. J. Neurosci. 28, 13649 (2008)
S. Fusi, M. Mattia, Collective behavior of networks with linear (VLSI) integrate-and-fire neurons. Neural Comput. 11, 633 (1999)
D.Q. Nykamp, D. Tranchina, A population density approach that facilitates large-scale modeling of neural networks: analysis and an application to orientation tuning. J. Comput. Neurosci. 8, 19 (2000)
B.W. Knight, A. Omurtag, L. Sirovich, The approach of a neuron population firing rate to a new equilibrium: an exact theoretical result. Neural Comput. 12, 1045 (2000)
A. Renart, J. De La Rocha, P. Bartho, L. Hollender, N. Parga, A. Reyes, K.D. Harris, The asynchronous state in cortical circuits. Science 327, 587 (2010)
J. Trousdale, Y. Hu, E. Shea-Brown, K. Josic, Impact of network structure and cellular response on spike time correlations. PLoS Comput. Biol. 8, e1002408 (2012)
B. Lindner, Superposition of many independent spike trains is generally not a Poisson process. Phys. Rev. E 73, 022901 (2006)
R.F.O. Pena, S. Vellmer, D. Bernardi, A.C. Roque, B. Lindner, Self-consistent scheme for spike-train power spectra in heterogeneous sparse networks. Front. Comput. Neurosci. 12, 9 (2018)
E. Soetens, L.C. Boer, J.E. Hueting, Expectancy or automatic facilitation? Separating sequential effects in two-choice reaction time. J. Exp. Psychol. Hum. Percept. Perform. 11(5), 598 (1985)
R.Y. Cho, L.E. Nystrom, E.T. Brown, A.D. Jones, T.S. Braver, P.J. Holmes, J.D. Cohen, Mechanisms underlying dependencies of performance on stimulus history in a two-alternative forced-choice task. Cogn. Affect. Behav. Neurosci. 2(4), 283–299 (2002)
A.D. Jones, R.Y. Cho, L.E. Nystrom, J.D. Cohen, T.S. Braver, A computational model of anterior cingulate function in speeded response tasks: effects of frequency, sequence, and conflict. Cogn. Affect. Behav. Neurosci. 2(4), 300–317 (2002)
M. Jones, T. Curran, M.C. Mozer, M.H. Wilder, Sequential effects in response time reveal learning mechanisms and event representations. Psychol. Rev. 120(3), 628 (2013)
S. Vellmer, B. Lindner, Decision-time statistics of nonlinear diffusion models: characterizing long sequences of subsequent trials. J. Math. Psychol. 99, 102445 (2020)
R. Ratcliff, P.L. Smith, S.D. Brown, G. McKoon, Diffusion decision model: current issues and history. Trends Cogn. Sci. 20(4), 260–281 (2016)
J. Palmer, A.C. Huk, M.N. Shadlen, The effect of stimulus strength on the speed and accuracy of a perceptual decision. J. Vis. 5(5), 376–404 (2005)
A. Roxin, A. Ledberg, Neurobiological models of two-choice decision making can be reduced to a one-dimensional nonlinear diffusion equation. PLoS Comput. Biol. 4(3), e1000046 (2008)
R.L. Stratonovich, Topics in the Theory of Random Noise (Gordon and Breach, New York, 1967)
M.J.E. Richardson, Effects of synaptic conductance on the voltage distribution and firing rate of spiking neurons. Phys. Rev. E 69, 051918 (2004)
R. Cao, A. Pastukhov, M. Mattia, J. Braun, Collective activity of many bistable assemblies reproduces characteristic dynamics of multistable perception. J. Neurosci. 36(26), 6957–6972 (2016)
B. Lindner, Interspike interval statistics of neurons driven by colored noise. Phys. Rev. E 69, 022901 (2004)
R. Moreno-Bote, N. Parga, Response of integrate-and-fire neurons to noisy inputs filtered by synapses with arbitrary timescales: firing rate and correlations. Neural Comput. 22, 1528 (2010)
T. Schwalger, B. Lindner, Analytical approach to an integrate-and-fire model with spike-triggered adaptation. Phys. Rev. E 92, 062703 (2015)
T.D. Oleskiw, W. Bair, E. Shea-Brown, N. Brunel, Firing rate of the leaky integrate-and-fire neuron with stochastic conductance-based synaptic inputs with short decay times (2020). arXiv preprint arXiv:2002.11181
L. Wolff, B. Lindner, A method to calculate the moments of the membrane voltage in a model neuron driven by multiplicative filtered shot noise. Phys. Rev. E 77, 041913 (2008)
F. Rieke, D. Warland, R. de Ruyter van Steveninck, W. Bialek, Spikes: Exploring the Neural Code (MIT Press, Cambridge, 1996)
S.P. Strong, R. Koberle, R.R.D. van Steveninck, W. Bialek, Entropy and information in neural spike trains. Phys. Rev. Lett. 80, 197 (1998)
F. Droste, B. Lindner, Exact analytical results for integrate-and-fire neurons driven by excitatory shot noise. J. Comput. Neurosci. 43, 81 (2017)
D.J. Mar, C.C. Chow, W. Gerstner, R.W. Adams, J.J. Collins, Noise shaping in populations of coupled model neurons. Proc. Natl. Acad. Sci. 96, 10450 (1999)
E. Ledoux, N. Brunel, Dynamics of networks of excitatory and inhibitory neurons in response to time-dependent inputs. Front. Comput. Neurosci. 5, 25 (2011)
F. Droste, B. Lindner, Up-down transitions in the background activity can be beneficial for neural information transmission. eNeuro 4, e0282–17 (2017)
Z. Bostner, G. Knoll, B. Lindner, Information filtering by coincidence detection of synchronous population output: analytical approaches to the coherence function of a two-stage neural system. Biol. Cybern. 114, 403 (2020)
M. Deger, T. Schwalger, R. Naud, W. Gerstner, Fluctuations and information filtering in coupled populations of spiking neurons with adaptation. Phys. Rev. E 90, 062704 (2014)
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Appendix A: Numerical calculation of mean response times and error rates
Appendix A: Numerical calculation of mean response times and error rates
1.1 A.1 Discretization
To determine the stationary solution, the start distribution for a given stimulus history and thereby the mean response times and error rates, we use a finite-difference method similarly to the one introduced in [47]. The variables x and a are discretized to N bins:
with \(j,k \in [0,\dots ,N-1]\). x is defined in between the thresholds such that \(x_{-1}=x_i=-1\) and \(x_{N}=x_c=1\) are not considered. The increment between two neighboring bins is \(\delta x=2/(N+1)\). The relevant range of a was estimated by the maximum increment within five decisions \(a_1=-5\delta _a\) and \(a_N=5\delta _a\) such that \(\varDelta _a=10\delta _a/N\). For the fitting procedure, \(N=80\) was sufficient. Discretized probability densities are N-dimensional vectors \(\mathbf {P}\) with the components:
1.2 A.2 Subthreshold dynamics
By the symmetric approximation of the first and second derivatives with respect to x and a, the discretized version of the subthreshold operator \({{\,\mathrm{\hat{\mathcal {L}}}\,}}\) in Eq. (49) is a \(N^2 \times N^2\) matrix of which the components are given by:
where the \(\delta _{j,k}\) are Kronecker symbols and \(\bar{\delta }_{j,k}=1-\delta _{j,k}\) are ’anti’-Kronecker symbols.
1.3 A.3 Reset operations
The decision-and-reset operators \({{\,\mathrm{\hat{\mathcal {R}}}\,}}_{\mathrm{R},c}\), \({{\,\mathrm{\hat{\mathcal {R}}}\,}}_{\mathrm{R},i}\), \({{\,\mathrm{\hat{\mathcal {R}}}\,}}_{\mathrm{A},c}\) and \({{\,\mathrm{\hat{\mathcal {R}}}\,}}_{\mathrm{A},i}\) in Eqs. (52) and (53) perform five steps: they measure the efflux of probability at the respective threshold, they shift probability along the a axis, if the stimulus alternates, they flip the sign of the variable a, they account for the exponential decay of a during the non decision time and, finally, they reinsert the probability at the reset point. In the discretized version, we perform each step by a single operator, for instance, \({{\,\mathrm{\hat{\mathcal {R}}}\,}}_{\mathrm{A},c}\)=\(\hat{R} \hat{E} \hat{F}^{\text {A}} \hat{S}^{c} \hat{D}^c\). The efflux of probability at the correct and incorrect threshold can be calculated by the operators \(\hat{D}^c\) and \(\hat{D}^i\), respectively, that read in their discretized versions:
Note that these are the components of \(N\times N^2\) matrices. For a correct decision, a is increased by \(\delta _a\) corresponding to a shift of \(\delta _a\) along the a axis, for an incorrect decision, a is decreased. The probability from the m-th bin is transferred into the \((m+n_a)\)-th or the \((m-n_a)\)-th bin with \(n_a=\delta _a/ \varDelta _a\). For our choice of discretization, \(n_a=8\) is an integer number. The discretized shift operators are given by the \(N\times N\) matrices:
The flip of the sign of a for the alternation of the stimulus is incorporated by the \(N \times N\) matrix:
The exponential decay during the non-decision time \(\varDelta \) yields that probability located at \(a_{m''}\) has to be inserted at \(a_{m''}e^{-\varDelta / \tau _a}\) which lies in between two bins. Thus, we split the probability and insert it into two neighboring bins at \(a_{n_E}\) and \(a_{n_E+1}\) with the fraction \(1-\kappa \) and \(\kappa \) given by:
Finally, the reinsertion of probability is performed by an \(N^2\times N\) matrix that is for an even number N given by:
1.4 A.4 Stationary solution
The partial differential equation for the stationary probability density in Eq. (54) can be approximated as a homogeneous linear system by approximating the operators as the matrices and probability density as a vector:
To exclude the trivial solution of the homogeneous system that is \(P_{0\,j+kN}=0\) for all j and k, we force the \(N^2/2+N/2\)-th component to be one yielding:
We determined \(\mathbf {P}_0'\) numerically using the linear algebra package scipy.sparse.linalg.spsolve in Python. Subsequently, the stationary probability density \(\mathbf {P}_0\) that fulfills the normalization condition in Eq. (55) is determined by:
1.5 A.5 Mean response times and error rates
The discretized initial distributions of the first trial in the sequence for a repetition and for an alternation of the stimulus \(\mathbf {P}_\text {R}\) or \(\mathbf {P}_\text {A}\) with \(P_{\mathrm{R}\,j+kN}=P_\text {R}(x_j,a_k,0)\) are given by Eq. (60):
As the next step, we have to calculate the time integral of the probability densities that are given as the solution of the partial differential equation (59) that reads in discretized version:
We solve this linear system numerically as Eq. (77). The initial probability density for the subsequent trial can be calculated according to Eq. (57):
Applying Eqs. (80) and (81) iteratively, initial probability density for any given sequence of repetitions and alternation can be calculated. Subsequently, the error rate of the last considered trial is given by Eq. (61):
The mean response time can be calculated from the solution of the partial differential equation (64):
We determine \(\mathbf {Q}_\text {X}\) numerically and calculate the mean response time with Eq. (62):
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Vellmer, S., Lindner, B. Fokker–Planck approach to neural networks and to decision problems. Eur. Phys. J. Spec. Top. 230, 2929–2949 (2021). https://doi.org/10.1140/epjs/s11734-021-00172-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1140/epjs/s11734-021-00172-3