Coherent structure modification by a shear acting at the surface of a turbulent open channel

Abstract

Recent experiments in the river Seine have revealed the presence of persistent large rolls. This finding has motivated the present numerical study of a turbulent open channel flow. Our pseudo-spectral direct numerical simulations are aimed at understanding how the shear at the surface, for instance produced by an external wind, can change vortical structures in the bulk. Simulations are run at a Reynolds number in the range $[5\times 10^3\div 10^4]$, in line with similar laboratory experiments. We investigate how flow structures located near the bottom wall, near the surface or inside the bulk are modified by a surface shear. Statistical signatures are extracted through Fourier analysis of the simulated fields, and typical wavelengths of vortices or streaks are computed. Moreover, instantaneous fields are used to show the existence of upwelling and downwelling motions. These motions can be hindered by the presence of a large enough surface shear. This condition turns out to be necessary for the existence of streaks at the surface as well. Our investigation clarifies the dynamics of vortices in an open channel flow at moderate Reynolds number, indicating that unsteady vortex structures are indeed present, but the existence of long coherent rolls cannot be accounted for by the sole presence of shear at the surface. Numerical studies with a much longer domain and possibly at higher Reynolds numbers are needed to provide a firm answer to the question.

1 Introduction

The presence of coherent structures in turbulent flows has motivated a huge research effort in the last decades [1,2,3]. While coherent structures are also present in isotropic flows [4], we focus here on the properties of coherent vortices in the presence of physical boundaries, and in particular for the archetypal case of an open channel flows. Vortical structures can manifest either as a permanent secondary flow in a cross-stream direction or as an instantaneous pattern of the flow dynamics. In both cases, they are particularly important in environmental situations, since they may play a major role in sediment transport and dispersion [5].

Triggered by the influential work of Barenblatt [6], a major effort has been made to understand better wall flows at moderate and high Re numbers. In such flows, experiments and numerical simulations revealed the existence of different near-wall vortical structures, spatially correlated and with different temporal persistency [7, 8]. Particularly interesting for boundary layers are the long streamwise elongated vortices [9,10,11]. These streamwise structures seem to be 100–1000 long in terms of the wall unit distance [12], defined as the viscous scale $\delta _{\nu }=\nu /u_{\tau }$ where $\nu$ is the kinematic viscosity and friction velocity is $u_{\tau }=\sqrt{{\tau _w}/{\rho }}$, based on the averaged wall stress $\tau _w$ and the fluid density $\rho$. Along the spanwise direction, these vortices generate streaks that generally extend over distances of approximately 100 wall unit distance or less.

More recently, visualizations, experiments and numerical studies have revealed an even more complex situation with the existence of large-scale (LS) and very-large-scale motions (VLS) [13,14,15]. The typical length scale of these structures is the outer scale h rather than the viscous scale, and they can extend over very long distances in the streamwise direction (even up to 10h). It is worth noting that all these structures may be energetically important, but they are generated randomly in time and space, and are instantaneous representation of the Reynolds stress dynamics [16].

In hydraulic flows, such as open channels, the situation is less clear-cut. In rough open channels, there is some evidence that large structures are present as streamwise rotating rolls, which actively participate to the bed dynamics [17,18,19,20]. Smooth channels are equally relevant when the interaction with the rough bed may be neglected. In this case, the presence of streaky structures at the bottom has been corroborated by many studies [21, 22]. Similar low- and high-speed streaks have also been found in free surface flows [23,24,25]. Streaks exist at the free surface at least when some large enough external shear is imposed at the free surface. This result is non-trivial since, contrary to a solid wall, vortex lines can attach at a free surface and a wall-normal vorticity component can exist. This is one classical instance of modification of vorticity dynamics by a free surface [26]. Similarly to what was proposed for closed wall flows, some authors have linked the presence of streaks near the surface to vortical motions spanning the entire channel height in the cross-stream direction rather than being localized near boundaries [27,28,29,30,31,32].

In addition, in smooth open channel flows, some in situ experiments have pointed out the presence of vortices, which look like secondary flows [33] in the transverse plane, i.e., contrary to LS and VLS in pipe and boundary layer flows, they are not random in space and time. Under which conditions these vortices are encountered in natural flows, and what is their impact on sediment/species transport, hydraulic resistance, mixing and morphodynamics are still a matter of debate that requires further analyses [19, 33].

To provide some insights on this issue, in the present work, we study numerically an open channel flow, focusing in particular on the upwelling and downwelling motions of fluid, and investigating whether there exists a clear statistical signature of rolls scaling with the height of the channel. Some recent works have particularly motivated the present one. Experiments by Chauvet et al. [34] have analyzed velocity and vorticity in the river Seine. Through Doppler measurements, these authors have provided evidence of a secondary flow in the transverse plane. More precisely they have measured a time-averaged vertical velocity, thus showing the existence of a typical wavelength along the spanwise direction that may be related to the presence of large circulation rolls. These structures appear to be robust, yet they are of much smaller amplitude than the main streamwise component: For the river Seine, the average speed is of about 1.6 $[\textrm{ms}^{-1}],$ whereas the vertical velocity turns out to be of the order of $0.5 10^{-2}$ ms⁻¹. How these structures are formed is not yet clear. Of even more interest for the present work, Zhong et al. [35] recently studied the dynamics of large vortical structures performing laboratory experiments in a smooth and large open channel (i.e., with a large width-to-height aspect), at Reynolds numbers similar to those used in our study. Given the close similarity with our study, we will make explicit reference to Zhong et al. [35] in discussing our results.

In this context, as pioneering shown by Lam and Banerjee [24] and  Pan and Banerjee [36], direct numerical simulations (DNS)—because of the large amount of data and information that generate—can be a valuable tool to probe the physics of turbulent open channel flow and to test hypotheses and theories. The major disadvantage of DNS is the limited value of the Reynolds number that can be achieved, which is typically rather small compared to that of geophysical flows. This has motivated the use of large-eddy simulations (LES) [37, 38] for large-scale geophysical flow simulations, despite the tendency of LES to smoothen out streaky structures [39].

The main goal of the present work is thus to provide a careful statistical analysis of a turbulent open channel flow, in order to understand whether large vortices appear and whether their manifestation may be linked to the presence of streaks at the surface. For such a purpose, we decided to run DNS. The setup and the value of the main parameters of the simulations are consistent with those of similar laboratory experiments [32, 35]. Because of the moderate Reynolds number considered here, the work is intended firstly as a complement to these ones. Furthermore, as in 2D simulations at low Re [40], several shear rates are imposed at the surface via the boundary conditions to assess the possible effect of the shear stress in triggering the growth of large vortices. As mentioned above, the ratio between the amplitude of the rolls and the mean flow is quite small in natural conditions, and therefore, we have performed simulations at high external shear compared to natural configurations, to improve the signal/noise ratio in the hope of better revealing such structures.

2 Methods

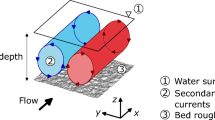
Let us consider a turbulent open channel flow driven by a mean pressure gradient, which is formerly equivalent to study the case of a free surface flow flowing by gravity over an inclined plane. The geometric configuration is represented by a rectangular domain of length ${\hat{L}}_x$ along the streamwise direction, height ${\hat{L}}_z$ and width ${\hat{L}}_y$. We assume:

$$\begin{aligned} {\hat{L}}_x =4 \pi {\hat{h}}, \qquad {\hat{L}}_y = 2 \pi {\hat{h}} \qquad \hbox {and} \qquad {\hat{L}}_z = 2 {\hat{h}}, \end{aligned}$$

(1)

where ${\hat{h}}$ is the half channel height (Fig. 1), symbol ${}^{\hat{\cdot }}$ indicating dimensional quantities. A Cartesian frame is used, where the streamwise, spanwise and normal coordinates are denoted, respectively, ${\hat{x}}$, ${\hat{y}}$ and ${\hat{z}}$. The flow is assumed to be incompressible:

$$\begin{aligned} \frac{\partial {\hat{u}}_j}{\partial {\hat{x}}_j}=0, \end{aligned}$$

(2)

and governed by the Navier–Stokes equations

$$\begin{aligned} \frac{\partial {\hat{u}}_i}{\partial {\hat{t}}} + {\hat{u}}_j \frac{\partial {\hat{u}}_i}{\partial {\hat{x}}_j} = -{1 \over {\hat{\rho }}}\frac{\partial {\hat{p}}}{\partial {\hat{x}}_i} + {{\hat{\nu }}} \frac{\partial ^2 {\hat{u}}_i}{\partial {\hat{x}}_j \partial {\hat{x}}_j}, \end{aligned}$$

(3)

where $\hat{u} \equiv \hat{u}_1$, $\hat{v} \equiv \hat{u}_2$ and $\hat{w} \equiv \hat{u}_3$ are the streamwise, spanwise and normal velocity components and $\hat{p}$ pressure. Fluid density $\hat{\rho }$ and kinematic viscosity $\hat{\nu }$ are assumed to be constant. Periodic conditions are imposed along the spanwise direction ${\hat{y}}$, so to mimic a flow that is contained in a channel but located away from lateral walls and therefore not much influenced by them. Along the streamwise direction ${\hat{x}}$, periodicity is also imposed for the velocity field. For pressure, we assume that there exists a constant mean pressure gradient ${\hat{\Pi }}$ and that pressure perturbations around the mean value are periodic along the streamwise ${\hat{x}}$ and spanwise ${\hat{y}}$ directions. The mean pressure is related here to boundary conditions, but it could be also introduced from constant forces in Eq. (3) representing the gravity component along the bed. A larger length is imposed along ${\hat{x}}$ to take into account the correlation of streamwise vortices [12]. In our simulations, a no-slip condition is imposed at the bottom, i.e., $({\hat{u}}, {\hat{v}}, {\hat{w}})=(0,0,0)$ at $({\hat{x}}, {\hat{y}},-{\hat{h}})$ and the free surface displacements along the vertical direction are assumed to be small with respect to the channel depth. This implies that the vertical velocity component and the vertical surface displacements can be neglected: ${\hat{w}}=0$ at ${\hat{z}}={\hat{h}}$. This rigid-lid approximation eliminates surface waves. While the presence of waves may add important effects [41, 42], this choice is considered as an adequate first order model for the purpose of the present work [43, 44], which considers flow at moderate Reynolds numbers. For streamwise and spanwise velocity components, we impose at the surface ${\hat{z}}={\hat{h}}$ either a free-slip condition (FSC) or an imposed stress condition (ISC). The FSC corresponds to a free surface with no imposed shear (that is, neglecting the shear imposed by the atmosphere). This leads to the following conditions at the free surface:

$$\begin{aligned} {{\hat{\mu }}} \frac{\partial }{\partial {\hat{z}}} {\hat{u}}({\hat{x}}, {\hat{y}}, +{\hat{h}})= 0 \qquad \hbox {and} \qquad {{\hat{\mu }}} \frac{\partial }{\partial {\hat{z}}} {\hat{v}}({\hat{x}}, {\hat{y}}, +{\hat{h}})= 0, \end{aligned}$$

(4)

where ${{\hat{\mu }}}={\hat{\rho }} {{\hat{\nu }}}$ is the dynamic viscosity. For the ISC, we impose a shear ${\hat{\tau }}_{s} \ne 0$ at the free surface plane ${\hat{z}}={\hat{h}}$ which is directed along the stream and results in the following conditions at the free surface:

$$\begin{aligned} {{\hat{\mu }}} \frac{\partial }{\partial {\hat{z}}} {\hat{u}}({\hat{x}}, {\hat{y}}, +{\hat{h}})= {\hat{\tau }}_{s} \qquad \hbox {and} \qquad {{\hat{\mu }}} \frac{\partial }{\partial {\hat{z}}} {\hat{v}}({\hat{x}}, {\hat{y}},+{\hat{h}})= 0. \end{aligned}$$

(5)

Because of the presence of a mean pressure gradient and of an imposed shear at the surface, this flow may be called a turbulent Poiseuille–Couette flow. For the FSC, the global equilibrium of forces between mean pressure gradient ${\hat{\Pi }}$ and the mean shear stress at the bottom wall ${\hat{\tau }}_w$ gives ${\hat{\tau }}_w = -2 {\hat{h}} {\hat{\Pi }}$. For the ISC, the mean pressure gradient is always balanced by a combination of the shear at the bottom ${\hat{\tau }}_w$ and the shear at the surface ${\hat{\tau }}_{s}$, that is, ${\hat{\tau }}_w -{\hat{\tau }}_{s} = -2 {\hat{h}} {\hat{\Pi }}$.

Fig. 1

Sketch of the flow configuration. The fluid domain is rectangular of length ${\hat{L}}_x$, width ${\hat{L}}_y$ and height ${\hat{L}}_z$. The origin is located at $({\hat{x}},{\hat{y}}, {\hat{z}})=(0,0,0)$ so that bottom and surface are situated, respectively, at ${\hat{z}}=-{\hat{h}}$ and ${\hat{z}}={\hat{h}}$, and horizontal coordinates ${\hat{x}}$, ${\hat{y}}$ are positive

The system is solved in dimensionless form by introducing a characteristic length [L] and velocity [U]. The length [L] is based on the half channel height $\hat{h}$ and the velocity on the mean pressure gradient, i.e., $[U] = \sqrt{ \frac{ {\hat{h}} }{\hat{\rho }} \mid {\hat{\Pi }} \mid }$. The following dimensionless variables are thus defined: $(x,y,z) = \frac{1}{[L]}({\hat{x}}, {\hat{y}}, {\hat{z}}), \quad (u,v,w) = \frac{1}{[U]}({\hat{u}}, {\hat{v}}, {\hat{w}}), \quad t = \frac{1}{[L][U]^{-1}} {\hat{t}}, \quad p = \frac{1}{{\hat{\rho }} [U]^{2}} {\hat{p}}, \quad \tau = \frac{1}{{\hat{\rho }} [U]^2} \hat{\tau }.$ In dimensionless form, the computational domain becomes  $x:[0,4\pi ]$,  $y:[0,2\pi ]$  and  $z:[-1,+1]$, and the governing Eqs. (2) and (3) read:

$$\begin{aligned} \frac{\partial u_j}{\partial x_j}=0, \end{aligned}$$

(6)

$$\begin{aligned} \frac{\partial u_i}{\partial t} + u_j \frac{\partial u_i}{\partial x_j} = -\frac{\partial p}{\partial x_i} + \frac{1}{\textrm{Re}} \frac{\partial ^2 u_i}{\partial x_j \partial x_j}. \end{aligned}$$

(7)

where the Reynolds number is defined $\textrm{Re} \equiv \frac{{\hat{h}} \sqrt{ \frac{ {\hat{h}} }{{\hat{\rho }}} |\hat{\Pi }|}}{\nu }$.

Several other Reynolds numbers can be introduced. First, a bulk Reynolds number,

$$\begin{aligned} \textrm{Re}_{\textrm{m}} = 2 u_{\textrm{m}} \textrm{Re}, \qquad \hbox {with a bulk velocity }~~~~ u_m \equiv {1 \over 2} \int ^{1}_{-1} ~ \langle ~ u ~ \rangle ~\textrm{d}z, \end{aligned}$$

(8)

where angular brackets $\langle \rangle$ denote averaging in time and over the homogeneous directions x and y. Second, a friction Reynolds number $\textrm{Re}_\tau \equiv {\hat{h} {\hat{u}}_\tau }/{\hat{\nu }}$, based on the bottom friction velocity ${\hat{u}}_\tau \equiv \sqrt{ {\hat{\tau }}_w \over {\hat{\rho }}}$. For FSC, the dimensionless bottom friction velocity is equal to $u_\tau \equiv {\hat{u}}_\tau /[U] = \sqrt{2}$ so that $\textrm{Re}_\tau =\sqrt{2} \textrm{Re}$. For the ISC, $u_{\tau } =\sqrt{ 2 + \tau _{s} }$ with $\tau _{s} \equiv {{\hat{\tau }}_{s} \over {\hat{\rho }} [U]^2}$ leading to $\textrm{Re}_\tau =\sqrt{2+\tau _{s}} \textrm{Re}$. For a standard Poiseuille flow, the shear at the surface is opposite to that at the bottom $\tau _s =- \tau _{w}$, and thus, $u_{\tau } =1$. Finally, a Reynolds number $\textrm{Re}_{\tau _s} =u_{\tau _s} ~ \textrm{Re}$, based on the friction velocity $u_{\tau _s} \equiv \sqrt{ | ~ \tau _s ~|}$ at the surface.

From a numerical point of view, Eqs. (6) and (7) are solved via a standard pseudo-spectral method [45, 46]. Further details on the numerics can be found in Appendix A.

Table 1 Mean flow parameters: the Reynolds number; the mean bulk velocity $u_{\textrm{m}}$; the associated bulk Reynolds number $\textrm{Re}_{\textrm{m}}$; the measured square of bottom friction velocity $u_{\tau }^{ 2}$; the associated friction Reynolds number $\textrm{Re}_{\tau }$; the square of surface friction velocity $u_{\tau _s}^{ 2}$ ; and the associated surface friction Reynolds number $\textrm{Re}_{\tau _s}$

We present five numerical simulations of the turbulent Poiseuille–Couette flow: a single $\textrm{FSC}$ and four $\textrm{ISC}$ simulations. In each $\textrm{ISC}$ simulation, the imposed shear stress $\tau _s$ corresponds to a given mean streamwise velocity $V_s$ at the surface. These simulations are sorted in ascending order according to the imposed shear stress $\tau _s$. Simulation $\textrm{ISC}_0$ with the imposed velocity value $V_s=0$ is similar, but not identical, to a standard Poiseuille flow since, differently for the standard Poiseuille flow, the stream- and spanwise velocity components can fluctuate at the top surface. $\textrm{ISC}_0$ and $\textrm{ISC}_1$ correspond to a negative shear $\tau _s$ while $\textrm{ISC}_2$ and $\textrm{ISC}_3$ correspond to a positive shear $\tau _s$. The different parameters are presented in Table 1. In order to indicate which real experiment could be directly related to our results, we present in Table 2 the case without shear applied at the surface with typical dimensional units, together with the parameters of the experiments reported in  [35].

Table 2 Flow conditions in dimensional units: ${{\hat{h}}}$ is the height, $\nu$ the kinematic viscosity, ${{\hat{W}}}$ the channel width, ${{\hat{W}}}/{{\hat{h}}}$ the aspect ratio. To make the comparison, we have used the definitions from Zhong et al. [35].Note that, for this reason, the $Re_\tau$ here corresponds to the double of that obtained in Table 1

To run the above simulations, we proceed as follows. We start from a realization of a closed channel flow, we changed the boundary condition at the top wall from a no-slip boundary into a free-slip one (FSC), and we let this new simulation to evolve until a statistically steady state is reached. We then use a single realization of this field as initial condition for the other simulations. For each simulated case, after an initial transient, the flow attained a new statistically steady state, in which statistics can be computed. All the statistics that will be shown below have been checked to be converged with respect to the number of mesh points and time discretization.

3 Results

3.1 Analysis of velocity statistics

Since we are particularly interested in coherent structures, we decided to present most of our results concerning classical statistics in appendix (see appendix B–C). As a brief statement, current results confirm previous analyses carried out at lower Reynolds numbers [24, 36]. For instance, we clearly observe (see Table 1) that, compared to FSC, the mean streamwise velocity $u_m$ decreases for $\textrm{ISC}_0$ and $\textrm{ISC}_1$, and increases for $\textrm{ISC}_2$ and $\textrm{ISC}_3$. The boundary condition at the top surface influences the local gradient of $\langle u \rangle$ near the bottom. Compared to $\textrm{FSC}$, we find larger (respectively, smaller) bottom shear stress when the imposed mean surface velocity $V_s$ is larger (respectively, smaller) than the mean surface velocity of $\textrm{FSC}$. The wall-normal profile of the dimensionless mean shear stress, given by:

$$\begin{aligned} \tau (z)= \frac{1}{\textrm{Re}}~\frac{\textrm{d} \langle u \rangle }{\textrm{d} z} -\langle u' w' \rangle , \end{aligned}$$

(9)

with velocity fluctuations $u_{i}'= u_{i} - \langle ~ u_{i} ~ \rangle$, is expected to be $\tau (z)=\tau _s + (1 - z)$ and $\tau _w=\tau _s + 2$, where $\tau _w \equiv \tau (-1)$ and $\tau _s \equiv \tau (1)$. The agreement of the numerical shear stress with the profile given by Eq. (9) is excellent (see appendix B). This result constitutes also a check of the statistical convergence of our computations. To properly quantify the effects due to viscosity near the two boundaries, we can further analyze the mean stress by decomposing it into its viscous and turbulent part and by rescaling the viscous and turbulent stresses as follows.

Fig. 2

Behavior of viscous and Reynolds stress (both normalized by the total mean shear stress) as a function of the wall-normal coordinate. Panel a: Situation near the bottom wall, as a function of $z^{+}$. Panel b: situation near the surface, as a function of $z^{+}_{s}$. Case $\textrm{FSC}$ is not computed at the surface, and therefore, it is plotted only in panel (a)

For the bottom boundary, the distance from the bottom is measured in wall units as

$$\begin{aligned} z^{+} \equiv \frac{1}{\delta _{\nu }} (z+1) \qquad \hbox {with} \qquad \delta _{\nu } \equiv \frac{1}{\textrm{Re}_{\tau }}, \end{aligned}$$

(10)

with $\delta _{\nu }$ the characteristic length scale of the viscous sublayer. Quantity $z^{+}$ can be viewed as a local Reynolds number based on velocity $u_\tau$ and distance from the wall $(z+1)$. In the same manner, we measure the distance from the surface in surface units as

$$\begin{aligned} z^{+}_{s} \equiv \frac{1}{\delta _{\nu _s}} (1-z), \qquad \hbox {with} \qquad \delta _{\nu _s} \equiv \frac{1}{\textrm{Re}_{\tau _s}} \end{aligned}$$

(11)

with $\delta _{\nu _{s}}$ the viscous sublayer length scale at the surface. In Fig. 2, the ratio $\frac{\textrm{Re}^{-1}}{\tau (z)}~\frac{\textrm{d} \langle u \rangle }{\textrm{d} z}$ (respectively, $-\frac{1}{\tau (z)}~\langle u' w' \rangle$) of the viscous stress (respectively, Reynolds stress ) to mean shear stress $\tau (z)$ is plotted with emphasis on the viscous layer near the bottom (as a function of $z^{+}$) and near the surface (as a function of $z^{+}_{s}$). Near the bottom boundary, these profiles nicely collapse regardless of the imposed $\tau _s$. A similar behavior is found near the surface boundary for the different $\textrm{ISC}$, with the possible exception for $\textrm{ISC}_2$, which corresponds to the smallest imposed shear $\tau _s$. $\textrm{ISC}_2$ is probably a limit case where the surface does not differ much from a solid wall. For $\textrm{FSC}$, the structure of shear is different near the surface since both viscous and Reynolds stress are zero at the surface, (Hence, it is not shown in Fig. 2b.)

These results together with the statistical analysis of mean streamwise velocity and fluctuations (see Appendix B–C) allow us to conclude the following: (i) Considering previous results obtained at lower Re number, no appreciable Reynolds number effect is found on the main statistics of the flow, at least for the range of Reynolds number considered here; (ii) the flow near the surface is similar to a boundary layer, as far as the mean velocity is concerned; (iii) the same conclusion applies to fluctuations statistics; and (iv) the stresses, upon proper rescaling, appear independent of the imposed external shear.

3.2 Flow structures at the bottom boundary

We switch now to the main focus of this work, namely coherent flow structures. Due to the significant shear stress present at the bottom boundary, the near-wall region is dominated by local streamwise vortices and low-speed streaks (velocity deficits). These structures have also been widely observed in laboratory experiments [47, 48] and reproduced in numerical simulations at low Reynolds number [24]. To characterize the near-wall dynamics in the present problem, in Fig. 3 we plot the contour maps of the fluctuations $u'$ of the streamwise velocity on the plane $z^{+} = 5$ at the upper limit of the viscous sublayer. Results are shown for the cases $\textrm{ISC}_0$, $\textrm{FSC}$ and $\textrm{ISC}_3$ only, and only a part of the domain is shown to highlight the structures (in appendix D, the plots of all cases and in the entire domain can be found). Figure 3, as well as the subsequent plots displaying instantaneous fields, presents the general behavior. The flow has similar characteristics for all cases, with the presence of low- and high-speed streaks populating the near-wall region. However, the length and width of these streaks do depend on the applied shear. In particular, the width of streaks decreases with decreasing the bottom shear. A more quantitative indication of the streak separation is obtained from the average Fourier spectrum of the vertical velocity component w as a function of the spanwise wavelength $\lambda _{y}$. This quantity is computed at $z^{+}=5$ and averaged in space (along the x direction) and in time (Fig. 4).

Fig. 3

Fluctuation $u'$ of the instantaneous streamwise velocity, normalized by $\max _{x,y}\!|\,u'|$, on the plane $z^{+}=5$ located near the bottom boundary. Snapshots have been taken after reaching the statistically steady state. Only a portion of the numerical domain is shown to highlight the structures. The color bar is presented in quadratic scale. Top left figure, $\textrm{ISC}_0$; Top right figure, $\textrm{ISC}_3$; Bottom figure, $\textrm{FSC}$

Fig. 4

Fourier spectrum (averaged in time and along the streamwise direction x) of the vertical velocity component as a function of the spanwise wavelength $\lambda _{y}$ expressed in dimensionless outer units (i.e., normalized by the half channel height h). The analysis is performed at the vertical location $z^{+}=5$

For all cases, the spectrum displays a peak that represents a characteristic wavelength $\lambda _y$: 0.53 for $\textrm{ISC}_0$, 0.45 for $\textrm{ISC}_1$, 0.39 for $\textrm{FSC}$, 0.33 for $\textrm{ISC}_2$, 0.28 for $\textrm{ISC}_3$. Streaks exhibit a shorter separation as the shear stress at the bottom boundary is increased (which is in turn a consequence of the increased module of the shear at the top surface). Nevertheless the same quantity normalized by the shear velocity $\langle ~ {\tilde{w}} ~ \rangle /u_{\tau }$ and presented against the wavelength expressed in wall units $\lambda _{y}^{+}\!\! \equiv {1 \over \delta _{\nu }}\lambda _{y}$, displays similar characteristic separation $\lambda _{y}^{+}(z^{+}\!\!=5)\approx 90\div 100$ for all cases, see also Fig. 6.

Fig. 5

Streamwise velocity u normalized by $\max _{y,z}\!|u|$ in the transversal plane $y-z$ at the lower half of channel $z^{+}\in [0,80]$. Top panel, $\textrm{ISC}_0$; Central panel, $\textrm{FSC}$; Bottom panel, $\textrm{ISC}_3$

Fig. 6

Fourier spectrum of the vertical velocity component (averaged in time and along the streamwise direction x, and normalized by the friction velocity) as a function of the spanwise wavelength expressed in wall units, $\lambda _{y}^{+}$. Different positions from the bottom in wall units $z^{+}$ are presented: Left, $z^{+}=5$; Center, $z^{+}=15$; Right, $z^{+}=30$

To get an idea on how these patterns are changing with respect to the distance from the wall, two pictures are presented. First (Fig. 5), the instantaneous streamwise velocity u is plotted in the transverse plane $y-z$. Low-velocity streaks, having a height of about 40–50 wall units, are observed for all cases. Second (Fig. 6), the average Fourier spectrum of $\langle {\tilde{w}} \rangle /u_{\tau }$ is also presented at three positions $z^{+}$ within the buffer layer ($z^+<30$), as a function of wavelength expressed in wall units $\lambda _{y}^{+}\!\!={1 \over \delta _{\nu }}\lambda _{y}$. The separation of streaks does not depend much on the different cases at any particular position $z^{+}$. However, streaks spacing slightly increases with the distance from the wall: $\lambda _{y}^{+}(z^{+}\!\!=5)\approx 90$,  $\lambda _{y}^{+}(z^{+}\!\!=15)=100,$  $\lambda _{y}^{+}(z^{+}\!\!=30)=135$. The $\lambda _{y}$ values for the FSC case agree with those obtained by Kim et al. [49], in particular $\lambda _{y}^{+}\approx 100$ for $z^+\lesssim 10$. Beyond the buffer layer, viscosity effects are negligible and wall units cannot adequately characterize the flow. Hence, the dominant wavelengths $\lambda _{y}^{+}$ computed from the different cases do not collapse when considering planes at $z^{+}\gtrsim 50$. By contrast, for such planes, the wavelength at which the maximum amplitude is reached is similar in terms of $\lambda _{y}$ for the different cases (Fig. 7). Furthermore, for $z^{+}\!\! >50$ spectra are similar and amplitudes do not change much. This confirms that streaks have a height of the order of 50 wall units.

Fig. 7

Fourier spectrum of the vertical velocity component (averaged in time and along the streamwise direction x, and normalized by the friction velocity) as a function of the spanwise wavelength $\lambda _{y}$. Different positions from the bottom in wall units $z^{+}$ are presented: Left, $z^{+}=60$; Center, $z^{+}=70$; Right, $z^{+}=80$

3.3 Flow structures at the free surface

One issue concerns the interaction of turbulence with the free surface and the effect of the shear imposed at the surface on the flow structures close to the surface. In Fig. 8 (and in appendix D), we present the fluctuations $u'$ of the streamwise velocity component in the horizontal plane located at $z^{+}_{s}=5$ (in surface units) (but for FSC, for which the plot is at $\frac{1-z}{\delta _{\nu }} =5$). Streak-like patterns are clearly visible for $\textrm{ISC}_0$ and $\textrm{ISC}_3$ (see Fig. 8 top and bottom, respectively), and also $\textrm{ISC}_1$. For $\textrm{FSC}$ (see Fig. 8 center) and $\textrm{ISC}_2,$ a streak-like pattern is not observed. This suggests that flow streaks are likely to appear only when the shear exceeds a critical value, as previously found by [24]. To quantify these observations, we compute (i) the average Fourier spectrum of the vertical velocity component as a function of the spanwise wavelength $\lambda _{y}$ (see Fig. 9 left) and (ii) the average Fourier spectrum of the vertical velocity component normalized by the surface shear velocity $u_{\tau _s}$ as a function of the wavelength in surface units $\lambda _{y,s}^{+}\!\!={1 \over \delta _{\nu _s}}\lambda _{y}$ at $z^{+}_{s}\!\!=5$ (see Fig. 9 right). One observes a dominant wavelength only for $\textrm{ISC}_0,$ $\textrm{ISC}_1$ and $\textrm{ISC}_3$ at $\lambda _y=0.45,~0.57,~0.48$, respectively. This wavelength corresponds to a value $\lambda _{y,s}^{+}=80$, similar to the value obtained for the bottom streaks. As a consequence, elongated structures of streamwise vorticity appear at the surface for $\textrm{ISC}_0$, $\textrm{ISC}_1$ and $\textrm{ISC}_3$, but not for $\textrm{FSC}$ and $\textrm{ISC}_2$.

Fig. 8

Instantaneous contour maps of the fluctuation $u'$ of the streamwise velocity, normalized by $\max _{x,y}\!|\,u'|$, at the horizontal plane $z^{+}_{s}=5$, in surface units (but for $\textrm{FSC}$, in which the plot is located at $\frac{1-z}{\delta _{\nu }}$ =5). The color bar is presented in quadratic scale. Top panel, $\textrm{ISC}_0$; Central panel, $\textrm{FSC}$; Bottom panel, $\textrm{ISC}_3$. Instantaneous snapshots are taken after a statistically steady state is reached

Fig. 9

Left panel: Average Fourier spectrum of the vertical velocity component as a function of the spanwise wavelength $\lambda _{y}$ for $\textrm{ISC}$. Right panel: Average Fourier spectrum of the vertical velocity component normalized by the surface friction velocity as a function of the spanwise wavelength in surface units $\lambda _{y,s}^{+}$. This analysis is performed at the vertical location $z^{+}_{s}=5$

3.4 Horizontal velocity divergence at the surface

To characterize further the interaction between the flow structures in the bulk of the channel and the free surface, we compute the horizontal flow divergence:

$$\begin{aligned} \nabla _{H}\!\cdot {\textbf{u}}\equiv \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y} \end{aligned}$$

(12)

at the surface, i.e., at $z=1$. The two-dimensional flow divergence is associated with the exchange of mass between the surface and the bulk of the flow [50]. Regions of positive horizontal divergence are regions of local flow expansion. These are due to incoming upwellings impinging on the free surface. Regions of negative horizontal divergence are regions of local flow compression, likely responsible for subsequent downwelling events. Contour maps of the instantaneous distribution of $\nabla _{H}\!\cdot {\textbf{u}}$ for the different flow cases are shown in Fig. 10. When the shear at the surface is weak ($\textrm{ISC}_2$) or vanishing ($\textrm{FSC}$), upwellings (red regions) and downwellings (blue regions) are lumps of positive or negative $\nabla _{H}\! \cdot {\textbf{u}}$ with no specific spatial orientation. For $\textrm{ISC}_0$, $\textrm{ISC}_1$ (not shown for brevity) and $\textrm{ISC}_3$ in which a large shear is present, the situation changes drastically: Upwellings and downwellings appear as longitudinal structures. These motions are hence distorted by the shear applied at the surface and tend to align with high- and low-speed streaks. They are also weaker than for $\textrm{ISC}_2$ (not shown for brevity) or $\textrm{FSC}$. Therefore, the presence of a shear is found to disrupt upwellings and downwellings (large-scale flow events). This in turn allows the presence of streaks at the surface. To fully characterize the flow structure near the upper surface, the concept of the flow compressibility is introduced. A dimensionless compressibility factor [51], linked to the local flow divergence, can be computed on $x-y$ planes at different z locations:

$$\begin{aligned} C=\frac{\left\langle ~ \left( ~\nabla _{H}\!\cdot {\textbf{u}}~\right) ^2 ~ \right\rangle }{\left( \left\langle \frac{\partial u}{\partial x}^2\right\rangle + \left\langle \frac{\partial u}{\partial y}^2\right\rangle + \left\langle \frac{\partial v}{\partial x}^2\right\rangle + \left\langle \frac{\partial v}{\partial y}^2\right\rangle \right) }. \end{aligned}$$

(13)

This factor is nonzero because of the 3D incompressibility of the flow. Figure 11 shows its profile for the top half of the domain. The free-shear case reproduces the result recently discussed by [50]. The value observed at the surface ($z=1$) in these simulations is $C\simeq 0.6$, which is higher than that found in experiments and numerical simulations considering the free-shear surface of an otherwise 3D incompressible turbulent isotropic flow [52]. In this case, the compressibility factor turns out to be $C\approx 0.5$ [52]. The value at the surface is close but higher also than the theoretical value $C=0.5$ that characterizes the strong compressible Kraichnan flow [53, 54]. This indicates an important compressibility effect in the surface case, even though it seems that time correlations of real flows tend to weaken the compressibility effect with respect to the Kraichnan model [55]. However, this is still a matter of debate, and the role of flow time correlations on the flow compressibility, and on the corresponding flow mixing, should be clarified better [56].

Fig. 10

Instantaneous contour maps of the horizontal velocity divergence $\nabla _{H}\cdot {\textbf{u}}$ at the surface normalized by $\max _{x,y}\!|\nabla _{H}\cdot {\textbf{u}}|$ for the different cases. The color bar is displayed in quadratic scale. Top panel: $\textrm{ISC}_0$; Central panel, FSC; Bottom panel, $\textrm{ISC}_3$. Instantaneous snapshots are taken after a statistically steady state is reached

Fig. 11

Compressibility factor C (13) on the top half of the domain for all the simulated cases

The compressibility factor decreases to a value near $C\approx 0.2$ in the bulk of the channel. This value is close to the value 1/6 which is expected for a two-dimensional cut of a three-dimensional homogeneous, isotropic flow.

The imposition of a shear (both positive or negative) does not modify the value of C in the channel core ($z=0$) but strongly reduces its value at the surface. Moreover, the value is decreased also in a large region below the surface $0.5<z<0.9$. This should be related to the distortion of the upwelling and downwelling motions operated by shear. The ${\text{ISC}}_2$ case is the only one in which the effect is smaller. In this case, the value of C is almost everywhere 0.2 as in the bulk. The results show a two dimensionalization of the flow in the region below the surface in the presence of shear. Since streaks are quasi-2D structures, this finding is consistent with the fact that streaks are only observed when a sufficiently high shear is present (otherwise they are not observed).

3.5 Flow structures inside the channel

We investigate now whether a shear applied at the surface promotes or hinders the formation of large-scale structures inside the bulk. Away from the boundaries, the formation of recirculation cells may be identified by using the vertical velocity w in the transversal $y-z$ plane (Fig. 12, left column) and in horizontal $x-y$ plane (Fig. 12, right column). Some difference between cases can be pointed out. For $\textrm{FSC}$ (and $\textrm{ISC}_2$, not shown here), large-scale structures generated in the central region of the channel can extend up to the surface (central panel in Fig. 12). They consist of adjacent upwelling and downwelling structures alternating in space. Without a shear (or with a small positive one), these large-scale vertical motions occur with a rather random horizontal spatial distribution, as highlighted in Fig. 12 (right column). A negative shear at the surface of the channel promotes the formation of smaller rollers close to the surface, with the consequent weakening of the large-scale structures (see case $\textrm{ISC}_0$, top panel in Fig. 12). The results obtained in the $\textrm{ISC}_3$ case (bottom panel in Fig. 12) might suggest that a strong positive shear increases the persistence along the stream of large-scale rolls.

Fig. 12

Left column: Instantaneous vertical velocity w normalized by $\max _{y,z}\!|w|$ in a transversal plane $y-z$. Right column: Instantaneous vertical velocity w normalized by $\max _{x,y}\!|w|$ at the center of the channel, i.e., in the horizontal plane $z=0$. Top panels, $\textrm{ISC}_0$; Central panels, $\textrm{FSC}$; Bottom panels, $\textrm{ISC}_3$

Fig. 13

Average Fourier spectrum of the vertical velocity component normalized by friction velocity as a function of the spanwise wavelength $\lambda _{y}$ at $z=-0.5$ (left panel), the center of the channel, $z=0$, (central panel) and at $z=0.5$ (right panel)

To quantify these observations, we compute the average Fourier spectrum (on a $x-y$ plane) of the vertical velocity component as a function of the spanwise wavelength $\lambda _{y}$. Results are shown in Fig. 13 for three different vertical positions ($z=-0.5$, $z=0$ and $z=0.5$). Regardless of the vertical location of planes, the dominant wavelength for the case of surface positive shear ($\textrm{ISC}_2$ and $\textrm{ISC}_3$) is at $\lambda _y \sim 2$, i.e., the channel height. In addition, a positive shear seems to increase the amplitude of the large-scale rolls. For negative shear cases ($\textrm{ISC}_0$ and $\textrm{ISC}_1$), the spectrum shows that the amplitude is reduced compared to the previous two cases and the optimal length is also less pronounced as we approach the wall or the free surface ($z=-0.5,~z=0.5$). These evidences corroborate the existence of some large-scale coherent dynamics, at least of modest intensity because of the relative importance of the peak in the Fourier spectrum. In order to highlight whether the vertical movements are correlated in the horizontal direction, the vertical velocity is visualized in the horizontal plane at the center of the channel (Fig. 12 right column). From these results, it is possible to argue that large-scale structures might be also more correlated when a sufficient and positive shear is imposed at the surface ($\textrm{ISC}_3$), indicating that a strong favorable wind triggers the formation of large-scale vortices, as in similar hydrodynamic unstable shear flows, i.e., Couette flows. Yet, the streamwise correlation remains poor, and results cannot be considered conclusive.

4 Discussion and conclusions

We have carried out a numerical analysis of the dynamics of vortical structures in turbulent open channel flows. This issue, which is of great fundamental interest, is also relevant for river dynamics, for which experimental and numerical studies seem to highlight the presence of large elongated rolls, whose size in the cross-plane scales with the river height h, and whose length can be several times h. Our numerical experiments have been made with parameters that can be considered similar to the recent laboratory experiments by Zhong et al. [35]. This numerical study complements those laboratory experiments, since numerical simulations have the advantage of providing all possible information with great accuracy. We have carried out different simulations choosing different shears applied at the surface, which mimic the presence of a wind, either opposite or along the streamwise direction. It is worth emphasizing that our simulations are made in idealized conditions and comparison with field experiments, always at much higher Reynolds numbers, must be taken cum grano salis. We discuss here our main points.

(i) Streaks at the surface are found only when a sufficient shear is imposed at the surface, and the separation of these streaks is found to be of the order of $50\div 100 \delta _{\nu }$. In this context, our results confirm and extend previous results obtained at lower Re [36], hence indicating, at least for the considered range of Reynolds numbers, very small (if any) Reynolds number effect. For the range of parameters investigated here, the observed streamwise vortices seem to scale in inner units, as those encountered in near-walls flows.

(ii) The boundary layer at the bottom is almost unaffected by the shear at the surface. Therefore, an external shear does not seem to be responsible for important changes in the near-wall region (river bed).

(iii) We have investigated the dynamics of upwelling and downwelling motions, and the influence of the shear on them. Upwelling and downwelling motions are always present along the full height of the channel, but the applied shear can modify their dynamics: While in the free shear or in the presence of a very low one, these motions are randomly organized in the horizontal plane, in the other cases, these motions are more regular and oriented, and streaks are also more visible.

(iv) Our analysis indicates that the streaky structures, and in particular their size, are sensitive to varying the amplitude and the direction of the shear. We have also tried to understand whether the structures, present along the vertical direction, extend also for several channel height in the streamwise one. A strong positive shear seems to trigger the horizontal organization of large rolls. Yet this result cannot explain the persistency of such vortices found in several in situ experiments. When a negative shear is present, the vertical structures appear not to be well correlated in the streamwise direction. That seems to imply that a low negative shear is probably necessary to deform the large upwelling and downwelling movements, but is not sufficient to justify the presence of large-scale vortices. It is worth noting that the general case for in situ experimental observations would be of negative shear. In any case, we have not found in our simulations sufficient signature of large elongated roll in smooth open channels due to shear. Those large elongated rolls found by other authors are not produced by simple shear at the surface, at least in the conditions considered here. Large rolls are in any case of small amplitude, an occurrence that makes their observation somehow tricky. Our results are in agreement with recent laboratory experiments [32, 35], in which authors measured a small correlation in the vertical and longitudinal plane, and linked it to large streamwise vortices. The experiments were performed at similar Reynolds numbers, but the domain was longer, possibly allowing for the development of larger rolls. Our analysis of the correlation in the horizontal plane suggests that these results cannot be considered conclusive for the existence of coherent large rolls.

According to our findings, the presence of a shear seems a necessary, but not sufficient, condition. Hence, large-scale structures should arise via some other physical mechanisms. The first idea is to invoke the effect of very high Re number [15]. Unfortunately, a parametric study of a well resolved long open channel at high Reynolds is prohibitive from the computational point of view. Stratification may trigger also large convection rolls, but in hydraulic flows it would be stable in most of the cases, making this hypothesis improbable. A promising perspective is to look at the possible effect of surface waves, which are known to be responsible for large vortices, as the Langmuir circulation in oceans [57, 58]. We plan to make some numerical simulations with a moving free surface, instead of using the rigid-lid approximation to analyze the effect of waves on the fluid motion.

Appendices

A Numerical method

The Navier–Stokes equations are solved applying the no-slip condition at the bottom, $(u,v,w)=(0,0,0)$ at $z=-1$. At the top surface $z=1$, the rigid-lid condition becomes $w=0$ and

$$\begin{aligned} \frac{\partial }{\partial z} u(x, y, +1)= 0, \qquad \qquad \frac{\partial }{\partial z} v(x, y, +1)= 0, \qquad \qquad{} & {} \hbox {for ~ FSC}, \end{aligned}$$

(14)

$$\begin{aligned} \frac{\partial }{\partial z} u(x, y, +1)= \textrm{Re}~\tau _{s}, \qquad \qquad \frac{\partial }{\partial z} v(x, y, +1)= 0, \qquad \qquad{} & {} \hbox {for ~ ISC}. \end{aligned}$$

(15)

This set of governing equations is discretized using a pseudo-spectral method [45, 46], which is based on transforming the field variables into wavenumber space, through Fourier representations for the (homogeneous) periodic directions x and y and Chebyshev polynomials $T_{n_z}(z)=\cos (n_z \arccos (z))$ for the non-homogeneous wall-normal direction z

$$\begin{aligned} u_i(x,y,z;t) \equiv \sum _{|n_x|} \sum _{|n_y|} \sum _{|n_z|} {\tilde{u}}_i(k_x,k_y,n_z;t) T_{n_z}(z)\,e^{~\textrm{i}(k_x x + k_y y)}. \end{aligned}$$

(16)

The summation is performed over the integer $n_x$, $n_y$ and $n_z$, which vary in the range $-N_x/2+1 \le n_x \le N_x/2$, $-N_y/2+1 \le n_y \le N_y/2$ and $0 \le n_z \le N_z$ where $N_x$, $N_y$ and $N_z-1$ are powers of two. The associated spatial grid points are, respectively, $N_x$, $N_y$ and $N_z$ along the x, y and z directions

$$\begin{aligned}&x(i) = (i-1) \, \frac{L_x}{N_x-1}{} & {} i = 1,2,3,...,N_x \end{aligned}$$

(17a)

$$\begin{aligned}&y(j) = (j-1) \, \frac{L_y}{N_y-1}{} & {} j = 1,2,3,...,N_y \end{aligned}$$

(17b)

$$\begin{aligned}&z(k) = \cos \left( \frac{k-1}{N_z-1} \, \pi \right){} & {} k = 1,2,3,...,N_z . \end{aligned}$$

(17c)

Time advancement of the governing equations is achieved by a combination of an implicit Crank–Nicolson scheme for the viscous terms and an explicit Adams–Bashforth scheme for the convective nonlinear terms. As commonly done in pseudo-spectral methods, the convective nonlinear terms are first computed in physical space and then transformed in the wavenumber space using a de-aliasing procedure based on the 2/3 rule [45]; derivatives are evaluated directly in the wavenumber space to maintain spectral accuracy. Further details about the numerical approach can be found in the literature [24, 46]. As far as computational time is concerned, each of the 5 simulations has taken about 4 weeks using 256 cores on an Intel PC cluster. A summary of the main simulation parameters is given in Table 3

Table 3 Summary of the main simulation parameters: the mean streamwise velocity at the surface $V_s$; the Reynolds number; the grid resolution in the streamwise direction in wall units $\Delta x^+=\Delta x \times {\text{Re}}_{\tau }$, in the spanwise direction $\Delta y^+=\Delta y \times {\text{Re}}_{\tau }$ and in the normal wall direction $\Delta z^+=\Delta z \times {\text{Re}}_{\tau }$ (minimum and maximum values are indicated); the number of points along each direction, $N_x\times N_y\times N_z$; the time step $\Delta t$

B Mean velocity and stress

In Fig. 14a, we present the wall-normal behavior of the mean streamwise velocity profile $\langle ~ u ~ \rangle$ for all cases. Although the behavior of the mean streamwise velocity for the case $\textrm{FSC}$ is similar to that observed in one-half of a turbulent Poiseuille channel flow, there exists a difference between the two cases: Vorticity is normal to the surface in $\textrm{FSC}$ but not at the center of a turbulent Poiseuille flow. For $\textrm{ISC}$, we observe (Fig. 14c) that the top boundary condition enables momentum transfer by diffusion at the free surface (boundary layer behavior close to the free surface). At the free surface, the rigid-lid condition imposes a zero Reynolds stress (Fig. 14d) through the prescription of $w^{\prime }=0$. The mean streamwise velocity profile (see Fig.  15) is computed in wall units as:

$$\begin{aligned} u^{+} \equiv \frac{\langle ~ u ~\rangle }{u_\tau } =\frac{\textrm{Re}~~}{\textrm{Re}_{\tau }} \langle ~ u ~\rangle . \end{aligned}$$

(18)

For all the cases, within the viscous sublayer ($z^{+}<5$), $u^{+}$ collapses onto the linear behavior $u^{+}=z^+$ prescribed by the law of the wall. In the core region ($z^{+}>30$), the logarithmic law is satisfied up to $40\%$ of the half channel height h, although with slightly different values for the von Kármán constant $\kappa$ and translation constant C for the various cases, as verified through data fitting. The behavior is similar to what was found previously [24] at lower Reynolds number. In addition, there is no clear trend for the values of $\kappa$ and C for increasing $u_{\tau }$. For $\textrm{FSC}$, we found $\kappa =2.5^{-1}$ and $C=4.94$: The value of $\kappa$ is the same obtained by [24], and their constant $C=5.1$ is very slightly larger. That is probably within the combined error but it may also be due to the fact that present simulations are at a higher Re.

Fig. 14

a Mean streamwise velocity profile $\langle ~ u ~ \rangle$; b mean shear stress $\tau$; and its decomposition in viscous (c) and Reynolds stresses (d). All cases are shown

Fig. 15

Wall-normal behavior of the mean streamwise velocity profile $\langle u^{+} \rangle$ for the different cases at $\textrm{Re}=180$ (symbols). The best fit to our data is also shown by the dash dotted lines. Note that the classical law of the wall [16] usually prescribes a slope $\kappa ^{-1}=0.41^{-1}=2.44$ and an offset $C=5.2$

Fig. 16

Mean velocity profile $u^{+}_{s}$ computed from the surface boundary for the different ISC cases at $\textrm{Re}=180$: a ISC0, b ISC1, c ISC2, d ISC3. The behavior of the law of the wall is also shown for comparison (with parameters adjusted to fit to our data)

We also characterize the mean streamwise velocity profile close to the free surface when a shear stress is applied ($\textrm{ISC}$ cases). To do this, the surface mean velocity $\langle ~ u(1) ~\rangle \equiv F_{s}$ is subtracted to the total mean velocity profile. The velocity given by:

$$\begin{aligned} u^{+}_{s} \equiv \frac{\textrm{abs}\big (\langle ~ u ~\rangle -V_s\big )}{u_{\tau _s}}. \end{aligned}$$

(19)

which is measured in surface units (Fig. 16). The velocity profiles follow the law of the wall with characteristic constants that depend on the flow configuration. This means that the velocity profile can be approximated in the viscous sublayer, respectively, in the core by

$$\begin{aligned} u^{+}_{s} = z^{+}_{s} \qquad \hbox {respectively} \qquad u^{+}_{s} = \frac{1}{\kappa } \ln z^{+}_{s} + C. \end{aligned}$$

(20)

The viscous sublayer at the surface ($0 \le z^{+}_{s}$ $\lesssim$$\;3$) is smaller than its counterpart at the bottom. Similarly, the characteristic coefficients $\frac{1}{\kappa }$ and C are generally smaller than their counterparts at the bottom, but no clear trend is observed. From the above considerations, we conclude that the flow near the surface is similar to a boundary layer as far as the mean velocity is concerned.

C Statistics of velocity fluctuations

Regarding fluctuations statistics, we focus on the root mean square (RMS) $u_{i~\textrm{rms}} \equiv \sqrt{\left\langle ~ u_{i}'\; ^2 ~ \right\rangle }$ of the velocity component $u_{i}$. The wall-normal behavior of $u_{i~\textrm{rms}}$ for the three fluctuating velocity components normalized by the friction velocity $u_{\tau }$ is shown in Fig. 17 for a region close to the bottom wall $0<z^+<80$ (the upper limit being about $z\approx 0.4$). As commonly observed in wall-bounded turbulence, the values of $u_{\text{rms}}$ are larger than the corresponding values of $v_{\text{rms}}$ and $w_{\text{rms}}$. For all cases, the $u_{\textrm{rms}}/u_{\tau }$ collapses for $z^{+}\le 15$ and reaches its largest value for $z^{+}\simeq 15$, while the $v_{\text{rms}}/u_{\tau }$ and $w_{\text{rms}}/u_{\tau }$ profiles do not collapse. However, they all agree with the analytic form imposed by the no-slip condition near the bottom boundary [16]

$$\begin{aligned} u_{\text{rms}}=b_1 z,~~~~v_{\text{rms}}= b_2 z,~~~w_{\text{rms}}= c_3 z^2, \end{aligned}$$

(21)

where $b_1$, $b_2$, $c_3$ are constant coefficients. Fluctuations of the three velocity components are also significant within the logarithmic layer [24, 49], where they increase monotonically as the imposed shear increases. They remain proportional to the turbulent kinetic energy with a constant of proportionality that does not change with $u_{\tau }$.

Fig. 17

Root mean square of a streamwise, b spanwise, c wall-normal velocities, normalized by the friction velocity $u_{\tau }$ and computed near the bottom boundary

Fig. 18

Root mean square of a streamwise, b spanwise, c wall-normal velocities normalized by the friction velocity $u_{\tau _s}$ (respectively, $u_{\tau }$) for ISC (respectively, FSC), computed near the top surface. The curves of ISC (respectively, FSC) are plotted against $z^{+}_{s}$ (respectively, $(1-z) / \delta _{\nu }$). All cases are shown, but $\textrm{ISC}_0$

A similar analysis can be done near the top surface ($0<z_s^+<80$). In that region (see Fig. 18), $u_{\textrm{rms}}/u_{\tau }$ profiles of cases $\textrm{ISC}_0$, $\textrm{ISC}_1$ and $\textrm{ISC}_3$ reach a local peak at the surface, where momentum is injected by the imposed shear. This is an expected behavior, since a Taylor expansion of the various stresses near the top boundary implies that

$$\begin{aligned} u_{rms}=a'_1 + c'_1 z^2,~~~~v_{rms}=a'_2 + c'_2 z^2,~~~w_{rms}= b'_3 z, \end{aligned}$$

(22)

where $a'_1$, $a'_2$, $b'_3$, $b'_3$ and $c'_2$ are constant coefficients. Similar to what was observed for the bottom boundary, fluctuations are also significant within the logarithmic layer. The rms fluctuations remain proportional to the turbulent kinetic energy as for the bottom wall, yet the constant of proportionality varies with $u_{\tau }$ for the free surface.

D Structures

In this section, we present some qualitative pictures of the flow structure observed at horizontal planes located near the bottom wall (Fig. 19) and near the top surface (Fig. 20).

Fig. 19

Fluctuation $u'$ of the instantaneous streamwise velocity, normalized by $\max _{x,y}\!|\,u'|$, at the horizontal plane $z^{+} = 5$ located near the bottom boundary. Instantaneous fields are taken at one representative time inside the statistically steady regime for a $\textrm{ISC}_0$; b $\textrm{ISC}_01$; c $\textrm{FSC}$; d $\textrm{ISC}_2$. e $\textrm{ISC}_3$. Color bar is presented in quadratic scale

Fig. 20

Fluctuation $u'$ of the instantaneous streamwise velocity, normalized by $\max _{x,y}\!|\,u'|$, at the horizontal plane $z^{+}_{s}=5$ located near the surface (except for the case FSC, for which the plot is located at $\frac{1-z}{\delta _{\nu }} =5$). Instantaneous fields are taken at one representative time inside the statistically steady regime for a $\textrm{ISC}_0$; b $\textrm{ISC}_01$; c $\textrm{FSC}$; d $\textrm{ISC}_2$; e $\textrm{ISC}_3$. Color bar is presented in quadratic scale