1 Introduction

A comprehensive knowledge of open-channel flows (OCFs) is required to address traditional engineering problems (e.g., hydraulic resistance and sediment transport) as well as more recent challenges, such as the preservation of the biodiversity of aquatic ecosystems, or the renaturalisation of watercourses highly impacted by human activity.

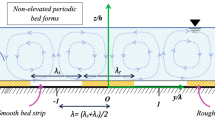
Despite the often used conventional assumption of two-dimensional flow, time-averaged flow fields in open channels are generally heterogeneous in space, leading to significant changes in the flow dynamics. Common examples of heterogeneous flow fields in OCFs are: (i) flow alterations near the bed induced by roughness elements; and (ii) secondary currents (SCs), streamwise time-averaged rotational motions of size comparable to the flow depth (Fig. 1). Based on classical Prantl’s classification, SCs can be divided into two categories: (i) SCs of the first kind generated by spatial gradients of the time-averaged velocity field; and (ii) SCs of the second kind induced by turbulence anisotropy. Given that OCFs are generally turbulent, both types of SCs can emerge and interact. In the case of uniform OCF in a prismatic rectangular channel, SCs form at the channel sidewalls due to turbulence anisotropy [e.g., 9, 10, 21]. The strength of these SCs weakens as we move away from the sidewalls, where the flow gradually becomes spatially homogeneous. In addition, SCs can also be triggered by spanwise bed heterogeneities. In their simplest form, these heterogeneities apply exclusively across the flow while being homogeneous along the channel, e.g., streamwise sediment ridges or strips of varying roughness, generating SCs of the second kind [4, 9, 19, 23, 24]. However, they may also assume more complex forms, such as discontinuous ridges, vegetation patches or random bed elevation distributions [1,2,3, 6, 7, 15, 17, 20, 22]. The generation mechanisms of SCs induced by multiscale roughness patterns remains poorly understood. Depending on the roughness characteristics and flow conditions, roughness-induced SCs may appear as SCs of the first kind, of the second kind, or a combination of the two.

Fig. 1
figure 1

Simplified representation of SCs in rough-bed open-channel flow

Full size image

If the flow is heterogeneous in space, time-averaging may be supplemented by spatial averaging within thin slabs parallel to the mean bed, allowing to quantify the contribution of mean flow spatial variations to the total fluid stresses, and to other flow quantities emerging in double-averaged hydrodynamic equations [e.g., 13, 14]. Thus, a generic time-averaged flow quantity \(\bar{\theta }\) (overbar indicates time averaging) can be then decomposed as \(\bar{\theta }=\langle \bar{\theta }\rangle +\tilde{\bar{\theta }}\), where angular brackets denote spatial averaging and tilde indicates spatial fluctuations. Extending this decomposition to the ith component of the time-averaged velocity vector \(\bar{u}_i=\langle \bar{u}_i\rangle +\tilde{\bar{u}}_i\), we may define dispersive fluid stresses \(-\rho \langle \tilde{\bar{u}}_i \tilde{\bar{u}}_j \rangle\) due to flow spatial heterogeneties, where i and j are notation indexes and \(\rho\) is fluid density. It follows that the total kinetic energy of the flow \(0.5\langle \overline{u_i u_i}\rangle\) per unit fluid mass (summation over repeated indices is implied throughout the paper) can be partitioned as:

$$\begin{aligned} \frac{1}{2} \langle \overline{u_i u_i} \rangle = \underbrace{\frac{1}{2} \langle \bar{u}_i \rangle \langle \bar{u}_i\rangle }_{\text {DMKE}} + \underbrace{\frac{1}{2} \langle \tilde{\bar{u}}_i \tilde{\bar{u}}_i\rangle }_{\text {DKE}} + \underbrace{\frac{1}{2} \langle \overline{u'_i u'_i} \rangle }_{\text {SATKE}} \end{aligned}$$
(1)

where \(0.5\langle \bar{u}_i \rangle \langle \bar{u}_i\rangle\) is double-mean kinetic energy (DMKE), \(0.5\langle \tilde{\bar{u}}_i \tilde{\bar{u}}_i\rangle\) is dispersive kinetic energy (DKE), \(0.5\langle \overline{u'_i u'_i} \rangle\) is spatially-averaged turbulent kinetic energy (SATKE), and prime denotes time fluctuations of the instantaneous velocity \(u_i\) relative to its time-averaged value, i.e., \(u_i=\bar{u}_i+u'_i\). Double-averaged conservation equations for momentum, fluid stresses and kinetic energy have been proposed for the cases of fixed [13, 25] and mobile bed conditions [14, 16].

In general, dispersive fluctuations \(\tilde{\bar{u}}_i\) include contributions from all types of spatial heterogeneities of the mean flow, without distinction. To overcome this limitation, Nikora et al. [15] proposed a spatial averaging procedure to partition the contributions of bed roughness and SCs to dispersive fluctuations. In this paper, their methodology is expanded by deriving double-averaged conservation equations for momentum, fluid stresses and kinetic energy. The proposed equations will be used to analyse energy exchanges in a simulated flow over a self-affine rough bed with SCs [15]. In Sect. 2, the spatial averaging methodology is outlined. In Sect. 3, the double-averaged continuity equations and conservation equations for momentum and kinetic energy accounting for the separate contributions of bed roughness and SCs are presented. Section 4 will be dedicated to the analysis of the numerical data set using the newly proposed equations. Finally, the main outcomes of the work are summarised in Sect. 5.

2 Spatial averaging

In this section, we propose an approach for the partitioning of dispersive fluctuations due to bed roughness and SCs based on two spatial averaging schemes. The flow is assumed to be uniform and fully developed, for which SCs do not change their characteristics in the streamwise direction. We use a right-hand coordinate system where the spatial coordinate \(x_i\) in the ith direction is denoted as \(x_1=x\), \(x_2=y\) and \(x_3=z\) in the streamwise, spanwise and bed-normal directions, respectively (Fig. 2).

2.1 Methodology

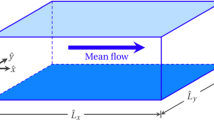
Spatial averaging is first applied within a ‘global’ domain (Fig. 2a), with a vertical thickness \(L_z\) sufficiently small to capture the strong vertical gradients of the flow, and a horizontal extent \(L_x {\times } L_y\) larger than the characteristic dimensions of both roughness and SCs. This procedure follows the double-averaging approach described by Nikora et al. [13, 14]. Superficial and intrinsic global spatial averages of \(\bar{\theta }\) are defined as, respectively:

$$\begin{aligned} \langle \bar{\theta }\rangle ^s =\frac{1}{V_0}\int _{V_0}{\bar{\theta }\gamma \text {d}V}{} && {} \text {and}{} && {} \langle \bar{\theta }\rangle =\frac{1}{V_f}\int _{V_0}{\bar{\theta }\gamma \text {d}V} =\frac{1}{V_f}\int _{V_f}{\bar{\theta }\text {d}V}, \end{aligned}$$
(2)

where \(V_0\) is the volume of the global averaging domain, \(\gamma\) is 1 within the fluid phase and 0 within the solid phase, \(\text {d}V\) is an infinitesimal volume and \(V_f=\int _{V_0}{\gamma \text {d}V}\) is the volume of fluid within the averaging domain of volume \(V_0\). Superficial and intrinsic averages are linked as \(\langle \bar{\theta }\rangle ^s=\phi \langle \bar{\theta }\rangle\), where \(\phi =V_f/V_0\) is the roughness geometry function [12].

Fig. 2
figure 2

a Global (in yellow) and b roughness-scale (in blue) averaging domains. Shape and sizes of the domains may vary

Full size image

Then, we define a \(l_x\times l_y\times l_z\) ‘roughness-scale’ averaging domain (Fig. 2b) with the same streamwise (\(l_x=L_x\)) and vertical (\(l_z=L_z\)) extents as the global averaging domain, but with a spanwise size \(l_y\) much smaller than the spanwise size of the SCs. Similar to Eq. (2), superficial and intrinsic spatial averages within the roughness-scale averaging domain are defined as, respectively:

$$\begin{aligned} \langle \bar{\theta }\rangle _r^s =\frac{1}{V_0^r}\int _{V_0^r}{\bar{\theta }\gamma \text {d}V}{} && {} \text {and}{} && {} \langle \bar{\theta }\rangle _r =\frac{1}{V_f^r}\int _{V_0^r}{\bar{\theta }\gamma \text {d}V} =\frac{1}{V_f^r}\int _{V_f^r}{\bar{\theta }\text {d}V}, \end{aligned}$$
(3)

where \(V_0^r\) is the volume of the roughness-scale averaging domain and \(V_f^r=\int _{V^r_0}{\gamma \text {d}V}\) is the volume of fluid within \(V_0^r\). Once again, superficial and intrinsic averages may be linked as \(\langle \bar{\theta }\rangle _r^s=\phi _r\langle \bar{\theta }\rangle _r\), where \(\phi _r=V_f^r/V_0^r\) is the roughness geometry function defined for the roughness-scale averaging domain.

Spatial averages within the global (Eq. 2) and roughness-scale (Eq. 3) averaging domains are connected through additional spatial averaging in the spanwise direction (\(\langle \ldots \rangle _y\)) as

$$\begin{aligned} \langle \bar{\theta }\rangle ^s = \langle \langle \bar{\theta }\rangle _r^s\rangle _y = \frac{1}{L_y}\int _{L_y}{\langle \bar{\theta }\rangle _r^s\text {d}y}. \end{aligned}$$
(4)

Global and roughness-scale averaging lead to the decompositions \(\bar{\theta } = \langle \bar{\theta }\rangle + \tilde{\bar{\theta }}\) and \(\bar{\theta } = \langle \bar{\theta }\rangle _r + \tilde{\bar{\theta }}^r\), respectively, where \(\tilde{\bar{\theta }}\) and \(\tilde{\bar{\theta }}^r\) are deviations of \(\bar{\theta }\) relative to the corresponding spatial averages, i.e., \(\langle \tilde{\bar{\theta }}\rangle = 0\), \(\langle \tilde{\bar{\theta }}^r\rangle _r = 0\) and \(\langle \tilde{\bar{\theta }}^r\rangle =\phi ^{-1}\langle \langle \tilde{\bar{\theta }}^r\rangle ^s_r\rangle _y=0\). With appropriate selection of the averaging domains, spatial averaging within the roughness-scale domain acts as a low-pass filter by removing dispersive fluctuations associated with the bed roughness. As a result, \(\tilde{\bar{\theta }}^r\) should include contributions from the bed roughness only, enabling us to define dispersive fluctuations due to SCs as \(\widetilde{\langle \bar{\theta }\rangle }_r = \tilde{\bar{\theta }}-\tilde{\bar{\theta }}^r = \langle \bar{\theta }\rangle _r - \langle \bar{\theta }\rangle\), i.e., \(\langle \widetilde{\langle \bar{\theta }\rangle }_r\rangle = \phi ^{-1}\langle \phi _r\widetilde{\langle \bar{\theta }\rangle }_r\rangle _y=0\). Thus, a time-averaged variable can now be decomposed as:

$$\begin{aligned} \bar{\theta } = \langle \bar{\theta }\rangle + \underbrace{\tilde{\bar{\theta }}^{r} + \widetilde{\langle \bar{\theta }\rangle }_{r}}_{\textstyle {=\tilde{\bar{\theta }}}}, \end{aligned}$$
(5)

where \(\tilde{\bar{\theta }}^{r}\) and \(\widetilde{\langle \bar{\theta }\rangle }_{r}\) are dispersive fluctuations due to bed roughness (Fig. 3a) and to SCs (Fig. 3b), respectively. For a reliable dispersive stress partitioning, a large scale separation between the characteristic dimensions of the bed roughness and the SCs is required.

Fig. 3
figure 3

Illustration of dispersive velocity fluctuations a due to bed roughness (\(\tilde{\bar{u}}^{r}_i\)) and b due to SCs (\(\widetilde{\langle \bar{u}_i\rangle }_{r}\)). Contours show the streamwise component (\(i=1\)), whereas vectors in (b) represent spanwise (\(i=2\)) and vertical (\(i=3\)) components

Full size image

2.2 Spatial averaging theorems

Considering flows over fixed boundaries, we may introduce spatial averaging theorems for both global and roughness averaging schemes, which are required for the derivation of the conservation equations introduced in Sect. 3. For brevity, we report theorems for superficial averages only, but theorems for intrinsic averages can be easily obtained as \(\langle \bar{\theta }\rangle ^s=\phi \langle \bar{\theta }\rangle\) and \(\langle \bar{\theta }\rangle _r^s=\phi _r\langle \bar{\theta }\rangle _r\) (see Sect. 2.1). The spatial averaging theorems for superficial global spatial averages of time and spatial derivatives for the case of an immobile solid surface are [13]

$$\begin{aligned} \left\langle \frac{\partial \bar{\theta }}{\partial t}\right\rangle ^s = \frac{\partial \langle \bar{\theta }\rangle ^s}{\partial t} \end{aligned}$$
(6)

and

$$\begin{aligned} \left\langle \frac{\partial \bar{\theta }}{\partial x_i}\right\rangle ^s = \frac{\partial \langle \bar{\theta }\rangle ^s}{\partial x_i} - \frac{1}{V_0}\iint \limits _{S_{int}}{\bar{\theta }m_i\text {d}S}, \end{aligned}$$
(7)

respectively, where t is time, \(S_{int}\) is the area of the fluid-bed interface within \(V_0\), and \(m_i\) is the unit vector normal to the bed surface and directed into the fluid. Similarly, the averaging theorems for superficial averages within the roughness-scale averaging domain are

$$\begin{aligned} \left\langle \frac{\partial \bar{\theta }}{\partial t}\right\rangle _r^s = \frac{\partial \langle \bar{\theta }\rangle _r^s}{\partial t} \end{aligned}$$
(8)

and

$$\begin{aligned} \left\langle \frac{\partial \bar{\theta }}{\partial x_i}\right\rangle _r^s = \frac{\partial \langle \bar{\theta }\rangle ^s_r}{\partial x_i} - \frac{1}{V_0^r}\iint \limits _{S_{int}^r}{\bar{\theta }m_i\text {d}S}, \end{aligned}$$
(9)

where \(S_{int}^r\) is the area of the fluid-bed interface within \(V_0^r\).

Similar to Eq. (4), theorems for globally-averaged and roughness-scale-averaged derivatives may be linked through spanwise averaging as:

$$\begin{aligned} \left\langle \frac{\partial \bar{\theta }}{\partial t}\right\rangle ^s =\left\langle \left\langle \frac{\partial \bar{\theta }}{\partial t}\right\rangle _r^s\right\rangle _{y} =\frac{1}{L_y}\int _{L_y}{\frac{\partial \langle \bar{\theta }\rangle _r^s}{\partial t}\text {d}y} \end{aligned}$$
(10)

and

$$\begin{aligned} \begin{aligned} \left\langle \frac{\partial \bar{\theta }}{\partial x_i}\right\rangle ^s&=\left\langle \left\langle \frac{\partial \bar{\theta }}{\partial x_i}\right\rangle _r^s\right\rangle _{y}\\&=\frac{1}{L_y}\int _{L_y}{\left( \frac{\partial \langle \bar{\theta }\rangle _r^s}{\partial x_i} - \frac{1}{V_0^r}\iint _{S_{int}^r}{\bar{\theta }m_i\text {d}S}\right) \text {d}y}. \end{aligned} \end{aligned}$$
(11)

In the next section, double-averaged conservation equations for momentum and kinetic energy separately accounting for contributions of roughness and SC effects are presented.

3 Double-averaged equations

In this section, the double-averaged continuity equation, momentum conservation equation, and conservation equations for the different components of the total kinetic energy are presented. The channel bed is assumed to be fixed, and the kinematic and no-slip conditions are applied at the solid–fluid interface. The velocity components in the streamwise x (\(i=1\)), spanwise y (\(i=2\)) and vertical z (\(i=3\)) directions are denoted as \(u_1=u\), \(u_2=v\) and \(u_3=w\), respectively.

3.1 Double-averaged continuity and momentum conservation equations

The globally double-averaged continuity equation for incompressible fluids (\(\rho\) is constant) can be derived by spatially averaging (Eqs. 2 and 7) the time-averaged continuity equation \(\partial \bar{u}_i/\partial x_i=0\) [e.g., 8], obtaining:

$$\begin{aligned} \frac{\partial \phi \langle \bar{u}_i\rangle }{\partial x_i} = 0. \end{aligned}$$
(12)

By space averaging the equation \(\partial \bar{u}_i/\partial x_i=0\) within the roughness-scale averaging domain (Eqs. 3 and 9), one may additionally obtain the roughness-scale-averaged continuity equation \(\partial \left( \phi _r\langle \bar{u}_i\rangle _r\right) /\partial x_i=0\).

Starting from the Reynolds equations [e.g., 8, i.e., time-averaged momentum conservation equations], the globally double-averaged momentum conservation equations may be obtained by decomposing time-averaged velocity and pressure as \(\bar{u}_i = \langle \bar{u}_i\rangle + \tilde{\bar{u}}_i^r + \widetilde{\langle \bar{u}_i\rangle }_r\) and \(\bar{p} = \langle \bar{p}\rangle + \tilde{\bar{p}}^r + \widetilde{\langle \bar{p}\rangle }_r\) (Eq. 5), respectively, and by applying global spatial averaging (Eqs. 2, 6 and 7):

$$\begin{aligned} \begin{aligned}&\left. \begin{aligned} \frac{\partial \phi \langle \bar{u}_{i}\rangle }{\partial t}&=\\ \end{aligned}\right\} \text {Time rate of change}\\&\left. \begin{aligned} &+\phi g_i-\frac{1}{\rho }\frac{\partial \phi \langle \bar{p}\rangle }{\partial x_i}\\ \end{aligned}\right\} \text {Source}\\&\left. \begin{aligned} &-\underbrace{ \frac{\partial \phi \langle \bar{u}_i\rangle \langle \bar{u}_j\rangle }{\partial x_j} }_{\text {mean flow}} -\underbrace{ \frac{\partial \phi \langle \tilde{\bar{u}}_i^r\tilde{\bar{u}}_j^r\rangle }{\partial x_j} }_{\begin{array}{c} \text {roughness} \\ \text {-induced} \end{array}} -\underbrace{ \frac{\partial \phi \langle \widetilde{\langle \bar{u}_i\rangle }_r\widetilde{\langle \bar{u}_j\rangle }_r\rangle }{\partial x_j} }_{\text {SC-induced}}\\&-\underbrace{ \frac{\partial \phi \langle \overline{u'_i u'_j}\rangle }{\partial x_j} }_{\text {turbulent}} +\underbrace{ \frac{\partial }{\partial x_j}\left( \phi \nu \left\langle \overline{\frac{\partial u_i}{\partial x_j}}\right\rangle \right) }_{\text {viscous}}\\ \end{aligned}\right\} \text {Transport}\\&\left. \begin{aligned}&+\frac{\phi }{\rho }\left( \frac{1}{V_f}\iint \limits _{S_{int}}{\bar{p}m_i\text {d}S} -\frac{1}{V_f}\iint \limits _{S_{int}}{\rho \nu \frac{\partial \bar{u}_i}{\partial x_j} m_j\text {d}S} \right) \\ \end{aligned}\right\} \text {Sink}\\ \end{aligned} \end{aligned}$$
(13)

where \(g_i\) is the gravity acceleration component in the \(i^\text {th}\) direction and \(\nu\) is fluid kinematic viscosity. The conservation equation for the roughness-scale-averaged momentum \(\langle \bar{u}_i\rangle _r\) may be derived in a similar manner by decomposing velocity and pressure as \(\bar{u}_i = \langle \bar{u}_i\rangle _r + \tilde{\bar{u}}_i^r\) and \(\bar{p} = \langle \bar{p}\rangle _r + \tilde{\bar{p}}^r\) (Sect. 2.1), respectively, and by applying spatial averaging within the roughness-scale domain (Eqs. 3, 8 and 9). This equation is essentially a ‘conventional’ double-averaged momentum equation [e.g., 13] and thus it is not shown for brevity.

Compared to the double-averaged momentum conservation equations based on non-partitioned dispersive velocity and pressure fluctuations [e.g., 13, 25], Eq. (13) includes the separate contributions of bed roughness and SCs to the transport (or spatial rate of change) of momentum. In addition, compared to the classical Reynolds equations, Eq. (13) explicitly accounts for the sink of momentum due to pressure (\(-\phi V_f^{-1}\iint _{S_{int}}{\bar{p}m_i\text {d}S}\)) and viscous (\(\phi V_f^{-1}\iint _{S_{int}}{\rho \nu (\partial \bar{u}_i/\partial x_j)m_j\text {d}S}\)) drag at the bed.

If the double-averaged flow is stationary (\(\partial \langle \bar{ }\rangle/\partial t = 0\)), uniform (\(\partial \langle \bar{}\rangle /\partial x = 0\)) and two-dimensional (\(\partial \langle \bar{}\rangle /\partial y = \langle \bar{v}\rangle = \langle \bar{w}\rangle = 0\)), the streamwise component (\(i=1\)) of the momentum conservation Eq. (13) reduces to:

$$\begin{aligned} 0 = \phi g S_b -\underbrace{\frac{\partial \phi \langle \tilde{\bar{u}}^r\tilde{\bar{w}}^r\rangle }{\partial z}}_{M_{1R}} -\underbrace{\frac{\partial \phi \langle \widetilde{\langle \bar{u}\rangle }_r\widetilde{\langle \bar{w}\rangle }_r\rangle }{\partial z}}_{M_{1SC}} -\underbrace{\frac{\partial \phi \langle \overline{u' w'}\rangle }{\partial z}}_{M_{2}} +\underbrace{\frac{\partial }{\partial z}\left( \phi \nu \left\langle \overline{\frac{\partial u}{\partial z}}\right\rangle \right) }_{M_{3}} -\frac{F_D}{\rho } \end{aligned}$$
(14)

where \(gS_b\approx g_1\), g is gravity acceleration, \(S_b\) is bed slope and

$$\begin{aligned} F_D(z) = \phi \left( -\frac{1}{V_f}\iint \limits _{S_{int}}{\bar{p}m_1\text {d}S} +\frac{1}{V_f}\iint \limits _{S_{int}}{\rho \nu \frac{\partial \bar{u}}{\partial x_j} m_j\text {d}S} \right) \end{aligned}$$
(15)

is the sum of pressure and viscous drag per unit volume. Equation (14) may be integrated between z and the water surface elevation (\(z_{ws}\)) obtaining:

$$\begin{aligned} \underbrace{\rho g S_b\int _z^{z_{ws}}{\phi (z)\text {d}z}}_{S_1} = \phi (z)\tau (z) + \underbrace{\int _z^{z_{ws }}{F_D(z)\text {d}z}}_{S_2}, \end{aligned}$$
(16)

where

$$\begin{aligned} \tau (z) = -\rho \langle \tilde{\bar{u}}^r\tilde{\bar{w}}^r\rangle -\rho \langle \widetilde{\langle \bar{u}\rangle }_r\widetilde{\langle \bar{w}\rangle }_r\rangle -\rho \langle \overline{u'w'}\rangle + \rho \nu \left\langle \overline{\frac{\partial u}{\partial z}}\right\rangle \end{aligned}$$
(17)

is the total fluid shear stress. Equation (16) represents the balance between momentum fluxes due to gravity, roughness-induced dispersive stresses (\(-\rho \langle \tilde{\bar{u}}^r\tilde{\bar{w}}^r\rangle\)), dispersive stresses due to SCs (\(-\rho \langle \widetilde{\langle \bar{u}\rangle }_r\widetilde{\langle \bar{w}\rangle }_r\rangle\)), spatially averaged Reynolds (turbulent) stresses (\(-\rho \langle \overline{u'w'}\rangle\)), double-averaged viscous stresses (\(\rho \nu \langle \overline{\partial u/\partial z}\rangle\)) and momentum sink due to drag at the bed (\(\int _z^{z_{ws}}{F_D\text {d}z}\)). By setting z equal to the minimum roughness elevation (\(z_t\)) in Eq. (16), we obtain the bed shear stress \(\tau _0=\rho g S_b H=\int _{z_t}^{z_{ws}}{F_D(z)\text {d}z}\), where \(H=\int _{z_t}^{z_{ws}}{\phi (z) \text {d}z}\) is mean flow depth. Thus, the shear (or friction) velocity is \(u_*=\sqrt{\tau _0/\rho }=\sqrt{g S_b H}\).

3.2 Conservation equations for kinetic energy

Following the spatial averaging schemes introduced in Sect. 2, time-averaged velocities can be decomposed as the sum \(\bar{u}_i = \langle \bar{u}_i\rangle + \tilde{\bar{u}}_i^r + \widetilde{\langle \bar{u}_i\rangle }_r\) (Eq. 5), where \(\tilde{\bar{u}}_i^r\) and \(\widetilde{\langle \bar{u}_i\rangle }_r\) represent dispersive velocity fluctuations due to bed roughness and to SCs, respectively. With this in mind, the total flow kinetic energy (Eq. 1) can now be expressed as:

$$\begin{aligned} \frac{1}{2} \langle \overline{u_i u_i} \rangle = \underbrace{\frac{1}{2} \langle \bar{u}_i \rangle \langle \bar{u}_i\rangle }_{\text {DMKE}} + \underbrace{\underbrace{\frac{1}{2} \langle \tilde{\bar{u}}_i^r \tilde{\bar{u}}_i^r\rangle }_{\text {RKE}} + \underbrace{\frac{1}{2} \langle \widetilde{\langle \bar{u}_i\rangle }_r \widetilde{\langle \bar{u}_i\rangle }_r\rangle }_{\text {SCKE}}}_{\text {DKE}} + \underbrace{\frac{1}{2} \langle \overline{u'_i u'_i} \rangle }_{\text {SATKE}}, \end{aligned}$$
(18)

where DKE is \(0.5\langle \tilde{\bar{u}}_i\tilde{\bar{u}}_i\rangle = 0.5\langle \tilde{\bar{u}}_i^r \tilde{\bar{u}}_i^r\rangle + 0.5\langle \widetilde{\langle \bar{u}_i\rangle }_r\widetilde{\langle \bar{u}_i\rangle }_r\rangle\), RKE is roughness-induced dispersive kinetic energy and SCKE is the dispersive kinetic energy due to SCs. Here, we will present conservation equations for the different components of the total kinetic energy appearing in Eq. (18), which can be easily obtained from the conservation equations for the fluid stresses (Appendix B) by setting \(i=k\) and dividing by 2. The key steps for the derivation of the conservation equations for the fluid stresses are summarised in Appendix A.

The conservation equation for DMKE is:

$$\begin{aligned} \begin{aligned}&\left. \begin{aligned} \frac{1}{2}\frac{\partial \phi \langle \bar{u}_i\rangle \langle \bar{u}_i\rangle }{\partial t}&= \\ \end{aligned}\right\} \text {Time rate of change}\\&\left. \begin{aligned}&+\underbrace{ \phi \langle {\bar{u}}_i\rangle g_i }_{G}\\ \end{aligned}\right\} \text {Source}\\&\left. \begin{aligned}&+\underbrace{ \phi \langle \tilde{\bar{u}}_i^r\tilde{\bar{u}}_j^r\rangle \frac{\partial \langle \bar{u}_i\rangle }{\partial x_j} }_{I_{1R}} +\underbrace{ \phi \langle \widetilde{\langle \bar{u}_i\rangle }_r\widetilde{\langle \bar{u}_j\rangle }_r\rangle \frac{\partial \langle \bar{u}_i\rangle }{\partial x_j} }_{I_{1SC}}\\&+\underbrace{ \phi \langle \overline{u'_i u'_j}\rangle \frac{\partial \langle \bar{u}_i\rangle }{\partial x_j} }_{I_2} +\underbrace{ \frac{\phi }{\rho }\langle \bar{p}\rangle \frac{\partial \langle \bar{u}_i\rangle }{\partial x_i} }_{I_3}\\&+\underbrace{ \frac{\langle \bar{u}_i\rangle }{\rho V_0}\iint \limits _{S_{int}}{\bar{p}m_i\text {d}S} }_{I_4} -\underbrace{ \frac{\langle \bar{u}_i\rangle }{V_0}\iint \limits _{S_{int}}{\nu \frac{\partial \bar{u}_i}{\partial x_j}m_j\text {d}S} }_{I_5}\\ \end{aligned}\right\} \begin{aligned}\text {Interbudget}\\ \text {exchange}\end{aligned}\\&\left. \begin{aligned}&-\underbrace{ \frac{1}{2}\frac{\partial \phi \langle \bar{u}_i\rangle \langle \bar{u}_i\rangle \langle \bar{u}_j\rangle }{\partial x_j} }_{T_1} -\underbrace{ \frac{\partial \phi \langle \bar{u}_i\rangle \langle \tilde{\bar{u}}_i^r\tilde{\bar{u}}_j^r\rangle }{\partial x_j} }_{T_{2R}} -\underbrace{ \frac{\partial \phi \langle \bar{u}_i\rangle \langle \widetilde{\langle \bar{u}_i\rangle }_r\widetilde{\langle \bar{u}_j \rangle }_r\rangle }{\partial x_j} }_{T_{2SC}}\\&-\underbrace{ \frac{\partial \phi \langle \bar{u}_i\rangle \langle \overline{u'_i u'_j}\rangle }{\partial x_j} }_{T_3} -\underbrace{ \frac{1}{\rho }\frac{\partial \phi \langle \bar{p}\rangle \langle \bar{u}_i\rangle }{\partial x_i} }_{T_4} +\underbrace{ \nu \frac{\partial }{\partial x_j} \left( \langle \bar{u}_i\rangle \frac{\partial \phi \langle \bar{u}_i\rangle }{\partial x_j} \right) }_{T_5}\\ \end{aligned}\right\} \text {Transport}\\&\left. \begin{aligned}&-\underbrace{ \phi \nu \frac{\partial \langle \bar{u}_i\rangle }{\partial x_j}\frac{\partial \langle \bar{u}_i\rangle }{\partial x_j} }_{D_1}-\underbrace{ \phi \nu \frac{\partial \langle \bar{u}_i\rangle }{\partial x_j} \left\langle \frac{\partial \tilde{\bar{u}}_i^r}{\partial x_j}\right\rangle }_{D_{2R}} -\underbrace{ \phi \nu \frac{\partial \langle \bar{u}_i\rangle }{\partial x_j} \left\langle \frac{\partial \widetilde{\langle \bar{u}_i\rangle }_r}{\partial x_j}\right\rangle }_{D_{2SC}}\\ \end{aligned}\right\} \begin{aligned}\text {Dissipation}\\ \text {to heat}\end{aligned}\\ \end{aligned} \end{aligned}$$
(19)

The conservation equation for RKE is:

$$\begin{aligned} \begin{aligned}&\left. \begin{aligned} \frac{1}{2}\frac{\partial \phi \langle \tilde{\bar{u}}_i^r\tilde{\bar{u}}_i^r\rangle }{\partial t}&=\\ \end{aligned}\right\} \text {Time rate of change}\\&\left. \begin{aligned}&-\underbrace{ \phi \langle \tilde{\bar{u}}_i^r\tilde{\bar{u}}_j^r\rangle \frac{\partial \langle \bar{u}_i\rangle }{\partial x_j} }_{I_{1R}} +\underbrace{ \phi \left\langle \overline{u'_i u'_j}\frac{\partial \tilde{\bar{u}}_i^r}{\partial x_j} \right\rangle }_{I_{6R}} -\underbrace{ \phi \left\langle \tilde{\bar{u}}_i^r\tilde{\bar{u}}_j^r\frac{\partial \widetilde{\langle \bar{u}_i\rangle }_r}{\partial x_j} \right\rangle }_{I_7}\\&-\underbrace{ \frac{\phi }{\rho }\langle \bar{p}\rangle \frac{\partial \langle \bar{u}_i\rangle }{\partial x_i} }_{I_3} -\underbrace{ \frac{\phi }{\rho }\left\langle \bar{p}\frac{\partial \widetilde{\langle \bar{u}_i\rangle }_r}{\partial x_i}\right\rangle }_{I_8}\\&-\underbrace{ \frac{\langle \bar{u}_i\rangle }{\rho V_0}\iint \limits _{S_{int}}{\bar{p}{m_i}\text {d}S} }_{I_4} +\underbrace{ \frac{\langle \bar{u}_i\rangle }{V_0}\iint \limits _{S_{int}}{\nu \frac{\partial \bar{u}_i}{\partial x_j}{m_j}\text {d}S} }_{I_5}\\&-\underbrace{ \phi \left\langle \frac{\widetilde{\langle \bar{u}_i\rangle }_r}{\rho V_f^r}\iint \limits _{S_{int}^r}{\bar{p}m_i\text {d} S}\right\rangle }_{I_9} +\underbrace{ \phi \left\langle \frac{\widetilde{\langle \bar{u}_i\rangle }_r}{V_f^r}\iint \limits _{S_{int}^r}{\nu \frac{\partial \bar{u}_i}{\partial x_j}m_j\text {d}S} \right\rangle }_{I_{10}}\\ \end{aligned}\right\} \begin{aligned}\text {Interbudget}\\ \text {exchange}\end{aligned}\\&\left. \begin{aligned}&-\underbrace{ \frac{1}{2}\frac{\partial \phi \langle \tilde{\bar{u}}_i^r\tilde{\bar{u}}_i^r\rangle \langle \bar{u}_j\rangle }{\partial x_j} }_{T_{6R}} -\underbrace{ \frac{1}{2}\frac{\partial \phi \langle \tilde{\bar{u}}_i^r\tilde{\bar{u}}_i^r \widetilde{\langle \bar{u}_j\rangle }_r\rangle }{\partial x_j}}_{T_{7R\text {-}SC}} -\underbrace{ \frac{1}{2}\frac{\partial \phi \langle \tilde{\bar{u}}_i^r\tilde{\bar{u}}_i^r\tilde{\bar{u}}_j^r \rangle }{\partial x_j} }_{T_{7R}}\\&-\underbrace{ \frac{\partial \phi \langle \tilde{\bar{u}}_i^r\overline{u'_i u'_j}\rangle }{\partial x_j} }_{T_{8R}} -\underbrace{ \frac{1}{\rho }\frac{\partial \phi \langle \tilde{\bar{p}}^r\tilde{\bar{u}}_i^r\rangle }{\partial x_i} }_{T_{9R}} +\underbrace{ \nu \frac{\partial }{\partial x_j} \left( \phi \left\langle \tilde{\bar{u}}_i^r\frac{\partial \tilde{\bar{u}}_i^r}{\partial x_j} \right\rangle \right) }_{T_{10R}}\\ \end{aligned}\right\} \text {Transport}\\&\left. \begin{aligned}&-\underbrace{ \phi \nu \frac{\partial \langle \bar{u}_i\rangle }{\partial x_j} \left\langle \frac{\partial \tilde{\bar{u}}_i^r}{\partial x_j}\right\rangle }_{D_{2R}}-\underbrace{ \phi \nu \left\langle \frac{\partial \tilde{\bar{u}}_i^r}{\partial x_j} \frac{\partial \tilde{\bar{u}}_i^r}{\partial x_j}\right\rangle }_{D_{3R}} -\underbrace{ \phi \nu \left\langle \frac{\partial \widetilde{\langle \bar{u}_i\rangle }_r}{\partial x_j}\frac{\partial \tilde{\bar{u}}_i^r}{\partial x_j}\right\rangle }_{D_{3R\text {-}SC}}\\ \end{aligned}\right\} \begin{aligned}\text {Dissipation}\\ \text {to heat}\end{aligned}\\ \end{aligned} \end{aligned}$$
(20)

The conservation equation for SCKE is:

$$\begin{aligned} \begin{aligned}&\left. \begin{aligned} \frac{1}{2}\frac{\partial \phi \langle \widetilde{\langle \bar{u}_i\rangle }_r\widetilde{\langle \bar{u}_i\rangle }_r\rangle }{\partial t}&=\\ \end{aligned}\right\} \text {Time rate of change}\\&\left. \begin{aligned}&-\underbrace{ \phi \langle \widetilde{\langle \bar{u}_i\rangle }_r\widetilde{\langle \bar{u}_j\rangle }_r\rangle \frac{\partial \langle \bar{u}_i\rangle }{\partial x_j} }_{I_{1SC}} +\underbrace{ \phi \left\langle \overline{u'_i u'_j}\frac{\partial \widetilde{\langle \bar{u}_i\rangle }_r}{\partial x_j}\right\rangle }_{I_{6SC}}\\&+\underbrace{ \phi \left\langle \tilde{\bar{u}}_i^r\tilde{\bar{u}}_j^r\frac{\partial \widetilde{\langle \bar{u}_i\rangle }_r}{\partial x_j}\right\rangle }_{I_7} +\underbrace{ \frac{\phi }{\rho }\left\langle \bar{p}\frac{\partial \widetilde{\langle \bar{u}_i\rangle }_r }{\partial x_i}\right\rangle }_{I_8}\\&+\underbrace{ \phi \left\langle \frac{\widetilde{\langle \bar{u}_i\rangle }_r}{\rho V_f^r}\iint \limits _{S_{int}^r}{\bar{p}m_i\text {d}S}\right\rangle }_{I_9} -\underbrace{ \phi \left\langle \frac{\widetilde{\langle \bar{u}_i\rangle }_r}{V_f^r}\iint \limits _{S_{int}^r}{\nu \frac{\partial \bar{u}_i}{\partial x_j}m_j\text {d}S} \right\rangle }_{I_{10}}\\ \end{aligned}\right\} \begin{aligned}\text {Interbudget}\\ \text {exchange}\end{aligned}\\&\left. \begin{aligned}&-\underbrace{ \frac{1}{2}\frac{\partial \phi \langle \widetilde{\langle \bar{u}_i\rangle }_r \widetilde{\langle \bar{u}_i\rangle }_r\rangle \langle \bar{u}_j\rangle }{\partial x_j} }_{T_{6SC}} -\underbrace{ \frac{\partial \phi \langle \widetilde{\langle \bar{u}_i\rangle }_r \tilde{\bar{u}}_i^r \tilde{\bar{u}}_j^r\rangle }{\partial x_j} }_{T_{7SC\text {-}R}}\\&-\underbrace{ \frac{1}{2}\frac{\partial \phi \langle \widetilde{\langle \bar{u}_i\rangle }_r \widetilde{\langle \bar{u}_i\rangle }_r \widetilde{\langle \bar{u}_j\rangle }_r\rangle }{\partial x_j} }_{T_{7SC}} -\underbrace{ \frac{\partial \phi \langle \widetilde{\langle \bar{u}_i\rangle }_r \overline{u'_i u'_j}\rangle }{\partial x_j} }_{T_{8SC}}\\&-\underbrace{ \frac{1}{\rho }\frac{\partial \phi \langle \widetilde{\langle \bar{p}\rangle }_r\widetilde{\langle \bar{u}_i\rangle }_r \rangle }{\partial x_i} }_{T_{9SC}} +\underbrace{ \nu \frac{\partial }{\partial x_j} \left( \phi \left\langle \widetilde{\langle \bar{u}_i\rangle }_r\frac{\partial \widetilde{\langle \bar{u}_i\rangle }_r}{\partial x_j} \right\rangle \right) }_{T_{10SC}}\\ \end{aligned}\right\} \text {Transport}\\&\left. \begin{aligned}&-\underbrace{ \phi \nu \frac{\partial \langle \bar{u}_i\rangle }{\partial x_j} \left\langle \frac{\partial \widetilde{\langle \bar{u}_i\rangle }_r}{\partial x_j}\right\rangle }_{D_{2SC}}-\underbrace{ \phi \nu \left\langle \frac{\partial \widetilde{\langle \bar{u}_i\rangle }_r}{\partial x_j}\frac{\partial \widetilde{\langle \bar{u}_i\rangle }_r}{\partial x_j} \right\rangle }_{D_{3SC}} -\underbrace{ \phi \nu \left\langle \frac{\partial \widetilde{\langle \bar{u}_i\rangle }_r}{\partial x_j}\frac{\partial \tilde{\bar{u}}_i^r}{\partial x_j}\right\rangle }_{D_{3R\text {-}SC}}\\ \end{aligned}\right\} \begin{aligned}\text {Dissipation}\\ \text {to heat}\end{aligned}\\ \end{aligned} \end{aligned}$$
(21)

Finally, the conservation equation for SATKE is:

$$\begin{aligned} \begin{aligned}&\left. \begin{aligned} \frac{1}{2}\frac{\partial \phi \langle \overline{u'_i u'_i}\rangle }{\partial t}&= \end{aligned}\right\} \text {Time rate of change}\\&\left. \begin{aligned}&-\underbrace{ \phi \langle \overline{u'_i u'_j}\rangle \frac{\partial \langle \bar{u}_i\rangle }{\partial x_j} }_{I_2} -\underbrace{ \phi \left\langle \overline{u'_i u'_j}\frac{\partial \tilde{\bar{u}}_i^r}{\partial x_j}\right\rangle }_{I_{6R}} -\underbrace{ \phi \left\langle \overline{u'_i u'_j}\frac{\partial \widetilde{\langle \bar{u}_i\rangle }_r}{\partial x_j}\right\rangle }_{I_{6SC}}\\ \end{aligned}\right\} \begin{aligned}\text {interbudget}\\ \text {exchange}\end{aligned}\\&\left. \begin{aligned}&-\underbrace{ \frac{1}{2}\frac{\partial \phi \langle \overline{u'_i u'_i}\rangle \langle \bar{u}_j\rangle }{\partial x_j} }_{T_{11}} -\underbrace{ \frac{1}{2}\frac{\partial \phi \langle \overline{u'_i u'_i}\tilde{\bar{u}}_j^r\rangle }{\partial x_j} }_{T_{12R}} -\underbrace{ \frac{1}{2}\frac{\partial \phi \langle \overline{u'_i u'_i}\widetilde{\langle \bar{u}_j\rangle }_r\rangle }{\partial x_j} }_{T_{12SC}}\\&-\underbrace{ \frac{1}{2}\frac{\partial \phi \langle \overline{u'_i u'_i u'_j}\rangle }{\partial x_j} }_{T_{13}} -\underbrace{ \frac{1}{\rho }\frac{\partial \phi \langle \overline{p' u'_i}\rangle }{\partial x_i} }_{T_{14}} +\underbrace{ \frac{1}{2}\nu \frac{\partial }{\partial x_j}\left( \frac{\partial \phi \langle \overline{u'_i u'_i}\rangle }{\partial x_j}\right) }_{T_{15}}\\ \end{aligned}\right\} \text {Transport}\\&\left. \begin{aligned}&-\underbrace{ \phi \nu \left\langle \overline{\frac{\partial u'_i}{\partial x_j}\frac{\partial u'_i}{\partial x_j}}\right\rangle }_{D_4}\\ \end{aligned}\right\} \begin{aligned}\text {Dissipation}\\ \text {to heat}\end{aligned}\\ \end{aligned} \end{aligned}$$
(22)

The kinetic energy is initially generated by gravity and fed into the DMKE conservation equation through the source term G. Then, it is exchanged between the components of the total kinetic energy through the interbudget exchange terms I, redistributed in space by the transport terms T and converted to heat by the dissipation terms D. Except for the appearance of new terms due to the dispersive fluctuation partitioning, conservation equations for DMKE  (19) and SATKE (22) are analogous to those presented by Zampiron et al [25]. The conservation equation for DKE \(0.5\langle \tilde{\bar{u}}_i\tilde{\bar{u}}_i\rangle\) can be recovered by summing Eqs. (20) and (21) together. For clarity, terms of Eqs. (19) to (22) are labelled as in  Zampiron et al [25], with the addition of subscripts R and SC indicating whether a term is associated with dispersive fluctuations due to bed roughness or SCs, respectively, e.g., \(I_{1}=I_{1R}+I_{1SC}\).

In the next section, the newly introduced double-averaged equations will be applied to a case study of OCF with roughness-induced SCs over a self-affine rough bed [15].

4 Application

4.1 Background

Fig. 4
figure 4

a self-affine rough bed; b distribution of roughness-scale-averaged streamwise velocity \(\langle \bar{u}\rangle _r\) with \((\langle \bar{v}\rangle _r,\langle \bar{w}\rangle _r)\) vectors

Full size image

In this section, we apply the double-averaged conservation equations presented in Sect. 3 to a simulated OCF over a self-affine rough bed with roughness-induced SCs [15].

The roughness was designed through spectral synthesis as a periodic square tile with a side length of \(b=392\) mm (Figure 4a; see Stewart et al, 2019, for details). The spectrum of the bed elevations exhibited a scaling range \(\propto k^{-1}\) (k is wavenumber) for wavelengths between \(\lambda =5\) mm and 50 mm (corresponding to \(k=2\pi /\lambda =1.26\,\text {mm}^{-1}\) and \(0.126\,\text {mm}^{-1}\), respectively). The bed elevations were normally distributed and followed the same scaling in both the streamwise and spanwise directions, ensuring the roughness isotropy. The roughness height \(\Delta =6\) mm was defined as four standard deviations of the bed elevations. The top of the roughness was assumed at \(z=\Delta /2\), with \(z=0\) at the mean bed level.

A large-eddy simulation (LES) was carried out using the in-house code Hydro3D. The flow was steady and uniform, with a relative submergence \(H/\Delta =20.2\), a bulk Reynolds number \(Re=UH/\nu =31\,300\) (\(U=H^{-1}\int _{z_t}^{z_{ws}}{\phi \langle \bar{u}\rangle \text {d}z}\) is bulk flow velocity), a friction Reynolds number \(H^+=u_*H/\nu =2\,600\) (superscript ‘+’ denotes normalisation with the viscous length \(\nu /u_*\)), a roughness Reynolds number \(\Delta ^+=u_*\Delta /\nu =131\), and a Froude number \(Fr=U/\sqrt{gH}=0.24\). The spatial extent of the simulation domain was equal to \(2{\times } b\) and b in the x and y directions, respectively. The simulation mesh was partitioned into a coarse mesh in the upper flow region, and a fine mesh near the bed. The wall-normal distance between grid points was 0.64 mm for the coarse mesh and 0.32 mm for the fine mesh, corresponding to \(\approx 14\) and \(\approx 7\) viscous units, respectively. The grid spacings in the x and y directions were \(\approx 2.4\) times the spacing in the z direction. The wall-adapting local eddy viscosity (WALE) proposed by Nicoud and Ducros [11] was used as subgrid-scale model. The flow was driven by a streamwise pressure gradient \(\text {d}\widehat{\langle \bar{p}\rangle }/\text {d} x\) (\(\widehat{\langle \bar{p}\rangle }=H^{-1}\int _{z_t}^{z_{ws}}{\phi \langle \bar{p}\rangle \text {d}z}\) is depth-averaged pressure) acting in place of the body force \(\rho g S_b\), which was adjusted at each time step to maintain a constant mass flux. Periodic boundary conditions were applied to the streamwise and spanwise directions. The water surface was simulated as a rigid lid with a free-slip boundary condition, whilst an immersed boundary method was used to represent the bed roughness. Full details on the simulation can be found in Nikora et al. [15].

The roughness-scale-averaged velocity field (Fig. 4b) shows the presence of SCs induced by the bed roughness, making this an ideal case for illustrating the equations presented in this paper. The SCs can be identified in the \(\langle \bar{v}\rangle _r\) and \(\langle \bar{w}\rangle _r\) distributions as streamwise rotational motions in the \(y{-}z\) plane. For the spatial averaging, we set the horizontal extent of the global averaging domain equal to the simulation domain (\(L_x = 2{\times }b\) and \(L_y = b\)), and \(L_z\) equal to the vertical distance between simulation grid points. The roughness-scale averaging domain featured the same streamwise and vertical sizes of the global averaging domain (\(l_x=L_x\) and \(l_z=L_z\)), while \(l_y\) was set equal to the spanwise distance between grid points. The selected value for \(l_y\) was significantly smaller than the spanwise size of the SCs (\(\approx 2H\)), ensuring that the SCs were not removed by the roughness-scale averaging procedure. As a result of the roughness isotropy, the statistical properties of the near-bed flow heterogeneities could be adequately estimated by adjusting the averaging domain size interchangeably in either the streamwise or spanwise directions, allowing for an \(l_y\) smaller than the range of scales characterising the roughness (5 mm \(\le \lambda \le 50\)  mm).

In the next sections, we will use the LES data to analyse the double-averaged streamwise momentum balance (Sect. 4.2) and the interbudget exchange terms of the conservation equations for the kinetic energy components (Sect. 4.3). Finally, we will examine the energy exchanges between the different normal components of the dispersive stresses due to SCs (Sect. 4.4).

4.2 Momentum conservation and fluxes

Fig. 5
figure 5

a,b terms of the conservation equation for the streamwise momentum (14) and c, d terms of the integrated streamwise momentum conservation Eq. (16 and 17) as functions of the normalised vertical coordinates z/H and \(z/\Delta\): a, c for \(z/H\le 0.1\) and (b,d) for \(z/H\ge 0.1\). Dashed lines show the roughness tops elevation at \(z=\Delta /2\); \(z=0\) at the mean bed level

Full size image

The terms of the streamwise momentum conservation Eq. (14) are presented in Fig. 5a,b, with \(F_D\) (the only term that could not be computed directly) estimated as a residual. Positive and negative values denote local gain and loss of momentum, respectively. The data show that momentum is supplied by gravity (\(\phi g S_b=-\phi \rho ^{-1}\text {d}\widehat{\langle \bar{p}\rangle }/\text {d}x\)), with the drag force (\(-F_D\)) acting as a momentum sink at the bed. This results in a net transport of momentum from the outer flow towards the bed. Most of this downward transport of momentum is due to turbulence (\(-M_{2}\)), but significant contributions are provided by viscous stresses (\(M_3\)) and roughness-induced dispersive stresses (\(-M_{1R}\)) near the bed, and by SCs (\(-M_{1SC}\)) at higher elevations.

By integrating Eq. (14) in the bed-normal direction, one may obtain the integrated streamwise momentum conservation Eq. (16). Near the bed (Fig. 5c), the gravitational term (\(S_1\)) is offset by the integral of the drag force (\(S_2\)), and by viscous, turbulent and roughness-induced dispersive stresses. Away from the bed (Fig. 5d), \(S_1\) is balanced by the sum of turbulent stresses and dispersive stresses due to SCs. Roughness-induced dispersive stresses reach their maximum value near the roughness tops, with a magnitude about two times that of the viscous stresses; whereas dispersive stresses due to SCs attain their maximum at \(z/H\approx 0.4\), near the elevation of the SC centres (Fig. 4b).

4.3 Energy exchanges

Table 1 Interbudget exchange terms for the kinetic energy components (Eq. 19 to 22)
Full size table
Fig. 6
figure 6

Kinetic energy components (Eq. 18) and corresponding velocity variances: a, b DMKE; c, d RKE; e, f SCKE; and g, h SATKE. Data shown as functions of z/H and \(z/\Delta\): a, c, e, g for \(z/H\le 0.1\) and b, d, f, h for \(z/H\ge 0.1\). Dashed lines show the roughness tops elevation at \(z=\Delta /2\); \(z=0\) at the mean bed level

Full size image
Fig. 7
figure 7

Interbduget exchange terms of the conservation equations for a, b DMKE, c, d RKE, e, f SCKE and g, h SATKE (19)–(22) (Table 1) as functions of z/H and \(z/\Delta\): a, c, e, g for \(z/H\le 0.1\) b, d, f, h for \(z/H\ge 0.1\). Dashed lines show the roughness tops elevation at \(z=\Delta /2\); \(z=0\) at the mean bed level

Full size image

Kinetic energy components (Eq. 18) and their constituents (i.e., velocity variances) are shown in Fig. 6. Similar to the fluid shear stresses (Fig. 5c,d), the variances of roughness- (Fig. 6c,d) and SC-induced (Fig. 6e,f) dispersive velocity fluctuations are larger near the roughness tops and away from the bed, respectively. In particular, the trends of \(\langle \widetilde{\langle \bar{v}\rangle }_r\widetilde{\langle \bar{v}\rangle }_r\rangle\) (non-zero near the bed and the water surface) and \(\langle \widetilde{\langle \bar{w}\rangle }_r\widetilde{\langle \bar{w}\rangle } _r\rangle\) (non-zero in the middle of the water column) reflect the distributions of the respective roughness-scale-averaged velocity components (Fig. 4b). The distributions of SCKE and \(\langle \widetilde{\langle \bar{u}\rangle }_r\widetilde{\langle \bar{u}\rangle } _r\rangle\) (Fig. 6e) exhibit a noticeable peak around the roughness tops (not observed in the distributions of \(\langle \widetilde{\langle \bar{v}\rangle }_r\widetilde{\langle \bar{v}\rangle } _r\rangle\) and \(\langle \widetilde{\langle \bar{w}\rangle }_r\widetilde{\langle \bar{w}\rangle } _r\rangle\)), which will be briefly discussed at the end of the section in relation to energy exchanges.

The interbudget exchange terms in the DMKE, RKE, SCKE and SATKE balance Eq. (19)–(22) are summarised in Table 1 and presented in Fig. 7, where positive and negative values denote energy gain and loss, respectively. For a uniform and two-dimensional double-averaged flow, the term \(I_3\) is zero.

The DMKE receives energy from gravity (G, Fig. 7a,b). This energy supply is essentially balanced by energy losses near the bed to the other kinetic energy components, indicating a downward transport of DMKE with negligible dissipation. The RKE receives energy from the DMKE near the bed via \(-I_{1R}\) and \(-I_4+I_5\) (Fig. 7c). This energy is partly dissipated, as indicated by the large excess of incoming energy, and partly passed onto the SATKE via \(I_{6R}\). The SCKE receives most of its energy from the DMKE (\(-I_{1SC}\), Fig. 7e,f), which is primarily offset by an energy loss to the SATKE (\(I_{6SC}\)). Energy exchanges between the SCKE and the RKE are limited in comparison (\(I_{7}\) and \(I^u_9-I^u_{10}\)), thereby concealing the role of bed roughness in the formation of SCs. The peaks observed in the SCKE and \(\langle \widetilde{\langle \bar{u}\rangle }_r\widetilde{\langle \bar{u}\rangle }_r \rangle\) distributions near the roughness tops (Fig. 6e) are likely due to \(-I_{1SC}\) (Fig. 7e), which indicates a substantial supply of energy from the DMKE to the SCKE at a similar elevation. Finally, the SATKE interbudget exchange terms exclusively act as energy gains (Fig. 7g,h), indicating large turbulent dissipation of energy, as expected.

In the next section, we will provide a more detailed analysis of the mechanisms that drive the formation of SCs. Specifically, we will examine the energy exchanges associated with each SC-induced dispersive normal stress.

4.4 Energy source for the secondary currents

By setting \(i=k=1,2,3\) in the conservation equation for the SC-induced dispersive stresses (B8), and assuming a uniform and two-dimensional double-averaged flow, we obtain the interbudget exchange terms for \(\langle \widetilde{\langle \bar{u}\rangle }_r\widetilde{\langle \bar{u}\rangle }_r\rangle\):

$$\begin{aligned} -I^u_{1SC}&= -2\phi \langle \widetilde{\langle \bar{u}\rangle }_r\widetilde{\langle \bar{w}\rangle }_r\rangle \frac{\partial \langle \bar{u}\rangle }{\partial z}\end{aligned}$$
(23a)
$$\begin{aligned} I^u_{6SC}&= 2\phi \left\langle \overline{u' u'_j}\frac{\partial \widetilde{\langle \bar{u}\rangle }_r}{\partial x_j} \right\rangle \end{aligned}$$
(23b)
$$\begin{aligned} I^u_{7}&= 2\phi \left\langle \tilde{\bar{u}}^r\tilde{\bar{u}}_j^r\frac{\partial \widetilde{\langle \bar{u}\rangle }_r}{\partial x_j} \right\rangle \end{aligned}$$
(23c)
$$\begin{aligned} I^u_{9}-I^u_{10}&= 2\phi \left\langle \frac{\widetilde{\langle \bar{u}\rangle }_r}{\rho V_f^r}\iint \limits _{S_{int}^r}{\bar{p}m_1\text {d}S} \right\rangle -2\phi \left\langle \frac{\widetilde{\langle \bar{u}\rangle }_r}{V_f^r}\iint \limits _{S_{int}^r}{\nu \frac{\partial \bar{u}}{\partial x_j}m_j\text {d}S} \right\rangle , \end{aligned}$$
(23d)

for \(\langle \widetilde{\langle \bar{v}\rangle }_r\widetilde{\langle \bar{v}\rangle }_r\rangle\):

$$\begin{aligned} I^v_{6SC}&= 2\phi \left\langle \overline{v' u'_j}\frac{\partial \widetilde{\langle \bar{v}\rangle }_r}{\partial x_j} \right\rangle \end{aligned}$$
(24a)
$$\begin{aligned} I^v_{7}&= 2\phi \left\langle \tilde{\bar{v}}^r\tilde{\bar{u}}_j^r\frac{\partial \widetilde{\langle \bar{v}\rangle }_r}{\partial x_j} \right\rangle \end{aligned}$$
(24b)
$$\begin{aligned} I^v_{8}&= 2\frac{\phi }{\rho }\left\langle \bar{p}\frac{\partial \widetilde{\langle \bar{v}\rangle }_r}{\partial y}\right\rangle \end{aligned}$$
(24c)
$$\begin{aligned} I^v_{9}-I^v_{10}&= 2\phi \left\langle \frac{\widetilde{\langle \bar{v}\rangle }_r}{\rho V_f^r}\iint \limits _{S_{int}^r}{\bar{p}m_2\text {d}S} \right\rangle -2\phi \left\langle \frac{\widetilde{\langle \bar{v}\rangle }_r}{V_f^r}\iint \limits _{S_{int}^r}{\nu \frac{\partial \bar{v}}{\partial x_j}m_j\text {d}S} \right\rangle \end{aligned}$$
(24d)

and, finally, for \(\langle \widetilde{\langle \bar{w}\rangle }_r\widetilde{\langle \bar{w}\rangle }_r\rangle\):

$$\begin{aligned} I^w_{6SC}&= 2\phi \left\langle \overline{w' u'_j}\frac{\partial \widetilde{\langle \bar{w}\rangle }_r}{\partial x_j} \right\rangle \end{aligned}$$
(25a)
$$\begin{aligned} I^w_{7}&= 2\phi \left\langle \tilde{\bar{w}}^r\tilde{\bar{u}}_j^r\frac{\partial \widetilde{\langle \bar{w}\rangle }_r}{\partial x_j} \right\rangle \end{aligned}$$
(25b)
$$\begin{aligned} I^w_{8}&= 2\frac{\phi }{\rho }\left\langle \bar{p}\frac{\partial \widetilde{\langle \bar{w}\rangle }_r}{\partial z}\right\rangle \end{aligned}$$
(25c)
$$\begin{aligned} I^w_{9}-I^w_{10}&= 2\phi \left\langle \frac{\widetilde{\langle \bar{w}\rangle }_r}{\rho V_f^r}\iint \limits _{S_{int}^r}{\bar{p}m_3\text {d}S} \right\rangle -2\phi \left\langle \frac{\widetilde{\langle \bar{w}\rangle }_r}{V_f^r}\iint \limits _{S_{int}^r}{\nu \frac{\partial \bar{w}}{\partial x_j}m_j\text {d}S} \right\rangle . \end{aligned}$$
(25d)
Table 2 Interbudget exchange terms for the dispersive normal stresses due to SCs (Eqs. 23 to 25)
Full size table
Fig. 8
figure 8

Interbduget exchange terms of the conservation equations for the normal dispersive stresses due to SCs a, b \(\langle \widetilde{\langle \bar{u}\rangle }_r\widetilde{\langle \bar{u}\rangle }_r\rangle\), c, d \(\langle \widetilde{\langle \bar{v}\rangle }_r\widetilde{\langle \bar{v}\rangle }_r\rangle\) and e, f \(\langle \widetilde{\langle \bar{w}\rangle }_r\widetilde{\langle \bar{w}\rangle }_r\rangle\) (Eq. 23 – 25 and Table 2) as functions of z/H and \(z/\Delta\): a, c for \(z/H\le 0.1\) and b, d for \(z/H\ge 0.1\). Dashed lines show the roughness tops elevation at \(z=\Delta /2\); \(z=0\) at the mean bed level

Full size image
Fig. 9
figure 9

Energy exchanges between different energy components. Terms defined in Eqs. (19)–(22) and (23)–(25). Pressure strain rate (PSR) terms for turbulent and roughness-induced dispersive stresses are defined in Eqs. (B7) and (B9), respectively

Full size image

The same notation as in the equations for the kinetic energy components (19)–(22) is used, with the addition of superscripts indicating the normal stress that each term refers to, i.e., superscript u, v and w for \(\langle \widetilde{\langle \bar{u}\rangle }_r\widetilde{\langle \bar{u}\rangle }_r\rangle\), \(\langle \widetilde{\langle \bar{v}\rangle }_r\widetilde{\langle \bar{v}\rangle }_r\rangle\) and \(\langle \widetilde{\langle \bar{w}\rangle }_r\widetilde{\langle \bar{w}\rangle }_r\rangle\), respectively. The terms of Eqs. (23)–(25) are summarised in Table 2 and shown in Fig. 8. In Fig. 9, a summary of the energy exchanges between the different fluid normal stresses is presented.

Similar to the SCKE, the streamwise stress \(\langle \widetilde{\langle \bar{u}\rangle }_r\widetilde{\langle \bar{u}\rangle }_r \rangle\) acquires energy from the double-mean flow via \(-I_{1SC}^u\). This energy gain is essentially balanced by a loss of energy to the streamwise turbulent stresses via \(I_{6SC}^u\), indicating little energy dissipation. Spanwise \(\langle \widetilde{\langle \bar{v}\rangle }_r\widetilde{\langle \bar{v}\rangle }_r\rangle\) and vertical \(\langle \widetilde{\langle \bar{w}\rangle }_r\widetilde{\langle \bar{w}\rangle }_r\rangle\) stress components do not exchange energy with \(\langle \widetilde{\langle \bar{u}\rangle }_r\widetilde{\langle \bar{u}\rangle }_r\rangle\) or with the double mean flow. Instead, \(\langle \widetilde{\langle \bar{v}\rangle }_r\widetilde{\langle \bar{v}\rangle }_r\rangle\) gains energy from the spanwise roughness-induced dispersive stress via \(I_7^v\) near the bed (Fig. 8c), whereas \(I_7^w\approx 0\) (figure 8e,f). Distributions of \(I_8^v\approx -I_8^w\) and \(I_{6SC}^v\approx -I_{6SC}^w\) suggest that \(\langle \widetilde{\langle \bar{w}\rangle }_r\widetilde{\langle \bar{w}\rangle }_r\rangle\) is sustained by an energy redistribution between \(\langle \widetilde{\langle \bar{v}\rangle }_r\widetilde{\langle \bar{v}\rangle }_r \rangle\) and \(\langle \widetilde{\langle \bar{w}\rangle }_r\widetilde{\langle \bar{w}\rangle }_r\rangle\) via pressure and turbulence.

Our analysis shows that SCs are initiated and sustained by the bed roughness, harvesting energy from spanwise roughness-induced dispersive velocity fluctuations near the bed via \(I^v_7\). The \(I_7\) terms do not include any turbulent contributions, possibly indentifying the SCs examined in this study as SCs of the first kind (definition in Sect. 1), capable of developing regardless of the flow regime (laminar or turbulent). Nevertheless, considering its large contribution to energy redistribution, turbulence is expected to play an important role in the development of SCs, influencing their final shape and characteristics.

5 Conclusions

In this paper, we proposed a new double-averaging approach, aiming to separate the contributions of bed roughness and SCs to dispersive fluid stresses. First, the conservation equations for momentum, fluid stresses and kinetic energy components were derived theoretically. Then, the new approach and resulting equations were applied to a LES of an OCF over a rough bed. The main results from the analysis of the LES data can be summarised as follows:

  • Dispersive stresses due to roughness and to SCs are dominant near and away from the bed, respectively, as expected.

  • Analysis of the energy exchanges between the different kinetic energy components showed that gravity supplies energy to the DMKE (kinetic energy of the double-mean flow), which is then redistributed to RKE (roughness-induced dispersive kinetic energy), SCKE (dispersive kinetic energy due to SCs) and SATKE (spatially-averaged turbulent kinetic energy). Within the RKE budget, energy is partly transferred to SATKE and partly dissipated. Within the SCKE budget, most of the energy is transferred to SATKE, with negligible energy dissipation. In the SATKE budget, all energy exchange terms act as energy gains, which are balanced by large energy dissipations to heat.

  • Analysis of the budgets for SC-induced dispersive stress showed that SCs draw energy near the bed from the spanwise dispersive velocity fluctuations induced by the roughness, revealing a direct link between SCs and the bed roughness. The energy of the SCs is then spatially redistributed by pressure and turbulence.

  • The absence of a turbulent component in the energy exchange term \(I_7^v\), which governs the supply of energy from the RKE to SCs, suggests that the roughness-induced SCs examined in this study are of the first kind. Despite this, turbulence plays a critical role in spatial energy redistribution and should not be overlooked.

The last point highlights the importance that roughness may have in the case of laminar flow conditions [‘rough-bed laminar flows’, 15]. In this scenario, the bed roughness may enhance momentum transfer through the introduction of additional roughness-induced dispersive stresses and the generation of SCs. This flow type may not be frequently encountered in OCFs, but it may be significant in other fields where the flow is often laminar, such as blood flows in vessels or microfluidics [e.g., 5].

Further research is still needed for a better understanding of the physical mechanisms responsible for the formation of roughness-induced SCs. The Authors intend to continue working on this issue, exploring different flow types, conditions and roughness patterns.