1 Introduction

Extensions of Einstein’s general theory of relativity (GR), often denoted as modified gravity or higher-order gravity theory, have aroused interest in their ability to address anomalous behaviour of gravitational phenomena within a cosmological setting. Such phenomena include the late-time accelerated expansion of the universe [1] which is supported by Wilkinson Microwave Anisotropy Probe (WMAP) data. Corrections to gravitational theory are required when higher derivative curvature terms contribute to the dynamics. Modification of the field equations of general relativity was made initially by Einstein himself by introducing the cosmological constant in order to describe a static universe that was sought after at the time. The inclusion of this constant has had a turbulent history as a result of the progress in observational data; however, it demonstrates that modifications of the general theory of relativity are necessary when considering the large-scale structure of the universe. The cosmological constant came to be interpreted as a vacuum energy and is now associated with the concepts of dark energy and the more variable form of dark energy known as quintessence. To date, there is only indirect evidence for the existence of dark energy and other exotic matter fields which cannot be detected at present, and this welcomes the possibility of higher dimensional effects. Kaluza and Klein [2, 3] originally proposed the idea that spacetime might encompass more than four dimensions. Although perhaps inaccessible from a physical point of view, additional spatial dimensions might help augment the range of stability for matter under extreme conditions where higher-order curvature effects become important [4].

The original generalisation of Einstein’s theory of relativity, known as the Lovelock theory of gravity [5], allows for extensions to higher-dimensional metrics. A particular case of Lovelock theory, namely Einstein–Gauss–Bonnet (EGB) gravity or sometimes referred to as Gauss–Bonnet gravity, contains geometrical features that favour a covariant theory of gravity. Thus it has gained interest and is being extensively studied. The Lagrangian in EGB theory includes the Gauss–Bonnet term which is quadratic in the Riemann tensor; however, second-order quasilinear equations of motion are obtained and so no additional dynamical degrees of freedom are introduced as in f(R) gravity. The quadratic nature of the Gauss–Bonnet term is consistent with the low energy effective action in heterotic string theory. This has contributed to Lovelock theory having acquired a reputation of being a string-theory-inspired gravity theory. More recently, EGB gravity has also been shown to be connected with classical electrodynamics [6].

Pioneering work involving Gauss–Bonnet gravity with a proposed connection to string theory in the context of vacuum spacetimes was done by Boulware and Deser [7] and by Wheeler [8]. Boulware and Deser generalised the higher dimensional solutions in Einstein gravity to include the contribution of the EGB theory with quadratic curvature terms. More recently, Dadhich et al. [9] have made notable contributions by proving that the constant density Schwarzschild interior solution is valid in both higher dimensional Einstein theory as well as in EGB gravity. Unfortunately, non-causality of the sound speed renders the constant density solution non-physical; however, the framework for investigating and comparing Einstein and EGB gravity in higher dimensions was established.

Thermodynamics of black holes within the framework of EGB gravity was considered by Hu et al. [10]. In cosmology, emergent universe theories within an EGB framework have also been studied [11], thus Einstein–Gauss–Bonnet theory with its extension to higher dimension is an active field of research.

Models of compact stellar objects, with static spherically symmetric spacetime metrics, have been widely studied in general relativity. Exact solutions have been found for both the Einstein and the Einstein-Maxwell system of field equations [12]. In terms of physical viability, the solutions obtained need to satisfy certain criteria. These include well-behaved gravitational potentials and matter quantities within the stellar interior, smooth matching of the interior and exterior metrics, sound speed causality and stability with respect to radial oscillations or perturbations. In EGB gravity, the higher degree of nonlinearity and the appearance of the Gauss–Bonnet coupling constant complicates the search for exact solutions. Apart from obtaining solutions, quantities calculated in higher dimensional systems might be un-physical unless they can be rescaled in both magnitude and dimension to give standard quantities in four-dimensional spacetime. This seems to be the case when attempts are made at comparing EGB gravity to GR and excessively large deviations in the energy density and pressures are obtained [13]. In particular, calculation of a mass in five-dimensions would yield a quantity of dimension \([length]^2\) in geometrical units and requires dimensional reduction before comparison can be made with physical masses. Other quantities in higher dimensions are likewise affected. In our study, we consider such a problem and transform all of the quantities obtained into a four-dimensional representation before applying an equation of state and performing calculations.

2 Einstein–Gauss–Bonnet gravity

An extension of general relativity into higher dimensions may be given by

$$\begin{aligned} G^{(d)}_{\textrm{ab}} = \frac{d-2}{d-3}S_{d-2}G_d T^{(d)}_{\textrm{ab}} \end{aligned}$$
(1)

where \(G^{(d)}_{\textrm{ab}}\) and \(T^{(d)}_{\textrm{ab}}\) represent the Einstein and energy-momentum tensors, respectively, in d-dimensions [14, 15]. \(G_d\) is an extension of Newton’s gravitational constant to d-dimensions, and the area of unitary hypersphere is given by \(S_{d-2} = 2\pi ^{(d-1)/2}/\Gamma [(d-1)/2]\). The standard approach used to explore the structure of \(G^{(d)}_{\textrm{ab}}\) is via the construction of the Lagrangian and subsequent minimisation of the action integral. This was done by Lovelock for gravity in an arbitrary number of spacetime dimensions [5].

Einstein–Gauss–Bonnet gravity is a specific case of Lovelock gravity. In five dimensions, the action integral according to the Gauss–Bonnet formalism is given by

$$\begin{aligned} S = \frac{1}{2\kappa _5}\int {\sqrt{-g}\left( R - 2\Lambda + \alpha L_{\textrm{GB}}\right) d^5x} + S_{\textrm{matter}} \end{aligned}$$
(2)

where the Einstein gravitational constant in five dimensions is \(\kappa _5 = \frac{3}{2}S_3 G_5 = 3\pi ^2 G_5\) with \(G_5\) representing Newton’s constant in 5-D. The Gauss–Bonnet coupling constant is denoted by \(\alpha \) and may be related to the string tension in string theory [16]. Research has been done on the constraints on Gauss–Bonnet gravity, mostly within a cosmological setting [17]. It was determined that the energy density due to the Gauss–Bonnet term should not exceed 15%. Stronger constraints have been obtained more recently from gravitational wave observational data [18].

The strength of the action \(L_{\textrm{GB}}\) lies in the fact that despite the Lagrangian being quadratic in the Ricci tensor, Ricci scalar and the Riemann tensor, the equations of motion turn out to be second-order quasilinear which is consistent with a theory of gravity. The Gauss–Bonnet term does not contribute to the dynamics of stellar evolution for \(n = 4\) but is generally nonzero for \(n > 4\). Specifically, it has been shown that for the Gauss–Bonnet case only dimensions five and six need be considered. Since the 5-D case leads to certain mathematical simplifications, it is a popular choice; however, solutions in 6-D have also recently been considered [19]. The EGB field equations may be written as

$$\begin{aligned} G_{\textrm{ab}} + \alpha H_{\textrm{ab}} = 3\pi ^2 T_{\textrm{ab}} \end{aligned}$$
(3)

where we have adopted the metric signature \((-++++)\) and where \(G_{\textrm{ab}}\) is the usual Einstein tensor. The Einstein gravitational constant \(G_5\) has been set to unity according to the geometrised system of units.

The Lanczos tensor is given by

$$\begin{aligned} H_{\textrm{ab}}= & {} 2\left( RR_{\textrm{ab}} - 2R_{\textrm{ac}}R^c_b - 2R^{\textrm{cd}}R_{\textrm{acbd}} + R^{\textrm{cde}}_a R_{\textrm{bcde}}\right) \nonumber \\{} & {} - \frac{1}{2}g_{\textrm{ab}}L_{\textrm{GB}}, \end{aligned}$$
(4)

where the Lovelock term has the form

$$\begin{aligned} L_{\textrm{GB}} = R^2 - 4R_{\textrm{cd}}R^{\textrm{cd}} + R_{\textrm{abcd}}R^{\textrm{abcd}}. \end{aligned}$$
(5)

Varying the action against the metric then generates the Einstein–Gauss–Bonnet equations which follow below.

3 The 5-D Einstein–Gauss Bonnet field equations

The line element in 5-D Einstein–Gauss–Bonnet (EGB) gravity is given by

$$\begin{aligned} ds^2= & {} - e^{2\nu } dt^2 + e^{2\lambda } dr^2 \nonumber \\{} & {} + r^2(d\theta ^2 + \sin ^2{\theta }d\phi ^2 + \sin ^2{\theta }\sin ^2{\phi }d\psi ^2), \end{aligned}$$
(6)

where \(\nu (r)\) and \(\lambda (r)\) are the gravitational potentials. We utilise a co-moving fluid velocity of the form \(u^a = e^{-\nu }\delta ^a_0\). The matter field for a shear-free, pressure anisotropic stellar fluid is given by the energy momentum tensor,

$$\begin{aligned} T_{\textrm{ab}} = \textsf {diag} (-\rho , p_r, p_t, p_t, p_t). \end{aligned}$$
(7)

Accordingly, the EGB field equations obtained from (2) reduce to

$$\begin{aligned} 3\pi ^2 \rho= & {} -\frac{3 e^{-2\lambda }}{r^2}\left[ 1 - e^{2\lambda } - \frac{\lambda '}{r} \left( r^2 + 4\alpha \left( 1 - e^{-2\lambda }\right) \right) \right] , \end{aligned}$$
(8)
$$\begin{aligned} 3\pi ^2 p_r= & {} \frac{3 e^{-2\lambda }}{r^2 }\left[ 1 - e^{2\lambda } + \frac{\nu '}{r} \left( r^2 + 4\alpha \left( 1 - e^{-2\lambda }\right) \right) \right] , \end{aligned}$$
(9)
$$\begin{aligned} 3\pi ^2 p_t= & {} \frac{e^{-2\lambda }}{r^2}\bigg [1 - e^{2\lambda } + 2 \nu ' \lambda ' \left( r^2 + 4 \alpha - r \left( \frac{1}{\nu '} - \frac{1}{\lambda '}\right) \right) \nonumber \\{} & {} + \nu ' \left( \frac{\nu ''}{\nu '} + \nu ' - 3 \lambda ' \right) \left( r^2 + 4\alpha \left( 1 - e^{-2\lambda }\right) \right) \bigg ], \end{aligned}$$
(10)

where the coefficients (\(3\pi ^2\)) reflect the higher dimensional character, namely the 3-sphere. The mass in five dimensions is given by

$$\begin{aligned} m(r) = 2\pi ^2 \int _0^r r'^3 \rho dr' \end{aligned}$$
(11)

and yields quantities of dimension \([length]^2\) in geometrised units.

The field equations satisfy

$$\begin{aligned} \frac{dp_r}{dr} = - \nu ' \left( \rho + p_r \right) + \frac{3}{r}\left( p_t - p_r \right) \end{aligned}$$
(12)

which is a generalised Tolman-Oppenheimer-Volkoff (TOV) equation in five dimensions [13].

In an attempt to obtain solutions, we make use of the Durgapal and Bannerji transformation [20], given by

$$\begin{aligned} e^{2\nu } = y^2(x), e^{-2\lambda } = Z(x), x = Cr^2, \end{aligned}$$
(13)

where C is a constant. It is set when applying the boundary condition, \(p_r(R) = 0\), where R is the stellar radius. The above transformation recasts the field equations as differential equations in terms of y and Z, such that the process of integration is facilitated. By implementing functional forms for Z(x), the field equations are linearised and complete integration is possible. This approach has been successfully applied to charged anisotropic relativistic matter in four-dimensional Einstein gravity [12, 21].

The field equations (8)–(10) may then be expressed as

$$\begin{aligned} \frac{3\pi ^2 \rho }{C}= & {} -3\dot{Z} + \frac{3(1 - Z)(1-4\alpha C \dot{Z})}{x} \end{aligned}$$
(14)
$$\begin{aligned} \frac{3\pi ^2 p_r}{C}= & {} -\frac{3(1 - Z)}{x} + 6Z\left[ 1 + \frac{4\alpha C (1 - Z)}{x}\right] \frac{\dot{y}}{y} \end{aligned}$$
(15)
$$\begin{aligned} \frac{3\pi ^2 p_t}{C}&= \, 4Z\left[ x + 4\alpha C(1 - Z) \right] \frac{\ddot{y}}{y} \nonumber \\{} & {} + 2\bigg [(x + 4\alpha C)\dot{Z} + 3Z(1 - 4\alpha C \dot{Z}) \nonumber \\{} & {} + \frac{4\alpha C Z(1 - Z)}{x}\bigg ]\frac{\dot{y}}{y} + \left[ 2\dot{Z} - \frac{1 - Z}{x} \right] \end{aligned}$$
(16)

and gravitational models may be obtained provided an explicit form for \(\dot{y}/y\) is determined or ideally a solution for y(x). We also note that solutions obtained in this way are with respect to the five-dimensional metric (6). In proceeding to a compactified form in four-dimensions, we would expect modification of \(\dot{y}/y\) and hence the metric function \(e^{2\nu }\).

4 The colour-flavour-locked equation of state

For a physically realistic relativistic star, we expect that the matter distribution should satisfy a barotropic equation of state (EoS) \(p_R = p_R(\rho )\). Under extreme densities and pressures as expected in the cores of neutron stars, quark matter is hypothesised to exist in a colour-superconducting, degenerate state. The colour-flavour-locked (CFL) equation of state has been proposed for this so-called strange-quark matter. The EoS for CFL quark matter was well motivated by Rocha et al. [22, 23] in which they assumed that the stellar interior was composed entirely of superconducting CFL matter. In order to make the problem mathematically tractable while retaining the essential physics involved, they were able to write the CFL EoS entirely as a function of the fluid density. We thus make use of the standard form of the CFL EoS in terms of the energy density, given by

$$\begin{aligned} p_{r3} = \beta \rho _3 + \gamma \rho _3^{1/2} - \xi \end{aligned}$$
(17)

where \(\beta \), \(\gamma \) and \(\xi \) are real constants. In particular, we set \(\beta = 1/3\) and adopt the associated forms for \(\gamma \) and \(\xi \) which are connected with the microphysics of quark matter in the colour-flavour-locked superconducting phase. The explicit form is then

$$\begin{aligned} p_{r3} = \frac{1}{3} \rho _3 + \frac{2\eta }{\pi } \rho _3^{1/2} - \left( \frac{3\eta ^2}{\pi ^2} + \frac{4}{3} B \right) , \end{aligned}$$
(18)

where

$$\begin{aligned} \eta = - \frac{m_s^2}{6} + \frac{2\Delta ^2}{3} \end{aligned}$$
(19)

and B is the MIT Bag constant. The parameters \(m_s\) and \(\Delta \) correspond to the strange-quark mass and the superconducting energy gap, respectively. Use of the CFL EoS requires appropriate conversion of units. [24]

5 Towards a stellar model

In developing a stellar model based on quark matter at nuclear saturation density or greater, we impose a colour-flavour-locked equation of state of the form

$$\begin{aligned} p_{r3} = \frac{1}{3} \rho _3 + \gamma \sqrt{\rho _3} - \xi . \end{aligned}$$
(20)

where \(\rho _3\) and \(p_{r3}\) are the three-dimensional density and pressure, respectively. Thus, in proceeding further we dimensionally reduce all quantities obtained in five dimensions to a representation in four dimensions so that the standard notions of matter and energy are regained. Our approach draws on basic string theoretical techniques [25] and has been used in Kaluza-Klein models involving compactification [26]. We apply compactification of the five-dimensional density onto a one-dimensional sphere, given by

$$\begin{aligned} \rho = \frac{1}{2\pi l_c} \rho _3 \end{aligned}$$
(21)

and in addition,

$$\begin{aligned} p_r = \frac{1}{2\pi l_c} p_{r3} \end{aligned}$$
(22)

where \(l_c\) is a parameter which represents the compactification radius. Compactification of the pressure follows in a similar way [25], and we give further support to this shortly. The above compactification is similar to the connection between six dimensional \(\rho \) and four dimensional \(\rho _3\) as given by Chopovsky et al. [27] which requires reduction with respect to a two-dimensional sphere. In an effort to obtain an expression for \(l_c\), we normalise the 5-D field equations to those of GR by equating at \(\alpha = 0\). Thus,

$$\begin{aligned} \rho _{(\textrm{GR})} = (2\pi l_c) \rho |_{\alpha = 0} \end{aligned}$$
(23)

where \(\rho _{(\textrm{GR})}\) is the energy density obtained from standard 4-D general relativity which via the Durgapal-Bannerji transformation is given by,

$$\begin{aligned} \frac{8\pi \rho _{(\textrm{GR})}}{C} = \frac{1 - Z}{x} - 2\dot{Z}. \end{aligned}$$
(24)

The compactification radius (at \(\alpha = 0\)) is thus computed to be,

$$\begin{aligned} l_c(x)|_{\alpha = 0} = \frac{1-Z-2x \dot{Z}}{16(1-Z-x \dot{Z})}. \end{aligned}$$
(25)

At this stage, we also confirm that the compactification radius, \(l_c\), is consistent with the compactification of the radial pressure (22). If the expression for \(l_c\) is computed via \(p_{r(\textrm{GR})} = (2\pi l_c) p_r |_{\alpha = 0}\), where \(p_{r(\textrm{GR})}\) is the radial pressure from 4-D general relativity, then the same expression given by (25) is obtained. In addition, it is assumed that \(\dot{y}/y\) is the same for both sets of field equations when the coupling constant \(\alpha = 0\). We now propose that the compactification radius is insensitive to variation of \(\alpha \) and make a first-order approximation near \(\alpha = 0\). Then for departure from \(\alpha = 0\), we conjecture that

$$\begin{aligned} l_c(x,\alpha ) = \frac{1-Z-2x \dot{Z}}{16(1-Z-x \dot{Z})(1 + \epsilon \alpha )} \end{aligned}$$
(26)

where \(\epsilon \ll 1\).

In order to close the system of equations for our model, we require an expression for \(\dot{y}/y\) in the compactified spacetime. Upon substituting (21) and (22) into the 5-D field Eqs. (14) and (15), we apply the CFL EoS (17) which then yields

$$\begin{aligned} \frac{\dot{y}}{y}= & {} \frac{1}{2 \left( x + 4 \alpha C(1 - Z) \right) } \nonumber \\{} & {} \times\bigg [\frac{8 \pi x (1 - Z - \dot{Z} x)(1 + \epsilon \alpha )}{C Z (1 - Z - 2 \dot{Z} x)} \nonumber \\{} & {}\times \bigg (\gamma \sqrt{\frac{C (1 - Z - 2 \dot{Z} x) \left[ 1 - Z -\dot{Z} (x + 4 \alpha C(1 - Z) )\right] }{8\pi x(1 - Z - \dot{Z} x)(1 + \epsilon \alpha )}} \nonumber \\{} & {} +\frac{C (1 - Z - 2 \dot{Z} x) \left[ 1 - Z -\dot{Z} (x + 4 \alpha C(1 - Z) )\right] }{24 \pi x (1 - Z - \dot{Z} x)(1 + \epsilon \alpha )}-\xi \bigg ) \nonumber \\{} & {} +\frac{1}{Z}-1\bigg ]. \end{aligned}$$
(27)

A suitable form for Z is now required which would allow us to complete the gravitational behaviour of our model. The Finch-Skea potential is a popular choice and well-suited to describing the gravitational behaviour of compact stellar objects while retaining algebraic simplicity [24, 28]. More sophisticated potentials include that of Vaidya and Tikekar [29]. Within the transformed setting, the Finch-Skea ansatz is given by

$$\begin{aligned} Z(x) = \frac{1}{1 + x}. \end{aligned}$$
(28)

As defined in (13), \(x = C r^2\), and C becomes a scaling parameter whose square-root is related to the curvature of the gravitational potential. Applying Z(x), we then obtain

$$\begin{aligned} \frac{\dot{y}}{y}= & {} \frac{\left( 4 \alpha C + x^2 + 3 x + 2\right) }{(1 + x)(1 + x + 4\alpha C)} \nonumber \\{} & {}\times \bigg [\frac{2}{3} + \gamma \sqrt{\frac{2\pi (1 + x)^3 (2 + x) (1 + \epsilon \alpha )}{C(3 + x) \left( 4 \alpha C + x^2 + 3 x + 2\right) }} \nonumber \\{} & {} -\frac{4 \pi \xi (2 + x) (1 + \epsilon \alpha )}{C(3 + x)(1 + x)\left( 4 \alpha C + x^2 + 3 x + 2\right) } \bigg ] \end{aligned}$$
(29)

which is not easily integrated. Since we will apply the restriction \(|x| < 1\), integration to a desired order in x may be performed in order to calculate quantities explicitly dependent on y(x). For computing the density and pressure, \(\dot{y}/y\) is sufficient. To third order in x we obtain,

$$\begin{aligned}{} & {} y(x) \approx J\exp \bigg [\frac{1}{6} \log (1 + x) - \frac{8 \alpha C \log (1 + x + 4 \alpha C)}{3} \nonumber \\{} & {} \quad + \frac{2}{3}(1 + x) + \frac{\gamma }{(1 + 4\alpha C)}\sqrt{\frac{\pi (1 + \epsilon \alpha )(1 + 2 \alpha C)}{6C}} \nonumber \\{} & {}\quad \times \bigg (4 x + \frac{\left( 28 \alpha ^2 C^2 + 27 \alpha C + 2\right) }{3 (1 + 2 \alpha C) (1 + 4 \alpha C)}x^2 \nonumber \\{} & {} \quad -\frac{\left( 176 \alpha ^4 C^4 - 40 \alpha ^3 C^3+51 \alpha ^2 C^2 + 46 \alpha C + 1\right) }{18 (1 + 2 \alpha C)^2 (1 + 4 \alpha C)^2}x^3 \bigg ) \nonumber \\{} & {} \quad + \xi \frac{2\pi (1 + \epsilon \alpha )}{C(1 - 2 \alpha C)}\bigg ((1 - 2 \alpha C)(1 + x)(1 - x + 8 \alpha C) \nonumber \\{} & {} \quad - 4 \log (3 + x) - 16 \alpha ^2 C^2 (1 - 4 \alpha C) \log (1 + x + 4 \alpha C) \bigg ) \bigg ] \nonumber \\ \end{aligned}$$
(30)

where J is a constant of integration which is set according to the matching of the interior metric potentials at the boundary, \(e^{2\nu (r = R)} = e^{-2\lambda (r = R)}\). At the stellar boundary, it is also necessary to match the internal and external spacetime metrics. The exterior spacetime in 5-D is described by the Boulware-Deser solution [7, 8],

$$\begin{aligned} ds^2= & {} - F(r) dt^2 + [F(r)]^{-1} dr^2 \nonumber \\{} & {} + r^2(d\theta ^2 + \sin ^2{\theta }d\phi ^2 + \sin ^2{\theta }\sin ^2{\phi }d\psi ^2), \end{aligned}$$
(31)

where

$$\begin{aligned} F(r) = 1 + \frac{r^2}{4\alpha }\left( 1 - \sqrt{1 + \frac{8\alpha M}{r^4}}\right) \end{aligned}$$
(32)

and M is the total mass in five dimensions. Matching the exterior and interior metrics at the boundary then requires, \(F(r) = e^{-2\lambda (r = R)}\). This provides an explicit expression for the mass,

$$\begin{aligned} M = \frac{C R^4 \left( 1 + C(R^2 + 2\alpha ) \right) }{\left( 1 + C R^2 \right) ^2} \end{aligned}$$
(33)

which may also be obtained via equation (11).

5.1 Physical quantities in four-dimensional spacetime

We require the calculation of physical quantities in standard 4-D spacetime. The compactification radius is now used to compactify the energy density given in the 5-D system (8) as prescribed by Eq. (21), for which we obtain,

$$\begin{aligned} \rho _3 = \frac{C \left( 3 + C r^2\right) \left[ (1 + C r^2)(2 + C r^2) +4 \alpha C\right] }{8 \pi \left( 1 + C r^2 \right) ^3 \left( 2 + C r^2 \right) \left( 1 + \epsilon \alpha \right) }. \end{aligned}$$
(34)

The radial and tangential pressures are then obtained via the CFL equation of state and the generalised Tolman-Oppenheimer-Volkov (TOV) equation, respectively,

$$\begin{aligned} p_{r3}= & {} \frac{1}{3} \rho _3 + \gamma \sqrt{\rho _3} - \xi \end{aligned}$$
(35)
$$\begin{aligned} p_{t3}= & {} \frac{1}{3}\rho _3 \left( 1 + 4 C r^2 \frac{\dot{y}}{y}\right) + \left( \gamma \sqrt{\rho _3} - \xi \right) \left( 1 + C r^2 \frac{\dot{y}}{y}\right) \nonumber \\{} & {} + \frac{r}{6}\rho _3 ' \left( 1 + \frac{3\gamma }{2 \sqrt{\rho _3}}\right) . \end{aligned}$$
(36)

We note that the tangential pressure \(p_t\) does not compactify in the same way as \(\rho \) and \(p_r\) in (21) and (22), respectively. Thus, use of the generalised TOV equation in 4-D assists in obtaining \(p_{t3}\). We plan to investigate this further in the future studies.

The mass may be calculated by integrating the density in the standard way, namely

$$\begin{aligned} m_3(r) = 4\pi \int _0^r r'^2 \rho _3 dr' . \end{aligned}$$
(37)

We note that the mass in the 5-D system which has geometrical units of \(\textrm{km}^2\) is readily transferred to physical mass by diametrical division,

$$\begin{aligned} \frac{m}{2R} = m_3. \end{aligned}$$
(38)

This allows for projection from the 3-sphere to 2-sphere geometry in which we assume that the projection of mass from higher to lower dimensions is not affected by the coupling constant, consistent with the conservation of mass-energy. This assists us in calculating the compactification radius scaling parameter, \(\epsilon \). After performing the integrations needed for m and \(m_3\) we obtain,

$$\begin{aligned} \epsilon= & {} \bigg [R^3\sqrt{C}\left( 1 + C(R^2 + 2\alpha )\right) \bigg ]^{-1} \nonumber \\{} & {}\times \left( 1 + C R^2\right) \bigg (R\sqrt{C} - \left( 1 + C R^2\right) \nonumber \\{} & {}\times \left( 5 \arctan {(R\sqrt{C})} - 4\sqrt{2}\arctan {(R\sqrt{C/2})}\right) \bigg ). \end{aligned}$$
(39)

Quantities arising from the 5-D field equations can now be projected into 4-D spacetime in which the quantities regain their standard physical nature and interpretations. The nature of quantities in higher dimensional EGB gravity has previously been an issue.

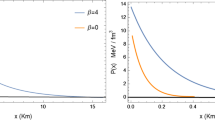
6 Physical application

In gaining insight into the benefits of 5-D Einstein–Gauss–Bonnet gravity applied to compact stellar objects described by a colour-flavour-locked (CFL) equation of state (EoS), we model a compact object of radius \(R = 9.5 \mathrm{\, km}\) which is a typical value for a strange star candidate. Using equation (39), a relationship between the compactification radius scaling parameter \(\epsilon \) and the curvature parameter C is then obtained as shown in Fig. 1. Although a relationship for \(\alpha = 0\) is not required, it is included for completeness. We see that the product \(\epsilon \alpha < 1.2\%\) for \(\alpha < 30\) which supports our first-order approximation of \(l_c\) in (26). The quark parameters are set to typical values [30], namely \(m_s = 150 \mathrm{\, MeV}\) for the strange-quark mass and \(\Delta = 100 \mathrm{\, MeV}\) for the gap energy. The MIT Bag constant is set at \(B = 90 \mathrm{\, MeV}/\textrm{fm}^3\) which is higher than the more typical value of \(60 \mathrm{\, MeV}/\textrm{fm}^3\); however, higher values have been considered recently in studies of strange-matter compact objects which follow the CFL EoS [22, 23]. Bag constants as high as \(300 \mathrm{\, MeV/fm}^3\) have been investigated in other studies [31]. Calculated masses, radii, central densities and central pressures are shown in Table 1. The masses, densities and pressures obtained are typical of those calculated for highly dense neutron stars.

Table 1 Calculated physical properties for \((R = 9.5\, \textrm{km}\); \(B = 90 \mathrm{\,MeV}/\textrm{fm}^3\); \(m_s = 150\, \mathrm{\, MeV}\); \(\Delta = 100 \mathrm{\, MeV})\)
Full size table
Table 2 Physical parameters of some strange-star candidates [31]
Full size table

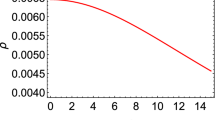
Plots of energy density and pressure are generated using equations (34), (35) and (36) as shown in Figs. 2 and 3, respectively. The pressure anisotropy parameter (\(\delta = p_{t3} - p_{r3}\)) is given in Fig. 4.

Fig. 1
figure 1

Compactification radius scaling parameter for \(R = 9.5\mathrm{\,km}\)

Full size image
Fig. 2
figure 2

Density profiles for \(R = 9.5\mathrm{\, km}\)

Full size image
Fig. 3
figure 3

Pressure profiles (R = 9.5 km)

Full size image
Fig. 4
figure 4

Anisotropy parameter profiles \((R = 9.5\mathrm{\, km})\)

Full size image
Fig. 5
figure 5

Adiabatic index

Full size image
Fig. 6
figure 6

Mass-Radius relationship. Points denote strange-star candidates given in Table 2

Full size image

7 Discussion

The effect of the Gauss–Bonnet coupling constant \(\alpha \) is shown in all of the plots. Increasing values of \(\alpha \) with the radius held constant result in lower densities and pressures, most notably towards the core. We see that the energy density does not change by more than 15% for \(\alpha = 30 \mathrm{\,km}^2\). In some 4-D EGB studies, central densities and pressures appear to be unaffected by \(\alpha \) [32]. Higher dimensional Einstein–Gauss–Bonnet gravity thus appears to offset the physical quantities of compact matter with respect to increasing density and pressure. Recent research has also shown that EGB gravity can assist in describing stable compact objects with masses in excess of \(2 M_\odot \) [33]. The importance of implementing the notion of compactification in order to represent 5-D quantities in standard 4-D spacetime is highlighted as small increments of \(\alpha \) show reasonable deviation of the basic physical quantities of density and pressure from that obtained in general relativity (GR). Large offsets from GR for \(\alpha \ne 0\) are not encountered as shown in other studies [13] and convergence to GR at \(\alpha = 0\) is a desired feature in our study. The effect of \(\alpha \) on anisotropy is shown in Fig. 4. We see that the effect of the coupling constant is to reduce the degree of anisotropy, proceeding to negative values where the radial pressure dominates the tangential. This is usually undesirable due to instability; however, other measures of stability, notably the adiabatic index (Fig. 5) favour the addition of the Lanczos term. Our study was also restricted to a shear-free matter distribution and the inclusion of shearing stresses and additional effects such as electric fields and surface tension could have a strong effect in overcoming unfavourable pressure anisotropies. The Finch-Skea framework also has certain pathologies especially towards the surface of the body where pressure anisotropy gradients tend to become negative. Nonzero values of \(\alpha \) seem to assist in reducing this feature. Other potential formalisms such as that of Vaidya and Tikekar [29] are also worthy of consideration in this regard. The mass-radius (M-R) relationships in which the mass and radius are parametrised in terms of (C) are shown in Fig. 6. Selected strange-star candidates are also included. Increasing the value of the coupling constant allows of larger radii for a fixed mass. Although this could be obtained by adjusting the MIT Bag constant and the quark parameters, the coupling constant allows for an additional degree of freedom.

8 Conclusion

We have presented a stellar model based on five-dimensional Einstein–Gauss–Bonnet (EGB) gravity theory. In so doing, we have focused on the importance of transforming quantities computed in five dimensions to the physical quantities within four-dimensional spacetime. It is a simple exercise to consider an object that is initially restricted to two spatial dimensions, being given the freedom to move into a third spatial dimension. When projected back to the 2D plane it would appear to have contracted. Likewise, reductions from higher dimensions would produce similar results albeit elusive from a geometrical point of view. At present, higher dimensions remain a mathematical tool and are physically inaccessible; however, this does not exclude the possibility of existence. Indeed, much progress has been made in investigations of physical phenomena such as fluid pulsation modes in higher dimensions, leading to the possibility of quarks propagating in extra dimensions [15]. Higher dimensional gravity theory, especially the Einstein–Gauss–Bonnet formalism in five dimensions, is showing promise in correcting for some of the shortcomings in Einstein’s general theory of relativity. Working in higher dimensions might also facilitate with some of the complexities associated in solving field equations for more complex gravitational systems.