1 Introduction

In higher-dimensional gravity theories (HDG) i.e., \(D \ge 5\) dimensions, the gravity action may be modified to include higher order curvature terms while keeping the equations of motion to second order, provided the higher order terms appear in specific combinations. Among the HDG theories, Lovelock gravity is one of the most natural generalizations of Einstein’s general relativity (GR), introduced originally by Lanczos [1], and rediscovered by David Lovelock [2, 3]. More precisely, the standard argument for the uniqueness of the Einstein field equation is based on Lovelock’s theorem, the relevant statement being restricted to 4-dimensions. In particular, the equations of motion of Lovelock gravity are quasi-linear and of second order with respect to the metric and Ostrogradsky instability (ghost) is avoided.

EGB gravity involves the second order Lovelock polynomial terms, appears in the low energy effective action of heterotic string theory [4] and leads to ghost-free nontrivial gravitational self-interactions [5]. For these reasons the role of the GB contribution has been actively studied in recent times. Moreover, EGB theory provides the simplest laboratory to study nontrivial higher curvature effects in dimensions higher than 4. Note that the critical dimensions in Lovelock theory are \(2N + 1\) and \(2N + 2\) where N is the order of the Lovelock polynomial [6]. For example, the cubic order terms, \(N = 3\) are only dynamic in dimensions 7 and 8. A principal feature of Lovelock theory is that the Lovelock terms become topological invariants and consequently do not contribute to the gravitational dynamics when the spacetime dimension equals to four. However, Glavan and Lin [7] proposed a novel theory of EGB gravity which bypasses the conclusions of Lovelock’s theorem and avoids Ostrogradsky instability in 4-dimensional spacetime. Their basic idea was to rescale the GB coupling constant \(\alpha \rightarrow \alpha /(D -4)\) and then taking the limit \(D \rightarrow 4\). The resultant theory is now dubbed as the novel four-dimensional 4D EGB theory. With this rescaling, authors in [7] have found a non-trivial black hole solution.

This idea evoked great interest amongst researchers and was extensively investigated in many configurations such as spherically symmetric and static black hole solutions including their physical properties [8,9,10,11,12,13,14], charged black hole [15, 16], black holes coupled with magnetic charge and nonlinear electrodynamics [17,18,19]. In this framework the strong/ weak gravitational lensing by black holes [20,21,22], quasi-normal modes [23,24,25], black hole shadows [26,27,28], wormholes and thin-shell wormholes [29, 30] and some other relevant works have also been investigated in [31]. Recently a rotating generalization was reported in [32, 33] using the Newman–Janis algorithm. However, the Newmann–Janis trick is not generally applicable in higher curvature theories (see Ref. [34]). It is worthwhile noting that several criticisms against the Glavan–Lin proposal have emerged, including the above limiting procedure being invalid [35,36,37,38]. The dimensional regularization procedure discussed by Tomozawa [39] dealt with this difficulty in a related context and it was shown that a factor of \(n -4\) in his analysis actually cancelled off. Lovelock’s theorem states that the only metric theory of gravity in four dimensions admitting up to second order equations of motion is general relativity. Additionally Lovelock’s polynomial construction gives the most general tensorial theory yielding second order equations of motion in any number of spacetime dimensions. In the case of the 4D EGB proposition Gurses et al. [37, 38] showed that a description in terms of a covariantly-conserved rank-2 tensor in four dimensions is not evident. Additionally through dimensional regularization one part of the GB tensor always remains higher dimensional. In other words, 4D EGB is well behaved in certain highly-symmetric spacetimes such as static spherically symmetric spacetimes. Thus, it is worth investigating the various applications of this 4DEGB gravity and exploring its relevant effects on gravitational dynamics.

In fact, this gravity theory has attracted significant attention of late that includes finding astrophysical solutions and investigating their properties. Thus, the main motivation of this paper is to study compact stars and their properties. Lovelock theory and its special case EGB gravity are essentially higher dimensional theories and some have questioned whether investigations into higher dimensional stars are fruitful exercises since extra dimensions are not physically accessible. The procedure we are following herein does not suffer this drawback. We can now study higher curvature effects in a standard four dimensional setting. However, we hasten to add that experiments into modified theories of gravity are often justified due to the inadequacy of general relativity to explain phenomena such as the observed accelerated expansion of the universe without resorting to exotic matter fields such as dark matter and dark energy. So if a modified theory is able to provide a cogent explanation for this observed behaviour then it is natural to check the self consistency of such a theory in other physically relevant areas such as stellar distributions and galaxy formation. On these grounds, this problem merits attention as did general relativity over the past century. Along these lines we may develop insights into the composition and properties of neutron stars (NSs), which are the remains of very massive stars (10–30 \(M_{\odot }\)) that ended their lives in supernova explosions [40, 41]. Such compact objects (NSs or QSs) impose restrictions on the equation of state (EoS) that is required to describe the matter content inside them. Additionally, strange stars and their phenomenological properties have been extensively investigated with different EoS in [42] (see Ref. [43, 44] for more). Moreover, in Ref. [45] the mass-radius relations are obtained for realistic hadronic and for strange quark star EoS.

Several recent treatments, including the work of Hansraj et al. [46], demonstrate new classes of exact solutions for 4D EGB stars by prescribing the temporal potential to be proportional to the stellar radius. The master field equations are extremely complicated and ad hoc prescriptions on mathematical grounds are made to obtain an exact solution. Note that imposing a physical constraint such as an EoS renders the problem totally intractable from a mathematical point of view and an appeal to numerical techniques must be made. Extending this work we would like to develop exact solutions that may be used to describe the dynamics of charged compact objects in strong gravitational fields such as is applicable to neutron/quark stars (NS/QS). It is believed that if such compact object exist in the Universe, they ought to be made of chemically equilibrated strange matter, which requires the presence of electrons inside them. At the same time, substantial evidence suggests that matter acquires large amounts of electric charge during an accretion process onto a compact object or during the gravitational collapse [47, 48]. Some studies have also concluded that Coulomb repulsion will add up to the internal pressure of the system which creates an effective pressure and prevents further gravitational collapse [49, 50]. In order to see any appreciable effect on the phenomenology of the compact stars, several efforts have been made starting from Bekenstein [51]. He generalized the Tolman–Oppenheimer–Volkoff (TOV) equations of hydrostatic equilibrium to the charged case, and discussed their applicability. In the Maxwell–Einstein context, Ivanov [52] and Sharma et al. [53] demonstrate that the presence of the electric charge affects the values of redshifts, luminosities and maximum mass of a compact objects.

Since then a substantial volume of work on relativistic charged stars has emerged studying the impact of the electromagnetic field on the global physical behaviour of relativistic superdense stars [54,55,56,57,58,59]. Hansraj and Maharaj [60] have obtained solutions for charged Finch–Skea stars; these models are given in terms of Bessel functions and obey a barotropic equation of state. We also mention the works of De and Raychaudhuri [61], where the condition for a charged star to reach equilibrium was established. Another important factor that seems to have a significant role in the stellar modelling is charged anisotropic solutions. For example, see the works of [62,63,64,65,66,67].

Our aim here is to explore new classes of exact spherically symmetric charged fluid spheres, in the novel 4D EGB gravity. From a mathematical perspective, the problem boils down to solving a system of four partial differential equations in six unknowns. Despite the fact that there is freedom to choose two of the matter or geometrical variables a priori the problem is more formidable than its Einstein counterpart. We achieve some progress by introducing a relationship between the space potential (effectively the energy density) and the electric field intensity to facilitate the location of exact solutions. The paper is organized as follows: after a brief introduction in Sect. 1, we derive the equations of motion for charged fluid sphere in Sect. 2. In particular, we explicitly generate the set of equations governing the static spherically symmetric configuration in Schwarzschild-like coordinates and expressed in the TOV form. In the same section we rewrite the field equations as an equivalent set of differential equations employing a transformation which transforms the master field equation to a linear second order ordinary differential equation with improved prospects of integrating. On specifying known physically well studied ansatze for superdense stars and by assuming a relationship between the potential and electric field intensity we determine a class of solutions which contain a well known special case. The full dynamics and geometry are now known and we are in a position to examine the physical viability of our model in Sect. 3. Next we analyze the physical properties of the model such as their energy density, pressure, energy conditions, speed of sound and adiabatic stability. Finally, we conclude by pointing out some interesting features of our model in section Sect. 4. Throughout the study we employ natural (geometrized) units \(G = c = 1\) and the metric signature \((-,+,+,+)\).

2 Basic construction of charged stellar model in 4D EGB gravity

Before we start our discussion on 4D EGB gravity, we would like to mention that the novel 4D EGB theory [7] has received several criticisms. Concerning these points, some criticisms on the validity of taking the \(D\rightarrow 4\) limit have been raised [68, 69]. However, the authors in Ref. [37] (see [35, 36] for more) pointed out that in 4D spacetime the resulting equations of motion is not regular in general and there is no regular action that reproduces the proposed regularized equations of motion [70]. In fact, Kaluza–Klein-reduction approach of the \(D\rightarrow 4\) limit leads to a particular class of scalar–tensor theories within the Horndeski family, see e.g. [71, 72]. Analogous approach was also employed in [73, 74] by adding a counter term in D-dimensions and then taking the \(D\rightarrow 4\) limit.

On the other hand, some proposals have been put forward to circumvent the aforementioned shortcomings coming from the novel 4D EGB gravity. Indeed, depending on the choice of the“regularisation scheme”, many other theories have been offered with different number of degrees of freedom and different properties. Following Ref. [75], the treatment was found to be consistent by breaking the four-dimensional diffeomorphism invariance (see also [76] in the cosmological context). However, it is interesting to note that the spherically symmetric 4D solutions still remain valid in these regularized theories [43]. In fact, the black hole solutions via rescaling procedure [7] still remains valid in these regularized theories [73, 77]. Thus it turns out that the spherically symmetric solution obtained using any of these regularization methods will be the same form as the original theory.

In this regard, the spherically symmetric charged star solution itself is meaningful and worthy of study. Thus, we decide to derive the equations of motion starting with scenarios based on the novel 4D EGB gravity. The action in D-dimensional Gauss-Bonnet theory minimally coupled to matter fields is given by,

$$\begin{aligned} {\mathcal {I}}_{A}=\frac{1}{16 \pi }\int d^{D}x\sqrt{-g}\left[ R +\frac{\alpha }{D-4} {\mathcal {L}}_{\text {GB}} \right] +\int d^{D}x\sqrt{-g} {\mathcal {L}}_m. \end{aligned}$$
(1)

Here, R is the Ricci scalar which provides the general relativistic part of the action, and g is determinant of the metric tensor \(g_{\mu \nu }\). The GB coupling constant \(\alpha \) has dimension of \([length]^2\), and Einstein–Gauss–Bonnet Lagrangian given by

$$\begin{aligned} {\mathcal {L}}_{\text {GB}}=R^{\mu \nu \rho \sigma } R_{\mu \nu \rho \sigma }- 4 R^{\mu \nu }R_{\mu \nu }+ R^2. \end{aligned}$$
(2)

Here, the Lagrangian density \({\mathcal {L}}_m\) of matter depends only on the metric tensor components \(g_{\mu \nu }\), and not on its derivatives, we obtain

$$\begin{aligned} T_{\mu \nu }= -\frac{2}{\sqrt{-g}}\frac{\delta \left( \sqrt{-g}{\mathcal {L}}_m\right) }{\delta g^{\mu \nu }}. \end{aligned}$$
(3)

Now, applying variation of the action (1) with respect to metric \(g_{\mu \nu }\) leads to the following equations of motion

$$\begin{aligned} G_{\mu \nu }+\frac{\alpha }{D-4} H_{\mu \nu }= 8 \pi T_{\mu \nu }, \end{aligned}$$
(4)

where \(G_{\mu \nu }\) and \(H_{\mu \nu }\), are the Einstein tensor and the Lanczos tensor with the following expressions

$$\begin{aligned} G_{\mu \nu }= & {} R_{\mu \nu }-\frac{1}{2}R~ g_{\mu \nu },\nonumber \\ H_{\mu \nu }= & {} 2\Bigr ( R R_{\mu \nu }-2R_{\mu \sigma } {R}{^\sigma }_{\nu } -2 R_{\mu \sigma \nu \rho }{R}^{\sigma \rho } \nonumber \\&- R_{\mu \sigma \rho \delta }{R}^{\sigma \rho \delta }{_\nu }\Bigl )- \frac{1}{2}~g_{\mu \nu }~{\mathcal {L}}_{\text {GB}}, \end{aligned}$$
(5)

with R the Ricci scalar, \(R_{\mu \nu }\) the Ricci tensor and \(R_{\mu \sigma \nu \rho }\) the Riemann tensor, respectively. As a result the above theory is free from Ostrogradski instability and the static and spherically symmetric black hole solution was discovered [7].

Since we are interested in charged stars, we assume \(T_{\mu \nu }= M_{\mu \nu }+E_{\mu \nu }\) in (4) stands for the energy-momentum tensor, which in this study is written as a sum of two terms,

$$\begin{aligned} M_{\mu \nu }= & {} (\rho +p)u_{\mu }u_{\nu }+ pg_{\mu \nu },~~~~ \text{ and }~~~~~~ E_{\mu \nu }\nonumber \\= & {} \frac{1}{4\pi }\left( F_{\mu }^{\gamma }F_{\nu \gamma }- \frac{1}{4}g_{\mu \nu } F_{\gamma \beta }F^{\gamma \beta }\right) , \end{aligned}$$
(6)

where \(M_{\mu \nu }\) is the energy–momentum tensor of a perfect fluid in D dimension with \(p=p(r)\) is the pressure, \(\rho =\rho (r)\) is the energy density of matter, and \(u_{\nu }\) is the fluid’s D-velocity. The \(E_{\mu \nu }\) is the electromagnetic energy–momentum tensor, which is given in terms of the Faraday–Maxwell tensor \(F_{\mu \nu }\) described by \(F_{\mu \nu } =\nabla _{\nu } A_{\mu }-\nabla _{\mu } A_{\nu }\) with \(\nabla _{\nu }\) representing the covariant derivative, and \(A_{\mu }\) the electromagnetic gauge field. The latter satisfies the covariant Maxwell equations, \([(-g)^{1/2} F^{\mu \nu } ]_{,\nu }=4 \pi j^{\mu }(-g)^{1/2}\) with \(j^{\mu }\) stands for the electromagnetic D-current and \(g \equiv \text {det}(g^{\mu \nu })\). Only the radial component \(F^{01}\) is non-zero, and the last equation is satisfied if \(F^{01}= -F^{10}\).

To achieve the compact charged spheres we take the following static, spherically symmetric D-dimensional metric ansatz as follows:

$$\begin{aligned} ds^2_{D}= - e^{2\Phi (r)}dt^2 + e^{2\lambda (r)}dr^2 + r^{2}d\Omega _{D-2}^2, \end{aligned}$$
(7)

where \(d\Omega _{D-2}^2\) is the metric on the unit \((D-2)\)-dimensional sphere. The functions \(\Phi (r)\) and \(\lambda (r)\) are depending on the radial coordinate r, respectively.

Taking all of these into account and using the metric (7) with stress tensor (6), in the limit \(D \rightarrow 4\), the non-zero components of the field equations are

$$\begin{aligned}&\frac{\alpha (1-e^{-2\lambda })}{r^3}\left[ 4\lambda ' e^{-2\lambda }-\frac{(1-e^{-2\lambda })}{r}\right] \nonumber \\&+e^{-2\lambda }\left( {2\lambda ' \over r}-{1\over r^2}\right) +{1\over r^2}= 8 \pi \rho +E^2 \end{aligned}$$
(8)
$$\begin{aligned}&\frac{\alpha (1-e^{-2\lambda })}{r^3}\left[ 4\Phi ' e^{-2\lambda }+\frac{(1-e^{-2\lambda })}{r}\right] \nonumber \\&+e^{-2\lambda }\left( {2\Phi ' \over r}+{1\over r^2}\right) -{1\over r^2}= 8 \pi p - E^2, \end{aligned}$$
(9)
$$\begin{aligned}&e^{-2\lambda }\left[ \Phi ''+\Phi '^2+\frac{1}{r}\left( \Phi '-\lambda ' \right) \right. \nonumber \\&\left. +\Phi ' \lambda ' \left( \frac{8\alpha e^{-2\lambda } }{r^2}-1\right) - \frac{2\alpha (1-e^{-2\lambda })}{r^2} \right. \nonumber \\&\left. \times \Bigg \{ \frac{1}{r}\left( \Phi '-\lambda ' \right) \right. \left. -2\left( \Phi ''+\Phi '^2 -\Phi ' \lambda ' \right) + \frac{1}{r^2}(e^{2\lambda }-1) \Bigg \} \right] \nonumber \\&= 8 \pi p+ E^2. \end{aligned}$$
(10)
$$\begin{aligned}&4 \pi {\sigma } r^2= e^{-\lambda }\left( r^2 E\right) ' . \end{aligned}$$
(11)

In the above system the quantities E and \(\sigma \) are the electric field intensity and the proper charge density respectively and primes denote differentiation with respect to r. Finally, Eqs. (8–11) are invariant under the transformation \(E \rightarrow -E\), \(\sigma \rightarrow - \sigma \). We observe that in the absence of the electric field, i.e., with \(E(r) = 0\), the above expression reduces to the standard relation for isotropic perfect fluid in 4D EGB gravity [46]. The proper charge density \(\sigma \) appears explicitly in the inhomogeneous Maxwell equation (11). It determines the net electric charge within a sphere of radius r is given by

$$\begin{aligned} q(r)= 4\pi \int ^{r}_{0} \sigma (r) e^{\lambda (r)} r^2 dr, \end{aligned}$$
(12)

where the electric charge is connected to the electric field through the relation \(E(r)=q(r)/r^2\). Finally, the conservation of the matter energy momentum tensor yields the following equation,

$$\begin{aligned} \frac{dp}{dr}= & {} - (\rho + p)\frac{d\Phi }{dr} +\frac{q }{4 \pi r^4}{dq \over dr},\nonumber \\= & {} - (\rho + p)\frac{d\Phi }{dr} +\frac{1 }{4 \pi }\left( EE'+{2 \over r} E^2\right) . \end{aligned}$$
(13)

At this stage we introduce the coordinate transformation followed by Durgapal and Bannerji [78],

$$\begin{aligned} x = Cr^2,~~ e^{-2\lambda } = Z(x)~~~ \mathrm {and}~~~ e^{2\Phi } = y^2(x), \end{aligned}$$
(14)

where C is an arbitrary constant. The benefit of this transformation is that the master nonlinear isotropy field equation (10) is transformed to a linear differential equation and we can profit from the vast knowledge on such equations. Under the transformation (14), we are able to express the components of the field Eqs. (8–11), which yield

$$\begin{aligned} 8\pi \rho +E^2= & {} \frac{C}{2 x^2} \bigg [4 x (\beta (Z-1) -x) \dot{Z}\nonumber \\&- (Z-1) (2 x+\beta (Z-1))\bigg ], \end{aligned}$$
(15)
$$\begin{aligned} 8\pi p-E^2= & {} \frac{C}{2 x^2 y} \bigg [ 8 x Z \dot{y} (x-\beta ( Z-1))\nonumber \\&+y (Z-1) (2 x+\beta (Z-1)) \bigg ], \end{aligned}$$
(16)
$$\begin{aligned} 0= & {} \beta \left( 4x^2Z(1-Z)\ddot{y} + 2x\left[ 2Z(Z - 1) \right. \right. \nonumber \\&\left. \left. + x\dot{Z}(1-3Z)\right] \dot{y} -(1-Z)(\dot{Z}x -Z +1)y \right) + \nonumber \\&x(4x^2 Z\ddot{y} + 2x^2\dot{Z}\dot{y}\nonumber \\&+ (\dot{Z}x -Z + 1-\frac{E^2 x }{C})y) , \end{aligned}$$
(17)
$$\begin{aligned} \frac{\sigma ^2}{C}= & {} \frac{Z}{4 \pi ^2 x}\left( x\dot{E} + E \right) ^2 \end{aligned}$$
(18)

where dots denote differentiation with respect to the variable x. The parameter \(\beta = 2\alpha C\), and here we measure in \(\text {km}^{2}\). In the above we have a system of four equations with six unknowns \(\rho \), p, E, \(\sigma \), y and Z, respectively. Hence, to solve the system, we are free to specify two of the six unknowns; in this treatment we assume forms for Z and E. In general, when the metric potential Z and the electric field intensity E are specified then one can easily get the metric function y by integrating (17). Next, we explain how we construct charged compact stars with isotropic matter.

3 Exact solutions

We now analyze the static and spherically symmetric (SSS) field equations for a class of exact 4D EGB models. It makes sense to follow processes that have led to success in the standard theory of general relativity namely prescribing one of the metric potentials and the electric field intensity. In this case it turns out that even after prescribing a potential, it is still nontrivial finding a suitable function for E to allow the integration of the master isotropy equation. Rewriting the isotropy equation (17) in the form

$$\begin{aligned}&4x^2Z\left( x + \beta (1-Z)\right) \ddot{y} \nonumber \\&+ 2x\left( x^2\dot{Z} + \beta \left( 2Z(Z-1) + x\dot{Z}(1-3Z) \right) \right) \dot{y}\nonumber \\&+ \left( (\dot{Z}x -Z+1)(x-\beta (1-Z)) -\frac{E^2 x^2}{C} \right) y = 0 \qquad \end{aligned}$$
(19)

offers a possible route to find rich classes of exact solution. Connecting the electric field intensity E and the spatial metric potential Z via

$$\begin{aligned} \frac{E^2}{C} = \frac{(\dot{Z}x -Z+1)(x-\beta (1-Z))}{x^2} \end{aligned}$$
(20)

results in the suppression of the y term thus effectively reducing the differential equation to first order and with better prospects of finding exact solutions.

4 Physical models

4.1 Vaidya–Tikekar model

In our investigation we study the gravitational potential in the form

$$\begin{aligned} Z=\frac{1+a x}{1+b x}, \end{aligned}$$
(21)

where a and b are constants with units in \(\text {km}^{-2}\). The chosen form ensures that the metric function \(e^{2\lambda }\) is regular and finite at the centre of the sphere for the wide range of values of parameters a and b. Since the potential Z contains known physically acceptable uncharged and charged relativistic stars for particular values of a and b i.e. when \(a=-\frac{1}{2}\) and \(b=1\) we regain the uncharged dense neutron star of Durgapal and Bannerji [78] and Tikekar super dense star model [79] for the values \(a = -1\), \(b = 7\). On substituting (21) in (19) and using (20) we obtain the function of y(r) which is

$$\begin{aligned} y= & {} c_1 \left( \frac{(2 a \beta +1) (a-b)^{3/2} \sqrt{\frac{a b x+a}{a-b}} \xi _1}{a^2 \sqrt{b(b x+1)}}\right. \nonumber \\&\left. +\frac{2 (b \beta (a-b))^{3/2} \xi _2}{b^2 \sqrt{(b-a) (a \beta -1)}}+\frac{\sqrt{a x+1} \sqrt{b x+1}}{a}\right) +c_2,\nonumber \\ \end{aligned}$$
(22)

where \(\xi _1=\sinh ^{-1}\left( \frac{\sqrt{b} \sqrt{a x+1}}{\sqrt{a-b}}\right) \) and \(\xi _2=\tan ^{-1}\left( \frac{\sqrt{b \beta (a x+1)} }{\sqrt{b x+1} \sqrt{ (1-a \beta )}}\right) \). Hence the complete solution of the field equations (15) and (16) is then given by

$$\begin{aligned} 8\pi \rho= & {} \frac{C (a-b) (\beta (a-b) (b x+3)-6 (b x+1))}{2 (b x+1)^3}, \end{aligned}$$
(23)
$$\begin{aligned} 8\pi p= & {} \frac{4 a^2 b C c_1 (a \beta -1) \sqrt{a x+1}}{\sqrt{b} c_1 \sqrt{a-b} \xi _3 +a^2 b c_2 (a \beta -1) \sqrt{b x+1}+a b c_1 (a \beta -1) \sqrt{a x+1} (b x+1)}\nonumber \\&+\frac{C (a-b) (\beta (b-a) (b x-1)+2 b x+2)}{2 (b x+1)^3}, \end{aligned}$$
(24)

where \(\xi _3^2= \Big ((a-b) (a \beta -1) (2 a \beta +1) \sqrt{\frac{a b x+a}{a-b}} \xi _1-2 a^2 \beta ^{3/2} \sqrt{b x+1} \sqrt{(b-a) (a \beta -1)} \xi _2\Big )\), and the speed of sound is given by

$$\begin{aligned}&\frac{d p}{d \rho } = \bigg [\frac{a^2 b^2 c_1 x (a-b) (1-a \beta ) (b x+1)^4 (\zeta _1 (-(a-b)) (a \beta -b \beta +2 b x+2)-\zeta _2)}{\zeta _1^2 \sqrt{a x+1} \sqrt{(b-a) (a \beta -1)} (-a \beta +b (\beta +x)+1)} \nonumber \\&-(b x+1) \bigg (-\frac{a (\text {bx}+1) \zeta _3}{(\text {ax}+1) b} -\zeta _5 (a-b) (a \beta +2 b^2 x^2-b \beta +4 b x+2) +\frac{1}{2} \zeta _2 x (a-b) \nonumber \\&\times (-a \beta +b (\beta +x)+1) (b (2 a \beta x+3 \beta +x)-a \beta +1)\nonumber \\&+\zeta _5 (b-a) (a \beta -b \beta +2 b x+2)+\zeta _4 (a-b) (b x+1) -\frac{b \xi _3 (b x+1)}{x}+\zeta _3-\zeta _4\bigg ) \nonumber \\&\times \frac{1}{\zeta _5}\bigg ] \bigg / 2 b x (b-a) (-x \beta b^2-4 \beta b +x (a \beta -6) b+4 a \beta -6), \end{aligned}$$
(25)

where

$$\begin{aligned} \zeta _1= & {} a^2 b^2 c_2 \sqrt{b x+1} \sqrt{(b-a) (a \beta -1)}\\&+c_1 \left( 2 a^2 \sqrt{b x+1} (b \beta (a-b))^{3/2} \xi _2\right. \\&+a b^2 \sqrt{a x+1} (b x+1) \sqrt{(b-a) (a \beta -1)} +b^{3/2} (a-b)^{3/2} \nonumber \\&\left. (2 a \beta +1) \sqrt{-(a-b) (a \beta -1)} \sqrt{\frac{a b x+a}{a-b}} \xi _1 \right) , \nonumber \\&\zeta _2=8 a^2 b^2 c_1 \sqrt{a x+1} (b x+1)^2 \sqrt{(b-a) (a \beta -1)}, \nonumber \\&\zeta _3= b x \sqrt{a x+1} (-a \beta +b (\beta +x)+1)^2 \zeta _2,\nonumber \\&\zeta _4=\zeta _2 \sqrt{a x+1} (a \beta -b (\beta +x)-1)\\&\left( a \beta -b^2 x^2-b (\beta +2 x)-1\right) ,\nonumber \\&\zeta _5=\zeta _1 \sqrt{a x+1} (-a \beta +b (\beta +x)+1)^2. \end{aligned}$$
Fig. 1
figure 1

The pressure profile is plotted as a function of radius for Vidya–Tikekar (VT) and Finch–Skea (FS) metric potential for \(\beta = 4\) and 0, respectively. For left diagrams the chosen values are \(a=7,~b=0.1,~c_1=0.5,~c_2=10,~C=0.05\); and for right diagrams we consider \(c_1=-0.009,~c_2=-0.1,~C=10\), respectively

Full size image
Fig. 2
figure 2

Variation of energy density as a function of the radial coordinate x for compact star. The labels of the curves are the same as given in Fig. 1

Full size image
Fig. 3
figure 3

Variation of the electric charge q as a function of the radial coordinate x inside the stellar interior

Full size image

4.2 Finch–Skea model

Now we turn our attention to another physically admissible ansatz, namely, Finch and Skea [80] which can be regained by setting \(a = 0\) and \(b=1\) in (21). This space-time geometry is well behaved and satisfies all criteria of physical acceptability by Delgaty and Lake [81]. The choice of Z is

$$\begin{aligned} Z=\frac{1}{1+x}. \end{aligned}$$
(26)

On substituting (26) in (19) and using (20), we obtain the solution

$$\begin{aligned} y=c_1 \left( 2 \beta ^{3/2} \eta _1+\frac{2}{3} \sqrt{x+1} (-3 \beta +x+1)\right) +c_2, \end{aligned}$$
(27)

where \(\eta _1=\tan ^{-1}\left( \frac{\sqrt{x+1}}{\sqrt{\beta }}\right) .\) With these assumptions we obtain the energy density and pressure using the expression (15) and (16), are

$$\begin{aligned} 8 \pi \rho= & {} \frac{c (3 (\beta +2)+(\beta +6) x)}{2 (x+1)^3},\end{aligned}$$
(28)
$$\begin{aligned} 8 \pi p= & {} -\frac{c \left( 2 c_1 \left( -3 \beta ^2 \left( x^2-1\right) +3 \beta ^{3/2} \eta _1 \eta _2+\beta (x-7) (x+1)^2-10 (x+1)^3\right) +3 c_2 \eta _2\right) }{2 (x+1)^{7/2} \left( 2 c_1 \left( 3 \beta ^{3/2} \eta _1+\sqrt{x+1} (-3 \beta +x+1)\right) +3 c_2\right) }, \end{aligned}$$
(29)

where \(\eta _2= \sqrt{x+1} (-\beta +(\beta +2) x+2), \) and the speed of sound is given by

$$\begin{aligned} \frac{dp}{d\rho }= & {} \bigg [-4 c_1^2 (3 \beta ^{3/2} \eta _1 (x+1) (12 \beta ^3-4 \beta ^2-15 \beta \nonumber \\&+(-4 \beta ^2-11 \beta +3) x^2+(2 \beta +1) x^3 \nonumber \\&-(6 \beta ^3+8 \beta ^2+28 \beta -3) x+1)\nonumber \\&+9 \beta ^3 \eta _1^2 \sqrt{x+1} (-2 \beta ^2\nonumber \\&+(\beta +2) x^2+(\beta ^2+\beta +4) x+2) \nonumber \\&+(x+1)^{3/2} (-18 \beta ^4+12 \beta ^3+25 \beta ^2-6 \beta \nonumber \\&-(5 \beta ^2+3 \beta +40) x^3+3 (\beta ^3+5 \beta ^2-5 \beta -20) x^2 \nonumber \\&+(\beta -10) x^4+(9 \beta ^4+15 \beta ^3+45 \beta ^2-17 \beta -40)\nonumber \\&x-10))-6 c_2 c_1 (\beta +x+1) \nonumber \\&((x+1) (12 \beta ^2-16 \beta +(2 \beta +1) x^2-2 (3 \beta ^2\nonumber \\&+7 \beta -1) x+1)+6 \beta ^{3/2} \eta _1\nonumber \\&\sqrt{x+1} (-2 \beta +(\beta +2) x+2)) \nonumber \\&-9 c_2^2 \sqrt{x+1} \bigg (-2 \beta ^2+(\beta +2) x^2\nonumber \\&+(\beta ^2+\beta +4) x+2\bigg )\bigg ] \bigg /\nonumber \\&\sqrt{x+1} (\beta +x+1) (4 \beta +(\beta +6) x+6) \eta _3, \end{aligned}$$
(30)

where \(\eta _3= \big (2 c_1 \big (3 \beta ^{3/2} \eta _1+\sqrt{x+1} (-3 \beta +x+1)\big )+3 c_2\big ){}^2.\)

5 Matching

At this stage the interior solution is smoothly connected to the vacuum exterior Reissner–Nordström metric at the junction surface with radius \(r = R\). In this case the line element for the star at the boundary \((r=R)\) has the form

$$\begin{aligned} {ds}^2= & {} - \left( \left( 2 \beta ^{3/2} \tan ^{-1}\left( \frac{\sqrt{CR^2+1}}{\sqrt{\beta }}\right) \right. \right. \nonumber \\&\left. \left. +\frac{2}{3} \sqrt{CR^2+1} (-3 \beta +CR^2+1)\right) c_1+c_2\right) ^2 {dt}^2 \nonumber \\&+ \left( 1+CR^2 \right) dr^2 +r^2(d\theta ^2 + \sin ^2 \theta d\phi ^2), \end{aligned}$$
(31)

The metric (31) should be matched with the exterior line element. Accordingly the arbitrary constant C may be expressed as

$$\begin{aligned} C= & {} \frac{1}{R^2}\left[ \left( 1-\frac{2M}{R}+ \frac{Q^2}{R^2} \right) ^{-1} -1\right] , \end{aligned}$$
(32)

in terms of the radius R and mass M of the sphere. Since, the pressure vanishing at the boundary results in the following relation

$$\begin{aligned} c_2= & {} -\frac{2 c_1}{3 \kappa _1} (\beta (CR^2)^2 \sqrt{(CR^2)+1}-10 (CR^2)^2 \sqrt{(CR^2)+1}\nonumber \\&+6 \beta ^{3/2} (CR^2) \kappa _2+6 \beta ^{3/2} \kappa _2 \nonumber \\&+3 \beta ^{5/2} (CR^2) \kappa _2-3 \beta ^{5/2} \kappa _2-3 \beta ^2 (CR^2) \sqrt{(CR^2)+1}\nonumber \\&+3 \beta ^2 \sqrt{(CR^2)+1}-6 \beta (CR^2) \sqrt{(CR^2)+1} \nonumber \\&-7 \beta \sqrt{(CR^2)+1}-20 (CR^2)\nonumber \\&\sqrt{(CR^2)+1}-10 \sqrt{(CR^2)+1}) \end{aligned}$$
(33)

where \(\kappa _1= (-\beta +\beta CR^2+2 CR^2+2)\) and \(\kappa _2= \tan ^{-1}\left( \frac{\sqrt{(CR^2)+1}}{\sqrt{\beta }}\right) \) and using the condition in (31) we are able to write \(c_1\) as

$$\begin{aligned} c_1= & {} \frac{\kappa _1 \sqrt{-2 M R+Q^2+R^2}}{8R \left( CR^2+1\right) ^{5/2}} \end{aligned}$$
(34)

which settles the integration constants \(c_1\) and \(c_2\).

Fig. 4
figure 4

Variation of the sound speed with radial coordinate x inside the stellar interior

Full size image
Fig. 5
figure 5

Variation of mass–radius relation

Full size image
Fig. 6
figure 6

Variation of energy conditions with the radial coordinate x

Full size image
Fig. 7
figure 7

Variation of adiabatic index with radius

Full size image
Fig. 8
figure 8

The three different forces, viz. gravitational force (\(F_g\)), hydrostatic force (\(F_h\)) and electric force (\(F_e\)) are plotted against x

Full size image

6 Physical properties of the spheres

We now proceed to analyse the physical viability of the charged solutions obtained in this paper. We will show that obtained solutions are physically reasonable. We utilise the exact solution obtained in Sect. 4 for a graphical analysis. The physical characteristics of the Vaidya–Tikekar ansatz are displayed in the left panels of each of the figures while the plots for Finch–Skea ansatz appear on the right. In the case of left and right plots we have selected the parameters as follows after extensive empirical fine-tuning: \(a=7 \text {km}^{-2}\), \(b=0.1 \text {km}^{-2}\), \(\beta = 4 \text {km}^{2}\), \(c_1=0.5,~c_2=10,~C=0.05\) and \(\beta =4 \text {km}^{2},~c_1=-0.009,~c_2=-0.1,~C=10\), respectively. In Figs. 1, 2, 3, 4 and 5 the EGB model (\(\beta = 4\)) together with its Einstein (\(\beta = 0\)) are depicted. The software package Mathematica (Wolfram [82]) was used to generate plots for the matter variables.

  1. (i)

    From Fig. 1 we observe that the pressure decreases smoothly towards the surface layer of the star. Since, the pressure vanishes at some finite distance which identify the boundary of the star at \(x = 15\) km and \(x = 1\) km, respectively. This immediately suggests that the model may represent a charged compact star. Moreover, the effect of the higher curvature terms is clear in each model. When the higher EGB terms are switched off (\(\alpha = 0\)) the Einstein model is obtained and it may be noted that there is a significant decrease in the radius of the sphere. Evidently higher curvature terms admit larger spheres by total volume.

  2. (ii)

    As it is clear from the Fig. 2 that the density profile is a monotonically decreasing function as one moves from the stellar center towards the stellar boundary. Figure 2, therefore, conveys an important message that the model is regular and well-behaved at all interior points of the star. Contrasting with the standard (\(\alpha = 0\)) sphere it may be observed that for the same radial value there is a substantially higher density in both variants of the model suggesting that higher curvature effects admit more compact objects than their Einstein versions.

  3. (iii)

    The electric charge within the radius r can be obtained by computing the volume integral of the charge density in Eq. (12). As a consequence of our definition q(x) vanishes at the centre, remains continuous and bounded in the interior of the star. Note that other choices of \(E^2\) in Eq. (20) generates different profiles as indicated in different literature. Moreover, we see that the electric charge is \(q \sim 10^{20} \mathrm{Coulomb}\) inside the fluid sphere. It is worth mentioning that the Coulomb repulsive force will add up to the internal pressure of the system and the entire repulsive force will be balanced by the gravitational force. We illustrate this situation in Fig. 3 which is positive, continuous and monotonically increasing for a certain region and then decreasing towards the boundary. Compared to GR, we see that the effect of net electric charge is higher for EGB gravity due to the presence of GB coupling constant \(\alpha \), and consequently leads to the higher mass of the compact stars.

  4. (iv)

    The causality condition required that inside the static configuration the speed of sound should be less than the speed of light i.e., \(0 \le v^2_s=\frac{dp}{d\rho } \le 1\). With the use of Eqs. (25) and (30) one can obtain an expression for \(v^2_s\). Figure 5 shows the sound speed of electrically charged compact stars. Thus, we argue that this criterion is met everywhere inside the star. In addition, it is noticeable that near the stellar centre there is about a two-fold increase in the sound speed when the EGB configuration is contrasted with the Einstein case. It should be borne in mind that the sound speed squared \(\frac{dp}{d\rho }\) is exhibited. Moving towards the stellar surface we find that the difference in sound speed decreases but causality is never violated in all cases.

  5. (v)

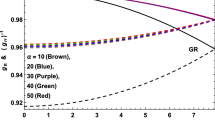
    The variation of the mass-radius \((M-R)\) relationship for all configurations is portrayed in Fig. 5. For both models it is observed that the compactification decreases when the higher curvature EGB effects are present. At the centre there is no difference however as the boundary is approached the EGB and Einstein cases appear to bifurcate uniformly to some maximum separation on the boundary. It is evident from the Fig. 5 that the maximum mass of compact stars can be much larger than that in GR when the parameter \(\alpha \) in EGB gravity is positive. In fact, Ray et al. [83] have pointed out that the charge can be as high as \(10^{20}\) Coulomb to bring in any significant effect on the \(M-R\) relation of the stellar configuration. Moreover, the existence of ultra-strong electric fields on the surfaces of quark stars, which may lead to huge electric fields as high as \(10^{19}\) V/cm was inferred by [84]. Notice that compact star model with Vaidya and Tikekar metric ansatz are able to reach a higher mass about \(\sim 2 M_{\odot }\), as can be seen in Fig. 5 (left panel). Accumulated all the above information our results provide circumstantial evidence in favor of quark stars in EGB gravity. In addition to this the \(M-R\) relationship is an indicator of the equation of state. From both models it may be observed that when higher curvature terms are active the equation of state becomes more stiff. That is for a given mass, the EGB models admit a larger radius. Consequently a larger maximum mass would result from the inclusion of the EGB effects. Alternatively this means that for a change in density there is a larger change in pressure when EGB models are compared to their Einstein counterparts.

  6. (vi)

    The energy conditions (ECs) are local inequalities, depending on the energy momentum tensor, that capture the idea of energy should be positive for strange star. Our analysis require that the following energy conditions, viz., (i) weak energy condition (WEC), (ii) strong energy condition (SEC) and (iii) dominant energy condition (DEC) hold true at each interior point of the star. These conditions are equivalent to

    $$\begin{aligned}&\text {NEC}: \rho + p \ge 0,~~~\text {WEC}: \rho + p \ge 0, ~~\text {and}~~ \rho + \frac{E^2}{8\pi } 0, \nonumber \\\end{aligned}$$
    (35)
    $$\begin{aligned}&\text {SEC}: \rho + p \ge 0, ~~\text {and}~~ \rho + 3p+ \frac{E^2}{4\pi } \ge 0, ~~ \nonumber \\&\quad \text {DEC}: \rho + \frac{E^2}{8\pi } \ge 0, ~~\text {and}~~ \rho - p+ \frac{E^2}{4\pi } \ge 0, \end{aligned}$$
    (36)

    Variations of ECs for the charged fluid star are represented in Fig. 6 for our choice of parametric space. The plot shows that ECs are obeyed everywhere, which means that the ECs are satisfied for all values of x.

  7. (iv)

    Our main result for the charged fluid sphere is the adiabatic index (\(\Gamma \)) which is related to the thermodynamical quantity. Addressing the instability problem Chandrasekhar [85] introduced a criterion for dynamical stability based on the variational method. To be more specific, the expression for the adiabatic index reads

    $$\begin{aligned} \Gamma =\frac{p+\rho }{p}\,\frac{dp}{d\rho }\, , \end{aligned}$$
    (37)

    The Eq. (37) is a dimensionless quantity measuring the stiffness of the EoS. This result has been extended to include pressure anisotropy, viscosity and heat flow by Herrera and co-workers [86, 87]. It is notable that for dynamical stability \(\gamma \) should be more than 4/3 \((i.e~ \gamma > 1.33)\). For investigating its effects, we plot Fig. 7 shows that our solution is stable against the radial adiabatic infinitesimal perturbations.

  8. (v)

    A system is considered to be in equilibrium, if the summation of all active forces on the system is Zero. This can be achieved by formulating the modified TOV equation given in Eq. (13), where the first term represents the hydrodynamic force (\(F_h \)), the second term is gravitational force (\(F_g\)) and the final term corresponds to electric force (\(F_e \)), respectively. For further investigation, we plot Fig. 8. As one can see that the equilibrium of the forces is achieved for our chosen parametric values and confirms stability of the system.

7 Summary and discussion

Among the higher curvature gravitational theories, the recently proposed novel 4D Einstein–Gauss–Bonnet gravity has received intensive interest because the GB coupling constant could contribute to the Einstein’s field equations by introducing a redefinition \(\alpha \rightarrow \alpha /(D-4)\) in D dimension and taking the limit \(D \rightarrow 4\). Motivated by this gravity theory, in this work, we thoroughly investigate static and spherically symmetric compact charged spheres made of a charged perfect fluid. Two new classes of exact solutions have been reported. Utilizing the coordinate transformation (14), we first convert the field equations in a different, but equivalent form. This transformation has been successfully utilized in the Einstein case to generate exact solutions.

After converting the master pressure isotropy equation we obtained an exact solution by prescribing an ansatz for the gravitational potential Z and by connecting the electric-field intensity E with Z to simplify the master field equation. This gravitational potential contained a number of interesting special cases such as the Vaidya–Tikekar and Finch–Skea potentials, and was used to find the structure of the second potential y. The simple form of the solutions found facilitate the analysis of the physical features of a charged sphere. We find that, in both the Vaidya–Tikekar and Finch–Skea cases, models exist satisfying the elementary physical requirements for representing a dense compact star through a graphical approach. We have shown that in the presence of such an adjustable parameter, it is possible to accommodate a large class of charged solutions satisfy the usual requirements of positivity of density and pressure, existence of a surface of vanishing pressure, all the energy conditions being met, a subluminal sound speed and equilibrium condition. We also found that the maximum mass of a compact star can be much larger than that in GR when the parameter \(\alpha \) is positive in 4D EGB gravity. In summary, it is interesting to observe that the 4D EGB theory admits physically palatable models consistent with basic conditions in the case of static spherically symmetric spacetimes.