1 Introduction

The energy loss of ions in matter has been long studied. There are several methods that accurately describe and reproduce the widely available experimental data in solids [1,2,3,4]. However, the interactions of charged particles in plasmas are still not fully understood and only few experimental data are available [5, 6]. This is a subject of great interest for different areas of research, such as the development of magnetic and inertial confinement fusion and for better understanding of Warm Dense Matter (WDM), etc [7,8,9].

On the other hand, experiments in the past few years have shown that the stopping power contribution of target bound electrons is relatively important in a considerable range of plasma temperatures and densities [10,11,12,13]. The relevance of this contribution depends on the degree of ionization and temperature of the plasma.

Free electron stopping power contribution can be estimated through the dielectric formalism, based on dielectric functions of the plasma target [14, 15]. The random phase approximation (RPA) dielectric function is interesting as it is valid for plasmas of all degeneracies, although does not consider collisions between target electrons [16].

There are several theoretical techniques for treating the bound stopping power. Many methods use either an ad hoc combination of independent free and bound electrons or an inhomogeneous WDM theory. For the first case, the most usual approach for the bound contribution is to use a Bethe-Bloch formula at high energies with a mean ionization potential following the method proposed by Mehlhorn [17] which also includes the LSS [18] approximation for the low projectile velocities regime. A similar approach is that used by Zimmerman [19]. Unified Wave Packet model (UWPM) [20] is a recent model that relies on this scheme, but uses the Kaneko’s dielectric function instead.

In the second case, a common theory is the average-atom local-density approximation (AA-LDA) method. These methods consider an inhomogeneous density with a mean ionization potential. Different formulations of the LDA can be found like those proposed by Wang et al [20], which use the “atom-in-jellium” model, where the atom is represented as a point nucleus embedded in a spherical cavity in a continuous background of positive charge; the MUZE model [21], that describes the distribution of electrons in an average atom within a Wigner–Seitz cell; or the SCAALP model [22], based on the neutral-pseudo-atom concept.

In this work, a method is presented that lies in the first mentioned technique, an ad hoc combination of free and bound electrons. A dielectric function for free electrons at any degeneracy [23] is used with the addition of the shellwise local plasma approximation (SLPA) [24, 25] for bound electrons. SLPA is specially suitable when dealing with multi-electronic targets and high energy collisions in which the target bound shells are involved. The main characteristic of the SLPA is the independent-shell consideration, meaning that only the electrons of the same binding energy respond collectively to the ion perturbation.

The paper is organized as follows. In Sect. 2, an explanation of the dielectric formalism, functions used in this work and detailed description of the SLPA formalism are given. In Sect. 3, our theoretical results are shown, first at a \(T=0\) comparing with SRIM code [26] for solids, showing excellent agreement. Then, a study of the variation of the stopping with ionization and temperature is carried out. First, ionization effect is studied in a cold gas. Second, the temperature effect is analyzed in plasmas. Comparison at diverse conditions with other methods is provided. Finally, in Sect. 4, conclusions of our method are summarized.

Atomic units (a.u.),  \(e=\hbar = m_{e}=1\), are used through all the work, unless other units are stated.

2 Dielectric formalism

Above certain energy, the energy loss of a charged particle in matter is mainly caused by target electrons. There are many theoretical methods to calculate the electronic stopping power of different targets, being one of the most common the dielectric formalism introduced by Fermi [27] and further developed by Fermi and Teller [28]. In the dielectric formalism, the electron response of an isotropic and homogeneous material to a perturbation produced by an external charge density is contained in the dielectric function \(\epsilon (k,\omega )\) of the medium. The expression to calculate the electronic stopping power is

$$\begin{aligned} S = \frac{2Z^{2}}{\pi v^{2}} \int _{0}^{\infty } \frac{dk}{k}\int _{0}^{kv} d \omega \omega \text {Im}\left[ \frac{-1}{\epsilon (k,\omega ) } \right] , \end{aligned}$$
(1)

where \(\omega \) is the energy transferred, k the momentum transferred and v is the projectile velocity. \(\text{ Im }\left[ \frac{-1}{\epsilon (k,\omega )}\right] \) is called the energy loss function. The dielectric formalism implies linear response, perturbative approximation, thus square dependence with the projectile charge Z, as can be noted in Eq. (1)

As mentioned before, free and bound electron contributions to the stopping power are considered separately. Therefore, the total stopping is

$$\begin{aligned} S=S_{free}+S_{bound}. \end{aligned}$$
(2)

2.1 Free electrons stopping

The dielectric function of a collisionless free electron gas was calculated first by Lindhard [14] in the Random Phase Approximation. Lindhard’s treatment is limited to free electrons at \(T = 0\). However, the same analysis can be done for matter at any temperature [23, 29, 30], starting from the general expression of the dielectric function

$$\begin{aligned} \epsilon (k,\omega )=1+\left( \frac{1}{\pi k}\right) ^{2} \int d^{3}k' \frac{\hat{f}(\vec {k}+\vec {k'})-\hat{f}(\vec {k'})}{\omega +i\delta - (E_{\vec {k}+\vec {k'}}-E_{\vec {k'}})}, \end{aligned}$$
(3)

where \(E_{k} = \hbar ^{2}k^{2}/2m\), f(k) is the Fermi function, \(\delta \) is the collision frequency between electrons and

$$\begin{aligned} f(\vec {k})=\{ 1 + exp\left[ \beta (E_{k}-\mu )\right] \} ^{-1}, \end{aligned}$$
(4)

where \(\beta = 1/k_{B}T\) with \(k_{B}\) being the Boltzmann’s constant. \(\mu \) is the chemical potential of the plasma and can be calculated using the Femi-Dirac integral of order 1/2.

The imaginary part of the dielectric function can be obtained by direct integration for \(\delta \rightarrow 0\).

$$\begin{aligned} \text {Im}\epsilon _{A}=\frac{\pi \chi _{0}^{2}}{8z^{3}}\theta ln\left( \frac{1+\exp [\eta -D(u-z)^{2}]}{1+\exp [\eta -D(u+z)^{2}]}\right) , \end{aligned}$$
(5)

where \(\chi _{0}^{2}=1/\pi k_{F}\) is the coupling parameter for degenerated plasmas, \(\theta =1/D=k_{B}T/E_{F}\) is the reduced temperature, \(\eta =\beta \mu \), \(u=\omega /kv_{F}\), \(z=k/2k_{F}\) are the dimensionless Lindhard variables, being \(E_{F}=\hbar ^{2}k_{F}^{2}/2m\) the Fermi energy and \(k_{F}=(3\pi ^{2}n_{e})^{1/3}\) the corresponding momentum, with \(n_{e}\) being the free electron density. When T tends to 0

$$\begin{aligned} \lim _{T\rightarrow 0}\text {Im}\epsilon _{A}(k,\omega )= \left\{ \begin{array}{lll} \frac{\pi \chi _{0}^{2}\hbar \omega }{8z^{3}E_{F}}, &{} (u\pm z)^{2}<1 \\ \frac{\pi \chi _{0}^{2}}{8z^{3}}[1-(u-z)^{2}], &{} (u-z)^{2}<1<(u+z)^{2}, \\ 0, &{} 1<(u-z)^{2} \end{array} \right. \end{aligned}$$
(6)

which is the Lindhard dielectric function, and thus, it can be applied for solids and cold gases.

The real part of this dielectric function may be obtained from \(\text {Im}\epsilon _{A}\) using the Kramers–Kronig relations,

$$\begin{aligned} \text {Re}\epsilon _{A}(k,\omega )=1+\frac{\chi _{0}^{2}}{4z^{3}}[g(u+z)-g(u-z)], \end{aligned}$$
(7)

where the function g(x) is given by

$$\begin{aligned} g(x)=\int _{0}^{\infty } \frac{ydy}{e^{Dy^{2}-\eta }+1}ln\left| \frac{x+y}{x-y}\right| , \end{aligned}$$
(8)

which has some useful (in terms of computational time) limiting expressions for the high and low degeneracy cases explained in detail in the original Arista et al work [23]. In what follows, this function will be referred as the Arista dielectric function.

2.2 Bound electron stopping

Bound electrons must be considered to give a full, high precision description of the projectile stopping in partially ionized matter. In order to take bound electrons into account, the SLPA is used. The SLPA formulation lays over two assumptions.

2.2.1 Shellwise method

The first one is the shellwise consideration, which describes independently the stopping power of projectiles with each nl sub-shell of target bound electrons, where n and l are the principal and azimuthal quantum numbers, respectively. The stopping power for a given nl sub-shell is

$$\begin{aligned} S_{nl}=\frac{2Z^{2}}{\pi v^{2}} \int _{0}^{\infty } \frac{dk}{k}\int _{0}^{kv} d \omega \omega \text {Im}\left[ \frac{-1}{\epsilon _{nl} (k,\omega ) } \right] , \end{aligned}$$
(9)

where each \(\epsilon _{nl}\) is a Levine-Louie dielectric function for the nl shell. The total stopping will be the addition of the shell contributions \(S_{t}=\sum _{nl}S_{nl}\). Levine-Louie function is a dielectric function which includes explicitly the excitation energy given by the binding energy [31]. Levine-Louie original work uses the Lindhard function, i.e. \(T=0\) and it is defined as

$$\begin{aligned} \text {Im}\epsilon _{LL}(k,\omega )= \left\{ \begin{array}{ll} \text {Im}\epsilon _{L}(k,\omega _{g}) &{} \text{ if } |\omega |>\omega _{m} \\ 0 &{} \text{ if } |\omega |<\omega _{m}, \end{array} \right. \end{aligned}$$
(10)

with \(\omega _{m}\) being the binding energy, \(\omega _{g}=\sqrt{\omega ^{2}-\omega _{m}^{2}}\), and \(\epsilon _{L}\) being the Lindhard dielectric function as defined before. If no binding energy is taken, \(\omega _{m}=0\), the usual expressions for the dielectric function, Eqs. (5) and (7) are recovered. This method for the dielectric function satisfies the so-called f-sum rule, or particle number conservation, which is a desirable feature for a dielectric function.

2.2.2 Shellwise local plasma approximation

The second one, LPA, extends the dielectric formalism to deal with atomic bound electrons as a free-electron gas of local density. In this case, \(\epsilon _{nl}(k,\omega )\) in Eq.(9) is a mean value of a local response that depends on the electron density of the shell, \(\rho _{nl}(r)\). Thus, the \(k_{F}\) definition given before changes to \(k_{Fnl}=(3\pi ^{2}\rho _{nl}(r))^{1/3}\) and the new energy loss function is calculated as

$$\begin{aligned} \text {Im}\left[ \frac{-1}{\epsilon _{nl}(k,\omega )}\right] =\int 4\pi r^{2}\text {Im}\left[ \frac{-1}{\epsilon _{LLnl}(k,\omega ,\rho _{nl}(r))}\right] dr. \end{aligned}$$
(11)

The electron density of the shell, \(\rho _{nl}(r)\), and the binding energy are the only inputs for SLPA. For atoms, they can be obtained from the Hartree–Fock wave functions [32].

The combination of both assumptions is what is called SLPA. Note that the LPA assumption is equivalent to LDA and the main difference of our SLPA method with LDA methods is the shellwise consideration. In [33] the validity of the LDA is studied concluding that this approximation gives an overall good agreement with the “exact” results obtained by first Born approximation. A small overestimation of the stopping cross section is obtained, specially at low projectile velocities. This overestimation comes from the neglect of the threshold in the excitation. However, in the results obtained in [25, 34], SLPA offers an excellent approximation to the experimental data in solids, even around the stopping maximum, which is a very sensitive region for the stopping theories. This will also be illustrated in the next section.

To understand the effect of the LPA in the stopping power estimations, the results of applying the shellwise method and the full SLPA method are studied. In Fig. 1, it is plotted the stopping power cross section of the three carbon shells independently and the total sum at \(T=0\). It can be seen that the main effect of the LPA is to lower the peak and to broaden the distribution. Also, it can be seen clearly the gap in the projectile velocities introduced by the binding energy of the Levine-Louie dielectric function. The inner-shells have greater binding energies and thus, the gap is larger and the peak is lowered. Then, the corresponding contribution to the total stopping is small.

Fig. 1
figure 1

Shell contributions to the total stopping power cross section of solid carbon at \(T=0\) and \(\rho =2.26\) g/cm\(^{3}\) as a function of the proton velocity for shellwise and SLPA methods

Full size image

3 Theoretical results

The plasma response to a traversing charged particle depends on plasma degeneracy, i.e. density and temperature, and plasma ionization. Following this, an analysis of the ionization and temperature effects on the stopping calculations is carried out. First both effects are considered separately, changing one while maintaining the other constant. Finally, ionization as a function of temperature is implemented to consider both effects simultaneously. Density is kept constant at normal solid density, \(\rho =2.26\) \(\hbox {g/cm}^{3}\) during all the analysis. The analysis is done using a carbon target because of his interest in multiple applications. Also silicon is used in the comparison with Unified Wave Packet model.

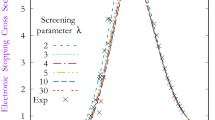
As SLPA can be used for solids, as all their electrons are bound, a comparison with SRIM code for solid carbon is shown in Fig. 2a. Within the theoretical method here presented, stopping power of inner bound electrons is calculated as described before, using SLPA with a Levine-Louie dielectric function for each shell. However, valence shells stopping are calculated using a collisional dielectric function. Here, the Mermin dielectric function [15, 29, 35] is used with a target electron-electron collision frequency of \(\delta =0.61\). This value can be found in literature [36] or obtained from the optical limit of the energy loss function, i.e. at \(k=0\) [37].

In Fig. 2a, only 1s shell is calculated using SLPA while Mermin function is used for 2s and 2p shells. Although the 1s contribution is small, in addition with the valence shells gives a very good fit to experimental results.

Fig. 2
figure 2

a Stopping power cross section of solid carbon as a function of proton velocity. b Stopping power cross section of bound electrons of a cold carbon gas target at \(T=0\) and different ionizations q

Full size image

To study the ionization effect decoupled from the temperature effect in the stopping power, a gas at \(T=0\) is considered. Figure 2b shows the results calculated with our method for the stopping power cross sections for protons interacting with the bound electrons of a cold carbon gas at different ionization states as a function of proton velocity. Notice that, as only bound contribution is shown, temperature is not relevant. q is the number of ionized electrons. In this case, every sub-shell is obtained with SLPA. The fitting curve to experimental data from the SRIM code is drawn for comparison. As it may be seen, the bound contribution suffers two effects as the ionization increases. The inner-shells have greater binding energies than outer-shells and these are increased when outer electrons are removed. As a consequence, the maximum of the stopping power caused by the bound electrons decreases drastically and also is shifted to higher projectile velocities. Therefore, the ionization is an essential parameter to determine the relevance of the bound electrons stopping power contribution. The comparison with SRIM code in Fig. 2b for carbon gas shows a good agreement, though not as good as for the solid case.

The next step of this analysis is to consider temperature effects in the projectile-target interaction using the proper ionization given by the temperature in conditions of thermal equilibrium. The mean ionization q as a function of temperature for carbon plasma is obtained from FLYCHK code [38]. These values are used to calculate the appropriate stopping power for each temperature. Notice that in the present case, considering solid-state density, the carbon ionization maintains almost constant for a wide range of temperatures. In particular, in the range 30–90 eV the ionization only suffers a minor increase. However, this is not always the case. For heavier target atoms, where ionization increases more gradually, or at lower densities, where pressure ionization does not occur, the ionization would change and so will do the free and bound contributions of the stopping power. In Fig. 3, the total stopping power cross section results at different temperatures with their associated ionization are shown. Despite bound electron contribution not changing significantly, the total stopping power is highly reduced due to the temperature effect in the free electron stopping power. In our calculation, bound electrons contribution is up to a 20 % of the total stopping at high projectile velocities in the 30–90 eV temperature range, fact that coincides with previous works [39].

Fig. 3
figure 3

Stopping power cross section as a function of proton velocity of carbon plasma at density 2.26 g/cm\(^{3}\) and at different temperatures for SLPA method

Full size image

Temperature tends to reduce the total stopping power of the plasma. On the other hand, the ionized electrons counteract this effect leading to the enhanced stopping power of hot plasmas [13]. This effect is not observed in the cases here analyzed for carbon, being the stopping reduction due to temperature the predominant effect. Taking all this into account, it is clear that temperature and ionization cannot be considered separately to describe the realistic stopping power of the plasma.

The final step of this analysis is the comparison of our method results with other models. As mentioned before, there is a wide range of temperatures in which the ionization maintains almost constant for the studied case. For simplicity, only this range of temperatures is considered in the comparison and also, ionization is taken as constant. Figure 4 shows the stopping power cross sections of a carbon plasma as a function of proton velocity at a constant ionization, \(q=4\) and different temperatures. In this graph, results of our method are compared with other theoretical models: Mehlhorn [17], Zimmerman [19] and Unified Wave Packet [40] models.

The Mehlhorn model [17] uses an expression that considers binary and collective effects in the free electrons stopping following Jackson procedure [41], and takes the minimum between the LSS method and the Bethe high energy limit for bound electrons. Results obtained are shown in subfigure a) of Fig. 4. It can be seen that better agreement is obtained at higher temperatures, but with great discrepancies found in any case. Indeed, Jackson procedure is valid for the approximation \(T\rightarrow \infty \). Furthermore, the LSS model has a very low velocity limit of validity in the case of protons, being the Bethe results the effective stopping for bound electrons. Therefore, big differences with our method at low-medium projectile velocities are expected.

Zimmerman method [19] uses a numerical approximation of the Maynard dielectric function [42] for free electrons and a Bethe-like expression with mean ionization potential expression for bound electrons. In subfigure b) of Fig. 4, results of this method are shown. Some differences arise again in the medium velocities regime. Also, a little deviation at high velocities is found. Partially, this can be explained by the usage of a mean ionization potential. As before, the difference between the two models is less significant as the temperature increases.

Fig. 4
figure 4

Stopping power cross section of a partially ionized carbon plasma as a function of proton velocity. For various methods at different temperatures, constant ionization \(q=4\) and \(\rho =2.26\) \(\hbox {g/cm}^{3}\). Solid lines: SLPA; dashed lines: a Mehlhorn [17]; b Zimmerman [19]. \(T=30\) eV: thin black lines; \(T=60\) eV; normal blue lines; \(T=90\) eV: thick red line

Full size image

A more recent model is the UWPM [40]. This model relies in Kaneko’s wave-packet model [43] for the contribution of bound electrons. It also extends the wave-packet model to describe with the same formulation the dielectric response of a plasma of free electrons in thermal equilibrium. Figure 5 shows a comparison with this model of the results obtained by SLPA. In this case, calculations of carbon are shown as before, but also those of silicon, for different temperatures at a fixed degree of ionization. For carbon, only the 1s shell provides a bound electron contribution to the stopping, which is very small compared with the free electron contribution. For silicon instead, ten electrons remain bounded, being their contribution dominant over the free electrons.

Fig. 5
figure 5

Stopping power cross section as a function of proton velocity of a carbon plasma, \(q=4\), \(\rho =2.26\) \(\hbox {g/cm}^{3}\); b silicon plasma, \(q=4\), \(\rho =2.33\) \(\hbox {g/cm}^{3}\)

Full size image

In contrast with Mehlhorn and Zimmerman models, UWPM is valid for a large range of ions, temperatures and densities. Furthermore, UWPM extension of Kaneko’s dielectric function for free electrons make use of the Arista dielectric function, which has been used in our method too. Therefore, the free electron contribution should be very similar for both models, aside from the differences caused by the effective temperature used by UWPM. Indeed, it can be seen in Fig. 5a that for carbon, which is almost entirely ionized, both models are equal in the high energy range, and very alike at low medium energies. On the other hand, the silicon shows higher discrepancies in the low-medium energies region due to the larger relative importance of the bound contributions. Overall, there is a good agreement between both models.

4 Conclusions

Recent experiments have been observed that bound electron contribution is relevant in the stopping power of partially ionized plasmas. Free and bound electron stopping power depends on both ionization and temperature simultaneously.

A new method is presented to calculate the stopping power of partially ionized plasmas, including its free and bound electrons by means of dielectric formalism. Free plasma electrons are accurately described by the Arista dielectric function for quantum plasmas, in which temperature is taken into account. Bound electrons are considered within the shellwise local plasma approximation through the Levine-Louie type dielectric function which introduces the binding energy. This binding energy produces a shift to higher values on projectile velocity to consider its stopping. The shellwise assumption allows to calculate each sub-shell contribution independently. LPA introduces an r dependent density that lowers the maximum and broadens the stopping with respect to constant density method. The SLPA describes appropriately the shells of any kind of target atoms. The whole method gives, a priori, a correct description of the stopping power according with previous results.

The excellent agreement obtained for the solid case serves as a basic test of the method. For the gas case, some differences are found. Also, it can be observed the displacement in projectile velocities for the bound stopping as outer electrons are removed.

Comparison with Mehlhorn and Zimmerman models for plasmas gives a reasonable agreement. The results of the high projectile velocity regime are shared by both methods as the behavior of this region is well known by the Behte expression. Bigger differences are found in the low-medium velocities results. Mehlhorn model is more accurate for heavier projectiles and targets, where the LSS model has a greater range of validity. Also it behaves better at high temperatures, where the Jackson limit applies. Zimmerman model is very general and can be applied to a large variety of projectiles and targets, but Bethe expression still limits the accuracy at low energies. Therefore, disagreement between the results found in those regions is expected. Comparison with UWPM serves to test the validity of our method for different elements. The agreement between both models is notable and comparison with future experimental results of plasmas should be made. Many of the methods that have been used for long time for the description of bound electrons are based on a Bethe function and other expressions that impose limits on the range of applicability of the method. On the other hand, our SLPA method is valid for the whole range of projectile velocities, temperatures and densities.