Electron acoustic shock waves in nonisothermal dissipative plasmas

Abstract

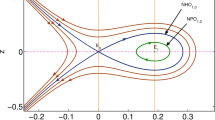
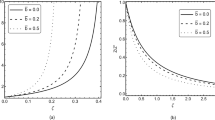
The propagation characteristics of weakly nonlinear electron acoustic waves in the presence of nonisothermal (trapped) hot electrons are investigated in collisional plasmas. The dynamics of the nonlinear waves are found to be governed by Schamel–Burgers and Schamel–Korteweg–de Vries–Burgers-type equations depending on the strength of the nonisothermal parameter. Burgers’ terms appear due to the anomalous dissipation introduced by the collisions between cold electrons and immobile ions in the presence of collective phenomena (plasma current). The derived nonlinear equations are solved analytically with the help of the Tanh method. The time-dependent computational results well agree with the analytical results and predict the possibility of the oscillatory and monotonic shock-like structures depending on the strength of the collisional drag and nonisothermality of hot electrons. The trapped electrons significantly modify the amplitude and width of the nonlinear pulse. The results may explain the shock formation and the particle acceleration mechanism in auroral plasma region.

Graphical Abstract

Appendix A: Derivations of the analytical shock solutions

In Eq. (35), we put $\phi _{1}(\chi )=f_1^2(Y)$ [where $Y=\tanh (c\chi )$ and $c^{-1}$ is the characteristic width of the solution] to eliminate the square root term and substituting this, we obtain

$$\begin{aligned}{} & {} \mu c\left[ (1-Y^2)\frac{\mathrm{{d}}}{\mathrm{{d}}Y}\left[ 2(1-Y^2)f_1\frac{\mathrm{{d}} f_1}{\mathrm{{d}} Y}\right] \right] \nonumber \\{} & {} \quad =2\left( u_f-\alpha _1 f_1+\alpha _2f_1^2\right) (1-Y^2)f_1\frac{\mathrm{{d}} f_1}{\mathrm{{d}} Y} \nonumber \\{} & {} \qquad +lc^2 (1-Y^2)\frac{\mathrm{{d}}}{\mathrm{{d}} Y}\left[ (1-Y^2)\frac{\mathrm{{d}}}{\mathrm{{d}}Y}\left[ 2(1-Y^2)f_1\frac{\mathrm{{d}} f_1}{\mathrm{{d}} Y}\right] \right] .\nonumber \\ \end{aligned}$$

(A.1)

Following the standard procedure [53], $f_1(Y)$ is expressed as the power series of Y as

$$\begin{aligned} f_1(Y)=\sum \limits _{n=0}^N a_n Y^n. \end{aligned}$$

(A.2)

Substituting this expansion in (A.1) and then balancing the highest powers (the second and fourth terms in right-hand side), we obtain $N=1$. Finally, we assume the solution of Eq. (35) of the form

$$\begin{aligned} \phi _1(\chi )=\varPhi \left[ \frac{1-\tanh (c\chi )}{2}\right] ^2. \end{aligned}$$

(A.3)

Putting this solution into the ODE [Eq. (35)] and equating the coefficients of like powers of $\tanh (c\chi )$, we obtain the system of simultaneous homogeneous equations as

$$\begin{aligned} \begin{bmatrix} 1 &{} \;\;\;2 &{} \;\;1 &{}\; -1 &{} \;\;\;1\\ 1 &{} \;\;\;8 &{} -2 &{} \;-2 &{} \;\;\;3\\ 1 &{} \;\;\;8 &{}\;\; 4 &{}\;\;\; 0 &{} \;-2\\ 1 &{} \;\;\;20 &{} -2 &{}\; -2 &{} \;\;\;2\\ 0 &{} \;\;\;6 &{} \;\;3 &{}\;\;\; 1 &{} \;-3\\ 0 &{} \;-12 &{}\;\; 0 &{}\;\;\; 0 &{} \;\;\;1\\ \end{bmatrix} \begin{bmatrix} u_f\\ lc^2\\ \mu c\\ \frac{\sqrt{\varPhi }}{2 \alpha _1}\\ \frac{\varPhi }{4 \alpha _2}\\ \end{bmatrix} = \begin{bmatrix} 0\\ 0\\ 0\\ 0\\ 0\\ \end{bmatrix}. \end{aligned}$$

(A.4)

After some elementary matrix operations, we obtain the following system of equations

$$\begin{aligned} u_f= & {} \frac{2\;\sqrt{\varPhi }\alpha _1}{3}-\frac{\varPhi \alpha _2}{2}, lc^2=\frac{\varPhi \alpha _2}{48}, \nonumber \\ \mu c= & {} -\frac{\sqrt{\varPhi }\alpha _1}{6}+\frac{5}{24}\varPhi \alpha _2. \end{aligned}$$

(A.5)

The last two equations are independent of $u_f$, and therefore, solving the first equation, we obtain

$$\begin{aligned} \sqrt{\varPhi }_{\pm }=\frac{2\alpha _1}{3\alpha _2}\pm \sqrt{\left( \frac{2\alpha _1}{3\alpha _2}\right) ^2-\frac{2u_f}{\alpha _2}}. \end{aligned}$$

(A.6)

However, only the $\varPhi _{-}$ root yields the physically consistent solution (see Sect. 5) and thereby we consider only the root $\varPhi _{-}$ as

$$\begin{aligned} \sqrt{\varPhi }=\left( 1+\frac{3}{\alpha }\right) ^{-1}\left[ b-\sqrt{b^2-\frac{4u_f \left( 1+\frac{3}{\alpha }\right) }{\sqrt{\alpha }}}\right] . \end{aligned}$$

(A.7)

This result well agree with our fixed point analysis of the SKdVB equation Eq.(18). Finally, the last two equations of Eq. (A.5) yields

$$\begin{aligned} c=\frac{\mu }{10l}\pm \frac{\alpha _1}{\sqrt{75\alpha _2 l}}. \end{aligned}$$

(A.8)

This clearly shows in case of − sign, the $c^{-1}$ (width) becomes infinite at a critical value of $\mu$, which is unphysical, and therefore, we consider

$$\begin{aligned} c=\left[ \frac{\alpha _1}{\sqrt{75\alpha _2 l}}+\frac{\mu }{10l}\right] =\frac{1}{10}\left[ \sqrt{\frac{3b^2}{\alpha +3}}+\frac{\nu }{\sqrt{\alpha }}\right] . \end{aligned}$$

(A.9)

Similarly, for SB equation [Eq. (21); $b\gg O(\sqrt{\epsilon })$], proceeding as before, we determine $N=2$ and the solution is then assumed as

$$\begin{aligned} \phi _1(\chi )=\varPhi _s\left[ \frac{1-\tanh (c\chi )}{2}\right] ^4, \end{aligned}$$

(A.10)

Substituting Eq. (A.10) into Eq. (44) and then equating the coefficients of different powers of $\tanh (c\chi )$, we obtain the system of equations as

$$\begin{aligned} \begin{bmatrix} \;4 &{} \;-16 &{} \;\;12 &{}\;\; -1\\ -12 &{} \;-72 &{} -16 &{} \;\;\;\;\;5\\ \;\;8 &{} \;\;\;208 &{}\; -36 &{}\;\;\; -9\\ \;\;8 &{} \;\;\;88 &{} \;\;64 &{}\;\;\;\;\; 5\\ -12 &{} \;-432 &{}\;\; 4 &{}\;\;\;\;\; 5\\ \;\;4 &{} \;\;\;104 &{} \;\;\;48 &{}\;\;\; -9\\ \;\;0 &{} \;\;\;240 &{} \;\;\;20 &{}\;\;\;\;\; 5\\ \;\;0 &{} \;\;-120 &{} \;\;\;0 &{}\;\;\; -1 \end{bmatrix} \begin{bmatrix} u_f\\ lc^2\\ \mu c\\ \frac{\sqrt{\varPhi }}{2 \alpha _1}\\ \end{bmatrix} = \begin{bmatrix} 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ \end{bmatrix} \end{aligned}$$

(A.11)

Again after some elementary matrix operations, we obtain the following system of equations,

$$\begin{aligned}{} & {} 4u_f-16lc^2-12\mu c-\alpha _1\sqrt{\varPhi _s}=0,\nonumber \\{} & {} \quad -120lc^2-\alpha _1\sqrt{\varPhi _s}=0,\;20\mu c+3\alpha _1\sqrt{\varPhi _s}=0. \nonumber \\ \end{aligned}$$

(A.12)

From these equations, we obtain

$$\begin{aligned} \sqrt{\varPhi _s}=\frac{2u_f}{b\sqrt{\alpha }},\;\;c=\frac{\nu }{18\sqrt{\alpha }}. \end{aligned}$$

(A.13)

These results are also well agree with our fixed point analysis of SB equation [Eq. (21)].